1. На главную
  2. Электронные версии
  3. Известия РАН. Серия физическая
  4. T. 86, № 12, 2022

Известия РАН. Серия физическая, 2022, T. 86, № 12, стр. 1694-1699

Динамика предельно коротких импульсов в оптически анизотропной среде с примесными двухуровневыми системами в рамках подхода Глаубера

М. Б. Белоненко 1, *, Н. Н. Конобеева 1

1 Федеральное государственное автономное образовательное учреждение высшего образования “Волгоградский государственный университет”
Волгоград, Россия

* E-mail: yana_nn@volsu.ru

Поступила в редакцию 29.07.2022
После доработки 15.08.2022
Принята к публикации 22.08.2022

Полный текст (PDF)

Аннотация

Изучены особенности распространения предельно коротких оптических импульсов в примесной двухуровневой системе с углеродными нанотрубками, обладающей анизотропными оптическими свойствами. На основании уравнений Максвелла, а также кинетических уравнений для средних значений операторов псевдоспина, полученных с помощью метода Глаубера, выведена система эффективных уравнений для расчета векторного потенциала электромагнитного поля и псевдоспина. Проанализировано влияние параметров системы (температуры и угла наклона вектора поляризации к оси УНТ) на пространственные характеристики предельно короткого импульса.

ВВЕДЕНИЕ

В данной работе мы продолжаем исследование распространения предельно коротких импульсов [1, 2] в оптически анизотропных средах, когда учитывается не только вторая поляризация поля, но и разные величины компонент скорости [3, 4]. В качестве анизотропной среды выступает примесный сегнетоэлектрический кристалл (т.е. его сегнетоэлектрические свойства определяются примесями) со спонтанной поляризацией в определенном интервале температур. Сегнетоэлектрики представляют собой один из наиболее удобных инструментов при изучении конфигурационных фазовых переходов. Как известно, такие кристаллы испытывают фазовый переход второго рода типа “порядок–беспорядок” [5]. Это дает возможность изменять их свойства с помощью температуры, что важно с практической точки зрения [6].

При этом мы учитываем, что сегнетоэлектрическая среда содержит двухуровневую примесь. Эти примеси мы будем описывать в дальнейшем в рамках псевдоспинового формализма [7]. В этом формализме z компонента псевдоспина задает различные (противоположные) направления поляризации примеси. Так собственное значение +1/2 соответствует поляризации вдоль полярной оси, а –1/2 – в противоположном направлении. Ненулевое среднее значение псевдоспина в равновесном состоянии будет соответствовать фазовому переходу. Отметим, что в оптике двухуровневая система играет важную роль, подобную роли гармонического осциллятора в классической физике. А именно, данная модель используется при описании взаимодействия лазерного излучения с веществом.

Введение в сегнетоэлектрический кристалл углеродных нанотрубок (УНТ) [8] обусловлено тем, что они способствуют стабильному распространению импульса.

МОДЕЛЬ И ОСНОВНЫЕ УРАВНЕНИЯ

Рассмотрим примесный сегнетоэлектрик c оптически анизотропными свойствами, в который помещены углеродные нанотрубки, оси которых сонаправлены и находятся под углом θ к оси OX. Полярная ось сегнетоэлектрика направлена под углом ψ к оси OX (рис. 1). Оси OX, OY и OZ показаны на рис. 1 [9]. Считаем, что в начальный момент времени электрическое поле направлено вдоль оси OX. Под действием этого поля в УНТ начинает течь ток и возникает поле вдоль оси OY.

Рис. 1.

Геометрия задачи.

Ранее при изучении фазовых переходов мы использовали феноменологический подход для записи уравнения движения [10]. В данной работе динамические свойства рассматриваемой системы будем изучать в рамках метода Глаубера [11].

Поскольку поляризация пропорциональна псевдоспину, то кинетическое уравнение для описания динамики псевдоспина можно записать в виде [12]:

(1)
$\begin{gathered} \left\langle {{{{\dot {S}}}_{x}}} \right\rangle = - \frac{{\left\langle {{{S}_{x}}} \right\rangle - 0.5{\text{th}}\left( {\beta \left( {J\left\langle {{{S}_{x}}} \right\rangle + {{\Delta }_{ \bot }}\left\langle {{{S}_{x}}} \right\rangle \alpha + \gamma {{{\left\langle {{{S}_{x}}} \right\rangle }}_{{zz}}} + \delta {{E}_{x}}} \right)} \right)}}{{{{T}_{{imp}}}}}, \\ \left\langle {{{{\dot {S}}}_{y}}} \right\rangle = - \frac{{\left\langle {{{S}_{y}}} \right\rangle - 0.5{\text{th}}\left( {\beta \left( {J\left\langle {{{S}_{y}}} \right\rangle + {{\Delta }_{ \bot }}\left\langle {{{S}_{y}}} \right\rangle \alpha + \gamma {{{\left\langle {{{S}_{y}}} \right\rangle }}_{{zz}}} + \delta {{E}_{y}}} \right)} \right)}}{{{{T}_{{imp}}}}}, \\ \end{gathered} $
где Timp – время релаксации примеси, α, γ – константы, определяемые величиной обменного взаимодействия (J), $\left\langle {{{S}_{i}}} \right\rangle ,$ $i = \left( {x,y} \right)$ – среднее значение x и y компонент псевдоспина, точкой здесь обозначается производная по времени, ${{\Delta }_{ \bot }}$ – Лапласиан в направлении перпендикулярном оси УНТ, β = 1/(kBT), kB – постоянная Больцмана, T – температура, δ – дипольный момент, (Ex, Ey) – компоненты электрического поля вдоль осей OX и OY соответственно.

Уравнения Максвелла можно записать в следующем виде:

(2)
$\frac{1}{{{{c}^{2}}}}\frac{{{{\partial }^{2}}\vec {E}}}{{\partial {{t}^{2}}}} - {{\nabla }^{2}}\vec {E} = - \mu \cdot \left\langle {\ddot {\vec {S}}} \right\rangle + \frac{{4\pi }}{c}\frac{{\partial{ \vec {j}}}}{{\partial t}},$
где c – скорость света, µ – константа, связанная с поляризацией примесной системы.

С учетом калибровки: $\vec {E} = - {{c}^{{ - 1}}}{{\partial{ \vec {A}}} \mathord{\left/ {\vphantom {{\partial{ \vec {A}}} {\partial t}}} \right. \kern-0em} {\partial t}},$ и вида векторного потенциала $\vec {A} = ({{A}_{x}}(x,y,z,t)$, ${{A}_{y}}(x,y,z,t),0),$ а также плотности электрического тока $\vec {j} = \left( {{{j}_{x}}\left( {x,y,z,t} \right),{{j}_{y}}\left( {x,y,z,t} \right),0} \right),$ уравнение (2) примет вид:

(3)
$\frac{1}{{{{c}^{2}}}}\frac{{{{\partial }^{2}}\vec {A}}}{{\partial {{t}^{2}}}} - {{\nabla }^{2}}\vec {A} = - \mu \cdot \left\langle {\dot {\vec {S}}} \right\rangle + \frac{{4\pi }}{c}\vec {j}\left( {\vec {A}} \right).$

Далее перейдем в цилиндрическую систему координат и перепишем уравнение (3) на две компоненты векторного потенциала:

(4)
$\begin{gathered} \frac{1}{{V_{e}^{2}}}\frac{{{{\partial }^{2}}{{A}_{x}}}}{{\partial {{t}^{2}}}} - \frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{{\partial {{A}_{x}}}}{{\partial r}}} \right) - \frac{{{{\partial }^{2}}{{A}_{x}}}}{{\partial {{z}^{2}}}} - \frac{1}{{{{r}^{2}}}}\frac{{{{\partial }^{2}}{{A}_{x}}}}{{\partial {{\phi }^{2}}}} = \\ = - \mu {\text{cos}}\psi \frac{{\partial \left\langle {{{S}_{x}}} \right\rangle }}{{\partial t}} + \frac{{4\pi }}{c}{{j}_{x}}\left( {{{A}_{x}},{{A}_{y}}} \right), \\ \frac{1}{{V_{o}^{2}}}\frac{{{{\partial }^{2}}{{A}_{y}}}}{{\partial {{t}^{2}}}} - \frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{{\partial {{A}_{y}}}}{{\partial r}}} \right) - \frac{{{{\partial }^{2}}{{A}_{y}}}}{{\partial {{z}^{2}}}} - \frac{1}{{{{r}^{2}}}}\frac{{{{\partial }^{2}}{{A}_{y}}}}{{\partial {{\phi }^{2}}}} = \\ = - \mu {\text{sin}}\psi \frac{{\partial \left\langle {{{S}_{y}}} \right\rangle }}{{\partial t}} + \frac{{4\pi }}{c}{{j}_{y}}\left( {{{A}_{x}},{{A}_{y}}} \right),\,\,\,\, \\ {{V}_{o}} = {c \mathord{\left/ {\vphantom {c {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}},\,\,\,\,{{V}_{e}} = {c \mathord{\left/ {\vphantom {c {{{n}_{e}}}}} \right. \kern-0em} {{{n}_{e}}}} \\ \end{gathered} $
r, z, φ – координаты в цилиндрической системе, ne, no – показатели преломления в направлении x и y соответственно.

Запишем стандартное выражение для плотности тока вдоль оси УНТ [8]:

(5)
$j = 2e\sum\limits_{s = 1}^m {\int {{{v}_{s}}\left( p \right)f\left( {p,s} \right)dp} } ,$
где e – заряд электрона, интегрирование ведется по первой зоне Бриллюэна, p – компонента квазиимпульса электрона, ${{v}_{s}}(p) = {{\partial {{\varepsilon }_{s}}\left( p \right)} \mathord{\left/ {\vphantom {{\partial {{\varepsilon }_{s}}\left( p \right)} {\partial p}}} \right. \kern-0em} {\partial p}}$ – скорость электронов, $f\left( {p,s} \right)$ – функция распределения Ферми, ${{\varepsilon }_{s}}\left( p \right)$ – закон дисперсии электронов УНТ [13]:
(6)
${{\varepsilon }_{s}}\left( p \right) = \pm {{\gamma }_{0}}\sqrt {1 + 4{\text{cos}}\left( {ap} \right){\text{cos}}\left( {\frac{{\pi s}}{m}} \right) + 4{\text{co}}{{{\text{s}}}^{2}}\left( {\frac{{\pi s}}{m}} \right)} ,$
где s = 1, 2, …, m, нанотрубка имеет тип (m,0), ${{\gamma }_{0}} \approx 2.7$ эВ, a = 3b/2ℏ, b – расстояние между соседними атомами углерода

Согласно выполненным в работе [14] расчетам можно утверждать, что эффект накопления заряда, возникающий из-за неоднородности поля, для импульсов рассматриваемой нами длительности можно не учитывать. Это позволяет положить производную по углу равной нулю. В этом случае систему уравнений (4) можно переписать в виде:

(7)
$\begin{gathered} \left\{ \begin{gathered} \Delta {{A}_{x}} + \frac{{4e\sigma {{\gamma }_{0}}a{\text{cos}}\theta }}{c} \times \hfill \\ \times \,\,\sum\limits_{q = 1}^\infty {{{b}_{q}}{\text{sin}}\left( {\frac{{aeq\left( {{{A}_{x}}{\text{cos}}\theta + {{A}_{y}}sin\theta } \right)}}{c}} \right)} - \hfill \\ - \,\,\mu {\text{cos}}\psi \frac{{\partial \left\langle {{{S}_{x}}} \right\rangle }}{{\partial t}} = \frac{1}{{V_{e}^{2}}}\frac{{{{\partial }^{2}}{{A}_{x}}}}{{\partial {{t}^{2}}}}, \hfill \\ \Delta {{A}_{y}} + \frac{{4e\sigma {{\gamma }_{0}}a{\text{sin}}\theta }}{c} \times \hfill \\ \times \,\,\sum\limits_{q = 1}^\infty {{{b}_{q}}{\text{sin}}\left( {\frac{{aeq\left( {{{A}_{x}}{\text{cos}}\theta + {{A}_{y}}{\text{sin}}\theta } \right)}}{c}} \right)} - \hfill \\ - \,\,\mu {\text{sin}}\psi \frac{{\partial \left\langle {{{S}_{y}}} \right\rangle }}{{\partial t}} = \frac{1}{{V_{0}^{2}}}\frac{{{{\partial }^{2}}{{A}_{y}}}}{{\partial {{t}^{2}}}}, \hfill \\ \end{gathered} \right. \\ \Delta = \frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{\partial }{{\partial r}}} \right) + \frac{{{{\partial }^{2}}}}{{\partial {{z}^{2}}}} \\ \end{gathered} $
σ – концентрация электронов,
(8)
${{b}_{q}} = \sum\limits_s {\frac{q}{{{{\gamma }_{0}}}}{{a}_{{sq}}}\int\limits_{ZB} {dp{\kern 1pt} '{\text{cos}}\left( {p{\kern 1pt} 'q} \right)} } \frac{{{\text{exp}}\left( { - {{{{\varepsilon }_{s}}\left( {p{\kern 1pt} '} \right)} \mathord{\left/ {\vphantom {{{{\varepsilon }_{s}}\left( {p{\kern 1pt} '} \right)} {{{k}_{B}}T}}} \right. \kern-0em} {{{k}_{B}}T}}} \right)}}{{1 + {\text{exp}}\left( { - {{{{\varepsilon }_{s}}\left( {p{\kern 1pt} '} \right)} \mathord{\left/ {\vphantom {{{{\varepsilon }_{s}}\left( {p{\kern 1pt} '} \right)} {{{k}_{B}}T}}} \right. \kern-0em} {{{k}_{B}}T}}} \right)}},$
asq – коэффициенты в разложении закона дисперсии электронов (6) в ряд Фурье.

Отметим, что вследствие убывания коэффициентов bq с ростом q в сумме можно ограничиться первыми 10 слагаемыми.

Система уравнений (1) и (7) после обезразмеривания решалась численно с начальными условиями следующего вида:

(9)
$\begin{gathered} {{A}_{x}} = Q{\text{exp}}\left( { - {{{\left( {\frac{z}{{{{l}_{z}}}}} \right)}}^{2}}} \right){\text{exp}}\left( { - \frac{{{{x}^{2}} + {{y}^{2}}}}{{l_{r}^{2}}}} \right), \\ \frac{d}{{dt}}{{A}_{x}} = \frac{{2uQ}}{{{{l}_{z}}^{2}}}{\text{exp}}\left( { - {{{\left( {\frac{z}{{{{l}_{z}}}}} \right)}}^{2}}} \right){\text{exp}}\left( { - \frac{{{{x}^{2}} + {{y}^{2}}}}{{l_{r}^{2}}}} \right), \\ {{A}_{y}} = 0,\,\,\,\,\frac{d}{{dt}}{{A}_{y}} = 0,\,\,\,\,{{S}_{x}} = {{S}_{0}}, \\ {{S}_{y}} = 0,\,\,\,\,\beta = \frac{{a{\text{tg}}\left( {2{{S}_{0}}} \right)}}{{J{{S}_{0}}}}, \\ \end{gathered} $
где Q – амплитуда электромагнитного импульса на входе в среду с УНТ, ${{l}_{z}},{{l}_{r}}$ – определяют ширину импульса вдоль направлений z и r соответственно, u – начальная скорость импульса вдоль оси z, S0 – величина псевдоспина в начальный момент времени, которая позволяет определить обратную температуру β при t = 0.

РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ

Как показали результаты вычислений, пространственные производные от псевдоспина в уравнении (1) не оказывают влияния на динамику импульса. Это позволяет пренебречь ими в последующих расчетах.

Возникающая эволюция x и y компоненты электрического поля импульса представлена на рис. 2. При этом мы рассматриваем фазу, которой соответствует значение S0 = 0. Отметим, что ${{I}_{x}} \propto E_{x}^{2},$ ${{I}_{y}} \propto E_{y}^{2}.$

Рис. 2.

Зависимость интенсивности для компонент электрического поля Ex (a–в) и Ey (г–е) от координат в различные моменты времени: (a, г) t = 1; (б, д) t = 5; (в, е) t = 9. Единица по времени соответствует 10–13 с, по координатам (z и r) – 2 · 10–5 м. Ix0, Iy0 – максимальная интенсивность для x и y компонент.

Рисунок 2 иллюстрирует сильное расплывание импульса, причем также наблюдается существенное возрастание интенсивности для обеих компонент поля. Это можно объяснить дополнительной поляризацией примесей под действием импульса переменного электрического поля

Далее проанализируем влияние углов θ и ψ на форму предельно короткого импульса (рис. 3). Мы будем сравнивать два случая: когда поляризация сонаправлена с осью УНТ и нет, т.е. когда θ ≠ ψ.

Рис. 3.

Зависимость интенсивности для компонент электрического поля Ex (верхний ряд рисунков) и Ey (нижний ряд рисунков) от координат (t = 9): (a, в) S0 = 0; (б, г) S0 = 0.25. Точечная кривая – θ ≠ ψ; сплошная кривая – θ = ψ. Единица по координатам (z и r) – 2 · 10–5 м. Im – максимальная интенсивность для всех случаев.

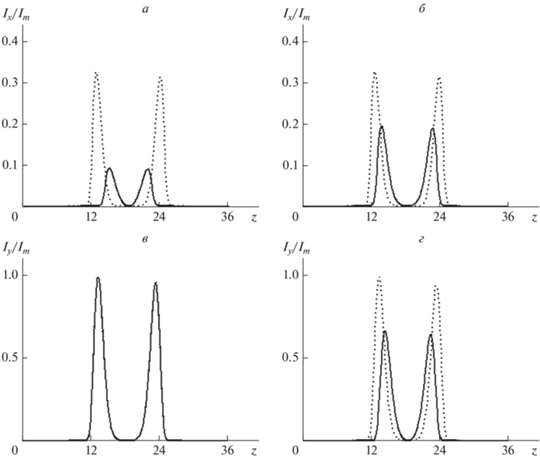
Согласно рис. 3 можно заключить, что угол, который составляет вектор поляризации с осью УНТ, не играет никакой роли для второй компоненты поля при S0 = 0, что соответствует температуре в наших расчетах T = 123 K. Для второго фазового состояния (Т = 56 К) величины углов оказывают влияние как на амплитуду поля импульса, так и на его пространственную локализацию.

Влияние температуры на характеристики предельно короткого импульса в сегнетоэлектрической среде с углеродными нанотрубками в случае, когда θ ≠ ψ представлено на рис. 4.

Рис. 4.

Зависимость интенсивности для компонент электрического поля Ex (a, в) и Ey (б, г) от координат (t = 9, θ ≠ ψ): верхний ряд рисунков – продольные срезы (при r = 0), нижний ряд рисунков – поперечные срезы интенсивности по максимуму интенсивности. Сплошная линия соответствует T = 123 K, точечная – T = 56 K. Единица по координатам (z и r) – 2 · 10–5 м. Ix0, Iy0 – максимальная интенсивность для x и y компонент.

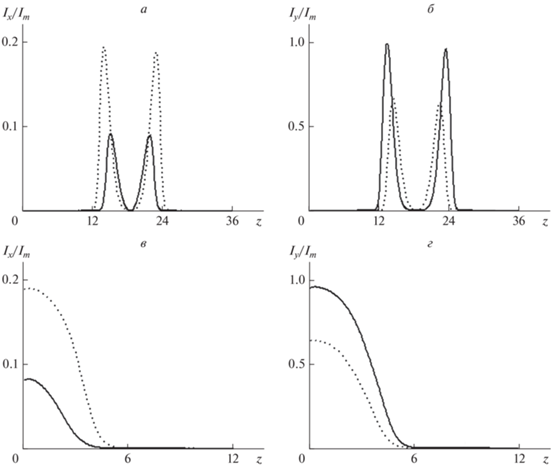
Построенные зависимости позволяют сделать вывод, что температура оказывает существенное влияние не только на амплитуду предельно короткого оптического импульса, но и на величину его продольного и поперечного расплывания. Таким образом, по ширине и амплитуде импульса можно определить фазовое состояние, в котором находится система.

ЗАКЛЮЧЕНИЕ

Таким образом, построена модель, описывающая динамику предельно короткого импульса в сегнетоэлектрической среде с оптически анизотропными свойствами в присутствии углеродных нанотрубок, в рамках подхода Глаубера. Установлено, что угол, который составляет вектор поляризации с осью УНТ, влияет на амплитуду электромагнитного импульса. Показано, что температура позволяет управлять пространственными характеристиками импульса (амплитудой и шириной).

Исследование выполнено при поддержке Минобрнауки РФ и Совета по грантам Президента РФ (проект № MД-3173.2021.1.2).

Список литературы

  1. Kärtner F.X. Few-cycle laser pulse generation and its applications. Berlin: Springer, 2004. 448 p.

  2. Krausz F., Ivanov M. // Rev. Mod. Phys. 2009. V. 81. No. 1. P. 163.

  3. Konobeeva N.N., Belonenko M.B. // Int. J. Mod. Phys. B. 2021. V. 35. No. 19. Art. No. 2150197.

  4. Konobeeva N.N., Belonenko M.B. // Nanosyst. Phys. Chem. Math. 2021. V. 12. No. 4. P. 430.

  5. Blinc R. // Ferroelectrics. 2010. V. 2004. No. 1. P. 3.

  6. Zhang C.X., Yang K.L., Ji P. et al. // J. Appl. Phys. 2018. V. 123. Art. No. 094102.

  7. Блинц Р., Жекш Б. Сегнетоэлектрики и анти-сегнетоэлектрики. Динамика решетки. М.: Мир, 1975. 402 с.

  8. Елецкий А.В. // УФН. 1997. Т. 167. С. 945; Eletskii A.V. // Phys. Usp. 1997. V. 40. No. 9. P. 899.

  9. Матвеев А.Н. Оптика. М.: Высшая школа, 1985. 351 с.

  10. Паташинский А.З., Покровский В.Л. Флуктуационная теория фазовых переходов. М.: Наука, 1982. 381 с.

  11. Glauber R.J. // J. Math. Phys. 1963. V. 4. P. 294.

  12. Белоненко М.Б., Сасов А.С. // ЖТФ. 2007. Т. 77. № 4. С. 131; Belonenko M.B., Sasov A.S. // Tech. Phys. 2007. V. 52. No. 4. P. 524.

  13. Dresselhaus M.S., Dresselhaus G., Eklund P.C. Science of fullerenes and carbon nanotubes. Oxford: Academic Press, 1996. 965 p.

  14. Zhukov A.V., Bouffanais R., Fedorov E.G., Belonenko M.B. // J. Appl. Phys. 2013. V. 114. Art. No. 143106.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал