1. На главную
  2. Электронные версии
  3. Известия РАН. Серия физическая
  4. T. 86, № 6, 2022

Известия РАН. Серия физическая, 2022, T. 86, № 6, стр. 770-774

Эффекты квази-фазового согласования в газах при генерации терагерцевого излучения в двухчастотных лазерных полях

С. Ю. Стремоухов 1, 2, *

1 Федеральное государственное бюджетное образовательное учреждение высшего образования “Московский государственный университет имени М.В. Ломоносова”
Москва, Россия

2 Федеральное государственное бюджетное учреждение “Национальный исследовательский центр “Курчатовский институт”
Москва, Россия

* E-mail: sustrem@gmail.com

Поступила в редакцию 17.01.2022
После доработки 07.02.2022
Принята к публикации 21.02.2022

Полный текст (PDF)

Аннотация

Представлены результаты численного исследования генерации терагерцевого излучения при взаимодействии двухчастотного лазерного поля, образованного линейно поляризованными первой (ω) и второй (2ω) гармониками Ti:Sa лазера, с газовыми средами, сформированными из набора струй аргона. Показано влияние эффектов квази-фазового согласования на эффективность и частотно-угловые спектры терагерцевого излучения.

ВВЕДЕНИЕ

Развитие методов генерации терагерцевого (ТГц) излучения открывает возможности его использования в различных сферах: от спектроскопии высокомолекулярных состояний до высокоскоростной передачи информации. Существует множество методов генерации ТГц излучения: от отрыва обычной клейкой ленты (генерация ТГц излучения происходит за счет ее трибозаряда при отрыве с последующим разрядом) до движения релятивистских электронов в лазерах на свободных электронах [1–7]. Среди этого многообразия лазерные методы генерации занимают особое положение, поскольку позволяют получить когерентное излучение, образуя компактный “table-top” источник ТГц излучения [8]. Вместе с тем, основным вектором развития генерации ТГц излучения лазерными методами в настоящее время является повышение эффективности преобразования лазерного излучения в область ТГц спектра для генерации мощных ТГц импульсов и исследования нелинейного отклика среды на воздействие такого излучения [9]. Источником когерентного ТГц излучения могут быть кристаллические [10], жидкие [11] и газовые среды [12], взаимодействующие как с одночастотными, так и многочастотными лазерными полями [13].

Важным направлением исследования генерации ТГц излучения в кристаллических средах является развитие методов управления квази-фазовым согласованием (КФС) излучения в кристалле для генерации мощных ТГц импульсов [14]. Эффекты КФС в газовых (плазменных) средах, в основном, изучаются для повышения эффективности генерации гармоник высокого порядка [15‒17]. Вместе с тем, исследования влияния эффектов КФС при генерации ТГц излучения в газовых средах не проводилось. Настоящая работа посвящена демонстрации влияния эффектов КФС на параметры ТГц излучения, генерируемого в газовых средах, состоящих из набора струй, отстоящих друг от друга на некотором расстоянии. Для упрощения анализа полученных результатов (для исключения влияния плазмы на параметры частотно-угловых спектров), был выбран доионизационный режим генерации ТГц излучения [18, 19].

ПАРАМЕТРЫ ЧИСЛЕННОГО ЭКСПЕРИМЕНТА

Для исследования эффектов КФС в газовых средах была проведена серия расчетов отклика протяженной газовой среды, взаимодействующей с двухчастотным лазерным полем, образованным сополяризованными первой и второй гармониками Ti:Sa лазера (λ = 800 нм), длительности импульсов были выбраны равными 30 фс для обоих компонент двухчастотного поля, интенсивности компонент поля I1 = 6.77 ⋅ 1012 Вт/см2 и I2 = 5.85 ⋅ 1011 Вт/см2 были выбраны таким образом, чтобы обеспечить доионизационный режим генерации ТГц излучения [18, 19]. Как было показано в [19], при таких параметрах ТГц часть фотоэмиссионного спектра отклика одиночного атома имеет максимум на частоте ~11 ТГц. Исследования проводились для несфокусированного гауссовского пучка, имеющего ширину σ.

Для того, чтобы продемонстрировать влияние профилирования газовой среды были выбраны 2 частоты в спектре 1 и 11 ТГц. Расчет проводился с помощью интерференционной модели, представленной в [19] и использованной ранее для исследования частотно-угловых спектров ТГц излучения, генерируемого протяженной газовой средой в случае, когда направления поляризации компонент двухчастотного поля сонаправлены [19] и имеют ненулевой угол друг относительно друга [20]. В рамках интерференционной модели с помощью непертурбативного подхода, представленного в [18, 21], рассчитывались параметры ТГц откликов одиночных атомов (амплитуды и фазы поля на определенной частоте), расположенных в различных точках исследуемой среды. Информация, полученная из квантово-механических расчетов, использовалась для расчета пространственного распределения излучения в области, окружающей среду [19]. Численные расчеты были проведены как для протяженных аргоновых газовых сред, так и для аргоновых сред, состоящих из набора газовых струй шириной d, разделенных вакуумными промежутками такой же ширины. Ранее, было показано, что такая организация среды взаимодействия позволяет увеличить эффективность генерации группы гармоник высокого порядка [16, 22].

ЧАСТОТНО-УГЛОВЫЕ СПЕКТРЫ ТГЦ ИЗЛУЧЕНИЯ

Наиболее типичные частотно-угловые спектры ТГц излучения представлены на рис. 1 (расчет проводился для газовой среды длиной 6 см и для поперечного пространственного размера гауссовского пучка σ = 0.3 см) и на рис. 2 (расчет проводился для газовой среды длиной 40 см и для поперечного пространственного размера гауссовского пучка σ = 0.3 см). Черным прямоугольником условно обозначена среда взаимодействия (которая является либо протяженной газовой средой, либо набором газовых струй). На рис. 1а, 1в, 1д, 1ж представлено пространственное распределение излучения на частоте 1 ТГц, на рис. 1б, 1г, 1е, 1з представлено пространственное распределение излучения на частоте 11 ТГц, рассчитанное для случая сплошной газовой среды (рис. 1а, 1б), газовой среды, состоящей из 30 газовых струй с d = 0.1 см (рис. 1в, 1г), из 10 газовых струй с d = 0.3 см (рис. 1д, 1е) и из 5 газовых струй с d = 0.6 см (рис. 1ж, 1з). Количество газовых струй было выбрано таким образом, чтобы общая длина среды оставалась неименной и соответствовала длине сплошной среды (в данном случае, общая длина составной среды равна 6 см).

Рис. 1.

Пространственное распределение излучения на частоте 1 ТГц (а, в, д, ж) и 11 ТГц (б, г, е, з), построенное для случая сплошной газовой среды длиной 6 см (а, б), газовой среды, состоящей из 30 газовых струй с d = 0.1 см (в, г), из 10 газовых струй с d = 0.3 см (д, е) и из 5 газовых струй с d = 0.6 см (ж, з). Расчеты проводились для аргоновой среды, взаимодействующей с двухчастотным лазерным полем, образованным линейно поляризованными первой и второй гармониками Ti:Sa лазера (параметры поля указаны в тексте).

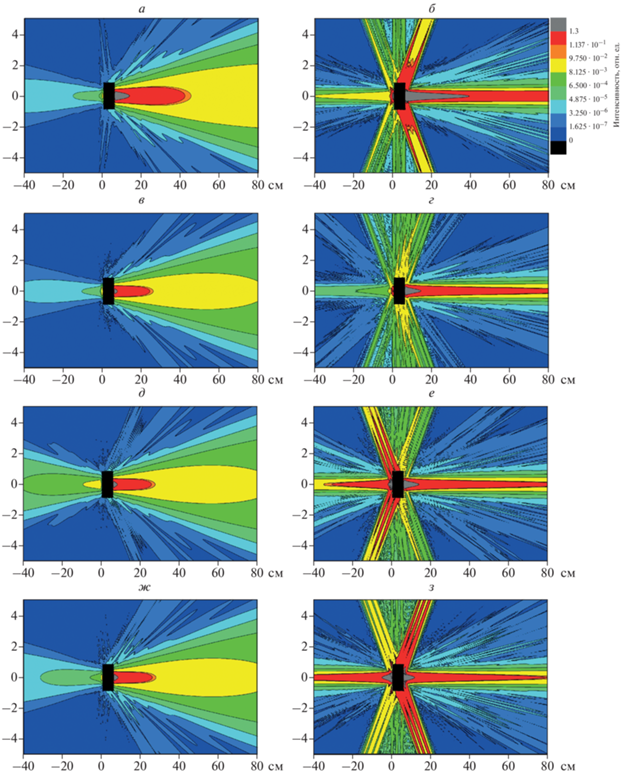
Видно, что профилирование среды приводит к изменению углового спектра генерируемого излучения. Так, профилирование среды может существенно усилить излучение, распространяющееся в обратном (по отношению к направлению распространения лазерного излучения) направлении (например, для d = 0.3 см излучение как на частоте 1 ТГц, так и на частоте 11 ТГц имеет более ярко выраженный “обратный лепесток” [23], чем излучение, генерируемое непрофилированной средой), также можно существенно усилить коническую эмиссию ТГц излучения (особенно ярко выражено для 10 ТГц и d = 0.6 см). Указанные особенности влияния профилирования среды наблюдаются и для более длинных сред (см. рис. 2, на котором представлены пространственные спектры, рассчитанные для излучения 1 ТГц (рис. 2а, 2в, 2д) и 11 ТГц (рис. 2б, 2г, 2е) для сплошной газовой среды (рис. 2а, 2б), газовой среды, состоящей из 20 газовых струй с d = 1 см (рис. 2в, 2г), из 5 газовых струй с d = 4 см (рис. 2д, 2е). Таким образом, профилирование среды оказывает существенное влияние на частотно-угловой спектр ТГц излучения.

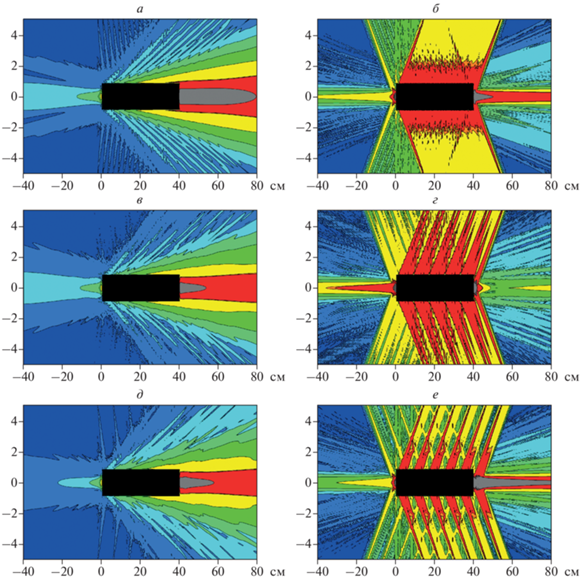
Рис. 2.

Пространственное распределение излучения на частоте 1 ТГц (а, в, д, ж) и 11 ТГц (б, г, е, з), построенное для случая сплошной газовой среды длиной 40 см (а, б), газовой среды, состоящей из 20 газовых струй с d = 1 см (в, г), из 5 газовых струй с d = 4 см (д, е). Расчеты проводились для аргоновой среды, взаимодействующей с двухчастотным лазерным полем, образованным линейно поляризованными первой и второй гармониками Ti:Sa лазера (параметры поля указаны в тексте). Цветовая палитра такая же, как и на рис. 1.

ОБСУЖДЕНИЕ

Сравнение частотно-угловых спектров демонстрирует некоторое уменьшение общей эффективности генерации ТГц излучения при взаимодействии с набором газовых струй по сравнению с протяженной средой. Это связано с различием в количестве атомов в среде: за счет большего количества атомов в сплошной протяженной среде, генерация ТГц излучения в ней происходит более эффективно. Вместе с тем, наличие отдельных газовых струй позволяет эффективно управлять угловым спектром излучения, влияя на конструктивную интерференцию вкладов отдельных атомов, формирующих набор газовых струй. Так, например, можно существенно уменьшить (см. рис. 1г), либо увеличить (рис. 1з) эффективность конической эмиссии, сохранив генерацию излучения в направлении распространения лазерного поля, либо существенно увеличить эффективность ТГц излучения в обратном направлении (рис. 1д, 1е, рис. 2г).

ЗАКЛЮЧЕНИЕ

Представлены первые результаты исследования влияния эффекта КФС на генерацию ТГц излучения в газовой среде, состоящей из набора струй. Показано, что, варьируя ширины газовых струй d, можно изменять угловой спектр генерируемого излучения. Таким образом, представлен дополнительный управляющий параметр, позволяющий контролировать не только эффективность генерации ТГц излучения, но и его угловой спектр, что может быть использовано для оптимизации схем тандемного использования ТГц излучения для проведения pump-probe экспериментов.

Работа выполнена при частичной финансовой поддержке Российского фонда фундаментальных исследований (проект № 18-02-40014).

Список литературы

  1. Horvat J., Lewis R.A. // Opt. Lett. 2009. V. 34. No. 14. P. 2195.

  2. Knyazev B.A., Kulipanov G.N., Vinokurov N.A. // Meas. Sci. Technol. 2010. V. 21. No. 5. Art. No. 054017.

  3. Byrd J.M., Leemans W.P., Loftsdottir A. et al. // Phys. Rev. Lett. 2002. V. 89. No. 22. Art. No. 224801.

  4. Pérez S., González T., Pardo D., Mateos J. // J. Appl. Phys. 2008. V. 103. No. 9. Art. No. 094516.

  5. Ozyuzer L., Koshelev A. E., Kurteret C. et al. // Science. 2007. V. 318. No. 5854. P. 1291.

  6. Williams B.S. // Proc. AOE-2008 (Shanghai, 2008). Art No. SuG3.

  7. Kim K.Y., Taylor A.J., Glownia J.H., Rodriguez G. // Nature Photon. 2008. V. 2. No. 10. P. 605.

  8. Dai J., Karpowicz N., Zhang X.-C. // Phys. Rev. Lett. 2009. V. 103. Art. No. 023001.

  9. Zhang X.-C., Shkurinov A., Zhang Y. // Nature Photon. 2017. V. 11. No. 1. P. 1.

  10. Shalaby M., Hauri C.P. // Nature Commun. 2015. V. 6. P. 5976.

  11. Dey I., Jana K., Fedorov V. et al. // Nature Commun. 2017. V. 8. No. 1. P.1184.

  12. Andreev A.V., Angeluts A.A., Balakin A.V. et al. // IEEE Trans. Terahertz Sci. Technol. 2020. V. 10. No. 1. P. 85.

  13. Cook D.J., Hochstrasser R.M. // Opt. Lett. 2000. V. 25. P. 1210.

  14. Shijia Z., Zhiming R., Wenjiang T., Enshuai Zh. // Laser. Phys. 2020. V. 30. Art. No. 115401.

  15. Hareli L., Shoulga G., Bahabad A. // J. Phys. B. 2020. V. 53. Art. No. 233001.

  16. Ganeev R.A., Stremoukhov S.Y., Andreev A.V., Alnaser A.S. // Appl. Sci. 2019. V. 9. P. 1701.

  17. Ganeev R.A., Boltaev G.S., Stremoukhov S.Y. et al. // Eur. Phys. J. D. 2020. V. 74. P. 199.

  18. Andreev A.V., Stremoukhov S.Yu. // Phys. Rev. A. 2013. V. 87. Art. No. 053416.

  19. Stremoukhov S.Yu., Andreev A.V. // Laser. Phys. Lett. 2015. V. 12. Art. No. 015402.

  20. Stremoukhov S.Yu., Andreev A.V. // J. Opt. Soc. Amer. B. 2017. V. 34. No. 2. P. 232.

  21. Andreev A.V., Stremoukhov S.Yu., Shoutova O.A. // Eur. Phys. J. D. 2012. V. 66. Art. No. 16.

  22. Stremoukhov S.Yu., Andreev A.V. // Laser Phys. 2018. V. 28. Art. No. 035403.

  23. Ushakov A.A., Panov N.A., Chizhov P.A. et al. // Appl. Phys. Lett. 2019. V. 114. No. 8. Art. No. 081102.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал