1. На главную
  2. Электронные версии
  3. Известия РАН. Серия физическая
  4. T. 86, № 7, 2022

Известия РАН. Серия физическая, 2022, T. 86, № 7, стр. 989-996

Влияние режимов теплоотдачи на поле температуры в кристаллах в методе Чохральского

К. А. Митин 1, *, В. С. Бердников 1

1 Федеральное государственное бюджетное учреждение науки “Институт теплофизики имени С.С. Кутателадзе Сибирского отделения Российской академии наук”
Новосибирск, Россия

* E-mail: mitin@ngs.ru

Поступила в редакцию 14.02.2022
После доработки 28.02.2022
Принята к публикации 23.03.2022

Полный текст (PDF)

Аннотация

Численно в системе, геометрически подобной упрощенной схеме верхней части ростового узла в методе Чохральского, изучено влияние равномерного вращения кристалла на закономерности сопряженного радиационно-конвективного теплообмена. Показано, что под действием вращения пространственная форма конвективных течений теряет устойчивость, возникают вторичные вихри, в результате значительно возрастает эффективность охлаждения кристалла.

ВВЕДЕНИЕ

Метод Чохральского является одним из наиболее часто применяемых методов получения монокристаллов широкой номенклатуры материалов [1–3]. В этом методе монокристалл вытягивается со свободной поверхности расплава на затравочный кристалл с заданной кристаллографической ориентацией. На начальной стадии разращивания кристалла до заданного диаметра отвод тепла от фронта кристаллизации (ФК) происходит в основном за счет теплопроводности через монокристалл в охлаждаемый шток, на котором он закреплен. По мере роста монокристалла теплоотдача все в большей степени осуществляется от его боковых образующих за счет конвективного и радиационного механизмов теплообмена [1–8]. Относительная роль кондуктивного теплоотвода через монокристалл и шток зависит от длины кристалла и от коэффициентов теплопроводности монокристалл и штока [2, 3, 7]. Интенсивность радиационно-конвективной теплоотдачи от кристалла зависит от перепада температуры между ФК и холодными стенками ростовой камеры, заполненной газом. Структурное совершенство получаемых монокристаллов зависит не только от конвективного теплообмена под ФК, определяющего формы ФК, но и от нестационарных полей температуры и термических напряжений внутри кристалла [1, 4–8]. В процессе роста кристалла необходимо обеспечить симметрию поля температуры внутри кристалла и минимальные градиенты температуры [1–7]. Нелинейность задач сопряженного радиационно-конвективного теплообмена между кристаллом, расплавом и окружающей средой приводит к необходимости решения большого количества задач при различных геометриях расчетной области, изменяющейся по мере роста кристалла. В рамках глобального моделирования затраты ресурсов значительные, поэтому результаты расчетов в опубликованных работах получены в узких диапазонах управляющих параметров [4–6]. Для понимания общих закономерностей зависимости полей температуры в кристаллах от интенсивности теплоотдачи с их образующих и соответствующих термических напряжений целесообразно решать задачи в рамках частичного моделирования [6–8]. Не претендуя на полное описание этих процессов, частичное моделирование позволяет определить основные тенденции в поведении рассматриваемых систем при изменении отдельных управляющих параметров или их группы. Численно методом конечных элементов [9] исследовано влияние скорости равномерного вращения кристалла на поля температуры в кристалле при различных длинах кристалла в диапазоне скоростей вращения от 1 до 25 об./мин.

ПОСТАНОВКА ЗАДАЧИ

Учитывая свойства осесимметрии тепловых узлов, применяемых при выращивании монокристаллов методом Чохральского, расчеты проведены в двумерной осесимметричной постановке. Геометрия расчетной области соответствует упрощенной схеме верхней части ростовой камеры, состоящей из монокристалла, затравочного кристалла, штока, стенок ростовой камеры и экрана, отделяющего поверхность расплава от газовой среды (аргона) в ростовой камере. Для моделирования смешанной конвекции в газе использована безразмерная нестационарная система уравнений Навье–Стокса, энергии и неразрывности в приближении Буссинеска, записанная в переменных вихрь, функция тока, азимутальная скорость и температура:

(1)
$\left\{ \begin{gathered} \frac{{\partial T}}{{\partial t}} - \frac{1}{{Pr}}\left( {\frac{{{{\partial }^{2}}T}}{{\partial {{r}^{2}}}} + \frac{1}{r}\frac{{\partial T}}{{\partial r}} + \frac{{{{\partial }^{2}}T}}{{\partial {{z}^{2}}}}} \right) + u\frac{{\partial T}}{{\partial r}} + \upsilon \frac{{\partial T}}{{\partial z}} = 0, \hfill \\ \frac{{\partial {{\omega }}}}{{\partial t}} - \left( {\frac{{{{\partial }^{2}}{{\omega }}}}{{\partial {{r}^{2}}}} + \frac{1}{r}\frac{{\partial {{\omega }}}}{{\partial r}} + \frac{{{{\partial }^{2}}{{\omega }}}}{{\partial {{z}^{2}}}}} \right) + u\frac{{\partial {{\omega }}}}{{\partial r}} + \upsilon \frac{{\partial {{\omega }}}}{{\partial z}} + \hfill \\ + \,\,\frac{{{\omega }}}{{{{r}^{2}}}} - u\frac{{{\omega }}}{r} - \frac{1}{r}\frac{{\partial {{W}^{2}}}}{{\partial z}} = - Gr\frac{{\partial T}}{{\partial r}}, \hfill \\ \frac{{\partial W}}{{\partial t}} - \left( {\frac{{{{\partial }^{2}}W}}{{\partial {{r}^{2}}}} + \frac{1}{r}\frac{{\partial W}}{{\partial r}} + \frac{{{{\partial }^{2}}W}}{{\partial {{z}^{2}}}}} \right) + u\frac{{\partial W}}{{\partial r}} + \hfill \\ + \,\,\upsilon \frac{{\partial W}}{{\partial z}} + \frac{W}{{{{r}^{2}}}} - u\frac{W}{r} = 0, \hfill \\ \left( {\frac{{{{\partial }^{2}}{{\psi }}}}{{\partial {{r}^{2}}}} + \frac{1}{r}\frac{{\partial {{\psi }}}}{{\partial r}} + \frac{{{{\partial }^{2}}{{\psi }}}}{{\partial {{z}^{2}}}}} \right) - \frac{2}{r}\frac{{\partial {{\psi }}}}{{\partial r}} = r \cdot \omega , \hfill \\ u = \frac{1}{r}\frac{{\partial {{\psi }}}}{{\partial z}},~\,\,\,\,\upsilon = - \frac{1}{r}\frac{{\partial {{\psi }}}}{{\partial r}}, \hfill \\ \end{gathered} \right.$
где T, ω, W, ψ, u, ${{\upsilon }}$ – это соответственно температура, вихрь скорости, азимутальная скорость, функция тока, радиальная и осевая компоненты скорости соответственно. В безразмерных уравнениях Gr = (βg/ν2)$\Delta TR_{S}^{3}$ – число Грасгофа. Здесь β – коэффициент объемного расширения газа, g – ускорение силы тяжести, ν – кинематическая вязкость аргона, ΔT – перепад температуры между фронтом кристаллизации и стенками ростовой камеры, RS – радиус кристалла. Число Прандтля аргона Pr = ν/a = 0.68, где a = λG/ρCP – коэффициент температуропроводности, λG – коэффициент теплопроводности газа, ρ – плотность, CP – теплоемкость при постоянном давлении. При приведении уравнений к безразмерному виду в качестве геометрического масштаба использован RS – радиус кристалла. За масштаб температуры принят ΔT – перепад температуры. Масштаб скорости – ν/RS. Масштаб радиационных потоков – RS2/λGΔT. Масштаб времени – ${{R_{S}^{2}} \mathord{\left/ {\vphantom {{R_{S}^{2}} {{\nu }}}} \right. \kern-0em} {{\nu }}}.$

Поля температуры внутри твердого тела вычислялись с помощью уравнения теплопроводности, записанного в безразмерном виде при тех же масштабах, что и система уравнений Навье–Стокса:

(2)
$\frac{{\partial T}}{{\partial t}} - \frac{1}{{Pr}}\frac{{{{{{\lambda }}}_{S}}}}{{{{{{\lambda }}}_{G}}}}\frac{{{{\partial }^{2}}T}}{{\partial {{r}^{2}}}} + \frac{1}{r}\frac{{\partial T}}{{\partial r}} + \frac{{{{\partial }^{2}}T}}{{\partial {{z}^{2}}}} = 0,$
где λG – коэффициент теплопроводности монокристалла.

Расчет радиационных потоков проводился на основе зонального метода [10] при следующих предположениях: расчетная область ограничена замкнутой системой поверхностей; все поверхности системы – серые, диффузно-излучающие и диффузно-отражающие; поверхности разбиты на зоны, в пределах которых радиационные свойства и температура могут считаться постоянными; среда, заполняющая ростовую камеру – диатермична. С использованием метода обратной трассировки лучей определялись области видимости зон, затем вычислялись угловые коэффициенты – доля радиационной энергии, излученной одной зоной, и непосредственно достигшей другой зоны. По известным угловым коэффициентам, с учетом до 10 отражений радиационного потока, вычислялись эффективные угловые коэффициенты. То есть доля радиационной энергии, излученной одной зоной, и поглощённой другой зоной. В том числе учитывались эффект облучения зоной самой себя и эффект самозатенения.

Зная распределения температуры по поверхностям системы и эффективные угловые коэффициенты, вычислялись исходящие с поверхностей результирующие радиационные потоки. Затем они учитывались, как добавка к условию идеального контакта: $ - {{{{\lambda }}}_{S}}{{\left. {\frac{{\partial T}}{{\partial n}}} \right|}_{{\text{Г}}}} = - {{{{\lambda }}}_{G}}{{\left. {\frac{{\partial T}}{{\partial n}}} \right|}_{{\text{Г}}}} + Q,$ где Q – это значение результирующего радиационного потока.

При поиске полей термических напряжений решалась квазистационарная задача термоупругости, используя концепцию термоупругого потенциала перемещений [11]. Пусть деформация тела, вызванная объемным расширением под воздействием температуры, задана перемещениями вдоль направлений осей координат ui. Примем, что перемещения можно выразить посредством выражений: ${{u}_{i}} = \frac{{\partial F}}{{\partial i}}.$ Здесь F – термоупругий потенциал перемещения. Поля термических напряжений можно найти по распределению термоупругого потенциала перемещений, используя следующее соотношение:

(3)
${{{{\sigma }}}_{{ij}}} = \frac{E}{{1 + {{\mu }}}}\left( {\frac{{{{\partial }^{2}}F}}{{\partial i\partial j}} - {{\Delta }}F{{{{\delta }}}_{{ij}}}} \right){\text{,}}\,\,\,\,{{\delta }} = \left\{ {1\,\,{\text{при}}\,\,i = j} \right\}.$
Здесь σ – величина термических напряжений, μ – коэффициент Пуассона, E – модуль Юнга, Δ – лапласиан, δij – символ Кронекера. Значения термоупругого потенциала перемещений может быть найдено из решения следующего уравнения Пуассона [11]:
(4)
$\frac{{{{\partial }^{2}}F}}{{\partial {{r}^{2}}}} + \frac{1}{r}\frac{{\partial F}}{{\partial r}} + \frac{{{{\partial }^{2}}F}}{{\partial {{z}^{2}}}} = \frac{{1 + {{\mu }}}}{{1 - {{\mu }}}}{{\alpha }}T,$
где α – коэффициент линейного расширения, T – поле температуры в конкретный момент времени.

Таким образом, по известному распределению поля температуры в момент времени сначала находится поле термоупругого потенциала перемещения, затем из термоупругого потенциала перемещения находятся поля компонент термического напряжения. После чего, по известным распределениям полей компонент термических напряжений находилось эквивалентное напряжение по фон Мизесу, которые определяются соотношением [11]:

(5)
${{{{\sigma }}}_{i}} = \sqrt {\frac{{{{{\left( {{{{{\sigma }}}_{{ii}}} - {{{{\sigma }}}_{{zz}}}} \right)}}^{2}} + {{{\left( {{{{{\sigma }}}_{{rr}}} - {{{{\sigma }}}_{{{{\varphi \varphi }}}}}} \right)}}^{2}} + {{{\left( {{{{{\sigma }}}_{{zz}}} - {{{{\sigma }}}_{{{{\varphi \varphi }}}}}} \right)}}^{2}} + 6\left( {{{\sigma }}_{{rz}}^{2} + {{\sigma }}_{{r{{\varphi }}}}^{2} + {{\sigma }}_{{z{{\varphi }}}}^{2}} \right)}}{2}} .$

Задача решалась при следующих краевых условиях. На фронте кристаллизации задана максимальная температура в системе (1683 К): ${{\left. T \right|}_{{{{{\text{Г}}}_{1}}}}} = 1.$ На экране, отделяющем поверхность расплава от ростовой камеры, заданы условия теплоизолированности, непротекания и прилипания: ${{\left. {\frac{{\partial T}}{{\partial n}}} \right|}_{{{{{\text{Г}}}_{2}}}}} = 0,$ ${{\left. {{\psi }} \right|}_{{{{{\text{Г}}}_{2}}}}} = 0,$ ${{\left. {{\omega }} \right|}_{{{{{\text{Г}}}_{2}}}}} = {{\left. {\frac{{\partial {{V}_{r}}}}{{\partial z}}} \right|}_{{{{{\text{Г}}}_{2}}}}}.$ На стенках ростовой камеры поддерживается минимальная температура в системе, задано условие непротекания и прилипания: ${{\left. T \right|}_{{{{{\text{Г}}}_{3}}}}} = 0,$ ${{\left. {{\psi }} \right|}_{{{{{\text{Г}}}_{3}}}}} = 0,$ ${{\left. {{\omega }} \right|}_{{{{{\text{Г}}}_{3}}}}} = {{\left. { - \frac{{\partial {{V}_{z}}}}{{\partial r}}} \right|}_{{{{{\text{Г}}}_{3}}}}}.$ На образующих кристалла заданы условия непротекания, прилипания, задана скорость вращения и условие идеального контакта с учетом радиационных потоков: ${{\left. {{\psi }} \right|}_{{{{{\text{Г}}}_{4}}}}} = 0,$ ${{\left. {{\omega }} \right|}_{{{{{\text{Г}}}_{4}}}}} = {{\left. {\frac{{\partial {{V}_{r}}}}{{\partial z}}} \right|}_{{{{{\text{Г}}}_{4}}}}}{{\left. { - \frac{{\partial {{V}_{z}}}}{{\partial r}}} \right|}_{{{{{\text{Г}}}_{4}}}}},$ ${{\left. W \right|}_{{{{{\text{Г}}}_{4}}}}} = w,$ ${{\left. T \right|}_{{{{{\text{Г}}}_{{{\text{4 - }}}}}}}} = {{\left. T \right|}_{{{{{\text{Г}}}_{{4 + }}}}}},$ $ - {{{{\lambda }}}_{S}}{{\left. {\frac{{\partial T}}{{\partial n}}} \right|}_{{{{{\text{Г}}}_{{{\text{4 - }}}}}}}} = - {{{{\lambda }}}_{G}}{{\left. {\frac{{\partial T}}{{\partial n}}} \right|}_{{{{{\text{Г}}}_{{4 + }}}}}} + Q.$ Нормальное напряжение на всех поверхностях кристалла равно нулю: ${{\left. {{{{{\sigma }}}_{{nn}}}} \right|}_{{\text{Г}}}} = 0.$

Численное моделирование проводилось методом конечных элементов на неравномерной сетке размером 101 × 501 узлов, состоящей из треугольных конечных элементов с заданными на них линейными функциями. Вычисления проводились при теплопроводности кристалла λS = 26 Вт · м–1 · К–1, характерной для монокристаллического кремния. Теплопроводность аргона λG = 5.83 · 10–2 Вт · м–1 · К–1, температуропроводность газа a = 3.74 · 10–4 м2 · с–1, коэффициент объемного расширения газа β = 6.4 · 10–4 K–1, кинематическая вязкость газа ν = 2.54 · 10–4 м2 · с–1. Свойства аргона взяты при температуре 1600 К [12]. Радиус кристалла RS – 0.05 м. Один безразмерный шаг по времени соответствует 0.098 с. Степень черноты всех поверхностей системы – 0.5. Коэффициент Пуассона μ – 0.25, коэффициент линейного расширения кристалла α – 5.2 · 10–6 К–1, модуль Юнга E – 1.59 · 10–11 Па.

РЕЗУЛЬТАТЫ И ИХ АНАЛИЗ

Проведены расчеты в режиме сопряженного теплообмена при различных комбинациях совместного действия кондуктивного, радиационного и конвективного механизмах теплообмена. При конвективном теплообмене отдельно рассмотрено влияние сил плавучести, центробежных сил и их совместное действие. Расчеты выполнены в диапазоне скоростей вращения кристалла от 0 до 25 об./мин, числе Грасгофа Gr = 16 000, соответствующему перепаду температуры ΔT = 1330 K и наборе длин кристаллов H/RS = 2, 4, 6, 8.

Результаты расчетов показывают, что во всех режимах поле температуры внутри кристалла неоднородно, соответственно неоднородно распределение радиальных и осевых градиентов температуры в различных частях кристалла (рис. 1). В кондуктивном и радиационно-кондуктивном режиме (рис. 1а) неоднородность распределения градиентов температуры прежде всего связана со сложной формой монокристалла и существенным вкладом в теплоотдачу от кристалла кондуктивного теплоотвода через затравочный кристалл и шток к холодной верхней стенке корпуса.

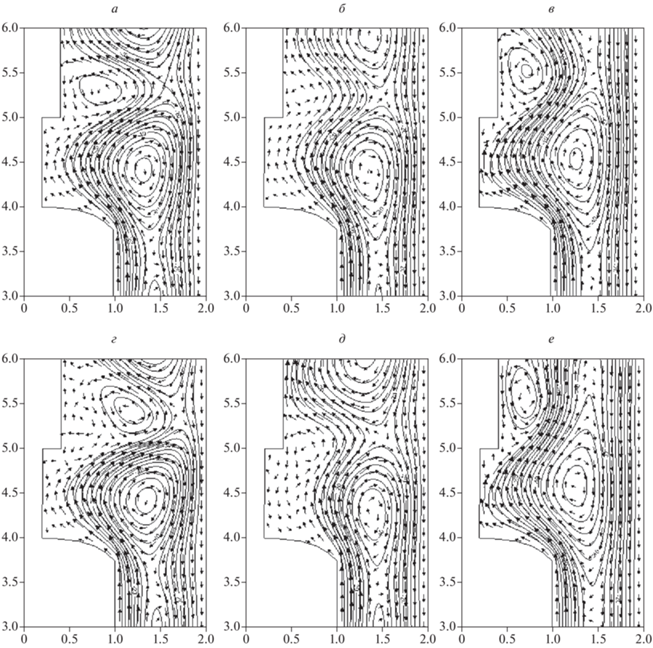
Рис. 1.

Изотермы (справа) и изолинии функции тока (слева) при высоте кристалла H/RS = 4 в момент времени t = 200 в режимах: изотермы в кондуктивном (слева) и радиационно-кондуктивном (справа) режиме (а); радиационно-конвективном с учетом центробежных сил при 25 об./мин (б); радиационно-конвективном с учетом сил плавучести (в); радиационно-конвективном с учетом центробежных сил и сил плавучести при 1 об./мин (г); радиационно-конвективном с учетом центробежных сил и сил плавучести при 10 об./мин (д); радиационно-конвективном с учетом центробежных сил и сил плавучести при 25 об./мин (е).

Под действием центробежной силы без учета влияния сил плавучести, но с учетом радиационной теплоотдачи, возникает стационарная система вихрей Тейлора (рис. 1б) в области над кристаллом. В придонной области течение газа низкоскоростное и практически не влияет на поле изотерм кристалла. Тепло от кристалла отдается в окружающую среду практически в режиме радиационно-кондуктивной теплоотдачи. В результате видно, что падает общая эффективность охлаждения кристалла.

Под действием сил плавучести формируется стационарная пространственная форма конвективных течений из трех вихрей с эффектом отрыва пограничного слоя от образующей штока на уровне z = 5.5 (рис. 1в). Между образующими монокристалла и холодными стенками корпуса образуется конвективный вихрь с направлением движения в нижней части от стенок корпуса к основанию кристалла и с восходящим течением вдоль его образующих. Этот же вихрь занимает часть пространства над кристаллом. Между образующими штока и стенками корпуса образуются аналогичный вихрь, который частично блокирует проникновения разогретого у основания кристалла газа в верхнюю область ростовой камеры. За счет существенно большего размера конвективного вихря вблизи монокристалла и более высокой интенсивности конвективных течений в придонной области, радиальные градиенты у основания кристалла растут заметно сильнее, чем при конвекции под влиянием центробежных сил. Под действием поднимающегося по образующей монокристалла, разогретого у фронта кристаллизации газа, снижается эффективность теплоотдачи с боковой поверхности монокристалла и общая эффективность охлаждения монокристалла, который более равномерно прогревается по высоте. В данном случае кристалл находится при высокой температуре, радиальные градиенты температуры относительно высокие, а осевые градиенты температуры относительно низкие.

При совместном действии сил плавучести и центробежных сил пространственная форма конвективных течений теряет устойчивость и течение газа становится нестационарным (рис. 1г, 1д и 1е). В верхней части ростовой камеры формируются вторичные вихри, опускающиеся вдоль по штоку до области затравочного кристалла, и сталкиваются с вихрем, занимающим область над кристаллом и между образующей монокристалла и холодными стенками корпуса. В режиме гравитационно-центробежной конвекции и учете радиационной теплоотдачи резко увеличиваются осевые градиенты температуры (рис. 1г, 1д и 1е).

На рис. 2 представлена эволюция поля скорости во времени в области над монокристаллом, при высоте кристалла H/RS = 4 и скорости вращения 10 оборотов в минуту. Видно, что при столкновении вторичного вихря с вихрем над кристаллом, вторичный вихрь отбрасывает на холодные стенки корпуса, по которым он впоследствии поднимается. Вследствие чего происходит выброс разогретого газа в верхнюю часть ростовой камеры. Как результат, резко возрастает эффективность охлаждения монокристалла. По мере роста скорости вращения форма конвективных течений начинает стабилизироваться, но остается нестационарной. Над кристаллом начинает усиливаться вихрь, частично блокирующий проникновение разогретого у основания газа в верхнюю часть ростовой камеры. Вследствие чего эффективность охлаждения кристалла падает, и он более равномерно разогревается по высоте (рис. 1е).

Рис. 2.

Эволюция векторного поля скорости и поля изолиний функции тока во времени при совместном действии сил плавучести и центробежных сил, H/RS = 4 и скорости вращения 10 об./мин в моменты времени: t = 35 (а), 70 (б), 105 (в), 140 (г), 175 (д), 210 (е).

После того, как под воздействием центробежных сил течение теряет свою устойчивость и приобретает флуктуирующий характер, поле температуры внутри монокристалла, затравочного кристалла и штока начинает осциллировать (рис. 3). В монокристалле распространяется тепловая волна, которая достигает максимальной амплитуды в верхней части кристалла. На рис. 4 представлены профили отклонений размерных эквивалентных напряжений по фон Мизесу на уровнях z = 0.15 м и z = 0.05 м, соответствующим безразмерным высотам z = 3 и z = 1, от распределения эквивалентных напряжений в момент времени t = 0, при высоте кристалла при высоте кристалла H/RS = 4 и скорости вращения 10 оборотов в минуту при совместном действии сил плавучести и центробежных сил в радиационно-конвективном режиме. Видно, что вместе с осцилляциями поля температуры внутри кристалла осциллируют и термические напряжения, которые так же максимальны в верхней части кристалла.

Рис. 3.

Реализация температуры на уровне z = 3.75 при совместном действии сил плавучести и центробежных сил, H/RS = 4 и скорости вращения 10 об./мин в точке 1 – r = 1, 2 – 0.5, 3 – 0.25, 4 – 0.

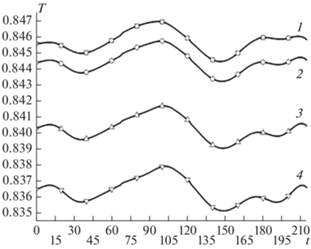
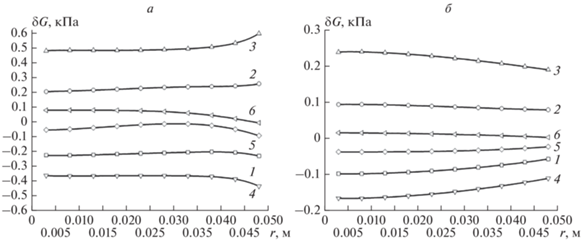
Рис. 4.

Профиль отклонений эквивалентных напряжений по фон Мизесу на уровне: z = 0.15 м (z = 3) (а), 0.05 м (z = 1) (б), от распределения эквивалентных напряжений в момент времени t = 0 при совместном действии сил плавучести и центробежных сил, H/RS = 4 и скорости вращения 10 об./мин в моменты времени: 1 – t = 3.4 с (t = 35), 2 – 6.9 с (70), 3 – 10.3 с (105), 4 – 13.8 с (140), 5 – 17.2 с (175), 6 – 20.7 с (210).

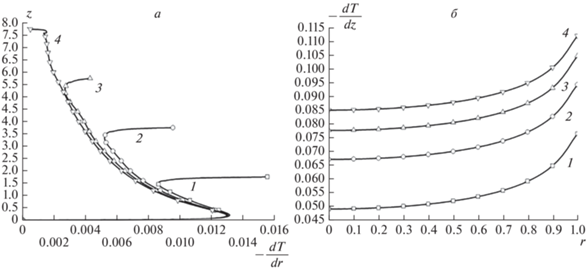
Расчеты проведены при дискретном наборе длин кристаллов H/RS = 2, 4, 6, 8. На качественном уровне закономерности эволюции полей изолиний функции тока и изотерм над верхним торцом кристаллов совпадают. Но тепловые потоки с образующих кристаллов зависят от их длины. На рис. 5а представлены зависимости распределений по высоте кристаллов радиальных градиентов температуры на образующих от их длины. Эти зависимости показывают распределения безразмерных локальных тепловых потоков с боковых поверхностей кристаллов. От теплоотдачи на образующих кристаллов зависят радиальные распределения осевых градиентов температуры в кристаллах (рис. 5б). Видно, что с ростом длины кристалла и увеличением площади боковых поверхностей растут интегральные тепловые потоки и вблизи ФК растут осевые градиенты температуры, пропорционально которым растут интегральные тепловые потоки.

Рис. 5.

Профили радиального градиента температуры в сечении r = 1 (а) и осевого градиента температуры в сечении z = 0.02 (б) в радиационно-конвективном режиме с учетом центробежных сил и силы плавучести при скорости вращения 10 об./мин и различных высотах кристалла: 1 – H/RS = 2; 2 – 4; 3 – 6; 4 – 8.

ЗАКЛЮЧЕНИЕ

Численно, методом конечных элементов, исследован сопряженный теплообмен в системе “кристалл–окружающая среда–стенки ростовой камеры”, геометрически подобной упрощенной схеме верхней части теплового узла в методе Чохральского. Расчеты проведены в кондуктивном, радиационно-кондуктивном, радиационно-конвективном режимах с учетом влияния центробежных сил и сил плавучести. Исследования проведены при скоростях вращения кристалла от 0 до 25 об./мин, при числе Грасгофа Gr = 16 000, соответствующем перепаду температуры ΔT = 1330 К, в диапазоне относительных длин кристалла 2 ≤ H/RS ≤ 8. Показано, что под влиянием центробежных сил пространственная форма конвективных течений теряет устойчивость и при всех длинах кристаллов течения газа переходят к флуктуирующим режимам. Наблюдаются выбросы нагретых у основания кристалла масс газа в верхнюю часть ростовой установки. Это приводит к колебательному характеру теплоотдачи с образующих кристалла и распространению тепловых волн в объеме кристалла при всех длинах кристаллов. Увеличение скорости вращения до 25 об./мин оказывает стабилизирующее влияние на пространственную форму конвективных течений. С ростом длины кристалла падает амплитуда колебания тепловых потоков в кристалле.

Исследования выполнены в рамках темы государственного задания ИТ СО РАН (код темы: 0257-2021-0003, номер гос. рег. 121031800213-0) при частичной поддержке Российского фонда фундаментальных исследований (проект № 19-08-00707).

Список литературы

  1. Мильвидский М.Г. Полупроводниковые материалы в современной электронике. М.: Наука, 1986. 144 с.

  2. Вильке К.-Т. Выращивание кристаллов. Л.: Недра, 1977. 600 с.

  3. Горилецкий В.И., Гринев Б.В., Заславский Б.Г. и др. Рост кристаллов. Галогениды щелочных металлов. Харьков: Акта, 2002. 536 с.

  4. Простомолотов А.И., Верезуб Н.А., Ильясов Х.Х. // Изв. вузов. Матер. электрон. техн. 2015. Т. 18. № 1. С. 31.

  5. Верезуб Н.А., Простомолотов А.И. // Изв. РАН. МТТ. 2020. № 5. С. 51; Verezub N.A., Prostomolotov A.I. // Mech. Solids. 2020. V. 55. No. 5. P. 643.

  6. Бердников В.С., Митин К.А. // Изв. РАН. Сер. физ. 2016. Т. 80. № 1. С. 75; Berdnikov V.S., Mitin K.A. // Bull. Russ. Acad. Sci. Phys. 2016. V. 80. No. 1. P. 68.

  7. Бердников В.С., Митин К.А., Григорьева А.М., Клещенок М.С. // Изв. РАН. Сер. физ. 2017. Т. 81. № 9. С. 1198; Berdnikov V.S., Mitin K.A., Grigoreva A.M., Kleshchenok M.S. // Bull. Russ. Acad. Sci. Phys. 2017. V. 81. No. 9. P. 1080.

  8. Mitin K.A., Berdnikov V.S. // J. Phys. Conf. Ser. 2018. V. 1105. Art. No. 012027.

  9. Соловейчик Ю.Г., Рояк М.Э., Персова М.Г. Метод конечных элементов для решения скалярных и векторных задач. Новосибирск: изд-во НГТУ, 2007. 896 с.

  10. Спэрроу Э.М., Сесс Р.Д. Теплообмен излучением. Л.: Энергия, 1971. 296 с.

  11. Мелан Э., Паркус Г. Термоупругие напряжения, вызываемые стационарными температурными полями. М.: Физматгиз, 1958. 167 с.

  12. Варгафтик Н.Б. Справочник по теплофизическим свойствам газов и жидкостей. М.: Наука, 1972. 720 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал