Известия РАН. Серия физическая, 2022, T. 86, № 8, стр. 1162-1165

ВВЕДЕНИЕ

Эффективность термодинамики и гидродинамики для физики была отмечена в трудах классиков [1–3], соответствующий подход успешно использовался авторами [4–7] и остается актуальным. Зачастую [3], для описания столкновений тяжелых ионов используют равновесную гидродинамику. В наших работах [4–11] было показано, что локальное термодинамическое равновесие в процессе столкновений тяжелых ионов устанавливается не сразу. С этой целью в настоящей работе использован результат решения кинетического уравнения [8, 9] для нахождения функции распределения нуклонов, которое при низких энергиях приводит к уравнениям неравновесной длиннопробежной гидродинамики [4].

Решение этих уравнений гидродинамики в одномерном случае найдено аналитически с использованием односолитонных решений уравнения Кортевега-де Фриза (см., например, [12–15]). Это представляет самостоятельный интерес, поскольку солитоны играют большую роль в физике элементарных частиц, ядерной физике, физике вообще, и это открывает путь к точному интегрированию уравнений гидродинамики. На этой основе получено обоснование образования горячего пятна hot spot – источника быстрых частиц с учетом дисперсии в эффективных силах.

НЕРАВНОВЕСНЫЙ ГИДРОДИНАМИЧЕСКИЙ ПОДХОД И ВОЗМОЖНОСТЬ ОБРАЗОВАНИЯ HOT SPOT

При средних энергиях сталкивающихся тяжелых ионов мы ищем решение кинетического уравнения [8, 9] для нахождения нуклонной функции распределения $f(\vec {r},\vec {p},t)$ ($\vec {r}({{x}_{1}},{{x}_{2}},{{x}_{3}})$ – пространственная координата, $\vec {p}({{p}_{1}},{{p}_{2}},{{p}_{3}})$ – импульс, $t$ – время) в виде:

где ${{f}_{0}}(\vec {r},\vec {p},t)$ – локально равновесная функция распределения, ${{f}_{1}}(\vec {r},\vec {p},t)$ – неравновесная функция распределения, являющаяся удобной формой описания возбуждений в теории ферми-жидкости, $q$ – релаксационный фактор. В результате получается [5–9] замкнутая система уравнений для нахождения плотности $\rho = g\int {f\frac{{{{d}^{3}}\vec {p}}}{{{{{(2\pi \hbar )}}^{3}}}}} ,$ плотности i-й компоненты импульса $m\rho {{\upsilon }_{i}} = g\int {{{p}_{i}}f\frac{{{{d}^{3}}\vec {p}}}{{{{{(2\pi \hbar )}}^{3}}}}} ,$ плотности внутренней энергии $e = {{e}_{{kin}}} + {{e}_{{int}}},$ где $\hbar $ – постоянная Планка, $g = 4$ – спин-изоспиновый фактор, $m$ – масса нуклона. Члены взаимодействия для плотности энергии ${{e}_{{int}}}$ и давления ${{P}_{{int}}}$ соответственно равны где $W(\rho )$ – зависящий от плотности $\rho $ одночастичный самосогласованный потенциал.

Как показано в [8, 9], при энергиях ${{E}_{0}} < 100$ МэВ/ нуклон релаксационный фактор максимален, $q = 1,$ приводя к уравнениям неравновесной длиннопробежной гидродинамики [4]. С увеличением энергии он уменьшается, приводя к большей изотропии функции распределения.

Взаимодействие двух ядер сводится к взаимодействию их областей перекрытия [5–9]. Это сопровождается сжатием, что можно интерпретировать приближенно как процесс образования hot spot – источника быстрых частиц. Ранее нами, в отсутствии дисперсии в эффективных силах, процесс сжатия рассматривался путем образования ударных волн. Включение дисперсионных членов может затруднить образование ударных волн и процесс сжатия.

В следующем разделе настоящей работы будет проанализирован механизм образования hot spot, исходя из уравнений гидродинамики, путем их точного аналитического решения c учетом дисперсии в эффективном взаимодействии.

РЕШЕНИЕ УРАВНЕНИЙ ГИДРОДИНАМИКИ В ОДНОМЕРНОМ СЛУЧАЕ И ОБСУЖДЕНИЕ

В настоящей работе нас интересует влияние на процесс столкновения, которое оказывают дисперсионные члены для эффективных сил, опущенные в выражениях (2) в работах [5–9]. Здесь для простоты это рассмотрение проведено в плоской одномерной геометрии, и задача столкновения ядер сведена к взаимодействию ядерных слоев-слэбов. Будет найдено аналитическое решение этой задачи путем сведения ее к столкновению солитонов уравнения Кортевега–де Фриза. Само по себе представляющее новый подход и определенный интерес для решения уравнений гидродинамики.

Уравнения гидродинамики [8, 9] при релаксационном факторе $q = 1$ (неравновесный случай) в одномерном случае сводятся к следующей системе уравнений для нахождения плотности $\rho (x,t),$ скорости $\upsilon (x,t),$ плотности тепловой энергии $I(x,t){\text{:}}$

где давление $P(x,t)$ = задано в приближении эффективных ядерных сил типа сил Скирма. При этом коэффициенты $a$ и $b$ связаны соотношением $a{{\rho }_{0}} + b\rho _{0}^{2} = 0,$ где ${{\rho }_{0}} = 0.15$ фм^–3 – равновесная ядерная плотность, а дисперсионный член с коэффициентом $\alpha $ определяет дисперсию (скоростной член), величина которого будет определена ниже.

Из уравнений (3) и (5) следует, что $I = {{I}_{1}}{{\left( {\frac{\rho }{{{{\rho }_{0}}}}} \right)}^{3}},$ где ${{I}_{1}}$ – независящий от $\rho $ коэффициент. Совместное решение уравнений (3) и (4) ищем в виде $\upsilon = \upsilon (\rho ).$ Откуда получаем соотношение

Следовательно

и где скорость звука ${{c}_{{s0}}} = \sqrt {\frac{{a + 2b{{\rho }_{0}}}}{m}} \approx 1{\text{/}}3c$ ≈ 10⁸ м/с, $\beta = \frac{b}{{m{{c}_{{so}}}}},$ $\frac{\alpha }{{2mc_{{so}}^{2}}}$ = (фм)².

После подстановки (7), (8) в уравнение (3) получаем два уравнения Кортевега–де Фриза

То есть уравнения гидродинамики сведены к двум уравнениям Кортевега–де Фриза [12, 13]. Уравнения (9), (10) можно привести к безразмерному виду

$t{\kern 1pt} ' = {{ \pm t} \mathord{\left/ {\vphantom {{ \pm t} \gamma }} \right. \kern-0em} \gamma },$ $x{\kern 1pt} ' = x{\text{/}}\lambda ,$ $A = \gamma = {{6}^{{6{\text{/}}10}}}{{\Theta }^{{1{\text{/}}5}}},$ $\lambda = {{6}^{{1{\text{/}}5}}}{{\Theta }^{{2{\text{/}}5}}},$ $\Theta = {{c}_{{so}}}2$(фм)². Как хорошо известно [14, 15], уравнение (11) сводится подстановкой к билинейному однородному уравнению для s, которое содержит солитонные решения и, в частности, односолитонное решение где $\omega = - {{k}^{3}}.$

Замечательным свойством уравнения Кортевега–де Фриза являются интегралы движения. Очевидным интегралом (11) является сумма $\int_{ - \infty }^\infty {\zeta dx{\kern 1pt} '} $ односолитонных решений. Это позволяет перейти к представлению столкновения ядер, как столкновению солитонов, если простую волну уравнения Кортевега–де Фриза (13), (14) проинтегрировать по ${{x}_{1}}.$ То есть найти приближенное решение

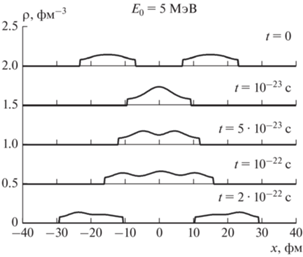
поскольку одинаковые солитоны движутся с постоянной скоростью, не взаимодействуя. Здесь $L$ – толщина слоя, на концах которого значение $Z$ пренебрежимо мало, $Z$ – является простой волной Кортевега–де Фриза, испущенной этим слоем. Пользуясь (12), затем можно найти плотность $\rho $ и скорость ${{\upsilon }_{0}},$ как функции $x$ и $t$ для двух простых волн уравнений (9) и (10). Это относится к каждому ядерному слою – источнику простых волн. Учитывая многократные отражения волн Кортевега–де Фриза от границ системы, можно рассмотреть всю динамику столкновения ядерных слоев-слэбов. Что мы и сделали.

На рис. 1. представлены мгновенные фотографии- профили плотности для столкновения ядерных слоев при энергии ${{E}_{0}} = 5$ МэВ на нуклон в различные моменты времени при t = 0; 0.1; 0.5; 1 и 2 в единицах времени 10^–22 с. Можно видеть первоначальное сжатие и образование hot spot, его распад и последующий разлет системы с образованием двух ядер.

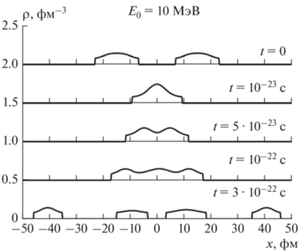
На рис. 2 представлены мгновенные профили плотности для столкновения ядерных слоев при энергии ${{E}_{0}} = 10$ МэВ на нуклон в моменты времени t = 0; 0.1; 0.5; 1 и 3 в единицах времени 10^–22 с. После первоначального сжатия, образования hot spot и последующего расширения на стадии разлета наблюдается фрагментация, т.е. образуются слои-фрагменты (их четыре) вместо двух первоначальных ядер.

Эти результаты получены аналитически, они совершенно не требуют затрат машинного времени. Из аналитических выражений находятся плотность $\rho (x,t),$ скорость $\upsilon (x,t),$ а также находится из сохранения энергии плотность тепловой энергии.

В результате мы убедились, что введение дисперсии в эффективные силы и в давление не нарушает представления о сжатии и образовании hot spot. Введение дополнительных размерностей не нарушит это представление кардинально. А сам подход на основе уравнения Кортевега–де Фриза представляет самостоятельный интерес и может быть использован и в других областях физики и техники.

ЗАКЛЮЧЕНИЕ

Таким образом, мы показали, что введение дисперсии в эффективные силы не нарушает представления об образовании hot spot и при относительно низких энергиях. Использование неравновесных гидродинамических уравнений с образованием hot spot, как было показано в [5‒11], позволяет описывать экспериментальные данные лучше, чем уравнения традиционной гидродинамики.

Нами также открыт путь к точному интегрированию уравнений гидродинамики. Сведение неравновесных уравнений гидродинамики к решению двух уравнений Кортевега–де Фриза в виде солитонов позволило найти аналитическое решение задачи, что представляет самостоятельный фундаментальный интерес для физики вообще и может быть использовано в различных прикладных областях.