Известия РАН. Серия физическая, 2022, T. 86, № 9, стр. 1243-1246

В последние годы активно развивается новое направление спинтроники – стрейнтроника [1]. В элементах стрейнтроники присутствует магнитный слой, обладающий высокими магнитострикционными свойствами. Наличие этого слоя позволяет управлять физическими параметрами элементов спинтроники посредством его деформации. В одной из первых экспериментальных работ продемонстрировавшей такую возможность [2] использовался спин-туннельном магниторезистивный элементе квадратной формы. В качестве слоя с положительной магнитострикцией использовался нано слой FeCo, а с отрицательной магнитострикцией – нано слой Ni.

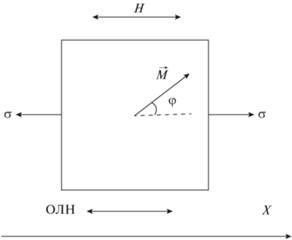
Следуя работе [2], рассмотрим свободный слой туннельного магниторезистивного элемента, подвергнутого однородной деформации растяжения или сжатия как показано на рис. 1.

Элемент имеет квадратную форму. Ось легкого намагничивания (ОЛН) и направление однородной деформации направлены вдоль координатной оси $X.$ Вектор намагниченности $\vec {M}$ лежит в плоскости пленки и под действием внешнего поля $H$ может быть ориентирован относительно оси $X$ под углом $\varphi .$ Для теоретического исследования обратного магнитострикционного эффекта на магниторезистивное сопротивление спин-туннельного магнитного перехода воспользуемся моделью однородного вращения вектора намагниченности (см, например, [3]). Плотность магнитной энергии в этом случае с учетом магнитоупругой энергии будет равна, [3, 4]:

Здесь первое слагаемое слева является плотностью энергии одноосной анизотропии. Второе слагаемое – это плотность магнитоупругой энергии [4], где верхний знак соответствует положительной магнитострикции, а нижний – отрицательной. Третье слагаемое плотность энергии взаимодействия внешнего магнитного поля с вектором намагниченности, где верхний знак соответствует направлению поля $H$ вдоль оси $X,$ нижний – против оси $X.$ Величина ${{K}_{u}}$ – константа одноосной анизотропии, $\lambda $ – относительное изменение длины образца, $\sigma $ – напряжение.

Введем обозначения

тогда выражение (1) можно записать в виде

Разделим обе части равенства (3) на модуль величины (плотность энергии эффективной анизотропии)

для безразмерной плотности магнитной энергии $\tilde {w}$ получим

где введена безразмерная величина напряженности внешнего магнитного поля

Знак (+) в (5) соответствует случаю, когда ${{H}_{{anef}}} > 0,$ знак (–) если ${{H}_{{anef}}} < 0.$

Дифференцируя функцию (5) по переменной $\varphi $ находим уравнение для определения экстремумов плотности энергии $\tilde {w}$

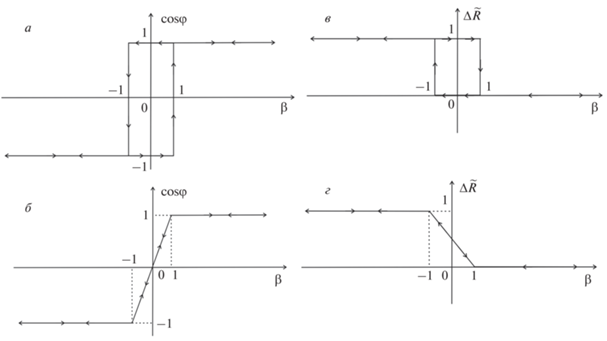
Из (5) и (6) следует, что при ${{H}_{{anef}}} > 0$ и $\beta < 1$ энергия $\tilde {w}$ будет иметь два локальных минимума при ${{\varphi }} = {\text{0,}}\,\,{{\pi }}{\text{.}}$ При $\beta > 1$ имеется только один минимум плотности энергии. Если проекция вектора внешнего магнитного поля $\vec {H}$ на ось X равна H, то минимум энергии достигается при $\varphi = 0$. Если же проекция вектора внешнего магнитного поля $\vec {H}$ на ось X равна – H, то минимум энергии достигается при ${{\varphi }} = {{\pi }}{\text{.}}$ Соответственно зависимость $\cos \varphi $ от безразмерного внешнего магнитного поля $\beta $ при перемагничивании будет иметь зависимость, представленную на рис. 2a.

В случае ${{H}_{{anef}}} < 0,$ то минимум плотности энергии (5) при $\left| \beta \right| < 1$ будет достигаться если

При $\left| \beta \right| > 1$ минимум энергии $\tilde {w}$ будет при

Соответствующая, зависимость $\cos \varphi $ от безразмерного внешнего магнитного поля $\beta $ при перемагничивании изображена на рис. 2б.

Как видно из рис. 2б при указанных параметрах происходит безгистерезисное перемагничивание свободного слоя спин-туннельного магниторезистивного элемента.

Используя приведенную выше теорию, несложно рассчитать изменение гигантского магнитосопротивления спин-туннельного элемента стрейнтроники от внешнего магнитного поля $H$ для случая, изображенного на рис. 1 по формуле [5]

Для безразмерного изменения магнитосопротивления $\Delta \tilde {R}$ находим

Тогда используя полученные выше решения, находим следующие зависимости безразмерного сопротивления $\Delta \tilde {R}$ от безразмерного внешнего магнитного поля $\beta $, которые приведены на рис. 2в (при ${{H}_{{anef}}} > 0$) и рис. 2г (при ${{H}_{{anef}}} < 0$).

Из полученных результатов следует, что в случае материала с положительной магнитострикцией при растяжении, то есть когда $\sigma > 0$ и ${{K}_{\sigma }} > 0$ происходит увеличение эффективной анизотропии ${{H}_{{anef}}} = {{H}_{{an}}} + {{H}_{\sigma }}.$ Следовательно, ширина гистерезисной петли увеличивается. При сжатии образца $\sigma < 0$ и ${{K}_{\sigma }} < 0,$ поэтому ${{H}_{{anef}}} = {{H}_{{an}}} - \left| {{{H}_{\sigma }}} \right|.$ Соответственно происходит уменьшение ширины гистерезисной петли. Если ${{H}_{\sigma }} > {{H}_{{an}}},$ то ${{H}_{{anef}}} < 0,$ тогда ось легкого намагничивания будет перпендикулярна оси $X.$ В этом случае гистерезис в зависимости безразмерного магнитосопротивления $\Delta \tilde {R}$ от безразмерного магнитного поля $\beta $ пропадает, а сама зависимость будет иметь вид, представленный на рис. 2г. При отрицательной магнитострикции закономерности на рис. 2в и 2г будут обратными.

Следует отметить, что теория когерентного вращения довольно хорошо совпадает (в том числе количественно) с экспериментальными результатами, полученными в [2]. Однако имеются и несовпадения с данной простой теорией, связанные с тем, что экспериментальные кривые в области резких углов имеют закругления, а сами петли имеют небольшой горизонтальный сдвиг и не являются, строго говоря, симметричными относительно начала координат. Были попытки объяснить эту зависимость наклоном оси одноосной анизотропии ${\text{в}}$ [6]. Однако наилучшее совпадение теоретической кривой с экспериментом получалось при довольно большом отклонении оси одноосной анизотропии (5°–10°), что, по нашему мнению, является маловероятным. Это подтверждается и тем, что те же авторы в [2] уже не используют эту гипотезу для объяснения плавного изгиба гистерезисной кривой, а приводят только экспериментальные результаты. По нашему мнению, это несовпадение экспериментальных результатов с теорией имеет иную физическую природу и обусловлено возникновением неоднородного перемагничивания в магнитной пленке или даже возникновением доменной структуры. В связи с этим мы выполнили численное моделирование процесса перемагничивания квадратной магнитной пленки методом крупных частиц.

В работе использовался популярный программный пакет для решения задач микромагнитного моделирования OOMMF [7], в основе которого лежит метод динамического установления для определения результирующей микромагнитной структуры в зависимости от внешних условий и параметров образца. В основе лежит решение динамического микромагнитного уравнения Ландау–Лифшица–Гильберта

где ${{\vec {H}}_{{ef}}}$ – эффективное магнитное поле, которое определяется вариационной производная свободной энергии по магнитному моменту. При этом исследуемый образец разбивается на ячейки в форме прямоугольного параллелепипеда, в объеме которых распределение намагниченности $\vec {M}$ можно считать практически однородным. В таком случае уравнение (12) преобразуется в систему дискретных уравнений, решение которой производится численно исходя из начальных и граничных условий. С течением времени система стремится к результирующему распределению намагниченности благодаря диссипативному члену в уравнении (12). Данное распределение является численным решением задачи.

Моделирование было выполнено для квадратного образца размерами 25 × 25 мкм² и толщиной 2.5 нм. Физические параметры образца: H_an = 10 Э, намагниченность насыщения M_s = 1960 Гс, константа обменного взаимодействия A = 1.3 ⋅ 10^–6 эрг/см. Результаты этого моделирования представлены на рис. 3.

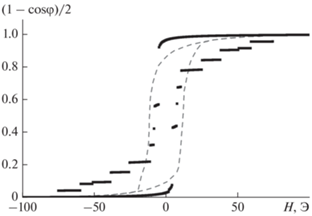
Разрывы в теоретической зависимости (1 – cosφ)/2 от величины внешнего магнитного поля H, по-видимому, связаны с дискретностью ячеек, а именно с единовременным перемагничиванием отдельных больших участков квадрата, что в свою очередь приводит к резкому скачку на графике. Вероятно, теоретическая кривая примет более плавный вид при увеличении числа ячеек в моделировании, однако это приводит к непропорциональному увеличению времени вычислений, которые могут быть не под силу даже суперкомпьютерам. В данной работе моделирование выполнено при 10  000 ячеек.

При сравнении результатов расчета с аналогичной зависимостью на рис. 4 , полученной в случае использования модели когерентного перемагничивания, можно заметить более плавный ход теоретической кривой в случае неоднородного перемагничивания, при этом рассмотренная теория полностью соответствуют основополагающей экспериментальной работе [2].