Известия РАН. Серия физическая, 2022, T. 86, № 9, стр. 1247-1250

ВВЕДЕНИЕ

В настоящее время широкое применение в спинтронике находят спин-туннельные гетероструктуры [1–3]. Типичные экспериментальные зависимости изменения сопротивления таких структур, обусловленного наличием гигантского магниторезистивного (ГМР) эффекта при их перемагничивании, имеют вид, изображенный на рис. 1 (пунктирные линии). Теоретический анализ процесса квазистационарного перемагничивания указанных структур требует решения вариационной задачи на нахождение такого распределения вектора намагниченности $\vec {M}\left( {x,y,z} \right)$, которое минимизирует функционал полной магнитной энергии

где $w\left( {\vec {M}\left( {x,y,z} \right)} \right)$ – объемная плотность полной магнитной энергии в заданной точке магнетика с координатами x, y и z. В случае справедливости модели когерентного вращения вектора намагниченности свободного слоя спин-туннельного наноэлемента можно воспользоваться теорией Стонера–Вольфарта [4]. Тогда для плотности магнитной энергии получим следующее выражение [5]:

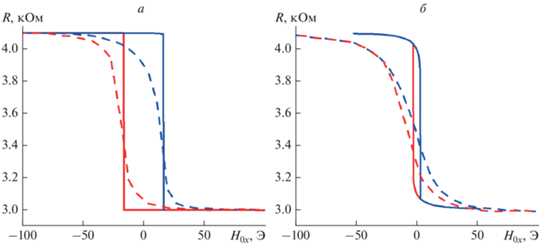
Здесь φ – угол поворота вектора намагниченности $\vec {M}$ относительно оси легкого намагничивания (ОЛН), вдоль которой направлена ось X декартовой системы координат. Соответственно координатная ось Y направлена вдоль направления трудного намагничивания в плоскости свободного слоя. Величины H_0x и H_0y – проекции вектора напряженности ${{\vec {H}}_{0}}$ внешнего магнитного поля на координатные оси X и Y соответственно, H_an – эффективное поле одноосной анизотропии, n_x и n_y – диагональные компоненты тензора размагничивающего фактора вдоль координатных осей X и Y соответственно.

Согласно выражению (1), полная магнитная энергия может иметь два равновесных состояния с наименьшим значением энергии: когда составляющая вектора намагниченности $\vec {M}$ вдоль оси X направлена по этой оси или против. При перемагничивании свободного слоя внешним магнитным полем, направленным вдоль оси X, при некотором критическом значении этого поля происходит изменение ориентации вектора намагниченности. Причем при прямом и обратном ходе этого поля критические значения имеют разные величины, что приводит к гистерезису кривой перемагничивания. Критические значения магнитного поля, согласно теории Стонера–Вольфарта [4], можно получить из условий [5]:

На рис. 1 сплошными линиями показаны теоретические зависимости сопротивления R спин-туннельного элемента от проекции H_0x внешнего магнитного поля, полученные в рамках этой теории. Качественно эта теория удовлетворительно описывает ход кривой и основные особенности гистерезиса ГМР сопротивления, но количественно экспериментальные графики изменяются более плавно. В этой работе сделана попытка объяснить это расхождение наличием некогерентного изменения вектора намагниченности в свободном слое.

ПАРАМЕТРЫ ИССЛЕДУЕМОГО ОБРАЗЦА

В работе исследуется ГМР сопротивление спин-туннельного магниторезистивного (СТМР) элемента следующей конфигурации: Ta(10 нм)/ CoFe(2 нм)/CoFeB(3 нм)/MgO(3.5 нм)/CoFeB(3 нм)/ Ru(0.85 нм)/CoFe(2 нм)/FeMn(10 нм)/Ta(10 нм). Данный СТМР элемент содержит так называемую синтетическую антиферромагнитную структуру, состоящую из двух противоположно намагниченных слоев (CoFe и CoFeB), связанных косвенным антиферромагнитным взаимодействием через слой рутения (Ru). Это позволяет исключить (или существенно уменьшить) влияние магнитостатического поля фиксирующего магнитного слоя на свободный слой СТМР элемента.

Нанослои СТМР элемента имеют форму эллипсов с полуосями a = 12 мкм и b = 6 мкм. Ось обменной (однонаправленной) анизотропии (ООА) между антиферромагнитным слоем (FeMn) и ферромагнитным слоем (CoFe) и ось легкого намагничивания (ОЛН) свободного слоя CoFeB направлены вдоль большей полуоси a эллипсов. Внешнее магнитное поле ${{\vec {H}}_{0}}$ можно разложить на две проекции: постоянная H_0y, направленная вдоль оси трудного намагничивания (т.е. вдоль полуоси b эллипсов), а также H_0x, направленная вдоль ОЛН. Изменение проекции H_0x внешнего магнитного поля приводит к изменению ориентации вектора намагниченности $\vec {M}$ свободного слоя, в результате чего возникает неоднородное распределение намагниченности.

Физические параметры материала свободного слоя, использующиеся в дальнейших расчетах: намагниченность насыщения M_s = 931 Гс, эффективное поле одноосной анизотропии H_an = 15 Э, константа обменного взаимодействия A = 1.3 ⋅ 10^–6 эрг/см.

ТЕОРЕТИЧЕСКИЙ РАСЧЕТ

Неоднородное перемагничивание моделировалось в рамках микромагнитной двумерной теории с использованием метода динамического установления, основанного на решении динамического уравнении Ландау–Лифшица–Гильберта:

где t – время, γ – гиромагнитное отношение, α – параметр затухания, $\vec {M}$ – вектор намагниченности, ${{\vec {H}}_{{ef}}}$ – эффективное магнитное поле, равное вариационной производной от функционала полной магнитной энергии. Ферромагнитный образец разбивается на N одинаковых прямоугольных ячеек, при этом их размер подбирается таким образом, чтобы в пределах этих ячеек было практически однородное распределение намагниченности $\vec {M}$. Магнитный момент каждой такой ячейки равен ${{\vec {p}}_{{mi}}} = {{\vec {M}}_{i}} \cdot \Delta V,$ где ∆V – объем ячейки. Поместив эквивалентный диполь в центр ячейки можно свести континуальное уравнение Ландау–Лифшица–Гильберта (4) к системе N дискретных уравнений:

Эта система решается численно при задании начальных и граничных условий. С течением времени система стремится к некоторому стационарному распределению магнитных моментов ${{\vec {p}}_{{mi}}}$ в ферромагнетике. Это происходит за счет диссипативного члена, выраженного последним слагаемым в уравнении (5). Данное распределение является результирующим при заданных условиях.

Для реализации описанного выше численного метода использовался распространенный программный пакет OOMMF [6]. В результате расчетов действительно было зафиксировано возникновение неоднородных магнитных структур (доменов) в свободном слое. Одна из таких структур представлена на рис. 2.

Расчет зависимости ГМР сопротивления СТМР элемента R от компоненты H_0x напряженности внешнего магнитного поля производился на основе полученных распределений намагниченности с использованием известной формулы:

где φ – угол между векторами намагниченности фиксированной и свободной соседних магнитных пленок, R₀ – минимальное сопротивление СТМР элемента при параллельном расположении векторов намагниченности в соседних слоях (φ = 0), ΔR – изменение сопротивления СТМР элемента, Δρ/ρ – величина ГМР эффекта.

На рис. 3 представлены результаты теоретических расчетов изменения ГМР сопротивления при некогерентном перемагничивании свободного слоя спин-туннельного элемента, которая значительно лучше приближается к экспериментальной кривой.

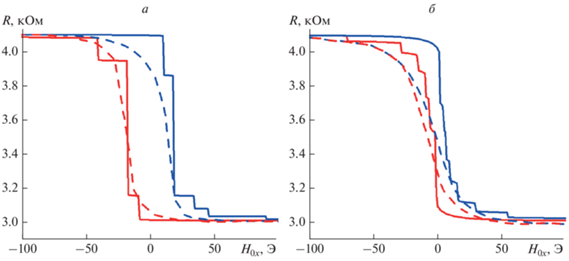
ЗАКЛЮЧЕНИЕ

Можно отметить, что график на рис. 3 имеет ступенчатый вид, что связано с особенностью неоднородного перемагничивания эллипсоида, а именно с возникновением доменов (рис. 2). Вследствие этого, при изменении внешнего магнитного поля происходит резкое перемагничивание определенных участков эллипсоида, в результате чего направление намагниченности в этих областях меняется практически на противоположное. Было установлена, что величина скачков зависит от выбора размеров ячейки при численном счете, однако дальнейшее уменьшение размеров ячейки в данной работе сопряжено с трудностями в виде кратного увеличения времени счета. Решение проблемы требует гораздо больших вычислительных ресурсов. Тем не менее показано, что расчет на основе модели некогерентного перемагничивания демонстрирует лучшее сходство с экспериментальными данными.

Работа поддержана Фондом развития теоретической физики и математики “БАЗИС”.