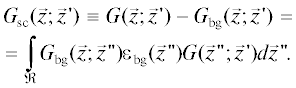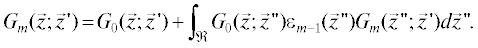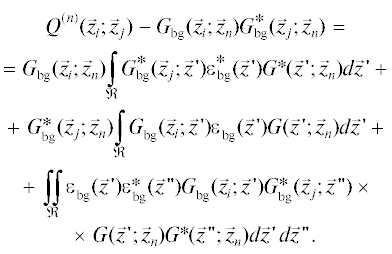Известия РАН. Серия физическая, 2023, T. 87, № 1, стр. 79-83

Методы определения внутренней структуры и параметров упругой неоднородной среды по данным измерений акустического поля представляют большой интерес. “Классическая” постановка задачи акустической томографии состоит в облучении исследуемого объекта заданными полями с разных ракурсов и в приеме рассеянных сигналов с последующей их обработкой. Таким методам посвящена обширная литература, например, [1‒4]. В последнее время получили развитие подходы, в которых акустическое поле создается естественными или антропогенными источниками шумового типа. Например, в гидроакустике [5, 6] такие источники могут быть связаны с судоходством или с естественными шумами моря; в геоакустике [7] – с микросейсмами; в медицинской термотомографии [3, 8] – с тепловым акустическим шумом среды и полями дополнительной “подсветки”. При этом алгоритмы обработки регистрируемых шумовых сигналов используют в качестве входных данных статистические характеристики этих сигналов, например, матрицу когерентности, в отличие от алгоритмов “классической” томографии, обычно основанных на обработке фазы и амплитуды.

В настоящей работе предлагается метод корреляционной обработки сигналов в томографической схеме с использованием шумовых зондирующих сигналов. Пусть исследуемая неоднородность занимает конечную область пространства $\Re ,$ вне которой находится однородная непоглощающая среда со скоростью звука ${{c}_{0}}.$ Внутри $\Re $ фазовая скорость звука и амплитудный коэффициент поглощения равны $с(\vec {z})$ и $\alpha (\vec {z}),$ соответственно. Кроме этого, внутри $\Re $ присутствуют неизвестные некоррелированные случайные источники поля $F(\vec {z}).$

Томографическая схема содержит $N$ элементов малого размера, расположенных в точках ${{\vec {z}}_{i}} \notin \Re .$ Каждый из элементов последовательно выступает в роли источника сигнала, в то время как остальные – в роли приемников. Это обеспечивает $N$ ракурсов томографирования. Еще один (нулевой) “ракурс” реализуется, когда ни один из элементов не излучает, и все они регистрируют только поля источников $F(\vec {z}).$ При заданной геометрии возможны два режима работы такой томографической схемы. Первый режим, монохроматический, предполагает использование гармонических зондирующих сигналов с частотой $\omega .$ На всех приемниках регистрируется поле акустического давления $p_{{}}^{{(n)}}(\vec {z})$ при каждом $n$-м ракурсе излучения. Во втором режиме, шумовом, излучаются случайные узкополосные сигналы со средней частотой ω, и регистрируются значения функции когерентности поля ${{\Gamma }^{{(n)}}}({{\vec {z}}_{i}};{{\vec {z}}_{j}}) = \left\langle {{{p}^{{(n)}}}({{{\vec {z}}}_{i}})\left\{ {{{p}^{{(n)}}}({{{\vec {z}}}_{j}})} \right\}{\text{*}}} \right\rangle $ для каждой пары приемников $(i;j).$ Здесь символ $\left\langle \ldots \right\rangle $ означает усреднение по реализациям, а звездочкой обозначено комплексное сопряжение. Временнáя зависимость полей в каждом из режимов выбирается в виде $\sim {\kern 1pt} \exp ( - i\omega t)$ и для краткости здесь и далее опускается.

Для описания волновых процессов в среде вводится запаздывающая функция Грина $G(\vec {z};\vec {z}{\kern 1pt} ').$ Она удовлетворяет условию излучения Зоммерфельда на бесконечности и уравнению Гельмгольца

где ${{k}^{2}}(\vec {z}) = {{{{\omega }^{2}}} \mathord{\left/ {\vphantom {{{{\omega }^{2}}} {{{c}^{2}}(\vec {z})}}} \right. \kern-0em} {{{c}^{2}}(\vec {z})}} + {{2i\omega \alpha (\vec {z})} \mathord{\left/ {\vphantom {{2i\omega \alpha (\vec {z})} {c(\vec {z})}}} \right. \kern-0em} {c(\vec {z})}}$ – квадрат волнового числа $k(\vec {z}).$ При $n$-м ракурсе излучения источники поля представлены суммой $F(\vec {z}) + {{F}^{{(n)}}}\delta ({{\vec {z}}_{n}} - \vec {z})$ неизвестных случайных источников $F(\vec {z})$ и текущего зондирующего источника ${{F}^{{(n)}}}\delta ({{\vec {z}}_{n}} - \vec {z}).$ Для нулевого ракурса при этом полагается ${{F}^{{(0)}}} = 0.$ Тогда поле акустического давления в каждом из случаев равно

Функция когерентности принимает вид

где учтено, что все источники некоррелированные, и введены их плотность мощности и мощность, соответственно: $\left\langle {F(\vec {z})F{\text{*}}(\vec {z}{\kern 1pt} ')} \right\rangle = I(\vec {z})\delta (\vec {z} - \vec {z}{\kern 1pt} ')$ и $\left\langle {{{F}^{{(n)}}}\left\{ {{{F}^{{(n)\,}}}} \right\}{\text{*}}} \right\rangle = {{I}^{{(n)}}}.$

В монохроматическом режиме работы первое слагаемое в (2) является помехой, а второе – полезным сигналом. Поэтому целесообразно выбирать частоту $\omega $ и мощность ${{I}^{{(n)}}}$ так, чтобы второе слагаемое преобладало. Тогда при известных амплитудах ${{F}^{{(n)}}}$ вычисляются значения $G({{\vec {z}}_{i}};{{\vec {z}}_{n}})$ функций Грина, где $i = \overline {1,N} ;$ $i \ne n.$ В шумовом режиме работы при известных мощностях ${{I}^{{(n)}}}$ вычисляются значения

где $i,j = \overline {1,N} ;$ $i,j \ne n.$ Величины $G({{\vec {z}}_{i}};{{\vec {z}}_{n}})$ и ${{Q}^{{(n)}}}({{\vec {z}}_{i}};{{\vec {z}}_{j}})$ не зависят от источников $F(\vec {z})$ и служат входными данными для одного из возможных алгоритмов решения обратной задачи рассеяния. В рамках этой задачи определяется $k(\vec {z})$, а значит, и функция Грина $G(\vec {z};\vec {z}{\kern 1pt} ')$ для всех значений своих аргументов. Восстановление $F(\vec {z})$ при известной функции Грина $G(\vec {z};\vec {z}{\kern 1pt} ')$ – обратная задача излучения, которая является некорректной, и ее решение не единственно [1–3]. Эта задача не рассматривается в настоящей работе.

Если предположить, что область ℜ заполнена фоновой средой с известным волновым числом ${{k}_{{{\text{bg}}}}}(\vec {z})$ (нижний индекс “bg” – сокращение от “background”, т.е. “фоновый”), то акустические поля будут определяться запаздывающей функцией Грина ${{G}_{{{\text{bg}}}}}(\vec {z};\vec {z}{\kern 1pt} ')$ для этой среды. Такая функция Грина удовлетворяет уравнению (1), в котором следует положить ${{k}_{{{\text{bg}}}}}(\vec {z})$ вместо $k(\vec {z}).$ Для описания различия между исследуемой средой и фоновой средой вводится функция рассеивателя ${{\varepsilon }_{{{\text{bg}}}}}(\vec {z}) = k_{{{\text{bg}}}}^{2}(\vec {z}) - {{k}^{2}}(\vec {z}).$ Тогда для функций Грина этих двух сред справедливо уравнение Липпмана–Швингера [1–3]:

Здесь ${{G}_{{{\text{sc}}}}}(\vec {z};\vec {z}{\kern 1pt} ')$ – функция, определяющая рассеянное поле. В частном случае, когда фоновая среда однородная и занимает все пространство, т.е. ${{k}_{{{\text{bg}}}}}(\vec {z}) = {{k}_{0}} \equiv {\omega \mathord{\left/ {\vphantom {\omega {{{c}_{0}}}}} \right. \kern-0em} {{{c}_{0}}}},$ ее функция Грина известна аналитически и равна ${{G}_{{{\text{bg}}}}}(\vec {z};\vec {z}{\kern 1pt} ') = {{G}_{0}}(\vec {z};\vec {z}{\kern 1pt} ').$ Для функции рассеивателя, вычисляемой относительно такой среды, вводится обозначение без нижнего индекса “bg”: $\varepsilon (\vec {z}) = k_{0}^{2} - {{k}^{2}}(\vec {z}).$

Решение уравнение (4) относительно ${{\varepsilon }_{{{\text{bg}}}}}(\vec {z})$ – трудная задача, поскольку в правую его часть наряду с неизвестной функцией ${{\varepsilon }_{{{\text{bg}}}}}(\vec {z})$ входит неизвестная функция Грина неоднородной среды $G(\vec {z};\vec {z}{\kern 1pt} ').$ Для слабых рассеивателей (для них везде выполнено ${{G}_{{{\text{sc}}}}}(\vec {z};\vec {z}{\kern 1pt} ') \ll {{G}_{{{\text{bg}}}}}(\vec {z};\vec {z}{\kern 1pt} ')$) в правой части (4) можно заменить $G(\vec {z};\vec {z}{\kern 1pt} ')$ на ${{G}_{{{\text{bg}}}}}(\vec {z};\vec {z}{\kern 1pt} ')$ (борновское приближение). Тогда это уравнение упрощается и может быть решено численно путем дискретизации и сведения его к системе линейных уравнений. Для рассеивателей средней силы (для них везде выполнено ${{G}_{{{\text{sc}}}}}(\vec {z};\vec {z}{\kern 1pt} ') < {{G}_{{{\text{bg}}}}}(\vec {z};\vec {z}{\kern 1pt} ')$) борновского приближения недостаточно, но можно применить итерационную процедуру [1, 4]. Она состоит в следующем:

1. На нулевой итерации ($m = 0$) фоновая среда полагается однородной с волновым числом, равным ${{k}_{0}},$ и задается априорная оценка рассеивателя ${{\varepsilon }_{0}}(\vec {z}) = k_{0}^{2}(\vec {z}) - k_{{{\text{apriori}}}}^{2}(\vec {z}).$ Если такой информации нет, то полагается ${{\varepsilon }_{0}}(\vec {z}) = 0.$

2. Пусть в результате предыдущей, $(m - 1)$-й, итерации была получена оценка рассеивателя ${{\varepsilon }_{{m - 1}}}(\vec {z}).$ Тогда на первом шаге $m$-й итерации решается прямая задача рассеяния и находится функция Грина среды ${{G}_{m}}(\vec {z};\vec {z}{\kern 1pt} ').$ С этой целью можно, например, воспользоваться уравнением (4), где произведены замены функций Грина $G(\vec {z};\vec {z}{\kern 1pt} ')$ на ${{G}_{m}}(\vec {z};\vec {z}{\kern 1pt} ');$ ${{G}_{{{\text{bg}}}}}(\vec {z};\vec {z}{\kern 1pt} ')$ на ${{G}_{0}}(\vec {z};\vec {z}{\kern 1pt} ')$ и функции 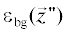на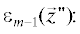

3. На втором шаге $m$-й итерации среда, заданная функцией рассеивателя ${{\varepsilon }_{{m - 1}}}(\vec {z}),$ считается фоновой. Тогда уравнение (4) в борновском приближении имеет вид

где вместо произвольных точек $\vec {z}$ и $\vec {z}{\kern 1pt} '$ указаны координаты ${{\vec {z}}_{i}}$ и ${{\vec {z}}_{n}}$ элементов томографической схемы. Значения функции Грина $G({{\vec {z}}_{i}};{{\vec {z}}_{n}})$ считаются заданными, поэтому такое уравнение решается относительно ${{\varepsilon }_{{{\text{bg}}}}}(\vec {z}),$ и делается новая оценка ${{\varepsilon }_{m}}(\vec {z}) = {{\varepsilon }_{{m - 1}}}(\vec {z}) + {{\varepsilon }_{{{\text{bg}}}}}(\vec {z}).$

Наконец, если рассеиватель сильный (в некоторых точках ${{G}_{{{\text{sc}}}}}(\vec {z};\vec {z}{\kern 1pt} ') > {{G}_{0}}(\vec {z};\vec {z}{\kern 1pt} ')$), его восстановление представляет наибольшую сложность, и описанная процедура может не приводить к верному решению задачи.

В шумовом режиме работы величины $G({{\vec {z}}_{i}};{{\vec {z}}_{n}})$ неизвестны. Поэтому нужно модифицировать третий шаг описанного итерационного алгоритма. Для этого выполняется подстановка (4) в (3) и получается

Это уравнение сходно с уравнением Липпмана–Швингера (4), но содержит квадратичный относительно ${{\varepsilon }_{{{\text{bg}}}}}(\vec {z})$ член в правой части. Считая ${{\varepsilon }_{{{\text{bg}}}}}(\vec {z})$ малым и ограничиваясь в правой части только слагаемыми, линейными по ${{\varepsilon }_{{{\text{bg}}}}}(\vec {z}),$ можно записать

Уравнение (6) можно использовать вместо уравнения (5) в модифицированном алгоритме, который пригоден для обработки данных в шумовом режиме.

В качестве иллюстрации, проводилось численное моделирование процесса восстановления для неоднородностей скорости звука в шумовом и, для сравнения, в монохроматическом режимах. Томографическая схема состояла из $N = 20$ элементов, которые располагались вокруг неоднородности равномерно по окружности радиусом $R = 5{{\lambda }_{0}},$ где ${{\lambda }_{0}} = {{2\pi {{с}_{0}}} \mathord{\left/ {\vphantom {{2\pi {{с}_{0}}} \omega }} \right. \kern-0em} \omega }$ – длина волны в фоновой среде. Шаг дискретизации при моделировании полагался равным ${{{{\lambda }_{0}}} \mathord{\left/ {\vphantom {{{{\lambda }_{0}}} 8}} \right. \kern-0em} 8}.$

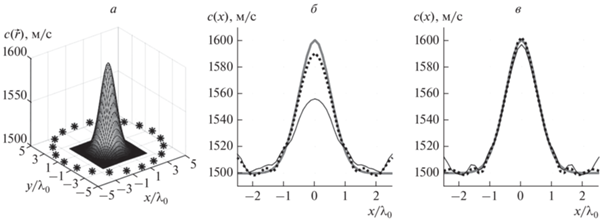
В первом случае моделируемая двумерная неоднородность задавалась функцией $c(\vec {r}),$ которая представлена на рис. 1а и имеет радиально-симметричную гауссову форму. Для такой неоднородности численно рассчитанная величина $\left| {{{{{G}_{{{\text{sc}}}}}(\vec {z};\vec {z}{\kern 1pt} ')} \mathord{\left/ {\vphantom {{{{G}_{{{\text{sc}}}}}(\vec {z};\vec {z}{\kern 1pt} ')} {{{G}_{{{\text{bg}}}}}(\vec {z};\vec {z}{\kern 1pt} ')}}} \right. \kern-0em} {{{G}_{{{\text{bg}}}}}(\vec {z};\vec {z}{\kern 1pt} ')}}} \right|$ достигает максимального значения $ \approx {\kern 1pt} 0.65 < 1,$ и поэтому она относится к классу рассеивателей средней силы. На рис. 1б и 1в представлены результаты ее восстановления в каждом из режимов после $m = 10$ и $m = 100$ итераций, соответственно. Можно видеть, что при большом $m$ итерационный процесс в итоге сходится к искомой зависимости в каждом из случаев, но скорость сходимости для шумового режима значительно выше.

Во втором случае моделируемая зависимость $c(\vec {r})$ представлена на рис. 2а. Такая неоднородность относится к классу сложных для восстановления сильных рассеивателей, поскольку для нее рассчитанная величина $\left| {{{{{G}_{{{\text{sc}}}}}(\vec {z};\vec {z}{\kern 1pt} ')} \mathord{\left/ {\vphantom {{{{G}_{{{\text{sc}}}}}(\vec {z};\vec {z}{\kern 1pt} ')} {{{G}_{{{\text{bg}}}}}(\vec {z};\vec {z}{\kern 1pt} ')}}} \right. \kern-0em} {{{G}_{{{\text{bg}}}}}(\vec {z};\vec {z}{\kern 1pt} ')}}} \right|$ превышает $ \approx {\kern 1pt} 1.9 > 1.$ На рис. 2б представлены результаты восстановления, полученные после $m = 5000$ итераций в каждом из режимов, а на рис. 2в изображены зависимости относительной погрешности восстановления $\delta (m),$ которые вычисляются для каждой $m$-й итерации как $\delta (m) = {{\left\| {{{\varepsilon }_{m}}(\vec {r}) - \varepsilon (\vec {r})} \right\|} \mathord{\left/ {\vphantom {{\left\| {{{\varepsilon }_{m}}(\vec {r}) - \varepsilon (\vec {r})} \right\|} {\left\| {\varepsilon (\vec {r})} \right\|}}} \right. \kern-0em} {\left\| {\varepsilon (\vec {r})} \right\|}}.$

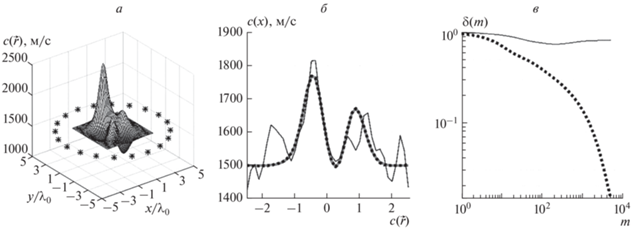
Можно видеть, что, результат, полученный при обработке данных в шумовом режиме, сходится к моделируемой зависимости, и $\delta (m)$ стремится к нулю с увеличением $m$ (рис. 2б и 2в). В монохроматическом режиме результат итераций сильно отличается от моделируемой зависимости. Однако проверка показывает, что он удовлетворяет уравнению (4). Это иллюстрирует неединственность решения уравнения (4) при небольшом $N.$ Можно предположить, что нахождение истинного решения при шумовом режиме обусловлено бóльшим объемом данных, который равен в этом случае${{{{N}^{2}}(N - 1)} \mathord{\left/ {\vphantom {{{{N}^{2}}(N - 1)} {2\sim {{N}^{3}}}}} \right. \kern-0em} {2\sim {{N}^{3}}}},$ в то время как при монохроматическом режиме – только ${{N(N - 1)} \mathord{\left/ {\vphantom {{N(N - 1)} {2\sim {{N}^{2}}}}} \right. \kern-0em} {2\sim {{N}^{2}}}}.$ Потенциально данное обстоятельство может дать шумовому режиму преимущество. Однако этот вопрос требует отдельного изучения, особенно в отношении наличия линейных зависимостей между компонентами ${{Q}^{{(n)}}}({{\vec {z}}_{i}};{{\vec {z}}_{j}}).$

При моделировании исследовалось влияние помех в исходных данных. Эти помехи вводились в виде нормально распределенной случайной добавки к функциям Грина $G({{\vec {z}}_{i}};{{\vec {z}}_{n}})$ со стандартным отклонением в 1–2% от среднего значения $G({{\vec {z}}_{i}};{{\vec {z}}_{n}}),$ вычисленного по всем элементам антенной решетки. Такая добавка существенно ухудшает результат восстановления, как в монохроматическом, так и в шумовом режимах, что является проявлением неустойчивости решения обратной задачи при восстановлении сильных рассеивателей. С учетом наличия помехи результат восстановления в шумовом режиме по-прежнему оказался лучше, чем результат восстановления в монохроматическом режиме.

Исследование выполнено при финансовой поддержке Российского фонда фундаментальных исследований и Правительства Москвы (проект № 21-32-70003).