Известия РАН. Серия физическая, 2023, T. 87, № 1, стр. 141-147
Математическая модель глобального ионосферного электрического поля, создаваемого грозами
В. В. Денисенко 1, 2, *, М. Дж. Райкрофт 3, Р. Дж. Харрисон 4
1 Институт вычислительного моделирования Сибирского отделения Российской академии наук –
обособленное подразделение Федерального государственного бюджетного научного учреждения
Федеральный исследовательский центр “Красноярский научный центр Сибирского отделения
Российской академии наук”
Красноярск, Россия
2 Калининградский филиал Федерального государственного бюджетного учреждения науки
“Институт земного магнетизма ионосферы и распространения радиоволн имени Н.В. Пушкова
Российской академии наук”
Калининград, Россия
3 Цезарь консалтинг
Кембридж, Великобритания
4 Университет Рэдинга, Факультет метеорологии
Рэдинг, Великобритания
* E-mail: denisen@icm.krasn.ru
Поступила в редакцию 29.08.2022
После доработки 16.09.2022
Принята к публикации 26.09.2022
- EDN: JVCZXA
- DOI: 10.31857/S0367676522700260
Аннотация
Данные об атмосферном электрическом поле хорошей погоды, полученные во время круиза VII миссии Карнеги, представлены в виде диаграммы в координатах универсальное время и месяцы, чтобы показать как суточные, так и сезонные вариации. Максимум поля наблюдается в момент времени около 18 UT в январе. Для этого момента времени создана модель ионосферной части глобальной электрической цепи, связанной с грозами. Построенная токовая система состоит из среднеширотной части и экваториальных электроструй, дневных и ночных, направленных на запад и восток, с силой тока до 120 А.
ВВЕДЕНИЕ
Существует несколько физических процессов, создающих ионосферное электрическое поле. Токи, создаваемые всеми этими генераторами, называются глобальной электрической цепью (ГЭЦ) [1]. Здесь мы изучаем только ту часть ГЭЦ, которая генерируется токами, поднимающимися из атмосферы. Хотя связанная с грозами часть ГЭЦ анализируется в многочисленных статьях, ее ионосферная часть все еще недостаточно изучена. Цель настоящей статьи – представить нашу модель электрических полей и токов, являющихся ионосферным проявлением части ГЭЦ, связанной с грозами. Первые результаты нашего моделирования были представлены в [2] с исправлением опечаток в [3]. Важной особенностью глобальных ионосферных токов является их концентрация вблизи геомагнитного экватора. Для ГЭЦ это было показано в [4]. Здесь мы кратко опишем модель [2] и представим новые результаты, полученные с использованием модели глобального распределения гроз [5], полученной на основе данных Всемирной наземной сети определения местоположения молнии (WWLLN) [6].
МОДЕЛЬ ГЛОБАЛЬНОГО ИОНОСФЕРНОГО ПРОВОДНИКА
Наша модель глобального проводника, состоящего из атмосферы, ионосферы, магнитосферы и литосферы, построенная для описания ГЭЦ с допустимыми упрощениями, детально описана в статье [2]. Мы рассматриваем атмосферу, ионосферу и магнитосферу как единый проводник, ограниченный снизу идеальным проводником, включающим океаны и сушу. Основными уравнениями для стационарного электрического поля $\vec {E}$ и плотности тока $\vec {j}$ являются закон Фарадея, закон сохранения заряда и закон Ома с тензором проводимости $\hat {\sigma }{\text{.}}$ Вводится электрический потенциал $V,$ для которого система уравнений сводится к уравнению электропроводности
Мы используем сферические геомагнитные координаты ${{\theta }_{m}},{{\varphi }_{m}},$ геомагнитную широту ${{\lambda }_{m}} = \frac{\pi }{2} - {{\theta }_{m}}$ и высоту над средним уровнем моря $h.$ Проводимость ионосферы Земли представляет собой гиротропный тензор, одна ось которого определяется направлением магнитной индукции $\vec {B}.$ Мы используем компоненты векторов, параллельных и нормальных к $\vec {B},$ которые отмечаем символами $\parallel $ и $ \bot ,$ при этом $B = \vec {B}.$ Тогда закон Ома имеет вид(2)
$~{{\vec {j}}_{\parallel }} = {{{{\sigma }}}_{\parallel }}{{\vec {E}}_{\parallel }},\,\,\,\,~{{\vec {j}}_{ \bot }} = {{{{\sigma }}}_{P}}{{\vec {E}}_{ \bot }} - {{{{{{\sigma }}}_{H}}\left[ {{{{\vec {E}}}_{ \bot }} \times \vec {B}} \right]} \mathord{\left/ {\vphantom {{{{{{\sigma }}}_{H}}\left[ {{{{\vec {E}}}_{ \bot }} \times \vec {B}} \right]} B}} \right. \kern-0em} B},$(3)
${{\vec {J}}_{ \bot }} = \left( {\begin{array}{*{20}{c}} {{{{{\Sigma }}}_{P}}}&{{{{{\Sigma }}}_{H}}} \\ { - {{{{\Sigma }}}_{H}}}&{{{{{\Sigma }}}_{P}}} \end{array}} \right){{\vec {E}}_{ \bot }},$Закон сохранения заряда (1) в двумерной модели выполняется в проинтегрированном вдоль магнитной силовой линии виде. Для численного решения задачи полезно построить некоторую опорную область на плоскости с декартовыми координатами $x,y,$ точки которой идентифицируют все рассматриваемые силовые линии магнитного поля. В приближении дипольного геомагнитного поля двумерное уравнение электропроводности в такой области может быть записано в виде
(4)
$\begin{gathered} - \frac{\partial }{{\partial x}}\left( {{{\Sigma }_{P}}\frac{{\partial V}}{{\partial x}} + {{\Sigma }_{H}}\frac{{\partial V}}{{\partial y}}} \right) - \\ - \,\,\frac{\partial }{{\partial y}}\left( { - {{\Sigma }_{H}}\frac{{\partial V}}{{\partial x}} + {{\Sigma }_{P}}\frac{{\partial V}}{{\partial y}}} \right) = Q, \\ \end{gathered} $Рассмотрение проводников в магнитосфере [8] показывает, что авроральные зоны эквивалентны почти идеальным проводникам, поскольку они соединены параллельно как между собой, так и с хорошими магнитосферными проводниками. Мы считаем их идеальным проводником с нулевым электрическим потенциалом $V = 0,$ что дает граничное условие Дирихле. Вторую границу проводника образуют самые нижние магнитные силовые линии, рассматриваемые как ионосферные. На них задан ток из атмосферы. Получается смешанная краевая задача для дифференциального уравнения в частных производных (4), которое является уравнением эллиптического типа. Она имеет единственное решение [9].
МОДЕЛЬ ГЛОБАЛЬНОГО ГРОЗОВОГО ГЕНЕРАТОРА
Генератором ГЭЦ является совокупность всех гроз на Земле [10]. Их единым параметром является суммарный электрический ток в ионосферу. К сожалению, нет способа измерить этот ток. Поэтому приходится использовать процедуру [5], которая кратко описана ниже.
Сначала, по диаграмме Карнеги, описанной в следующем разделе, мы берем напряженность электрического поля хорошей погоды вблизи поверхности океана для исследуемого момента времени. Это поле E0 и одномерная модель атмосферной проводимости дают разность потенциалов между поверхностью Земли и ионосферой ${{U}_{0}}.$ Затем мы получаем токи хорошей погоды на всем земном шаре и путем интегрирования получаем суммарный ток хорошей погоды, текущий из ионосферы на землю ${{I}_{0}}.$ Параметр $R = {{{{U}_{0}}} \mathord{\left/ {\vphantom {{{{U}_{0}}} {{{I}_{0}}}}} \right. \kern-0em} {{{I}_{0}}}}$ представляет собой полное сопротивление атмосферы.
Сохранение заряда в стационарном случае означает, что такой же ток течет из грозовых областей в ионосферу Istorm = I0. Поскольку распределение грозового тока по Земле неизвестно, мы заменяем его глобальным распределением молниевой активности, предполагая, что ток в ионосферу и количество вспышек молнии линейно пропорциональны некоторому скрытому параметру, который характеризует грозовую активность. Мы используем модель [5] глобального распределения грозовой активности, построенную на основе данных Всемирной наземной сети определения местоположения молнии (WWLLN) [6].
ДИАГРАММА КРУИЗА VII МИССИИ КАРНЕГИ
В статье [11] построены аппроксимации кривых Карнеги, т.е. зависимостей E0 от UT, полученных для разных сезонов во время круиза VII. Аппроксимирующие функции были выбраны в виде
(5)
${{E}_{0}}\left( t \right) = {{A}_{0}} + \sum\limits_{n = 1}^4 {{{A}_{n}}\sin \left( {nt~15^\circ + {{\varphi }_{n}}} \right)} ,$Сезонную зависимость удобно анализировать, если от этих четырех функций времени ${{E}_{0}}\left( t \right)$ перейти к единой функции ${{E}_{0}}\left( {m,t} \right),$ где параметр $m$ описывает время в течение года, например, в месяцах. Параметр $m$ мы считаем не дискретным, а непрерывно меняющимся в интервале $0 < m < 12.$ Все функции считаем периодически продолженными вне этого интервала.
Для определения ${{E}_{0}}\left( {m,t} \right)$ следует определить зависимость параметров (5) от $m,$ например, ${{A}_{0}}\left( m \right).$ Естественно предполагать, что приведенные в [11] значения параметров (5) получены как средние для этих сезонов, например:
(6)
$\begin{gathered} A_{0}^{{{\text{NDJ}}}} = \frac{1}{3}\int\limits_{ - 2}^1 {{{A}_{0}}\left( m \right)~dm} ~,\,\,\,\,A_{0}^{{{\text{FMA}}}} = \frac{1}{3}\int\limits_1^4 {{{A}_{0}}\left( m \right)~dm} ~, \\ A_{0}^{{{\text{MJJ}}}} = \frac{1}{3}~\int_4^7 {{{A}_{0}}\left( m \right)~dm} ,\,\,\,\,A_{0}^{{{\text{ASO}}}} = \frac{1}{3}~\int\limits_7^{10} {{{A}_{0}}\left( m \right)~dm} . \\ \end{gathered} $(7)
$\begin{gathered} {{A}_{0}}\left( m \right) = a + b\cos \left( {{{2\pi \left( {m - 0.5} \right)} \mathord{\left/ {\vphantom {{2\pi \left( {m - 0.5} \right)} {12}}} \right. \kern-0em} {12}}} \right) + \\ + \,\,c\sin \left( {{{2\pi \left( {m - 0.5} \right)} \mathord{\left/ {\vphantom {{2\pi \left( {m - 0.5} \right)} {12}}} \right. \kern-0em} {12}}} \right) + \\ + \,\,e\cos \left( {{{4\pi \left( {m - 0.5} \right)} \mathord{\left/ {\vphantom {{4\pi \left( {m - 0.5} \right)} {12}}} \right. \kern-0em} {12}}} \right). \\ \end{gathered} $Сдвиг на полмесяца соответствует сдвигу в усреднениях (6) и позволяет не включать в (7) еще один член $\sin \left( {{{4\pi \left( {m - 0.5} \right)} \mathord{\left/ {\vphantom {{4\pi \left( {m - 0.5} \right)} {12}}} \right. \kern-0em} {12}}} \right),$ поскольку его средние значения по всем четырем интервалам (6) равны нулю. Средние значения функции (7) по каждому интервалу несложно вычислить. Подставив их в уравнения (6), получаем четыре линейных алгебраических уравнения для четырех неизвестных $a,b,c,e.$ Их решением являются
(8)
$\begin{gathered} a = {{\left( {A_{0}^{{{\text{NDJ}}}} + A_{0}^{{{\text{FMA}}}} + A_{0}^{{{\text{MJJ}}}} + A_{0}^{{{\text{ASO}}}}} \right)} \mathord{\left/ {\vphantom {{\left( {A_{0}^{{{\text{NDJ}}}} + A_{0}^{{{\text{FMA}}}} + A_{0}^{{{\text{MJJ}}}} + A_{0}^{{{\text{ASO}}}}} \right)} 4}} \right. \kern-0em} 4}, \\ ~b = {{\left( {A_{0}^{{{\text{NDJ}}}} - A_{0}^{{{\text{MJJ}}}}} \right)\pi } \mathord{\left/ {\vphantom {{\left( {A_{0}^{{{\text{NDJ}}}} - A_{0}^{{{\text{MJJ}}}}} \right)\pi } {\left( {4\sqrt 2 } \right)}}} \right. \kern-0em} {\left( {4\sqrt 2 } \right)}}, \\ c = {{\left( {A_{0}^{{{\text{FMA}}}} - A_{0}^{{{\text{ASO}}}}} \right)\pi } \mathord{\left/ {\vphantom {{\left( {A_{0}^{{{\text{FMA}}}} - A_{0}^{{{\text{ASO}}}}} \right)\pi } {\left( {4\sqrt 2 } \right)}}} \right. \kern-0em} {\left( {4\sqrt 2 } \right)}}, \\ e = {{\left( {A_{0}^{{{\text{NDJ}}}} - A_{0}^{{{\text{FMA}}}} + A_{0}^{{{\text{MJJ}}}} - A_{0}^{{{\text{ASO}}}}} \right)\pi } \mathord{\left/ {\vphantom {{\left( {A_{0}^{{{\text{NDJ}}}} - A_{0}^{{{\text{FMA}}}} + A_{0}^{{{\text{MJJ}}}} - A_{0}^{{{\text{ASO}}}}} \right)\pi } {16}}} \right. \kern-0em} {16}}. \\ \end{gathered} $Аналогично вычисляем коэффициенты полиномов вида (7) для остальных восьми функций$.$ Подставив полученные девять функций ${{A}_{0}}\left( m \right),~ \ldots ,{{\varphi }_{4}}\left( m \right)$ в представление (5), получаем искомую функцию ${{E}_{0}}\left( {m,t} \right).$ Ее линии уровня показаны на рис. 1. По построению, ее усреднение за три месяца дает кривую Карнеги для этого периода. Рисунок 1 можно назвать диаграммой Карнеги VII. Она дает наглядное представление не только UT вариаций, как кривая Карнеги, но и вариации в течение года.
Рис. 1.
Вертикальное электрическое поле ${{E}_{0}}$ над поверхностью океана, полученное из данных VII круиза Карнеги [11]. Линии ${{E}_{0}} = {\text{const}}$ в зависимости от времени (UT) и месяца года построены с интервалом 10 В ⋅ м–1. Штриховые линии соответствуют значениям ${{E}_{0}} \leqslant 120$ В ⋅ м–1.
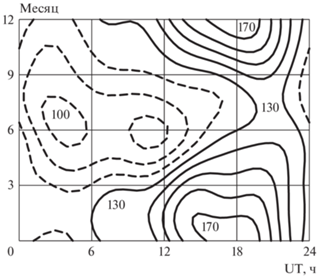
Как видно по рис. 1, напряженность электрического поля в атмосфере над океаном минимальна (около 100 В/м) в период 02–12 UT в июне-июле и максимальна (до 170 В/м) в период 15–19 UT в январе. Последним обстоятельством определяется выбор 1 января для детального представления результатов моделирования в настоящей статье.
РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ
Описанным выше способом мы получили глобальное распределение грозовых токов в ионосферу для первого дня года, когда диаграмма Карнеги на рис. 1 показывает абсолютный максимум ${{E}_{0}} = 177$ В ⋅ м–1 в момент времени 18 UT. Затем мы добавили токи хорошей погоды, которые имеют противоположное направление, ${{J}_{{atm}}} < 0.$ Жирные контуры на рис. 2 выделяют грозовые области, в которых ${{J}_{{atm}}} > 0.$
Рис. 2.
Глобальное распределение проводимости Каулинга ${{{{\Sigma }}}_{C}}$ в 18:00 UT 1 января при низкой солнечной активности. Жирными контурами выделены области грозы, где ${{J}_{{atm}}} > 0.$ Точками показан геомагнитный экватор.
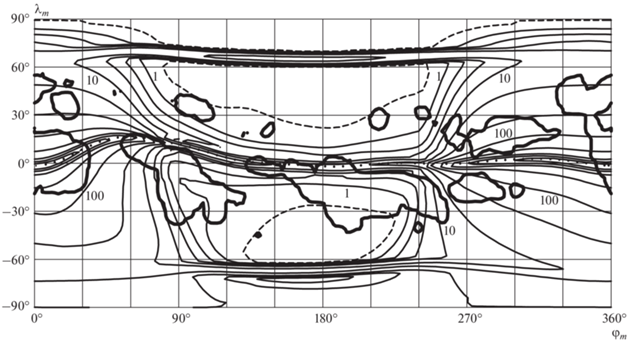
Поскольку диаграмма Карнеги представляет измерения над океаном, мы используем соответствующие значения атмосферных параметров σ(0) = 3.09 · 10–14 См ⋅ м–1 и Σ(λ, $~\varphi $) = 1.09 · 10–17 См в соответствии с моделью [2]. Для ${{E}_{0}} = 177$ В/м получаем ${{U}_{0}} = 502$ кВ и Istorm = 2.79 кА при R = = 180 Ом. Если мы используем параметры, соответствующие суше, σ(0) = 1.54 · 10–14 См ⋅ м–1 и Σ(λ, $~\varphi $) = 0.80 ⋅ 10–17 См для того же ${{E}_{0}},$ мы получим ${{U}_{0}} = 340$ кВ и Istorm = 1.89 кА.
Решение смешанной краевой задачи для уравнения (4) в основной части ионосферы в 18 ч UT представлено на рис. 3. Распределение электрического потенциала $V({{\varphi }_{m}},{{\lambda }_{m}})$ на высоте $h$ = 120 км в ионосфере показано с помощью эквипотенциалей, построенных с интервалом 20 В. Для малых значений $V < 40$ В интервал взят равным 4 В; на рис. 3 они показаны тонкими линиями, штриховые линии соответствуют отрицательным значениям.
Рис. 3.
Распределение электрического потенциала на высоте 120 км в ионосфере. Эквипотенциали построены с интервалом 20 В, дополнительно тонкими линиями для $V < 40$ В с интервалом 4 В. Штриховые линии соответствуют отрицательным значениям потенциала. Жирными контурами выделены области грозы, где ${{J}_{{atm}}} > 0.$ Карта рассчитана для 18:00 UT 1 января при низкой солнечной активности. Точками показан геомагнитный экватор.
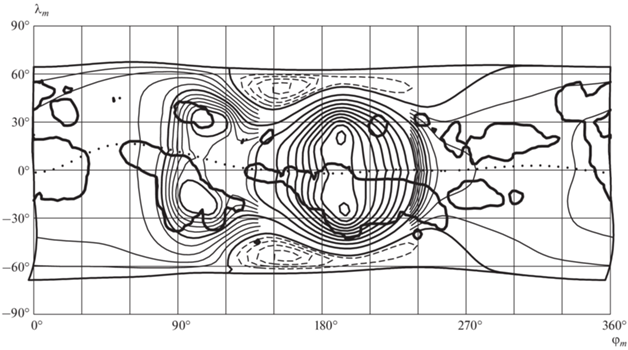
Максимальная разность потенциалов в ионосфере составляет около 220 В. Это на три порядка меньше, чем напряжение между землей и ионосферой, которое в этой модели составляет 502 кВ. Соответствующая напряженность электрического поля также невелика. Его горизонтальная составляющая не превышает 90 мкВ ⋅ м–1. Тем не менее, именно это небольшое электрическое поле обеспечивает распределение ионосферных токов, которые замыкают токи из атмосферы и в атмосферу.
Положение области максимального значения ионосферного потенциала $V = 205$ В соответствует большому грозовому генератору над Северо-Западной Австралией. Видны лишь незначительные возрастания потенциала над другими грозовыми областями из-за высокой дневной ионосферной проводимости (вблизи экватора местный полдень наступает при ${{\varphi }_{m}}$ = 340°). Рисунок 3 демонстрирует естественное свойство напряженности электрического поля: она намного больше в ночной ионосфере, поскольку там мала проводимость.
Теперь обратим внимание на окрестность геомагнитного экватора, на котором магнитное поле $\vec {B}$ по определению имеет нулевую вертикальную составляющую. Геомагнитный экватор показан точками на рис. 2 и 3. Эквипотенциали примерно перпендикулярны геомагнитному экватору. Строго говоря, они параллельны магнитному полю $\vec {B},$ а направление $\vec {B}$ точно перпендикулярно геомагнитному экватору только для дипольного поля. Мы видим изменение потенциала вдоль геомагнитного экватора на рис. 3, что означает ненулевую составляющую ${{E}_{{{\varphi }}}}$ напряженности электрического поля.
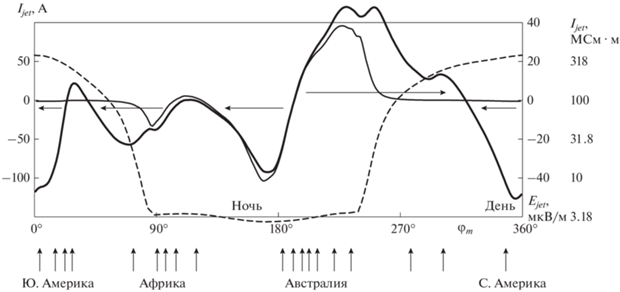
Из-за существенного увеличения проводимости на геомагнитном экваторе ${{E}_{{{\varphi }}}}$ создает экваториальные электроструи [12]. Строго говоря, нам нужна составляющая ${{E}_{{jet}}},$ которая нормальна к магнитному полю и не сильно отличается от Eφ. Это поле незначительно меняется с высотой на силовых линиях магнитного поля, вершины которых находятся ниже 200 км. Как видно на рис. 4, оно не превышает 40 мкВ ⋅ м–1. Ток электроструи Ijet может быть получен численным интегрированием по силовым линиям магнитного поля с вершинами в интервале высот $90 < H < 135$ км [12]. Интегрирование проводимости Каулинга по той же области дает полную проводимость области электроструи ${{A}_{{jet}}}.$ Ток электроструй показан жирной линией на рис. 4. Направления электроструй также показаны горизонтальными стрелками (положительный ток направлен на восток). Вертикальными стрелками отмечены токи, поднимающиеся в ионосферу из основных грозовых областей, каждая стрелка соответствует 100 А в данном секторе. Большая часть этого тока возникает в огромной грозовой области, включающей Северо-Западную Австралию и Юго-Восточную Азию. Именно эта область порождает основную восточную электрострую к востоку от нее (до 120 А) и сильную западную электрострую к западу от нее (до 90 А). Такие направления означают, что заряды, доставляемые в ионосферу из атмосферы, разносятся ионосферными токами, в том числе, этими электроструями.
Рис. 4.
Ток электроструй ${{I}_{{jet}}}\left( {{{\varphi }_{m}}} \right)$ (жирная линия), компонента ${{E}_{{jet}}}\left( {{{\varphi }_{m}}} \right)$ электрического поля (тонкая линия), проводимость области электроструи ${{A}_{{jet}}}\left( {{{\varphi }_{m}}} \right)$ в логарифмическом масштабе (штриховая линия). Горизонтальные стрелки показывают направления экваториальных электроструй в ионосфере. Вертикальные стрелки характеризуют токи, поступающие в ионосферу из грозовых областей; каждая стрелка соответствует 100 А вблизи этого меридиана.
ЗАКЛЮЧЕНИЕ
Создана модель ионосферной части ГЭЦ, связанной с грозами, для январского вечера (18 UT). Эта токовая система содержит четыре экваториальных электроструи, дневные и ночные, направленные на запад и на восток, с токами, достигающими 120 А. Они создают магнитные возмущения на земле, которые, по оценкам, находятся в диапазоне 0.1 нТл. В принципе, эти магнитные возмущения можно было бы измерить на геомагнитном экваторе ночью, когда они не замаскированы сильными электроструями, порождаемыми всеми ионосферными и магнитосферными генераторами.
Данные миссии Карнеги представлены в виде диаграммы в координатах UT и время года, чтобы показать как суточные, так и сезонные вариации. Рисунок 1 построен для VII круиза Карнеги.
Работа выполнена при финансовой поддержке Российского научного фонда (проект № 21-17-00208).
Список литературы
Hays P.B., Roble R.G. // J. Geophys. Res. 1979. V. 84. No. A7. P. 3291.
Denisenko V.V., Rycroft M.J., Harrison R.G. // Surv. Geophys. 2019. V. 40. No. 1. P. 1.
Denisenko V.V., Rycroft M.J., Harrison R.G. // Surv. Geophys. 2019. V. 40. No. 1. P. 37.
Denisenko V.V., Rycroft M.J. // J. Atmos. Terr. Phys. 2021. V. 221. No. 3. Art. № 105704.
Денисенко В.В., Ляхов А.Н. // Солн.-земн. физ. 2021. Т. 7. № 4. С. 111; Denisenko V.V., Lyakhov A.N. // Sol.-Terr. Phys. 2021. V. 7. No. 4. P. 104.
Rodger C.J., Brundell J.B., Dowden R.L., Thomson N.R. // Ann. Geophys. 2004. V. 22. P. 747.
Denisenko V.V., Biernat H.K., Mezentsev A.V. et al. // Ann. Geophys. 2008. V. 26. P. 2111.
http://arxiv.org/abs/1802.07955.
Денисенко В.В. // Сибир. мат. журн. 1994. Т. 35. № 3. С. 554; Denisenko V.V. // Siberian Math. J. 1994. V. 35. No. 3. P. 495.
Мареев Е.А. // УФН. 2010. Т. 180. С. 527; Mareev E.A. // Phys. Usp. 2010. V. 53. No. 5. P. 504.
Harrison R.G. // Surv. Geophys. 2013. V. 34. P. 209.
Richmond A.D. // J. Atmos. Terr. Phys. 1973. V. 3. No. 6. P. 1083.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Серия физическая


