Известия РАН. Серия физическая, 2023, T. 87, № 3, стр. 417-421
Управление режимами распространения спиновой волны в волноводе из железо-иттриевого граната посредством локального лазерного нагрева
В. А. Губанов 1, *, В. В. Кругляк 2, А. В. Садовников 1
1 Федеральное государственное бюджетное образовательное учреждение высшего образования
“Саратовский национальный исследовательский государственный университет имени Н.Г. Чернышевского”
Саратов, Россия
2 Факультет физики и астрономии, Эксетерский университет
Эксетер, Великобритания
* E-mail: vladmeen@gmail.com
Поступила в редакцию 28.09.2022
После доработки 27.10.2022
Принята к публикации 25.11.2022
- EDN: HGRFAB
- DOI: 10.31857/S0367676522700739
Аннотация
Представлены результаты микромагнитного моделирования магнитной структуры на поверхности пленки железо-иттриевого граната (ЖИГ), где создавалась область измененной намагниченности насыщения путем фокусированного лазерного излучения. На основе построенных амплитудно-частотных характеристик прохождения сигнала через магнонную структуру с областью нагрева показана возможность реализации режимов фильтрации спин-волнового сигнала при изменении диаметра нагреваемой области на поверхности ЖИГ.
В настоящий момент отчетливо проявились недостатки существующей компонентной базы систем обработки информационных сигналов, основанных на полупроводниковой электронике. Сложности, ограничивающие рост тактовых частот полупроводниковых микросхем, связаны с повышением тепловыделения за счет увеличения плотности транзисторов как в латеральном направлении отдельно взятого слоя интегральной микросхемы, так и за счет увеличения количества слоев и элементов межсоединений в ультра больших интегральных схемах [1, 2]. Использование магнонов – квантов спиновых волн (СВ) – позволяет в одном модуле устройства совместить узлы генерации, передачи и обработки информационного сигнала, при этом обработки без выделения тепла ввиду отсутствия переноса электрического заряда [3–7].
В последнее время большой интерес представляет интеграция магнонных логических устройств с полупроводниковыми для создания нового класса логически устройств. Первым шагом такой интеграции можно назвать развитие технологий создания ферромагнитных структур на полупроводниковых подложках [8, 9]. В полупроводниковой электронике создаются трехмерные логические устройства, то перспективным является создание комплементарной базы для создания многомерных топологических систем (МТС). МТС создаются из примитивных функциональных блоков с частотными и/или пространственными режимами селекции распространения сигнала и могут лежать в основе парадигмы устройств обработки данных следующего поколения [10]. Материалом, который может быть применим для решения данных задач, могут выступать пленки ЖИГ [11] за счет сверхнизкого затухания спиновых волн, и как следствие, значительно большим значением длины распространения СВ по сравнению с проводящими ферромагнитными маетeриалами, используемыми в магнонике (NiFe, CoFeB, Co) [12].
Свойства СВ в многомерных системах определяются дипольными и обменными взаимодействиями и могут управляться, к примеру, при использовании упругих деформаций [9, 13], лазерного излучения для изменения свойств ферритовых пленок [8] или лазерного излучения для локального лазерного нагрева структуры [14]. Последняя концепция основана на механизме поглощения лазерного излучения и локального нагрева, приводящему к изменению величины намагниченности насыщения и созданию нерегулярного спин-волнового канала в магнонных волноводах. В работе [15] показан эффект управления характеристиками передачи спиновой волны и формы сигнала при быстром нагреве и медленном охлаждении ферромагнитной пленки. Создаваемая область нагрева может иметь разные формы: в виде прямоугольника, треугольника [16] и виде круга [17].
В волноводной системе ферромагнитных волноводов возможно создавать многогодовое распространение спиновых волн в конфигурации Дэймона–Эшбаха (ДЭ) [18]. Раздельное возбуждение мод СВ является сложной задачей, т.к. источником в большинстве случаев является микрополосковая антенна, которая возбуждает всевозможные моды вдоль ширины волновода [19, 20]. Каждая ширинная мода обладает своей дисперсией и, как следствие, они обладают различными частотными диапазонами при одинаковых волновых числах (и наоборот). Для распространения определенной ширинной моды СВ могут использоваться L и T образные волноводы [21, 22], в которых при переходе из разных сегментов структуры могут трансформироваться типы СВ, и таким образом проводить модовую селекцию спиновых волн.
В данной работе показана возможность перестройки при помощи лазерного излучения режима распространения СВ в пленке ЖИГ. Показано, как при изменении величины локального лазерного нагрева и диаметра нагреваемой области, наблюдается трансформация передаточной характеристики СВ и структуре возникает режим непропускания спин-волнового сигнала. Предложенный метод управления изменением коэффициента передачи и фазы спин-волнового сигнала при изменении интенсивности лазерного излучения и диаметра лазерного пятна, сфокусированного на магнонном волноводе, может найти применение для создания устройств магнонной логики.
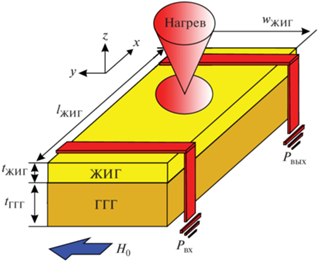
В качестве исследуемой структуры, приведенной на рис. 1, была использована пленка ЖИГ толщиной tЖИГ= 10 мкм, сформированная методом жидкофазной эпитаксии на подложке гадолиний галлиевого граната (ГГГ) толщиной tГГГ= = 500 мкм. При помощи метода лазерного скрайбирования был сформирован волновод шириной wЖИГ = 2 мм и длиной lЖИГ = 6 мм. Структура помещалась во внешнее магнитное поле величиной 1830 Э, ориентированное вдоль оси y. При таких условиях эффективно возбуждались поверхностные магнитостатические волны (ПМСВ) с помощью микрополоскового преобразователя Pвх шириной 30 мкм и принимались выходной микрополосковой антенной Pвых.
На расстоянии в 4.25 мм от левого края волновода формировался центр лазерного пятна, при помощи которого создавалась область с измененной намагниченностью насыщения MS. Для изменения MS. от температуры нагрева T используется следующее соотношение:
(1)
$~{{M}_{{S\left( {x,y} \right)}}} \approx {{M}_{0}} - \beta \left[ {T\left( {x,y} \right) - {{T}_{{RT}}}} \right],$Было проведено микромагнитное моделирование в программе MuMax3 [23], в котором решается уравнение Ландау–Лифшица–Гильберта при помощи метода конечных разностей:
(2)
$\frac{{\partial{ \vec {M}}}}{{\partial t}} = \gamma \left[ {{{{\vec {H}}}_{{eff}}} \cdot \vec {M}} \right] + \frac{\alpha }{{{{M}_{{s\left( {x,y} \right)}}}}}\left[ {\vec {M} \cdot \frac{{\partial{ \vec {M}}}}{{\partial t}}} \right],$Первым этапом было проведено экспериментальное измерение степени нагрева при помощи лазера Excelsior (Spectra Physics) EXLSR-532-200-CDRH с длиной волны 532 нм и мощностью 200 мВт, лазерное пятно которого наводилось на пленку ЖИГ. Полученные результаты лазерного нагрева были использованы для микромагнитного моделирования. По формуле (1) была пересчитана MS в области нагрева пленки ЖИГ. В дальнейшем вводится безразмерный параметр
(3)
$\delta = {{{{M}_{S}}} \mathord{\left/ {\vphantom {{{{M}_{S}}} {{{M}_{{RT}}}}}} \right. \kern-0em} {{{M}_{{RT}}}}}{\kern 1pt} ,$На рис. 2 представлены передаточные характеристики, полученные на выходной микрополосковой антенне PВЫХ для разных диаметров лазерного пятна: d = 250 мкм (синяя линия), d = 500 мкм (красная линия), d = 1000 мкм (коричневая линия) и d =1500 мкм (зеленая линия) при параметре δ = 0.9. Из рис. 2а было выделено два частотных диапазона: 7.2–7.3 ГГц (рис. 2б) и 7.3–7.36 ГГц (рис. 2в). Также на рис. 2б и 2в отмечены цифрами 1–5 провалы на передаточных характеристиках. При диаметре лазерного пятна d = = 250 мкм провалов передачи сигнала на передаточной характеристике не наблюдаются. Как видно на рис. 2б, на частоте 7.26 ГГц при диаметрах лазерного пятна d = 500 мкм и d = 1000 мкм наблюдается провал на АЧХ, при этом уровень провала в случае для пятна d = 500 мкм отличается на 10 дБ. Также можно сказать о том, что при увлечении диаметра лазерного пятна происходит снижение среднего уровня прохождения сигнала.
Рис. 2.
Передаточные характеристики спиновой волны для случаев разных диаметров создаваемых локальным лазерным нагревом (а): d = 250 мкм (синяя линия), d = 500 мкм (красная линия), d = 1000 мкм (коричневая линия), d = 1500 мкм (зеленая линия) при изменении намагниченности насыщения $\partial $ = 0.9; сегменты передаточных характеристик для частотного диапазона 7.2–7.3 ГГц (б) и 7.3–7.26 ГГц (в). Цифрами на рисунке отмечены провалы на передаточных характеристиках: 1 – 7.26 ГГц для d = 500 мкм, 2 – 7.26 ГГц для d = 1000 мкм, 3 – 7.31 ГГц для d = 1000 мкм, 4 – 7.345 ГГц для d = 1000 мкм, 5 – 7.35 ГГц для d = 1500 мкм.
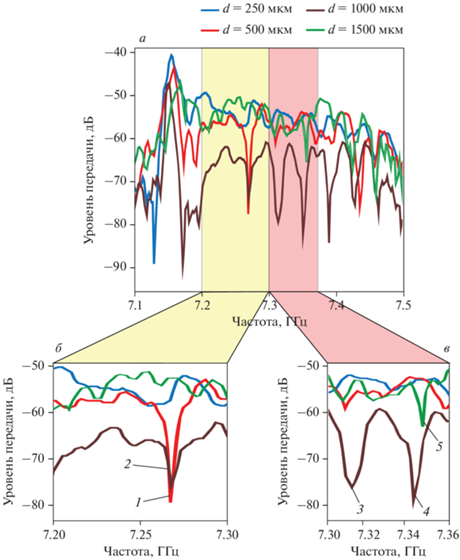
На рис. 2 в детально показаны режимы, при которых на АЧХ наблюдаются провалы для лазерного пятна диаметром 1000 мкм на частотах 7.31 и 7.345 ГГц. Можно говорить о том, что при создании области нагрева с диаметром d = 1000 мкм в структуре наблюдается 4 режима непропускания спин волнового сигнала.
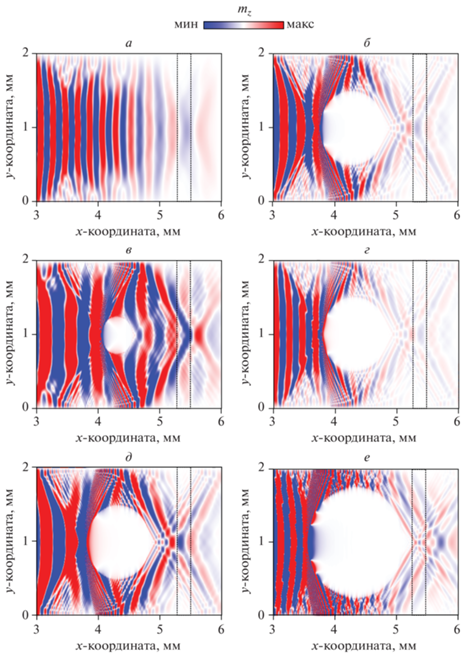
Для объяснения режимов непропускания спин-волнового сигнала были построены карты распределения mz компоненты намагниченности СВ для выбранных частот, представленных на рис. 3: $\partial $ = 1, f = 7.26 ГГц, d = 0 мкм (а); $\partial $ = 0.9, f = = 7.26 ГГц, d = 500 мкм (б); $\partial $ = 0.9, f = 7.26 ГГц, d = 1000 мкм (в); $\partial $ = 0.9, f = 7.31 ГГц, d = 1000 мкм (г); $\partial $ = 0.9, f = 7.345 ГГц, d = 1000 мкм (д); $\partial $ = 0.9, f = 7.35 ГГц, d = 1500 мкм (е). Видно, что для случая $\partial $ = 1, f = 7.26 ГГц, d = 0 мкм (рис. 3а) в области выходной антенны Pвых распространяется первая ширинная мода и при этом достигается максимальный режим пропускания СВ. Для дальнейших случаев, при которых на передаточных характеристиках наблюдаются провалы, в рассматриваемой структуре возникают условия распространения третьей ширинной моды за счет огибания СВ области нагрева. При этом интегральное значение компоненты намагниченности mz, полученное в области выходной микрополосковой антенны Pвых (от 5.25 до 5.5 мм вдоль x-координаты – обозначено пунктирной линией), становится ниже, чем в случае распространения первой ширинной моды без приложения локального лазерного нагрева. Необходимо отметить, что при параметрах $\partial $ = = 0.9, f = 7.26 ГГц, d = 500 мкм (рис. 3б) влияние лазерного нагрева на модовый состав минимально и поэтому на передаточной характеристике не наблюдаются провалы. Для остальных случаев уровень передачи падает за счет распространения третьей ширинной моды. При этом наблюдаются две пучности с отрицательным направлением и одна пучность с положительным направлением mz компоненты намагниченности. Именно такое распределение дает в интегральном значении уменьшение уровня передачи СВ.
Рис. 3.
Карты распределения mz компоненты намагниченности в структуре в срезе от 3 до 6 мм по x-координате для случаев: $\partial $ = 1, f = 7.26 ГГц, d = 0 мкм (а); $\partial $ = 0.9, f = 7.26 ГГц, d = 500 мкм (б); $\partial $ = 0.9, f = 7.26 ГГц, d = 1000 мкм (в); $\partial $ = 0.9, f = 7.31 ГГц, d = 1000 мкм (г); $\partial $ = 0.9, f = 7.345 ГГц, d = 1000 мкм (д); $\partial $ = 0.9, f = 7.35 ГГц, d = 1500 мкм (е). Пунктирной линией отмечена область выходной микрополосковой антенны Pвых.
Таким образом, показана возможность управления режимами распространения СВ в планарном ЖИГ волноводе посредством локального лазерного нагрева. Были получены режимы распространения СВ при изменении диаметра лазерного пятна и величины нагрева. Приведены передаточные характеристики и карты распределения mz компоненты намагниченности, описывающие характер распространения СВ и возникновение трансформации первой ширинной моды в третью ширинную моду за счет локального лазерного нагрева приводящие к появлению в спектре передаточных характеристик провалов. Предложенный метод управления при изменении коэффициента передачи и фазы спин-волнового сигнала в структуре из пленки ЖИГ может найти применение для создания устройств магнонной логики.
Исследование выполнено при финансовой поддержке Российского фонда фундаментальных исследований (проект № 20-37-90020).
Список литературы
Kruglyak V.V., Demokritov S.O., Grundler D. // J. Phys. D. 2010. V. 43. No. 26. Art. No. 264001.
Sadovnikov A.V., Beginin E.N., Sheshukova S.E. // Appl. Phys. Lett. 2015. V. 107. No. 20. Art. No. 202405.
Barman A., Gubbiotti G., Ladak S. // J. Phys. Cond. Matt. 2021. V. 33. No. 41. Art. No. 413001.
Neisser M., Wurm S. // Adv. Opt. Tech. 2015. V. 4. No. 4. P. 235.
Beginin E.N., Kalyabin D.V., Popov P.A. et al. // In: Three-dimensional magnonics. N.Y.: Jenny Stanford Publishing, 2019. P. 67.
Chumak A.V., Vasyuchka V.I., Serga A.A., Hillebrands B. // Nature Phys. 2015. V. 11. No. 6. P. 453.
Wang Q., Pirro P., Verba R. et al. // Sci. Advances. 2018. V. 4. No. 1. Art. No. e1701517.
Sadovnikov A.V., Beginin E.N., Sheshukova S.E. et al. // Phys. Rev. B. 2019. V. 99. No. 5. Art. No. 054424.
Sadovnikov A.V., Grachev A.A., Serdobintsev A.A. et al. // IEEE Magn. Lett. 2019. V. 10. Art. No. 5506405.
Никитов С.А., Сафин А.Р., Калябин Д.В. и др. // УФН. 2020. Т. 190. № 10. С. 1009; Nikitov S.A., Safin A.R., Kalyabin D.V. et al. // Phys. Usp. 2020. V. 63. No. 10. P. 945.
Cherepanov V., Kolokolov I., L’vov V. // Phys. Reports. 1993. V. 229. No. 3. P. 81.
Gurevich A.G., Melkov G.A. Magnetization oscillations and waves. London: CRC Press, Boca Raton, 1996. 464 p.
Gusev N.S., Sadovnikov A.V., Nikitov S.A. et al. // Phys. Rev. Lett. 2020. V. 124. No. 15. Art. No. 157202.
Borys P., Kolokoltsev O., Gomez–Arista. I. et al. // JMMM. 2020. V. 498. Art. No. 166154.
Fetisov Y.K., Makovkin A.V. // J. Appl. Phys. 1996. V. 79. No. 8. P. 5721.
Vogel M., Aßmann R., Pirro P. et al. // Sci. Reports. 2018. V. 8. Art. No. 11099.
Whitehead N.J., Horsley S.A.R., Philbin T.G., Kruglyak V.V. // Appl. Phys. Lett. 2018. V. 113. No. 21. Art. No. 212 404.
Damon R.W., Eshbach J.R. // J. Phys. Chem. Sol. 1961. V. 19. No. 3–4. P. 308.
O’keeffe T.W., Patterson R.W. // J. Appl. Phys. 1978. V. 49. No. 9. P. 4886.
Bajpai S.N. // J. Appl. Phys. 1985. V. 58. No. 2. P. 910.
Sadovnikov A.V., Davies C.S., Kruglyak V.V. et al. // Phys. Rev. B. 2017. V. 96. No. 6. Art. No. 060401.
Brächer T., Pirro P., Westermann J. et al. // Appl. Phys. Lett. 2013. V. 102. No. 13. Art. No. 132411.
Vansteenkiste A., Leliaert J., Dvornik M. et al. // AIP Advances. 2014. V. 4. Art. No. 107133.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Серия физическая