Химическая физика, 2019, T. 38, № 11, стр. 5-15
Кинетическое моделирование изотерм адсорбции
С. О. Травин 1, *, О. Б. Громов 2, Д. В. Утробин 2, А. В. Рощин 1
1 Институт химической физики им. Н.Н. Семёнова Российской академии наук
Москва, Россия
2 Акционерное общество “Высокотехнологический научно-исследовательский
институт неорганических материалов им. акад. А.А. Бочвара”
Москва, Россия
* E-mail: TravinSO@yandex.ru
Поступила в редакцию 29.11.2018
После доработки 17.03.2019
Принята к публикации 20.03.2019
Аннотация
Рассмотрены возможности расчета адсорбционных равновесий с помощью моделирования набора кинетических стадий сорбции и десорбции. Предложен подход, в котором изотерма адсорбции получается путем сканирования в моделирующей программе концентрации сорбируемого вещества как линейной функции времени. Показана принципиальная возможность получения изотерм адсорбции пяти типов из шести, утвержденных IUPAC (кроме многоступенчатой – тип VI). Для получения неискаженных изотерм адсорбции необходимо и достаточно использовать шаг сканирования, больший постоянной времени установления адсорбционного равновесия. Показано, что изотерма полимолекулярной адсорбции Брюнауэра–Эммета–Теллера может быть с высокой точностью промоделирована с помощью простой кинетической схемы.
1. КЛАССИФИКАЦИЯ АДСОРБЕНТОВ
При описании явлений адсорбции имеется значительная терминологическая путаница [1, 2], в связи с чем мы в данной работе будем придерживаться предложенной академиком М.М. Дубининым [3] классификации адсорбентов, принятой в 1972 году IUPAC. Эта классификация подразделяет пористые адсорбенты на три основные типа с микро-, мезо- и макропорами. Нанометровый размер исторически оказался отнесенным к классу микропор.
В случае микропор силовые поля, создаваемые противоположными стенками, перекрываются, что приводит к существенному возрастанию адсорбционных потенциалов и величины адсорбции. На долю мезо- и макропор отводится лишь транспортная функция, влияющая на динамику, но не на константу связывания адсорбционного равновесия. С появлением современных непористых высокодисперсных материалов с удельной поверхностью 1000 и более м2/г открылись широкие возможности их использования в качестве адсорбентов.
Если для пористых адсорбентов важную роль играет не только размер, но и форма пор, то универсальным способом выражения дисперсности любых, в том числе и непористых материалов, является их удельная поверхность. Такой подход оказался весьма продуктивен, например, в гетерогенном катализе. Он позволил Г.К. Борескову [4] сформулировать для ряда платиновых катализаторов правило приблизительно постоянной удельной каталитической активности, т.е. активности, отнесенной к единице поверхности.
Дисперсность может быть выражена и другими единицами: средним размером частиц или распределением числа частиц по размерам, отношением числа поверхностных, доступных для адсорбции атомов к общему числу атомов в частице, которое и является собственно дисперсностью. Чем меньше частицы, тем это отношение больше. Особенно велико оно для непористых адсорбционных наноматериалов.
Как показали проведенные в Институте катализа СО РАН исследования, весьма эффективным средством определения дисперсности является хемосорбционный метод, позволяющий достаточно надежно и с хорошей относительной точностью оценить величину активной поверхности или число поверхностных атомов, доступных для реагирующих веществ, а также средний размер частиц.
2. КАНОНИЗИРОВАННЫЕ ФОРМЫ ИЗОТЕРМ АДСОРБЦИИ
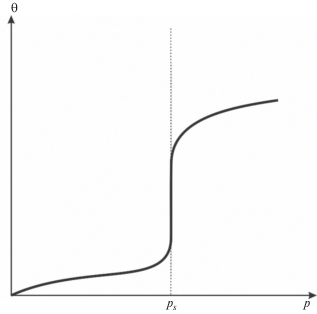
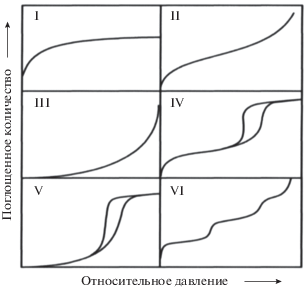
Настоящий обзор не претендует на полноту рассмотрения теории адсорбции. Более того, выбор материала продиктован целью авторов – промоделировать, исходя из первых принципов химической кинетики, основные формы изотерм адсорбции. В настоящее время их известно шесть. Первые пять были предложены Брюнауэром [5], шестая добавлена позже (см. рис. 1).
Рис. 1.
Принятая IUPAC классификация форм изотерм адсорбции. Обращает на себя внимание наличие гистерезиса на кривых форм IV и V.
Очевидно, что наличие уравнений, описывающих экспериментальные данные по равновесию адсорбции, существенно сокращает объем экспериментальных исследований и позволяет получать важные характеристики адсорбционных систем. В этой связи рассмотрим кратко наиболее важные и широко применяющиеся уравнения изотерм адсорбции.
Последние 100 лет (а точнее, с опубликования в 1918 г. статьи Лэнгмюра о монослойной адсорбции [6]) основные теоретические дискуссии развертываются вокруг уточнения вида изотерм адсорбции для разных случаев взаимодействия адсорптива с адсорбентом. Классическое уравнение Лэнгмюра для адсорбции на однородной поверхности (слово “пористость” и тем более размеры пор в этом контексте не упоминаются) может быть легко выведено из схемы равновесия [7].
Модель Лэнгмюра проста, наглядна и исключительно удобна для модельных расчетов. В этой модели предполагается, что на поверхности адсорбента есть конечное количество связывающих центров, каждый из которых может быть либо свободен, либо связан с молекулой адсорбтива. Предполагается также, что центры не взаимодействуют между собой, т.е. что свободная энергия Гиббса адсорбции (или, что то же самое, константа равновесия) адсорбции постоянна, т.е. не зависит ни от концентрации адсорбтива, ни от степени заполнения поверхности.
Схема процесса описывается всего двумя реакциями – прямой и обратной:
Скорость сорбции равна
а скорость десорбции
Учитывая баланс свободных и занятых мест:
и приравнивая скорости прямого и обратного процессов в состоянии равновесия, получаем уравнение изотермы Лэнгмюра:
(6)
$~{{k}_{{1~}}}pS = {{k}_{{1~}}}p({{[{\text{S]}}}_{0}} - [{\text{AS]}}) = {{k}_{{ - 1~}}}[{\text{AS]}},$(7)
$\left[ {{\text{AS}}} \right] = {{\left[ {\text{S}} \right]}_{0}}\frac{{Kp}}{{1 + Kp}},\,\,\,\,K = \frac{{~{{k}_{{1~}}}}}{{~{{k}_{{ - 1~}}}}};$тогда степень заполнения поверхности
или $\theta = {{\left[ {{\text{AS}}} \right]} \mathord{\left/ {\vphantom {{\left[ {{\text{AS}}} \right]} {{{{\left[ {\text{S}} \right]}}_{0}}}}} \right. \kern-0em} {{{{\left[ {\text{S}} \right]}}_{0}}}}$ – степень заполнения поверхности; ${\text{Г}}$ – количество адсорбированного вещества; ${{{\text{Г}}}_{\infty }}$ – полная емкость монослоя, достигаемая при “бесконечном” значении давления p адсорбата; $K$ – константа равновесия.
Столь подробное внимание уделено хорошо всем известной модели Ленгмюра по причине того, что именно ее мы будем в дальнейшем усложнять и адаптировать для различных приложений численного моделирования адсорбции. Уравнение Лэнгмюра, хотя и соответствует “всего лишь” простейшему случаю монослойной адсорбции однородной поверхности, совершенно безупречно с точки зрения формальной кинетики и классической термодинамики. Все константы являются действительно константами, т.е. не зависят от степени заполнения поверхности. В подавляющем большинстве случаев отклонение от классического лэнгмюровского типа связано с неоднородностью центров связывания [7], а также с возможностью налипания адсорбирующихся молекул более толстым слоем, чем мономолекулярный слой.
Все дальнейшие модели изотермы адсорбции сводились к учету неоднородности центров по энергии связывания:
(9)
$\theta \left( p \right) = \mathop \smallint \limits_{{{Q}_{{min}}}}^{{{Q}_{{max}}}} \theta \left( {p,Q} \right)F\left( Q \right)dQ,\,\,\,\,~\mathop \smallint \limits_{{{Q}_{{min}}}}^{{{Q}_{{max}}}} F\left( Q \right)dQ = 1.$Знаковым событием в построении адсорбционных теорий и моделей стала изотерма полимолекулярной адсорбции Брюнауэра–Эммета–Теллера (БЭТ) [5]:
(10)
$\Gamma = {{\Gamma }_{{mono}}}\frac{{C{p \mathord{\left/ {\vphantom {p {{{p}_{s}}}}} \right. \kern-0em} {{{p}_{s}}}}}}{{\left( {1 - {p \mathord{\left/ {\vphantom {p {{{p}_{s}}}}} \right. \kern-0em} {{{p}_{s}}}}} \right)\left[ {1 + \left( {C - 1} \right){p \mathord{\left/ {\vphantom {p {{{p}_{s}}}}} \right. \kern-0em} {{{p}_{s}}}}} \right]}}~.$Здесь ${{\Gamma }_{{mono}}}$ – емкость монослоя, ${{p}_{s}}$ – давление насыщенного пара адсорбата, C – константа равновесия, остальные обозначения те же, что и в уравнениях (3)–(7).
При этом вызывает возражение высказывание известного специалиста в адсорбции М.А. Толмачева [8]: “Уравнение БЭТ термодинамически некорректно, что признавали и его авторы. Наиболее точную характеристику ему дал В.В. Серпинский: “Брюнауэр, Эммет и Теллер вывели термодинамически некорректное уравнение, их величайшая заслуга состоит в том, что они убедили весь мир использовать это уравнение”. Добавим к этому “за неимением лучшего”.
В следующем разделе мы покажем, что уравнение БЭТ может быть получено практически теми же самыми приемами, что и уравнение Лэнгмюра. Хотя сам Брюнауэр критически относился к надежности исходных постулатов модели [9].
При выводе этих, а равно и любых других уравнений для равновесия адсорбции необходимо иметь в виду следующее:
1) разделение системы на адсорбционную и объемную фазы не может быть проведено строго;
2) адсорбционная фаза, выделенная на основании каких-либо дополнительных (всегда приближенных) соображений, энергетически неоднородна (вследствие неоднородности адсорбционного поля), и, поскольку эта неоднородность не может быть учтена в рамках феноменологической термодинамики, описание свойств адсорбционной фазы приходится проводить с использованием средних по фазе значений параметров (концентраций, химических потенциалов и т.д.) [10];
3) наличие адсорбционного поля необходимо учитывать в выражении для химического потенциала, т.е. использовать полные химические потенциалы для компонентов адсорбционной фазы.
Учет этих требований приводит к практической неосуществимости модельно-теоретических расчетов, основанных на строгом использовании уравнений классической термодинамики Гиббса. В результате практически одновременно с уравнением изотермы БЭТ появляется основное уравнение теории объемного заполнения микропор (ТОЗМ) в работе Дубинина и Радушкевича [11] в 1947 году. Ими было предложено следующее эмпирическое уравнение для определения объема микропор W0 активных углей:
где k – параметр системы; $\gamma $ – коэффициент аффинности, или степени сродства, связывающий адсорбционные потенциалы данного и стандартного адсорбата (для бензола условно принято γ = 1); $\varepsilon = RT{\text{ln}}\left( {{{{{p}_{s}}} \mathord{\left/ {\vphantom {{{{p}_{s}}} p}} \right. \kern-0em} p}} \right)$ – адсорбционный потенциал (свободная энергия Гиббса) или работа по изотермическому сжатию пара от давления p до давления насыщенного пара ${{p}_{s}}.$
Исходной предпосылкой к выводу уравнения послужила концепция равномерности заполнения всего объема микропор н термодинамическая потенциальная теория Поляни. В расчетах величина ${{p}_{s}}$ берется из данных для объемной фазы при температуре эксперимента Т.
В логарифмической форме уравнение Дубинина–Радушкевича принимает вид
(12)
${\text{ln}}W = {\text{ln}}{{W}_{0}} - {{\left( {\frac{{RT}}{{{{E}_{0}}}}} \right)}^{2}}{\text{l}}{{{\text{n}}}^{2}}\left( {\frac{p}{{{{p}_{s}}}}} \right).$В этом виде уравнение (12) более пригодно для анализа практически полученных графиков сорбции.
Исследования 80-х годов, выполненные М.М. Дубининым совместно с проф. Ф. Стекли (университет г. Невшатель, Швейцария), привели к существенному развитию представлений о форме микропор активного угля и позволили сделать вывод, что наиболее рациональной моделью микропор является щелевидная. На основе этой модели удалось связать уравнение ТОЗМ с геометрическими параметрами щелевидной микропоры. Методами статистической термодинамики и численного эксперимента было установлено, что для очень тонких щелевидных микропор физическая адсорбция может иметь активированный характер, не связанный с молекулярно-ситовым эффектом. Оказалось, что модель ограниченной щелевидной поры приводит к достоверным значениям объема микропор, вычисляемым из констант Генри, а также позволяет предсказывать ход графиков дифференциальных теплот адсорбции, удовлетворительно совпадающих с предсказанными ТОЗМ.
В обоснование уравнений (11), (12), следующих из концепции ТОЗМ, были сформулированы следующие положения:
1. Каждая микропора характеризуется определенным средним значением величины ε. Для плоской поверхности средние значения ε равны нулю. Отличия ε от нуля обусловлены свойствами микропор. Пористые системы обладают энергетической неоднородностью величин ε.
2. По мере увеличения отношения $x = {p \mathord{\left/ {\vphantom {p {{{p}_{s}}~}}} \right. \kern-0em} {{{p}_{s}}~}}$ последовательно заполняются поры со значениями ε, большими, чем ε(x). В то же время при малых x адсорбцией на активных местах пренебрегают, поэтому уравнение (10) не может перейти в уравнение Генри при малых заполнениях, что является необходимым требованием в термодинамически строгих теориях адсорбции.
3. Процесс заполнения и освобождения микропор при увеличении и уменьшении давления считается полностью обратимым (отсутствует капиллярная конденсация и тем более адсорбционный гистерезис).
Примерно в это же время (т.е. в начале 80-х гг.) на семинаре отдела адсорбции в ИФХ АН СССР под руководством М.М. Дубинина был сделан доклад Ю.К. Товбиным “Двумерная конденсация адсорбированных атомов на неоднородной поверхности”. Эта работа затем была представлена акад. М.М. Дубининым для публикации в Докладах АН СССР [12]. Товбин вспоминает: “Ни руководитель семинара, ни докладчик тогда еще не могли себе представить, что именно с этой работы начнется создание количественных моделей, объясняющих поведение адсорбата в микропорах, в узких каналах любого типа и малых полостях цеолитов” [13]. И далее в том же обзоре [13] Ю.К. Товбин сообщает: “Систематическое изучение фазовых диаграмм адсорбированных молекул в пористых системах началось в 90-х годах. В данном обзоре обсуждаются вопросы, непосредственно связанные с теорией объемного заполнения: 1) о теории адсорбции для микропористых систем, в которых определяющее влияние оказывает поверхностный потенциал стенок пор, и 2) классификация пор по размерам, связанная как со значением нижней границы пор, так и со всем диапазоном размеров пор, в которых существует петля адсорбционною гистерезиса”.
При этом, несмотря на несомненные успехи и достижения, при составлении практически важных справочников и баз данных по адсорбции вопросы теории остаются открытыми и далекими от понимания. Первый из них касается применения всем известного правила фаз Гиббса [14] к адсорбционным равновесиям. Оно определяет количество степеней свободы термодинамической системы, находящейся в равновесии, в зависимости от числа ее компонентов и фаз:
Если применять это правило к изотермическим системам, то при фиксации температуры число степеней свободы уменьшается на единицу и (13) переходит в выражение
В адсорбционной системе можно (с определенными, уже сформулированными оговорками) выделить два компонента (адсорбат + адсорбент) и две фазы: газообразный свободный адсорбат и связанный монослойно “двумерный решеточный газ”. Такой системе соответствует моновариантное равновесие (с одной степенью свободы), т.е. по мере увеличения давления растет и степень занятости узлов двумерной адсорбционной решетки.
Ситуация драматически меняется при возникновении полимолекулярного сорбирования и капиллярной конденсации. В этом случае мы имеем три фазы: обычную газовую и решеточный газ и еще одну – жидкую. При этом совершенно неважно, считать ли жидкую фазу относящейся к свободному либо к адсорбированному состоянию. Увеличение числа фаз на единицу приводит к уменьшению степеней свободы до нуля, т.е. к нонвариантному равновесию, подобному тройной точке воды, т.е. формально подобное равновесие возможно лишь при единственном значении давления. Формы изотерм IV и V по классификации IUPAC лишь отчасти подходят под такое определение.
Напротив, при хемосорбции (а в этих случаях капиллярная конденсация, как правило, отсутствует, поскольку при переходе в адсорбированный слой молекула адсорбтива меняет свое химическое состояние, чем заметно уменьшает свое сродство к другим подобным молекулам) можно говорить о появлении третьего компонента – химически связанного с адсорбентом слоя адсорбата. Тогда даже при наличии трех фаз (двух газовых и жидкой) равновесие остается моновариантным, т.е. соответствующим случаям IV и V из номенклатуры IUPAC и описываемым уравнениями типа Дубинина–Радушкевича, БЭТ, Фрейндлиха или иным уравнением для полимолекулярной адсорбции.
Нам не удалось найти в литературных источниках какой-либо формулы, описывающей приведенную на рис. 2 зависимость, которая моделирует формы изотерм IV, V по классификации IUPACK, что само по себе неудивительно. В то же время в ряде работ (см., например, [13]) приводятся подобные расчетные графики, полученные численными методами на основе молекулярной динамики в рамках модели решеточного газа. К сожалению, в работе [13] (как и во многих других) идет систематическое упоминание о том, что “уравнения МРГ многократно использовались в литературе, поэтому нигде не приводятся”. В итоге, несмотря на известность модели, для практического использования она доступна лишь авторам и их непосредственному окружению. К тому же в литературе недостаточно освещены вопросы, касающиеся кинетики адсорбционного связывания в случае неоднородных центров.
Для наиболее очевидного и распространенного случая больцмановского распределения центров по теплоте связывания очевидно, что
(15)
$F\left( Q \right) = {{F}_{0}}{\text{exp}}\left( {{{ - Q} \mathord{\left/ {\vphantom {{ - Q} {kT}}} \right. \kern-0em} {kT}}} \right).$Реакционная способность центров при неизменной энергии активации будет иметь зависимость вида
Сопоставляя (15) и (16), получаем уравнение
(17)
$k\left( Q \right)F\left( Q \right) = {{F}_{0}}{{A}_{0}}{\text{exp}}\left( {\frac{{ - {{E}_{a}}}}{{kT}}} \right) = {\text{const}},$в котором и правая, и левая части от Q не зависят.
И далее, избавляясь от Q, получаем
т.е. количество реагирующих центров обратно пропорционально их реакционной способности. При этом аналитическое решение для зависимости степени заполнения подложки от времени дается логарифмическим законом:
(19)
$\theta = {{\theta }_{\infty }}\ln \left( {1 + kt} \right) \approx {{\theta }_{\infty }}\left\{ {\ln \left( k \right) + \ln \left( t \right)} \right\}.$Таким образом, если для заполнения матрицы на 10% достаточно, допустим, 10 с, то на следующие 10% потребуется 100 с, затем – тысяча и т.д. до 10 млрд с, т.е. с практической точки зрения реакция будет длиться вечно. Иными словами, термодинамическое равновесие не наступит никогда, и необходимо переопределять статсуммы и иные термодинамические характеристики системы с учетом реального времени наблюдения. “Логарифмически затянутые” кинетические кривые – это случай распределенной константы скорости или (в обратных величинах) характерного времени сорбции. Такие закономерности достаточно часто встречаются в химической физике.
Наконец, значительного пересмотра аппарата описания требуют случаи гистерезиса. При этом речь не может идти не только о законе действующих масс в его классическом представлении, но даже о законе действующих масс с любым наперед заданным распределением центров по реакционной способности. Фактически для таких систем реакционная способность зависит не только от концентраций, но еще и от предыстории. При этом, по-видимому, даже марковские цепи, в которых система “помнит” свое предыдущее состояние, могут оказаться недостаточными для моделирования, ибо память может оказаться более глубокой, чем на один шаг назад.
Разумеется, для подобных организованных систем едва ли применимы методы равновесной термодинамики (учитывая почти бесконечную затянутость времени установления равновесия), столь успешно применяемой в классических уравнениях (1)–(8). Необходима разработка практически удобного инструментария практически “с нуля” для математического моделирования таких систем, практическая значимость которых не вызывает сомнений.
3. УРАВНЕНИЯ ИЗОТЕРМ АДСОРБЦИИ ПРОСТЫХ ФОРМ
Основным недостатком (правильнее сказать – ограничением) модели Лэнгмюра является ее неприменимость к случаям многослойной, полимолекулярной адсорбции. Ее развитием и распространением на многослойный случай стала изотерма БЭТ.
Основные допущения теории БЭТ сводятся к следующему:
1) после установления равновесия при некотором давлении p и температуре Т доля поверхности адсорбента θ0 свободна, доля θ1 занята мономолекулярным слоем, доля θ2 покрыта бимолекулярным слоем и т.д.;
2) равновесие между мономолекулярным слоем и паром, а также между верхними слоями полимолекулярных слоев и паром определяется уравнениями Лэнгмюра, но с константами равновесия, зависящими от количества адсорбированных слоев;
3) образование первого слоя сопровождается выделением теплоты адсорбции, а всех последующих – теплоты конденсации. Иными словами, вместо плавной зависимости энергии Гиббса от толщины слоя в модели используется Θ-функция, скачком изменяющая свое значение на первом слое и остающаяся в дальнейшем постоянной.
С учетом этих предположений выведено уравнение изотермы полимолекулярной адсорбции БЭТ – (10). В некоторых случаях сродство молекул адсорбтива к молекулам, находящимся в связанном состоянии на поверхности, может оказаться даже выше, чем для связывания первого слоя. Тогда полагают, что для всех последующих слоев энергия Гиббса будет не фиксированной константой, а переменной величиной, распределенной в некотором диапазоне. Такие модели адсорбции на “однородно неоднородной” поверхности, т.е. поверхности с центрами связывания, однородно распределенными в диапазоне энергий [15, 16], приводят к уравнениям изотермы Темкина –
и Фрейндлиха –
Изотерма Темкина подразумевает действительно равномерную плотность распределения энергетических уровней по диапазону, тогда как изотерма Фрейндлиха предполагает более реалистичную картину экспоненциального закона распределения энергетически неоднородных мест.
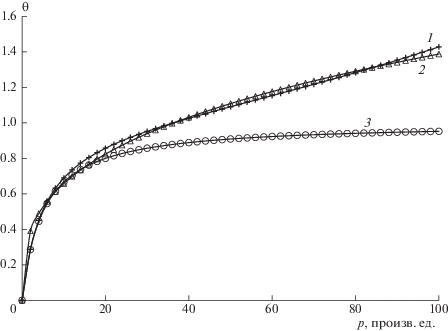
До тех пор, пока средняя толщина слоя не сильно отклоняется от единицы, реальное различие между моделями пренебрежимо мало. Естественно, лэнгмюровская модель ограничена единичной степенью заполнения поверхности, но вот модели Фрейндлиха и БЭТ едва различимы между собой (см. рис. 3).
Фактически модель БЭТ специально сконструирована для описания режимов капиллярной конденсации. В тех случаях, когда количество слоев заметно превышает единицу, поведение моделей начинает сильно расходиться.
4. МОДЕЛИРОВАНИЕ ИЗОТЕРМ АДСОРБЦИИ НА ОСНОВЕ КИНЕТИЧЕСКИХ СХЕМ
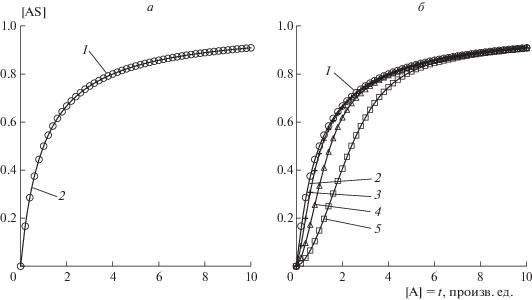
Численное моделирование процессов адсорбции весьма удобно делать в программной среде надстройки “Кинетика”, специально созданной авторами для моделирования сложных многостадийных процессов [17]. Само по себе моделирование процесса из двух реакций: (1), (2), не представляет труда. Кинетические кривые могут быть рассчитаны в аналитическом виде при любых соотношениях начальных концентраций и констант скорости отдельных стадий. Формальный алгоритм построения модельной изотермы мог бы заключаться в том, чтобы последовательно задавать разные значения давления адсорптива и рассчитывать соответствующую ему равновесную степень заполнения поверхности (при $t \to \infty $). Но, поскольку надстройка допускает внешнее управление любым из параметров системы, то добавив алгебраическое уравнение [A] = t и используя значения констант скорости стадий (1), (2), гарантирующих время установления адсорбционного равновесия, в разы меньшее, чем “время сканирования концентрации”, мы можем получить (с помощью все того же инструментария) расчетную форму изотермы адсорбции. На рис. 4а показано, что описанный прием работает с хорошей точностью. Следует обратить внимание, что в случаях, когда адсорбционное равновесие не успевает установиться за один шаг скрининга по времени, возможны искажения, подобные изображенным на рис. 4б. Так или иначе, при t/τ > 100 совпадение модельной изотермы с точно рассчитанной по уравнению Лэнгмюра может рассматриваться как идеальное. На рис. 4б режим специально “загрублен” так, чтобы установление адсорбционного равновесия не успевало за разверткой по времени.
Рис. 4.
Сравнение результатов кинетической модели изотермы Лэнгмюра с расчетом по равновесному уравнению: а – [S]0 = [A]0 = 1, шаг Δt = 0.01 с, 1/τ = k1 = 100, k–1 = 100, Δt/τ = 100, К = 1. Кривая 1 (кружки) – уравнение Лэнгмюра, кривая 2 (непрерывная линия) – кинетическая модель. На рисунке б показана чувствительность модели к характерному времени установления адсорбционного равновесия при S0 = A0 = 1, Δt = 0.01 с, k1 = k–1, К = 1. Кривая 1 (кружки) – равновесное значение по уравнению Лэнгмюра, кривая 2 (непрерывная линия) – Δt/τ = 10, кривая 3 (крестики) –Δt/τ = 3, кривая 4 (треугольники) – Δt/τ = 1, кривая 5 (квадратики) –Δt/τ = 0.3.
Научившись моделировать простейшее адсорбционное равновесие, мы можем перейти к модели изотермы БЭТ. Схема реакций (1), (2) дополнится еще четырьмя стадиями, включающими переходы из монослоя в гиперслой, испарения из гиперслоя и обратные им. Было бы ошибочно стадию налипания адсорбата на гиперслой записать в виде ${\text{AAS}} + {\text{A}} \to {\text{AAS}} + {\text{AAS}},$ поскольку это привело бы к экспоненциальному (взрывному) размножению числа связывающих центров и неустойчивости всей модели.
Вместо этого в стадии № 5 из табл. 1 показано сохранение числа центров “толстого” слоя и увеличение числа адсорбированного вещества, обозначенного переменной Precursor. Псевдопеременная ADS и незначимая реакция № 6 введены для удобства возможности суммирования в ней всех адсорбированных состояний: монослоя AS, наружного полимолекулярного слоя AAS и внутренних молекул полимолекулярной адсорбции “Precursor”. Итоговая схема для моделирования полимолекулярной адсорбции представлена в табл. 1.
Таблица 1.
Схема, использованная для моделирования изотермы БЭТ
| № стадии | Реагент 1 | Реагент 2 | Продукт 1 | Продукт 2 | Константа |
|---|---|---|---|---|---|
| 1 | A+ | S→ | AS | 9.00E + 03 | |
| 2 | AS→ | S+ | A | 4.00E + 02 | |
| 3 | AS+ | A→ | AAS | 2.00E + 02 | |
| 4 | AAS→ | AS+ | A | 4.40E + 03 | |
| 5 | AAS+ | A→ | AAS+ | Precursor | 7.00E + 01 |
| 6 | ADS→ | ADS | 1.00E + 00 |
Добавив к этой схеме “развертку по времени” в виде алгебраического условия [A] = t и суммируя все типы адсорбированных молекул [ADS] = = [AS] + [AAS] + [Precursor], мы получаем изотерму БЭТ совершенно аналогично тому, как в предыдущем пункте получали развертку изотермы Лэнгмюра. Результат представлен на рис. 5.
Рис. 5.
Сравнение кинетической развертки изотермы БЭТ (сплошная линия) с расчетом по формуле (10) (крестики).
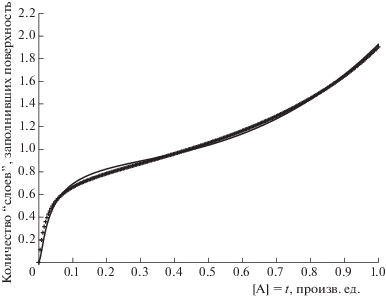
Подчеркнем, что схема реакций №№ 1–6 из табл. 1 в точности соответствует всем трем постулатам, заложенным в модель БЭТ. В то же время никакой вариацией параметров уравнения (10) не удается передать в точности вид изотермы, полученной “модельным скринингом”, в частности получить столь выразительный “прогиб спинки”.
Совершенно аналогичным приемом, введя зависимость константы равновесия в изотерме Лэнгмюра от степени заполнения поверхности, можно промоделировать и другие типы (по классификации IUPAC) изотерм адсорбции. На рис. 6 представлена одна из таких модельных изотерм – S-образная изотерма адсорбции разновидности V, полученная из уравнения Лэнгмюра после добавления в модель следующей зависимости константы связывания от степени заполнения поверхности:
(22)
$K = \frac{{{{k}_{1}}}}{{{{k}_{{ - 1}}}}}{\text{exp}}\left\{ { - {\text{th}}\left( {\alpha \left( {\theta - {{\theta }_{c}}} \right)} \right)} \right\}.$Рис. 6.
S-образная модельная изотерма адсорбции формы V, полученная из уравнения Лэнгмюра с зависящей от степени заполнения поверхности константой связывания. Изменение константы адсорбции задано уравнением (22). Графики даны для следующих значений параметров: ${{k}_{1}} = 30$ – константа скорости налипания адсорбтива на поверхность, ${{k}_{{ - 1}}} = 0.33$ константа скорости отрыва от поверхности, ${{\theta }_{c}} = 0.33.$ Энергетический параметр конденсации $\alpha = {{{{Q}_{{cond}}}} \mathord{\left/ {\vphantom {{{{Q}_{{cond}}}} {RT}}} \right. \kern-0em} {RT}}$ принимает следующие значения: кривая 1 – $\alpha = - 2$ (расталкивание между адсорбированными молекулами), кривая 2 – $\alpha = 0$ (отсутствие взаимодействия между адсорбированными молекулами, изотерма Лэнгмюра), кривая 3 – $\alpha = 1$ (слабое притяжение между адсорбированными молекулами), кривая 4 – $\alpha = 2$ (умеренное притяжение между адсорбированными молекулами (сравнимое с kT)), кривая 5 – $\alpha = 5~$ (сильное притяжение между адсорбированными молекулами), кривая 6 – $\alpha = 10$ (очень сильное притяжение между адсорбированными молекулами), кривая 7 – $\alpha = 20$ (очень сильное притяжение между адсорбированными молекулами).
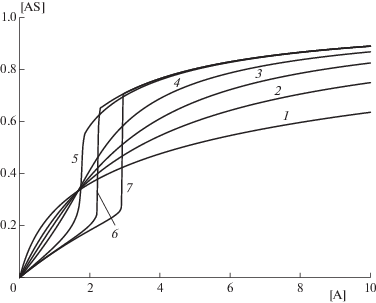
Такая зависимость подразумевает плавное увеличение теплоты адсорбции от некоего исходного значения до теплоты конденсации. Здесь параметр θс соответствует степени заполнения, при которой происходит капиллярная конденсация.
Если развивать подход к числовому моделированию, довольно привлекательной выглядит идея описания изотермы любого вида схемой Лэнгмюра из двух реакций путем искусственного отнесения всех отклонений реальной изотермы от дробно-линейной функции к функциональной зависимости псевдоконстанты связывания от концентрации адсорптива:
Откуда
На рис. 7 представлена зависимость псевдо-лэнгмюровской констант от давления адсорптива, рассчитанных для разных моделей по формуле (25).
Рис. 7.
Зависимость лэнгмюровской “псевдоконстанты” K от давления p. Кривая 1 (квадратики) – модель БЭТ, кривая 2 (крестики) – кинетическая развертка БЭТ, кривая 3 (сплошная лия) – сплайн кинетической развертки.
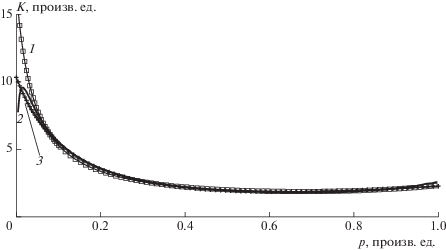
Имитацию формы кривой (для целей дальнейшего моделирования) проводили по формуле
Подчеркнем, что использованная функция для $K\left( p \right)$ была нами “сконструирована” исключительно для выбранной модельной изотермы с рис. 3. При более “толстых” слоях полимолекулярной конденсации, очевидно, необходимо искать другие варианты (см. рис. 8). Очевидно, что зависимость, описываемая формулой (26), неадекватна модели.
Рис. 8.
Искажение функционального вида лэнгмюровской “псевдоконстанты” при числе слоев от двух и более. Кривая 1 (крестики) – модель БЭТ, кривая 2 (кружки) – кинетическая развертка БЭТ, кривая 3 (треугольники) – сплайн кинетической развертки.
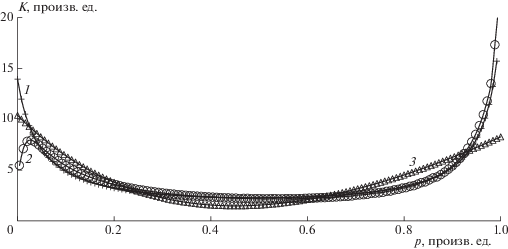
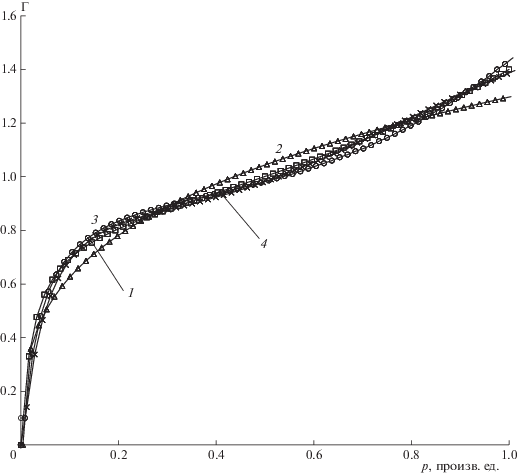
Возвращаясь к набору моделей полимолекулярной конденсации, мы можем получить “синтетическую” изотерму, основанную на использовании имитации формы. На рис. 9 приведены и расчеты по другим моделям. Видно, что при малых степенях насыщения имитация формы ближе к “кинетической развертке”, тогда как после начала капиллярной конденсации она максимально приближена к изотерме БЭТ с уравнением (10).
Рис. 9.
Сводный график моделей полимолекулярной сорбции. Кривая 1 (квадратики) – уравнение БЭТ, кривая 2 (треугольники) – уравнение Фрейндлиха, кривая 3 (кружки) – кинетическая развертка БЭТ, кривая 4 (косые крестики) – аппроксимация кинетической развертки по формуле (26).
Подбор коэффициентов формулы (26) по методу наименьших квадратов показывает высокую степень совпадения кривых, полученных по формуле БЭТ (10) и по кинетической развертке (табл. 2).
ВЫВОДЫ
1. С помощью набора нескольких равновесных стадий можно промоделировать развертку концентрации адсорбата и получить модельные изотермы адсорбции основных типов.
2. Для практического моделирования удобно использовать модель изотермы Лэнгмюра, в которую дополнительно вносятся эмпирические зависимости константы (или “псевдоконстанты”) равновесия от концентрации.
Работа выполнена в рамках Программы фундаментальных исследований ИХФ РАН № 46.15 госзадания № 0082-2014-0005 (номер государственной регистрации ЦИТИС: АААА-А17-117091220076-4).
Список литературы
Адсорбция, адсорбенты и адсорбционные процессы в нанопористых материалах. Сб. статей / Под ред. Цивадзе А.Ю. М.: Изд-во “Граница”, 2011; http://www.rfbr.ru/rffi/ru/books/o_1781651#1
Толмачев A.M. Адсорбция, адсорбенты и адсорбционные процессы в нанопористых материалах. Сб. статей / Под ред. Цивадзе А.Ю. М.: Изд-во “Граница”, 2011. С. 106.
Волощук А.М., Петухов Г.А., Фомкин А.А. // Там же. С. 12.
Боресков Г.К. Гетерогенный катализ в химической промышленности. М.: Госхимиздат, 1955. С. 5.
Brunauer S., Emmett P.H., Teller E. // J. Amer. Chem. Soc. 1938. V. 60. P. 309.
Langmuir I. // J. Amer. Chem. Soc. 1918. V. 40. № 9. P. 1361; https://doi.org/10.1021/ja02242a004
Halsey G.D. // Adv. Catal. 1952. V. 4. P. 259.
Толмачев А.М. Термодинамика адсорбции газов, паров и растворов (спецкурс). Уч.-метод. пособие. М.: Изд-во МГУ, 2012. С. 118.
Брюнауэр С. Адсорбция газов и паров. М.: Изд-во иностр. лит., 1948.
Tolmachev A.M. // Langmuir. 1991. № 7. P. 1400.
Дубинин M.M., Радушкевич Л.В. // Докл. АН СССР. 1947. Т. 55. С. 331.
Товбин Ю.К. // Докл. АН СССР. 1981. Т. 260. № 3. С. 679.
Товбин Ю.К. // Адсорбция, адсорбенты и адсорбционные процессы в нанопористых материалах. Сб. статей / Под ред. Цивадзе А.Ю. М.: Изд-во “Граница”, 2011. С. 64.
Жуховицкий А.А., Шварцман Л.А. Физическая химия. 4-е изд., перераб. и доп. М.: Металлургия, 1987.
Товбин Ю.К., Петухов А.Г. // ЖФХ. 2007. Т. 81. № 8. С. 1527.
Дамаскин Б.Б., Петрий О.А., Подловченко Б.И. и др. Практикум по электрохимии Учеб. пособие для хим. спец. вузов / Под ред. Дамаскин Б.Б. М.: Высш. шк., 1991.
Травин С.О., Громов О.Б. // Хим. безопасность. 2018. Т. 2. № 1. С. 50; https://doi.org/10.25514/CHS.2018.1.12882
Дополнительные материалы отсутствуют.
Инструменты
Химическая физика