Химическая физика, 2019, T. 38, № 4, стр. 23-27

Одним из основных постулатов химической кинетики является кинетический закон (КЗ), который служит базой для теоретического анализа моделей химических реакций. Классический закон действующих масс (ЗДМ) является простейшим КЗ, который выражает степенную зависимость скорости элементарной реакции от концентраций A_j реагентов: r_i ∼ $A_{j}^{{aij}},$ где a_ij − стехиометрические коэффициенты. Однако ЗДМ выполняется достаточно точно только для идеальных изотермических систем. Теория более общих КЗ сформировалась в работах R. Marcelin, deDonder, Van Rysselberghe, И. Пригожина, M. Feinberg и др. (см., например, работы [1–5]). В этих работах скорость элементарной реакции определена через новую термодинамическую функцию состояния – химическое сродство (affinities). Развитие теории общих КЗ было продолжено Г.С. Яблонским, А.Н. Горбанем, В.И. Быковым и др. [6–11], которые систематизировали кинетические и термодинамические аспекты применения неидеальной кинетики к исследованию химических реакций. Неидеальные КЗ общего вида использованы также при исследовании каталитических реакций на неоднородных поверхностях (см. работы [12–15]). Сродство выражает более сложную гипотезу для скорости элементарной реакции, которую можно представить в виде r_i ∼ $A_{j}^{{aij}}$[1 + f_j(A_j)], где f_j − “уровень” неидеальности (кинетический). Эта зависимость справедлива для широкого класса неидеальных систем и при f_j = 0 совпадает с идеальным ЗДМ. Если сродство связать с химическими потенциалами реагентов, m_j = g_j(A_j), то функция скорости реакции для неидеальных систем может быть записана как КЗ общего вида: r_i ∼ $A_{j}^{{aij}}$[1 + F_j(m_j(A_j)], где F_j − “уровень” неидеальности (термодинамический). Необходимо отметить, что термодинамический подход к определению КЗ общего вида накладывает существенные ограничения на вид потенциальных функций, который необходимо учитывать при моделировании неидеальных систем (см., например, [10, 11, 16–18]). Так, в работах [16–18] показано, что химическая неидеальность без учета термодинамических ограничений может приводить к ложным критическим явлениям (множественность равновесий и автоколебания) даже в закрытых системах. В то же время для открытых систем химическая неидеальность может быть причиной критических эффектов даже при соблюдении термодинамических ограничений. Новое направление неравновесной химической кинетики представляют методы дуальных экспериментов (см. работы [19, 20]) и мультиэкспериментов (см. [21]). Эти методы позволяют по результатам нескольких неравновесных экспериментов, проведенных при различных начальных условиях, определить точные термодинамические временны́е инварианты химических реакций для систем, имеющих точные решения [19, 20], или приближенные кинетические инварианты (квазиинварианты) для систем, точные решения которых неизвестны [21]. Квазиинварианты представляют собой комбинации неравновесных концентраций реагентов, остающиеся почти постоянными в течение всей реакции. Это свойство позволяет использовать их как дополнительный инструмент решения обратных задач нестационарной химической кинетики. Обобщим эти результаты и определим кинетические квазиинварианты реакций, протекающих в неидеальных системах с кинетикой общего вида.

Пусть химическая реакция с участием веществ A_j включает стадии

где a_ij ≥ 0, b_ij ≥ 0 – стехиометрические коэффициенты; i = 1, …, s – номер стадии, j = 1, …, n – номер реагента. Динамика реакции (1) в неизотермическом реакторе идеального смешивания описывается системой обыкновенных дифференциальных уравнений (n + 1)-го порядка [22]:

где r_i(k_±i, A_j, T) − скорости стадий, определяемые по некоторому неидеальному КЗ, 1/с; k_±i = = k_±i0exp(−E_±i/RT) − константы скоростей стадий, 1/с; k_±i0 и E_±i − предэкспоненты и энергии активации стадий; A_j – концентрации реагентов, мол. доли; T – температура, K; A_j0, T₀ – начальные условия (н.у.); q₀ и q − начальная и текущая скорости потока, 1/с; T_x − температура стенки реактора, К; α – коэффициент теплопередачи через стенку реактора, 1/с; Q_i − относительные тепловые эффекты стадий, К.

Выберем неидеальный КЗ в форме Марселина–де Донде [10–18]:

где φ_i > 0 − кинетический множитель стадии; μ_j = = μ_j0 + lnA_j0 + f_j(A_j) = m_j/RT − псевдохимические потенциалы (термин Фейнберга [5]), индекс “0” соответствует идеальной кинетике; уровень неидеальности зададим линейной функцией f_j = = $\sum {{{\alpha }_{j}}{{A}_{j}}} $, α_j − вещественные параметры (вектор неидеальности); R − универсальная газовая постоянная. Для идеальной кинетики из (4) следует классический ЗДМ: $\quad{{r}_{i}} = {{k}_{i}}\prod {A_{j}^{{aij}}} - {{k}_{{ - i}}}\prod {A_{j}^{{bij}}} .$

Система (2)–(4) не решается аналитически, т.е. ее точные инварианты неизвестны и не могут быть найдены. Найдем квазиинварианты. Разложим решения системы (2)–(4) в ряд и подставим в них значения производных:

здесь r_i0 − начальные скорости стадий. Вычислим значения выражений (5), (6) для двух н.у.: A_j01, T₀₁ и A_j02, T₀₂, отличных от равновесных значений. Получим

где

Исключим из каждой пары (7), (8) время и получим n + 1 основных потенциальных квазиинвариантов:

где

Очевидно, любые линейные комбинации этих выражений также являются квазиинвариантами. Квазиинварианты (9), (10) можно “улучшить” с помощью критерия улитки [21], который принимает вид

где A_j∞ = A_j1∞ = A_j2∞ и T_∞= T_1∞ = T_2∞ − равновесные концентрации и температура, которые определяются из решения системы уравнений $A_{j}^{'}$ = T  ' = 0. Соотношения (11), (12) определяют наилучшие условия для проведения пар экспериментов и наблюдения квазиинвариантов. Для идеальных систем из (9)–(12) следуют результаты, полученные в работе [21].

Применим полученные соотношения к двухстадийной реакции

Для этой реакции система (2)–(4) примет вид

где k_±1 = k_±10exp(−E_±1/RT), k_±2 = k_±20exp(−E_±2/RT); a = α₁, b = α₂, c = α₃ − вектор неидеальности. Для системы (1.2)–(1.4) соотношения (9)–(12) дают n + 1 = 4 основных квазиинварианта:

где

Условия (11), (12) запишутся следующим образцом:

Рассчитаем условия экспериментов с учетом того, что из выражений (1.2)–(1.4) следуют два равновесных закона сохранения: q(A_∞ + B_∞ + С_∞)/q₀ = = A₀ + B₀ + С₀ = const₁ и qQ₁A_∞ − qQ₂C_∞ + (q + α)T_∞ = = q₀Q₁A₀ − q₀Q₂С₀ + q₀T₀ + αT_x = const₂. Пусть вектор неидеальности a = b = c = 1; константы скоростей и энергии активации стадий: k₁₀ = 1, k₋₁₀ = 0, k₂₀ = 1, k₋₂₀ = 0 и E₁= E₂= 2; скорости потока q₀= 1, q = 1, температуры T₀= 300, T_x = 200; другие параметры: R = 2, α = 1, Q₁ = 1, Q₂ = 1, A₀ = 1, B₀ = 0, С₀ = 0. Тогда const₁ = 1 и const₂= 501, A_∞ ≈ 0.40, B_∞ ≈ 0.26, C_∞ ≈ 0.34, T_∞ ≈ 250.5. Выберем для пары экспериментов н.у., например A₀₁ = 0.7, B₀₁ = 0.2, тогда C₀₁ = const₁ − A₀₁ − B₀₁ = 0.1, T₀₁ = (const₂ − q₀Q₁A₀₁ + + q₀Q₂C₀₁ − αT_x)/q₀ ≈ 300.4; и A₀₂ = 0.8, B₀₂ = 0.1, тогда C₀₂ = 0.1, T₀₂ ≈ 300.3 и K_A0 = 0.07, K_A∞ = 0.08, K_B0 = 0.13, K_B∞ = 0.08, K_C0 = −0.12, K_C∞ = −0.41, K_T0 ≈ −0.93, K_T∞ ≈ −0.86. Квазиинварианты (1.5), (1.6) для заданного вектора неидеальности, рассчитанные по этой паре экспериментов, показаны на рис. 1.

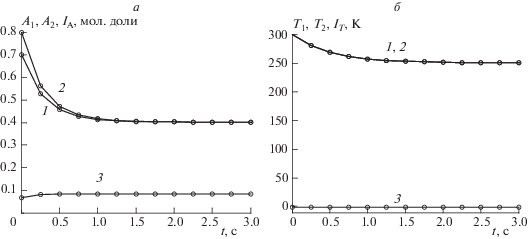
Проведем вторую пару экспериментов, например для вектора неидеальности a = 2, b = 1, c = 0. Тогда для тех же н.у. получим A_∞ ≈ 0.34, B_∞ ≈ 0.28, C_∞ ≈ 0.38, T_∞ ≈ 250.5, K_A0 = 0.13, K_A∞ = 0.1, K_B0 = 0.13, K_B∞ = 0.09, K_C0 = −0.12, K_C∞ = −0.46, K_T0 ≈ −3.29, K_T∞ ≈ −2.83. Квазиинварианты (1.5), (1.6) для этого вектора неидеальности, рассчитанные для той же пары экспериментов, показаны на рис. 2. Из рис. 1 и 2 видно, что зависимости I_A(t) и I_Т(t) изменяются в меньшем интервале, чем соответственно неравновесные концентрации реагента A₁(t), A₂(t) и температуры Т₁(t), Т₂(t) в двух экспериментах, т.е. почти постоянны во времени при разных векторах неидеальности. Отметим, что на рис. 1б и 2б кривые 1 и 2 практически совпадают так как начальные значения температур T₀₁ и T₀₂ почти одинаковы.

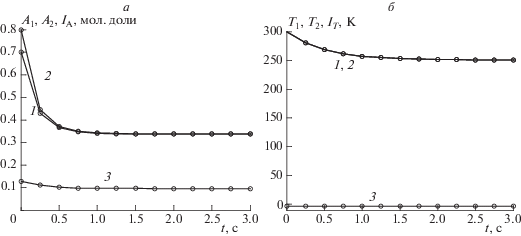
Таким образом, разработано обобщение метода мультиэкспериментов для химических реакций, протекающих в неидеальных системах, применимое к различным кинетическим законам (действующих масс, Марселина–де Донде и др.) в реакторе идеального смешения. Метод позволяет определять приближенные временны́е кинетические инварианты (квазиинварианты) нелинейных многостадийных химических реакций в открытых и закрытых изотермических и неизотермических системах с кинетикой достаточно общего вида, т.е. остается справедливым при любом типе неидеальности. Такие квазиинварианты представляют собой комбинации неравновесных значений концентраций реагентов, измеренных в двух или более экспериментах и остающихся почти постоянными в течение всей реакции. Они позволяют предсказывать и исследовать неизвестные кинетические закономерности в реакциях, протекающих в неидеальных условиях с кинетическими законами общего вида. Разработанный метод расширяет набор новых инструментов для решения обратных задач химической кинетики и может быть использован для более адекватной идентификации механизмов химических реакций, а также повышения эффективности режимов работы химических реакторов.