Химическая физика, 2019, T. 38, № 8, стр. 69-79
Трехмерное прямое численное моделирование турбулентного горения водородно-воздушных смесей в синтетическом поле турбулентности
В. Я. Басевич 1, А. А. Беляев 1, В. С. Иванов 1, С. Н. Медведев 1, С. М. Фролов 1, 2, 3, *, Ф. С. Фролов 1, 3, Б. Басара 4
1 Институт химической физики им. Н.Н. Семёнова Российской академии наук
Москва, Россия
2 Национальный исследовательский ядерный университет “МИФИ”
Москва, Россия
3 Федеральный научный центр Научно-исследовательский институт системных исследований
Российской академии наук
Москва, Россия
4 AVL List GmbH
Gras, Austria
* E-mail: smfrol@chph.ras.ru
Поступила в редакцию 05.12.2018
После доработки 06.03.2019
Принята к публикации 20.03.2019
Аннотация
Предложена методика трехмерного прямого численного моделирования распространения турбулентного пламени в газовых реагирующих смесях в условиях стационарной, однородной и изотропной турбулентности. Методика основана на детальном кинетическом механизме горения многокомпонентной смеси, не содержит каких-либо подгоночных параметров и применена к расчету турбулентного горения водородно-воздушных смесей, обедненных горючим. Рассчитанные скорости распространения турбулентного пламени удовлетворительно согласуются с измеренными значениями. Расчетные концентрации активных центров реакции – гидроксила ОН, атомов Н и О в турбулентном пламени меньше, чем в ламинарном, что также согласуется с экспериментом.
ВВЕДЕНИЕ
Прямое численное моделирование турбулентного горения предполагает неэмпирический подход на основе применения детального кинетического механизма (ДКМ) и учета поля пульсационных скоростей. Первые работы по математическому моделированию турбулентного горения появились достаточно давно [1, 2], однако общепринятых методов математического описания физико-химических процессов в турбулентном пламени до сих пор в литературе нет (см. [3–9]). Существующие подходы, как правило, включают всякого рода “замыкающие” гипотезы, основанные на экспериментальных наблюдениях. Поскольку область применимости той или иной гипотезы ограничена, такие полуэмпирические подходы неуниверсальны.
Сегодня наиболее перспективным универсальным подходом к неэмпирическому теоретическому описанию турбулентного горения считают прямое численное моделирование (ПЧМ, в англоязычной литературе – Direct Numerical Simulation (DNS)), при котором в рассмотрение включены все основные особенности трехмерного турбулентного реагирующего течения с полным спектром турбулентных пульсаций скорости, полным набором исходных, промежуточных и конечных химических компонентов с их индивидуальными термохимическими свойствами и свойствами молекулярного переноса, а также с адекватными граничными условиями [7–9]. Численное интегрирование определяющих уравнений течения проводят на расчетных сетках, обеспечивающих пространственное разрешение турбулентных вихрей колмогоровского масштаба, используя схемы высокого порядка аппроксимации.
Несмотря на значительные успехи в развитии ПЧМ турбулентного горения, на этом пути есть еще много проблем. Так, при сравнении самых “свежих” приведенных в литературе решений для скорости распространения турбулентного пламени, полученных с помощью ПЧМ (см., например, работу [10]), с известными экспериментальными данными выясняется, что их точность все еще заметно уступает точности, достигаемой при решении задач ламинарного горения (авторы работы [10] получили величины скорости распространения турбулентного пламени в метановоздушной смеси, в 3–5 раз большие экспериментальных значений, описанных в литературе). В теоретических работах в качестве причин расхождения результатов расчетов и экспериментов часто называют неучтенные эффекты, вызванные неопределенными граничными условиями в реальных экспериментах. Кроме того, применение ПЧМ к реальным турбулентным пламенам требует очень больших вычислительных ресурсов, в связи с чем в расчетах все еще приходится использовать различные упрощения, влияющие на точность решения.
В данной работе используется альтернативный подход к ПЧМ турбулентного горения гомогенной газовой смеси, который ранее был предложен в работе [11] в двумерном приближении. Вместо численного решения всех уравнений, определяющих распространение турбулентного пламени в реагирующем газе, в [11] предложено решать только уравнения переноса скалярных величин – концентраций реагентов и энергии – в искусственном (“синтетическом”) поле турбулентности, характеризуемом заданной (постоянной) среднеквадратичной интенсивностью пульсаций скорости с заданными (постоянными) интегральными пространственными и временными масштабами. При этом предполагалось, что химический процесс описывается одной глобальной реакцией, а само распространение пламени не влияет на характеристики синтетического поля турбулентности в предпламенной зоне.
В отличие от [11], в работе [12] химический процесс описывался уже не одной глобальной реакцией, а ДКМ с участием активных центров. В [12] результаты по моделированию турбулентного горения в двумерном приближении были получены для одного конкретного состава водородно-воздушной смеси в простейших условиях синтетического поля стационарной, однородной и изотропной турбулентности. В работе [13] методика из [12] была усовершенствована и применена для расчета распространения турбулентного пламени в водородно-воздушных гомогенных смесях разного состава и при разных давлениях.
Цель данной работы – переход от моделирования турбулентного горения в двумерном приближении к физически адекватной трехмерной задаче.
МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧИ
Постановка задачи в общем виде сформулирована в работе [13], но здесь целесообразно ее повторить. Система уравнений, определяющих распространение турбулентного пламени, основана на уравнениях Навье–Стокса в трехмерной постановке, уравнении сохранения энергии и уравнениях неразрывности для всех химических компонентов в смеси идеальных газов [14]:
(1)
$\rho \frac{{\partial {{Y}_{i}}}}{{\partial t}} + \rho {\mathbf{v}}\nabla {{Y}_{i}} = {{\omega }_{i}} - \nabla (\rho {{Y}_{i}}{{{\mathbf{V}}}_{i}}),\,\,\,\,i = 1,...,N,$Предполагается, что система (1) дополнена ДКМ окисления горючего, термохимическими данными каждого вещества ($h_{i}^{0},$ ${{c}_{{p,i}}}$) и соответствующими соотношениями для ${{{\mathbf{f}}}_{i}},$ ${\mathbf{q}},$ ${\mathbf{P}},$ ${{{\mathbf{V}}}_{i}}$ и ${{\omega }_{i}},$ а также начальными и граничными условиями. В результате решения задачи должны быть получены скорость стационарного распространения ${{u}_{t}}$ (скорость турбулентного горения) и структура турбулентного пламени в многокомпонентном реагирующем газе. Чтобы упростить решение задачи, введем следующие основные допущения:
1. Область течения имеет простейшую геометрию; турбулентность стационарная, однородная и изотропная.
2. Давление постоянно ($p = {{p}_{0}}$), а влиянием силы тяжести можно пренебречь. Благодаря этим допущениям задача существенно упрощается, так как отпадает необходимость решать уравнение сохранения количества движения.
3. Тепловой поток ${\mathbf{q}}$ определяется только молекулярной теплопроводностью (лучистым теплообменом можно пренебречь).
4. Эффекты термодиффузии малы.
5. Реагирующая смесь сильно разбавлена инертным газом (азотом), так что диффузионные потоки всех химических компонентов определяются законом Фика с коэффициентом бинарной диффузии.
С учетом допущений 2–5 система дифференциальных уравнений (1) сводится к виду
(2)
$\begin{gathered} \frac{{\partial \rho }}{{\partial t}} + \nabla (\rho {\mathbf{v}}) = 0,\,\,\,\,\rho \frac{{\partial e}}{{\partial t}} + \rho {\mathbf{v}}\nabla e = \nabla (\lambda \nabla T), \\ \rho \frac{{\partial {{Y}_{i}}}}{{\partial t}} + \rho {\mathbf{v}}\nabla {{Y}_{i}} = {{\omega }_{i}} + \nabla ({{D}_{i}}\rho \nabla {{Y}_{i}}),\,\,\,\,i = 1,...,N, \\ \end{gathered} $Для дальнейшего упрощения задачи предположим, что решение системы (2) стремится к некоторому стационарному решению, для которого
Поскольку нас интересует именно такое стационарное решение, уравнение (3) можно использовать вместо уравнений неразрывности смеси, т.е. вместо первого уравнения в системе (2). В этом случае постановка задачи допускает дальнейшее упрощение. Вектор мгновенной местной скорости ${\mathbf{v}} = (u,v,w)$ в (3), где $u,\,\,{v},\,\,w$ – компоненты вектора, можно представить в виде суммы вектора средней скорости ${\mathbf{V}} = (U,V,W)$ (здесь прописные буквы означают среднее значение) и вектора пульсаций скорости ${\mathbf{v}}{\text{'}} = (u{\text{'}},{v}{\text{'}},w{\text{'}})$ (штрихи относятся к пульсациям скорости): ${\mathbf{v}} = {\mathbf{V}} + {\mathbf{v}}{\text{'}}.$
Тогда (3) можно преобразовать к виду
(4)
$\nabla (\rho {\mathbf{v}}) = \nabla (\rho {\mathbf{V}} + \rho {\mathbf{v}}{\text{'}}) = \nabla (\rho {\mathbf{V}}) + \nabla (\rho {\mathbf{v}}{\text{'}}) = 0.$Основываясь на первом допущении (об однородной и изотропной турбулентности), предположим далее, что
и, следовательно,
В области течения с простейшей геометрией (см. допущение 1) всегда существует усредненное направление распространения турбулентного пламени, и можно устремить одну ось пространственных координат в этом направлении. Тогда выражение (6) можно проинтегрировать и получить
где ${\mathbf{B}}$ – постоянный поток вещества. С учетом (7) систему (2) можно привести к виду(8)
$\begin{gathered} \rho \frac{{\partial e}}{{\partial t}} + {\mathbf{B}}\nabla e = \nabla (\lambda \nabla T) - \nabla (\rho {\mathbf{v}}{\text{'}}u), \\ \rho \frac{{\partial {{Y}_{i}}}}{{\partial t}} + {\mathbf{B}}\nabla {{Y}_{i}} = {{\omega }_{i}} + \nabla ({{D}_{i}}\rho \nabla {{Y}_{i}}) - \nabla (\rho {\mathbf{v}}{\text{'}}{{Y}_{i}}), \\ i = 1,...,N. \\ \end{gathered} $Последние члены в обоих уравнениях системы (8) определяют перенос вещества и энергии с турбулентными пульсациями скорости. Если вектор ${\mathbf{B}}$ известен, то производные по времени в этих уравнениях можно положить равными нулю, чтобы получить структуру стационарного турбулентного пламени. Однако, как правило, значение вектора ${\mathbf{B}}$ заранее неизвестно. Поэтому, чтобы получить его значение, необходимо решить нестационарную систему (8), описывающую движение волны горения до достижения некоторой постоянной скорости. В этом случае конвективные члены в системе (8) можно опустить, а система уравнений примет вид
(9)
$\begin{gathered} \rho \frac{{\partial e}}{{\partial t}} = \nabla (\lambda \nabla T) - \nabla (\rho {\mathbf{v}}{\text{'}}e), \\ \rho \frac{{\partial {{Y}_{i}}}}{{\partial t}} = {{\omega }_{i}} + \nabla ({{D}_{i}}\rho \nabla {{Y}_{i}}) - \nabla (\rho {\mathbf{v}}{\text{'}}{{Y}_{i}}), \\ i = 1,...,N. \\ \end{gathered} $Наконец, можно упростить и последние члены в двух уравнениях (9), используя (5) и предполагая, что
(10)
${{\nabla }_{x}}(\rho u{\text{'}}) = {{\nabla }_{y}}(\rho {v}{\text{'}}) = {{\nabla }_{z}}(\rho w{\text{'}}) = 0,$где ${{\nabla }_{x}} = {\partial \mathord{\left/ {\vphantom {\partial {\partial x}}} \right. \kern-0em} {\partial x}},$ ${{\nabla }_{y}} = {\partial \mathord{\left/ {\vphantom {\partial {\partial y}}} \right. \kern-0em} {\partial y}}$ и ${{\nabla }_{z}} = {\partial \mathord{\left/ {\vphantom {\partial {\partial z}}} \right. \kern-0em} {\partial z}}.$ Интегрирование уравнений (10) дает
(11)
$\rho u{\text{'}} = {{\rho }_{0}}u_{0}^{'},\,\,\,\,\rho {v}{\text{'}} = {{\rho }_{0}}{v}_{0}^{'},\,\,\,\,\rho w{\text{'}} = {{\rho }_{0}}w_{0}^{'}.$После подстановки соотношений (11) в систему (9) окончательно получим
(12)
$\begin{gathered} \rho \frac{{\partial e}}{{\partial t}} = \nabla (\lambda \nabla T) - {{\rho }_{0}}{{c}_{{v}}}{\mathbf{v}}_{0}^{'}\nabla T, \\ \rho \frac{{\partial {{Y}_{i}}}}{{\partial t}} = {{\omega }_{i}} + \nabla ({{D}_{i}}\rho \nabla {{Y}_{i}}) - {{\rho }_{0}}{\mathbf{v}}_{0}^{'}\nabla {{Y}_{i}},\,\,\,\,i = 1,...,N. \\ \end{gathered} $Таким образом, как и в работах [11–13], вместо численного решения системы (1) предлагается решать систему (12), состоящую только из уравнений переноса скалярных величин – концентраций всех N реагентов и энергии – на заданном синтетическом поле турбулентности, характеризуемом среднеквадратичной интенсивностью пульсаций скорости v' с заданными интегральными пространственными и временны́ми масштабами. При трехмерном моделировании в системе координат (x, y, z) уравнения (12) в развернутом виде и с учетом калорического уравнения состояния будут выглядеть следующим образом:
(13)
$\begin{gathered} \rho {{c}_{p}}\frac{{\partial T}}{{\partial t}} = \sum\limits_{i = 1}^N {{{h}_{i}}{{\omega }_{i}}} + \left( {\frac{\partial }{{\partial x}}\lambda \frac{{\partial T}}{{\partial x}} + \frac{\partial }{{\partial y}}\lambda \frac{{\partial T}}{{\partial y}} + \frac{\partial }{{\partial z}}\lambda \frac{{\partial T}}{{\partial z}}} \right) - \\ - \,\,{{\rho }_{0}}{{c}_{p}}\left( {u_{0}^{'}\frac{{\partial T}}{{\partial x}} + {v}_{0}^{'}\frac{{\partial T}}{{\partial y}} + w_{0}^{'}\frac{{\partial T}}{{\partial z}}} \right),\,\,\,\,\rho \frac{{\partial {{Y}_{i}}}}{{\partial t}} = {{\omega }_{i}} + \\ + \,\,\left( {\frac{\partial }{{\partial x}}{{D}_{i}}\rho \frac{{\partial {{Y}_{i}}}}{{\partial x}} + \frac{\partial }{{\partial y}}{{D}_{i}}\rho \frac{{\partial {{Y}_{i}}}}{{\partial y}} + \frac{\partial }{{\partial z}}{{D}_{i}}\rho \frac{{\partial {{Y}_{i}}}}{{\partial z}}} \right) - \\ - \,\,{{\rho }_{0}}\left( {u_{0}^{'}\frac{{\partial {{Y}_{i}}}}{{\partial x}} + {v}_{0}^{'}\frac{{\partial {{Y}_{i}}}}{{\partial y}} + w_{0}^{'}\frac{{\partial {{Y}_{i}}}}{{\partial z}}} \right),\,\,\,\,i = 1,...,N, \\ {{p}_{0}} = \rho {{R}^{0}}T\sum\limits_{i = 1}^N {\frac{{{{Y}_{i}}}}{{{{\mu }_{i}}}}} . \\ \end{gathered} $Система (13) состоит из N + 2 уравнений для N + 2 переменных ($N$ веществ с массовой долей ${{Y}_{i}},$ температурой $T$ и плотностью $\rho $). Для замыкания системы используем следующие соотношения для ${{c}_{p}},$ $\lambda $ и ${{D}_{i}}{\text{:}}$
(14)
$\begin{gathered} {{c}_{p}} = \sum\limits_{i = 1}^N {{{c}_{{p,i}}}{{Y}_{i}}} , \\ {{c}_{{p,i}}} = \frac{{{{R}^{0}}}}{{{{\mu }_{i}}}}\left( {{{a}_{1}} + {{a}_{2}}T + {{a}_{3}}{{T}^{2}} + {{a}_{4}}{{T}^{3}} + {{a}_{5}}{{T}^{4}}} \right), \\ \lambda = \lambda (T,{{Y}_{1}},...,{{Y}_{N}},{{\mu }_{1}},...,{{\mu }_{N}},{{c}_{{p,1}}},...,{{c}_{{p,N}}}), \\ {{D}_{i}} = {{D}_{i}}(T,p,{{\mu }_{i}},{{\mu }_{{in}}}), \\ \end{gathered} $Для скорости химических реакций используется соотношение [14]
Уравнения (13) содержат параметры стационарной, однородной и изотропной турбулентности реагирующего газа (три компоненты вектора пульсационной скорости: $u_{0}^{'},\,\,{v}_{0}^{'},\,\,w_{0}^{'}$). Как и в работах [11–13], компоненты вектора пульсационной скорости получаем путем статистического разыгрывания методом Монте-Карло, предположив, что мгновенные местные компоненты вектора пульсационной скорости удовлетворяют нормальному распределению Гаусса φ, а вихревая структура турбулентности описывается экспоненциально затухающими пространственной (R') и временнóй (R) корреляционными функциями:
(15)
$\varphi \left( {u{\text{'}}} \right) = \frac{1}{{\sqrt {2\pi } \sigma }}\exp \left\{ { - \frac{{{{{\left( {u{\text{'}} - u} \right)}}^{2}}}}{{2{{\sigma }^{2}}}}} \right\},$(16)
$~R' = {\text{exp}}\left( {{{--{{r}_{k}}} \mathord{\left/ {\vphantom {{--{{r}_{k}}} {L{\text{'}}}}} \right. \kern-0em} {L{\text{'}}}}} \right),\,\,\,\,R = \exp \left( { - {t \mathord{\left/ {\vphantom {t \tau }} \right. \kern-0em} \tau }} \right).$Соотношение (15) для краткости записано только для x-составляющей мгновенной пульсационной скорости u' со среднеквадратичным значением u, причем индекс “0” в обозначениях опущен. Такое же соотношение используется для разыгрывания y- и z-составляющих мгновенной пульсационной скорости ${v}'$ и w' с соответствующими среднеквадратичными значениями ${v}$ и w. В (15) и (16) $\sigma $ – среднеквадратичное отклонение пульсаций скорости по направлению x, y или z; rk – расстояние в физическом пространстве; L' и τ – пространственный и временнóй масштабы турбулентности. В соответствии с первым допущением (см. выше) о стационарности и однородности поля турбулентности, масштабы τ и L' приняты постоянными.
Среднеквадратичная длина пространственного вектора пульсационной скорости $\bar {u}$ определяется по среднеквадратичным значениям его компонент u, ${v}$ и w соответственно по осям x, y и z с помощью соотношения
Подчеркнем, что задание вектора пульсационной скорости $\bar {u}$ и пространственного масштаба турбулентности L' равносильно заданию диссипации турбулентной энергии ε ~ ${{\bar {u}}^{3}}$/L' и колмогоровского масштаба турбулентности l0 ~ a3/4ε–1/4, где a = λ/ρcp – коэффициент температуропроводности, который для газов близок к коэффициенту кинематической молекулярной вязкости.
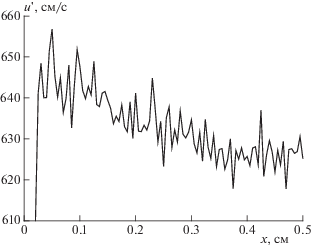
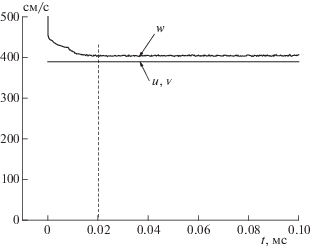
Пример статистического разыгрывания поля пульсационных скоростей u' по одной из координатных осей (по оси х) методом Монте-Карло представлен на рис. 1. Получающиеся при этом зависимости среднеквадратичных компонент скорости u, ${v}$ и w от времени приведены на рис. 2. Как видно, компоненты скорости u и ${v}$ строго соответствуют задаваемым исходным значениям, а компонента w, за счет которой выдерживается закон неразрывности, в самом начале процесса оказывается больше задаваемого значения, однако затем приближается к u и ${v}.$ Поэтому для выполнения условия изотропности турбулентности самое начало процесса (соответствующее области до вертикальной штриховой линии на рис. 1) в проведенных расчетах исключалось из рассмотрения. Граничные и начальные условия для системы (13) рассмотрены ниже для конкретной расчетной области.
МЕТОДИКА РАСЧЕТОВ
Расчетная область представляет собой параллелепипед, верхняя и нижняя грани которого – плоские квадраты. В начальный момент времени t = t0= 0 объем содержит два слоя, разделенных плоской поверхностью, параллельной основанию и отстоящей от него на некоторое расстояние. Нижний слой содержит продукты горения, верхний – свежую смесь. Нижняя и верхняя грани удалены от разделительной поверхности на достаточно большое расстояние, чтобы обеспечить постоянство давления в системе за все время расчета. Боковые грани – непроницаемые стенки со скольжением потока. Пламя распространяется снизу вверх. На рис. 3 для примера показана трехмерная поверхность распространяющегося пламени, искривленная турбулентными пульсациями скорости.
Рис. 3.
Поверхность распространяющегося турбулентного пламени. Водородно-воздушная смесь с содержанием водорода 9.09%, начальная температура Т0 = 293 К, давление атмосферное; характеристики турбулентности: $\bar {u}$ = 242 см/с, L' = 1 см, τ = 0.010 с.
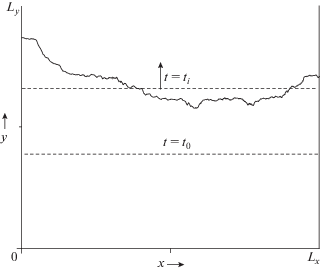
На рис. 4 представлена двумерная схема расчетной области в выбранной системе координат (x, y) при некотором значении z. Начальное положение поверхности пламени в момент времени t = t0= 0 показано горизонтальной штриховой линией. При t > 0 положение пламени условно представляется плоскостью, параллельной основанию параллелепипеда, выше которой находится только свежая смесь, а ниже – только продукты реакции. Подчеркнем, что это – условный фронт пламени, поскольку сама зона реакции в пламени имеет конечную толщину. Таким образом, для определения скорости распространения пламени условно принимается, что свежая смесь занимает пространство с температурой Т < Tm, а продукты реакции – пространство с температурой T > Tm. Значение Tm равно среднему арифметическому между начальной температурой свежей смеси, T0, и термодинамически равновесной температурой продуктов сгорания, T1:
На рис. 4 мгновенное положение фронта пламени в момент времени t = ti > 0 – след истинной поверхности пламени на плоскости ху – показан тонкой сплошной линией, а положение условного фронта пламени – горизонтальной штриховой линией.
Задачу о распространении турбулентного пламени решали с помощью численного интегрирования системы (13) с дополнительными соотношениями методом переменных направлений [15, 16]. Для решения уравнений по каждому из направлений (x, y, z) применялась неявная разностная схема с равномерным шагом по пространству и линеаризацией нелинейных “источниковых” слагаемых на верхнем слое. Эта схема имеет первый порядок точности по времени и пространству. Расчетная область пространства (x, y, z) имела размер 1 × 0.5 × 1 см3. Все расчетные ячейки имели форму куба размером 0.01 × 0.01 × 0.01 см3 или 0.005 × 0.005 × 0.005 см3. Полное количество расчетных ячеек составило 500 000 и 4 000 000 соответственно. Шаг интегрирования по времени изменялся в зависимости от числа итераций, но не превышал 10–6 с.
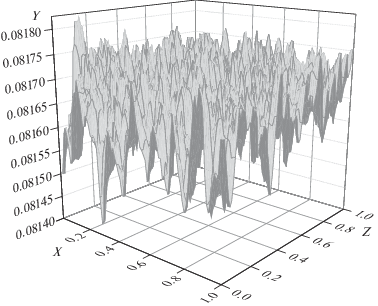
Важная операция – моделирование синтетического поля турбулентности $v_{0}^{'} = (u_{0}^{'},{v}_{0}^{'},w_{0}^{'})$ в уравнениях (13). Моделирование полей пульсационных скоростей $u{\text{'}}$(x, y, z, t), $v{\text{'}}$(x, y, z, t) и w'(x, y, z, t) проводилось путем разыгрывания их возможных значений при заданных параметрах турбулентности u, ${v},$ w, L' и τ. Процедура разыгрывания предусматривала выполнение закона неразрывности. Соответствующая методика описана в Приложении.
Ниже представлены используемые здесь начальные и граничные условия. Начальные условия –
(17)
$\begin{gathered} t = {{t}_{0}} = 0;\,\,\,\,y > y(t = {{t}_{0}}){\text{:}}\,\,{{Y}_{j}} = {{Y}_{{j0}}}, \\ T = {{T}_{0}},\,\,\,\,j = 1,...,N, \\ y < y(t = {{t}_{0}}){\text{:}}\,\,{{Y}_{j}} = {{Y}_{{j1}}},\,\,\,\,T = {{T}_{1}},\,\,\,\,j,...,N. \\ \end{gathered} $Граничные условия –
(18)
$\begin{gathered} y = 0{\text{:}}\,\,\frac{{\partial T}}{{\partial y}} = 0,\,\,\,\,\frac{{\partial {{Y}_{j}}}}{{\partial y}} = 0,\,\,\,\,j = 1,...,N; \\ y = {{L}_{y}}{\text{:}}\,\,\frac{{\partial T}}{{\partial y}} = 0,\,\,\,\,\frac{{\partial {{Y}_{j}}}}{{\partial y}} = 0,\,\,\,\,j = 1,...,N; \\ \end{gathered} $РЕЗУЛЬТАТЫ РАСЧЕТОВ
Как и в [13], в данной работе рассматривается турбулентное горение гомогенной водородно-воздушной смеси. Для описания кинетики химических превращений используется блок реакций окисления водорода из детального кинетического механизма окисления и горения нормальных углеводородов [17]. Значения коэффициентов полиномов для всех веществ взяты из работы [18]. Коэффициенты переноса $\lambda $ и ${{D}_{i}}$ рассчитывались по методике, описанной в [19].
Ниже данные, представленные в работе [20], используются для сравнения расчетных и измеренных значений скоростей турбулентного горения смесей разного состава в зависимости от интенсивности турбулентности. Максимальное физическое время расчета турбулентного пламени достигало 10–3 с, т.е. было меньше характерного временнóго масштаба τ. Поэтому решения представляют собой индивидуальные реализации положения поверхности фронта турбулентного пламени. На поверхности фронта пламени наблюдаются (см. рис. 3) и мелкомасштабные, и крупномасштабные пространственные неоднородности, характеризуемые линейными размерами, которые и меньше, и больше толщины фронта пламени. Мелкомасштабная турбулентность изменяет (увеличивает) скорость обменных процессов (обмен массой и энергией) внутри фронта пламени, а крупномасштабная турбулентность изменяет форму пламени и увеличивает площадь его поверхности.
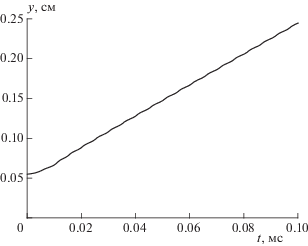
Определим истинную скорость турбулентного пламени ut как скорость движения разделительной плоскости между свежей смесью и продуктами горения, т.е. как скорость условного фронта пламени. Несмотря на относительно короткое физическое время расчета (t < τ), истинная скорость турбулентного пламени почти постоянна (см. наклон кривой на рис. 5). Проверка показала, что одновременное удвоение числа расчетных точек по трем осям при сохранении размеров расчетной области (вместо 500 000 получается 4 000 000 ячеек) не изменяет значения истинной скорости ut турбулентного пламени.
Рис. 5.
Расчетная зависимость расстояния, пройденного усредненным фронтом турбулентного пламени, от времени. Водородно-воздушная смесь c содержанием водорода 17.36%, начальная температура Т0 = = 293 К, давление атмосферное; характеристики турбулентности: $\bar {u}$ = 675 см/с, L' = 1 см, τ = 0.010 с.
Если учесть тепловое расширение продуктов реакции, то по видимой скорости турбулентного пламени ut можно определить истинную скорость его распространения U, используя соотношение
где m0 и m1 – число молей в свежей смеси и в продуктах реакции соответственно.
Отметим, что в редких случаях в расчетах получались сильно заниженные значения скорости (меньше нормальной скорости ламинарного пламени). Поскольку речь идет о синтетической турбулентности, вероятно, причина этого эффекта – необычные комбинации случайных чисел при нахождении функции y(t). При этом сама функция имела хотя и странную, но легко узнаваемую форму. Такие решения считались “паразитными” и не принимались во внимание.
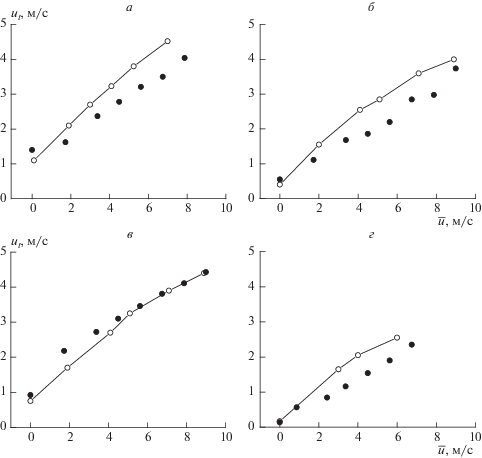
На рис. 6 проведено, как и в [20], сравнение расчетных и измеренных зависимостей истинной скорости ut распространения турбулентного пламени в смесях разного состава от пространственной среднеквадратичной пульсационной скорости $\bar {u}.$ Видно, что при увеличении турбулентности ut возрастает. Из приведенного сравнения следует вывод об удовлетворительном качественном согласии результатов.
Рис. 6.
Зависимости скорости распространения турбулентного пламени ut от среднеквадратичной пульсационной скорости $\bar {u}.$ Темные кружки – расчет, светлые кружки с линиями – эксперимент [19]; водородно-воздушные смеси с содержанием водорода 23.09% (а), 13.51% (б), 17.36% (в) и 9.09% (г); начальная температура Т0 = 293 К, давление атмосферное; характеристики турбулентности: L' = 1 см, τ = 0.010 с.
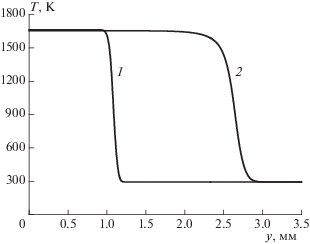
На рис. 7 проведено сравнение расчетных профилей температуры в ламинарном и турбулентном пламенах. По этим профилям можно оценить толщину пламени и сравнить ее с пространственными масштабами пульсаций скорости. Профиль температуры в турбулентном пламени более пологий, чем в ламинарном пламени, а само турбулентное пламя шире, чем ламинарное вследствие влияния мелкомасштабных обменных процессов.
Рис. 7.
Расчетные профили температуры в ламинарном (1) и турбулентном (2) пламенах. Водородно-воздушная смесь с содержанием водорода 17.36%, начальная температура Т0 = 293 К, давление атмосферное. Для турбулентного пламени характеристики турбулентности: $\bar {u}$ = 675 см/с, L' = 1 см, τ = 0.010 с.
На рис. 8 представлен пример расчетных профилей температуры и концентраций промежуточных и конечных продуктов реакции в турбулентном пламени. Несмотря на схожесть структур зон реакции в турбулентном и ламинарном пламенах, здесь все же есть некоторые количественные различия. Так, концентрации самых активных промежуточных продуктов реакции – гидроксила ОН, атомов Н и О – в турбулентном пламени оказываются ниже, чем в ламинарном. Это отчетливо видно на рис. 9, на котором представлены примеры расчетных зависимостей максимальных по зоне реакции концентраций гидроксила от среднеквадратичной пульсационной скорости $\bar {u}.$ Понижение концентрации активных центров является следствием увеличения интенсивности турбулентности, т.е. следствием ускорения обменных процессов. По косвенным данным такой вывод был сделан и в экспериментах, описанных в работе [21].
Рис. 8.
Расчетные профили температуры и концентраций разных веществ в турбулентном пламени. Водородно-воздушная смесь с содержанием водорода 17.36%, начальная температура Т0 = 293 К, давление атмосферное; характеристики турбулентности: $\bar {u}$ = 675 см/с, L' = 1 см, τ = 0.010 с.
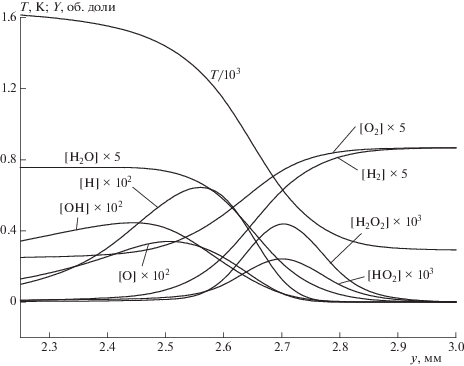
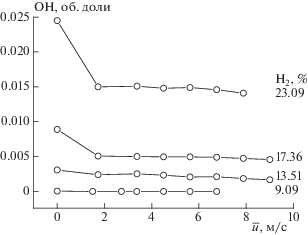
Рис. 9.
Расчетные зависимости концентрации гидроксила от среднеквадратичной пульсационной скорости $\bar {u}.$ Водородно-воздушные смеси разного состава, начальная температура Т0 = 293 К, давление атмосферное; характеристики турбулентности: L' = 1 см, τ = 0.010 с.
В заключение отметим еще один результат, который важен для понимания структуры зоны горения в турбулентном пламени: во всех проведенных расчетах поверхность фронта пламени была односвязной. Анализ расчетных распределений концентраций реагентов показал, что даже при максимальных интенсивностях турбулентности в поле течения не обнаруживаются “островки” свежей горючей смеси, окруженные продуктами горения. Это не согласуется с результатами расчетов в работе [10], где отмечалось наличие таких “островков”. По-видимому, здесь сказывается различие в методиках описания поля турбулентности или недостаточно длительное моделирование процесса распространения турбулентного пламени. Этот вопрос будет исследован дополнительно.
ЗАКЛЮЧЕНИЕ
Предложена методика трехмерного прямого численного моделирования распространения турбулентного пламени в газовых реагирующих смесях в поле синтетической стационарной, однородной и изотропной турбулентности. Методика основана на детальном кинетическом механизме горения многокомпонентной смеси, не содержит каких-либо подгоночных параметров и применена к расчету турбулентного горения водородно-воздушных смесей разного состава.
Сравнение результатов расчетов с экспериментальными данными показало, что между ними есть удовлетворительное качественное соответствие: согласно как расчету, так и эксперименту скорость турбулентного горения возрастает с увеличением интенсивности турбулентности. Расчеты показывают, что концентрации активных центров реакции – гидроксила ОН, атомов Н и О в турбулентном пламени меньше, чем в ламинарном, что также согласуется с экспериментом.
Дальнейшая работа будет направлена на применение предложенной методики к воздушным смесям углеводородных горючих, прежде всего метана. Важнейшая особенность турбулентного горения углеводородов, наблюдаемая экспериментально, – это погасание пламени при высоких интенсивностях турбулентности.
Работа выполнена при поддержке Российским научным фондом (проект 18-73-10196).
Список литературы
Damkoler G. // Z. Elektrochem. 1940. B. 46. S. 601.
Щелкин К.И. // ЖТФ. 1943. Т. 13. С. 520.
Lewis B., Elbe G. Combust., Flames and Explosions of Gases. Orlando: Acad. Press, 1987.
Соколик А.С.Самовоспламенение, пламя и детонация в газах. М.: Изд-во АН СССР, 1960.
Щетинков Е.С. Физика горения газов. М.: Наука, 1965.
Bernard J.A., Bradley J.N. Flame and Combustion. L.–N.Y.: Chapman and Hall, 1985.
Echekki T., Chen J.H. // Combust. and Flame. 2003. V. 134. P. 169.
Bell J.B., Day M.S., Grcar J.F. // Proc. Combust. Inst. 2002. V. 29. P. 1987.
Bell J.B., Cheng R.K., Day M.S., Shepherd I.G. // Ibid. 2006. V. 31. P. 1309.
Aspden A.J., Day M.S., Bell J.B. // Combust. and Flame. 2016. V. 166. P. 266.
Басевич В.Я., Володин В.П., Когарко С.М., Перегудов Н.И. // Хим. физика. 1982. Т. 1. № 8. С. 1130.
Басевич В.Я., Беляев А.А., Фролов С.М., Басара Б. // Горение и взрыв. 2017. Т. 10. № 1. С. 4.
Басевич В.Я., Беляев А.А., Фролов С.М., Фролов Ф.С. // Хим. физика. 2019. Т. 38. № 1. С. 27.
Williams F.A. Combustion Theory. California: Benjamin Cummings, 1985.
Годунов С.К., Рябенький В.С. Разностные схемы. М.: Наука, 1977.
Яненко Н.Н. Метод дробных шагов решения многомерных задач математической физики. Новосибирск: Наука, 1967.
Басевич В.Я., Беляев А.А., Посвянский В.С., Фролов С.М. // Хим. физика. 2013. Т. 32. № 4. С. 87.
Thermodynamic Data at the Web Site of the Laboratory for Chemical Kinetics. Alexander Burcat’s. Ideal Gas Thermodynamic Data in Polynomial Form for Combustion and Air Pollution Use; http://garfield.chem.elte.hu/Burcat/burcat.html
Reid R.C., Prausnitz J.M., Sherwood T.K. The Properties of Gases and Liquids. N.Y.: McGraw-Hill, 1977.
Карпов В.П., Северин Е.С. // Физика горения и взрыва. 1980. Т. 16. № 1. С. 45.
Басевич В.Я., Когарко С.М. // Там же. 1985. Т. 21. № 5. С. 12.
Дополнительные материалы отсутствуют.
Инструменты
Химическая физика