Химическая физика, 2020, T. 39, № 2, стр. 3-17

1. ИСТОРИЯ РАЗВИТИЯ ЭКОЛОГИЧЕСКИХ МОДЕЛЕЙ

О математическом моделировании экологических процессов написано уже столько, что от авторов потребовалась определенная смелость, чтобы совершить попытку донести до читателей что-нибудь практически полезное по этой теме. В работе Ю.М. Свирежева [1], одного из основоположников математического моделирования в экологии, сказано: “сложилась ситуация, при которой любой человек, мало-мальски овладевший тем или иным математическим аппаратом, обязательно строит “модель”, и обязательно “математическую” или “кибернетическую”.

В справочнике Йоргенсена с соавт. [2] предпринята попытка отразить опыт, накопленный за последнее десятилетие XX века при разработке около 1000 моделей. Идея авторов [2] – дать представления об уже созданных экологических моделях, с тем чтобы создатель новой модели мог бы “стоять на плечах” предыдущих разработчиков, иметь достаточно сведений о том, есть ли аналогичные прецеденты (use case) в ранее опубликованных работах, и, если кто-то ранее уже исследовал ту же или подобную проблему в похожей экосистеме, то весьма полезно было бы знать, каковы были его достижения, в чем состояли успехи, а где встретились непреодолимые сложности.

В справочнике [2] подробно рассмотрено 400 наиболее представительных моделей, однако влияние этого доброго начинания на последующее развитие экологических моделей следует отнести скорее к разряду благих намерений, чем давших плоды проектов. Причина того, что преемственность моделей на практике не срабатывает, кроется не только в том, что разработчики алгоритмов математического расчета экологических моделей в силу специфики своего образования слабо ориентируются в вопросах биологии, а пользователи разработанных алгоритмов, наполняющие их химико-биологическим содержанием, не представляют себе подводных камней вычислительной процедуры, но и в том, что в реальной жизни пока что задачи, которые решаются в математической физике и механике, как правило, куда сложнее и глубже, чем те, которые решают математические биологи. По сути, недостатков исследований по математической биологии только два: слабое проникновение в биологическую сущность проблем и низкий математический уровень [3].

Не менее важным негативным моментом, на наш взгляд, является коммерциализация программного обеспечения для моделирования. Доступные пакеты программ, как правило, имеют недоступную для массового пользователя цену. Но даже в тех случаях, когда составитель модели имеет доступ к требуемому пакету, крайне редки случаи, что у пакета при этом – открытый код (open source), что не только снижает привлекательность продукта, но и заметно ограничивает возможности его развития.

В ряде случаев возникает не только проблема применения тех или иных математических алгоритмов, но и проблема концептуального подхода к моделированию. Даже с оговоркой, что не все модели детерминированно описывают объект, отдельный интерес представляет ответ на вопрос о том, насколько детерминирован выбор самой модели? Утверждение о том, что теоретическое построение может быть однозначно выведено из экспериментальных данных, было тщательно проанализировано и уверенно отвергнуто еще в середине XX века в публикациях таких столпов теоретической физики, как Фейнман и Вигнер [4]. В настоящее время “модельный детерминизм” может появляться или необоснованно – из-за недостатка образования, или (редко) – из-за предельной примитивности объекта или явления.

Практически это означает, что в эмпирически доступных пределах альтернативные модели могут давать сопоставимый результат, а различие между выдвинутыми гипотезами не может быть обосновано статистически достоверно. Принципиальным моментом в разработке экологических моделей является тот факт, что экологический эксперимент не подразумевает сослагательного наклонения. В частности, все данные по глобальному потеплению климата имеют один единственный набор временны́х рядов (для различных географических координат), который не может быть воспроизведен или повторен ни при каких обстоятельствах.

В этом смысле понятие вероятности (как величины, равной отношению числа “благоприятных” исходов к их общему числу) применимо к экологическим моделям лишь с большой натяжкой, поскольку верификация вероятностных предсказаний основана на идее повторяемости испытаний. Для экологических процессов важную роль играют такие явления, как изменение климата, глобальные тектонические изменения, массовая миграция, исчезновение отдельных биологических видов и другие, где даже на мысленном уровне понятие воспроизводимости временны́х рядов требует представления об альтернативных параллельных мирах.

Казалось бы, ограничения в вероятностной трактовке экологических процессов должны были бы свести на нет попытки статистического анализа таких систем, но на практике все произошло с точностью до наоборот. В 1973 году Хиротугу Акаике опубликовал оценку “близости моделей”, основанную на максимизированном логарифмическом правдоподобии Фишера [5]. Его мера, называемая информационным критерием Акаике (AIC), породила новую парадигму выбора модели при статистическом анализе эмпирических данных и дала начало тысячам публикаций. Хотя этот подход имеет фундаментальную и достаточно простую связь с теорией информации, в естественных и прикладных науках перспективность его применения гораздо менее очевидна. В математической биологии этот подход привел к отказу от понятия “правильная” (“истинная”) модель. Моделирование при этом рассматривается как упражнение в наилучшем приближении расчета к эмпирическим данным в контексте выборки из некоторой четко определенной совокупности. Тем не менее на основании выбора наилучшей аппроксимирующей модели специалисты данного направления делают выводы о том, какие “эффекты” (представленные параметрами) могут быть поддержаны эмпирическими данными; при этом выбранная в экологии модель может существенно отличаться от модели, выбираемой на основе статистического тестирования исходных (нулевых) гипотез. При выборе модели для вероятностных распределений deLeeuw [6] приходит к выводу, что наиболее разумным (“убедительным”) критерием выбора модели является AIC, даже если модель не соответствует действительности. При этом поиск наилучшей аппроксимирующей модели превращается в самоцель, тогда как поиск физических закономерностей, лежащих в основе такой аппроксимации, отходит на второй план или даже вовсе выпадает из поля зрения исследователей.

Еще одной особенностью данного направления является то, что формальное предпочтение может быть оказано более чем одной модели (мультимодельный вывод). Такие процедуры среди сторонников AIC-подхода считаются более надежными [7].

В книге [7] приводится также простой пример сравнительной оценки ряда моделей. Были изучены закономерности накопления видов птиц среди лесных ландшафтов на востоке США с использованием индексных данных: y (зависимая переменная) – число накопившихся на территории видов, а x (аргумент) – численность общего поголовья [8, 9]. Были проведены расчеты с использованием априорного набора из девяти простейших элементарных функций для регрессии методом наименьших квадратов – степенная, показательная, логарифмическая, дробно-линейная и т.д. – с количеством подгоночных параметров от трех до пяти. Априори ясно (в том числе и самим авторам исследования), что ни одна из этих девяти моделей не будет “правдой”, которая формируется данными обследования гнездящихся птиц, а предпочтение отдается из соображений “разумной скупости”.

Нередко биологи собирают данные по 50–130 “экологическим” переменным и вслепую надеются, что какой-то метод анализа и компьютерная система будут находить “значимые” переменные и сортировать “интересные” результаты [10]. Авторы работы [11] назвали такой подход “стратегией стрельбы из дробовика”, причем данная стратегия превалирует в наивном использовании многих традиционных методов многомерного анализа (компоненты, пошаговый анализ дискриминантных функций, методы канонической корреляции и факторного анализа) и дает в основном ложные результаты. Никакое совершенство математических алгоритмов и увеличение вычислительной мощи компьютеров не должны поощрять исследователей к бездумному расширению набора предикторных переменных, хотя бы они и приводили к идеальному подгону первичных данных. Те же авторы сообщают об известных им случаях, когда набор переменных общим числом до 1500 применялся к числу измерений меньше 40 (что гарантирует абсолютную неопределенность поиска значимых отношений).

В предельно краткой форме проблему можно сформулировать так: специалисты, занимающиеся математическим моделированием сложных экологических систем, не понимают либо математики, либо химии и биологии, либо и того и другого.

2. ПРИМЕНЕНИЕ СИСТЕМНЫХ ОГРАНИЧЕНИЙ К ПОСТРОЕНИЮ МОДЕЛЕЙ

В работе Йоргенсена [12] приводится следующий пример. В течение многих лет люди использовали физические модели судов для определения профиля, который дает судну наименьшее сопротивление в воде. Такая модель имеет форму и относительные размеры реального корабля, но не содержит всех деталей, таких как приборы, планировка кают и т.д. Такие детали не имеют значения для целей этой модели. Подобным образом предлагается выделить и основные цели моделирования экосистем.

Экологические модели Йоргенсен сравнивает также с географическими картами (которые тоже являются моделями). Различные типы карт служат различным целям. Есть карты для самолетов, кораблей, автомобилей, железных дорог, геологов, археологов и т.д. Они все разные, потому что они фокусируются на разных объектах. Карты также доступны в различных масштабах в соответствии с применением и базовыми знаниями. Кроме того, карта никогда не содержит всех деталей для рассмотренной географической области, потому что было бы неуместно отвлекаться от основной цели карты.

Если с первой частью предыдущего образца [12] еще как-то можно согласиться, закрыв глаза на теорию подобия и необходимость одновременно с размерами модели изменять еще и вязкость среды, то вторая ее часть (про географические карты) вызывает больше возражений, чем имеет пунктов для согласия. Действительно, в зависимости от предназначения карты могут иметь различный масштаб и наполнение, т.е. на карте для туристов нет указания месторождений полезных ископаемых, а на картах для геологов обычно не указывают кафе и рестораны. И тем не менее – это одна и та же карта! В том смысле, что на любой из таких карт независимо от масштаба и предназначения расстояние от Мекки до Иерусалима будет (как и во времена Пророка) равно 1239 километров.

С математическими моделями экологических систем все обстоит совершенно иным образом. Например, одни только температурные модели дают в качестве прогноза и таяние шапок полярных льдов с одновременным повышением уровня мирового океана (либо в качестве варианта – повышение температуры без повышения уровня океана), и наступление очередного ледникового периода.

Йоргенсен [13] сформулировал общие ограничения по неопределенности моделей. Для того чтобы определить взаимозависимость двух компонентов, содержащихся в системе, необходимы как минимум три измерения (если их будет всего два, то невозможно даже отличить линейную зависимость от нелинейной). В случае трех компонент потребуется уже 3 ∙ 3 = 9 измерений. В общем случае при относительной точности измерений Δx должно выполняться следующее соотношение:

Так, уже для 18 компонентов требуется ни много ни мало 100 миллионов измерений. Тем самым исследователю, посвятившему свою жизнь статистическому направлению моделирования экосистем, предстоит нелегкий выбор: знать все ни о чем или ничего обо всем.

Приведенные ограничения исключают беспочвенную надежду на то, что со временем вычислительная мощь компьютеров позволит обрабатывать практически неограниченные наборы данных. Скорость работы компьютеров, действительно, становится выше в соответствии с законом Мура [14]. Но известен также и закон Вирта, который утверждает, что увеличение производительности аппаратной части еще не означает ускорения работы как таковой: оптимизация направлена на экономию времени работы программистов, но никак не на уменьшение времени исполнения алгоритмов самой программой. Это может происходить по нескольким причинам: добавление избыточных ненужных функций, плохой код, нежелание программистов дорабатывать программы и плохой менеджмент или частая смена команды.

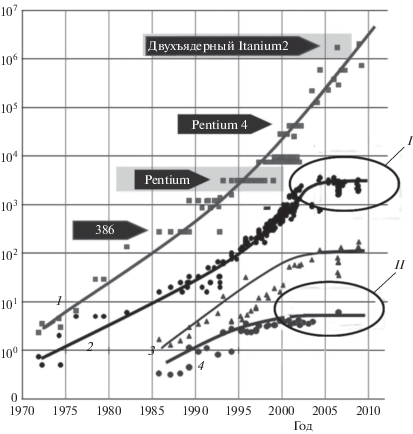
В качестве иллюстрации на рис. 1 показаны число транзисторов, тактовая частота, энергопотребление и степень параллелизма на уровне инструкций [15]. Как видно из приведенных на этом рисунке данных, рост числа транзисторов в процессоре ЭВМ перестал увеличивать производительность вычислений. Поэтому совершенно несбыточной мечтой остается возможность построения моделей с “достаточной степенью детализации”.

Рис. 1.

Иллюстрация закона Мура (источники: Intel, Википедия, К. Олукотун): 1 – плотность транзисторов, 2 – тактовая частота, 3 – вычислительная мощность, 4 – параллельные вычисления; I – частота процессора перестала расти, II – нет дальнейшего распараллеливания. Специалисты обратили внимание, что, несмотря на рост числа транзисторов в процессоре, ЭВМ перестали увеличивать производительность вычислений.

Наложение общих системных требований на модели, на первый взгляд, вносит заметное упорядочивающее действие в организацию исследований и выбор адекватной модели. Уравнения модели и их параметры должны соответствовать свойствам экосистемы. Контрольные условия, налагаемые на свойства моделей, имеют все более возрастающую сложность (а значит, и неопределенность) по мере продвижения от общефизических принципов к ограничениям химическим и далее – биологическим.

Последовательность усложнения требований к моделям отражает уменьшение отношения к физическим свойствам и увеличение отношения к биологическим свойствам экосистем. На фоне требований поддержания видового разнообразия или относительного постоянства химического состава в трофических цепях общефизические требования выглядят простыми и ясными. Но только на первый взгляд.

Принципы сохранения часто используются в качестве ограничений модели. Биогеохимические модели должны соблюдать законы сохранения массы, а биоэнергетические – в такой же степени подчиняться закону сохранения энергии.

Материя и энергия должны сохраняться в соответствии с основными физическими понятиями, что также справедливо для экосистем. Требуется, чтобы энергия и материя не создавались и не уничтожались. Взаимопревращение материи и энергии в соответствии с известной эйнштейновской формулой представляет интерес только для ядерной энергетики. Поэтому в подавляющем большинстве экологических моделей два основополагающих принципа рассматриваются раздельно:

1) экосистемы сохраняют материю;

2) экосистемы сохраняют энергию.

Тем не менее практическое применение, казалось бы, столь легко проверяемых принципов упирается в неожиданные сложности. Определить, какая часть потока солнечной энергии тратится на фотосинтез, а какая бесполезно рассеивается в виде тепла и переизлучается обратно в космос, – задача неразрешимая. По итогу практически все органические материалы: высушенные ткани инфузории, гидры, земляных червей, водной улитки, жуков, гуппи, имеют одинаковую теплоту сгорания – от 5500 до 5900 ккал/кг, что очень мало отличается от теплотворной способности дров. В этом контексте и рассуждения об избыточной эксергии высокоорганизованных видов, стоящих на верхних ступенях эволюционной лестницы, выглядят термодинамически несостоятельными. Все дрова горят одинаково!

Аналогичным образом очень трудно проверить и материальный баланс. Все экосистемы являются открытыми, но помимо учитываемых каналов приноса и уноса отдельных веществ и элементов далеко не всегда имеется возможность корректно оценить скорость массобмена толщи и поверхностных слоев воды, выпадения донных отложений и унос вещества в атмосферу. В итоге применение незыблемых законов сохранения в качестве контрольных требований остается скорее добрым пожеланием, чем реально используемым и работающим набором уравнений.

3. СТРУКТУРНО-ДИНАМИЧЕСКИЕ МОДЕЛИ

Модели последнего поколения, получившие названия структурно-динамических, обычно включают в себя некоторый биогеоценоз (основная структурная единица, которая может быть представлена как самостоятельная экосистема – термин, введенный В.Н. Сукачевым). Такие модели часто формализуются в виде набора дифференциальных уравнений в сочетании с некоторыми алгебраическими уравнениями и списком входных параметров: дифференциальные уравнения требуют определения начального состояния и задания граничных условий.

При этом молчаливо предполагается, что чем больше отдельных стадий включено в модель, тем она точнее приближает расчетные величины к истинным их значениям и тем сильнее прогностические возможности модели. В научном сообществе сформировалось стойкое и, скорее всего, ложное ощущение, что накопление первичных данных, получаемых инструментальными методами, дополнение химических реакций процессами трансформации веществ с участием гидробионтов и, наконец, учет процессов массопереноса между различными резервуарами экосистемы приведут в обозримом будущем к созданию всеобъемлющей модели формирования квазистационарного состояния того или иного водоема.

С другой стороны, усложнение системы уравнений и увеличение числа вычисляемых переменных, очевидно, может способствовать только уменьшению устойчивости системы и увеличению вероятности ее срыва в хаотический режим. Из теории хаоса Колмогорова, Арнольда и Мозера (КАМ) известно, что в общем случае движение распадается на два типа:

1) периодическое движение, происходящее в определенной ограниченной части фазового пространства;

2) случайное движение, “покрывающее” все фазовое пространство.

В теории динамических систем принято использовать понятие инвариантной меры, которая не изменяется с течением времени при эволюции положения системы в фазовом пространстве. Понятие инвариантной меры применяется при усреднении уравнений движения, в теории показателей Ляпунова, в теории метрической энтропии и вероятностных фрактальных размерностей.

Как периодическое, так и хаотическое движения могут иметь положительную меру. Наоборот, ограниченные движения эргодических систем (или систем с перемешиванием) имеют меру нуль.

Для систем, обладающих слабой устойчивостью, свойство упорядоченности типов движения утрачивается. В таких системах один тип движения может встречаться в сколь угодно малой окрестности другого типа движения. Увеличение точности наблюдений в данном случае не имеет смысла. Микроструктура фазового пространства становится чрезвычайно сложной, что вынуждает исследователя при долгосрочных прогнозах привлекать различного рода статистические соображения. Еще меньше смысла в таких случаях имеет увеличение числа наблюдаемых переменных. Понятно, что для систем, склонных к впадению в хаос, понятие прогнозирования также приобретает специфическое толкование.

Прогноз как попытка заглянуть в будущее всегда содержит в себе элемент вероятности. Но поскольку экологические системы в принципе не допускают повторения экспериментов “на воспроизводимость”, вероятностную оценку подменяет правдоподобность модели.

Принято считать, что при построении математической модели любой системы главная задача – создать модель достаточной полноты. Для этого необходимо стремиться учесть все существенные факторы, влияющие на рассматриваемые явления; уделить специальное внимание наличию в ней противоречивых элементов как одного из признаков полноты модели; учесть возможность появления неизвестных факторов, чтобы в случае необходимости дополнить модель новым элементом. Однако последние полсотни лет применения “тяжелой артиллерии” в виде компьютерного моделирования сложных явлений показали, что локальная точность совпадения модельного представления системы и прогностическая способность модели – это совершенно разнородные и даже частично не совпадающие свойства.

С современных позиций можно отметить два крайних варианта моделирования, дающего самые ненадежные прогнозы. С одной стороны, это полное отсутствие физической модели процесса. Тогда математическое моделирование временны́х рядов основывается на вероятностном описании случайных блужданий, что получило весьма широкое распространение в экономических расчетах биржевых котировок акций или курсов валют. Характерно, что, несмотря на десятки нобелевских премий за количественные модели экономики, еще ни разу не удалось ни предсказать, ни, тем более, купировать нежелательные последствия ни одного из кризисов.

Вторая крайность основана на исчерпывающем понимании сути происходящего процесса, вызывающем убежденность в том, что завтра будет так же, как вчера. Так, начиная с середины XIX столетия, появились многочисленные демографические прогнозы, в том числе и от весьма авторитетных ученых. Основывались эти модели на представлениях о законе первого порядка, согласно которому (как и в случае с законом Мура) прирост происходит от достигнутого и пропорционально ему, что математически однозначно сводится к экспоненциальной функции от времени. Этого соблазна не избежал даже великий Дмитрий Иванович Менделеев, который, исходя из модели экспоненциального роста населения и сопутствующего ему развития гужевого транспорта, рассчитал, что через 50 лет уровень навоза достигнет подоконников первого этажа, после чего дальнейшее развитие урбанизации станет невозможным.

В развитии сколько-нибудь сложной системы можно ожидать прохождение точек бифуркации, где траектория движения в фазовом пространстве может с той или иной вероятностью пойти по одной из нескольких ветвей, что делает надежность сколько-нибудь долгосрочного прогноза исчезающе малой. Но даже для систем, в которых описание носит не вероятностный, а полностью детерминированный характер, долгосрочные прогнозы ложны.

Основное положение лапласовского детерминизма было сформулировано следующим образом: “Современное состояние природы, очевидно, является следствием ее предыдущего состояния. Ум, который был бы способен знать в определенное время все взаимодействия между объектами Вселенной, был бы в состоянии установить соответствующие положения, движения и взаимодействия всех этих объектов в любой момент времени, как в прошлом, так и в будущем. Кривая, описываемая молекулой воздуха или пара, управляется столь же строго и определенно, как и планетные орбиты: между ними лишь та разница, что налагается нашим неведением”.

Тем не менее даже для небесной механики, в которой нет ни трения, ни заметного изменения массы участников, ничего, кроме идеально точно соблюдающегося закона всемирного тяготения, задача хорошо решается лишь для случая, если участников только двое, а уже задача трех тел в квадратурах не берется. Все же на ограниченном промежутке времени траектория любого из тел может быть рассчитана с любой наперед заданной точностью, чего, увы, нельзя сказать про химические, биологические и вообще экологические системы.

Экологические изыскания, направленные на прогнозирование рисков, особенно техногенных, чаще всего с поставленной задачей не справляются.

Попробуем дать обобщенный взгляд на то, какие именно системы дифференциальных уравнений могут встретиться применительно к вопросам химической безопасности. Не касаясь вопросов, связанных с взаимоотношением структуры и свойств загрязняющих веществ (ЗВ), равно как вопросов острой и хронической токсичности, ограничимся только попытками поиска ответа на вопросы – сколько, когда и где может образоваться представляющих опасность загрязняющих веществ.

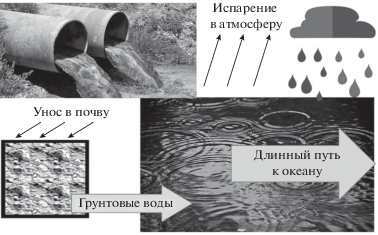
Все поступающие в атмосферу ЗВ, будь то промышленные выбросы, аммиачные испарения скотоферм или извержения вулканов, будут существовать в атмосфере максимум до первого дождя, после чего никуда, кроме как в водоемы, попасть им не суждено. Внесенные в почвы в ходе агротехнических мероприятий удобрения и пестициды с поверхностным стоком, движением грунтовых вод постепенно, в зависимости от сорбционной способности и растворимости, химической стойкости и биологической активности, рано или поздно в исходном либо измененном виде окажутся все в тех же водоемах, если только не будут произведены в них изначально (см. рис. 2).

Рис. 2.

Общая схема миграции загрязнителей в водных экосистемах.

Что будет происходить дальше? Все реки за довольно короткий промежуток времени доберутся до морей и океанов, в которых разбавление столь существенное, что, несмотря на все усилия человечества, внести заметный вклад в загрязнение мирового океана пока не удалось. Исключение составляет узкая прибрежная полоса, которую без ограничения общности можно причислить к эстуариям рек. Кроме того, если Мировой Океан не в состоянии справиться с каким-либо из поступающих в него потоков ЗВ, он вполне в состоянии включить вертикальный “конвейер” и удалить лишние ЗВ в виде донных отложений.

В ряде мест, особенно курортных, прибрежная зона – пелагиаль – загрязнена сплошным слоем полиэтилена и алюминия от всевозможной посуды и упаковок. Но это загрязнение, отвратительное с эстетической точки зрения и явно вредное для обитателей водной среды, практически не представляет угрозы с точки зрения химической безопасности.

Тем самым круг исследуемых задач можно сузить путем создания пространственно-временных рамок или ограничений. В конечном итоге основной интерес представляют лишь вещества, загрязняющие поверхностные воды суши до их поступления в океан. Если ЗВ докатились до океана, то по большому счету беда миновала. Что, конечно, не отменяет необходимости бороться с загрязнением океана нефтепродуктами, пластиком и т.д. Но эта часть задачи, за исключением случаев аварийных разливов нефти и нефтепродуктов, не требует решения уравнений и моделирования.

Остается водный поток с возможными разбавлениями и сбросами ЗВ, которые в водной среде подвержены разнообразным физико-химическим, химическим и биохимическим превращениям.

4. ВЫЧИСЛИТЕЛЬНЫЕ ПРОБЛЕМЫ ЭКОЛОГИЧЕСКИХ МОДЕЛЕЙ

Пространственно-временная картина распространения ЗВ в общем случае дается уравнением диффузии с массопереносом и химическими превращениями:

с соответствующими граничными и начальными условиями.

Первый член с градиентом концентрации соответствует диффузионному распространению вещества. Общий вид подразумевает пространственную неоднородность коэффициента диффузии, что на практике встречается довольно редко. Чаще всего коэффициент диффузии – это все-таки константа, которую можно вынести из-под знака дифференциального оператора. Второй член общего уравнения (с дивергенцией поля скоростей) отвечает за конвективный массоперенос. И, наконец, третий член соответствует интенсивности источников или стоков для вещества в точке, т.е. собственно кинетике химических превращений.

С помощью операторов Гамильтона и Лапласа уравнение записывается компактно:

Компактный вид не должен вводить в заблуждение относительно вычислительных сложностей при его решении. В нем скрыты двукратное дифференцирование по трем пространственным координатам и дифференцирование по времени. Это несколько сложнее, чем кажется при полном покомпонентном выписывании многочленного выражения:

Даже в простейшем случае, когда система обладает аксиальной симметрией и в ней имеется хорошее перемешивание, алгоритм численного решения дифференциального уравнения весьма далек от простоты, даже в случае всего одного компонента.

Чтобы понять смысл знаменитого выражения Пригожина: “Динамические системы не интегрируемы и не эргодичны”, нет необходимости разбираться с трехмерным случаем, осложненным химическими превращениями и потоковым массопереносом. Достаточно попытаться использовать любой из алгоритмов численного интегрирования для одномерного случая. Простейшее уравнение диффузионного “расплывания” залпового вброса ЗВ имеет вид

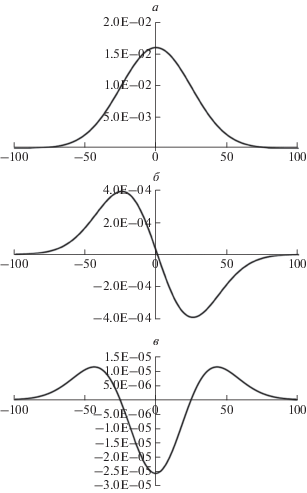
Фундаментальное решение данного уравнения известно – это функция Гаусса (см. уравнение (6) и рис. 3). Ее инвариантом является отношение квадрата линейной координаты ко времени или, что то же самое, – отношение линейного смещения от центра пятна загрязнения к корню квадратному из времени:

Рис. 3.

Функция Гаусса (а), ее первая (б) и вторая (в) производные.

Хотя точное аналитическое выражение для решения известно, можно попытаться получить пространственно-временные зависимости распространения загрязнения путем численного интегрирования уравнения (5) с использованием какой-либо модификации метода конечных разностей, с тем чтобы затем сравнить приближенное численное решение с точным. Заметим, что фундаментальное решение окажется сразу бесполезным, если включить в рассмотрение конвективное перемешивание и/или химическую реакцию. Поэтому правильный подход к численному моделированию такого процесса должен подразумевать возможность наращивания событий и процессов, а не ограничиваться простейшим случаем, когда решение могло быть получено в виде элементарной функции.

5. ИСПОЛЬЗОВАНИЕ РАЗНОСТНЫХ СХЕМ

Получив стартовое распределение концентраций, вычислив его как функцию Гаусса один раз (для момента времени t = 0), всю дальнейшую эволюцию необходимо рассчитывать, исходя из дифференциального уравнения диффузии (5). В него входят первая и вторая производные от концентрации по времени и по пространственной координате:

Поскольку для обработки экохимических процессов в реальных условиях использование аналитического выражения для гауссианы неуместно, приходится использовать приемы численного дифференцирования функции двух переменных, эволюция которой осложнена химическими и конвективными процессами.

Во избежание возможных проблем с точностью, при вычислении производных не будем ограничиваться простейшим отношением приращения абсциссы к приращению ординаты, а воспользуемся пятиточечным шаблоном, основанным на разложении в ряд Тейлора. Такой вариант дает на три порядка большую точность вычислений, чем линейное двухточечное приближение, хотя и усложняет вычислительную емкость модели.

Чтобы как-то компенсировать вычислительные затраты, воспользуемся элементарным соображением, что и первообразная и, соответственно, ее вторая производная являются четными функциями. Поэтому задачу можно решать только для положительной части полупространства (отрицательная часть будет просто ее зеркальным отражением).

Из рис. 3 видно, что вторая производная, по крайней мере на визуальном уровне, рассчитывается идеально. Тем не менее в уравнении диффузии (теплопроводности), включающем влияние второй производной на саму функцию, обнаруживается положительная обратная связь, которая приводит к экспоненциальному росту ошибок вычисления по мере увеличения числа шагов численного интегрирования. Даже ошибки машинной точности, связанной с округлением в последнем разряде, достаточно для возбуждения колебаний в интегрируемой функции. На рис. 4 наглядно показана неустойчивость явной разностной схемы для интегрирования уравнений диффузии.

Рис. 4.

Типичный результат численного интегрирования решений диффузионного уравнения с применением явной схемы метода конечных разностей.

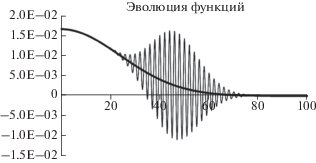
Обращает на себя внимание то, что самой “эволюции” как раз и не произошло – функция распределения концентрации не изменила ни положения максимума, ни ширины. Но на ней после 15–20 шагов по времени возникли осцилляции, которые являются вычислительным артефактом. Характерно, что “раскачка” функции, приводящая к ее неустойчивости, происходит в ее точке перегиба, т.е. там, где вторая производная ближе всего к нулю и малейшие флуктуации в состоянии сменить знак второй производной с “плюса” на “минус”, что и приводит к самым драматическим и неверным вычислительным последствиям.

Может показаться удивительным, что уменьшение шага интегрирования в разы или даже на порядки не спасает от появления осцилляций в численном решении. Хотя обычно численные методы с уменьшением шага становятся все более точными, для интегрирования уравнения теплопроводности внутренняя неустойчивость явной разностной схемы остается доминирующей и проявляется всегда. Более того, срыв в неустойчивый режим происходит тем раньше, чем меньше шаг по времени (шагов оказывается больше, но произведение величины шага на количество шагов до срыва уменьшается). Таким образом, метод “грубой силы” (“brute force”) приводит к результату, противоположному желаемому!

Можно перейти к неявной разностной схеме, которая гарантирует устойчивость расчетов. Но в общем случае это потребует решения системы линейных уравнений и инвертирования матриц на каждом шаге по времени. Вычислительная емкость неявной схемы – O(n³), где n – размерность сетки интегрирования по пространственным координатам (для сравнения вычислительная емкость явной схемы – O(n¹), что для большинства реальных задач означает проигрыш в тысячи раз при переходе от явной схемы к неявной).

Однако при использовании варианта Крэнка–Николсона (см. формулу (8)) устойчивость схемы счета достигается практически без увеличения вычислительной емкости:

Изящество схемы заключается в том, что матрица для вычисления правых частей получается трехдиагональной. В этом случае для решения системы линейных уравнений нет необходимости ее инвертировать – задача решается методом “прогонки”, который имеет вычислительную емкость O(n¹).

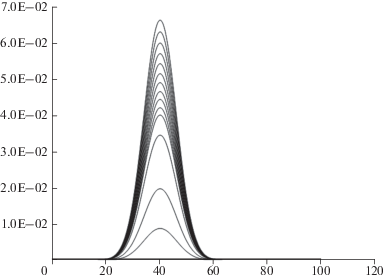
На рис. 5 представлены профили расползания пятна загрязнения, полученные путем расчета по схеме Крэнка–Николсона. Дрейф и химические превращения отсутствуют – площадь под кривыми, соответствующая общему количеству загрязнителя, сохраняется постоянной. Обращает на себя внимание то, что изначально прямоугольный профиль в ходе диффузии неизбежно приобретает форму гауссианы.

Рис. 5.

Численное интегрирование расползания пятна загрязнения методом тридиагонального прогона по схеме Крэнка–Николсона.

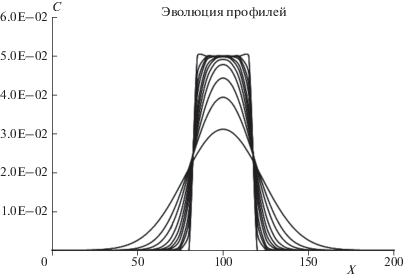
На рис. 6 представлены профили деградации загрязнителя в ходе химической реакции без учета диффузионного или потокового массопереноса. Методы и параметры те же, что и в случае рис. 5, но отсутствуют диффузия и дрейф. Чисто химическая деградация загрязнителя. Форма пространственного распределения загрязнителя изначально принята гауссовой.

Рис. 6.

Химическая деградация загрязнителя в пятне загрязнения. Диффузия и дрейф отсутствуют. Изначальная форма пространственного распределения загрязнителя принята гауссовой. Методы и параметры численного интегрирования эволюции пятна те же, что и в случае рис. 5.

На рис. 7 представлен случай “сползания” пятна загрязнения по течению водоема или при ветровом массопереносе, а на рис. 8 на эволюцию пятна загрязнения влияют все три фактора: диффузия, дрейф и химическая деградация. Для рис. 7 методы и параметры те же, что и в случае рис. 5, но отсутствуют диффузия и химическая деградация загрязнителя. Чистый дрейф при неизменной амплитуде и ширине пика. Обращает на себя внимание то, что даже при применении неявной схемы счета (устойчивой!) на больших временах эволюции появляются биения, аналогичные тем, что были в случае явной схемы на рис. 4.

Рис. 7.

Дрейф пятна загрязнения при неизменной амплитуде и ширине пика (диффузия и химическая деградация отсутствуют). Обращает на себя внимание то, что даже при применении неявной схемы счета (устойчивой!) на больших временах эволюции появляются биения, аналогичные тем, что были для явной схемы, приведенной на рис. 4. Методы и параметры численного интегрирования эволюции пятна те же, что и в случае рис. 5.

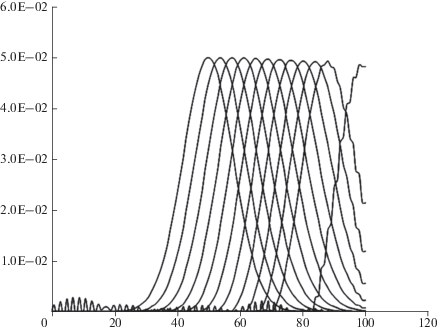
Рис. 8.

Исчезновение пятна загрязнения при одновременном воздействии трех факторов – диффузии, дрейфа и химической деградация. Из-за значительного уменьшения концентрации неустойчивость к дрейфу на больших временах не проявляется. Методы и параметры численного интегрирование те же, что и в случае рис. 5.

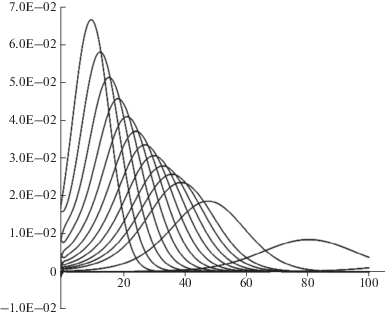
Для рис. 8 методы и параметры те же, что и в случае рис. 5. В эволюции представлены все три процесса – и диффузия, и дрейф, и химическая деградация. При этом неустойчивость к дрейфу на больших временах не проявляется.

На этих примерах достаточно убедительно видно, что при самых разнообразных процессах форма профиля довольно быстро перестает представлять интерес для исследования и моделирования. Какими бы ни были изначальная форма пятна загрязнения и параметры системы, через некоторое время профиль становится максимально близким к нормальному распределению. При этом моделирование показывает, что даже протяженные вдоль одной координаты залповые вбросы асимптотически стремятся к приобретению формы радиально-симметричного (круглого) пятна.

С учетом изложенного нет никакого смысла рассматривать сколько-нибудь подробную пространственную сетку – ничего принципиально нового детализация масштаба модели принести не может. Совершенно другое дело – выбор детализации по времени. Кинетическая картина, особенно в случае присутствия не единичного вещества, а набора веществ, может оказаться весьма разнообразной.

На рис. 9–12 представлены возможные нетривиальные особенности динамики концентраций основных компонентов водной экосистемы Куйбышевского водохранилища (по схеме Сердюцкой и Каменевой, приведенной в работе [16]). Хотя схема взаимодействия веществ включает в себя всего 18 реакций между шестью наиболее значимыми компонентами экосистемы, назвать временнýю динамику системы “ожидаемой” или хотя бы “интуитивно понятной” никак нельзя.

Рис. 9.

Модельная двадцатилетняя динамика концентраций (в единицах массы) планктона (сплошная линия), неорганического азота (штриховая линия) и органического азота (точечная линия) в Куйбышевском водохранилище (расчет по схеме из работы [16]).

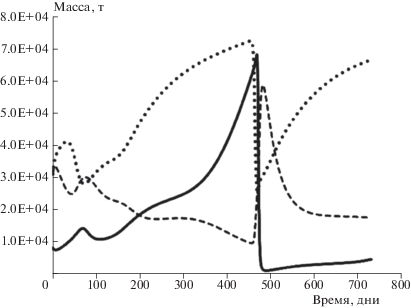
Рис. 10.

Фазовая диаграмма соотношения количеств зоопланктона и биопланктона в Куйбышевском водохранилище на двадцатилетнем промежутке времени (расчет по схеме из [16]).

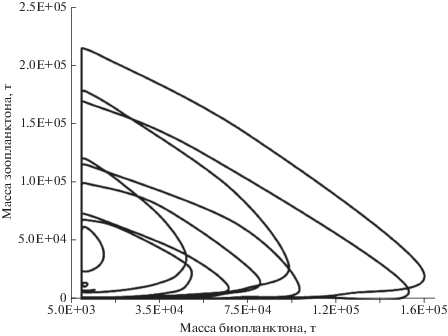
Рис. 11.

Фазовая диаграмма соотношения количеств органического и неорганического азота в Куйбышевском водохранилище на двадцатилетнем промежутке времени (расчет по схеме из [16]).

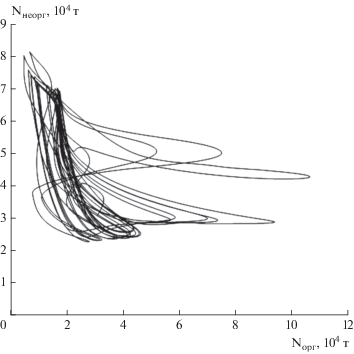
Рис. 12.

Модельная динамика массы зоопланктона в Куйбышевском водохранилище на двадцатилетнем промежутке времени (расчет по схеме из [16]).

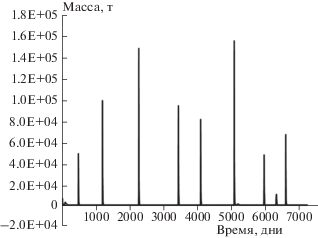
Полученные при численном моделировании кинетические кривые не слишком обнадеживают в ожидании прогноза. Еще меньше оснований полагаться на точность модельного прогноза остается после анализа фазовых траекторий в парах взаимопревращаемых веществ или биологических видов, находящихся в одной трофической цепи: зоопланктона и биопланктона (пара 1, рис. 10) и органического и неорганического азота (пара 2, рис. 11).

Хотя вынужденные колебания концентраций (или биомассы) тактируются сезонными колебаниями температуры, влияющими на скорость взаимопревращений, результирующая картина весьма далека от вынужденных колебаний с частотой вынуждающего фактора. В случае гармонических колебаний фазовые диаграммы представляли бы собой правильные окружности. Отклонение от гармонизма предполагает нарушение формы замкнутой фазовой траектории, но не дает априорных оснований ожидать или хотя бы подозревать псевдопериодическую сложную картину, которой соответствуют запутанные траектории на рис. 10 и особенно на рис. 11.

Еще большую непредсказуемость демонстрирует временна́я диаграмма количества зоопланктона на двадцатилетнем промежутке времени (рис. 12). Хотя смена сезонов и соответствующей им биологической активности происходит ежегодно, на всем двадцатилетнем промежутке мы можем насчитать всего лишь восемь кратковременных вспышек. Более внимательный анализ этого временнóго ряда показывает, что промежуток между вспышками может быть то два, то три года. Более того, максимум численности не обязательно приходится на весну или лето и может оказаться в межсезонье. Сам факт наличия периодичности (или псевдопериодичности) показывает качественную адекватность модели наблюдаемому явлению. Действительно, раз в несколько лет с не вполне понятной предсказуемостью наблюдается вспышка активности биоты. Но прогностическую силу подобной модели можно сопоставить разве что с прогнозом погоды, который утверждает, что вслед за летом непременно наступит зима, вот только не обязательно в этом году и может быть даже не в следующем. Но наступит.

К общим характеристикам такой модели можно добавить, что сравнительно небольшая вариация констант скорости в пределах 10–20% оставляет качественную картину динамики процесса столь же выразительной и разнообразной, но может поменять конкретные сроки наступления событий в разы.

ЗАКЛЮЧЕНИЕ

Последние десятилетия отмечены экспоненциальным ростом мощности компьютеров и снижением стоимости вычислений. Скорость вычислений удваивается каждые 24 месяца.

Применительно к математическому моделированию физико-химических процессов, определяющих качество природных вод, возросшие возможности вычислительной техники привели к развитию экстенсивного подхода, основанного на увеличении числа принимаемых в рассмотрение компонентов и реакций между ними. При этом молчаливо предполагается, что чем больше отдельных стадий включено в модель, тем она точнее приближает расчетные величины к истинным их значениям и тем сильнее прогностические возможности модели. Возникло стойкое ощущение, что накопление первичных данных, получаемых инструментальными методами, дополнение химических реакций процессами трансформации веществ с участием гидробионтов и учет процессов массопереноса между различными резервуарами экосистемы приведут в обозримом будущем к созданию всеобъемлющей модели формирования квазистационарного состояния того или иного водоема.

Однако, как показывает проведенный в данной работе анализ, это ощущение ошибочно. Приведенные в работе примеры показывают, что процессы массопереноса с диффузией и химическим превращением на вычислительной стадии охотно “срываются в осцилляции”. Оказалось, что это происходит не столько из-за несовершенства применяемых вычислительных алгоритмов, сколько из-за таковых свойств самих систем. А пошаговая вычислительная процедура – это не более чем “проявитель”, показывающий природу вещей.

Сложности, связанные с интегрированием динамических систем, каковыми являются экологические системы, связаны с тем, что малейшая флуктуация срывает систему из упорядоченного режима в хаотичный.

Формально задача моделирования звучит предельно просто: найти стационарный режим водоема (водной экосистемы) и время выхода на него. При этом необходимо быть готовым к тому, что экосистема будет претерпевать сезонные пульсации. При численном моделировании водной экосистемы биоорганизмы рассматриваются как псевдовещества, хотя и не химической природы, но подчиняющиеся закону действия масс.

Особую роль в математическом моделировании экологических систем (как и любых других динамических систем) играет случайное событие, исходно не закладываемое в параметры математической модели, но при реализации которого происходит качественное изменение модели – замена ранее действовавшей системы математических уравнений. Так или иначе, прогнозная модель работает лишь на каком-то интервале времени.

Хорошо рассчитываются лишь те системы, где проводится либо индивидуализация превращений, либо все очень хорошо перемешано. Настолько хорошо, что в течение интересного для моделирования промежутка времени система успеет побывать в каждой точке фазового пространства без нарушения законов сохранения. Причем не просто побывать, а еще и повести себя таким образом, что усреднение данных по всем участникам движения не будет ничем отличаться от длительного наблюдения за одной единственной частицей. Среднее по пространству равно среднему по времени. Это положение известно как эргодическая гипотеза, которую никто не доказал, но и не опроверг.

При рассмотрении эргодичных систем с хорошим перемешиванием обычно рассматриваются два предельных случая: реакторы идеального смешения и реакторы идеального вытеснения. В первом случае время считается, как оно есть (t = t) – от момента контакта реагентов (или от момента начала наблюдения) до текущего показания хронометра. Пространственную задачу можно вообще не рассматривать, поскольку во всех точках системы время контакта реагентов одинаково. Достаточно решить кинетическую задачу в одной точке, чтобы распространить полученное решение на все остальные фрагменты экосистемы. Во втором случае пространственная картина является временнóй разверткой происходящих событий, т.е. проекцией временны́х зависимостей на пространственную координату, когда время всецело определяется пространственными координатами (t = x/v).

Все остальные случаи находятся где-то между идеальным смешением и идеальным вытеснением. Но эта сложность незначительная, она сводится лишь к чуть более трудоемкому подсчету “локального времени” путем интегрирования по траектории. Тем самым первостепенное для прогнозирования значение получает умение моделировать временнóй ход реакции в точке.

В реакторах смешанного типа необходимо рассматривать пространственное распределение скоростей массовых потоков, которые могут также зависеть и от времени. При этом в отдельных фрагментах экосистемы участки объема неидеально вытеснились, тогда как в других местах они неидеально перемешались.

В общем случае “зрелость” того или иного фрагмента дается уравнением

Численное интегрирование систем со сложным кинетическим поведением и неоднородным пространственным распределением представляет собой весьма сложную вычислительную задачу. Решение ее с помощью разностных схем требует огромного ресурса машинного времени и вычислительных мощностей, которые недостижимы в настоящее время и не ожидаются в обозримом будущем. В то же время используемое в настоящей работе интегрирование подобных систем с применением метода Монте-Карло представляется весьма перспективным направлением моделирования.

Подводя итоги, можно подчеркнуть, что качественная картина изменения количеств компонентов экосистемы во времени несопоставимо богаче, чем их распределение по пространству. Именно по этой причине следует сосредотачивать основное внимание именно на кинетических параметрах экосистемы, отдавая себе отчет, что явления пространственного массопереноса в результате течений и диффузии носят второстепенный характер. Более того, пространственные картины фактически являются результатом проявления временнóй динамики с той оговоркой, что пространство – это время, затраченное на его преодоление.

Работа выполнена в рамках Программы фундаментальных исследований ИХФ РАН № 46.15 государственного задания № 0082-2014-0005 (номер государственной регистрации ЦИТИС: АААА-А17-117091220076-4).