Химическая физика, 2020, T. 39, № 9, стр. 3-8

ВВЕДЕНИЕ

Структурированные на наноуровне металлы и их соединения являются важной составной частью многих технологических устройств [1–4]. В частности, широко применяются наноразмерные проволочки (далее – нанопроволочки) и комплексы на их основе [1, 5]. Нанопроволочки также являются перспективными компонентами инновационных композитных материалов и естественными элементами каркасов комплексных наносистем [1]. Разработаны многочисленные методы получения нанопроволочек. Наиболее распространены различные вариации метода эпитаксии [5]. Однако применяемые методы имеют ограничения по производительности, особенно длинных нанопроволочек (длиной до сантиметра и более).

Ранее был реализован синтез нанопроволочек в объеме [6–10] и в свободно летящих каплях [11–13] жидкого гелия, обогащенного атомами металла. При этом атомы металла коагулируют в наноразмерные сферы (далее – наносферы), а наносферы частично объединяются в нанопроволочки. При приложении электрического поля напряженностью ~10² В/см удалось получить нанопроволочки длиной ~1 см$~$ [6]. Авторы перечисленных работ связывают формирование нанопроволочек с захватом квантовыми вихрями и быстрым объединением наносфер, диффундирующих вдоль вихря, при их частых столкновениях.

Однако нами было доказано [14–16], что механизм самосборки на квантовых вихрях не может обеспечить синтез нанопроволочек, поскольку:

1) огромное тепловыделение при сплавлении наносфер оторвет их от вихря;

2) нанопроволочки синтезируются не только ниже, но и выше λ-точки [8], когда нет квантовых вихрей;

3) нанопроволочки синтезируются также на поверхности жидкого гелия, нормальной к вихрям [17];

4) в летящих каплях гелия, имеющих размер ~1 мкм, формируется правильная решетка из ~200 вихрей [18], но атомы металла не распределяются по ним, а формируют несколько нанопроволочек [11–13], что статистически невероятно, если наносферы движутся в капле гелия независимо, и указывает на их взаимное притяжение.

С другой стороны, мы показали [14–16], что все экспериментальные факты, касающиеся синтеза нанопроволочек в жидком гелии, хорошо согласуются с известным дрейфовым механизмом формирования низкоразмерных структур [19, 20]. Так, раскаленные в ходе коагуляции наносферы, окруженные изолирующей прослойкой из гелиевого пара (наблюдалась их температура ∼(2÷4) ⋅ 10³ К [10]), приобретают заряд за счет термоэлектронной эмиссии [15, 16]; заряженные и поляризованные наносферы притягиваются друг к другу и к неоднородностям на поверхностях экспериментального оборудования [14–16]; конкуренция дрейфа наносфер под воздействием формирующихся электрических полей и термически обусловленной диффузии ведет к формированию системы с элементами самоподобия, структурными элементами которой являются квазиодномерные нанопроволочки, что мы и наблюдали в работах [14, 15]; при наличии однородного внешнего поля длина нанопроволочек может стать макроскопической, что наблюдалось в работе [6].

Еще раз подчеркнем: высокотемпературный синтез квазиодномерных структур за счет электростатических сил хорошо известен и широко распространен. Он реализуется в продуктах лазерной абляции в газах [21], во взрывной волне [22], в ходе поляризационной коагуляции [23], а также при диффузионно-контролируемой агрегации заряженных частиц во внешнем поле [19, 20, 24]. Такой синтез достаточно подробно изучен теоретически. Механизм коагуляции рассеянных атомов в наночастицы, формирующие далее квазиодномерные структуры, описан в работах [22, 25, 26]. Проанализирована кинетика перезарядки наночастиц за счет захвата ими присутствующих в системе свободных электронов [21]. Описан значительный вклад в свободную энергию энтропийного члена, обеспечивающего формирование одномерных систем при высокой температуре [21]. Рассмотрено электростатическое взаимодействие наночастиц за счет мультипольных моментов различных порядков [27]. Изучено влияние формы и ориентации частиц на структуру формирующихся нанопроволочек [27].

Наиболее существенно для нас то, что при приложении достаточно сильного внешнего поля за счет внесения в систему электродов со значительной разностью потенциалов между ними, в ней формируется два типа нанопроволочек: микроскопичкески короткие, создающиеся по всему объему, и макроскопически длинные, протянувшиеся от одного электрода к другому [6]. Короткие нанопроволочки могут формироваться за счет различных типов взаимодействия между наночастицами, рассмотренных выше. Но макроскопически длинные нанопроволочки очевидно формируются за счет притяжения заряженных наносфер к вершинам исходно незначительных возвышенностей на поверхности электродов, представляющих собой концентраторы поля [28]. Рост исходных возвышенностей увеличивает степень концентрации поля на их концах. Это формирует положительную обратную связь и обеспечивает эффективный рост начавших формироваться нанопроволочек до макроскопической длины [14–16].

Цель настоящей работы – исследование возможности роста между электродами именно таких, макроскопически длинных нанопроволочек в жидком азоте, обогащенном распыленным металлом, коагулировавшим в наносферы, приобретшие электрический заряд прежде всего за счет термоэлектронной эмиссии [15, 16]. Жидкий азот намного дешевле и технологичнее жидкого гелия, поэтому возможность формирования в нем нанопроволочек весьма существенна с точки зрения нанотехнологических приложений. При этом, как будет показано ниже, разупорядочивающее влияние относительно высокой температуры жидкого азота может быть скомпенсировано приложением достаточно сильного внешнего электростатического поля.

Отдельно обсудим вопросы о механизме формирования нанопроволочек из наносфер, об устойчивости формирующихся нанопроволочек и об их прочности. Многочисленные изображения нанопроволочек, полученные с помощью электронной микроскопии [7, 11–13], подтверждают тезис, отстаиваемый в работах [6–10], что нанопроволочки формируются путем частичного сплавления наносфер. При этом диаметр зон сплавления обычно чуть больше половины диаметра наносфер, так что прочность нанопроволочки в первом приближении можно оценить как прочность цилиндрической нанопроволочки, диаметр которой равен половине диаметра сплавившихся наносфер. Факт сплавления наносфер подтвержден прямым наблюдением излучения, исходящего из зоны формирования наносфер (в жидком гелии) и имеющего яркостную температуру ∼(2÷4) ⋅ 10³ К (в зависимости от металла) [10]. Энергия сплавления обеспечивается за счет уменьшения суммарной площади наносфер при сплавлении и тем самым уменьшения их поверхностной энергии, что хорошо подтверждается расчетами [7, 8]. При этом раскаленные сплавляющиеся наносферы отделены от жидкого гелия изолирующей прослойкой из испарившегося гелия [7, 8, 10]. Нанопроволочки устойчивы к воздействию тепловых флуктуаций, что подтверждено их электронно-микроскопическими изображениями, полученными после естественного нагрева образцов до комнатной температуры [7, 11–13]. Наличие у наносфер электрического заряда не способно повлиять на устойчивость формирующихся нанопроволочек. Действительно, энергия сплавления пары наносфер была оценена нами как ~(2÷5) ⋅ 10² эВ [14, 15], а энергия электростатического отталкивания наносфер радиусом r ~ 1 нм, имеющих элементарный заряд e, может быть оценена как ~e²/r ~ 1 эВ, что на два с половиной порядка меньше.

ОСНОВНЫЕ РЕЗУЛЬТАТЫ

Поскольку было установлено, что квантовые вихри не имеют существенного значения при самосборке нанопроволочек [14–16], этот процесс может быть осуществлен в жидком азоте – достаточно инертном, значительно более дешевом и существенно более технологичном, чем жидкий гелий. Достаточно высокая температура жидкого азота (T = 78 К) делает процесс диффузии, препятствующий формированию квазиодномерных элементов, более интенсивным, однако разупорядочивающее влияние температуры может быть скомпенсировано упорядочивающим влиянием внешнего электрического поля. Обоснуем предлагаемую концепцию.

Рассмотрим вначале движение в жидком азоте наносферы, приобретшей заряд e, в окрестности конца нанопроволочки на расстоянии R от него в отсутствие внешнего поля. Наносфера поляризует нанопроволочку. Основным концентратором поля выступает при этом именно ее конец [28]. Поэтому с разумной точностью можно считать, что наведенный заряд –e сосредоточен на самом ее конце. Наносфера будет захвачена концом нанопроволочки, если энергия их связи превосходит кинетическую энергию теплового движения наносферы:

(k – постоянная Больцмана), что в 30 раз превосходит типичный диаметр нанопроволочки, составляющий ~5 нм. Тот факт, что наносфера будет притянута именно к концу, а не к боковой поверхности нанопроволочки, соответствует представлению о концентрации наведенного заряда в конце проволочки и подробно обоснован нами в работах [15, 16].

Пусть теперь имеются два плоских параллельных друг другу электрода, левый и правый, расположенные на расстоянии Λ друг от друга. От левого электрода отходит нормально к нему проволочка длиной L с радиусом r, составляющим несколько нанометров. Будем полагать, что проволочка не является чрезвычайно короткой, т.е. L $ \gg $ r, и в то же время справа от нее остается достаточный зазор между проволочкой и электродом: Λ – L $ \gg $ r. Направим ось абсцисс вдоль проволочки. Начало координат поместим на поверхности левого электрода. Левый электрод заряжен отрицательно, правый – положительно. Разность потенциалов между ними равна U, так что напряженность поля в межэлектродном пространстве вдали от проволочки равна –E = –U/Λ. Межэлектродное пространство заполнено хорошо очищенным жидким азотом. Напряжение пробоя хорошо очищенных жидкостей E* ~ 10⁵ В/см. Поэтому положим E = 10⁴ В/см. Под воздействием разности потенциалов между электродами нанопроволочка приобретает некоторый отрицательный заряд –q, сосредоточенный в основном на ее конце [28].

Между двумя плоскими электродами реализуется нормальный к их поверхностям одномерный поток заряженных наносфер, сформированных в продуктах лазерной абляции, как это было реализовано в работах [6–10], или, возможно, за счет электрического взрыва проволочки. Эти наносферы положительно заряжены за счет термоэлектронной эмиссии. Под воздействием электрического поля они дрейфуют от правого электрода к левому. Часть наносфер захватывается отрицательно заряженным концом нанопроволочки. Поставим задачу: вычислим сечение захвата заряженных наносфер, дрейфующих в жидком азоте, концом проволочки.

Вновь, как и выше, будем приближенно считать, что весь заряд –q, наведенный на проволочке, сосредоточен в ее правом конце, на поверхности проволочки, т.е. в области размером ~r. Отметим, что фактически наведенный заряд распределен по проволочке, быстро убывая от ее конца. Это обеспечивает эквипотенциальность проволочки по ее длине. Поскольку основная часть заряда сосредоточена в окрестности конца проволочки [28], сделанное выше предположение о концентрации всего наведенного заряда в ее конце позволяет с разумной точностью вычислить электрическое поле в окрестности конца проволочки и тем самым определить сечение захвата заряженных наносфер этим концом. Картина поля в окрестности боковой поверхности проволочки будет при этом описана неточно: вместо нулевой напряженности поля во всей проволочке (представляющей собой эквипотенциальный элемент) практически на всей протяженности проволочки наш расчет даст неискаженное значение напряженности –E. Это внесет в полный поток наносфер в конце проволочки дополнительный поток, примерно отвечающий геометрическому сечению проволочки ~πr². Как мы увидим ниже, полное сечение захвата наносфер концом проволочки, S*, весьма велико: S* $ \gg $ πr². Этот результат подтвердит допустимость пренебрежения дополнительным малым потоком, т.е. допустимость использования (для подсчета потока наносфер в конец проволочки) расчетной модели, в которой весь заряд, наведенный на проволочке, сосредоточен в ее конце.

Далее пренебрежем искажением поля электродов зарядом, находящимся на конце проволочки. Действительно, оценка методом электростатических изображений показывает, что это искажение мало, так как в соответствии со сказанным выше выполняются условия r $ \ll $ L и r $ \ll $ (Λ – L), и потому справедливы соотношения

Окончательно для расчета потока наносфер в конец проволочки с разумной точностью можно считать, что поле между электродами складывается из однородного поля –E и поля от наносферы радиусом r, имеющей некоторый отрицательный заряд –q и располагающейся на конце проволочки. Тогда потенциал φ вдоль оси абсцисс равен (рис. 1)

Рис. 1.

Зависимость потенциала φ от расстояния x до левого электрода в используемой нами модели проволочки, находящейся между электродами. Фактически такая зависимость реализуется на некотором расстоянии от проволочки. Масштаб по оси абсцисс искажен для наглядности. При неискаженном масштабе область отклонения функциональной зависимости от линейной в окрестности точки x = L на несколько порядков уже.

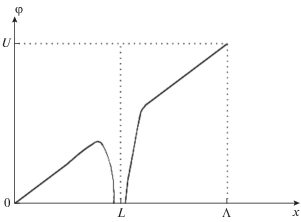
Отметим, что фактически такая зависимость потенциала от расстояния до левого электрода (т.е. линейная зависимость везде, кроме окрестности конца проволочки, где реализуется резкое падение, а затем резкое восстановление потенциала) реализуется на некотором расстоянии от проволочки.

Найдем величину q, исходя из того, что левый электрод и конец нанопроволочки находятся на эквипотенциальной поверхности, т.е. разность потенциалов между ними равна нулю; при этом разность потенциалов между концом нанопроволочки и правым электродом равна U:

Подставляя соотношение (3) в любое из равенств (4) и учитывая, что r ⪡ L, получим

Когда длина проволочки достаточно мала, наведенный заряд равен элементарному:

(численное значение указано для E = 10⁴ B/см и r = 5 нм). Если L < L*, то наведенный на конце нанопроволочки эффективный заряд, определяемый тепловым движением электронов проводимости в проволочке в окрестности ее конца, оказывается меньше элементарного.

Пусть теперь наносфера диаметром δ с зарядом e находится между электродами в окрестности конца проволочки. Разность потенциалов между электродами поляризовала конец нанопроволочки, наведя в нем заряд –q (см. (5)). Приблизившаяся наносфера навела дополнительно заряд –e.

Пока проволочка достаточно короткая: L < L*, можно учитывать только заряд, наведенный наносферой. При этом сечение S* захвата наносфер концом нанопроволочки равно площади круга радиусом R* (см. (1)):

Сопоставим его с сечением S₀ захвата незаряженных наносфер диаметром δ нанопроволочкой радиусом r :

При r = δ = 5 нм получим: S*/S₀ ≈ 350. Это говорит о селективном захвате заряженных наносфер концами даже коротких нанопроволочек.

Когда нанопроволочка становится достаточно длинной: L > L*, можно учитывать только заряд, наведенный на ее конце разностью потенциалов U. Наносфера будет захвачена концом проволочки, если энергия ее кулоновского взаимодействия с концом проволочки превосходит энергию ее теплового движения:

(численное значение указано для E = 10⁴ В/см, r = = 5 нм, T = 78 К). При этом сечение S** захвата заряженных наносфер определяется по формуле

Уже при L = 1 мкм S**/S₀ ≈ 5 ⋅ 10³. Соотношение (10) демонстрирует исключительно высокую селективность захвата заряженных наносфер концами нанопроволочек в присутствии внешнего электрического поля напряженностью E ~ 10⁴ В/см. Приведенная оценка обосновывает эффективность использования жидкого азота для формирования в нем нанопроволочек в присутствии внешнего поля.

Проследим за кинетикой движения заряженной наносферы диаметром δ между электродами. Отметим, что движение частиц в жидкости (на масштабе микрона и более), имеющих размер порядка нанометра и более, вполне удовлетворительно описывается в приближении механики сплошной среды. Это подтверждается близостью значений коэффициентов диффузии достаточно крупных молекул (имеющих размер порядка одного или нескольких нанометров), измеренных экспериментально и вычисленных с помощью формулы Эйнштейна–Стокса (при выводе которой предполагается, что сила трения крупной молекулы о жидкость задается формулой Стокса) [29]. Предположим, что число Рейнольдса при движении заряженной наносферы мало: Re $ \ll $ 1. Тогда сопротивление ее движению стоксово и наносфера движется со скоростью V при равновесии электростатической и стоксовой сил:

где η = 1.8 ⋅ 10^–3 г/(см ⋅ с) – вязкость жидкого азота. С учетом (11)

где ρ = 0.81 г/см – плотность жидкого азота. Численные значения в (11), (12) указаны для E = 10⁴ В/см, δ = 5 нм. Полученная оценка (12) подтверждает исходное предположение о малости числа Рейнольдса. Оценка (11) показывает, что время самосборки длинных нанопроволочек после формирования наносфер из распыленных атомов металла в поле с напряженностью E ~ 10⁴ В/см занимает секунды.

Кинетическая энергия W наносферы, связанная с дрейфом, составляет

где M – масса наносферы, ρ* – ее плотность. Численное значение указано для ρ* =10 г/см³, δ = 5 нм, V = 2 см/с. Энергия теплового движения наносферы, равная (3/2)kT ≈ 10^–2 эВ, превосходит эту величину на четыре порядка. Это показывает, что когда наносфера попадает в область эффективного сечения ее захвата концом нанопроволочки (см. (1), (7)), наличие дрейфа наносферы под воздействием однородного поля практически не сказывается на балансе кинетической и потенциальной энергии и частица будет притянута к концу нанопроволочки.

ЗАКЛЮЧЕНИЕ

Приведенные оценки показывают, что эффективное формирование макроскопически длинных металлических нанопроволочек из продуктов лазерной абляции или из продуктов электрического взрыва проволоки может проводиться в жидком азоте. Это существенно упрощает технологию производства и уменьшает его стоимость в сравнении с известным методом формирования нанопроволочек в жидком гелии. При этом деструктивное воздействие более высокой температуры компенсируется ориентирующим воздействием электрического поля напряженностью ~10⁴ В/см.

Работа выполнена в рамках госзадания (тема 45.9, 0082-2014-0011, АААА-А17-117111600093-8).