Химическая физика, 2021, T. 40, № 10, стр. 42-47

ВВЕДЕНИЕ

Изучению колебательных режимов в проточных химических реакторах, математические модели которых представляют собой систему двух дифференциальных уравнений, посвящено значительное количество исследований. Обзор моделей и некоторых полученных результатов выполнен авторами работ [1, 2].

В работе [3] для проточного реактора идеального смешения, в котором протекает простая экзотермическая реакция, впервые проведен систематический анализ возможных фазовых портретов. Авторы [3] исследовали эволюцию типа конкретного стационарного состояния и его устойчивость при изменении параметра, не влияющего на положение состояния, но существенным образом изменяющего его устойчивость. Таким параметром является множитель, стоящий в левой части нестационарного уравнения теплового баланса реактора. В той же работе приведено более тридцати простых фазовых портретов, выделены портреты с устойчивым предельным циклом, являющимся математическим образом термокинетических колебаний. Эта работа стимулировала дальнейшие исследования в этой области [4, 5]. Найдены более сложные фазовые портреты, содержащие два одновременно существующих предельных цикла, которые являются математическим образом колебательных режимов. Продолжаются исследования колебательных режимов взаимодействия в изотермических химических системах, основы которых заложили Белоусов и Жаботинский [6].

В работах [7, 8] проведены исследования колебательных режимов в неизотермическом проточном реакторе идеального смешения с гомогенной реакционной средой, в которой протекает двухстадийная последовательная реакция. В области множественности стационарных состояний обнаружены автоколебания. Авторами работы [9] в параметрическом пространстве системы определены различные возможные режимы работы реактора идеального смешения, включая области неединственности стационарных состояний и области колебательных режимов. Отметим работу [10], в которой для сложной кинетической схемы (шесть кинетических уравнений) обнаружены как устойчивые колебательные режимы, так и хаотические режимы, когда колебания теряют свою устойчивость. Наконец, упомянем работу [11], в которой подробно исследованы колебательные режимы в реакторе идеального вытеснения.

Значительный интерес представляет исследование реакторов идеального смешения с реакционной гетерогенной средой, поскольку такие реакторы важны в применении их на практике. Математическая модель такого реактора уже описывается системой трех обыкновенных дифференциальных уравнений с простыми начальными условиями.

Интересен также вопрос о механизме возникновения и эволюции колебательных режимов в таком реакторе идеального смешения. Ранее [12] мы исследовали динамическое поведение подобного реактора, в котором протекает бимолекулярная экзотермическая реакция в гетерогенной системе жидкость–жидкость, причем специальное внимание было уделено свойствам стационарных состояний. Настоящая работа выполнена в продолжение работы [12] и связана с изучением механизма возникновения и эволюции колебательных режимов.

ПОСТАНОВКА ЗАДАЧИ

В проточный реактор идеального смешения поступает приготовленная гетерогенная реакционная система жидкость–жидкость с объемной скоростью q. Дисперсионная среда представляет собой раствор компонента A, а дисперсная фаза – раствор компонента B. Дисперсионная среда экстрагирует компонент B, где он реагирует с компонентом A. Реакция экзотермическая и бимолекулярная. Предполагаем, что реагент A взят в избытке. Поэтому кинетика реакции описывается уравнением псевдопервого порядка, а концентрация реагента A в дисперсионной среде входит в выражение для наблюдаемой константы скорости.

В соответствии с работой [12] введем следующие обозначения: T – температура смеси в реакторе, T₀ – температура теплообменника, T_EN – температура смеси на входе в реактор, k – предэкспоненциальный множитель, E – энергия активации, R – универсальная газовая постоянная, Q – тепловой эффект реакции, α – коэффициент теплообмена, S – поверхность теплообмена реактора с теплообменником, V – объем реактора, c и ρ – соответственно удельная теплоемкость и плотность реакционной смеси, [B_A] – концентрация реагента B в дисперсионной среде, [B] – его концентрация в дисперсной фазе, [B₀] – его же концентрация на входе в реактор, ε – коэффициент распределения (отношение концентрации реагента B на межфазной поверхности со стороны дисперсионной среды к его концентрации в дисперсной фазе), δ – коэффициент массоотдачи, Σ – удельная поверхность раздела фаз, q – удельный объемный расход,

– масштабная температура. Обозначим выражение во вторых скобках как ${{\left( {{{\alpha S} \mathord{\left/ {\vphantom {{\alpha S} V}} \right. \kern-0em} V}} \right)}_{*}} = {{\alpha S} \mathord{\left/ {\vphantom {{\alpha S} V}} \right. \kern-0em} V} + {{c\rho q} \mathord{\left/ {\vphantom {{c\rho q} V}} \right. \kern-0em} V}.$

Для удобства решения задачи удобно перейти к безразмерным переменным:

Тогда подлежащая дальнейшему анализу система дифференциальных уравнений, описывающая динамическое поведение системы, и начальные условия примут вид

Здесь индекс “IN” соответствует значениям концентраций реагентов и температуры в начальный момент времени. Также использовались следующие безразмерные параметры:

Параметр γ заслуживает отдельного внимания. Дело в том, что варьирование величины этого параметра без изменения положения стационарного состояния влияет на его устойчивость. Это обстоятельство будет учтено ниже. При выполнении работы использован подход, предложенный в работе [3] и позволяющий анализировать эволюцию колебательной неустойчивости в зависимости от γ.

Система дифференциальных уравнений (1)–(3) с начальными условиями (4) решалась численно по неявной схеме Эйлера первого порядка точности с использованием программы, разработанной авторами представленной работы. В процессе вычислений величина шага по времени подбиралась по заданному алгоритму, учитывающему градиенты рассчитываемых значений температуры и концентраций.

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Еще в работе [12] было показано, что рассматриваемый реактор может иметь либо одно, либо три стационарных состояния. При этом единственное стационарное состояние, в зависимости от выбранных параметров, может быть как низкотемпературным, так и высокотемпературным. В данной работе мы исследуем поведение реактора, имеющего единственное стационарное состояние.

Примем следующие (весьма типичные для исследуемого реактора) значения параметров: β = 0.05, Da = 0.1, Se = 1.0, ε = 1.0, P = 100. Решая стационарную задачу, т.е. приравнивая нулю производные в системе уравнений (1)–(3), находим также стационарные значения температуры и степеней превращения: ${{\theta }_{{st}}}$ = 8.70494693, ${{\eta }_{{{{{\text{B}}}_{{st}}}}}}$ = 0.10928824, $\eta _{{{{{\text{B}}}_{{st}}}}}^{{\text{A}}}$ = 0.020217065. Согласно данным, полученным в [12], три последних величины соответствуют высокотемпературному единственному стационарному состоянию.

Для анализа механизма возникновения колебательных режимов необходим анализ корней λ_i (i = 1, 2, 3) характеристического (“векового”) уравнения для линеаризованной системы (1)–(3) [13, 14]:

где

В данном случае мы имеем вещественное кубическое характеристическое уравнение, которое может иметь три действительных либо один вещественный и два комплексных корня. В зависимости от расположения этих корней на плоскости комплексного переменного λ возможны различные типы тепловых режимов в реакторе.

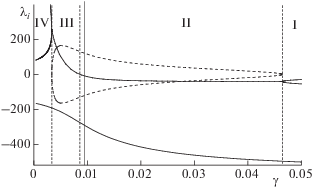
На рис. 1 показано, как параметр γ (о его роли сказано выше) влияет на корни характеристического уравнения, а следовательно, и на тип стационарного состояния. Действительные корни и реальная часть комплексных корней изображены сплошными кривыми. Штриховыми кривыми изображены мнимые части комплексных корней. Как видно из рис. 1, можно выделить четыре области, соответствующие различным типам стационарного состояния (римские цифры I–IV). При этом вертикальные штриховые линии разграничивают области с различными типами стационарного состояния.

Область I. Корни характеристического уравнения действительные и отрицательные. Стационарное состояние – устойчивый узел [14, 15].

Область II. Действительный корень и реальная часть комплексных корней отрицательны. Стационарное состояние – устойчивый фокус [14, 15].

Область III. Один действительный корень отрицательный, а реальная часть комплексных корней положительна. Стационарное состояние – седло – неустойчивый фокус [13].

Область IV. Все три корня действительные – два положительные и один отрицательный. Стационарное состояние – седло – неустойчивый узел [13]. Заметим, что это стационарное состояние абсолютно неустойчиво, поэтому оно должно быть окружено устойчивым предельным циклом, на который “наматываются” все траектории.

Возникает вопрос, где и как возникает устойчивый цикл, если он отсутствует в области I. Для этого проведем анализ эволюции стационарного состояния, начиная со значений параметра γ = 0.06. В области I стационарное состояние – устойчивый узел. При приближении к границе между областью I и областью II устойчивый узел начинает вырождаться (сближение двух корней). На границе (γ ≈ 0.04645) возникает “вырожденное” стационарное состояние с кратными корнями. Интересно, что если приближаться к границе слева, “вырожденное” состояние возникает при кратности мнимых частей комплексных корней. При переходе через границу справа в область II с уменьшением параметра γ формируется устойчивый фокус. Как показал численный анализ, при γ ≈ 0.00954 “жестко” возникают релаксационные колебания конечной амплитуды. Это отмечено в области II сплошной тонкой вертикальной прямой при γ = 0.00954. Реализуется структура устойчивый фокус – неустойчивый предельный цикл – устойчивый предельный цикл, которая сохраняется до границы между областями II и III.

На рис. 2 приведены результаты расчетов для γ = 0.0095, доказывающие существование неустойчивого предельного цикла. На рис. 2а представлена траектория, выходящая из точки Z (θ_IN = 13.96), она “наматывается” на устойчивый фокус. При выходе из точки Z на рис. 2б (θ_IN = 13.98) траектория, “разматываясь”, приходит к устойчивому предельному циклу.

Итак, образуется следующая структура: устойчивый фокус, окруженный неустойчивым и устойчивым циклами. Источником рождения пары циклов является полуустойчивый цикл, возникающий, по-видимому, из сгущения траекторий.

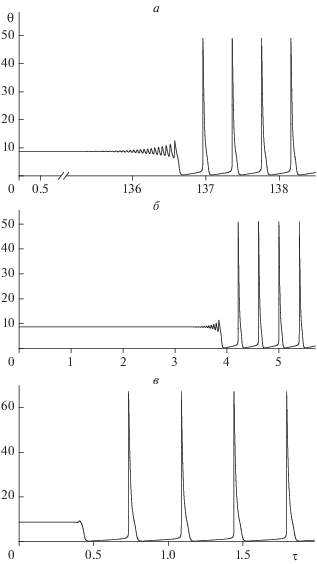
При переходе через границу в область III (γ ≈ ≈ 0.00861) возникает стационарное состояние – седло – неустойчивый фокус. Граница раздела представляет собой вырожденное состояние, которое характеризуется чисто мнимыми и одним действительным корнями. Устойчивый фокус меняет свою устойчивость за счет неустойчивого предельного цикла, который “садится” на стационарное состояние и исчезает. При выходе же из стационарного состояния траектория, разматываясь, резко выходит на устойчивый предельный цикл. Доказательством этого являются результаты, приведенные на рис. 3. Видно, что с уменьшением параметра γ, во-первых, уменьшается время выхода реактора на колебательный режим, а во-вторых, “раскрутка” траектории практически исчезает при малых значениях γ (рис. 3в).

При переходе в область IV (γ ≈ 0.00336) неустойчивый фокус переходит в неустойчивый узел через “вырожденное” состояние с кратными корнями. Колебания сохраняются и в этой области. На рис. 4 представлены зависимости периода осцилляций P_os и максимальной амплитуды θ_max цикла от параметра γ. Из этих данных следует, что с уменьшением параметра γ максимальная температура θ_max плавно растет. Это связано с тем, что с уменьшением γ увеличивается запас тепла в реакционной системе. Период колебаний P_os плавно уменьшается. При численном анализе обнаружено, что на “плавность” изменения характеристик колебаний, возникающих “жестко”, не влияет эволюция стационарного состояния.

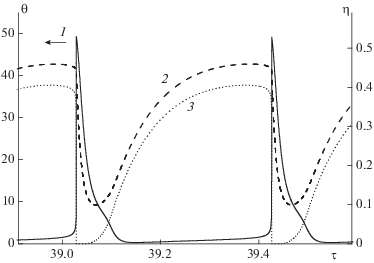
На рис. 5 представлена структура высокотемпературного колебания при γ = 0.0083. При этом значении γ наблюдается выход из исследуемого стационарного состояния. На этом рисунке сплошная кривая 1 – $\theta = {{f}_{1}}(\tau ),$ штриховая кривая 2 – ${{\eta }_{{\text{B}}}} = {{f}_{2}}(\tau )$ и точечная кривая 3 – $\eta _{{\text{B}}}^{{\text{A}}} = {{f}_{3}}(\tau ).$ Характер колебаний релаксационный. Из данных этого рисунка следует, что возникшие релаксационные колебания представляют собой ряд последовательных “вспышек”. Происходит резкий рост температуры (рис. 5, кривая 1), приводящий к полному выгоранию компонента B, экстрагированного реагентом A (рис. 5, кривая 3), а также к уменьшению концентрации компонента B в реакторе (рис. 5, кривая 2). После воспламенения за время ≈ 0.1 происходит резкое охлаждение реактора и наступает период “депрессии”, за который происходит накопление реагентов в фазах, и процесс повторяется.

Приведенные выше данные относятся к высокотемпературному единственному стационарному состоянию. Что касается единственного низкотемпературного стационарного состояния, то при изменении параметра γ эволюция стационарного состояния в области единственности происходит по простой схеме: устойчивый фокус → устойчивый узел → устойчивый фокус и т.д. Колебательная неустойчивость состояний в этом случае при изменении параметра γ не обнаружена.

ЗАКЛЮЧЕНИЕ

Разработанная ранее методика исследования типов стационарных состояний успешно применена для анализа механизма возникновения и эволюции колебательных режимов проточного реактора идеального смешения с реагирующей гетерогенной системой. Зависимость корней характеристического уравнения от параметра γ указывает на существование устойчивого предельного цикла, поскольку, например, в области IV стационарное состояние абсолютно неустойчиво. Выходящие из него траектории должны “наматываться” на предельный цикл. Показано, что колебания конечной амплитуды возникают “жестко” в области существования устойчивого фокуса. Доказано, что образование устойчивого предельного цикла (математический образ колебаний) сопровождается образованием неустойчивого предельного цикла.

Работа выполнена по теме госзадания (регистрационные номера: AAAA-A19-119022690098-3, АААА-А19-119071190040-5, АААА-А17-117040610346-5).