Химическая физика, 2021, T. 40, № 10, стр. 8-16
Особенности теории резонансного рассеяния электронов на атомах
С. О. Адамсон 1, *, Д. Д. Харлампиди 2, Г. В. Голубков 1, 3, Ю. А. Дьяков 1, 4, С. Я. Уманский 1, М. Г. Голубков 1
1 Федеральный исследовательский центр химической физики
им. Н.Н. Семёнова Российской академии наук
Москва, Россия
2 Московский педагогический государственный университет
Москва, Россия
3 Национальный исследовательский центр “Курчатовский институт”
Москва, Россия
4 Исследовательский центр экологических изменений, Академия Синика
Тайбэй, Тайвань
* E-mail: sergey.o.adamson@gmail.com
Поступила в редакцию 02.02.2021
После доработки 09.03.2021
Принята к публикации 22.03.2021
Аннотация
При рассмотрении многих задач физики плазмы используются кинетические уравнения, для решения которых требуются сечения упругого и неупругого рассеяния электронов на атомах и молекулах. Для построения сечений требуются современные расчеты характеристик резонансного рассеяния электронов, которые основаны на применении методов, оперирующих с комплексным гамильтонианом. Метод комплексного абсорбирующего потенциала (КАП) используется для подобного класса задач, но характеризуется неустойчивыми оценками параметров резонансов. В настоящей работе для одноканальной проблемы с явной параметризацией матрицы рассеяния проведен анализ особенностей метода КАП. Показано, что в зависимости от выбора начальных условий существует два типа КАП-траекторий с действительными пределами при стремлении комплексного масштабирующего множителя к нулю. Траектории первого типа характеризуются наличием оптимальной точки, а траектории второго типа – наличием замкнутого участка в окрестности резонанса. Также показано, что при конечных значениях масштабирующего множителя КАП-траектория не проходит через резонанс. Данные выводы качественно подтверждаются результатами независимого применения метода КАП к расчетам модельных и многоэлектронных систем.
1. ВВЕДЕНИЕ
При решении многих важных задач физики плазмы используются кинетические уравнения, для решения которых используются сечения упругого и неупругого рассеяния электронов на атомах и молекулах. Наибольший интерес для химической физики верхней атмосферы представляют сечения для энергий столкновения, не превышающих порога ионизации. Эти сечения рассчитываются теоретически или оцениваются в пучковых экспериментах [1].
Теоретические расчеты, большинство из которых основано на использовании метода парциальных волн, также весьма трудоемки. Основные сложности здесь обусловлены тем, что потенциалы взаимодействия электрона с атомами известны довольно плохо, а для многоэлектронных систем они не могут быть введены однозначно. Понятие потенциала взаимодействия в этом случае весьма условно, так как задача рассеяния электрона на атоме является многочастичной и в общем случае описывается оператором многоэлектронного взаимодействия. При решении многоэлектронной задачи используется “эффективный потенциал”, включающий поляризационное взаимодействие, кулоновское взаимодействие с остовом и потенциал обменного взаимодействия. Для большинства атомов хорошо установленным является поляризационный потенциал. Параметризация же потенциалов других типов связана с большими трудностями [2]. Более того, преобразование задачи рассеяния к одноэлектронному варианту с подгоночным эффективным потенциалом придает ей “полуэмпирический” характер. Тем не менее при соответствующем выборе параметров потенциала метод позволяет хорошо подогнать результаты расчета к экспериментальным данным.
В зависимости от постановки задачи фазы рассеяния и параметры автоионизационных резонансов вплоть до настоящего времени рассчитывались различными приближенными методами. Резонансам отвечают квазистационарные состояния непрерывного спектра электрона в поле возбужденного атома, где фазы рассеяния, как известно, резко изменяются [3].
Возможность расчета энергии и ширины резонансного состояния путем введения мнимого масштабируемого потенциала в исходный гамильтониан впервые была показана более тридцати лет назад [4–8]. Вычислительная процедура предполагала построение зависимости комплексных собственных значений стационарного уравнения Шредингера от масштабирующего множителя, а также проведение оценки энергии и ширины резонанса как геометрического центра замкнутой области при ее наличии у полученной зависимости (траектории). Теория подхода предполагала, что замкнутая область является следствием неполноты базиса, и при его пополнении должна стягиваться к одной из точек траектории [8]. Данный подход показал достаточную точность при решении модельных задач [4–9], хотя в работе [9] положение резонанса оценивалось по одной из точек траектории.
Ключевым моментом в развитии данного подхода стала работа [10], в которой было дано теоретическое обоснование и представлены результаты расчетов метастабильного 2Πg состояния аниона молекулы N2. Успешное применение данного подхода, получившего название “метод комплексного абсорбирующего потенциала” (КАП), и относительная простота его реализации в сравнении с методом комплексной координаты [11] стали причинами применения этого метода для расчетов резонансов в многоэлектронных системах. Достаточно полный список статей, посвященных расчетам многоэлектронных систем методом КАП, можно найти в [12]. Из работ, в него не вошедших, следует отметить работу [13], а также методические работы [14–20] и обзоры [21, 22].
При практическом использовании метода КАП используется единый базис атомных орбиталей (АО) для внутренней и внешней областей. Данный прием позволяет сохранить непрерывность волновой функции на границе внутренней и внешней областей, однако не позволяет отделить ошибки учета электронной корреляции во внутренней области от ошибок параметризации КАП. Эта особенность может быть устранена методом сшивки независимых решений на границе внутренней и внешней областей с использованием, например, формализма метода R-матрицы [23]. Подобные подходы с успехом использовались, в частности, для решения задач реакционного рассеяния [22, 24–26], а также при расчете параметров резонансов рассеяния методом комплексного масштабирования (комплексной координаты) [27, 28].
Разработку подхода, комбинирующего КАП и метод R-матрицы, необходимо начать с рассмотрения модельных проблем, решение которых позволит выявить его особенности и недостатки. По этой причине в настоящей работе рассматривается построение КАП-траекторий для случая явно параметризованной R-матрицы. Отметим, что данный тип модельных задач использовался при построении теории метода КАП [10], а также для качественного анализа поведения КАП-траекторий в окрестности резонансного полюса [12].
В разд. 2 работы рассмотрена модельная проблема, комбинирующая методы комплексного абсорбирующего потенциала и R-матрицы. В разд. 3 приведены детали расчета, а в разд. 4 обсуждаются полученные результаты.
2. ОСНОВНОЕ УРАВНЕНИЕ МЕТОДА КАП
Пусть в области $r \geqslant R$ функция ${{\psi }_{{ext}}}\left( {E,r} \right)$ является решением уравнения Шредингера
(1)
$\left[ { - \frac{{{{\hbar }^{2}}}}{{2m}}\frac{{{{\partial }^{2}}}}{{\partial {{r}^{2}}}} + {{V}_{{ext}}}\left( r \right) - E} \right]{{\psi }_{{ext}}}\left( {E,r} \right) = 0.$(2)
$\int\limits_R^\infty {{{{\tilde {\phi }}}_{n}}\left( r \right){{\phi }_{m}}\left( r \right)} dr = {{\delta }_{{nm}}},$(3)
${{\psi }_{{ext}}}\left( {E,r} \right) = \sum\limits_n {{{A}_{n}}{{\phi }_{n}}} = \sum\limits_n {{{{\tilde {A}}}_{n}}{{{\tilde {\phi }}}_{n}}} $Умножая уравнение (1) слева на функции ${{\tilde {\phi }}_{n}}\left( r \right)$ (n = 1, 2, …) и интегрируя по области $r \in \left[ {R,\infty } \right)$, получаем
(4)
$\begin{gathered} \int\limits_R^\infty {{{{\tilde {\phi }}}_{n}}\left( r \right)\left[ { - \frac{{{{\hbar }^{2}}}}{{2m}}\frac{{{{\partial }^{2}}}}{{\partial {{r}^{2}}}} + {{V}_{{ext}}}\left( r \right) - E} \right]{{\psi }_{{ext}}}\left( {E,r} \right)dr} = \\ {{\left. { = \,\,\frac{{{{\hbar }^{2}}}}{{2m}}W({{{\tilde {\phi }}}_{n}}\left( r \right),\;\,{{\psi }_{{ext}}}\left( {E,r} \right))} \right|}_{{r = R}}} + \\ + \,\,\int\limits_R^\infty {{{\psi }_{{ext}}}\left( {E,r} \right)\left[ { - \frac{{{{\hbar }^{2}}}}{{2m}}\frac{{{{\partial }^{2}}}}{{\partial {{r}^{2}}}} + {{V}_{{ext}}}\left( r \right) - E} \right]{{{\tilde {\phi }}}_{n}}\left( r \right)dr} = 0, \\ \end{gathered} $(5)
${{\hat {L}}_{b}} = \frac{{{{\hbar }^{2}}}}{{2m}}\delta \left( {r - R} \right)\left[ {\frac{\partial }{{\partial r}} - {{{\left. {b\left( E \right)} \right|}}_{{r = R}}}} \right],$(6)
$\begin{gathered} \frac{{{{\hbar }^{2}}}}{{2m}}W{{\left. {({{{\tilde {\phi }}}_{n}}\left( r \right),\,\,{{\psi }_{{ext}}}\left( {E,r} \right))} \right|}_{{r = R}}} = \\ = - \int\limits_R^\infty {{{\psi }_{{ext}}}\left( {E,r} \right){{{\hat {L}}}_{s}}{{{\tilde {\phi }}}_{n}}\left( r \right)dr} . \\ \end{gathered} $После этого преобразуем (4) в матричную форму:
(7)
$\begin{gathered} {{\left. {\frac{{{{\hbar }^{2}}}}{{2m}}\left( {\frac{{\partial {{\psi }_{{ext}}}\left( {E,r} \right)\left( {E,r} \right)}}{{\partial r}}\tilde {F} - {{\psi }_{{ext}}}\left( {E,r} \right)\tilde {F}{\kern 1pt} '} \right)} \right|}_{{r = R}}} + \\ + \,\,\left( {{{H}_{{ext}}} - IE} \right)A = 0. \\ \end{gathered} $Далее, умножая (7) слева на произведение вектора-строки ${{F}^{T}} = \left| {\begin{array}{*{20}{c}} {{{\phi }_{1}}}&{...}&{{{\phi }_{n}}} \end{array}} \right|$ и на матрицы G(E) = $ = {{\left( {{{H}_{{ext}}} - IE} \right)}^{{ - 1}}},$ получаем следующее уравнение:
(8)
${{\left. {\frac{{{{\hbar }^{2}}}}{{2m}}\left( {\frac{{\partial {{\psi }_{{ext}}}\left( {E,r} \right)}}{{\partial r}}{{F}^{T}}G\left( E \right)\tilde {F} - {{\psi }_{{ext}}}\left( {E,r} \right){{F}^{T}}G\left( E \right)\tilde {F}{\kern 1pt} '} \right)} \right|}_{{r = R}}} = - {{F}^{T}}{{\left. A \right|}_{{r = R}}} = - {{\left. {{{\psi }_{{ext}}}\left( {E,r} \right)} \right|}_{{r = R}}}.$После приведения подобных слагаемых это уравнение преобразуется к виду
(9)
$\begin{gathered} \frac{{{{\hbar }^{2}}}}{{2m}}{{\left. {{{F}^{T}}G\left( E \right)\tilde {F}} \right|}_{{r = R}}} = \\ = {{\left. {R\left( E \right)\left( {\frac{{{{\hbar }^{2}}}}{{2m}}{{F}^{T}}G\left( E \right)\tilde {F}{\kern 1pt} '\,\, - 1} \right)} \right|}_{{r = R}}}, \\ \end{gathered} $Если предположить, что при $0 \leqslant r \leqslant R$ имеется уравнение
(10)
$\left[ { - \frac{{{{\hbar }^{2}}}}{{2m}}\frac{{{{\partial }^{2}}}}{{\partial {{r}^{2}}}} + {{V}_{{int}}}\left( r \right) - E} \right]{{\psi }_{{int}}}\left( {E,r} \right) = 0,$(11)
${{\left. {{{\psi }_{{int}}}\left( {E,r} \right)} \right|}_{{r = R - 0}}} = {{\left. {{{\psi }_{{ext}}}\left( {E,r} \right)} \right|}_{{r = R + 0}}},$(12)
${{\left. {\frac{{\partial {{\psi }_{{int}}}\left( {E,r} \right)}}{{\partial r}}} \right|}_{{r = R - 0}}} = {{\left. {\frac{{\partial {{\psi }_{{ext}}}\left( {E,r} \right)}}{{\partial r}}} \right|}_{{r = R + 0}}},$В этом методе гамильтониан системы $\hat {H}{\kern 1pt} \left( s \right)$ представляется в виде
где ${{\hat {H}}_{0}}$ – исходный гамильтониан, s – масштабирующий параметр и ${{V}_{{{\text{КАП}}}}}$ – абсорбирующий потенциал, вид которого зависит от исходного гамильтониана системы. В частности, для радиальной проблемы (10) абсорбирующий потенциал будет удовлетворять условиям где R – точка наложения потенциала [10]. Строгих требований к виду абсорбирующего потенциала здесь не предъявляется, поэтому при решении радиальной задачи используются потенциалы $\sim {\kern 1pt} {{r}^{{{\beta }}}},$ $\beta \geqslant 2$ [9, 10].С целью оценки положения резонансного состояния для значений параметра $s = - i{{\eta }_{1}}, - i{{\eta }_{2}},...,$ $ - i{{\eta }_{n}}$ (${{\eta }_{n}}$ – действительное число и ${{\eta }_{{n + 1}}} > {{\eta }_{n}}$) решается уравнение
Здесь $\psi \left( s \right)$ – собственная функция и $E\left( s \right)$ – собственное число. Предполагается, что при наличии резонанса траектория $E\left( s \right)$ имеет так называемую оптимальную точку $E\left( {\tilde {s}} \right),$ в которой функция $\left| {E\left( {\tilde {s}} \right) - {{E}_{{res}}}} \right|$ имеет минимальное значение (величина ${{E}_{{res}}} = {{E}_{0}} - i{\Gamma \mathord{\left/ {\vphantom {\Gamma 2}} \right. \kern-0em} 2},$ где ${{E}_{0}}$ – энергия и Γ – ширина резонанса). Отметим, что оптимальная точка в методе КАП определяется неоднозначно, так как было предложено несколько вариантов ее определения, приводивших к близким оценкам энергии и ширины резонанса [10].Рассмотрим теперь применение уравнения (9) для построения КАП-траекторий. Как и в [10], возьмем абсорбирующий потенциал вида
где $s = - i\eta $ – масштабирующий множитель. Для разложения ${{\psi }_{{ext}}}\left( {E,r} \right)$ выберем функции Эрмита(18)
${{\tilde {\phi }}_{n}}\left( x \right) = {{C}_{n}}{{H}_{n}}\left( x \right)\exp \left( {{{ - {{x}^{2}}} \mathord{\left/ {\vphantom {{ - {{x}^{2}}} 2}} \right. \kern-0em} 2}} \right).$(19)
$\int\limits_{ - \infty }^{ + \infty } {{{{\tilde {\phi }}}_{n}}\left( x \right){{{\tilde {\phi }}}_{m}}\left( x \right)} dx = {{\delta }_{{nm}}}.$Это условие доказывает ортонормированность системы функций ${{\tilde {\phi }}_{n}}\left( x \right).$ Более того, эта система является полной и замкнутой [31, 32].
Представляя (19) в виде суммы интегралов:
(20)
$\begin{gathered} \int\limits_{ - \infty }^{ + \infty } {{{{\tilde {\phi }}}_{n}}\left( x \right){{{\tilde {\phi }}}_{m}}\left( x \right)} dx = \int\limits_0^{ + \infty } {{{{\tilde {\phi }}}_{n}}\left( x \right){{{\tilde {\phi }}}_{m}}\left( x \right)} dx + \\ + \,\,\int\limits_0^{ + \infty } {{{{\tilde {\phi }}}_{n}}\left( { - x} \right){{{\tilde {\phi }}}_{m}}\left( { - x} \right)} dx = {{\delta }_{{nm}}}, \\ \end{gathered} $(21)
$\int\limits_0^{ + \infty } {{{{\tilde {\phi }}}_{n}}\left( x \right){{{\tilde {\phi }}}_{m}}\left( x \right)} dx = {{{{\delta }_{{nm}}}} \mathord{\left/ {\vphantom {{{{\delta }_{{nm}}}} 2}} \right. \kern-0em} 2},$(22)
$\int\limits_0^{ + \infty } {{{{\tilde {\phi }}}_{n}}\left( x \right){{{\tilde {\phi }}}_{m}}\left( x \right)} dx \ne 0,$Так как ранее вывод уравнения (9) и его последующие преобразования проводились c использованием дополнительного условия ${{\left. {\tilde {F}{\kern 1pt} '{\kern 1pt} } \right|}_{{r = R}}} = 0$ [10, 23, 28], разложим решение уравнения (1) ${{\psi }_{{ext}}}\left( {E,r} \right)$ в ряд по системе функций Эрмита четных степеней. В этом случае ${{\left. {{{\partial {{\phi }_{n}}\left( x \right)} \mathord{\left/ {\vphantom {{\partial {{\phi }_{n}}\left( x \right)} {\partial r}}} \right. \kern-0em} {\partial r}}} \right|}_{{r = R}}} = 0,$ и, как следствие, ${{\left. {F{\kern 1pt} '{\kern 1pt} } \right|}_{{r = R}}} = {{\left. {\tilde {F}{\kern 1pt} '{\kern 1pt} } \right|}_{{r = R}}} = 0,$ что приводит к упрощению уравнения (9):
(23)
${{\left. {R\left( E \right)} \right|}_{{r = R}}} = - \frac{{{{\hbar }^{2}}}}{{2m}}{{\left. {{{F}^{T}}G\left( E \right)F} \right|}_{{r = R}}}.$Подставляя функции Эрмита в выражения для элементов матрицы ${{H}_{{ext}}},$ получаем
гдеИспользуя рекурсивное соотношение
Построение траектории $E\left( s \right)$ в методе КАП можно осуществить двумя способами: 1) определить функции $\left\{ {{{{\tilde {\phi }}}_{n}}\left( x \right)} \right\}$ и далее решать уравнение (16) для всех требуемых значений параметра s, 2) масштабировать функции ${{\phi }_{n}}\left( x \right)$ в каждой точке траектории. Первый способ применялся в большинстве исследований многоэлектронных систем, так как не требует пересчета одно- и двухэлектронных интегралов. Второй способ был введен в качестве модельной проблемы при построении теории КАП [10]. Оба способа легко реализуются при решении уравнения (23): первый – за счет выбора параметра $\lambda > 0,$ второй – наложением требования $s - \lambda = 0.$ В этом случае в матрице ${{H}^{{ext}}}$ сохраняются только диагональные элементы ($H_{{nm}}^{{ext}} = {{E}_{m}}{{\delta }_{{nm}}}$), что позволяет заменить (23) суммой
(25)
${{\left. {R\left( E \right)} \right|}_{{r = R}}} = - \frac{{{{\hbar }^{2}}}}{{2m}}{{\left. {\sum\limits_n {\frac{{{{{({{\phi }_{n}}(r))}}^{2}}}}{{{{E}_{n}} - E}}} } \right|}_{{r = R}}},$Подставляя в (25) значения ${{E}_{n}}$ и ${{\phi }_{n}}(r)$ из (18) с учетом изменения нормировки (${{C}_{n}} \to \sqrt 2 {{C}_{n}}$) и проводя необходимые преобразования, получаем
(26)
${{\left. {R\left( E \right)} \right|}_{{r = R}}} = - \frac{1}{{2\pi {{\beta }^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}\sum\limits_{l = 0} {\frac{{\Gamma (l + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2})}}{{l!(l + {1 \mathord{\left/ {\vphantom {1 {4 - z}}} \right. \kern-0em} {4 - z}})}}} .$(27)
$\begin{gathered} \sum\limits_{l = 0} {\frac{{\Gamma (l + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2})}}{{l!(l + {1 \mathord{\left/ {\vphantom {1 {4 - z}}} \right. \kern-0em} {4 - z}})}}} = \\ = \frac{{\Gamma (a)\Gamma ({a \mathord{\left/ {\vphantom {a {2 - z}}} \right. \kern-0em} {2 - z}})}}{{\Gamma ({{1 + a} \mathord{\left/ {\vphantom {{1 + a} {2 - z}}} \right. \kern-0em} {2 - z}})}}\left[ {{{{(a)}}_{0}} + \frac{{{{{(a)}}_{1}}{{{({a \mathord{\left/ {\vphantom {a {2 - z}}} \right. \kern-0em} {2 - z}})}}_{1}}}}{{{{{({{1 + a} \mathord{\left/ {\vphantom {{1 + a} {2 - z}}} \right. \kern-0em} {2 - z}})}}_{1}}}} + ...} \right] = \\ = \frac{{\Gamma (a)\Gamma ({a \mathord{\left/ {\vphantom {a {2 - z}}} \right. \kern-0em} {2 - z}})}}{{\Gamma ({{1 + a} \mathord{\left/ {\vphantom {{1 + a} {2 - z}}} \right. \kern-0em} {2 - z}})}}F(a,\,\,{a \mathord{\left/ {\vphantom {a {2 - z}}} \right. \kern-0em} {2 - z}},{{1 + a} \mathord{\left/ {\vphantom {{1 + a} {2 - z}}} \right. \kern-0em} {2 - z}};\,\,1), \\ \end{gathered} $(28)
$\begin{gathered} F(a,b,c;1) = \frac{{\Gamma (с)}}{{\Gamma (b)\Gamma (c - b)}}\int\limits_0^1 {{{t}^{{b - 1}}}{{{(1 - t)}}^{{c - b - a - 1}}}dt} = \\ = \frac{{\Gamma (c)}}{{\Gamma (b)\Gamma (c - b)}}B(b,c - b - a) = \frac{{\Gamma (c)\Gamma (c - b - a)}}{{\Gamma (c - b)\Gamma (c - a)}}, \\ \end{gathered} $(29)
$\sum\limits_{l = 0} {\frac{{\Gamma \left( {l + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}} \right)}}{{l!\left( {l + {1 \mathord{\left/ {\vphantom {1 {4 - z}}} \right. \kern-0em} {4 - z}}} \right)}}} = \pi \frac{{\Gamma \left( {{1 \mathord{\left/ {\vphantom {1 {4 - z}}} \right. \kern-0em} {4 - z}}} \right)}}{{\Gamma \left( {{3 \mathord{\left/ {\vphantom {3 {4 - z}}} \right. \kern-0em} {4 - z}}} \right)}},$(30)
${{\left. {R\left( E \right)} \right|}_{{r = R}}} = - \frac{1}{{2{{\beta }^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}\frac{{\Gamma \left( {{1 \mathord{\left/ {\vphantom {1 {4 - z}}} \right. \kern-0em} {4 - z}}} \right)}}{{\Gamma \left( {{3 \mathord{\left/ {\vphantom {3 {4 - z}}} \right. \kern-0em} {4 - z}}} \right)}}.$3. МЕТОД РАСЧЕТА
Для проверки эффективности метода КАП было проведено численное решение уравнений (23) и (30). В обоих случаях предполагалось, что функция ${{\psi }_{{int}}}\left( {E,r} \right)$ при $r \to R$ (для $r < R$) имеет вид
где $S\left( k \right)$ – матрица рассеяния, k – волновое число. При наличии в системе нескольких изолированных резонансов Брейта–Вигнера матрицу рассеяния S можно представить как сумму(32)
$S\left( k \right) = {{S}_{0}}\left( k \right) - \sum\limits_n {\frac{{i{{T}_{n}}}}{{E - {{E}_{n}}}}} ,$(33)
$S\left( k \right) = {{S}_{0}}\left( k \right)\prod\limits_n {\frac{{E - E_{n}^{*}}}{{E - {{E}_{n}}}}} .$Параметризация матрицы рассеяния (33) предполагает наличие единственного резонанса с энергией ${{E}_{0}} = 3.42639031 - 0.00638724i$ а.е., совпадающей с энергией низшего резонанса в потенциале из работы [37] и постоянной нерезонансной компонентой фазового сдвига ${{\delta }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}.$ Уравнения (23) и (29) решались итерационно с $R = 20$ а.е.; порог сходимости по энергии составлял 10–10 а.е. Масса частицы полагалась равной $m = 1$ а.е. Для вычисления гамма-функций комплексного аргумента был использован метод, описанный в работе [38]. Обращение трехдиагональной матрицы в (23) проводилось методом, предложенным в работе [39].
4. РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Умножение обеих частей (27) на величину $ - ik$ и подстановка выражения (31) в уравнение (23) позволяют записать последнее в окончательном виде:
(34)
${{\left. { - ikR\left( E \right)} \right|}_{{r = R}}} = \frac{{{{e}^{{ - ikr}}} - S\left( k \right){{e}^{{ikr}}}}}{{{{e}^{{ - ikr}}} + S\left( k \right){{e}^{{ikr}}}}} = i\sqrt z \frac{{\Gamma \left( {{1 \mathord{\left/ {\vphantom {1 {4 - z}}} \right. \kern-0em} {4 - z}}} \right)}}{{\Gamma \left( {{3 \mathord{\left/ {\vphantom {3 {4 - z}}} \right. \kern-0em} {4 - z}}} \right)}}.$Численное решение уравнений (23) и (34) позволяет построить КАП-траектории для случая явно параметризованной матрицы рассеяния. Для бесконечного набора функций при действительных значениях параметра $s$ ($\lambda = s$) оба уравнения имеют только действительные корни, причем $E\left( s \right)$ является многозначной функцией, ветви которой имеют общий предел $E\left( {s \to 0} \right) \to 0$ и конечные пределы при $s \to \infty .$ Для конечного набора функций конечные пределы при $\lambda \to \infty $ сохраняются, а при $s \to 0$ каждая ветвь имеет конечный, отличный от нуля предел. Также можно отметить, что при $s > {{s}_{c}},$ где ${{s}_{c}}$ – некоторое значение параметра $s$ (для рассматриваемого примера ${{s}_{c}} \approx 0.02$), решения (23) приближаются к решениям (34) – см. рис. 1.
Рис. 1.
Вид функции $E\left( s \right)$ при $s > 0.$ Сплошные линии соответствуют полному набору функций, штриховые линии с точками (○) – конечному набору функций ($\lambda = 1.6,$ $N = 100$).
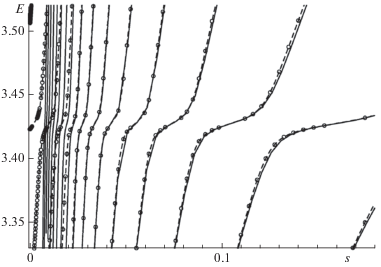
Из многозначности функции $E\left( s \right)$ при $s > 0$ следует, что для случая $s = \lambda - i\eta $ ($\eta > 0$) можно построить несколько КАП-траекторий с одинаковыми действительными пределами при $\eta \to 0.$ Если в одной из точек КАП-траектории выполняется условие $E\left( {s = i\eta } \right) = {{E}_{0}},$ где ${{E}_{0}}$ – положение резонанса, то уравнение (34) упрощается до трансцендентного уравнения:
(35)
${{\left. { - ikR\left( E \right)} \right|}_{{r = R}}} = i\sqrt z \frac{{\Gamma \left( {{1 \mathord{\left/ {\vphantom {1 {4 - z}}} \right. \kern-0em} {4 - z}}} \right)}}{{\Gamma \left( {{3 \mathord{\left/ {\vphantom {3 {4 - z}}} \right. \kern-0em} {4 - z}}} \right)}} = - 1.$Используя свойства гамма-функции, несложно убедиться, что уравнение (35) не имеет решения. Отсюда следует, что условие $E\left( {s = i\eta \to 0} \right) \to {{E}_{0}},$ сформулированное в работе [10] для метода КАП, не выполняется.
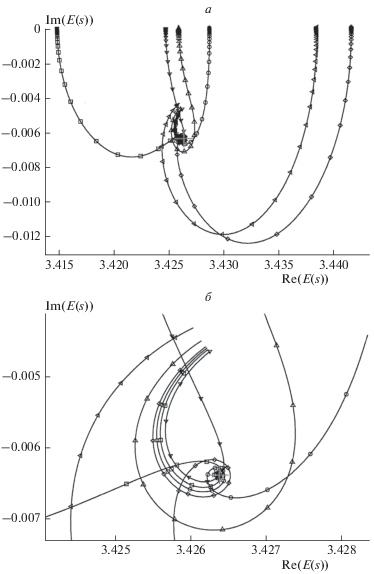
При численном решении уравнения (34) найдено два вида КАП-траекторий. Траектории первого типа ($\lambda \leqslant 0.1$) разбиваются на две области точкой $\eta = {{\eta }_{{opt}}},$ в которой выполняется условие $\min = \left| {\eta {{\partial E\left( {s = i\eta } \right)} \mathord{\left/ {\vphantom {{\partial E\left( {s = i\eta } \right)} {\partial \eta }}} \right. \kern-0em} {\partial \eta }}} \right|$ (в терминологии КАП – оптимальная точка [10]). В области $\eta < {{\eta }_{{opt}}},$ наблюдается сильная зависимость от малых изменений величины параметра $\lambda ,$ а при $\eta > {{\eta }_{{opt}}}$ – слабая. Оптимальная точка не совпадает с резонансом, но находится вблизи него (см. рис. 2, 3). Траектории второго типа ($\lambda > 0.1$) имеют оптимальную точку, и их вид полностью определяется выбором значения $\lambda $ (см. рис. 4). Данные результаты в целом согласуются с опытом применения метода КАП к расчетам модельных и реальных систем [8, 10].
Рис. 2.
КАП-траектории (полный набор функций) при следующих значениях $\lambda {\text{:}}$ ⚪ – 0.01, ◻ – 0.0103, ◇ – 0.0106, △ – 0.0109, ◁ – 0.0112; знак “плюс” – положение резонанса.

Рис. 3.
Оптимальные точки КАП-траекторий (полный набор функций) при следующих значениях $\lambda $: ⚪ – 0.01, ◻ – 0.0103, ◇ – 0.0106, △ – 0.0109, ◁ – 0.0112; знак “плюс” – положение оптимальной точки.
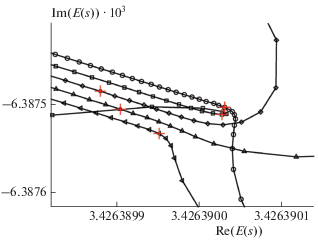
Рис. 4.
КАП-траектории (полный набор функций) при следующих значениях $\lambda $: ▷ – 0.1, ⚪ – 0.2, ◻ – 0.4, ◇ – 0.8, △ – 1.6, ◁ – 3.2; знак “плюс” – положение резонанса; а – общий вид траектории, б – окрестность оптимальной точки.
Оба типа траекторий обнаруживаются при решении уравнения (23), однако переход к траекториям второго типа имеет место только при больших значениях параметра $\lambda > 360$ (см. рис. 5, 6).
5. ЗАКЛЮЧЕНИЕ
В настоящей работе для одноканальной проблемы с явной параметризацией матрицы рассеяния проведен анализ особенностей метода КАП. Показано, что в зависимости от выбора начальных условий существует два типа КАП-траекторий с действительными пределами при стремлении комплексного масштабирующего множителя к нулю. Траектории первого типа характеризуются наличием оптимальной точки, а траектории второго типа – наличием замкнутого участка в окрестности резонанса. Также показано, что при конечных значениях масштабирующего множителя КАП-траектория не проходит через резонанс. Данные выводы качественно подтверждаются результатами независимого применения метода КАП к расчетам модельных и многоэлектронных систем.
Проведенное исследование открывает новые возможности для описания целого ряда прикладных приложений, которые представляют большой интерес для химической физики нижней ионосферы [40]. Например, во внешнем электрическом поле Земли на высотах 80–95 км образуются высоковозбужденные состояния атомов, которые являются автоионизационными [41]. При этом появляются медленные электроны, которые могут резонансно рассеиваться на атомах водорода и кислорода [42], что является особенно важным для кинетики формирования на этих высотах фотоионизационной плазмы [40]. Время жизни такой плазмы обычно не превышает 30 мин. В этот период наблюдается значительный рост ошибки позиционирования глобальных навигационных спутниковых систем [43]. Более детальное рассмотрение этих вопросов выходит за рамки настоящей работы и будет предметом будущих исследований.
Работа выполнена в рамках государственного задания Министерства науки и высшего образования Российской Федерации (тема № АААА-А19-119010990034-5).
Список литературы
Смирнов Б.М. Атомные столкновения и элементарные процессы в плазме. Москва: Атомиздат, 1968.
Друкарев Г.Ф. Столкновения электронов с атомами и молекулами. М.: Наука, 1978.
Nesbet R.K., Lyons J.D. // Phys. Rev. A. 1971. V. 4. № 5. P. 1812.
Jolicard G., Austin E.J. // Chem. Phys. Lett. 1985. V. 121. № 1–2. P. 106.
Jolicard G., Austin E.J. // Chem. Phys. 1986. V. 103. № 2–3. P. 295.
Jolicard G., Perrin M.Y. // Chem. Phys. 1987. V. 116. № 1. P. 1.
Jolicard G., Humbert J. // Chem. Phys. 1987. V. 118. № 3. P. 397.
Jolicard G., Leforestier C., Austin E.J. // J. Chem. Phys. 1988. V. 88. № 2. P. 1026.
Rom N., Lipkin N., Moiseyev N. // Chem. Phys. 1991. V. 151. № 2. P. 199.
Riss U.V., Meyer H.D. // J. Phys. B: At. Mol. Opt. Phys. 1993. V. 26. № 23. P. 4503.
Reinhardt W.P. // Ann. Rev. Phys. Chem. 1982. V. 33. P. 223.
Адамсон С.О., Харлампиди Д.Д., Голубков Г.В. и др. // Хим. физика. 2020. Т. 39. № 10. С. 9.
Ingr M., Meyer H.D., Cederbaum L.S. // J. Phys. B: At. Mol. Opt. Phys. 1999. V. 32. № 19. P. L547.
Sahoo S., Ho Y.K. // J. Phys. B: At. Mol. Opt. Phys. 2000. V. 33. № 12. P. 2195.
Santra R., Cederbaum L.S. // J. Chem. Phys. 2001. V. 115. № 15. P. 6853.
Sajeev Y., Vysotskiy V., Cederbaum L.S. et al. // J. Chem. Phys. 2009. V. 131. № 21. 21102.
Landau A., Moiseyev N. // J. Chem. Phys. 2016. V. 145. № 16. 164111.
White A.F., Epifanovsky E., McCurdy C.W. et al. // J. Chem. Phys. 2017. V. 146. № 23. 234107.
Thodika M., Fennimore M., Karsili T.N.V. et al. // J. Chem. Phys. 2019. V. 151. № 24. 244104.
Phung Q.M., Komori Y., Yanai T. et al. // J. Chem. Theor. Comp. 2020. V. 16. № 4. P. 2606.
Santra R., Cederbaum L.S. // Phys. Rep. 2002. V. 368. № 1. P. 1.
Muga J.G., Palao J.P., Navarro B. et al. // Phys. Rep. 2004. V. 395. № 6. P. 357.
Zvijac D.J., Heller E.J., Light J.C. // J. Phys. B: At. Mol. Opt. Phys. 1975. V. 8. № 7. P. 1016.
Huarte-Larranaga F., Gimenez H., Aguilar A. et al. // Chem. Phys. Lett. 1998. V. 291. № 3–4. P. 346.
Huarte-Larranaga F., Gimenez H., Aguilar A. // J. Chem. Phys. 1998. V. 109. № 14. P. 5761.
Huarte-Larranaga F., Gimenez H., Lucas J.M. et al. // J. Chem. Phys. 1999. V. 111. № 5. P. 1979.
Halley M.H., Delande D., Taylor K.T. // J. Phys. B: At. Mol. Opt. Phys. 1992. V. 25. № 21. P. L525.
Halley M.H., Delande D., Taylor K.T. // J. Phys. B: At. Mol. Opt. Phys. 1993. V. 26. № 12. P. 1775.
Bloch C. // Nucl. Phys. 1957. V. 4. P. 503.
Schneider B.I. // Phys. Rev. A. 1981. V. 24. № 1. P. 1.
Szego G. Orthogonal polynomials. Providence, Rhode Island: Amer. Mathem. Soc., 1939.
Ахиезер Н.И., Глазман И.М. Теория линейных операторов в гильбертовом пространстве. Т. 1. Харьков: Изд-во Харьк. ун-та, 1977.
Казьмин Ю.А. // Вестн. МГУ. Сер. 1, Математика, механика. 1960. № 2. С. 6.
Рындина В.В. // Изв. АН СССР. Сер. мат. 1962. Т. 26. № 1. С. 143.
Бейтмен Г., Эрдейи А. Высшие трансцендентные функции. Т. 1. М.: Наука, 1973.
Davies K.T.R., Baranger M. // Ann. Phys. 1962. V. 19. № 3. P. 383.
Bain R.A., Bardsley J.N., Junker B.R. et al. // J. Phys. B: At. Mol. Opt. Phys. 1974. V. 7. № 16. P. 2189.
Zhang S., Jin J. Computation of Special Functions. N.Y.: John Wiley & Sons, 1996.
Ting T.C.T. // Quart. Appl. Math. 1964. V. 22. № 2. P. 105.
Kuverova V.V., Adamson S.O., Berlin A.A. et al. // Adv. Space Res. 2019. V. 64. № 10. P. 1876.
Голубков Г.В., Бычков В.Л., Арделян Н.В. и др. // Хим. физика. 2019. Т. 38. № 7. С. 23.
Голубков Г.В., Маслов Т.А., Бычков В.Л. и др. // Хим. физика. 2020. Т. 39. № 10. С. 47.
Голубков Г.В., Манжелий М.И., Берлин А.А. и др. // Хим. физика. 2021. Т. 40. № 3. С. 86.
Дополнительные материалы отсутствуют.
Инструменты
Химическая физика




