Химическая физика, 2021, T. 40, № 10, стр. 17-21

Влияние трехспиновых групп на первичное эхо в линейных полимерах со свободными концами

Т. П. Кулагина^1, *, Г. Е. Карнаух¹, И. Ю. Голубева²

¹ Институт проблем химической физики Российской академии наук
Черноголовка, Россия

² Московский государственный университет им. М.В. Ломоносова
Москва, Россия

^* E-mail: tan@icp.ac.ru

Поступила в редакцию 18.03.2021
После доработки 07.04.2021
Принята к публикации 20.04.2021

DOI: 10.31857/S0207401X21100095

Полный текст (PDF)

Аннотация

На основе развитой ранее теории спада свободной индукции и спинового эха предложена теория первичного эха в гибкоцепных полимерах с изолированными группами трех спинов с произвольными константами диполь-дипольного взаимодействия (ДДВ). Показана возможность использования общей теории спиновых эхо в многоспиновых системах. Предложен метод оценки влияния трехспиновых групп на форму линии (ЯМР) при различной температуре по интегральной интенсивности сигнала. Показано, что при повышении температуры различия влияния одинаковых или произвольных значений констант ДДВ на спектр не наблюдается.

Ключевые слова: первичное эхо, группа трех спинов, произвольные константы диполь-дипольного взаимодействия.

ВВЕДЕНИЕ

Для проведения управляемого синтеза и применения линейных и сшитых полимеров необходимы данные об их структуре и молекулярной подвижности, которые определяются различными методами ЯМР. Импульсный метод ЯМР-релаксации является неинвазивным и информативным методом изучения структуры на различных уровнях, молекулярной подвижности, и в частности диффузии, в конденсированной среде [1–7]. При наличии в полимере выделенных трехспиновых групп наблюдается уширение спектров под влиянием окружающих спинов и частичного усреднения их дипольного взаимодействия [8, 9]. Обычно трехспиновые группы рассматриваются в модели эквивалентных ядер с одинаковыми значениями констант диполь-дипольного взаимодействия (ДДВ). В спектрах в этом случае наблюдаются три пика. Исследование трехспиновой группы с различными значениями констант ДДВ, проведенное в работах [9, 10] в твердом теле, показало, что могут наблюдаться 5 или 7 пиков.

Аналитические выражения для спада свободной индукции (ССИ) и первичного спинового эха (СЭ) в работах [1–5] не приведены, что затрудняет расчеты и получение информации о структуре и ориентации трехспиновых групп из сигналов ЯМР. В данной работе предложен новый метод расчета ССИ и СЭ в системе дипольно-связанных трех спинов 1/2 с произвольными константами ДДВ. В этом методе впервые использованы симметрии, определяемые спиновым обменом и операцией переворота всех спинов вокруг оси начальной поляризации и направлением импульсов при формировании солид-эха [8, 11]. Использование этих симметрий позволило свести расчеты с матрицей 8-го порядка к расчетам на двух матрицах 3-го порядка [8–10]. Расчеты показали качественное соответствие теории и эксперимента [4] в твердом теле.

МЕТОДЫ ИССЛЕДОВАНИЯ

В работе предложена теория сигналов первичного эха в линейных полимерах без зацеплений, содержащих группы дипольно-связанных трех спинов 1/2 с произвольными константами ДДВ. Предложен новый метод расчета сигналов СЭ ${{A}_{3}}\left( {t,~\tau } \right)$ после воздействия импульсной последовательности ${{\left( {{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} \right)}_{y}} - \tau - {{\left( {{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} \right)}_{x}} - t$ [8, 9].

Сигнал между первым и вторым импульсом является сигналом ССИ ${{G}_{3}}\left( t \right),$ который определяется следующей формулой [10]:

(1)

$\begin{gathered} {{G}_{3}}\left( t \right) = \frac{1}{8}\left( {1 + 3{{{\cos }}^{2}}\beta } \right) + \frac{3}{8}{{\sin }^{2}}\beta \cos {{\omega }_{{32}}}t + \\ + \,\,\frac{1}{2}{{\cos }^{2}}\frac{\beta }{2}\cos {{\omega }_{{12}}}t + \frac{1}{2}{{\sin }^{2}}\frac{\beta }{2}\cos {{\omega }_{{13}}}t. \\ \end{gathered} $

В случае эквивалентных ядер c константой ДДВ b формула ССИ принимает вид

(2)

${{G}_{3}}\left( t \right) = 1 - {\text{si}}{{{\text{n}}}^{2}}\frac{{3bt}}{2}.$

Для расчета ССИ в линейных полимерах без зацеплений использовалась динамическая модель полимера [6, 7], в которой полимерная цепь состоит из N₀ статистически независимых сегментов. Движение полимерной цепи в широком температурном интервале при температуре выше температуры стеклования Т_с представляется в виде нескольких типов движений: в низкотемпературной области проявляются только мелкомасштабное молекулярное движение внутри сегментов, а в среднетемпературной – крупномасштабное (сегментарное) движение сегментов. В этой модели динамики полимерной цепи корреляционная функция молекулярных движений k(τ) имеет вид

(3)

$k(\tau ) = (1 - \alpha ){{k}_{1}}(\tau ) + \alpha {{k}_{2}}(\tau ),$

где ${{k}_{1}}\left( \tau \right) - {\text{exp}}\left( {{{ - \tau } \mathord{\left/ {\vphantom {{ - \tau } {{{\tau }_{c}}}}} \right. \kern-0em} {{{\tau }_{c}}}}} \right)$ – корреляционная функция Бломбергена–Парселла–Паунда, характеризующая мелкомасштабные движения полимерной цепи, ${{\tau }_{c}}$ – характерное время корреляции молекулярных движений, которое связано с температурой $~T$ по закону Аррениуса: ${{\tau }_{c}} = {{\tau }_{0}}{\text{exp}}\left( {{E \mathord{\left/ {\vphantom {E {kT}}} \right. \kern-0em} {kT}}} \right);$

${{k}_{2}}\left( \tau \right) = \frac{1}{{{{N}_{0}}}}\sum\limits_{p = 1}^{{{N}_{0}}} {{\text{exp}}\left( { - \frac{{{{p}^{2}}{{\pi }^{2}}\tau }}{{{{\tau }_{c}}N_{0}^{2}}}} \right)} $

− корреляционная функция Каргина–Слонимского–Рауза, характеризующая крупномасштабные движения сегментов полимерной цепи; $\alpha $ − доля крупномасштабного движения (эмпирический коэффициент), для цепей со свободными концами $\alpha = 0.05.$

Спады свободной индукции в линейных полимерах без зацеплений рассчитываются в модели Андерсона–Вейса с корреляционной функцией молекулярных движений (3):

(4)

${{G}_{r}}(t) = \exp \left( { - \omega _{{loc}}^{2}\int\limits_0^t {(t - \tau )k(\tau )d\tau } } \right),$

где ${{\omega }_{{loc}}}$ – среднее локальное поле, создаваемое на любом спине всеми остальными спинами цепи.

Спад свободной индукции в линейном полимере, содержащем выделенные трехспиновые группы, выражается следующей формулой:

(5)

$G\left( t \right) = {{G}_{3}}\left( t \right){{G}_{r}}\left( t \right),$

где $~{{G}_{3}}\left( t \right)$ – ССИ в системе трех спинов (1).

Аналогично выглядит выражение СЭ для всей спиновой системы:

(6)

$A\left( {t,\tau } \right) = {{A}_{3}}\left( {t,\tau } \right){{A}_{r}}\left( {t,\tau } \right),$

где ${{A}_{r}}\left( {t,~\tau } \right)$ – сигнал первичного эха в полимерах [7].

Формула для расчета сигнала первичного эха ${{A}_{r}}\left( {t,~\tau } \right)$ в полимерах получена на основе общего теоретического подхода, предложенного в работе [6] и связана со средним квадратом случайного изменения фазы $\left\langle {{{\delta }^{2}}{{\varphi }_{i}}} \right\rangle $ вследствие изменения локального магнитного поля на спине ядра соотношением

(7)

${{A}_{{id}}} = \exp \left[ { - \frac{1}{2}\left\langle {{{\delta }^{2}}{{\varphi }_{i}}} \right\rangle } \right].$

Для определения связи $\left\langle {{{\delta }^{2}}{{\varphi }_{i}}} \right\rangle $ со средним квадратом смещения ядер получены формулы, справедливые для любых случайных процессов. По условию аддитивности смещений r(t_i, t_j) на отрезке времени [t_i, t_j] для каждой реализации случайного процесса справедливо равенство

(8)

$r\left( {{{t}_{1}},{{t}_{2}}} \right) + r\left( {{{t}_{2}},{{t}_{3}}} \right) = r\left( {{{t}_{1}},{{t}_{3}}} \right).$

Для корреляции смещений стационарных процессов получена эквивалентная формула:

(9)

$\left\langle {r\left( {{{t}_{1}},{{t}_{2}}} \right)r\left( {{{t}_{3}},{{t}_{4}}} \right)} \right\rangle = \frac{1}{2}\left( {\left\langle {{{r}^{2}}\left( {{{t}_{1}},{{t}_{4}}} \right)} \right\rangle + \left\langle {{{r}^{2}}\left( {{{t}_{2}},{{t}_{3}}} \right)} \right\rangle - \left\langle {{{r}^{2}}\left( {{{t}_{1}},{{t}_{3}}} \right)} \right\rangle - \left\langle {{{r}^{2}}\left( {{{t}_{2}},{{t}_{4}}} \right)} \right\rangle } \right).$

С помощью формулы (9) получено выражение среднего квадрата смещений для эха в стационарных условиях:

(10)

$\begin{gathered} \left\langle {{{{\left( {r\left( {0,\tau } \right) - r\left( {\tau ,\tau + t} \right)} \right)}}^{2}}} \right\rangle = 2\left\langle {{{r}^{2}}\left( \tau \right)} \right\rangle + 2\left\langle {{{r}^{2}}\left( t \right)} \right\rangle - \\ - \,\,\left\langle {{{r}^{2}}\left( {\tau + t} \right)} \right\rangle . \\ \end{gathered} $

Величина $\left\langle {{{r}^{2}}\left( t \right)} \right\rangle $ задается уравнением

(11)

$\left\langle {{{r}^{2}}\left( t \right)} \right\rangle = 2\left\langle {\omega _{{loc}}^{2}\left( 0 \right)} \right\rangle \int\limits_0^t {\left( {t - t{\kern 1pt} '} \right)k\left( {t{\kern 1pt} '} \right)dt{\kern 1pt} '} .$

Из формул (4), (9), (10) следует связь сигнала СЭ с ССИ:

(12)

${{A}_{r}}\left( {t,\tau } \right) = \frac{{{{G}_{r}}{{{\left( t \right)}}^{2}}{{G}_{r}}{{{\left( \tau \right)}}^{2}}}}{{{{G}_{r}}\left( {\tau + t} \right)}}.$

Для расчета сигналов СЭ ${{A}_{3}}\left( {t,~\tau } \right)$ после воздействия импульсной двухимпульсной последовательности рассмотрен гамильтониан диполь-дипольного взаимодействия

(13)

$\begin{gathered} \hat {H}_{d}^{z} = {{b}_{{12}}}\left( {2\hat {S}_{1}^{z}\hat {S}_{2}^{z} - \hat {S}_{1}^{x}\hat {S}_{2}^{x} - \hat {S}_{1}^{y}\hat {S}_{2}^{y}} \right) + \\ + \,\,{{b}_{{23}}}\left( {2\hat {S}_{2}^{z}\hat {S}_{3}^{z} - \hat {S}_{2}^{x}\hat {S}_{3}^{x} - \hat {S}_{2}^{y}\hat {S}_{3}^{y}} \right) + \\ + \,\,{{b}_{{31}}}\left( {2\hat {S}_{3}^{z}\hat {S}_{1}^{z} - \hat {S}_{3}^{x}\hat {S}_{1}^{x} - \hat {S}_{3}^{y}\hat {S}_{1}^{y}} \right) \\ \end{gathered} $

и проведены аналитические расчеты сигнала эха A₃(τ, t) от изолированной группы трех спинов с произвольными константами ДДВ [8, 9]:

(14)

где ${{\sigma }_{1}} = {{b}_{{12}}} + {{b}_{{23}}} + {{b}_{{31}}},$ ${{\sigma }_{2}} = {{b}_{{12}}}{{b}_{{23}}}$ + ${{b}_{{23}}}{{b}_{{31}}} + {{b}_{{31}}}{{b}_{{12}}},$ ${{\lambda }_{1}} = \frac{{{{\sigma }_{1}}}}{2},$ ${{\lambda }_{2}} = \frac{{ - {{\sigma }_{1}} - \chi }}{4},$ ${{\lambda }_{3}} = \frac{{ - {{\sigma }_{1}} + \chi }}{4},$ $\chi = (9\sigma _{1}^{2}$ – $ - \,\,24{{\sigma }_{2}}{{)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},$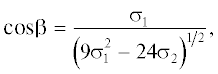

${{\omega }_{{ij}}}$ = ${{\lambda }_{i}} - {{\lambda }_{j}}.$

При $t = \tau $ получаем сигнал CЭ в трехспиновой группе с одинаковыми константами $b$ ДДВ:

(15)

${{A}_{3}}\left( t \right) = \frac{5}{8} + \frac{1}{2}\cos \left( {\frac{{3bt}}{2}} \right) - \frac{1}{8}{\text{cos}}\left( {3bt} \right).$

При ${{\sigma }_{1}} = 0$ введем $\omega = \frac{{{{{\left( { - 6{{\sigma }_{2}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}{2} = {{\left( {{M \mathord{\left/ {\vphantom {M 2}} \right. \kern-0em} 2}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ и М₂ = = $\omega _{{loc}}^{2}$ = 3/2($b_{{12}}^{2}$ + $b_{{12}}^{2}$ + $b_{{23}}^{2}$) – второй момент трехспиновой системы. Тогда СЭ определяется как

(16)

$\begin{gathered} {{A}_{3}}\left( t \right) = \frac{{41}}{{128}} + \frac{{11}}{{16}}\cos \left( {\omega t} \right) + \frac{5}{{32}}\cos \left( {2\omega t} \right) - \\ - \,\,\frac{3}{{16}}\cos \left( {3\omega t} \right) + \frac{3}{{128}}\cos \left( {4\omega t} \right) = \\ = 1 - 4{\text{si}}{{{\text{n}}}^{4}}\frac{{\omega t}}{2} + 3{\text{si}}{{{\text{n}}}^{8}}\frac{{\omega t}}{2}. \\ \end{gathered} $

При $t = \tau $ формула (14) приобретает вид

(17)

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

В данной работе рассматривалась модель при слабом влиянии спинов полимерной цепи на трехспиновую группу и без учета подвижности спинов внутри группы. Проведено моделирование сигналов ССИ и СЭ в гибкоцепных линейных полимерах со свободными концами, содержащих изолированные группы трех спинов 1/2, по формулам (5), (6) с корреляционной функцией (3) при различных значениях времени корреляции ${{\tau }_{c}}$ (время в расчетах безразмерное, т.е. в единицах ω_loc). На рис. 1, 2 представлено фурье-преобразование F_e(ω) сигнала СЭ, нормированного на максимальное значение, для линейного полимера с выделенной трехспиновой группой с одинаковыми и произвольными константами ДДВ. Из этих рисунков видно, что при одинаковых константах ДДВ наблюдаются, как и ожидалось, три пика в положительной и два пика в отрицательной областях. При произвольных константах ДДВ наблюдаются семь пиков в положительной области и два пика в отрицательной. Для исследования влияния трехспиновых групп на сигналы СЭ предложена методика расчета интегральной интенсивности F_e(ω), нормированной на максимальное значение (площадь спектра под кривой), и проведены расчеты в широком температурном интервале при различных значениях характерного времени молекулярных движений в полимере.

Рис. 1.

Форма линии F_e(ω) при одинаковых значениях констант ДДВ и N₀ = 20, b = 10^–5, τ_c = 0.01.

Рис. 2.

Фурье-преобразование СЭ F_e(ω) при различных значениях констант ДДВ и ${{\sigma }_{1}} = 0,$ $~{{\sigma }_{2}} = - 7 \cdot {{10}^{{ - 4}}}\,\,{{{\text{c}}}^{2}},$ $N = 20,$ ${{\tau }_{1}} = {{10}^{{ - 5}}}\,\,{\text{с}},$ ${{\tau }_{c}} = 0.001.$

Из рис. 3 видно, что для расчетных параметров при уменьшении ${{\tau }_{c}}$ влияние трехспиновых групп с одинаковыми и произвольными константами ДДВ практически одинаковое. Большее различие наблюдается при небольших значениях характерного времени корреляции ${{\tau }_{c}}$ молекулярной подвижности, т.е. при низкой температуре.

Рис. 3.

Зависимость от τ_с интегральной интенсивности S сигнала без трехспиновых групп (1), с одинаковыми (2) и произвольными (3) константами ДДВ.

Расчеты показали, что значения интегральной интенсивности сигналов практически совпадают при расчете по формулам (6) и (12), если вместо G_r(t) рассчитывать G(t) по формуле (5) с трехспиновой группой. Это позволит в дальнейшем проводить расчеты по формуле (12), что существенно сокращает время счета.

ЗАКЛЮЧЕНИЕ

В работе развита теория сигналов ССИ и СЭ в линейных полимерах, содержащих изолированные трехспиновые группы с произвольными константами ДДВ. На основе предложенной ранее теории [6, 7] получена формула для сигнала первичного эха в линейных полимерах, содержащих выделенные трехспиновые группы. Проведены расчеты сигналов ССИ и СЭ в линейных полимерах с группой трех спинов 1/2 с эквивалентыми и произвольными константами ДДВ с использованием точной аналитической формулы [9, 10]. Расчеты сигналов ССИ указывают на то, что в форме линии при одинаковых константах ДДВ наблюдаются три пика, а при различных константах ДДВ – 5 или 7 пиков.

Предложенная методика исследования влияния трехспиновых групп на сигналы СЭ позволяет по интегральной интенсивности сигнала качественно определять наличие выделенных групп в полимерной цепи и получать информацию о константах ДДВ.

Работа выполнена как часть госзадания (регистрационный номер АААА-А19-119071190017-7).

Список литературы

Andrew E.R., Bersohn R. // J. Chem. Phys. 1950. V. 18. № 2. P. 159.
Gutowsky H.S., Pake G.E. // J. Chem. Phys. 1950. V. 18. P. 162.
Powles J.G., Mansfield P. // Phys. Lett. 1962. V. 2. P. 58.
Moskvich Yu.N., Sergeev N.A., Dotsenko G.I. // Phys. Stat. Sol. (a). 1975. V. 86. P. 409.
Chizhik V.I., Chernyshev Yu.S., Donets A.V. et al. Magnetic Resonance and Its Applications. Berlin: Springer-Verlag, 2014.
Кулагина Т.П., Карнаух Г.Е., Кузина А.Н., Смирнов Л.П. // Хим. физика. 2013. Т. 32. № 3. С.62.
Кулагина Т.П., Карнаух Г.Е., Смирнов Л.П., Кузина А.Н. // Хим. физика. 2014. Т. 33. № 8. С. 59.
Kulagina T.P., Karnaukh G.E., Golubeva I.Yu. // Appl. Magn. Reson. 2020. V. 51. № 2. P. 155.
Кулагина Т.П., Карнаух Г.Е., Голубева И.Ю. // Хим. физика. 2020. Т. 39. № 4. С. 31.
Кулагина Т.П., Карнаух Г.Е., Андрианов С.А. // Бутлеров. сообщ. 2013. № 7. С. 35.
Кокорин А.И., Громов О.И., Kálai T., Hideg K., Путников А.Е. // Хим. физика. 2019. Т. 38. № 4. С. 58.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Химическая физика

Архивы выпусков Информация о журнале Отправить рукопись в журнал