1. На главную
  2. Электронные версии
  3. Химическая физика
  4. T. 40, № 5, 2021

Химическая физика, 2021, T. 40, № 5, стр. 81-85

Проекционные операторы для идентификации планетарных волн Россби и Пуанкаре в атмосфере

А. И. Клопова 1, С. Б. Лебле 1, И. В. Карпов 1, 2, *

1 Балтийский федеральный университет имени Иммануила Канта
Калининград, Россия

2 Калининградский филиал Института земного магнетизма, ионосферы и распространения радиоволн им. Н.В. Пушкова Российской академии наук
Калининград, Россия

* E-mail: ivkarpov@inbox.ru

Поступила в редакцию 24.07.2020
После доработки 01.09.2020
Принята к публикации 21.09.2020

Полный текст (PDF)

Аннотация

В статье рассматриваются возможности применения метода проекционных операторов для анализа результатов наблюдений параметров атмосферы с целью выделения вкладов планетарных волн Россби и Пуанкаре. В верхней атмосфере волновые возмущения планетарных масштабов регистрируются в периоды геомагнитных возмущений, а также в периоды мощных динамических процессов в нижних слоях атмосферы, таких как ураганы, метеорологические штормы, внезапные стратосферные потепления. Метод проекционных операторов расширяет возможности анализа таких возмущений параметров атмосферы, позволяя определить амплитудные характеристики планетарных волн, их пространственные и временны́е масштабы. В работе представлена процедура вывода конечно-разностных проекционных операторов, которая может быть применена к анализу временны́х рядов наблюдений, выполняемых отдельными станциями. Приведены результаты тестовых исследований проекционных операторов с оценкой точности определения характеристик волн Россби и Пуанкаре.

Ключевые слова: планетарные волны Россби и Пуанкаре, атмосфера, ионосфера, проекционный оператор, наблюдаемые параметры атмосферы.

1. ВВЕДЕНИЕ

В исследованиях динамики верхней атмосферы и ионосферы важное внимание уделяется изучению характеристик волновых процессов и, в частности, характеристик планетарных волновых возмущений. Такие возмущения наблюдаются в вариациях атмосферных и ионосферных параметров при развитии мощных метеорологических процессов в нижней атмосфере в периоды внезапных стратосферных потеплений и геомагнитных возмущений. Результаты наблюдений вариаций атмосферных и ионосферных параметров в таких условиях рассматривались в многочисленных работах и показали усиление вариаций с периодами планетарных волн [1–5]. Теоретические представления о причинах появления таких вариаций в ионосфере связывают с волновыми процессами, развивающимися в атмосфере в условиях возмущений на различных высотах.

Однако до настоящего времени типы планетарных волновых процессов, их характеристики и особенности возбуждения остаются недостаточно изученными, что усложняет задачу интерпретации экспериментальных данных. Проблемой экспериментальных исследований динамики атмосферы является ненадежная идентификация типов наблюдаемых волновых возмущений. Современные исследования волновых возмущений основываются на методах гармонического анализа результатов наблюдений, позволяющих выделить частотные характеристики возмущений, что, очевидно, недостаточно для идентификации типа волнового возмущения. Это связано, с одной стороны, с недостаточным количеством экспериментальных данных, а с другой – с недостатками методов обработки результатов наблюдений.

Важным инструментом в решении задач идентификации волн является метод проекционных операторов, успешно применяемый в различных областях физики, например в исследованиях электромагнитных и звуковых процессов [6–8]. В этом методе предполагается, что наблюдаемая пространственно-временная структура параметров среды определяется суперпозицией волн различных типов, для которых предполагаются известными дисперсионные и поляризационные соотношения. На основе таких предположений можно построить операторы проектирования исходного суперпозиционного состояния Ф на линейный базис, соответствующий известному типу волн:

$\Phi = \sum\limits_1^n {{{\Phi }_{i}}} = \sum\limits_1^n {{{P}_{i}}\Phi } .$

Здесь ${{P}_{i}}$ и ${{\Phi }_{i}}$ – оператор проектирования и волновой вектор, соответствующие i-ому типу волны. Вектор Фi содержит компоненты волнового поля, например меридиональную и зональную проекции вектора скорости, давление и т.д. Связь между компонентами вектора Фi для каждого типа волны определяется поляризационными соотношениями. Действие оператора проектирования на суперпозиционное состояние Ф, которое является результатом наблюдений, определяет амплитуды и фазы Фi волн известного типа. Для операторов проектирования, в соответствии с определением, предполагается выполнение следующих условий:

(2)
$P_{i}^{2} = {{P}_{i}}\,\,\,\,{\text{и}}\,\,\,\,\sum\limits_i {{{P}_{i}}} = I,$

где I – единичный оператор.

В более простой задаче атмосферной акустики в приближении вертикально распространяющихся плоских волн такие операторы были построены в работе [9]. Их применение к задаче модельной диагностики было представлено в [10]. В работе [11] к волновым модам подключено состояние подпространства нулевой частоты – так называемая энтропийная мода.

2. ОПЕРАТОРЫ ПРОЕКТИРОВАНИЯ ДЛЯ ПЛАНЕТАРНЫХ ВОЛН РОССБИ И ПУАНКАРЕ

В задаче идентификации типов баротропных планетарных волн в атмосфере Земли построение проекционных операторов основывается на решении уравнений гидродинамики для волн Россби и Пуанкаре в приближении β-плоскости, имеющих вид [12]

(3)
$\begin{gathered} {{U}_{t}} - fV + {{c}^{2}}{{\eta }_{x}} = 0, \\ {{V}_{t}} + fU + {{c}^{2}}{{\eta }_{y}} = 0, \\ {{\eta }_{t}} + {{V}_{y}} + {{U}_{x}} - \beta V = 0. \\ \end{gathered} $

В уравнениях (3) координаты x и y определяют зональное (на восток) и меридиональное (на юг) направления, t – время. Переменные U и V связаны с меридиональной (u) и зональной (v) компонентами вектора скорости: ${v}{{H}_{0}} = V,$ $u{{H}_{0}} = U;$ $\eta $ – геопотенциальная высота, H0 – высота однородной атмосферы, ${{c}^{2}} = g\gamma H$ (γ – показатель адиабаты), $H = {{H}_{0}}(1 - \beta y),$ $f = 2\Omega \cos \theta ,$ $\beta = \left( {{1 \mathord{\left/ {\vphantom {1 R}} \right. \kern-0em} R}} \right)\sin \theta ,$ R – радиус Земли, $\Omega $ – угловая скорость вращения Земли, $\theta $ – коширота, на которой определена $\beta $ – плоскость. Уравнения (3) описывают динамику газа в канале шириной L с непроницаемыми стенками и наклоном дна, определяемым параметром β.

В динамике атмосферы и ионосферы такого рода задачи возникают при анализе наблюдений атмосферных и ионосферных параметров в периоды геомагнитных возмущений, когда формируются разнесенные по широте области нагрева термосферы вследствие диссипации ионосферных токов в высоких широтах и поглощения солнечного излучения. Примеры результатов экспериментальных исследований ионосферы, выявивших возмущения планетарных масштабов во время прохождения геомагнитных бурь, представлены в работах [1–4]. Усиление активности планетарных волн в нижней термосфере также отмечается в периоды внезапных стратосферных возмущений и метеорологических процессов в тропосфере [2–5, 13–15].

Решение для этого случая можно представить в следующем виде:

(4)
$\begin{gathered} V = \sum\limits_n {{{Y}_{n}}{{\Theta }_{n}}} , \\ U = \sum\limits_n {{{Y}_{n}}{{\varphi }_{n}}} + {{Y}_{{ny}}}{{\phi }_{n}}, \\ \eta = \sum\limits_n {{{Y}_{n}}{{\mu }_{n}}} + {{Y}_{{ny}}}{{\nu }_{n}}. \\ \end{gathered} $

Здесь ${{Y}_{n}} = \sin ({{l}_{n}}y)\exp ({{\beta y} \mathord{\left/ {\vphantom {{\beta y} 2}} \right. \kern-0em} 2}),$ ${{l}_{n}} = {{\pi n} \mathord{\left/ {\vphantom {{\pi n} L}} \right. \kern-0em} L}.$

Выполняя преобразование Фурье системы (4) по переменной x, в котором

$\Theta = \int {\exp (ikx)\tilde {\theta }dk} ,$

переходим к новой системе уравнений для фурье-образов [6–8]:

(5)
$\begin{gathered} {{{\tilde {\mu }}}_{t}} + ik\tilde {\varphi } - \beta \tilde {\theta } = 0, \\ {{{\tilde {\varphi }}}_{t}} - f\tilde {\theta } + ik{{c}^{2}}\tilde {\mu } = 0, \\ {{{\tilde {\theta }}}_{t}} + f(1 - Q)\varphi + \beta {{c}^{2}}Q\tilde {\mu } = 0, \\ Q = {{({{l}^{2}} + {{{{\beta }^{2}}} \mathord{\left/ {\vphantom {{{{\beta }^{2}}} 4}} \right. \kern-0em} 4})} \mathord{\left/ {\vphantom {{({{l}^{2}} + {{{{\beta }^{2}}} \mathord{\left/ {\vphantom {{{{\beta }^{2}}} 4}} \right. \kern-0em} 4})} {({{\beta }^{2}} - {{{{f}^{2}}} \mathord{\left/ {\vphantom {{{{f}^{2}}} {{{c}^{2}}}}} \right. \kern-0em} {{{c}^{2}}}})}}} \right. \kern-0em} {({{\beta }^{2}} - {{{{f}^{2}}} \mathord{\left/ {\vphantom {{{{f}^{2}}} {{{c}^{2}}}}} \right. \kern-0em} {{{c}^{2}}}})}}. \\ \end{gathered} $

Условием разрешимости системы (5) являются дисперсионные соотношения для низкочастотной (волны Россби) и высокочастотной (волны Пуанкаре) составляющих, которые имеют вид

(6)
$\begin{gathered} {{\sigma }_{1}} = {{ - \beta fk} \mathord{\left/ {\vphantom {{ - \beta fk} {\left( {{{k}^{2}} + {{l}^{2}} + {{{{f}^{2}}} \mathord{\left/ {\vphantom {{{{f}^{2}}} {{{c}^{2}}}}} \right. \kern-0em} {{{c}^{2}}}}} \right)}}} \right. \kern-0em} {\left( {{{k}^{2}} + {{l}^{2}} + {{{{f}^{2}}} \mathord{\left/ {\vphantom {{{{f}^{2}}} {{{c}^{2}}}}} \right. \kern-0em} {{{c}^{2}}}}} \right)}},\,\,\,\,{{\sigma _{1}^{2}} \mathord{\left/ {\vphantom {{\sigma _{1}^{2}} {{{f}^{2}}}}} \right. \kern-0em} {{{f}^{2}}}} < 1; \\ {{\sigma }_{{2,3}}} = \pm c{{\left[ {{{{({f \mathord{\left/ {\vphantom {f c}} \right. \kern-0em} c})}}^{2}} + {{k}^{2}} + {{l}^{2}} + {{{{\beta }^{2}}} \mathord{\left/ {\vphantom {{{{\beta }^{2}}} 4}} \right. \kern-0em} 4}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},\,\,\,\,{{{{\sigma }_{{2,3}}}} \mathord{\left/ {\vphantom {{{{\sigma }_{{2,3}}}} f}} \right. \kern-0em} f} > 1. \\ \end{gathered} $

Здесь σ1 – частота волны Россби, а σ2,3 – частоты правой и левой волн Пуанкаре; k и l – компоненты волнового вектора в зональном и меридиональном направлениях соответственно. Компоненты вектора $\Phi = \sum\nolimits_1^3 {{{\Phi }_{i}}} $ для рассматриваемых волн определяются следующим образом:

(7)
$\begin{gathered} {{{\tilde {\varphi }}}_{i}} = \frac{{f{{\sigma }_{i}} + k\beta {{c}^{2}}}}{{\beta \sigma + kf}}{{{\tilde {\mu }}}_{i}} \equiv {{a}_{i}}{{{\tilde {\mu }}}_{i}}, \\ {{{\tilde {\theta }}}_{i}} = \frac{{\sigma _{i}^{2} - {{k}^{2}}{{c}^{2}}}}{{i(\beta \sigma + kf)}}{{{\tilde {\mu }}}_{i}} \equiv {{b}_{i}}{{{\tilde {\mu }}}_{i}}, \\ {{\Phi }_{i}} = \left( {\begin{array}{*{20}{c}} 1 \\ {{{a}_{i}}} \\ {{{b}_{{}}}} \end{array}} \right){{{\tilde {\mu }}}_{i}}. \\ \end{gathered} $

Для баротропных волн Россби и Пуанкаре в атмосфере общий вид проекционных операторов получен в [6]:

(8)
${{P}_{i}} = \left( {\begin{array}{*{20}{c}} {{{\alpha }_{i}}}&{{{\beta }_{i}}}&{{{\gamma }_{i}}} \\ {{{\alpha }_{i}}{{a}_{i}}(\sigma )}&{{{\beta }_{i}}{{a}_{i}}(\sigma )}&{{{\gamma }_{i}}{{a}_{i}}(\sigma )} \\ {{{\alpha }_{i}}{{b}_{i}}(\sigma )}&{{{\beta }_{i}}{{b}_{i}}(\sigma )}&{{{\gamma }_{i}}{{b}_{i}}(\sigma )} \end{array}} \right).$

Матричные элементы операторов Pi определяются соотношениями

(9)
$\begin{gathered} {{\Delta }_{1}} = {{b}_{2}}{{a}_{3}} - {{b}_{3}}{{a}_{2}},\,\,\,\,{{\Delta }_{2}} = {{b}_{3}}{{a}_{1}} - {{b}_{1}}{{a}_{3}}, \\ {{\Delta }_{3}} = {{b}_{1}}{{a}_{2}} - {{b}_{2}}{{a}_{1}},\,\,\,\,{{\alpha }_{i}} = \frac{{{{\Delta }_{i}}}}{\Xi },\,\,\,\,\Xi = \sum\limits_i {{{\Delta }_{i}}} , \\ {{\beta }_{1}} = \frac{{({{b}_{3}} - {{b}_{2}})}}{\Xi },\,\,\,\,{{\beta }_{2}} = \frac{{({{b}_{1}} - {{b}_{3}})}}{\Xi },\,\,\,\,{{\beta }_{3}} = \frac{{({{b}_{2}} - {{b}_{1}})}}{\Xi }, \\ {{\gamma }_{1}} = \frac{{({{a}_{2}} - {{a}_{3}})}}{\Xi },\,\,\,\,{{\gamma }_{2}} = \frac{{({{a}_{3}} - {{a}_{1}})}}{\Xi },\,\,\,\,{{\gamma }_{3}} = \frac{{({{a}_{1}} - {{a}_{2}})}}{\Xi }. \\ \end{gathered} $

Решение задачи выделения из суперпозиции той или иной волны предполагает определение амплитуды, частоты и волнового числа. При непосредственном применении операторов проектирования определяется только амплитуда волны (1). Частоту и волновое число можно определить из поляризационных соотношений (7). Соответствующие выражения для расчета этих параметров имеют вид

(10)
${{k}_{i}} = i{{b}_{i}}\frac{{({{a}_{i}}\beta - f)}}{{{{c}^{2}} - {{a}_{i}}^{2}}},\,\,\,\,{{\sigma }_{i}} = i{{b}_{i}}\frac{{(\beta {{c}^{2}} - f{{a}_{i}})}}{{{{c}^{2}} - a_{i}^{2}}}.$

Таким образом, методом проекционных операторов определяется процедура выделения характеристик известной планетарной волны (амплитуды, частоты и волнового числа) из суперпозиционного состояния с помощью поляризационных соотношений (7).

3. ПРИМЕНЕНИЕ ПРОЕКЦИОННЫХ ОПЕРАТОРОВ ДЛЯ АНАЛИЗА ВОЛНОВЫХ ПОЛЕЙ В АТМОСФЕРЕ

Для применения метода проекционных операторов для анализа волновой структуры атмосферы операторы проектирования (8) следует модифицировать, определив их действующими только на зависящие от времени функции. Зависимость $k(\sigma )$ определяется из дисперсионных соотношений и используется в выражениях для матричных элементов проекционных операторов (7)–(9).

Из дисперсионного соотношения (6) для волн Россби следует, что $k(\sigma )$ определяется алгебраическим уравнением:

(11)
${{k}^{2}} + k_{{max}}^{2} + \frac{{\beta fk}}{\sigma } = 0.$

Здесь $k_{{max}}^{2} = {{{{f}^{2}}} \mathord{\left/ {\vphantom {{{{f}^{2}}} {{{c}^{2}}}}} \right. \kern-0em} {{{c}^{2}}}} + {{l}^{2}}.$ Решения (11) определяют “длинные” ($k < {{k}_{{max}}}$) и “короткие” ($k > {{k}_{{max}}}$) волны Россби, соответствующие одной частоте. Параметр kmax – волновое число, соответствующее волне Россби с максимально допустимой частотой ${{\sigma }_{{max}}} = {{\beta f} \mathord{\left/ {\vphantom {{\beta f} {2{{k}_{{max}}}}}} \right. \kern-0em} {2{{k}_{{max}}}}}.$ Зависимость $k{\kern 1pt} \left( \sigma \right)$ с точностью до членов разложения ${{\left( {{\sigma \mathord{\left/ {\vphantom {\sigma f}} \right. \kern-0em} f}} \right)}^{3}}$ для “коротких” и “длинных” волн имеет соответственно вид

(12)
$k = - \frac{\beta }{\lambda } + \frac{{\beta \lambda }}{{{{{v}}^{2}}}},$
(13)
$\begin{gathered} k = - \frac{{\beta \lambda }}{{{{{v}}^{2}}}} - \frac{{\beta {{\lambda }^{3}}}}{{{{{v}}^{4}}}}, \\ \lambda = \frac{\sigma }{f},\,\,\,\,{v} = - \frac{\beta }{{{{k}_{{max}}}}}. \\ \end{gathered} $

Коэффициенты ${{a}_{1}}(\sigma ){{b}_{1}}(\sigma )$ в операторе (7) в приближении “коротких” и “длинных” волн будут иметь соответственно вид

(14)
${{a}_{1}} = {{\eta }}c + \frac{{c{{\lambda }^{2}}\left( {{{\eta }^{2}} - 1} \right)}}{\eta },\,\,\,\,{{b}_{1}} = - \frac{{\eta c\lambda }}{{i{{v}^{2}}}};$
(15)
${{a}_{1}} = - {{\eta }}c - \frac{{c{{\lambda }^{2}}\left( {{{\eta }^{2}} - 1} \right)}}{\eta },\,\,\,\,{{b}_{1}} = \frac{{\eta c\lambda }}{{i{{v}^{2}}}}.$

В (14), (15) приняты следующие обозначения: η = $ = \beta {c \mathord{\left/ {\vphantom {c f}} \right. \kern-0em} f},$ $i = \sqrt { - 1} .$

Для волн Пуанкаре проекционный оператор строится по такой же схеме. Дисперсионное соотношение для этих волн имеет вид

(16)
${{k}^{2}} + k_{{max}}^{2} + \frac{{{{\beta }^{2}}}}{4} - \frac{{{{\sigma }^{2}}}}{{{{c}^{2}}}} = 0.$

Решение (16) определяет две волны, которые распространяются на восток (индекс “2”) и на запад (индекс “3”):

(17)
${{k}_{{2,3}}} = \mp \left( {\frac{f}{{c{{\delta }}}} - \frac{{c{{\delta }}{{\beta }^{2}}}}{{4f{{{v}}^{2}}}}} \right),\,\,\,\,{{\delta }} = \frac{f}{\sigma }.$

Для волн Пуанкаре в качестве малого параметра для разложения выбран параметр δ = f/σ. Пренебрегая малыми членами выше второго порядка, можно получить следующие выражения для коэффициентов ${{a}_{{2,3}}}(\sigma )$ и ${{b}_{{2,3}}}(\sigma ){\text{:}}$

(18)
${{a}_{2}} = - c + \frac{{{{\eta }^{2}}c\left( {\eta + 1} \right)}}{{4{{{v}}^{2}}\left( {\eta - 1} \right)}}{{\delta }^{2}},\,\,\,\,{{b}_{2}} = \left( { - \frac{{{{\eta }^{2}}c)}}{{2i{{{v}}^{2}}\left( {1 - \eta } \right)}}} \right)\delta ,$
(19)
${{a}_{3}} = c - \frac{{{{\eta }^{2}}c\left( {\eta - 1} \right)}}{{4{{{v}}^{2}}\left( {\eta + 1} \right)}}{{\delta }^{2}},\,\,\,\,~{{b}_{2}} = \left( {\frac{{{{\eta }^{2}}с}}{{2i{{{v}}^{2}}\left( {1 + \eta } \right)}}} \right)\delta .$

Используя выражения (14), (15), (18), (19), можно получить аналитические выражения для матричных элементов операторов проектирования.

В качестве теста рассматривались результаты действия полученных в аналитическом виде операторов на собственные векторы волн Россби и Пуанкаре (7), определенные на широте 50° при ширине канала L = 3000 км для моды с n = 1. Такой выбор параметров определяется характерными масштабами планетарных возмущений в верхней атмосфере в периоды геомагнитных бурь и внезапных стратосферных потеплений.

Результаты тестовых расчетов показали, что амплитуда выделяемой волны Паункаре, определенная после действия оператора на волновое поле, практически совпадает с амплитудой этой волны в тестовом примере во всей области изменения параметра δ. Амплитуда волны Россби после применения оператора проектирования становится существенно меньше амплитуды анализируемой волны при λ > 0.4 (см. ниже рис. 1б). Это означает, что построенный оператор проектирования для волн Россби применим только при меньших значениях параметра λ, что соответствует периодам волн Россби более ~3 сут на средних широтах.

Рис. 1.

Амплитуды “длинной” волны Россби в анализируемом волновом поле (штрих-пунктирная линия), после применения оператора проектирования в аналитическом представлении (штриховая) и конечноразностного оператора (сплошная).

4. КОНЕЧНО-РАЗНОСТНЫЕ АНАЛОГИ ПРОЕКЦИОННЫХ ОПЕРАТОРОВ

Для непосредственного применения проекционных операторов к временны́м рядам экспериментальных данных необходимо переопределить оператор частоты σ в выражениях для матричных элементов операторов. Согласно исходным положениям построенные проекционные операторы действуют на волны вида $F{\kern 1pt} \left( {{\mathbf{r}},t} \right) = {{F}_{0}}{\text{exp}}\left\{ {i\left( {{\mathbf{kr}} - \sigma t} \right)} \right\}.$ Это позволяет в матричных элементах связать умножение на частоту $\sigma $ с оператором дифференцирования по времени, а деление – с интегрированием:

(20)
$\sigma F{\kern 1pt} \left( {{\mathbf{r}},t} \right) = i\frac{{\partial F{\kern 1pt} \left( {{\mathbf{r}},t} \right)}}{{\partial t}};\,\,\,\,{{\sigma }^{{ - 1}}}F{\kern 1pt} \left( {{\mathbf{r}},t} \right) = - i\int {F{\kern 1pt} \left( {{\mathbf{r}},t} \right)dt} .$

Матричные элементы в операторе проектирования удобно представить в виде разложения в степенные ряды по малым параметрам $\delta = {f \mathord{\left/ {\vphantom {f \sigma }} \right. \kern-0em} \sigma }$ и $\lambda = {\sigma \mathord{\left/ {\vphantom {\sigma f}} \right. \kern-0em} f}$ для волн Пуанкаре и волн Россби соответственно:

(21)
$P_{{ij}}^{{(1)}} = \sum\limits_n {A_{{ijn}}^{{(1)}}{{\lambda }^{n}}} ,\,\,\,\,P_{{ij}}^{{(2,3)}} = \sum\limits_n {A_{{ijn}}^{{(2,3)}}{{\delta }^{n}}} .$

В соответствии с (20) переменные λn и δn в операторах проектирования (21) при переходе от (σ, k)-пространства к (r, t)-пространству должны быть преобразованы в соответствующие конечно-разностные операторы дифференцирования и интегрирования по времени. Производные по времени от исходного волнового поля могут быть представлены конечно-разностными операторами вида

(22)
$\begin{gathered} \frac{{\partial f}}{{\partial t}} = \frac{{f(t) - f(t - \tau )}}{\tau },\,\,\,\,\frac{{{{\partial }^{2}}f}}{{\partial {{t}^{2}}}} = \\ = \frac{{f(t) - 2f(t - \tau ) + f(t - 2\tau )}}{{{{\tau }^{2}}}}. \\ \end{gathered} $

С применением таких аппроксимаций были построены конечно-разностные операторы и выполнены тестовые расчеты действия проекционного оператора на исходное волновое поле, изменяющееся во времени как $\exp (i\sigma t).$ Для заданной из области рассматриваемых планетарных волн частоты и нормированной амплитуды волны определялось изменяющееся во времени волновое поле в соответствии с поляризационными соотношениями (6), (7). Оператор проектирования для заданного типа волн применялся к построенному таким образом волновому полю. В этом случае можно сравнить характеристики выделенной, после применения оператора проектирования, волны с исходной, заданной гармонической волной.

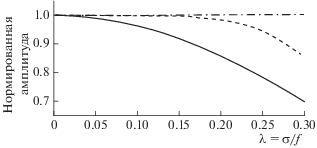
На рис. 1 показаны результаты тестового расчета действия конечно-разностного оператора для “длинных” волн Россби на исходное волновое поле, изменяющееся во времени как $\exp \left( {i\sigma t} \right)$ с нормированной амплитудой, соответствующей собственному волновому вектору для этих волн. В этих расчетах широта β-плоскости и ширина канала такие же, как и в тестовых расчетах с операторами в аналитическом виде.

Как следует из представленных результатов, точность определения амплитуды волны конечно-разностным оператором не превышает 5% при λ < 0.1 и 10% при λ < 0.15, что соответствует периодам волн ~7 и ~4 сут на средних широтах. Расчеты также показали, что изменение шага по времени (параметр τ в (22)) в диапазоне от 1 до 6 ч слабо влияет на результат.

На рис. 2 показаны результаты расчетов, демонстрирующих точность определения амплитуды “длинной” волны Россби конечно-разностным оператором проектирования в зависимости от широты для волн с различными периодами, определяемыми параметром λ.

Рис. 2.

Амплитуды “длинных” волн Россби в зависимости от кошироты θ при разных значениях параметра $\lambda = {\sigma \mathord{\left/ {\vphantom {\sigma f}} \right. \kern-0em} f}{\text{:}}$ 0.12 (сплошная линия), 0.15 (штриховая), 0.20 (штрих-пунктирная).

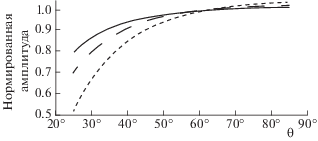
Как видно из этого рисунка, точность определения амплитуды снижается с уменьшением кошироты и периода волны (увеличением параметра λ). На средних широтах точность определения амплитуды волн не превышает 10% в области периодов ~4 сут.

Результаты расчетов показали, что в тех случаях, когда тип волны, заданной в исходном волновом поле, совпадал с типом проекционного оператора, амплитуда волны определялась с точностью ~5–10% на средних широтах. В противном случае, когда проекционный оператор применялся не к “своей волне”, амплитуда волны, определяемой проекционным оператором, была меньше амплитуды исходной волны не менее чем в 4–5 раз.

5. ЗАКЛЮЧЕНИЕ

Таким образом, предлагаемая процедура построения конечно-разностных операторов проектирования для планетарных волн Россби и Пуанкаре позволяет получить операторы, которые с приемлемой точностью решают задачу выделения характеристик этих волн в анализируемом волновом поле. Точность решения задачи, в принципе, может быть повышена путем включения в анализ членов более высокого порядка в разложениях (21) по параметрам δ и λ. Достоинство конечно-разностной формы операторов состоит в возможности решения задачи идентификации типа планетарной волны на основе анализа временны́х рядов наблюдений, получаемых на отдельной станции. Недостатком этого метода анализа волновых полей является необходимость иметь ряд наблюдений всех компонент анализируемого волнового поля – давления и компонент скорости, что является проблемой экспериментальных исследований. Однако можно предположить, что развитие методики применения операторов проектирования позволит решать задачу анализа волновых полей и в случае неполноты набора измеряемых параметров.

В теоретических исследованиях, выполняемых с применением гидродинамических моделей, этот недостаток отсутствует, и операторы проектирования будут служить полезным инструментом анализа результатов модельных экспериментов.

Работа выполнена при финансовой поддержке грантом Российского фонда фундаментальных исследований № 18-05-00184.

Список литературы

  1. Altadill D., Apostolov E.M. // J. Geophys. Res. 2003. V. 108. № A11. P. 1403.

  2. Pancheva D., Apostolov E., Laštovička J., Boška J. // J. Atmos. Terr. Phys. 1989. V. 51. P. 381.

  3. Laštovička J., Križan P., Novotná D. // Studia Geophys. Geod. 2003. V. 47. P. 161.

  4. Laštovička J., Križan P., Šauli P., Novotná D. // Ann. Geophysicae. 2003. V. 21. P. 1543.

  5. Rishbeth H., Mendillo M. // J. Atmos. Solar-Terr. Phys. 2001. V. 63. P. 1661.

  6. Лебле С.Б. Волноводное распространение нелинейных волн в стратифицированных средах. Л.: Изд-во ЛГУ, 1988.

  7. Leble S. Nonlinear Waves in Waveguides (with stratification). Berlin Heidelberg: Springer Verlag, 1991.

  8. Leble S., Perelomova A. Dynamical projectors method in hydro- and electrodynamics. London: Taylor & Francis Group, 2018.

  9. Лебле С.Б., Верещагин С.Д., Верещагина И.С. // Хим. физика. 2018. Т. 37. № 5. С. 68.

  10. Leble S., Vereshchagin S. // Pure Appl. Geophys. 2018. V. 175. № 8. P. 3023.

  11. Лебле С.Б., Верещагин С.Д., Верещагина И.С. // Хим. физика. 2020. Т. 39. № 4. С. 73.

  12. Pedlosky J. Geophysical fluid dynamics. N.Y.: Springer Verlag, 1987.

  13. Васильев П.А., Бессараб Ф.С., Карпов И.В., Клименко В.В., Клименко М.В., Суходолов Т.В., Розанов Е.В. // Изв. РАН. Физика атмосферы и океана. 2019. Т. 55. № 2. С. 41.

  14. Карпов И.В., Бессараб Ф.С., Борчевкина О.П., Артеменко К.А., Клопова А.И. // Геомагнетизм и аэрономия. 2018. Т. 58. № 4. С. 526.

  15. Карпов И.В., Бессараб Ф.С., Кореньков Ю.Н., Клименко В.В., Клименко М.В. // Хим. физика. 2016. Т. 35. № 1. С. 49.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Химическая физика

Архивы выпусков Информация о журнале Отправить рукопись в журнал