Химическая физика, 2022, T. 41, № 1, стр. 77-87
Влияние спонтанных флуктуаций на возникновение и развитие турбулентности. 1. Расчет вклада спонтанных флуктуаций
И. В. Лебедь *
Институт прикладной механики Российской академии наук
Москва, Россия
* E-mail: lebed-ivl@yandex.ru
Поступила в редакцию 09.03.2021
После доработки 27.04.2021
Принята к публикации 20.05.2021
- EDN: QMIRRQ
- DOI: 10.31857/S0207401X22010095
Аннотация
Уравнения многомоментной гидродинамики привлечены для изучения процесса искажения регулярных режимов течения в задаче обтекания покоящейся сферы. Исследуется влияние на эти искажения спонтанных флуктуаций, которые постоянно присутствуют в среде независимо от внешнего воздействия. После пересечения критического значения числа Рейнольдса стационарное решение уравнений многомоментной гидродинамики теряет устойчивость. Потеря устойчивости сопровождается качественным изменением в поведении спонтанных флуктуаций. Независимость в их поведении исчезает. Законы сохранения вынуждают спонтанные флуктуации подстраивать свое поведение во времени и в пространстве под поведение гидродинамических величин. При отсутствии неупорядоченных возмущений выполнение законов сохранения в системе, потерявшей устойчивость, обеспечивается спонтанными флуктуациями.
ВВЕДЕНИЕ
Анализ данных эксперимента привел исследователей к выводу, что возникновение турбулентности связано с появлением крупных вихрей (когерентных структур), зарождающихся вблизи ограничивающих течение поверхностей [1, 2]. В соответствии с существующими представлениями турбулентность интерпретируется в терминах эволюции когерентных структур. Полуэмпирический детерминистический подход к расчету турбулентности сформировался около 150 лет назад. Усредненные по Рейнольдсу уравнения Навье–Стокса (RANS), отражающие этот подход, выведены в те же далекие времена. Эти уравнения и их современная модификация (моделирование крупных вихрей (LES)) решаются вплоть до настоящего времени, несмотря на значительные количественные и качественные расхождения с данными эксперимента. В каждом конкретном случае необходимым условием корректности приближенных полуэмпирических методов является совпадение результатов RANS- и LES-расчетов с результатами прямого численного интегрирования уравнений Навье–Стокса. Прямое численное интегрирование является наиболее точным способом моделирования наблюдаемых явлений, простых и сложных.
Обтекание твердой сферы является простейшей задачей гидродинамики. Решение этой задачи при низких значениях числа Рейнодьдса (Re) найдено во времена создания уравнений Навье–Стокса. При умеренно высоких значениях $\operatorname{Re} $ в эксперименте регистрируется только одна регулярная когерентная структура в следе за сферой – зона закручивания. При повышении $\operatorname{Re} $ в эксперименте дополнительно регистрируется в дальнем следе за сферой набор регулярных когерентных структур, образующих вихревую дорожку. Дальнейшее повышение $\operatorname{Re} $ сопровождается постепенным замещением регулярной картины течения на турбулентную.
Прямое численное интегрирование уравнений Навье–Стокса позволяет успешно воспроизвести все устойчивые регулярные течения вокруг сферы, однако оно не в состоянии воспроизвести ни одного из наблюдаемых неустойчивых регулярных режимов (см. обзор [3]). Уравнения многомоментной гидродинамики позволяют сделать следующий шаг на пути продвижения по Re. В отличие от решений уравнений классической гидродинамики, решения уравнений многомоментной гидродинамики удовлетворительно воспроизводят все наблюдаемые регулярные течения, последовательно возникающие после того, как основное течение теряет свою устойчивость (периодические пульсации зоны закручивания и два режима вихревого испускания) [4, 5].
Сравнение результатов прямого численного интегрирования с экспериментом показывает, что детерминистическое многопериодическое решение уравнений Навье–Стокса не имеет ни малейших перспектив проинтерпретировать хаотический турбулентный режим обтекания сферы [6–8]. Регулярное движение когерентных структур (устойчивое и неустойчивое), которое описывается решениями детерминистических уравнений многомоментной гидродинамики, также не в состоянии воспроизвести турбулентную картину течения (смотри обзор [8]). Это является причиной интереса к исследованию влияния стохастических факторов на возникновение и развитие турбулентности, а именно, неупорядоченных возмущений и спонтанных флуктуаций.
Турбулентные процессы протекают в окружающей среде, на промышленных предприятиях, в экспериментальных установках. Влияние турбулентности необходимо учитывать при разработке химических технологий; турбулентность оказывает сильное воздействие на режим горения [9, 10]. При наблюдении за турбулентными процессами в поле течения регистрируется большое количество крупных вихрей. Картина течения, возникающая в результате эволюции большого числа регулярных когерентных структур, зачастую отождествляется с турбулентной картиной. Решения детерминистических уравнений (уравнений Навье–Стокса, RANS- и LES-уравнений) зачастую успешно интерпретируют устойчивое движение регулярных когерентных структур. Такой подход создает представление о возможности интерпретации турбулентных течений в терминах решений детерминистических уравнений. Провал детерминистических уравнений (уравнений Навье–Стокса и уравнений многомоментной гидродинамики) при попытке воспроизведения турбулентности в простейшей задаче гидродинамики, задаче обтекания сферы, развеивает эту иллюзию.
В работах [11–13] предложено искать возможность приведения детерминистических уравнений к пригодному для интерпретации турбулентности виду на пути включения в эти уравнения стохастических составляющих. Детерминистические уравнения многомоментной гидродинамики дополняются стохастическими составляющими, ответственными за неупорядоченные возмущения. Исследуется влияние неупорядоченных возмущений, возникающих в набегающем на неподвижную сферу потоке за счет внешнего воздействия. Исследование показало, что при определенных условиях интенсивность неупорядоченных возмущений резко возрастает. Это создает хаотическую картину течения в следе за сферой [11–13]. В отличие от неупорядоченных возмущений спонтанные флуктуации существуют в каждой точке среды постоянно, независимо от внешнего воздействия. Настоящая работа посвящена исследованию влияния спонтанных флуктуаций на возникновение и развитие турбулентности.
В разд. 1 детерминистические уравнения многомоментной гидродинамики дополняются стохастическими составляющими, ответственными за спонтанные флуктуации. В разд. 2 проводится учет вклада спонтанных флуктуаций в парную энтропию системы. Вносится существенное дополнение к критерию эволюции системы, потерявшей устойчивость. В дальнейших исследованиях сформулированы общие представления о спонтанных флуктуациях. Уравнения многомоментной гидродинамики, учитывающие вклад спонтанных флуктуаций, проинтегрированы численно в режиме неустойчивости.
1. УЧЕТ СПОНТАННЫХ ФЛУКТУАЦИЙ ПРИ ИНТЕРПРЕТАЦИИ НЕУСТОЙЧИВОГО РЕЖИМА ОБТЕКАНИЯ СФЕРЫ
Общий подход к решению уравнений многомоментной гидродинамики в терминах парных функций распределения изложен в работах [4, 14]. В соответствии с [4] в задаче с независящими от времени $t$ граничными условиями парная функция строится в виде ряда произведений так называемых траекторных инвариантов (уравнение (1.6) в [4]). Функция распределения используется для расчета гидродинамических величин [15, Гл. 4]. Подстановка рассчитанных распределений гидродинамических величин в уравнения многомоментной гидродинамики [15, Гл.5] приводит к замкнутой нелинейной системе дифференциальных уравнений $n$-порядка для безразмерных коэффициентов ${{\hat {С}}_{i}}(t){\text{:}}$
(1.1)
$\frac{{\partial {{{\hat {С}}}_{i}}}}{{\partial t}} = {{F}_{i}}({{\hat {С}}_{1}},...,{{\hat {С}}_{n}}),\,\,\,\,i = 1,...,n.$Рассмотрим твердую сферу с радиусом a, движущуюся с постоянной скоростью ${{U}_{0}}$ в неподвижном газе. Сфера покоится в декартовой системе $XYZ$ с началом, совпадающим с центром движущегося тела. Тогда скорость набегающего потока газа на бесконечном расстоянии от сферы равна ${{U}_{0}}.$ Пусть направление скорости совпадает с положительным направлением оси Z. Пусть r, θ и $\varphi $ являются сферическими координатами некоторой точки среды x.
В задаче обтекания сферы с радиусом $a$ сохранение трех низших членов разложения (1.6) из работы [4] дает классическое решение Стокса, справедливое при низких значениях числа Рейнольдса: $Re \ll 1.$ Здесь $\operatorname{Re} = {{m{{n}_{0}}{{U}_{0}}2a} \mathord{\left/ {\vphantom {{m{{n}_{0}}{{U}_{0}}2a} {{{{{\eta }}}_{{\text{0}}}}}}} \right. \kern-0em} {{{{{\eta }}}_{{\text{0}}}}}},$ ${{n}_{0}}$ и ${{T}_{0}}$ – плотность и температура невозмущенной среды, ${{{{\eta }}}_{{\text{0}}}}$ – коэффициент динамической вязкости, $m$ – масса частицы газа. Для продвижения по Re, помимо стоксовских членов, в разложении (1.6) из [4] сохранены следующие низшие члены разложения. Сохранение низших членов привело к замкнутой системе (1.1) из 20 уравнений для 20 коэффициентов ${{\hat {С}}_{i}},$ $i = 1,...,20.$ Система (1.1) состоит из 19 алгебраических уравнений, линейных и нелинейных, и одного линейного дифференциального уравнения. Пусть ${{\hat {С}}_{i}}^{{(0)}}(t) = \hat {\bar {С}}_{i}^{{(0)}} + \delta \hat {С}_{i}^{{r(0)}}(t),$ $i = 1,...,20,$ есть некоторое осесимметричное решение системы (1.1), тогда $\hat {\bar {С}}_{i}^{{(0)}}$ есть стационарная составляющая этого решение. Нестационарная составляющая $\delta \hat {С}_{i}^{{r(0)}}(t)$ названа в [4] регулярной флуктуацией стационарного решения $\hat {\bar {С}}_{i}^{{(0)}}.$ Решение ${{\hat {С}}_{i}}^{{(0)}}(t),$ $i = 1,...,20,$ позволяет рассчитать распределения всех главных гидродинамических величин. Коэффициенты $\hat {C}_{1}^{{(0)}},$ $\hat {C}_{2}^{{(0)}},$ $\hat {C}_{3}^{{(0)}}$ и $\hat {C}_{4}^{{(0)}}$ ответственны за распределение плотности числа частиц, коэффициенты $\hat {C}_{5}^{{(0)}},$ $\hat {C}_{6}^{{(0)}},$ $\hat {C}_{7}^{{(0)}},$ $\hat {C}_{8}^{{(0)}},$ $\hat {C}_{9}^{{(0)}},$ $\hat {C}_{{18}}^{{(0)}}$ и $\hat {C}_{{19}}^{{(0)}}$ задают распределение давления и напряжений, коэффициенты $\hat {C}_{{10}}^{{(0)}},$ $\hat {C}_{{11}}^{{(0)}},$ $\hat {C}_{{12}}^{{(0)}},$ $\hat {C}_{{13}}^{{(0)}},$ $\hat {C}_{{15}}^{{(0)}},$ $\hat {C}_{{16}}^{{(0)}}$ и $\hat {C}_{{17}}^{{(0)}}$ ответственны за распределения тепловых потоков, коэффициенты $\hat {C}_{{14}}^{{(0)}}$ и $\hat {C}_{{20}}^{{(0)}}$ задают распределение скорости течения.
Численное интегрирование системы (1.1) показало, что стационарное решение $\hat {\bar {C}}_{i}^{{(0)}},$ $i = 1,...,20,$ остается устойчивым вплоть до некоторого критического значения числа Рейнольдса $Re_{0}^{*} = 129.1$ [4]. Пересечение $Re_{0}^{*}$ сопровождается потерей устойчивости. Начиная с некоторого момента времени $t = 0,$ малые отклонения $\delta \hat {C}_{i}^{{r(0)}}(t)$ от стационарного решения $\hat {\bar {C}}_{i}^{{(0)}}$ начинают экспоненциально нарастать. Нарастание регулярной флуктуации $\delta \hat {C}_{i}^{{r(0)}}(t)$ происходит вплоть до момента времени $t = {{t}_{*}} > 0.$ В момент ${{t}_{*}}$ решение ${{\hat {С}}_{i}}^{{(0)}}(t) = $ $ = \hat {\bar {С}}_{i}^{{(0)}} + \delta \hat {С}_{i}^{{r(0)}}(t)$ обрывается. Однако в окрестности точки обрыва ${{t}_{*}}$ существует решение $\delta \hat {С}_{i}^{{ * r(0)}}(t*)$ системы так называемых обратных уравнений многомоментной гидродинамики [15, Гл.7], которое экспоненциально затухает. Системы прямых и обратных уравнений идентичны, однако время $t{\text{*}}$ отсчитывается в прогрессирующем направлении на временнóй оси, направленной из будущего в прошлое.
К моменту $t* = 2{{t}_{*}}$ решение ${{\hat {С}}_{i}}^{{ * (0)}}(t*) = $ $ = \hat {\bar {С}}_{i}^{{(0)}} + \delta \hat {С}_{i}^{{ * r(0)}}(t*)$ достигает окрестности неустойчивого стационарного решения $\hat {\bar {С}}_{i}^{{(0)}}.$ Процесс последовательного нарастания и затухания отклонения повторяется с периодом $T = 2{{t}_{*}}$ [4].
Стационарное решение $\hat {\bar {С}}_{i}^{{(0)}}$ удовлетворительно интерпретирует экспериментально наблюдаемую осесимметричную зону закручивания см. рис. 1 из работы [11]. Решения ${{\hat {С}}_{i}}^{{(0)}}(t) = $ $ = \hat {\bar {С}}_{i}^{{(0)}} + \delta \hat {С}_{i}^{{r(0)}}(t),$ $0 < t < {{t}_{*}},$ и ${{\hat {С}}_{i}}^{{ * (0)}}(t*) = \hat {\bar {С}}_{i}^{{(0)}} + $ $ + \,\,\delta \hat {С}_{i}^{{ * r(0)}}(t*),$ ${{t}_{*}} < t* < 2{{t}_{*}},$ удовлетворительно интерпретируют осесимметричные пульсации зоны закручивания в следе за сферой, наблюдаемые экспериментально [16, 17].
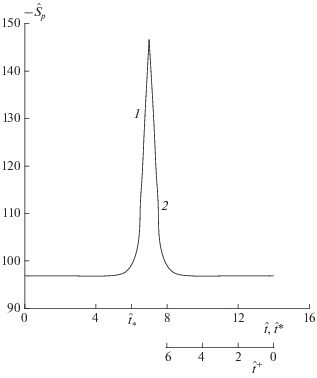
Рис. 1.
Поведение во времени парной энтропии $\hat {S}_{p}^{{}}$ при $\operatorname{Re} = 400,$ $t = ({{\operatorname{Re} a} \mathord{\left/ {\vphantom {{\operatorname{Re} a} {2{{U}_{0}}}}} \right. \kern-0em} {2{{U}_{0}}}})\hat {t}.$
При устойчивости течения $\left( {Re < Re_{0}^{*}} \right)$ каждое малое отклонение $\delta \hat {С}_{i}^{{r(0)}}(t = 0)$ от решения $\hat {\bar {С}}_{i}^{{(0)}}$ затухает, $\left| {\delta \hat {С}_{i}^{{r(0)}}(t)} \right| \ll \left| {\hat {\bar {С}}_{i}^{{(0)}}} \right|.$ После потери устойчивости $\left( {Re > Re_{0}^{*}} \right)$ нарастающая регулярная флуктуация $\delta \hat {С}_{i}^{{r(0)}}(t)$ достигает порядка величины коэффициента $\hat {\bar {С}}_{i}^{{(0)}}.$ Каждая флуктуация $\delta \hat {C}_{i}^{{r(0)}}(t = 0)$ начинает вести себя во времени сугубо индивидуально. Возможность интерпретации каждого из потерявших устойчивость решений в терминах некоторого среднего решения пропадает. Таким образом, нелинейная система (1.1) разводит первоначально близкие решения. Ансамбль Гиббса распадается. Такое поведение решений получило название “эффект бабочки Лоренца” [18].
Уравнения многомоментной гидродинамики, как и уравнения классической гидродинамики, описывают, вообще говоря, пространственно-временную эволюцию не какой-либо отдельной системы, а целого ансамбля систем (ансамбля Гиббса) [19]. Каждая отдельная система ансамбля обладает всеми возможными значениями микроскопических параметров, совместимых с изначально заданными значениями макроскопических параметров. При этом макроскопические параметры отдельной системы задаются не точно, а в определенных пределах, соответствующих порядку возможных флуктуаций. После распада ансамбля Гиббса возможность интерпретации каждой отдельной системы ансамбля в терминах некоторой средней системы пропадает. Более того, после распада ансамбля Гиббса представление диссипативных моментов (тензора вязких напряжений и вектора теплового потока) в терминах главных гидродинамических величин становится некорректным.
В работе [20] при моделировании индивидуальной системы каждая гидродинамическая величина в уравнениях классической гидродинамики дополнялась членами, ответственными за отклонения гидродинамических величин от их средних значений. В устойчивой среде $(Re < Re{\text{*}})$ малые отклонения (регулярные или хаотические), которые возникают в некоторый начальный момент времени $t = 0,$ затухают. Таким образом, малые отклонения вносят пренебрежимо малый вклад в распределения гидродинамических величин, представленные средним по ансамблю стационарным решением $\hat {\bar {С}}_{i}^{{(0)}},$ $i = 1,...,20.$ Необходимости в расчете отклонений не возникает. Качественно иной порядок наступает после потери системой устойчивости $\left( {Re > Re_{0}^{*}} \right).$ В неустойчивой среде регулярные флуктуации $\delta \hat {С}_{i}^{{r(0)}}(t)$ разрастаются, достигая величины решения $\hat {\bar {С}}_{i}^{{(0)}}.$ Регулярное решение $\hat {C}_{i}^{{(0)}}(t) = \bar {C}_{i}^{{(0)}} + \delta \hat {C}_{i}^{{r(0)}}(t)$ оказывается не в состоянии удовлетворить законам сохранения массы импульса и энергии (1.12)–(1.14) из [4]. Причиной этого является зависимость от времени, которую коэффициенты $\hat {C}_{i}^{{(0)}}$ приобретают в результате роста $\delta \hat {C}_{i}^{{r(0)}}(t)$ после потери устойчивости. В частности, закон сохранения импульса выполнится, если
Однако функция $\hat {C}_{i}^{{(0)}}(t) = \bar {C}_{i}^{{(0)}} + \delta \hat {C}_{i}^{{r(0)}}(t),$ i = 1, $...,20,$ является решением замкнутой системы (1.1). Таким образом, решение $\hat {C}_{i}^{{(0)}}(t),$ вообще говоря, не в состоянии удовлетворить уравнению (1.2). То есть, учет лишь регулярной составляющей $\delta \hat {C}_{i}^{{r(0)}}(t)$ нестационарного решения $\hat {C}_{i}^{{(0)}}(t)$ не обеспечивает выполнение закона сохранения импульса.
В соответствии с представлениями из работы [20] уравнения для регулярных коэффициентов $\hat {C}_{i}^{{(0)}}(t)$ следует дополнить членами, ответственными за эволюцию малых стохастических отклонений гидродинамических величин от их средних значений. Пусть среда не содержит неупорядоченных возмущений, возникающих за счет внешнего воздействия. В отличие от неупорядоченных возмущений спонтанные флуктуации присутствуют в реальной физической системе постоянно, независимо от внешнего воздействия. Спонтанная флуктуация является случайным событием в каждой точке среды x. Следуя представлениям из [20], проведем учет спонтанных флуктуаций. Будем искать малое отклонение $\delta \hat {C}_{{20,i}}^{{(0)}}(t,x)$ статистического коэффициента $\hat {\bar {C}}_{{20}}^{{(0)}},$ который доминирует в распределении скорости течения (3.9) из [4], в виде линейной комбинации независимых составляющих:
(1.3)
$\begin{gathered} \delta \hat {C}_{{20,i}}^{{(0)}}(t,x) = \delta \hat {C}_{{20}}^{{r(0)}}(t) + \delta \hat {C}_{{20,i}}^{{s(0)}}(t,x), \\ \hat {C}_{{20,i}}^{{(0)}}(t,x) = \hat {\bar {C}}_{{20}}^{{(0)}} + \delta \hat {C}_{{20.i}}^{{(0)}}(t,x). \\ \end{gathered} $В уравнении (1.3) составляющая, ответственная за неупорядоченные возмущения, опущена; $\delta \hat {C}_{{20,i}}^{{s(0)}}(t,x)$ является спонтанной флуктуацией стационарного решения $\hat {\bar {C}}_{{20}}^{{(0)}},$ отвечающей i-компоненте скорости течения, $i = r,\theta .$ Наряду с $\delta \hat {C}_{{20,i}}^{{s(0)}}(t,x)$ зададим спонтанную флуктуацию $\delta \hat {C}_{{20}}^{{s(0)}}(t,x),$ которая отвечает модулю скорости течения. Подставив выражение (1.3) для коэффициента $\hat {C}_{{20,i}}^{{(0)}}(t,x)$ в доминирующий член распределения плотности потока частиц $nU$ (уравнение (3.9) из [4]), получим
(1.4)
$\begin{gathered} n{{U}_{r}} = {{n}_{0}}{{U}_{0}}\cos {{\theta }}\left( {1 - \frac{3}{2}\frac{a}{r} + \frac{1}{2}\frac{{{{a}^{3}}}}{{{{r}^{3}}}}} \right) + {{n}_{0}}{{U}_{0}}\operatorname{Re} \hat {\bar {C}}_{{20}}^{{(0)}}\left( {3 - 30{{{\cos }}^{2}}{{\theta }} + 35co{{s}^{4}}{{\theta }}} \right)\frac{{{{a}^{2}}}}{{{{r}^{2}}}}{{\left( {1 - \frac{{{{a}^{2}}}}{{{{r}^{2}}}}} \right)}^{2}} + {{n}_{0}}\left( {\delta U_{r}^{{(r)}} + \delta U_{r}^{{(s)}}} \right), \\ n{{U}_{\theta }} = {{n}_{0}}{{U}_{0}}\sin {{\theta }}\left( { - 1 + \frac{3}{4}\frac{a}{r} + \frac{1}{4}\frac{{{{a}^{3}}}}{{{{r}^{3}}}}} \right) + {{n}_{0}}{{U}_{0}}\operatorname{Re} \hat {\bar {C}}_{{20}}^{{(0)}}\sin {{\theta }}\left( {12\cos {{\theta }} - 28co{{s}^{3}}{{\theta }}} \right)\frac{{{{a}^{4}}}}{{{{r}^{4}}}}\left( {1 - \frac{{{{a}^{2}}}}{{{{r}^{2}}}}} \right) + {{n}_{0}}\left( {\delta U_{\theta }^{{(r)}} + \delta U_{\theta }^{{(s)}}} \right). \\ \end{gathered} $В уравнении (1.4) $\delta {{U}^{{(s)}}}$ является спонтанной флуктуацией составляющей скорости течения,
(1.5)
$\begin{gathered} \delta U_{r}^{{(s)}} = {{U}_{0}}\delta \hat {U}_{r}^{{(s)}} = {{U}_{0}}\delta \hat {U}_{r}^{{s(0)}}\left( {3 - 30{{{\cos }}^{2}}{{\theta }} + 35co{{s}^{4}}{{\theta }}} \right)\frac{{{{a}^{2}}}}{{{{r}^{2}}}}{{\left( {1 - \frac{{{{a}^{2}}}}{{{{r}^{2}}}}} \right)}^{2}}, \\ \delta U_{\theta }^{{(s)}} = {{U}_{0}}\delta \hat {U}_{\theta }^{{(s)}} = {{U}_{0}}\delta \hat {U}_{\theta }^{{s(0)}}\sin \theta \left( {12\cos {{\theta }} - 28co{{s}^{3}}{{\theta }}} \right)\frac{{{{a}^{4}}}}{{{{r}^{4}}}}\left( {1 - \frac{{{{a}^{2}}}}{{{{r}^{2}}}}} \right). \\ \end{gathered} $Здесь $\delta \hat {U}_{i}^{{s(0)}} = \operatorname{Re} \delta \hat {C}_{{20,i}}^{{s(0)}},$ величина $\delta \hat {U}_{{}}^{{s(0)}} = $ $\operatorname{Re} \delta \hat {C}_{{20}}^{{s(0)}}$ является спонтанной флуктуацией модуля скорости течения, регулярная флуктуация $\delta {{U}^{{(r)}}}$ определена в [4].
Коэффициенты $\hat {C}_{5}^{{(0)}},$ $\hat {C}_{6}^{{(0)}},$ $\hat {C}_{7}^{{(0)}},$ $\hat {C}_{8}^{{(0)}},$ $\hat {C}_{9}^{{(0)}},$ $\hat {C}_{{18}}^{{(0)}}$ и $\hat {C}_{{19}}^{{(0)}}$ ответственны за распределение давления ${{p}^{G}}$ и тензора напряжений $p_{{kl}}^{G},$ создаваемых в результате движения центров масс пар частиц. По аналогии с уравнением (1.3), будем искать флуктуацию статистического коэффициента $\hat {\bar {C}}_{i}^{{(0)}},$ i = 5, 6, 7, 8, 9, 18, 19, в виде
(1.6)
$\begin{gathered} \hat {C}_{i}^{{(0)}}(t,x) = \hat {\bar {C}}_{i}^{{(0)}} + \delta \hat {C}_{i}^{{(0)}}(t,x),\,\,\,\,\delta \hat {C}_{i}^{{(0)}}(t,x) = \delta \hat {C}_{i}^{{r(0)}}(t) + \delta \hat {C}_{i}^{{s(0)}}(t,x), \\ i = 5,6,7,19,\,\,\,\,\hat {C}_{{i,kl}}^{{(0)}}(t,x) = \hat {\bar {C}}_{i}^{{(0)}} + \delta \hat {C}_{{i,kl}}^{{(0)}}(t,x),\,\,\,\,\delta \hat {C}_{{i,kl}}^{{(0)}}(t,x) = \\ = \delta \hat {C}_{i}^{{r(0)}}(t) + \delta \hat {C}_{{i,kl}}^{{s(0)}}(t,x),\,\,\,\,i = 5,6,7,8,9,18,19. \\ \end{gathered} $В уравнении (1.6) $\delta \hat {C}_{i}^{{s(0)}}$ и $\delta \hat {C}_{{i,kl}}^{{s(0)}}$ являются спонтанными флуктуациями коэффициента $\hat {\bar {C}}_{i}^{{(0)}}.$
Коэффициенты $\hat {C}_{i}^{{(0)}}(t,x)$ ответственны за давление ${{p}^{G}},$ коэффициенты $\hat {C}_{{i,kl}}^{{(0)}}(t,x)$ – за тензор напряжений $p_{{kl}}^{G}.$ Аналитические выражения для ${{p}^{G}}$ и $p_{{kl}}^{G},$ обладающее порядком величины ${{n}_{0}}k{{T}_{0}}M{{a}^{2}},$ имеют вид
(1.7)
$\begin{gathered} p_{{}}^{G} = {{n}_{0}}k{{T}_{0}}M{{a}^{2}}\sum\limits_i {\hat {\bar {C}}_{i}^{{(0)}}{{f}^{{(i)}}}(r,\theta ) + {{n}_{0}}k{{T}_{0}}\left( {\delta {{{\hat {p}}}^{{G(r)}}} + \delta {{{\hat {p}}}^{{G(s)}}}} \right)} , \\ i = 5,6,7,19,\,\,\,\,p_{{kl}}^{G} = {{n}_{0}}k{{T}_{0}}M{{a}^{2}}\sum\limits_i {\hat {\bar {C}}_{{i,kl}}^{{(0)}}f_{{kl}}^{{(i)}}(r,\theta )} + {{n}_{0}}k{{T}_{0}}\left( {\delta \hat {p}_{{kl}}^{{G(r)}} + \delta \hat {p}_{{kl}}^{{G(s)}}} \right), \\ i = 5,6,7,8,9,18,19. \\ \end{gathered} $Здесь $M{{a}^{2}} = {{mU_{0}^{2}} \mathord{\left/ {\vphantom {{mU_{0}^{2}} {k{{T}_{0}}}}} \right. \kern-0em} {k{{T}_{0}}}},$ $k$ – постоянная Больцмана; $\delta {{\hat {p}}^{{G(s)}}}$ и $\delta \hat {p}_{{kl}}^{{G(s)}}$ являются спонтанными флуктуациями давления ${{p}^{G}}$ и тензора напряжений $p_{{kl}}^{G}{\text{:}}$
(1.8)
$\begin{gathered} \delta {{{\hat {p}}}^{{G(s)}}} = M{{a}^{2}}\sum\limits_i {\delta \hat {C}_{i}^{{s(0)}}{{f}^{{(i)}}}(r,\theta )} , \\ i = 5,6,7,19, \\ \delta \hat {p}_{{kl}}^{{G(s)}} = M{{a}^{2}}\sum\limits_i {\delta \hat {C}_{{i,kl}}^{{s(0)}}f_{{kl}}^{{(i)}}(r,\theta )} , \\ i = 5,6,7,8,9,18,19. \\ \end{gathered} $Регулярные флуктуации $\delta {{\hat {p}}^{{G(r)}}}$ и $\delta \hat {p}_{{kl}}^{{G(r)}}$ определены в [4]. Пространственная структура безразмерных функций ${{f}^{{(i)}}}(r,\theta )$ и $f_{{kl}}^{{(i)}}(r,\theta )$ представлена в работах [4, 14].
Пусть ${{p}^{v}}$ и $p_{{kl}}^{v}$ являются соответственно давлением и тензором напряжений, которые создаются в результате относительного движения частиц в паре. Следуя представлениям из работы [20], учтем спонтанные флуктуации давления ${{p}^{v}}$ и тензора напряжений $p_{{kl}}^{v}$ в порядке величины ${{n}_{0}}k{{T}_{0}}M{{a}^{2}}$ (уравнение (4.5) из [14]):
(1.9)
$\begin{gathered} {{p}^{v}} = {{n}_{0}}k{{T}_{0}}M{{a}^{2}}\hat {\bar {C}}_{{20}}^{{(0)}}{{A}^{v}} + {{n}_{0}}k{{T}_{0}}\left( {\delta {{{\hat {p}}}^{{v(r)}}} + \delta {{{\hat {p}}}^{{v(s)}}}} \right), \\ p_{{kl}}^{v} = {{n}_{0}}k{{T}_{0}}M{{a}^{2}}\hat {\bar {C}}_{{20}}^{{(0)}}A_{{kl}}^{v} + {{n}_{0}}k{{T}_{0}}\left( {\delta \hat {p}_{{kl}}^{{v(r)}} + \delta \hat {p}_{{kl}}^{{v(s)}}} \right). \\ \end{gathered} $В уравнении (1.9) $\delta {{\hat {p}}^{{v(s)}}}$ и $\delta \hat {p}_{{kl}}^{{v(s)}}$ – спонтанные флуктуации давления ${{p}^{v}}$ и тензора напряжений $p_{{kl}}^{v}.$ Регулярные флуктуации $\delta {{\hat {p}}^{{v(r)}}}$ и $\delta \hat {p}_{{kl}}^{{v(r)}}$ определены в [4]. Пространственная структура безразмерных функций ${{A}^{v}}(r,\theta ),$ $A_{{kl}}^{v}(r,\theta )$ представлена в работах [4, 14]. Выражения для спонтанных флуктуаций выводятся по аналогии с выражениями для неупорядоченных возмущений из работы [11]:
(1.10)
$\begin{gathered} \delta {{{\hat {p}}}^{{v(s)}}} = M{{a}^{2}}\sum\limits_i {\delta \hat {C}_{i}^{{s(0)}}{{f}^{{(i)}}}(r,\theta )} ,\,\,\,\,i = 23,...,26, \\ \delta \hat {p}_{{kl}}^{{v(s)}} = M{{a}^{2}}\sum\limits_i {\delta \hat {C}_{{i,kl}}^{{s(0)}}f_{{kl}}^{{(i)}}(r,\theta )} ,\,\,\,\,i = 27,...,33. \\ \end{gathered} $Подставим выражение (1.4) для плотности потока частиц $nU,$ выражения (1.7) и (1.9) для давлений ${{p}^{G}},$ ${{p}^{v}}$ и тензоров напряжений $p_{{kl}}^{G},$ $p_{{kl}}^{v}$ в уравнение сохранения импульса из работы [15, Гл.5]. Следуя общей идеологии решения уравнений многомоментной гидродинамики, приравняем нулю выражения при каждом произведении ${{({a \mathord{\left/ {\vphantom {a r}} \right. \kern-0em} r})}^{j}}{{\cos }^{m}}\theta {{\sin }^{n}}\theta $ с четными $j$ и четными $m + n$ отдельно [4]. В результате получаем
(1.11)
$\frac{{\partial \delta C_{{20}}^{{r(0)}}(t)}}{{\partial t}} + \frac{{\partial \delta C_{{20,i}}^{{s(0)}}(t,x)}}{{\partial t}} + \frac{1}{{{{n}_{0}}ma}}F_{{20}}^{{(j,m + n)}}(t,x) = 0.$Здесь
(1.12)
$\begin{gathered} \delta C_{{20}}^{{r(0)}}(t) = {{U}_{0}}\operatorname{Re} \delta \hat {C}_{{20}}^{{r(0)}}(t), \\ \delta C_{{20,i}}^{{s(0)}}(t,x) = {{U}_{0}}\operatorname{Re} \delta \hat {C}_{{20,i}}^{{s(0)}}(t,x). \\ \end{gathered} $В уравнении (1.11) функция $F_{{20}}^{{(j,m + n)}}(t,x)$ является линейной комбинацией спонтанных флуктуаций $\delta C_{i}^{{s(0)}}$ и $\delta C_{{i,kl}}^{{s(0)}}{\text{:}}$
(1.13)
$\begin{gathered} \delta C_{i}^{{s(0)}}(t,x) = {{n}_{0}}k{{T}_{0}}M{{a}^{2}}\delta \hat {C}_{i}^{{s(0)}}(t,x), \\ i = 5,6,7,19,23,...,26, \\ \delta C_{{i,kl}}^{{s(0)}}(t,x) = {{n}_{0}}k{{T}_{0}}M{{a}^{2}}\delta \hat {C}_{{i,kl}}^{{s(0)}}(t,x), \\ i = 5,...,9,18,19,27,...,33. \\ \end{gathered} $Функция $F_{{20}}^{{(j,m + n)}}(t,x)$ не содержит пространственных производных коэффициентов из уравнения (1.13).
Система уравнений многомоментной гидродинамики (1.1) диктует характерный временнóй масштаб изменения гидродинамических величин: ${{\tau }_{h}} = {{\operatorname{Re} a} \mathord{\left/ {\vphantom {{\operatorname{Re} a} {2{{U}_{0}}}}} \right. \kern-0em} {2{{U}_{0}}}},$ т.е. временнóй интервал ${{\tau }_{h}}$ является характерным масштабом изменения регулярной флуктуации $\delta C_{{20}}^{{r(0)}}$ [4]. Крупномасштабные спонтанные флуктуации скорости течения ($\operatorname{Re} \left| {\delta C_{{20}}^{{s(0)}}} \right|\sim {{U}_{0}}$) также обладают характерным масштабом изменения ${{\tau }_{h}}.$ Мелкомасштабные спонтанные флуктуации скорости течения ($\operatorname{Re} \left| {\delta C_{{20}}^{{s(0)}}} \right| \ll {{U}_{0}}$) изменяются в порядке своей величины на масштабе ${{\tau }_{s}} \ll {{\tau }_{h}}.$ Мелкомасштабные спонтанные флуктуации вносят пренебрежимо малый вклад в распределения гидродинамических величин, однако, вообще говоря, их производные по времени имеют основной порядок величины. Таким образом, учет спонтанных флуктуаций (крупномасштабных и мелкомасштабных) позволяет, в принципе, обеспечить выполнение закона сохранения импульса (1.11).
2. ИНТЕРПРЕТАЦИЯ ПОВЕДЕНИЯ НЕУСТОЙЧИВОЙ СИСТЕМЫ В ТЕРМИНАХ ПАРНОЙ ЭНТРОПИИ
Понятия локальной парной энтропии $S_{p}^{{(0)}}(t,x)$ и парной энтропии системы $S_{p}^{{(0)}}(t)$ вводятся в работе [15, Гл. 6]; верхний индекс “0” соответствует решению $\hat {C}_{i}^{{(0)}}(t),$ $i = 1,...20,$ которое используется для расчета функций $S_{p}^{{(0)}}(t,x)$ и $S_{p}^{{(0)}}(t)$. Уравнение (6.1.12) в работе [15] определяет локальную парную энтропии $S_{p}^{{(0)}}(t,x)$ в терминах главных гидродинамических величин. В задаче обтекания сферы явные аналитические выражения для пространственных распределений главных гидродинамических величин (уравнения (4.4)–(4.10) в [14]) содержат двадцать безразмерных коэффициентов $\hat {C}_{i}^{{(0)}},$ $i = 1,...,20.$
В соответствии с представлениями из [20] при описании отдельной системы каждую гидродинамическую величину следует дополнить флуктуационной составляющей. В разд. 1 вклад спонтанных флуктуаций учитывается в безразмерных коэффициентах, формирующих гидродинамические величины. Коэффициенты $\hat {\bar {C}}_{i}^{{(0)}}$ и $\delta \hat {C}_{i}^{{r(0)}}(t),$ $i = 1,...,7,19$ содержатся в выражениях для скалярных гидродинамических величин: плотности среды $n$ и давления ${{p}^{G}}.$ Вклад спонтанных флуктуаций в $n$ и ${{p}^{G}}$ учитывается за счет членов, пропорциональных коэффициентам $\delta \hat {C}_{i}^{{s(0)}}(t,x)$, $i = 1,...,7,19$ (уравнение (1.8) для ${{p}^{G}}$). Коэффициенты $\hat {\bar {C}}_{{20}}^{{(0)}}$ и $\delta \hat {C}_{{20}}^{{r(0)}}(t)$ содержатся в выражениях для давления ${{p}^{v}}.$ Выражение для скалярной величины ${{p}^{v}}$ дополняется членами, пропорциональными коэффициентам $\delta \hat {C}_{i}^{{s(0)}}(t,x),$ $i = 23,...,26$ (уравнение (1.10)).
Коэффициенты $\hat {\bar {C}}_{i}^{{(0)}}$ и $\delta \hat {C}_{i}^{{r(0)}}(t),$ i = 10, ..., 13, 15, $...,\,\,17,\,\,14,\,\,20,$ содержатся в выражениях для векторных гидродинамических величин: скорости течения $U$ и теплового потока ${{q}^{v}}.$ Вклад спонтанных флуктуаций в $U$ и ${{q}^{v}}$ учитывается за счет членов, пропорциональных коэффициентам $\delta \hat {C}_{{i,j}}^{{s(0)}}(t,x),$ $i = 10,...,13,15,...,17,14,20$ (уравнение (1.5) для $U$). Коэффициенты $\hat {\bar {C}}_{i}^{{(0)}}$ и $\delta \hat {C}_{i}^{{r(0)}}(t),$ $i = 5,...,9,18,19,$ содержатся в выражениях для тензора напряжений $p_{{kl}}^{G}.$ Выражение для $p_{{kl}}^{G}$ содержит члены, пропорциональные коэффициентам $\delta \hat {C}_{{i,kl}}^{{s(0)}}(t,x),$ i = 5, ..., $9,18,19$ (уравнение (1.8)). Коэффициенты $\hat {\bar {C}}_{{20}}^{{(0)}}$ и $\delta \hat {C}_{{20}}^{{r(0)}}(t)$ входят в выражения для тензора напряжений $p_{{kl}}^{v}$. Вклад спонтанных флуктуаций в $p_{{kl}}^{v}$ учитывается за счет членов, пропорциональных коэффициентам $\delta \hat {C}_{{i,kl}}^{{s(0)}}(t,x),$ $i = 27,...,33$ (уравнение (1.10)).
Подстановка выражений для гидродинамических величин с коэффициентами $\hat {\bar {C}}_{i}^{{(0)}}$ и $\delta \hat {C}_{i}^{{r(0)}}(t),$ $i = 1,...,20,$ $\delta \hat {C}_{i}^{{s(0)}}(t,x),$ $i = 1,...,7,19,21,...,26,$ $\delta \hat {C}_{{i,j}}^{{s(0)}}(t,x)$, $i = 10,...,13,15,...17,14,20,$ $\delta \hat {C}_{{i,kl}}^{{s(0)}}(t,x),$ $i = 5,...,9,18,19,27,...,33,$ в уравнение для парной энтропии позволяет выделить составляющие энтропии, ответственные за спонтанные флуктуации. Выражения для пространственных распределений гидродинамических величин содержат безразмерные параметры $M{{a}^{2}}$ и Re. Зависимость от $\operatorname{Re} $ содержится в коэффициентах. Подставим уравнения (4.4)–4.10) из [14] с коэффициентами, формирующими стационарное решение, регулярные и спонтанные флуктуации, в уравнение (6.1.12) из [15] для локальной парной энтропии $S_{p}^{{(0)}}(t,x).$ Проинтегрируем полученную функцию по x в пределах объема $V$ системы. В результате выражение для парной энтропии системы представляется в виде бесконечного ряда по параметру $M{{a}^{2}}{\text{:}}$
(2.1)
$S_{p}^{{(0)}}(t) = \sum\limits_{l = 0}^\infty {S_{p}^{{(0,l)}}} (t) = {{S}_{0}}\sum\limits_{l = 0}^\infty {{{{(M{{a}^{2}})}}^{l}}\hat {S}_{p}^{{(0,l)}}} (t),$где ${{S}_{0}} = k{{n}_{0}}{{v}_{0}},$ ${{v}_{0}} = (4{\text{/}}3)\pi {{a}^{3}}.$ Твердая сфера, совершающая равномерное и прямолинейное движение в невозмущенной среде, является открытой системой с независящими от времени граничными условиями. Первые два члена разложения (2.1) могут быть опущены, так как эти члены являются постоянными величинами [21]. В пределе $M{{a}^{2}} \ll 1$ третий член доминирует в разложении (2.1):
(2.2)
$S_{p}^{{(0,2)}}(t) = k{{n}_{0}}{{v}_{0}}M{{a}^{4}}\left[ {\hat {\bar {S}}_{p}^{{(0,2)}} + \delta \hat {S}_{p}^{{(0,2)}}(t)} \right];$(2.3)
$\delta \hat {S}_{p}^{{(0,2)}}(t) = \delta \hat {S}_{p}^{{r(0,2)}}(t) + \delta \hat {S}_{p}^{{s(0,2)}}(t).$(2.4)
$\begin{gathered} \hat {\bar {S}}_{p}^{{(0,2)}} = \hat {\bar {S}}_{p}^{{(0,2)}}\left( {\hat {\bar {C}}_{1}^{{(0)}},...,\hat {\bar {C}}_{{20}}^{{(0)}}} \right),\,\,\,\,\delta \hat {S}_{p}^{{r(0,2)}}(t) = \hat {S}_{p}^{{r(0,2)}}\left[ {\hat {\bar {C}}_{1}^{{(0)}},...\hat {\bar {C}}_{{20}}^{{(0)}},\delta \hat {C}_{1}^{{r(0)}}(t),...,\delta \hat {C}_{{20}}^{{r(0)}}(t)} \right],\,\,\,\,\delta \hat {S}_{p}^{{s(0,2)}}(t) = \\ = \int\limits_V {\hat {F}_{p}^{{s(0,2)}}(x,} \hat {\bar {C}}_{1}^{{(0)}} + \delta \hat {C}_{1}^{{r(0)}}(t),...,\hat {\bar {C}}_{{20}}^{{(0)}} + \delta \hat {C}_{{20}}^{{r(0)}}(t),\,\,\,\,\delta \hat {C}_{1}^{{s(0)}}(t,x),...,\delta \hat {C}_{{33,kl}}^{{s(0)}}(t,x))dx. \\ \end{gathered} $В уравнении (2.4) безразмерная парная энтропия $\hat {\bar {S}}_{p}^{{(0,2)}}$ является нелинейной функцией безразмерных стационарных коэффициентов $\hat {\bar {C}}_{i}^{{(0)}},$ $i = 1,...,20,$ а безразмерная парная энтропия $\delta \hat {S}_{p}^{{r(0,2)}}(t)$ – нелинейной функцией коэффициентов $\hat {\bar {C}}_{i}^{{(0)}}$ и регулярных флуктуаций $\delta \hat {C}_{i}^{{r(0)}}(t),$ $i = 1,...,20$ (уравнения (4.4)–(4.10) в [14]). Функция $\hat {F}_{p}^{{s(0,2)}}$ является линейной комбинацией спонтанных флуктуаций $\delta \hat {C}_{i}^{{s(0)}}(t,x),$ $i = 1,...,7,19,21,...,26,$ $\delta \hat {C}_{{i,j}}^{{s(0)}}(t,x),$ $i = 10,...,13,15,...17,14,20,$ $\delta \hat {C}_{{i,kl}}^{{s(0)}}(t,x),$ $i = 5,...,9,18,19,27,...,33.$ Нелинейные по $\delta \hat {C}_{i}^{{s(0)}}(t,x),$ $\delta \hat {C}_{{i,j}}^{{s(0)}}(t,x)$ и $\delta \hat {C}_{{i,kl}}^{{s(0)}}(t,x)$ слагаемые опущены. Функция $\hat {F}_{p}^{{s(0,2)}}$ определена в работе [21].
Изменение парной энтропии $S_{p}^{{(0)}}(t)$ во времени происходит либо за счет ее оттока через ограничивающую систему поверхность, ${{\Delta }_{{EX}}}S_{p}^{{(0)}}(t),$ либо за счет производства ее самой системой, ${{\Delta }_{{IN}}}S_{p}^{{(0)}}(t){\text{:}}$
(2.5)
$\frac{{\partial S_{p}^{{(0)}}(t)}}{{\partial t}} + {{\Delta }_{{EX}}}S_{p}^{{(0)}}(t) = {{\Delta }_{{IN}}}S_{p}^{{(0)}}(t).$Общее выражение для производства локальной парной энтропии за счет столкновений, ${{\Delta }_{{IN}}}S_{p}^{{(0)}}(t{\text{,}}x),$ представлено уравнением (6.2.14) в работе [15]. В соответствии с уравнением (6.2.14) из [15] в каждой точке пространства $x$ и в каждый момент времени $t$ ${{\Delta }_{{IN}}}S_{p}^{{(0)}}(t{\text{,}}x)$ является величиной неотрицательной. Таким образом, столкновения частиц генерируют энтропию в каждый момент времени в каждой точке пространства. Уравнение (2.5) справедливо при отсчете времени в прогрессирующем направлении на временнóй оси, устремленной из прошлого в будущее.
Понятия обратной локальной парной энтропии $S_{p}^{{ * (0)}}(t*,x)$ и обратной парной энтропии системы $S_{p}^{{ * (0)}}(t*)$ вводятся в [15, Гл.7]. Уравнение (7.4.44) в [15] определяет локальную парную энтропии $S_{p}^{{ * (0)}}(t*,x)$ в терминах главных гидродинамических величин. Уравнение баланса энтропии имеет вид
(2.6)
$\frac{{\partial S_{p}^{{ * (0)}}(t*)}}{{\partial t{\text{*}}}} + {{\Delta }_{{EX}}}S_{p}^{{ * (0)}}(t*) = {{\Delta }_{{IN}}}S_{p}^{{ * (0)}}(t*).$Аналитическое выражение для производства локальной парной энтропии за счет столкновений ${{\Delta }_{{IN}}}S_{p}^{{ * (0)}}(t{\text{*,}}x)$ представлено уравнением (7.4.49) в работе [15]. В соответствии с (7.4.49) из [15] в каждой точке пространства $x$ и в каждый момент времени $t{\text{*}}$ ${{\Delta }_{{IN}}}S_{p}^{{ * (0)}}(t{\text{*,}}x)$ является величиной неположительной. То есть, столкновения частиц поглощают энтропию в каждый момент времени в каждой точке пространства. Уравнение (2.6) справедливо при отсчете времени в прогрессирующем направлении на временнóй оси, устремленной из будущего в прошлое.
Кривая 1 на рис. 1 представляет зависимость от времени парной энтропии $\hat {\bar {S}}_{p}^{{(0,2)}} + \delta \hat {S}_{p}^{{r(0,2)}}(t),$ рассчитанной по решению $\hat {C}_{i}^{{(0)}}(t),$ $i = 1,...,20,$ в доминирующем порядке (уравнение (2.2)). Параметры расчета парной энтропии приведены в [5]. С момента времени $t = 0$ и вплоть до момента времени t = ${{t}_{*}}$ обрыва решения энтропия системы непрерывно падает. Такое поведение энтропии соответствует удалению потерявшей устойчивость системы от состояния статистического равновесия. Кривая 2 на рис.1 дает зависимость от времени парной энтропии $\hat {\bar {S}}_{p}^{{(0,2)}} + \delta \hat {S}_{p}^{{ * r(0,2)}}(t*),$ рассчитанной по решению $\hat {C}_{i}^{{ * (0)}}(t*).$ Движение изображающей точки с момента $t* = {{t}_{*}}$ и вплоть до момента $t* = 2{{t}_{ * }}$ соответствует приближению состояния системы к состоянию статистического равновесия. Решение $\hat {C}_{i}^{{ * (0)}}(t*)$ позволяет проинтерпретировать эволюцию неустойчивой системы при отсчете времени ${{t}^{ + }}$ в регрессирующем направлении на шкале времени, направленной из прошлого в будущее; при этом [22]
(2.7)
$\begin{gathered} S_{p}^{{*(0,2)}}(t*) = S_{p}^{{ + (0,2)}}({{t}^{ + }}), \\ \frac{{\partial S_{p}^{{*(0,2)}}(t*)}}{{\partial t{\text{*}}}} = - \frac{{\partial S_{p}^{{ + (0,2)}}({{t}^{ + }})}}{{\partial {{t}^{ + }}}}. \\ \end{gathered} $Соотношение связи времен на разных осях принимает вид ${{t}^{ + }} = - t{\text{*}} + 2{{t}_{ * }}.$ Регрессирующий порядок отсчета времени ${{t}^{ + }}$ представлен на оси, расположенной под осью абсцисс на рис. 1. В работе [5] использовано одинаковое обозначение для регрессирующего направления отсчета времени ${{t}^{ + }}$ на временнóй оси, направленной из прошлого в будущее, и прогрессирующего направления отсчета времени $t{\text{*}}$ на временнóй оси, направленной из будущего в прошлое. Одинаковое обозначение создает некоторые трудности в понимании результатов работы [5]. Соотношения (2.7) способствуют устранению этих трудностей.
Принцип сохранения и потери устойчивости в открытой системе сформулирован в работе [21]. В соответствии с этим принципом система остается устойчивой, пока производство энтропии в системе ${{\Delta }_{{IN}}}S_{p}^{{(0)}}(t)$ превышает отток энтропии через ограничивающую систему поверхность, ${{\Delta }_{{EX}}}S_{p}^{{(0)}}(t).$ Нарушение этого условия сопровождается потерей устойчивости. При этом всякая флуктуация энтропии ${{\delta }}S_{p}^{{(0)}}(t = 0) < 0,$ порождаемая системой в некоторый начальный момент $t = 0,$ начинает нарастать. В частности, в системе с независящими от времени граничными условиями
(2.8)
$\frac{{\partial S_{p}^{{(0)}}(t)}}{{\partial t}} = \frac{{\partial \delta S_{p}^{{(0)}}(t)}}{{\partial t}} < 0\,\,\,\,{\text{для}}\,\,\,\,{{\delta }}S_{p}^{{(0)}}(t = 0) < 0.$В соответствии с уравнением (2.8), после пересечения первого критического значения числа Рейнольдса $\operatorname{Re} _{0}^{*}$ энтропия потерявшей устойчивость системы начинает удаляться от состояния статистического равновесия. По мере роста $\operatorname{Re} $ один неустойчивый режим обтекания замещается другим, тоже неустойчивым. Причина замещения состоит в том, что решение, соответствующее замещающему режиму обтекания, становится более предпочтительным по сравнению с решением, соответствующим замещенному режиму обтекания. Критерий эволюции [5] определяет приоритет при конкуренции решений уравнений многомоментной гидродинамики.
В соответствии с критерием эволюции потерявшая устойчивость открытая система с независящими от времени граничными условиями выбирает такое направление эволюции, которое обеспечивает наиболее быстрое падение энтропии. А именно, из двух направлений развития неустойчивости, обладающих в некоторый момент времени $t = t{\kern 1pt} {\text{'}}$ одинаковыми значениями энтропии и производной энтропии, флуктуация находит такое направление, которое обладает более низким значением второй производной энтропии:
(2.9)
$\begin{gathered} {{\left. {\frac{{{{\partial }^{2}}S_{p}^{{(\alpha )}}(t)}}{{\partial {{t}^{2}}}}} \right|}_{{t = t{\kern 1pt} '}}} < {{\left. {\frac{{{{\partial }^{2}}S_{p}^{{(\beta )}}(t)}}{{\partial {{t}^{2}}}}} \right|}_{{t = t{\kern 1pt} '}}}\,\,\,\,{\text{при}}\,\,\,\,{{\left. {S_{p}^{{(\alpha )}}(t)} \right|}_{{t = t{\kern 1pt} '}}} = {{\left. {S_{p}^{{(\beta )}}(t)} \right|}_{{t = t{\kern 1pt} '}}}, \\ {{\left. {\frac{{\partial S_{p}^{{(\alpha )}}(t)}}{{\partial t}}} \right|}_{{t = t{\kern 1pt} '}}} = {{\left. {\frac{{\partial S_{p}^{{(\beta )}}(t)}}{{\partial t}}} \right|}_{{t = t{\kern 1pt} '}}}\,\,\,\,{\text{для}}\,\,\,\,{{\delta }}S_{p}^{{(\alpha )}}(t = t{\kern 1pt} ') < 0\,\,\,\,{{\delta }}S_{p}^{{(\beta )}}(t = t{\kern 1pt} ') < 0. \\ \end{gathered} $То есть, в момент времени $t = t{\kern 1pt} '$ система выбирает $\alpha $-направление, так как вторая производная энтропии по времени обладает более низким значением по сравнению с $\beta $-направлением.
При конкуренции решений прямых уравнений многомоментной гидродинамики с решениями обратных уравнений критерий эволюции принимает вид
(2.10)
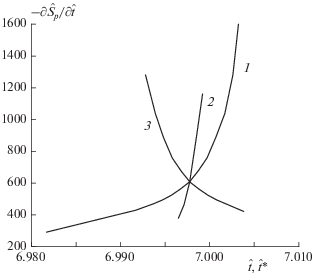
$\begin{gathered} {{\left. {\frac{{{{\partial }^{2}}S_{p}^{{(\alpha )}}(t)}}{{\partial {{t}^{2}}}}} \right|}_{{t = t{\kern 1pt} '}}} < {{\left. { - \frac{{{{\partial }^{2}}S_{p}^{{(\beta )}}(t*)}}{{\partial {{{(t*{\text{)}}}}^{2}}}}} \right|}_{{t* = t{\kern 1pt} '}}}\,\,\,\,{\text{при}}\,\,\,\,{{\left. {S_{p}^{{(\alpha )}}(t)} \right|}_{{t = t{\kern 1pt} '}}} = {{\left. {S_{p}^{{ * (\beta )}}(t*)} \right|}_{{t* = t{\kern 1pt} '}}}, \\ {{\left. {\frac{{\partial S_{p}^{{(\alpha )}}(t)}}{{\partial t}}} \right|}_{{t = t{\kern 1pt} '}}} = {{\left. { - \frac{{\partial S_{p}^{{ * (\beta )}}(t*)}}{{\partial t{\text{*}}}}} \right|}_{{t* = t{\kern 1pt} '}}}\,\,\,\,{\text{для}}\,\,\,\,{{\delta }}S_{p}^{{(\alpha )}}(t = t{\kern 1pt} ') < 0 \\ {{\delta }}S_{p}^{{ * (\beta )}}(t* = t{\kern 1pt} ') < 0. \\ \end{gathered} $Кривая 1 на рис. 2 представляет зависимость от времени производной парной энтропии ${{\left( {\hat {\bar {S}}_{p}^{{(0,2)}} + \delta \hat {S}_{p}^{{r(0,2)}}(t)} \right)} \mathord{\left/ {\vphantom {{\left( {\hat {\bar {S}}_{p}^{{(0,2)}} + \delta \hat {S}_{p}^{{r(0,2)}}(t)} \right)} {\partial{ \hat {t}}}}} \right. \kern-0em} {\partial{ \hat {t}}}},$ рассчитанной по решению прямых уравнений многомоментной гидродинамики $\hat {C}_{i}^{{(0)}}(t).$ Кривая 3 на рис. 2 представляет зависимость от времени производной парной энтропии ${{\left( {\hat {\bar {S}}_{p}^{{ * (0,2)}} + \delta \hat {S}_{p}^{{ * r(0,2)}}(t*)} \right)} \mathord{\left/ {\vphantom {{\left( {\hat {\bar {S}}_{p}^{{ * (0,2)}} + \delta \hat {S}_{p}^{{ * r(0,2)}}(t*)} \right)} {\partial{ \hat {t}}{\text{*}}}}} \right. \kern-0em} {\partial{ \hat {t}}{\text{*}}}},$ рассчитанной по решению обратных уравнений многомоментной гидродинамики $\hat {C}_{i}^{{ * (0)}}(t*).$ Решения $\hat {C}_{i}^{{(0)}}(t)$ и $\hat {C}_{i}^{{ * (0)}}(t*)$ удовлетворительно воспроизводят осесимметричные пульсации зоны закручивания в следе за сферой, наблюдаемые экспериментально [16, 17]. В соответствии с критерием (2.10) ни одно из этих решений не имеет приоритета в точке пересечения $t = t{\kern 1pt} '.$ Кривая 2 на рис. 2 задает зависимость от времени производной парной энтропии ${{\left( {\hat {\bar {S}}_{p}^{{(1,2)}} + \delta \hat {S}_{p}^{{r(1,2)}}(t)} \right)} \mathord{\left/ {\vphantom {{\left( {\hat {\bar {S}}_{p}^{{(1,2)}} + \delta \hat {S}_{p}^{{r(1,2)}}(t)} \right)} {\partial{ \hat {t}}}}} \right. \kern-0em} {\partial{ \hat {t}}}},$ рассчитанной по решению прямых уравнений многомоментной гидродинамики $\hat {C}_{i}^{{(1)}}(t).$ Решение $\hat {C}_{i}^{{(1)}}(t)$ удовлетворительно воспроизводит наблюдаемое вихревое кольцо, образующееся на периферии зоны закручивания [17]. В соответствии с критерием (2.10) решение $\hat {C}_{i}^{{(1)}}(t)$ имеет приоритет перед решением $\hat {C}_{i}^{{ * (0)}}(t*)$ в точке пересечения $t = t{\kern 1pt} '.$ Пусть изображающая точка движется по кривой 3 при отсчете времени $t{\text{*}}$ в положительном направлении. Тогда в соответствии с критерием (2.10) в момент $t = t{\kern 1pt} '$ изображающая точка покидает кривую 3, продолжая движение по кривой 2 в положительном направлении отсчета времени $t$ [5]. Переход изображающей точки от одного решения к другому удовлетворительно интерпретирует вихревое испускание, наблюдаемое экспериментально [17].
Рис. 2.
Поведение во времени производной парной энтропии ${{\partial {{{\hat {S}}}_{p}}} \mathord{\left/ {\vphantom {{\partial {{{\hat {S}}}_{p}}} {\partial{ \hat {t}}}}} \right. \kern-0em} {\partial{ \hat {t}}}}$ при $\operatorname{Re} = 400,$ $t = ({{\operatorname{Re} a} \mathord{\left/ {\vphantom {{\operatorname{Re} a} {2{{U}_{0}}}}} \right. \kern-0em} {2{{U}_{0}}}})\hat {t}.$
Таким образом, расчет энтропии есть необходимое условие интерпретации поведения системы, потерявшей устойчивость, в терминах решений уравнений многомоментной гидродинамики. Необходимость расчета энтропии возникает потому, что решения уравнений многомоментной гидродинамики предлагают системе несколько вариантов эволюции. Энтропия системы, а точнее ее производная во времени, указывают то единственное направление, в котором развивается система, потерявшая устойчивость.
3. ЗАКЛЮЧЕНИЕ
Уравнения классической гидродинамики выстроены на трех низших главных гидродинамических величинах. Высшие главные гидродинамические величины не используются при построении классической гидродинамики. Проведенный анализ показывает, что интерпретация явлений в терминах решений уравнений классической гидродинамики справедлива, вообще говоря, лишь в пределе слабого отклонения состояния среды от статистического равновесия, в частности при $\operatorname{Re} \ll 1$ [15, Гл.6]. Тем не менее решения уравнений классической гидродинамики удовлетворительно воспроизводят устойчивые течения при умеренно высоких значениях числа Рейнольдса [3, 23]. Это означает, что появляющаяся в решениях уравнений Навье–Стокса погрешность не на столько велика, чтобы заметно исказить рассчитываемые картины течения. Однако эта погрешность разрастается крайне быстро после потери устойчивости. Это объясняется свойством нелинейных уравнений разводить близкие решения даже в ограниченной области фазового пространства [18]. Таким образом, решения уравнений классической гидродинамики теряют направление развития системы, теряющей устойчивость [3, 23].
Возможность корректного воспроизведения направления развития неустойчивой системы появляется в результате увеличения количества главных гидродинамических величин. В работе [15, Гл.5] уравнения многомоментной гидродинамики выстроены на семи главных гидродинамических величинах, отвечающих измеряемым моментам функции распределения. Решения уравнений многомоментной гидродинамики ведут систему в направлении, качественно отличающемся от направления, задаваемого решениями уравнений классической гидродинамики.
Оказалось, что в зоне закручивания, потерявшей устойчивость, каждое регулярное решение системы (1.1) повело себя сугубо индивидуально. Перестало существовать некоторое среднее решение, пригодное для интерпретации всех изначально близких регулярных решений. Ансамбль Гиббса распался. Потерявшее устойчивость решение не смогло удовлетворить законам сохранения числа частиц, импульса и энергии.
Учет стохастических факторов позволяет обеспечить выполнение законов сохранения. В работах [11–13] система уравнений для гидродинамических величин решалась совместно с системой уравнений для неупорядоченных возмущений, возникающих в набегающем потоке за счет внешнего воздействия. При отсутствии внешнего воздействия уравнения сохранения дополняются составляющими, ответственными за спонтанные флуктуации. Таким образом, независимость в поведении спонтанных флуктуаций исчезает. В зоне закручивания спонтанные флуктуации вынуждены вести себя во времени и в пространстве вполне определенным образом, согласно уравнениям сохранения. А именно, спонтанные флуктуации должны подстраивать свое поведение во времени и в пространстве под поведение гидродинамических величин.
Список литературы
Лойцянский Л.Г. Механика жидкости и газа. М.: Наука,1987.
Townsend A.A. The structure of turbulent shear flow. Cambridge University Press, 1956.
Лебедь И.В., Уманский С.Я. // Хим. физика. 2007. Т. 26. № 1. С. 65.
Лебедь И.В. // Хим. физика. 1997. Т. 16. № 7. С. 72.
Лебедь И.В. // Хим. физика. 2014. Т. 33. № 4. С. 1.
Tomboulides A.G., Orszag S.A. // J. Fluid Mech. 2000. V. 416. P. 45.
Natarajan R., A. Acrivos A. // J. Fluid Mech. 1993. V. 254. P. 323.
Lebed I.V. // J. Adv. Phys. 2016. V. 12. P. 5460.
Басевич В.Я., Беляев А.А., Иванов В.С. и др. // Хим. физика. 2019. Т. 38. № 8. С. 69.
Бетев А.С., Киверин А.Д., Медведев С.П., Яковенко И.С. // Хим. физика. 2020. Т. 39. № 12. С. 17.
Киселев А.Ф., Лебедь И.В. // Хим. физика. 2021. Т. 40. № 1. С. 79.
Киселев А.Ф., Лебедь И.В. // Хим. физика. 2021. Т. 40. № 9. С. 80 .
Kiselev A.Ph., Lebed I.V. // Chaos, Solitons, Fractals. 2021. V. 142. 10491.
Lebed I.V. // Open J. Fluid Dynam. 2014. V. 4. P.163.
Lebed I.V. The foundations of multimoment hydrodynamics, Part 1: ideas, methods and equations. N.-Y.: Nova Sci. Publ., 2018.
Taneda S. // J. Phys. Soc. Jpn. 1956. V. 11. № 10. P. 1104.
Chomaz J.M., Bonneton P., Hopfinger E.J. // J. Fluid Mech. 1993. V. 234. P.1.
Schuster H.G. Deterministic chaos. Weinheim: Physik Verlag, 1984.
Liboff R.L. Introduction to the theory of kinetic equations. N.-Y.: Willey, 1969.
Лифшиц Е.М., Питаевский Л.П. Статистическая физика Ч. 2. М.: Наука, 1978.
Лебедь И.В. // Хим. физика. 1998. Т. 17. № 3. С. 25.
Lebed I.V. // J. Adv. Phys. 2015. V. 9. P. 2487.
Лебедь И.В., Уманский С.Я. // Хим. физика. 2012. Т. 31. № 2. С. 70.
Дополнительные материалы отсутствуют.
Инструменты
Химическая физика


