Химическая физика, 2022, T. 41, № 4, стр. 81-90

ВВЕДЕНИЕ

Настоящая работа посвящена исследованию влияния спонтанных флуктуаций на возникновение и развитие турбулентности. Уравнения многомоментной гидродинамики привлечены для численного моделирования хаотического искажения регулярных режимов течения в задаче обтекания покоящейся сферы. В первой части исследования [1] детерминистические уравнения многомоментной гидродинамики дополнены стохастическими членами, ответственными за спонтанные флуктуации. Проведен учет вклада спонтанных флуктуаций в парную энтропию системы. Показано, что потеря устойчивости течения сопровождается качественным изменением поведения спонтанных флуктуаций.

В разд. 1 исследования формулируются общие представления о спонтанных флуктуациях и обсуждаются характерные особенности поведения неустойчивой системы, являющегося зеркальным отражением ее поведения в режиме устойчивости. Исследуется также воздействие зеркально отраженного характера эволюции неустойчивой системы на вероятность возникновения спонтанной флуктуации. В разд. 2 уравнения многомоментной гидродинамики, в которых учитывается вклад спонтанных флуктуаций, интегрируются численно в режиме неустойчивости. Обсуждение полученных результатов проводится в разд. 3.

1. МОДЕЛИРОВАНИЕ СПОНТАННЫХ ФЛУКТУАЦИЙ

Неупорядоченные возмущения возникают в набегающем потоке за счет внешнего воздействия. Движущаяся жидкая частица приносит возникающие перед сферой неупорядоченные возмущения в зону закручивания за сферой. В отличие от неупорядоченных возмущений спонтанные флуктуации существуют в каждой точке среды постоянно, независимо от внешнего воздействия. Пусть ${{N}_{{\delta V}}}$ есть число частиц, содержащихся в выделенном элементе объема газа $\delta V{\text{,}}$ ${{N}_{{\delta V}}} \gg 1.$ Частицы пересекают границы выделенного элемента объема за счет самопроизвольного (спонтанного) хаотического движения. В результате величина ${{N}_{{\delta V}}}$ флуктуирует около своего среднего по ансамблю значения $\left\langle {{{N}_{{\delta V}}}} \right\rangle $ [2]:

Здесь ${{\delta }}N_{{\delta V}}^{{(s)}}$ есть спонтанная флуктуация числа частиц в выделенном объеме $\left\langle {{{N}_{{\delta V}}}} \right\rangle .$ Среднее квадратичное отклонение ${{\left[ {\left\langle {{{{\left( {{{\delta }}N_{{\delta V}}^{{(s)}}} \right)}}^{2}}} \right\rangle } \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ является мерой интенсивности спонтанной флуктуации:

В состоянии статистического равновесия [3]

Определим коэффициент ${{K}_{s}}$ как отношение характерной величины спонтанной флуктуации скорости течения $\delta {{U}^{{(s)}}}$ к характерной скорости течения U, ${{K}_{s}} = {{\left| {\delta {{U}^{{(s)}}}} \right|} \mathord{\left/ {\vphantom {{\left| {\delta {{U}^{{(s)}}}} \right|} U}} \right. \kern-0em} U} \ll 1.$ Пусть ${{L}_{h}}$ является характерным пространственным масштабом, на котором скорость течения изменяется в порядке своей величины, а ${{{{L}_{h}}} \mathord{\left/ {\vphantom {{{{L}_{h}}} U}} \right. \kern-0em} U}$ – характерным временны́м масштабом изменения скорости течения. Тогда ${{K}_{s}}{{L}_{h}}$ является характерным пространственным масштабом изменения спонтанной флуктуации скорости течения, а ${{\tau }_{{s1}}} = {{{{K}_{s}}{{L}_{h}}} \mathord{\left/ {\vphantom {{{{K}_{s}}{{L}_{h}}} U}} \right. \kern-0em} U}$ – характерным временны́м масштабом ее изменения.

В соответствии с представлениями из работы [4] каждую из измеряемых гидродинамических величин: плотность числа частиц n, скорость течения U, температуру T, тензор напряжений ${{p}_{{ij}}}$ и тепловой поток q, следует дополнить составляющей, ответственной за спонтанные флуктуации, – ${{\delta }}{{n}^{{(s)}}},$ ${{\delta }}{{U}^{{(s)}}},$ ${{\delta }}{{T}^{{(s)}}},$ ${{\delta }}p_{{ij}}^{{(s)}},$ ${{\delta }}{{q}^{{(s)}}}$ соответственно. Уравнения сохранения для гидродинамических величин, дополненных спонтанными флуктуациями, представлены в [4]. Уравнения сохранения выполняются в том случае, если каждая из флуктуаций ${{\delta }}{{n}^{{(s)}}},$ ${{\delta }}{{U}^{{(s)}}},$ ${{\delta }}{{T}^{{(s)}}},$ ${{\delta }}p_{{ij}}^{{(s)}},$ ${{\delta }}{{q}^{{(s)}}}$ пропорциональна ${{K}_{s}},$ а ${{K}_{s}}{{L}_{h}}$ и ${{\tau }_{{s1}}}$ являются характерными масштабами изменения спонтанных флуктуаций.

Спектральный метод решения уравнений многомоментной гидродинамики позволяет представить каждую гидродинамическую величину в терминах безразмерных коэффициентов ${{\hat {C}}_{i}}.$ Коэффициенты ${{\hat {C}}_{i}}$ находятся из решения системы уравнений (1.1) из [1]. В докритическом диапазоне $\operatorname{Re} < \operatorname{Re} _{0}^{ * }$ стационарное решение $\hat {\bar {C}}_{i}^{{(0)}},$ $i = 1,...,20,$ этой системы устойчиво. Возникающие малые отклонения от стационарного решения $\hat {\bar {C}}_{i}^{{(0)}}$ (регулярные и хаотические) распадаются. В результате малые отклонения дают пренебрежимо малый вклад в распределения гидродинамических величин.

Качественно иной порядок имеет место в закритическом диапазоне $\operatorname{Re} > \operatorname{Re} _{0}^{ * }.$ Пересечение критического значения числа Рейнольдса ${{\operatorname{Re} }_{0}}$ сопровождается ростом малых отклонений. Растущая регулярная флуктуация $\delta \hat {C}_{i}^{{r(0)}}$ достигает порядка величины стационарного решения $\hat {\bar {C}}_{i}^{{(0)}}.$ Ансамбль Гиббса распадается. После потери устойчивости решение $\hat {C}_{i}^{{(0)}}$ уже не может удовлетворить законам сохранения числа частиц, импульса и энергии. При отсутствии неупорядоченных возмущений выполнение законов сохранения обеспечивается за счет спонтанных флуктуаций. Система уравнений многомоментной гидродинамики (1.1) из [1] дополняется членами, ответственными за эволюцию спонтанных флуктуаций. Таким образом, уравнения для спонтанных флуктуаций решаются совместно с уравнениями для регулярных коэффициентов. Для выполнения уравнений сохранения поведение во времени и в пространстве спонтанных флуктуаций должно подстраиваться под поведение главных гидродинамических величин. Таким образом, в зоне закручивания в следе за сферой спонтанные флуктуации будут вести себя во времени и в пространстве вполне определенным образом в соответствии с законами сохранения.

В разд. 1 из [1] вклад спонтанных флуктуаций учтен в коэффициентах ${{\hat {C}}_{i}}.$ Пропорциональный коэффициенту $\hat {C}_{{20}}^{{(0)}}$ член доминирует в распределении скорости течения в следе за сферой (см. уравнение (3.9) из [5]). Поэтому спонтанную флуктуацию скорости течения следует интерпретировать в терминах спонтанной флуктуации $\delta \hat {C}_{{20}}^{{s(0)}}.$ В соответствии с уравнением (1.5) из [1] δU^s(0) = $ = {{U}_{0}}\operatorname{Re} \delta \hat {C}_{{20}}^{{s(0)}},$ тогда ${{K}_{s}} = \operatorname{Re} \left| {\delta \hat {C}_{{20}}^{{s(0)}}} \right|.$ Подставим распределения измеряемых гидродинамических величин (уравнения (4.4)–(4.10) из [6]), дополненные спонтанными флуктуациями, в уравнения сохранения из [4]. Уравнения сохранения выполняются в том случае, если

Таким образом, коэффициент ${{K}_{s}}$ будет одновременно характеризовать как интенсивность спонтанных флуктуаций скорости течения, так и интенсивность спонтанных флуктуаций остальных измеряемых гидродинамических величин. Наряду с локальным коэффициентом ${{K}_{s}}$ определим осредненный во времени и в пространстве коэффициент ${{\bar {K}}_{s}} = \operatorname{Re} \left| {\delta \hat {\bar {C}}_{{20}}^{{s(0)}}} \right|.$

Моделируя эволюцию спонтанной флуктуации, положим, что в некоторый момент времени флуктуация $\delta \hat {C}_{{20,i}}^{{s(0)}},$ $i = r,\theta ,$ мгновенно появляется в каждой элементарной ячейке среды объемом $\delta V$ в следе за сферой. Дальнейшее поведение спонтанной флуктуации $\delta \hat {C}_{{20,i}}^{{s(0)}}$ описывается уравнением сохранения импульса (1.11) из [1]. Решение этого уравнения раскрывает поведение во времени возникшей мгновенно спонтанной флуктуации $\delta \hat {C}_{{20,i}}^{{s(0)}}.$ В отличие от неупорядоченных возмущений спонтанные флуктуации возникают в каждой ячейке зоны закручивания за счет самопроизвольного хаотического движения частиц. Поэтому существует единственный интервал времени ${{{{\tau }}}_{{s2}}},$ соответствующий как поочередному возникновению, так и распаду спонтанной флуктуации в ячейке. Характерный интервал ${{{{\tau }}}_{{s2}}} = {{{{\tau }}}_{{s2}}}(t)$ определяется характерным временем изменения регулярной флуктуации в соответствии с уравнением сохранения импульса:

В соответствии с представляемой моделью эволюция спонтанной флуктуации $\delta \hat {C}_{{20,i}}^{{s(0)}},$ мгновенно возникшей в некоторый начальный момент $t = 0,$ протекает на отрезке времени ${{{{\tau }}}_{{s2}}}.$ Следующая спонтанная флуктуация $\delta \hat {C}_{{20,i}}^{{s(0)}}$ возникает в ячейке также мгновенно в момент времени $t = {{{{\tau }}}_{{s2}}}.$ Эволюция следующей спонтанной флуктуации также протекает в соответствии с уравнением (1.11) из [1]. Это уравнение решается на каждом отрезке времени ${{{{\tau }}}_{{s2}}}$ независимо от результата решения этого уравнения в предшествующий отрезок времени.

Представим спонтанную флуктуацию $\delta \hat {C}_{{20,i}}^{{s(0)}},$ $i = r,\theta ,$ в виде

Пусть осредненная флуктуация $\delta \hat {\bar {C}}_{{20}}^{{s(0)}}$ крайне слабо изменяется на масштабе, соответствующем размеру ячейки $\delta l,$ ${{(\delta l)}^{3}}\sim \delta V.$ Положим, что в каждой точке n-ячейки спонтанная флуктуация $\Delta \hat {C}_{{20,i(n)}}^{{s(0)}}$ имеет одно и то же значение. То есть флуктуация $\Delta \hat {C}_{{20,i(n)}}^{{s(0)}}$ моделируется функцией, которая постоянна внутри каждой ячейки. Случайная величина $\Delta \hat {C}_{{20,i(n)}}^{{s(0)}}$ мгновенно появляется в ячейке в некоторый начальный момент времени $t = 0.$ Номер ячейки n определяет ее место в пространстве, $n = n(x).$ Таким образом, пространственное распределение флуктуации $\Delta \hat {C}_{{20,i(n)}}^{{s(0)}}$ из уравнения (1.4) моделируется гистограммой в каждый момент времени t.

Решение уравнения сохранения импульса позволит отыскать некоторые статистические свойства стохастических флуктуаций $\delta \hat {C}_{{20,i}}^{{s(0)}}.$ Простота представленной модели исключает необходимость нахождения других статистических свойств флуктуаций.

В соответствии с представлениями, заложенными во времена Л. Больцмана [7], вероятность появления системы в некотором состоянии прямо пропорциональна объему W, который это состояние системы занимает в Г-пространстве:

В уравнении (1.5) ${{A}_{{dir}}}$ есть некоторая постоянная, 6N-мерное Г-пространство является фазовым пространством всех N частиц, составляющих систему. В соответствии с постулатом (1.5) вероятность появления системы в некотором состоянии возрастает с увеличением объема, занимаемого этим состояние в Г-пространстве. Соотношение, устанавливающее связь между объемом W и энтропией системы S, имеет вид [7]

Уравнение (1.6) справедливо как для энтропии Больцмана ${{S}_{B}},$ так и для определенной в работе [8, Гл.6] парной и одночастичной энтропии системы – ${{S}_{p}}$ и ${{S}_{1}}$ соответственно. Подстановка уравнения (1.6) в уравнение (1.5) приводит к выражению для вероятности, которое А. Эйнштейн впервые применил к исследованию флуктуаций [3]:

При формулировке постулата (1.5) и определения (1.6) не использовались какие-либо ограничения. Поэтому постулат (1.5) и определение (1.6) могут быть применены как для ансамбля систем (ансамбля Гиббса), так и для отдельной системы. При этом система может находиться как в состоянии статистического равновесия, так и в неравновесном состоянии. Система может оказаться в некотором состоянии как за счет спонтанной флуктуации, так и в результате внешнего воздействия. Внешнее воздействие способно повлиять на процесс спонтанного возникновения некоторого состояния системы – оно может внести поправку в уравнение (1.7).

Пусть некоторая система пребывает в состоянии статистического равновесия. В этом случае

Здесь ${{\bar {S}}^{{(Eq)}}}$ – средняя по ансамблю энтропия системы, находящейся в состоянии статистического равновесия; ${{\delta }}{{S}^{{s(Eq)}}}$ – спонтанная флуктуация энтропии ${{\bar {S}}^{{(Eq)}}}.$ Последняя обладает максимально возможным значением [3], поэтому состояние статистического равновесия исключает возможность появления положительно определенной спонтанной флуктуации энтропии, т.е. ${{{{\delta }}{{S}^{{s(Eq)}}}} \mathord{\left/ {\vphantom {{{{\delta }}{{S}^{{s(Eq)}}}} {k < 0}}} \right. \kern-0em} {k < 0}}.$ Подставим уравнение (1.8) в уравнение (1.7). Тогда получаем

здесь В соответствии с уравнением (1.9) ненормированная вероятность возникновения спонтанной флуктуации энтропии уменьшается по мере роста абсолютной величины флуктуации $\left| {{{{{\delta }}{{S}^{{s(Eq)}}}} \mathord{\left/ {\vphantom {{{{\delta }}{{S}^{{s(Eq)}}}} k}} \right. \kern-0em} k}} \right|.$

В отсутствие внешнего воздействия система находится в состоянии статистического равновесия. Внешнее воздействие, кратковременное или постоянное, переводит систему в неравновесное состояние. Пусть внешнее воздействие вынуждает твердую сферу радиуса a двигаться равномерно и прямолинейно через неподвижный газ со скоростью U₁, намного меньшей скорости звука. Число Рейнольдса Re₁ соответствует движению сферы со скоростью U₁. В условиях квазиизолированности описание системы может проводиться без учета взаимодействия этой системы с окружающей средой [4]. Пусть сфера внезапно останавливается в момент времени $t = {{t}^{{(1)}}}.$ Тогда к моменту времени $t = {{t}^{{(h)}}}$ система перейдет из неравновесного состояния в состояние статистического равновесия. В момент времени ${{t}^{{(1)}}}$ система имеет среднее по ансамблю значение энтропии $\bar {S}({{\operatorname{Re} }_{1}}),$ к моменту времени ${{t}^{{(h)}}} > {{t}^{{(1)}}}$ средняя по ансамблю энтропия системы станет равной ${{\bar {S}}^{{(Eq)}}}.$ Учитывая уравнение (1.7), получаем

здесь В соответствии с уравнением (1.10) вероятность положительно определенной спонтанной флуктуации ${{\delta }}{{S}^{s}}({{\operatorname{Re} }_{1}}) > 0$ превалирует над вероятностью отрицательно определенной спонтанной флуктуации ${{\delta }}{{S}^{s}}({{\operatorname{Re} }_{1}}) < 0.$ Флуктуация ${{\delta }}{{S}^{s}}({{\operatorname{Re} }_{1}}) > 0$ средней по ансамблю энтропии $\bar {S}({{\operatorname{Re} }_{1}})$ стремится направить систему к состоянию статистического равновесия. Менее вероятная флуктуация ${{\delta }}{{S}^{s}}({{\operatorname{Re} }_{1}}) < 0$ энтропии $\bar {S}({{\operatorname{Re} }_{1}})$ стремится направить систему в противоположную сторону. В соответствии с уравнением (1.10) спонтанная флуктуация ${{\bar {S}}^{{(Eq)}}} - \bar {S}({{\operatorname{Re} }_{1}}) > 0$ имеет максимальную вероятность. Эта флуктуация возникает в гидродинамическом масштабе времени, обладающем порядком величины ${{t}^{{(h)}}} - {{t}^{{(1)}}}.$ Пространственный масштаб флуктуации ${{\bar {S}}^{{(Eq)}}} - \bar {S}({{\operatorname{Re} }_{1}}) > 0$ превосходит радиус сферы a. Отметим, что само понятие спонтанной флуктуации энтропии $\bar {S}({{\operatorname{Re} }_{1}})$ теряет смысл на гидродинамическом масштабе [2].

Пусть в любой момент $t < {{t}^{{(1)}}}$ внешнее воздействие поддерживает систему в неравновесном стационарном состоянии, обладающем энтропией $\bar {S}({{\operatorname{Re} }_{1}}) < {{\bar {S}}^{{(Eq)}}}.$ Внешнее воздействие препятствует движению системы в направлении состояния статистического равновесия. Таким образом, внешнее воздействие исключает (или значительно уменьшает) вероятность появления положительно определенной спонтанной флуктуации ${{\delta }}{{S}^{s}}({{\operatorname{Re} }_{1}}) > 0,$ т.е. внешнее воздействие искажает уравнение (1.10). Внешнее воздействие вынуждает систему находиться в том или ином состоянии. Поэтому понятие вероятности появления системы в том или ином состоянии за счет спонтанной флуктуации теряет смысл. Таким образом, уравнение (1.10) становится некорректным при наличии внешнего воздействия.

Начиная со времени $t = {{t}^{{(1)}}},$ прямые уравнения описывают перевод системы в состояние статистического равновесия из состояния, имеющего энтропию $\bar {S}({{\operatorname{Re} }_{1}}).$ Изменим в момент времени $t = {{t}^{{(h)}}}$ – скорости всех частиц на противоположные по знаку величины. В этом случае к моменту времени $t = 2{{t}^{{(h)}}}$ система вернется в исходное неравновесное состояние, которое она имела в момент времени ${{t}^{{(1)}}}.$ Отметим, что возвращение в неравновесное состояние возможно лишь при полной изоляции системы. Переход из равновесного состояния в неравновесное описывается обратными уравнениями. Й. Лошмидт привел этот пример в своем диспуте с Л. Больцманом [8, Гл.7].

Таким образом, в устойчивой системе при отсутствии внешнего воздействия прямые уравнения гидродинамики описывают переход от состояния с меньшей энтропией $\bar {S}({{\operatorname{Re} }_{1}})$ к состоянию с большей энтропией ${{\bar {S}}^{{(Eq)}}},$ т.е. ведут систему в направлении состояния статистического равновесия. В отсутствие внешнего воздействия обратные уравнения описывают крайне маловероятный переход из состояния с большей энтропией ${{\bar {S}}^{{(Eq)}}}$ в состояние с меньшей энтропией $\bar {S}({{\operatorname{Re} }_{1}}),$ т.е. уводят систему из состояния статистического равновесия.

Пусть внешнее воздействие вынуждает твердую сферу двигаться равномерно и прямолинейно через неподвижный газ со скоростью ${{U}_{2}} > {{U}_{1}}.$ Движение сферы с более высокой скоростью ${{U}_{2}} > {{U}_{1}}$ соответствует более низкому значению энтропии $\bar {S}({{\operatorname{Re} }_{2}}) < \bar {S}({{\operatorname{Re} }_{1}}).$ В устойчивом стационарном режиме для достижения более низкого значения энтропии $\bar {S}({{\operatorname{Re} }_{2}}) < \bar {S}({{\operatorname{Re} }_{1}})$ необходимо усилить внешнее воздействие, т.е. требуется дополнительное внешнее воздействие. Пусть система после достижения критического значения энтропии $\bar {S}\left( {\operatorname{Re} _{0}^{ * }} \right) < \bar {S}({{\operatorname{Re} }_{2}})$ теряет свою устойчивость. После потери устойчивости происходит самопроизвольное удаление системы от состояния статистического равновесия. Таким образом, движение в направлении уменьшения энтропии происходит без всякого дополнительного внешнего воздействия. Процесс удаления от состояния статистического равновесия потерявшей устойчивость системы описывается прямыми уравнениями гидродинамики. В момент времени $t = {{t}_{ * }}$ решение прямых уравнений гидродинамики обрывается, однако в окрестности точки обрыва имеется решение обратных уравнений гидродинамики, которое ведет систему в направлении состояния статистического равновесия [9].

Таким образом, поведение неустойчивой системы является зеркальным отражением ее поведения в режиме устойчивости. Устранение внешнего воздействия сопровождается приближением состояния устойчивой системы к состоянию статистического равновесия. Напротив, состояние неустойчивой системы удаляется от состояния статистического равновесия без какого-либо дополнительного воздействия. Оба эти процесса описываются прямыми уравнениями гидродинамики. В отсутствие внешнего воздействия крайне маловероятный переход от статистического равновесия к устойчивому неравновесию описывается обратными уравнениями гидродинамики. Напротив, в режиме неустойчивости обратные уравнения гидродинамики ведут систему в направлении статистического равновесия.

Пусть внешнее воздействие вынуждает твердую сферу двигаться равномерно и прямолинейно через неподвижный газ со скоростью ${{U}_{3}}.$ Пусть число Рейнольдса ${{\operatorname{Re} }_{3}}$ соответствует движению сферы со скоростью ${{U}_{3}}.$ Пусть энтропия $\bar {S}({{\operatorname{Re} }_{3}})$ не превосходит энтропию критического состояния системы, $\bar {S}\left( {\operatorname{Re} _{0}^{ * }} \right){\text{:}}$ $\bar {S}({{\operatorname{Re} }_{3}}) < \bar {S}\left( {\operatorname{Re} _{0}^{ * }} \right).$ В этом случае рассматриваемая система неустойчива. Уравнение (1.10) для вероятности спонтанной флуктуации должно быть переформулировано для системы, потерявшей устойчивость. Учитывая зеркально отраженное поведение неустойчивой системы, находим

здесь

В уравнении (1.11) ${{A}_{{rev}}}$ есть некоторая постоянная, ${{\delta }}{{S}^{r}}({{\operatorname{Re} }_{3}})$ – регулярная флуктуация средней по ансамблю энтропии $\bar {S}({{\operatorname{Re} }_{3}}).$ Регулярная флуктуация ${{\delta }}{{S}^{r}}({{\operatorname{Re} }_{3}}) = {{\delta }}{{S}^{r}}({{\operatorname{Re} }_{3}},t)$ обеспечивает зависимость энтропии от времени в задаче с независящими от времени граничными условиями. В соответствии с уравнением (1.11) вероятность отрицательно определенной спонтанной флуктуации ${{\delta }}{{S}^{s}}({{\operatorname{Re} }_{3}}) < 0$ превалирует над вероятностью положительно определенной флуктуации ${{\delta }}{{S}^{s}}({{\operatorname{Re} }_{3}}) > 0.$ Спонтанная флуктуация ${{\delta }}{{S}^{s}}({{\operatorname{Re} }_{3}}) < 0$ энтропии $\bar {S}({{\operatorname{Re} }_{3}})$ направляет систему прочь от состояния статистического равновесия. Менее вероятная флуктуация ${{\delta }}{{S}^{s}}({{\operatorname{Re} }_{3}}) > 0$ энтропии $\bar {S}({{\operatorname{Re} }_{3}})$ стремится повести систему в направлении состояния статистического равновесия. Спонтанная флуктуация ${{\delta }}S_{{(*)}}^{s}({{\operatorname{Re} }_{3}}) = {{\delta }}S_{{(*)}}^{r}({{\operatorname{Re} }_{3}}) < 0$ имеет максимальную вероятность; здесь регулярная флуктуация ${{\delta }}S_{{( * )}}^{r}({{\operatorname{Re} }_{3}}) = \delta {{S}^{r}}({{\operatorname{Re} }_{3}},t = {{t}_{*}})$ соответствует моменту времени ${{t}_{ * }} = {{t}_{ * }}(\operatorname{Re} )$ обрыва решения прямых уравнений многомоментной гидродинамики. Эта флуктуация возникает в гидродинамическом масштабе времени ${{t}_{h}}$ (в задаче обтекания сферы ${{t}_{h}} = {{\operatorname{Re} a} \mathord{\left/ {\vphantom {{\operatorname{Re} a} {2{{U}_{0}}}}} \right. \kern-0em} {2{{U}_{0}}}}$). Пространственным масштабом спонтанной флуктуации ${{\delta }}S_{{( * )}}^{s}({{\operatorname{Re} }_{3}})$ является величина ${{l}_{h}} \geqslant a.$ Как и в устойчивом случае, само понятие спонтанной флуктуации теряет смысл в гидродинамическом масштабе. Как и ранее, уравнение (1.11) становится некорректным при появлении дополнительного внешнего воздействия.

Перепишем уравнение (1.11) в терминах объема W, который состояние системы занимает в Г‑пространстве. Тогда получим,

В соответствии с уравнением (1.12) вероятность появления неустойчивой системы в некотором состоянии обратно пропорциональна объему W который это состояние занимает в Г-пространстве.

2. РАСЧЕТ ВКЛАДА СПОНТАННЫХ ФЛУКТУАЦИЙ

Следуя изложенному в разд. 1, будем интерпретировать спонтанные флуктуации скорости течения $\delta {{U}^{{s(0)}}}$ в терминах спонтанных флуктуаций $\delta \hat {C}_{{20}}^{{s(0)}}.$ В соответствии с уравнением (1.5) из [1] $\delta {{U}^{{s(0)}}} = {{U}_{0}}\operatorname{Re} \delta \hat {C}_{{20}}^{{s(0)}},$ тогда ${{K}_{s}} = \operatorname{Re} \left| {\delta \hat {C}_{{20}}^{{s(0)}}} \right|$ и ${{\bar {K}}_{s}} = \operatorname{Re} \left| {\delta \hat {\bar {C}}_{{20}}^{{s(0)}}} \right|.$ Оценим порядок величины членов системы уравнений (1.1) из [1]. Оказывается, что левая часть этой системы, ${{\partial{ \hat {C}}_{i}^{{(0)}}} \mathord{\left/ {\vphantom {{\partial{ \hat {C}}_{i}^{{(0)}}} {\partial{ \hat {t}}}}} \right. \kern-0em} {\partial{ \hat {t}}}},$ $i = 1,...,19,$ ${{\partial \operatorname{Re} \hat {C}_{{20}}^{{(0)}}} \mathord{\left/ {\vphantom {{\partial \operatorname{Re} \hat {C}_{{20}}^{{(0)}}} {\partial{ \hat {t}}}}} \right. \kern-0em} {\partial{ \hat {t}}}},$ по абсолютной величине обладает порядком регулярной флуктуации $\left| {\delta \hat {C}_{i}^{{r(0)}}} \right|,$ i = 1, ..., 19. $\operatorname{Re} \left| {\delta \hat {C}_{{20}}^{{r(0)}}} \right|.$ Учитывая уравнения (1.12) и (1.13) из [1] приведем уравнение (1.11) из [1] к безразмерному виду. Пусть абсолютная величина любой из спонтанных флуктуаций $\delta \hat {C}_{i}^{{s(0)}},$ i = 5, 6, 7, 19, 23, ..., 26, $\delta \hat {C}_{{i,kl}}^{{s(0)}},$ $i = 5,\,\,6,\,\,7,\,\,8,\,\,9,\,\,18,\,\,19,\,\,27,...,\,\,33,$ значительно меньше абсолютной величины регулярной флуктуации $\delta \hat {C}_{i}^{{r(0)}},$ $i = 1,...,19,$ $\operatorname{Re} \delta \hat {C}_{{20}}^{{r(0)}}.$ В этом случае третий член левой части уравнения (1.11) из [1] значительно меньше первого члена. Тогда это уравнение упрощается:

В уравнении (2.1) спонтанная флуктуация $\delta \hat {C}_{{20,i}}^{{s(0,g)}}({{t}_{{in}}},x)$ разыгрывается случайным образом в момент времени ${{t}_{{in}}}$ в каждой n-ячейке ($n = n(x)$) около своего среднего значения $ \pm \left| {\delta \hat {\bar {C}}_{{20}}^{{s(0)}}} \right|$ с разбросом, равным $\left| {\delta \hat {\bar {C}}_{{20}}^{{s(0)}}} \right|.$ В уравнении (2.1) интервал времени $\tau _{{s2}}^{{(1)}} = \tau _{{s2}}^{{(1)}}(t)$ определяется из уравнения (1.3) в момент времени $t = {{t}_{{in}}}{\text{:}}$

Суммарное значение регулярной и спонтанной флуктуаций $\delta \hat {C}_{{20,i}}^{{rs(0)}}$ в момент времени ${{t}_{{in}}} + \tau _{{s2}}^{{(1)}}$ в каждой n-ячейке принимает вид

На следующем шаге спонтанная флуктуация $\delta \hat {C}_{{20,i}}^{{s(0,g)}}\left( {{{t}_{{in}}} + \tau _{{s2}}^{{(1)}},x} \right)$ разыгрывается около своего среднего значения в момент времени ${{t}_{{in}}} + \tau _{{s2}}^{{(1)}}.$ Пошаговый процесс повторяется. На $(l + 1)$-шаге спонтанная флуктуация $\delta \hat {C}_{{20,i}}^{{s(0,g)}}\left( {{{t}_{{in}}} + t_{{s2}}^{{(l)}},x} \right)$ разыгрывается случайным образом в момент времени ${{t}_{{in}}} + t_{{s2}}^{{(l)}}$ около своего среднего значения $ \pm \left| {\delta \hat {\bar {C}}_{{20}}^{{s(0)}}} \right|$ с разбросом, равным $\left| {\delta \hat {\bar {C}}_{{20}}^{{s(0)}}} \right|;$ здесь $t_{{s2}}^{{(l)}} = \tau _{{s2}}^{{(1)}} + $ $ + \tau _{{s2}}^{{(2)}} + ... + \tau _{{s2}}^{{(l)}}.$ Эволюция спонтанной флуктуации $\delta \hat {C}_{{20,i}}^{{s(0,g)}}\left( {{{t}_{{in}}} + t_{{s2}}^{{(l)}},x} \right)$ управляется уравнением (1.11) из [1]. В соответствии с этим уравнением к моменту времени ${{t}_{{in}}} + t_{{s2}}^{{(l + 1)}}$

В уравнении (2.3)

К моменту времени ${{t}_{{in}}} + t_{{s2}}^{{(l + 1)}}$ суммарный вклад регулярной и спонтанной флуктуаций $\delta \hat {C}_{{20,i}}^{{rs(0)}},$ $i = r,\theta ,$ в каждой n-ячейке достигнет величины

В соответствии с уравнением (2.3) положительно определенные спонтанные флуктуации $\delta \hat {C}_{{20,i}}^{{s(0,g)}}\left( {{{t}_{{in}}} + t_{{s2}}^{{(l)}},x} \right) > 0$ нарастают, в то время как отрицательно определенные спонтанные флуктуации $\delta \hat {C}_{{20,i}}^{{s(0,g)}}\left( {{{t}_{{in}}} + t_{{s2}}^{{(l)}},x} \right) < 0$ затухают. Пошаговый процесс завершается при обрыве решения $\hat {C}_{i}^{{(0)}},i = 1,...,20,$ в момент $t = {{t}_{ * }}.$

В стационарном случае нелинейная алгебраическая система уравнений (1.1) из [1] двадцатого порядка имеет решение $\hat {\bar {C}}_{i}^{{(0)}},$ $i = 1,...,20.$ Пусть $\delta \hat {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{C} }_{i}^{{(0)}}$ есть некоторое отклонение от решения $\hat {\bar {C}}_{i}^{{(0)}}{\text{:}}$ $\hat {C}_{i}^{{(0)}} = \hat {\bar {C}}_{i}^{{(0)}} + \delta \hat {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{C} }_{i}^{{(0)}}.$ Зададим отклонение $\delta \hat {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{C} }_{i}^{{(0)}}$ одного из коэффициентов, а именно коэффициента $\hat {\bar {C}}_{{19}}^{{(0)}}.$ Замена линейного уравнения ${{\hat {C}}_{{19}}} = 0$ стационарной системы (1.1) из [1] на уравнение ${{\hat {C}}_{{19}}} = \delta \hat {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{C} }_{{19}}^{{(0)}}$ позволяет определить отклонения $\delta \hat {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{C} }_{i}^{{(0)}},$ $i = 1,...,18,20$ всех остальных коэффициентов [5]. Полученное отклонение от стационарного решения $\hat {\bar {C}}_{i}^{{(0)}}$ может быть приравнено спонтанной флуктуации решения $\hat {\bar {C}}_{i}^{{(0)}}$ в некоторый начальный момент времени $t = 0{\text{:}}$ $\delta \hat {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{C} }_{i}^{{(0)}} = \delta \hat {C}_{i}^{{s(0)}}(t = 0),$ $i = 1,...,20.$

Для оценки величины спонтанной флуктуации $\delta \hat {C}_{{19}}^{{s(0)}}(t = 0)$ рассчитаем $\Delta {{N}_{{\delta V}}}$ из уравнения (1.1). При расчете использованы следующие параметры: ${{n}_{0}} = 2 \cdot {{10}^{{19}}}\,\,{\text{с}}{{{\text{м}}}^{{ - 3}}},$ $\delta l = {{10}^{{ - 2}}}\,\,{\text{см}}$ для ${{v}_{0}} = {{10}^{2}}\,\,{\text{с}}{{{\text{м}}}^{3}},$ тогда $\Delta {{N}_{{\delta V}}} = 2 \cdot {{10}^{{ - 7}}}$ (использованное значение ${{n}_{0}}$ соответствует плотности воздуха при нормальных условиях [7]). В разд. 1 установлено, что единый коэффициент ${{K}_{s}}$ может быть использован для оценки величины спонтанных флуктуаций всех измеряемых гидродинамических величин. Оценим величину ${{K}_{s}},$ используя рассчитанное значение $\Delta {{N}_{{\delta V}}}{\text{:}}$ ${{K}_{s}}\sim \Delta {{N}_{{\delta V}}}.$ Использование термодинамического соотношения (1.1) дает оценку снизу для ${{K}_{s}}.$ Тогда в соответствии с уравнением (1.2) $\delta \hat {C}_{{19}}^{{s(0)}}(t = 0)\sim \Delta {{N}_{{\delta V}}}.$ Решение системы двадцатого порядка позволяет рассчитать спонтанные флуктуации $\delta \hat {C}_{i}^{{s(0)}}(t = 0),$ $i = 1,...,18,20.$

Положим, что в каждой n-ячейке следа за сферой спонтанная флуктуация имеет рассчитанное значение $\delta \hat {\bar {C}}_{i}^{{s(0)}}(t = 0),$ $i = 1,...,20.$ Используем $\delta \hat {\bar {C}}_{i}^{{s(0)}}(t = 0)$ для расчета спонтанной флуктуации парной энтропии $\delta \hat {S}_{p}^{{s(0,2)}},$ определяемой уравнением (2.4) из [1]. При расчете использованы следующие параметры: $\operatorname{Re} = 400,$ $M{{a}^{2}} = {{10}^{{ - 7}}}.$ Расчеты показывают, что безразмерная парная энтропия $\delta S_{p}^{{s(0,2)}}{{(t = 0)} \mathord{\left/ {\vphantom {{(t = 0)} k}} \right. \kern-0em} k}$ является величиной, значительно превосходящей единицу: ${{n}_{0}}{{v}_{0}}M{{a}^{4}}\delta \hat {S}_{p}^{{s(0,2)}}(t = 0) \gg 1.$ Оказывается, что $\delta \hat {S}_{p}^{{s(0,2)}}(t = 0) > 0$ для $\delta \hat {\bar {C}}_{{20}}^{{s(0)}}(t = 0) > 0,$ $\delta \hat {S}_{p}^{{s(0,2)}}(t = 0) < 0$ для $\delta \hat {\bar {C}}_{{20}}^{{s(0)}}(t = 0) < 0.$

Высокое значение безразмерной парной энтропии $\delta S_{p}^{{s(0,2)}}{{(t = 0)} \mathord{\left/ {\vphantom {{(t = 0)} k}} \right. \kern-0em} k}$ обеспечивает асимметрию возникновения спонтанных флуктуаций разных знаков. А именно, вероятность ${{P}_{{rev}}}$ появления в каждой n-ячейке следа за сферой отрицательно определенной спонтанной флуктуации $\delta \hat {C}_{{20,i}}^{{s(0)}}(t = 0) < 0$ подавляюще велика по сравнению с вероятностью появления положительно определенной спонтанной флуктуации $\delta \hat {C}_{{20,i}}^{{s(0)}}(t = 0) > 0$ в соответствии с уравнением (1.11). Случайный розыгрыш спонтанных флуктуаций в следе за сферой допускает поочередное появление в ячейке как отрицательно, так и положительно определенных флуктуаций. Однако высокое значение парной энтропии $\delta S_{p}^{{s(0,2)}}{{(t = 0)} \mathord{\left/ {\vphantom {{(t = 0)} k}} \right. \kern-0em} k}$ обеспечивает подавляюще высокую вероятность появления в следе за сферой только отрицательно определенных спонтанных флуктуаций.

Согласно уравнению (2.1), положительно определенная спонтанная флуктуация $\delta \hat {C}_{{20,i}}^{{s(0,g)}}({{t}_{{in}}},x) > 0,$ $i = r,\theta ,$ растет, а отрицательно определенная спонтанная флуктуация $\delta \hat {C}_{{20,i}}^{{s(0,g)}}({{t}_{{in}}},x) < 0$ затухает в любой n-ячейке зоны закручивания. Отождествим момент появления спонтанной флуктуации $\delta \hat {C}_{{20}}^{{s(0)}}(t = 0)$ с моментом времени $t = {{t}_{{in}}}.$ Следуя уравнению (1.11), исключим возможность появления положительно определенной флуктуации в любой n-ячейке. В результате находим, что к моменту времени ${{t}_{{in}}} + \tau _{{s2}}^{{(1)}}$ возникшая в момент $t = {{t}_{{in}}}$ отрицательно определенная спонтанная флуктуация $\delta \hat {C}_{{20,i}}^{{s(0,g)}}({{t}_{{in}}},x) < 0$ исчезает: $\delta \hat {C}_{{20,i}}^{{s(0)}}\left( {{{t}_{{in}}} + \tau _{{s2}}^{{(1)}},x} \right) = 0.$ Тогда в соответствии с уравнением (2.2) суммарный вклад регулярной и спонтанной флуктуаций $\delta \hat {C}_{{20,i}}^{{rs(0)}}\left( {{{t}_{{in}}} + \tau _{{s2}}^{{(1)}},x} \right)$ в момент времени ${{t}_{{in}}} + \tau _{{s2}}^{{(1)}}$ в любой n-ячейке определяется вкладом регулярной флуктуации $\delta \hat {C}_{{20}}^{{r(0)}}\left( {{{t}_{{in}}} + \tau _{{s2}}^{{(1)}}} \right){\text{:}}$

В ходе дальнейшего пошагового процесса примем во внимание, что вероятность появления положительно определенной спонтанной флуктуации в любой n-ячейке среды пренебрежимо мала. В соответствии с уравнением (2.3) возникшая в момент времени ${{t}_{{in}}} + t_{{s2}}^{{(l)}}$ отрицательно определенная спонтанная флуктуация $\delta \hat {C}_{{20,i}}^{{s(0,g)}}\left( {{{t}_{{in}}} + t_{{s2}}^{{(l)}},x} \right) < 0$ исчезает к моменту времени ${{t}_{{in}}} + t_{{s2}}^{{(l + 1)}}.$ Тогда в соответствии с уравнением (2.4) суммарный вклад регулярной и спонтанной флуктуаций $\delta \hat {C}_{{20,i}}^{{rs(0)}}\left( {{{t}_{{in}}} + t_{{s2}}^{{(l + 1)}},x} \right)$ в момент времени ${{t}_{{in}}} + t_{{s2}}^{{(l + 1)}}$ в любой n-ячейке определяется вкладом регулярной флуктуации $\delta \hat {C}_{{20}}^{{r(0)}}\left( {{{t}_{{in}}} + t_{{s2}}^{{(l + 1)}}} \right){\text{:}}$ $\hat {C}_{{20,i}}^{{rs(0)}}\left( {{{t}_{{in}}} + t_{{s2}}^{{(l + 1)}},x} \right)$ $\hat {C}_{{20}}^{{r(0)}}\left( {{{t}_{{in}}} + t_{{s2}}^{{(l + 1)}}} \right),$ $i = r,\theta .$ Таким образом, спонтанные флуктуации вносят пренебрежимо малый вклад в зависимость от времени коэффициента $\hat {C}_{{20}}^{{(0)}}$ (уравнение (1.3) из [1]) в системе, потерявшей устойчивость.

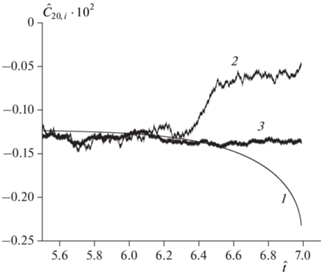
Кривая 1 на рис. 1 задает эволюцию коэффициента $\delta \hat {C}_{{20,i}}^{{rs(0)}}(t,x),$ $i = r,\theta ,$ в некоторой точке x следа за сферой. В каждой точке x эволюция коэффициента $\delta \hat {C}_{{20,i}}^{{rs(0)}}(t,x)$ строго следует эволюции коэффициента $\delta \hat {C}_{{20}}^{{r(0)}}(t).$ Такое поведение коэффициента $\delta \hat {C}_{{20,i}}^{{rs(0)}}(t,x)$ не зависит от величины коэффициента ${{\bar {K}}_{s}},$ задающего интенсивность спонтанных флуктуаций. Поведение коэффициента $\delta \hat {C}_{{20,i}}^{{rs(0)}}(t,x),$ ответственного за спонтанные флуктуации, качественно отличается от поведения коэффициента $\delta \hat {C}_{{20,i}}^{{rd(0)}}(t,x),$ $i = r,\theta ,$ ответственного за неупорядоченные возмущения (кривые 2 и 3 на рис. 1). Расчет кривых 2 и 3 проведен в соответствии с методом, изложенным в разд. 2 из [10]. Кривой 2 соответствует высокое значение коэффициента турбулентности ${{\bar {K}}_{d}} = 0.4\% .$ Кривая 3 рассчитана при ${{\bar {K}}_{d}} = 0.04\% .$ Расхождение значений коэффициентов $\delta \hat {C}_{{20,i}}^{{rd(0)}}(t,x)$ в разных точках следа за сферой x сильно зависит от величины коэффициента турбулентности ${{\bar {K}}_{d}},$ достигая основного порядка величины при ${{\bar {K}}_{d}} = 0.4\% .$ Сильное расхождение создает турбулентную картину течения в зоне закручивания за сферой (см. рис. 3 из [10]). Расхождение значений коэффициентов $\delta \hat {C}_{{20,i}}^{{rd(0)}}(t,x)$ в разных точках следа крайне незначительно при ${{\bar {K}}_{d}} = 0.04\% .$ Такое поведение коэффициентов крайне слабо искажает ламинарную картину течения (см. рис. 1 из [11]).

При отсутствии неупорядоченных возмущений закон сохранения импульса (1.11) из [1] выполняется за счет составляющих, ответственных за спонтанные флуктуации. Однако спонтанные флуктуации не в состоянии исказить ламинарную картину течения в следе за сферой. Картина течения, потерявшего устойчивость, будет полностью определяться регулярными составляющими скорости течения $U(t,x)$ (уравнение (1.4) из [1]).

3. ЗАКЛЮЧЕНИЕ

Анализ данных эксперимента позволяет сделать заключение, что поведение неустойчивой системы является зеркальным отражением ее поведения в режиме устойчивости. Действительно, при устранении внешнего воздействия состояние устойчивой системы устремляется в направлении статистического равновесия. Напротив, состояние системы, потерявшей устойчивость, без какого-либо дополнительного внешнего воздействия устремляется в противоположном направлении, прочь от состояния статистического равновесия. Прямые уравнения гидродинамики описывают оба процесса. В отсутствие внешнего воздействия крайне маловероятный переход от статистического равновесия к устойчивому неравновесному состоянию описывается обратными уравнениями гидродинамики. Напротив, в режиме неустойчивости обратные уравнения гидродинамики ведут систему в направлении статистического равновесия.

Во времена Л. Больцмана, после создания H‑теоремы, разгорелась дискуссия о ее справедливости. Оппоненты Больцмана привели примеры процессов, которые невозможно проинтерпретировать в терминах H-теоремы. Больцман признал возражения оппонентов. Однако он указал оппонентам на то, что процессы, представленные ими, крайне маловероятны. По Больцману, его уравнение описывает абсолютное большинство процессов, происходящих в природе [8, Гл. 7]. Время показало, что эволюция устойчивой системы протекает в соответствии с представлениями Больцмана. Качественно иной порядок возникает после потери системой устойчивости. Развитие системы как в направлении приближения к статистическому равновесию, описываемом обратными уравнениями многомоментной гидродинамики, так и в направлении удаления от статистического равновесия, описываемом прямыми уравнениями, идет с одинаковой вероятностью. То есть оба направления эволюции системы становятся равновероятными. Периодическая смена направлений эволюции предотвращает распад системы.

Критерий эволюции Гленсдорфа–Пригожина характеризует поведение устойчивой системы, стремящейся к равновесному состоянию [12]. В соответствии с этим критерием скорость изменения энтропии системы уменьшается по мере приближения к состоянию равновесия. Зеркально отраженный характер эволюции неустойчивой системы нашел свое выражение в критерии эволюции (2.9), (2.10) из [1]. Сформулированный критерий эволюции характеризует поведение неустойчивой системы, стремящейся прочь от состояния равновесия. В соответствии с этим критерием система стремится максимально быстро удалиться от равновесного состояния.

Критерий эволюции Гленсдорфа–Пригожина демонстрирует свойства найденных решений уравнений гидродинамики. При поиске решений уравнений гидродинамики никакой необходимости в привлечении этого критерия не возникает. На критерий эволюции (2.9), (2.10) из [1] возложена более ответственная задача. В соответствии с ним выбирается направление эволюции системы. То есть расчет распределений гидродинамических величин, характеризующих потерявшую устойчивость систему, невозможен без привлечения этого критерия.

Численное интегрирование показало, что решения детерминистических уравнений (уравнений классической гидродинамики Навье–Стокса и уравнений многомоментной гидродинамики) успешно воспроизводят регулярные режимы обтекания твердой сферы (устойчивые и неустойчивые) [5, 13]. Однако детерминистические уравнения не в состоянии воспроизвести турбулентные картины течения [14–16]. Это является причиной интереса к исследованию влияния стохастических факторов на возникновение и развитие турбулентности, а именно неупорядоченных возмущений и спонтанных флуктуаций. Возможность исследования влияния последних достигается путем введения стохастических составляющих в детерминистические уравнения [10, 11, 17].

Неупорядоченные возмущения возникают в среде за счет внешнего воздействия. В экспериментах по обтеканию сферы интенсивность неупорядоченных возмущений в набегающем потоке не превышает десятых долей процента. Для интерпретации турбулентности в терминах неупорядоченных возмущений необходимо понимание причин роста их интенсивности в турбулентном следе за сферой. Проведенное исследование показало, что причиной роста интенсивности неупорядоченных возмущений в зоне закручивания за сферой является распад ансамбля Гиббса, наступающий после потери системой устойчивости. Турбулентная картина возникает в результате хаотического движения когерентных структур, искаженных разросшимися неупорядоченными возмущениями [10, 11, 17].

При докритических значениях числа Рейнольдса $\operatorname{Re} < \operatorname{Re} _{0}^{*}$ решение системы уравнений многомоментной гидродинамики (1.4) из [10] стационарно и устойчиво. Это решение соответствует всему ансамблю систем (ансамблю Гиббса). Возникающие неупорядоченные возмущения затухают в некотором масштабе, который значительно меньше масштаба изменения гидродинамических величин.

Качественно иная картина имеет место после достижения критического значения числа Рейнольдса $\operatorname{Re} _{0}^{ * }.$ При $\operatorname{Re} > \operatorname{Re} _{0}^{ * }$ решение уравнений многомоментной гидродинамики теряет свою устойчивость, приобретая зависимость от времени. Ансамбль Гиббса распадается. В потерявшей устойчивость зоне закручивания каждое регулярное решение системы (1.4) из [10] повело себя сугубо индивидуально. Перестало существовать некоторое среднее решение, пригодное для интерпретации всех изначально близких регулярных решений. Такое поведение решений получило название эффекта бабочки Лоренца [18]. Потерявшее устойчивость решение не удовлетворяет законам сохранения числа частиц, импульса и энергии.

Учет неупорядоченных возмущений обеспечивает выполнение законов сохранения. В соответствии с преставлениями из работы [4] уравнения сохранения дополнялись членами, ответственными за неупорядоченные возмущения. В работах [10, 11, 17] система уравнений для неупорядоченных возмущений решалась совместно с системой уравнений для регулярных коэффициентов. Таким образом, независимость в поведении неупорядоченных возмущений исчезла. В зоне закручивания неупорядоченные возмущения будут вести себя во времени и в пространстве вполне определенным образом в соответствии с законами сохранения. Отрицательно определенные неупорядоченные возмущения по-прежнему затухали, в то время как положительно определенные – нарастали. Это различие в поведении и неравномерность возникновения положительно и отрицательно определенных неупорядоченных возмущений привело к накоплению возмущений в зоне закручивания.

Изменение в поведении неупорядоченных возмущений, в свою очередь, привело к качественному изменению регулярной картины течения в зоне закручивания. Перемещаясь по материальной линии, жидкая частица испытывала как хаотические изменения направления своего движения, так и хаотические изменения модуля скорости движения. В отличие от регулярных материальных линий искаженные материальные линии хаотически пересекались в зоне закручивания. Хаотическое движение жидкой частицы по искаженным неупорядоченными возмущениями пересекающимся материальным линиям создавало турбулентную картину течения как в зоне закручивания (рис. 3 из [10]), так и в вихревых кольцах, которые периодически отделялись от зоны закручивания и устремлялись вниз по потоку (рис. 7, 8 из [17]).

В отличие от неупорядоченных возмущений спонтанные флуктуации существуют в среде постоянно. Гидродинамическая величина флуктуирует около своего среднего по ансамблю значения за счет самопроизвольного хаотического движения частиц среды. В устойчивой зоне закручивания спонтанные флуктуации возникают и затухают в некотором масштабе времени, значительно уступающем характерному времени изменения гидродинамических величин.

Качественно иная картина имеет место после достижения критического значения числа Рейнольдса ${{\operatorname{Re} }_{0}}.$ В неустойчивом следе за сферой спонтанные флуктуации будут вести себя во времени и в пространстве вполне определенным образом в соответствии с уравнением сохранения импульса. А именно, спонтанные флуктуации должны подстраивать свое поведение во времени и в пространстве под поведение гидродинамических величин. Таким образом, при отсутствии внешнего воздействия выполнение законов сохранения в потерявшем устойчивость течении обеспечивается спонтанными флуктуациями.

В отличие от неупорядоченных возмущений, которые доставляются жидкой частицей в зону закручивания, спонтанные флуктуации появляются самопроизвольно в каждой точке зоны закручивания. Поэтому существует единственный интервал времени ${{{{\tau }}}_{{s2}}}$ (уравнение (1.3)), соответствующий как возникновению, так и распаду спонтанной флуктуации в неустойчивом следе за сферой. В соответствии с представленной моделью (см. разд. 1) спонтанная флуктуация появляется мгновенно случайным образом в каждой точке x неустойчивого следа за сферой в масштабе времени ${{{{\tau }}}_{{s2}}}.$ Дальнейшая эволюция спонтанной флуктуации скорости течения управляется законом сохранения импульса. Согласно уравнению (2.3) положительно определенные спонтанные флуктуации $\delta \hat {C}_{{20,i}}^{{s(0)}} > 0$ нарастают, в то время как отрицательно определенные спонтанные флуктуации $\delta \hat {C}_{{20,i}}^{{s(0)}} < 0$ затухают.

В соответствии с представлениями, существующими со времен Л. Больцмана, вероятность спонтанной флуктуации пропорциональна объему, который эта флуктуация занимает в Г-пространстве. Оказывается, что в устойчивой неравновесной системе вероятность появления положительно определенной спонтанной флуктуации превалирует над вероятностью появления отрицательно определенной флуктуации (уравнение (1.10)). Зеркально отраженный характер эволюции неустойчивой системы кардинально изменяет этот порядок. В неустойчивой системе вероятность появления отрицательно определенной спонтанной флуктуации начинает превалировать над вероятностью появления положительно определенной флуктуации (уравнение (1.11)).

Проведенный расчет показал, что в каждой точке х следа за сферой вероятность появления отрицательно определенной спонтанной флуктуации подавляюще велика по сравнению с вероятностью появления положительно определенной спонтанной флуктуации (см. разд. 2). В соответствии с уравнением (2.3) отрицательно определенная спонтанная флуктуация $\delta \hat {C}_{{20,i}}^{{s(0)}} < 0$ успевает полностью исчезнуть в масштабе времени ${{{{\tau }}}_{{s2}}}.$ Тогда при отсутствии внешнего воздействия картина течения, потерявшего устойчивость, полностью определятся регулярными составляющими скорости течения $U(t,x).$ То есть постоянно присутствующие в реальной физической системе спонтанные флуктуации не в состоянии исказить ламинарную картину течения, потерявшего устойчивость. Таким образом, ответственность за возникновение и развитие турбулентности полностью ложится на неупорядоченные возмущения, возникающие в среде за счет внешнего воздействия.