Кинетика и катализ, 2019, T. 60, № 6, стр. 756-762

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Рассмотрим линейную химическую реакцию с участием n реагентов А_j, протекающую через s элементарных стадий вида

где a_±ij ≥ 0, Σa_±ij = 1 – стехиометрические коэффициенты веществ А_j в стадии i. В закрытых системах каждая из стадий линейной реакции должна быть линейной, т.е. должен выполняться постадийный закон сохранения (ЗС)

В открытых системах линейные реакции могут включать также нелинейные стадии с участием других реагентов, изменениями которых можно пренебречь (гипотеза квазистационарности Боденштейна–Семенова [1, 2]). Динамика реакций (1), (2) в безградиентном изотермическом реакторе в рамках закона действующих масс описывается системой линейных обыкновенных дифференциальных уравнений (ОДУ)

где А_j – концентрации реагентов А_j (в мольных долях – мол. д.), ${{r}_{i}} = {{k}_{i}}\Pi A_{j}^{{aij}}$ и ${{r}_{{ - i}}} = {{k}_{{ - i}}}\Pi A_{j}^{{a - ij}}$ – линейные по А_j скорости стадий в прямом и обратном направлениях (в 1/с), k_–i – константы скоростей стадий (в 1/с), q₀ и q – начальная и текущая скорости потока (в 1/с). Начальные условия (н. у.)

Линейные реакции имеют только одно устойчивое равновесие A_j∞ [21], которое определяется из системы линейных алгебраических уравнений

и может быть записано в явном виде где Δ ≠ 0 и Δ_j – соответственно, главный и вспомогательные определители [22] системы (5). В закрытых системах всегда выполняются ЗС веществ

В открытых системах ЗС могут быть записаны в дифференциальной форме

Эти ЗС позволяют снизить порядок системы (3) на единицу и должны учитываться при выборе н. у. для экспериментов. Общее решение системы (3) определяется собственными числами (с. ч.) λ₁, λ₂, …, λ_1n – корнями характеристического уравнения (х. у.)

где φ = φ(k_i, k_–i, A_0j) – кинетические параметры (константы). Если все с. ч. действительны и различны, то общее решение (8) запишется [22] как где C_jk = С_jk(k_i, k_–i, A_0j) – константы, зависящие от кинетических параметров и н. у., С_j = С_j(k_i, k_–i) – константы, зависящие только от кинетических параметров. Если среди с. ч. есть комплексно-сопряженные пары λ = m ± in, i² = –1, то соответствующие пары слагаемых в (10) тоже будут комплексно-сопряженными C_jkexp(m + in)t + C_jkexp(m – in)t (с одинаковыми коэффициентами) и могут заменяться действительными выражениями [22] где P, Q, или R, α – новые действительные константы интегрирования. Частный случай кратных с. ч. здесь не рассматривается.

Применим к решениям (10) и (11) метод, аналогичный [17–20], немного модифицировав его. В исходном варианте этот метод допускает использование любых двух различных физичных н. у. Модификация состоит в более “жестком” выборе н. у., которые должны удовлетворять следующим достаточным условиям (критерию) применимости метода

Эти условия выражают требования равенства нулю всех коэффициентов при экспонентах в (10) и (11), кроме одного коэффициента с номером k₀, хотя бы для одного реагента с номером j₀, при физичных значениях н. у. Они представляют собой систему (n – 1) линейных уравнений с n неизвестными, которая имеет бесконечное число решений. Если среди этих решений есть хотя бы одно физичное, то критерий (12) выполним и решения (10) и (11) для двух различных н. у. могут быть представлены в виде

При наличии комплексно-сопряженных с. ч. соответствующие пары слагаемых в (13) имеют вид (11). Найдем из первого уравнения (13) единственную зависящую от t экспоненту и вычислим, с учетом (9), остальные зависящие от t экспоненты

где A_j1 > С_j. Подставим выражения (14) во второе уравнение (13) и получим или в нормированной форме

Левые части выражений (15) и (16) не зависят от времени, а зависят только от концентраций одного из реагентов, кинетических параметров и н. у. реакции, т.е. являются точными автономными инвариантами, существенно нелинейными относительно концентраций любого из реагентов, измеренных в двух неравновесных экспериментах. При выполнении условий A_j1 > С_j они принимают действительные значения, являются физичными и наблюдаются на графиках в виде горизонтальных линий.

Таким образом, в закрытых и открытых системах в рамках закона действующих масс аналитические выражения для инвариантов линейных химических реакций (15) и (16), протекающих в безградиентном изотермическом реакторе, могут быть представлены в виде суммы концентраций реагентов (в степенях от констант скоростей стадий), найденных из двух неравновесных значений концентраций с любой заданной парой начальных условий, удовлетворяющих критерию применимости метода (12). Максимальное число таких инвариантов для выбранной пары начальных условий равно числу реагентов. При выборе другой пары начальных условий можно построить еще столько же инвариантов и т.д. Для их экспериментальной проверки необходимо данные двух соответствующих экспериментов подставить в левые части любого из инвариантных выражений (15) и (16) и сравнить их с константами в правых частях этих соотношений. Выполнение или невыполнение этих равенств будет, соответственно, означать приемлемость или неприемлемость исследуемого механизма химической реакции, что может быть полезно при решении обратных задач.

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Пример 1. Пусть реакция A = C протекает по последовательной схеме

Динамика таких реакций в закрытой системе описывается ОДУ вида (3):

Координаты равновесия (5) и (6) для этой системы равны A_∞ = k_–1k_–2/Δ, B_∞ = k₁k_–2/Δ, C_∞ = = k₁k₂/Δ, Δ = k₁k₂ + k₁k_–2 + k_–1k_–2, а ЗС (7) запишется как

Выразим отсюда B = 1 – A – C, подставим в (1.2) и получим два ОДУ относительно A и C, т.е. понизим порядок системы (3) на единицу

Общее решение (1.4) определяется корнями х. у. (9), которое запишется как

где φ₁ = k₁ + k_–1 + k₂ + k_–2, φ₂ = k₁k₂ + k₁k_–2 + k_–1k_–2. Анализ показал, что уравнение (1.5) имеет только действительные корни. Пусть k₁ = 1, k_–1 = 1, k₂ = 1, k_–1 = 1, тогда φ₁ = 4, φ₂ = 3 и λ₁ = –1, λ₂ = –3, а решения (10) системы (1.4) запишутся как

Из (1.6) видно, что условие применимости метода (12) к любому реагенту A (j₀ = 1) или С (j₀ = 2) по первой (k = 1) экспоненте запишется как A₀ = C₀, а по второй (k = 2) экспоненте примет вид A₀ + C₀ = 2/3. Выполним с учетом ЗС (1.3), например, второе из этих условий. Оно представляет собой одно линейное уравнение с двумя неизвестными, которое имеет бесконечное число решений. Одним из физичных решений с учетом ЗС (1.3) является A₀₁ = 0, B₀₁ = 1/3, C₀₁ = 2/3. Второе н. у. выберем произвольно A₀₂ = 2/3, B₀₂ = 0, C₀₂ = 1/3, но тоже с учетом ЗС. Для этих н. у. соотношения (13) примут вид

Из (1.8) и (1.9) видно, что для реагентов A и С соотношения (14) запишутся как

Подставим (1.10) во второе уравнение (1.8) и найдем точный А-инвариант

или в нормированной форме

Подставим (1.11) во второе уравнение (1.9) и найдем точный C-инвариант

или в нормированной форме

Инварианты (1.13), (1.15) и решения двух задач Коши показаны на рис. 1а и 1б.

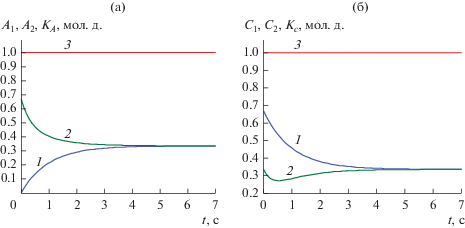
Как видно на рис. 1а и 1б, зависимости K_A(t) и K_C(t) представляют собой строго горизонтальные линии, т.е. не зависят от времени и являются точными инвариантами.

Если та же реакция A = С протекает по параллельной схеме

то ее динамика с учетом ЗС (1.3) описывается ОДУ

Коэффициенты х. у. (9) примут вид φ₁ = k₁ + k_–1 +_{+ 2k2 + k–2, φ2 = k1k2 + k1k–2 + 2k2k–2 + k–1k–2 + k2², откуда при тех же значениях констант получим φ1 = 5, φ2 = 6, т.е. λ1 = –2, λ2 = –3, и соотношения (13) по реагенту A запишутся как}

Из (1.18) с учетом (15) и (16) для той же пары н. у. A₀₁ = 0, B₀₁ = 1/3, C₀₁ = 2/3 и A₀₂ = 2/3, B₀₂ = 0, C₀₂ = 1/3 получим ненормированный и нормированный инварианты

Нетрудно убедиться, что графики этих зависимостей тоже представляют собой строго горизонтальные линии, т.е. являются точными инвариантами.

Пример 2. Рассмотрим линейную трехстадийную схему реакции A = D:

Динамика реакции (2.1) описывается ОДУ

Координаты равновесия (5) и (6) равны A_∞ = = k_–1k_–2k_–3/Δ, B_∞ = k₁k_–2k_–3/Δ, C_∞ = k₁k₂k_–3/Δ, D_∞ = k₁k₂k₃/Δ, где Δ = k₁k₂k₃ + k₁k_–2k_–3 + k₁k₂k_–3 + + k_–1k_–2k_–3, а ЗС (7) принимает вид

Выразим отсюда B, подставим в (2.2) и получим систему ОДУ третьего порядка

где B = 1 – A – C – D. Характеристическое уравнение (9) для этой системы принимает вид где φ₁ = k₁ + k_–1 + k₂ + k_–2 + k₃ + k_–3, φ₂ = (k₁ +  k_–1) × × (k₂ + k_–2 + k₃ + k_–3) – k₂k_–1 – k₃(k_–3–k₂) +  k_–3 ×× (k₂ + k_–2 + k₃), φ₃ = –k₁k_–3k₂– k₁k_–2k_–3– k₁k₂k₃–– k_–1k_–2k_–3. Пусть k₁ = 1, k_–1 = 1, k₂ = 1, k_–1 = 1, k₃ = 1, k_–3 = 1, тогда λ₁ = –2, λ_2,3 = –2 ± 2^1/2 = (–0.5858, –3.4142) и A-решения системы (2.2) для любых н. у. запишутся как

(2.6)

$\begin{gathered} A = ({{{{A}_{0}}} \mathord{\left/ {\vphantom {{{{A}_{0}}} 2}} \right. \kern-0em} 2} + {{{{C}_{0}}} \mathord{\left/ {\vphantom {{{{C}_{0}}} 2}} \right. \kern-0em} 2} - {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4})\exp ({{\lambda }_{1}}t) + \\ + \,\,{{С}_{{120}}}\exp ({{\lambda }_{2}}t) + {{С}_{{130}}}\exp ({{\lambda }_{3}}t) + {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}, \\ \end{gathered} $

где С₁₂₀ = α₁₂A₀ + β₁₂B₀ + γ₁₂C₀ + θ₁₂, С₁₃₀ = α₁₃A₀ + + β₁₃B₀ + γ₁₃C₀ + θ₁₃, α₁₂ = –3 730 904 090 310 553, β₁₂= 5 276 295 164 430 438, γ₁₂ = 9 007 199 254 740 991, θ₁₂ = –2 638 147 582 215 219, α₁₃ = 5 436 325 649 948 134, β₁₃ = 7 688 125 463 633 382, γ₁₃ = 2 251 799 813 685 248, θ₁₃ = –3 844 062 731 816 691 (приведены точные значения). Критерий применимости метода (12) для реагента А по второй и третьей экспонентам дает систему двух линейных уравнений с тремя неизвестными н. у.

(2.7)

$\begin{gathered} {{\alpha }_{{12}}}{{A}_{0}} + {{b}_{{12}}}{{B}_{0}} + {{\gamma }_{{12}}}{{C}_{0}} + {{\theta }_{{12}}} = {\text{ }}0, \\ {{\alpha }_{{13}}}{{A}_{0}} + {{b}_{{13}}}{{B}_{0}} + {{\gamma }_{{13}}}{{C}_{0}} + {{\theta }_{{13}}} = {\text{ }}0. \\ \end{gathered} $

Эта система имеет бесконечно много решений. Выберем из них одно физичное решение, например, А₀₁ = 0, B₀₁ = 1/2, C₀₁ = 0. Второе н. у. возьмем любое A₀₂ = 1, B₀₂ = 0, C₀₂ = 0. Решения (2.6) для этих двух н. у. примут вид

(2.8)

${{A}_{1}} = - {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}\exp ({{\lambda }_{1}}t) + {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4},$

(2.9)

$\begin{gathered} {{A}_{2}} = {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}\exp ({{\lambda }_{1}}t) + {{С}_{{120,2}}}\exp ({{\lambda }_{2}}t) + \\ + \,\,{{С}_{{130,2}}}\exp ({{\lambda }_{3}}t) + {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}, \\ \end{gathered} $

где С_120,2 = (2^1/2 + 1) × × 159 226 291 8131 443/9 007 199 254 740 992, С_130,2 == (2^1/2 – 1)1 592 262 918 131 443/9 007 199 254 740 992. Из (2.8) следует

(2.10)

$\begin{gathered} \exp ({{\lambda }_{1}}t) = 1 - 4{{A}_{1}},\,\,\,\,\exp ({{\lambda }_{2}}t) = {{(1 - 4{{A}_{1}})}^{{{{\lambda 2} \mathord{\left/ {\vphantom {{\lambda 2} {\lambda 1}}} \right. \kern-0em} {\lambda 1}}}}}, \\ \exp ({{\lambda }_{3}}t) = {{(1 - 4{{A}_{1}})}^{{{{\lambda 3} \mathord{\left/ {\vphantom {{\lambda 3} {\lambda 1}}} \right. \kern-0em} {\lambda 1}}}}}. \\ \end{gathered} $

Подставим (2.10) в (2.9) и найдем точный А-инвариант системы (2.2):

(2.11)

$\begin{gathered} {{I}_{A}}(t) \equiv {{A}_{2}} - (1 - {{4{{A}_{1}})} \mathord{\left/ {\vphantom {{4{{A}_{1}})} 4}} \right. \kern-0em} 4} - {{С}_{{120,2}}}{{(1 - 4{{A}_{1}})}^{{{{\lambda 2} \mathord{\left/ {\vphantom {{\lambda 2} {\lambda 1}}} \right. \kern-0em} {\lambda 1}}}}} - \\ - \,\,{{С}_{{130,2}}}{{(1 - 4{{A}_{1}})}^{{\lambda {3 \mathord{\left/ {\vphantom {3 {\lambda 1}}} \right. \kern-0em} {\lambda 1}}}}} = {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}, \\ \end{gathered} $

или в нормированной форме

(2.12)

$\begin{gathered} {{K}_{A}}(t) \equiv 4{{A}_{2}} + 4{{A}_{1}} - 1 - 4{{С}_{{120,2}}}{{(1 - 4{{A}_{1}})}^{{{{\lambda 2} \mathord{\left/ {\vphantom {{\lambda 2} {\lambda 1}}} \right. \kern-0em} {\lambda 1}}}}} - \\ - \,\,4{{С}_{{130,2}}}{{(1 - 4{{A}_{1}})}^{{{{\lambda 3} \mathord{\left/ {\vphantom {{\lambda 3} {\lambda 1}}} \right. \kern-0em} {\lambda 1}}}}} = {\text{ }}1. \\ \end{gathered} $

Рис. 2.

Решения задач Коши и A-инвариант для реакции (2.1) при k₁ = 1, k_–1 = 1, k₂ = 1, k_–1 = 1, k₃ = 1, k_–3 = 1, A₀₁ = 0, B₀₁ = 1/2, C₀₁ = 0, D₀₁ = 1/2, A₀₂ = 1, B₀₂ = 0, C₀₂ = 0, D₀₂ = 0: 1 – A₁(t), 2 – A₂(t), 3 – K_A(t).

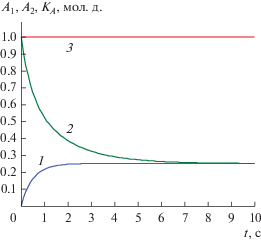
Инвариант (2.12) и решения двух задач Коши показаны на рис. 2. Решения системы (2.2) для других реагентов запишутся аналогично (2.6):

(2.13)

$\begin{gathered} C = ({1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4} - {{{{A}_{0}}} \mathord{\left/ {\vphantom {{{{A}_{0}}} 2}} \right. \kern-0em} 2} - {{{{C}_{0}}} \mathord{\left/ {\vphantom {{{{C}_{0}}} 2}} \right. \kern-0em} 2})\exp ({{\lambda }_{1}}t) + \\ + \,\,{{С}_{{220}}}\exp ({{\lambda }_{2}}t) + {{С}_{{230}}}\exp ({{\lambda }_{3}}t) + {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}, \\ \end{gathered} $

(2.14)

$\begin{gathered} D = ({{{{A}_{0}}} \mathord{\left/ {\vphantom {{{{A}_{0}}} 2}} \right. \kern-0em} 2} + {{{{C}_{0}}} \mathord{\left/ {\vphantom {{{{C}_{0}}} 2}} \right. \kern-0em} 2} - {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}){\text{exp}}({{\lambda }_{1}}t) + \\ + \,\,{{С}_{{320}}}{\text{exp}}({{\lambda }_{2}}t) + {{С}_{{330}}}{\text{exp}}({{\lambda }_{3}}t) + {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}, \\ \end{gathered} $

где С₂₂₀ = α₂₂A₀ + β₂₂B₀ + γ₂₂C₀ + θ₂₂, С₂₃₀ = α₂₃A₀ + + β₂₃B₀ + γ₂₃C₀ + θ₂₃, С₃₂₀ = α₃₂A₀ + β₃₂B₀ + γ₃₂C₀ + + θ₃₂, С₃₃₀ = α₃₃A₀ + β₃₃B₀ + γ₃₃C₀ + θ₃₃ и т.д. С их помощью находятся B- и C-инварианты для реагентов B и C соответственно.

Пример 3. Рассмотрим реакцию, протекающую по линейной циклической схеме

(3.1)

$1)\,\,{\mathbf{А}} = {\mathbf{В}},\,\,\,\,2)\,\,{\mathbf{В}} = {\mathbf{С}},\,\,\,\,3)\,\,{\mathbf{С}} = {\mathbf{D}},\,\,\,\,4)\,\,{\mathbf{D}} = {\mathbf{A}}.$

Эта реакция описывается ОДУ

(3.2)

$\begin{gathered} x{\kern 1pt} ' = {{r}_{1}} - {{r}_{2}},\,\,\,\,y{\kern 1pt} ' = {{r}_{2}} - {{r}_{3}}, \\ q{\kern 1pt} ' = {{r}_{3}} - {{r}_{4}},\,\,\,\,z{\kern 1pt} ' = {{r}_{4}} - {{r}_{1}}, \\ \end{gathered} $

где x ≡ [B], y ≡ [C], q ≡ [D] и z ≡ [A] – концентрации реагентов; r₁= k₁z – k_–1x, r₂= k₂x – k_–2y, r₃= k₃y – k_–3q, r₄= k₄q – k_–4z, а ЗС принимает вид

(3.3)

$x + y + q + z = 1.$

Пусть k₁= 1, k₂ = 2, k₃ = 3, k₄ = 4, k_–1 = 0.5, k_–2 = 0.3, k_–3 = 0.3, k_–4 = 1. Тогда λ₁ = –6.2002 (действительное), а λ_2,3 = –2.9499 ± 1.4520i (комплексно-сопряженные), и x-решения, с учетом (11), запишутся как

(3.4)

$\begin{gathered} x = {{С}_{{110}}}\exp ({{\lambda }_{1}}t) + ({{С}_{{120}}}\cos nt + \\ + \,\,{{С}_{{130}}}\sin nt)\exp \left( {mt} \right) + {{2676} \mathord{\left/ {\vphantom {{2676} {13\,405}}} \right. \kern-0em} {13\,405}}, \\ \end{gathered} $

где С₁₁₀ ≈ 0.1587x₀ – 0.1081y₀ + 0.2123q₀ – 0.0598, С₁₂₀ ≈ 0.8413x₀ + 0.1081y₀ – 0.2123q₀ – 0.1398, С₁₃₀ ≈ ≈ 0.0237x₀ + 0.7241y₀ + 0.2135q₀ – 0.1492. Критерий применимости метода (12) для x (С₁₂₀ = С₁₃₀ = 0) выполняется, например, при x₀₁ = 0.1403, y₀₁ = 0.2015, q₀₁ = 0, z₀₁ = 1 – x₀ – y₀ – q₀. Второе н. у. выберем произвольно x₀₂ = 0, y₀₂ = 0, q₀₂ = 0, z₀₂ = 1, но с учетом ЗС (3.3). Решения (3.4) для этих двух н. у. запишутся как

(3.5)

${{x}_{1}} = {{С}_{{110\_1}}}\exp ({{\lambda }_{1}}t) + {{С}_{1}},$

(3.6)

$\begin{gathered} {{x}_{2}} = {{С}_{{110\_2}}}\exp ({{\lambda }_{1}}t) + ({{С}_{{120\_2}}}\cos nt + \\ + \,\,{{С}_{{130\_2}}}\sin nt)\exp (mt) + {{C}_{1}}, \\ \end{gathered} $

где λ₁ = –6.2002, m = Re(λ_2,3) = –2.9499, n = Im(λ_2,3) = = 1.452, С_110,1 ≈ –0.0593, С_110,2 ≈ –0.0598, С_120,2 ≈ –0.1492, С_130,2 ≈ –0.1398, С₁ = 2676/13 405 ≈ 0.1996.

Из (3.5) получим

(3.7)

$\begin{gathered} {{E}_{1}} \equiv \exp ({{\lambda }_{1}}t) = ({{x}_{1}} - {{{{С}_{1}})} \mathord{\left/ {\vphantom {{{{С}_{1}})} {{{С}_{{110\_1}}}}}} \right. \kern-0em} {{{С}_{{110\_1}}}}}, \\ {{E}_{2}} \equiv \exp (mt) = {{E}_{1}}{{^{m}}^{{/\lambda 1}}}, \\ t = \ln {{[({{x}_{1}} - {{{{С}_{1}})} \mathord{\left/ {\vphantom {{{{С}_{1}})} {{{С}_{{110\_1}}}]}}} \right. \kern-0em} {{{С}_{{110\_1}}}]}}} \mathord{\left/ {\vphantom {{[({{x}_{1}} - {{{{С}_{1}})} \mathord{\left/ {\vphantom {{{{С}_{1}})} {{{С}_{{110\_1}}}]}}} \right. \kern-0em} {{{С}_{{110\_1}}}]}}} {{{\lambda }_{1}}}}} \right. \kern-0em} {{{\lambda }_{1}}}}. \\ \end{gathered} $

Подставим (3.7) в (3.6) и найдем точный x-инвариант системы (3.2), (3.3):

(3.8)

$\begin{gathered} {{I}_{x}} \equiv {{x}_{2}} - {{С}_{{110\_2}}}{{E}_{1}} - ({{С}_{{120\_2}}}\cos nt + \\ + \,\,{{С}_{{130\_2}}}\sin nt){{E}_{2}} = {{С}_{1}}, \\ \end{gathered} $

или в нормированной форме

(3.9)

$\begin{gathered} {{K}_{x}} \equiv {{x}_{2}} - {{С}_{{110\_2}}}{{{{E}_{{1~}}}} \mathord{\left/ {\vphantom {{{{E}_{{1~}}}} {{{С}_{1}}}}} \right. \kern-0em} {{{С}_{1}}}} - \\ - \,\,({{С}_{{120\_2}}}\cos nt + {{С}_{{130\_2}}}\sin nt){{{{E}_{2}}} \mathord{\left/ {\vphantom {{{{E}_{2}}} {{{С}_{1}}}}} \right. \kern-0em} {{{С}_{1}}}} = 1. \\ \end{gathered} $

Инвариант (3.9) и решения двух задач Коши показаны на рис. 3.

Рис. 3.

Решения задач Коши и x-инвариант для реакции (2.1) при k₁ = 1, k₂ = 2, k₃ = 3, k₄ = 4, k_–1 = 0.5, k_–2 = 0.3, k_–3 = 0.3, k_–4 = 1, x₀₁ = 0.1403, y₀₁ = 0.2015, q₀₁ = 0, z₀₁ = 1 – x₀ – y₀ – q₀, x₀₂ = 0, y₀₂ = 0, q₀₂ = 0, z₀₂ = 1: 1 – x₁(t), 2 – x₂(t), 3 – K_х(t).

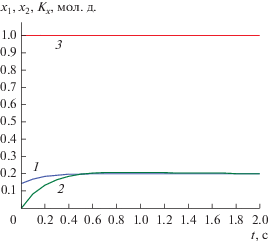
Решения (3.4) для других реагентов запишутся аналогично и дают точные y-, q- и z-инварианты для соответствующих реагентов.

Пример 4. Рассмотрим одну из возможностей применения инвариантов для решения обратных задач. Сравним две альтернативные линейные схемы (1.1) и (1.16) для реакции А = С. Пусть в результате экспериментов с двумя различными н. у. получены два набора данных A_1эксп(t) и A_2эксп(t). Рассчитаем для них инвариантные выражения K₁(t) и K₂(t) по соответствующим этим схемам формулам (1.13) и (1.20) (табл. 1). Анализ показал, что эти экспериментальные данные, с учетом погрешностей эксперимента, одинаково хорошо согласуются с обеими возможными схемами реакции – последовательной и параллельной. Однако среднее расчетное значение инвариантов K_сред ближе к теоретическим значениям K_теор у последовательной схемы, что позволяет считать ее более вероятной.

Таблица 1.  

Концентрации реагента А в реакции A = С по данным двух экспериментов с н. у.*

t, с	А1эксп	А2эксп	K1	K2
	мол. д.
0	0	0.67	1.0100	1.0050
1	0.10	0.55	1.1285	0.9750
2	0.15	0.50	1.1418	0.9750
3	0.20	0.37	0.8780	0.8550
4	0.25	0.35	0.9171	0.9000
5	0.30	0.33	0.9395	0.9450
6	0.33	0.33	0.9850	0.9900
7	0.33	0.33	0.9850	0.9900
Kсред			0.9981	0.9543
Kтеор			1	1

*  A₀₁ = 0, B₀₁ = 1/3, C₀₁ = 2/3 и A₀₂ = 2/3, B₀₂ = 0, C₀₂ = 1/3.

ЗАКЛЮЧЕНИЕ

Предложенный в работе метод определения автономных кинетических инвариантов многостадийных линейных химических реакций позволяет находить точные аналитические выражения, которые связывают неравновесные значения концентраций реагентов, измеренные в двух экспериментах с разными начальными условиями (не обязательно “термодинамическими”), но остаются строго постоянными в течение всего переходного процесса в безградиентном изотермическом реакторе. Этот метод представляет собой альтернативный подход к поиску и обнаружению аналитических выражений для неравновесных временных инвариантов химических реакций, впервые предложенный американо-брюссельской школой кинетиков [6–16]. В этих работах каждый механизм реакции характеризуется одним инвариантом в виде отношений концентраций всех реагентов, найденных в двух экспериментах с взаимно-обратными (“термодинамическими”) начальными условиями.

Отличия нашего метода состоят в следующем:

– каждый механизм реакции характеризуется множеством инвариантов (их число равно числу реагентов, причем для каждой пары начальных условий);

– инварианты представляются в виде суммы концентраций только одного (любого) из реагентов, измеренных в двух экспериментах с любыми неравновесными (не обязательно “термодинамическими”) начальными условиями;

– инварианты применимы как в закрытых, так и в открытых системах.

Такие инварианты могут быть использованы как новые средства идентификации механизмов химических реакций, проводимых с использованием релаксационных экспериментов. Метод может быть применен и к нелинейным реакциям в квазистационарных условиях, а также к некоторым нелинейным реакциям с тремя и более реагентами, допускающим точные аналитические решения.