Кинетика и катализ, 2021, T. 62, № 4, стр. 501-506

Влияние внутридиффузионного сопротивления на химический процесс в зерне катализатора несферической формы

С. Г. Заварухин^a, b, *, В. О. Родина^a

^a ФГБУН ФИЦ “Институт катализа им. Г.К. Борескова СО РАН”
630090 Новосибирск, просп. Акад. Лаврентьева, 5, Россия

^b ФГБОУ ВО Новосибирский государственный технический университет
630073 Новосибирск, просп. К. Маркса, 20, Россия

^* E-mail: zsg@catalysis.ru

Поступила в редакцию 20.01.2021
После доработки 05.04.2021
Принята к публикации 08.04.2021

DOI: 10.31857/S0453881121040158

Полный текст (PDF)

Аннотация

Рассмотрена задача о трехмерном зерне катализатора с тремя характерными размерами a, b и с при наличии внутридиффузионного сопротивления и реакции первого порядка. На основе точного решения в декартовой системе координат предложены зависимости для расчета эквивалентного размера зерна и степени его использования от параметра Тиле ψ. Особенностью решения является зависимость формы зерна от параметра Тиле. В безразмерных координатах при ψ → 0 поверхность зерна стремится к сфере единичного радиуса, а при ψ → ∞ принимает форму правильного октаэдра, вершины которого находятся на координатных осях на единичном расстоянии от начала координат. В размерных координатах в зависимости от соотношения параметров a, b и с зерно может принимать формы, похожие на эллипсоиды, диски или “сигары”. При больших значениях параметра Тиле степень использования зерна несферической и сферической форм описываются одной зависимостью, равной 3/ψ.

Ключевые слова: несферическое зерно катализатора, реакция первого порядка, эквивалентный размер зерна, степень использования катализатора

ВВЕДЕНИЕ

При исследовании влияния внутридиффузионного сопротивления на химический процесс в зерне катализатора, как правило, рассматривают следующую задачу.

Снаружи на поверхности зерна поддерживается постоянная концентрация C₀. Внутри зерна реагент участвует в двух процессах – химической реакции и массопереносе, который подчиняется закону Фика. Для необратимой реакции первого порядка А → В процесс в зерне в рамках квазигомогенной модели описывается следующим уравнением [1]:

(1)

$D{{\Delta }}C = kC,~$

где D – эффективный коэффициент диффузии; Δ – оператор Лапласа; C – концентрация реагента внутри зерна; k – константа скорости реакции. Граничное условие записывается в виде

${{\left. C \right|}_{\Gamma }} = \,\,~{{C}_{0}},$

где Г – внешняя граница зерна.

Для данной задачи аналитическое решение получено только для нескольких случаев, обладающих одним из видов симметрии. Это плоское, цилиндрическое и сферическое зерна. Для них выражение для концентрации реагента внутри зерна в безразмерных координатах имеют вид [2]

$\bar {с} = \frac{{{\text{ch}}\left( {{{\psi }}\bar {x}} \right)}}{{{\text{ch}}\left( {{\psi }} \right)}}~~~\left( {{\text{плоское\;зерно}}} \right),$

$~~\bar {с} = \frac{{{{I}_{0}}\left( {{{\psi }}\bar {r}} \right)}}{{{{I}_{0}}\left( {{\psi }} \right)}}~~~\left( {{\text{цилиндрическое\;зерно}}} \right),$

$~~\bar {с} = \frac{{{\text{sh}}\left( {{{\psi }}\bar {R}} \right)}}{{\bar {R}{\text{sh}}\left( {{\psi }} \right)}}~~~\left( {{\text{сферическое\;зерно}}} \right),$

где $\bar {c}$ – безразмерная концентрация, $\bar {c} = {C \mathord{\left/ {\vphantom {C {{{C}_{0}}}}} \right. \kern-0em} {{{C}_{0}}}}$; $\bar {x}$ – безразмерная декартова координата, $\bar {x} = {x \mathord{\left/ {\vphantom {x {{{x}_{0}}}}} \right. \kern-0em} {{{x}_{0}}}}$; x₀ – полуширина плоского зерна; $\bar {r}$ – безразмерный радиус в цилиндрической системе координат, $\bar {r} = {r \mathord{\left/ {\vphantom {r {{{r}_{0}}}}} \right. \kern-0em} {{{r}_{0}}}}$; r₀ – радиус цилиндрического зерна; $\bar {R}$ – безразмерный радиус в сферической системе координат, $\bar {R} = {R \mathord{\left/ {\vphantom {R {{{R}_{0}}}}} \right. \kern-0em} {{{R}_{0}}}}$; R₀ – радиус сферического зерна; ch и sh – гиперболические косинус и синус; I₀ – модифицированная функция Бесселя нулевого порядка; ψ – параметр Тиле, ${{\psi }} = {{x}_{0}}\sqrt {\frac{k}{D}} = {{r}_{0}}\sqrt {\frac{k}{D}} = {{R}_{0}}\sqrt {\frac{k}{D}} $.

Степень использования зерна η рассчитывается по следующим зависимостям [2]:

${{\eta }} = \frac{{{\text{th}}\left( {{\psi }} \right)}}{{{\psi }}}~\,\,\left( {{\text{плоское\;зерно}}} \right),$

$~{{\eta }} = \frac{2}{{{\psi }}}\frac{{{{I}_{1}}\left( {{\psi }} \right)}}{{{{I}_{0}}\left( {{\psi }} \right)}}~\,\,~\left( {{\text{цилиндрическое\;зерно}}} \right),$

${{\eta }} = \frac{3}{{{\psi }}}\left( {\frac{1}{{{\text{th}}\left( {{\psi }} \right)}} - \frac{1}{{{\psi }}}} \right)~~\left( {{\text{сферическое\;зерно}}} \right),$

где th – гиперболический тангенс, I₁ – модифицированная функция Бесселя первого порядка.

При фиксированном значении параметра Тиле наибольшим значением η характеризуется сферическое зерно, далее следует цилиндрическое, а затем плоское [2].

Чтобы описать зависимость η(ψ) для вышеуказанных зерен некоторой универсальной формулой, Aris R. [3] предложил в расчетах использовать эквивалентный размер зерна R_e, определяемый по следующей формуле:

(2)

${{R}_{e}} = \frac{V}{S}~,$

где V – объем зерна, S – внешняя поверхность зерна.

Согласно (2) для сферического зерна эквивалентный размер зерна равен R₀/3, для цилиндрического – r₀/2, для плоского зерна – совпадает с его полушириной x₀. Если рассчитывать параметр Тиле по эквивалентному размеру зерна, то зависимости η(ψ) для цилиндрического и сферического зерен ложатся на кривые, близкие к кривой для плоского зерна [3]. Расположение кривых становится обратным: сверху находится кривая для плоского зерна, под ней – кривая для цилиндрического зерна и ниже ‑ кривая для сферического зерна. Кривые совпадают в точке ψ → 0 и имеют одинаковое асимптотическое поведение η → 1/ψ при ψ → ∞, характерное для плоского зерна. Максимальное отклонение кривой для сферического зерна от кривой для плоского зерна составляет 16% в точке ψ = 1.6.

Зависимость (2) предлагается применять на практике и для зерен произвольной формы [2]. Действительно, если рассмотреть случай больших значений параметра Тиле, то каждый достаточно малый участок поверхности зерна эквивалентен поверхности плоского полубесконечного зерна (катализатор расположен в полупространстве х > 0), и удельный поток реагента на границе зерна равен

$j = \sqrt {kD} {{C}_{0}}.$

Степень использования зерна будет

${{\eta }} = \frac{{Sj}}{{Vk{{C}_{0}}}} = \frac{{S\sqrt {kD} {{C}_{0}}}}{{Vk{{C}_{0}}}} = \frac{1}{{\frac{V}{S}\sqrt {\frac{k}{D}} }} = \frac{1}{{{{R}_{e}}\sqrt {\frac{k}{D}} }} = \frac{1}{{{\psi }}}.$

Таким образом, при определении параметра Тиле через эквивалентный размер (2) при больших значениях ${{\psi }}$ степень использования зерна произвольной формы совпадает с зависимостью для плоского зерна.

Тем не менее расчет степени использования зерна произвольной формы на основе эквивалентного размера и зависимости η(ψ) для плоского зерна при конечных значениях параметра Тиле является приближенным. Поэтому представляют ценность точные решения для других трехмерных зерен, отличных от сферы. На основе этих решений можно получить дополнительную информацию о точности расчетов с применением эквивалентного размера зерна.

Цель настоящей работы – на основе точного решения для зерна с тремя характерными размерами a, b и c (по x, y и z) предложить зависимости для вычисления эквивалентного размера и степени использования зерна. Особенностью данного решения является универсальность, позволяющая, меняя соотношение параметров, описывать трехмерные зерна, похожие по форме на эллипсоиды, диски или “сигары”.

ПОСТРОЕНИЕ РЕШЕНИЯ

Уравнение (1) в декартовых координатах имеет вид

(3)

$D\left( {\frac{{{{\partial }^{2}}C}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}C}}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{2}}C}}{{\partial {{z}^{2}}}}} \right) = kC.$

Примем, что геометрия зерна характеризуется тремя параметрами a, b и c (по x, y и z) и крайние точки зерна имеют следующие координаты: (±a, 0, 0), (0, ±b, 0) и (0, 0, ±c).

В крайних точках, т.к. они принадлежат границе зерна, выполняются соотношения

(4)

$C\left( { \pm a,0,0} \right) = C\left( {0, \pm b,0} \right) = C\left( {0,0, \pm c} \right) = {{C}_{0}}.~$

Будем искать решение в виде

$C\left( {x,y,z} \right) = X\left( x \right)Y\left( y \right)Z\left( x \right).$

После подстановки в уравнение (3) получим

(5)

$\frac{1}{X}\frac{{{{{\text{d}}}^{2}}X}}{{{\text{d}}{{x}^{2}}}} + \frac{1}{Y}\frac{{{{{\text{d}}}^{2}}Y}}{{{\text{d}}{{y}^{2}}}} + \frac{1}{Z}\frac{{{{{\text{d}}}^{2}}Z}}{{{\text{d}}{{z}^{2}}}} = \frac{k}{D}.~$

Учитывая независимость переменных x, y и z, уравнение (5) распадается на три независимые уравнения

(6)

$\frac{1}{X}\frac{{{{{\text{d}}}^{2}}X}}{{{\text{d}}{{x}^{2}}}} = k_{x}^{2},\,\,\,\,~~\frac{1}{Y}\frac{{{{{\text{d}}}^{2}}Y}}{{{\text{d}}{{y}^{2}}}} = ~\,\,k_{y}^{2},~\,\,\,\,~~\frac{1}{Z}\frac{{{{{\text{d}}}^{2}}Z}}{{{\text{d}}{{z}^{2}}}} = ~\,\,k_{z}^{2},$

где k_x, k_y и k_z – константы, удовлетворяющие уравнению

(7)

$k_{x}^{2} + k_{y}^{2} + k_{z}^{2} = \frac{k}{D}.$

Решением каждого из уравнений (6) является суперпозиция гиперболических синуса и косинуса. Но, учитывая симметричность граничных условий, каждое решение должно быть четной функцией и представляет косинус гиперболический. В результате общее решение для C(x, y, z) будет:

(8)

$C\left( {x,y,z} \right) = B~{\text{ch}}\left( {{{k}_{x}}x} \right){\text{ch}}\left( {{{k}_{y}}y} \right){\text{ch}}\left( {{{k}_{z}}z} \right),~$

где B – неопределенная константа.

Подставляя (8) в граничные условия (4), получим

(9)

$B~{\text{ch}}\left( {{{k}_{x}}a} \right) = B~{\text{ch}}\left( {{{k}_{y}}b} \right) = B~{\text{ch}}\left( {{{k}_{z}}c} \right) = {{C}_{0}}.~$

Из (9) следует

(10)

${{k}_{x}}a = {{k}_{y}}b = {{k}_{z}}c = \psi ,~\,\,\,\,~B = \frac{{{{C}_{0}}}}{{{\text{ch}}\left( \psi \right)}},~$

где ψ – пока неопределенная константа, но, как будет показано ниже, она имеет смысл параметра Тиле.

Учитывая (10), решение (8) примет вид

(11)

$C\left( {x,y,z} \right) = \frac{{{{C}_{0}}~{\text{ch}}\left( {{{\psi }}\frac{x}{a}} \right){\text{ch}}\left( {{{\psi }}\frac{y}{b}} \right){\text{ch}}\left( {{{\psi }}\frac{z}{c}} \right)}}{{{\text{ch}}\left( {{\psi }} \right)}}.~~$

В безразмерных переменных зависимость (11) будет

(12)

$\bar {с}\left( {\bar {x},~\bar {y},\bar {z}} \right) = \frac{{{\text{ch}}\left( {{{\psi }}\bar {x}} \right){\text{ch}}\left( {{{\psi }}\bar {y}} \right){\text{ch}}\left( {{{\psi }}\bar {z}} \right)}}{{{\text{ch}}\left( {{\psi }} \right)}},$

где $\bar {x}$ = x/a, $\bar {y}$ = y/b, $\bar {z}$ = z/c.

Можно заметить, что на осях зерна зависимость концентрации от продольной координаты совпадает с зависимостью для плоского зерна.

Из уравнения (7), используя (10), следуют зависимости

$\frac{{{{{{\psi }}}^{2}}}}{{{{a}^{2}}}} + \frac{{{{{{\psi }}}^{2}}}}{{{{b}^{2}}}} + \frac{{{{{{\psi }}}^{2}}}}{{{{c}^{2}}}} = \frac{k}{D},~~$

${{\psi }} = L\sqrt {\frac{k}{D}{\kern 1pt} {\kern 1pt} } ,$

где L – характерный размер зерна, рассчитываемый по формуле

(13)

$\frac{1}{L} = \sqrt {\frac{1}{{{{a}^{2}}}} + \frac{1}{{{{b}^{2}}}} + \frac{1}{{{{c}^{2}}}}} .~$

Для частных случаев характерный размер зерна будет

$a = {{x}_{0}},\,\,\,\,~b \gg {{x}_{0}},~\,\,\,\,~c \gg {{x}_{0}},~\,\,\,~L = \,\,~{{x}_{0}},$

$a = b = {{r}_{0}},~\,\,\,\,~c \gg {{r}_{0}},~\,\,\,\,~L = \,\,~\frac{{{{r}_{0}}}}{{\sqrt 2 }},$

$a = b = c = {{R}_{0}},~~L = ~\frac{{{{R}_{0}}}}{{\sqrt 3 }}.$

Первый случай соответствует диску, второй – “сигаре” и третий – деформированной сфере.

Если зафиксировать параметр L, то соотношение (13) дает уравнение поверхности в координатах a, b, c, каждая точка которой соответствует зерну с характерным размером L и одним и тем же параметром Тиле. Например, зерно может быть “равносторонним” (a = b = c) или вытянутым по координате z, но при этом уменьшенным по координатам x и y.

Форма зерна в безразмерных переменных определяется уравнением

(14)

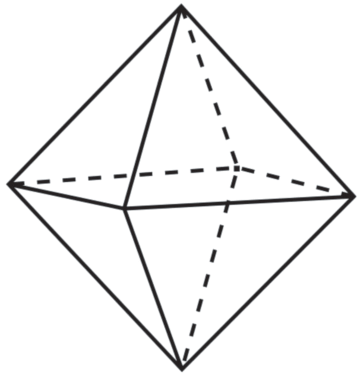
Следует отметить, что форма зерна зависит от параметра Тиле. Можно показать, что при ψ → 0 поверхность зерна в безразмерных переменных стремится к сфере единичного радиуса (${{\bar {x}}^{2}} + {{\bar {y}}^{2}} + {{\bar {z}}^{2}} = 1$), а при ψ → ∞ принимает форму правильного октаэдра, вершины которого находятся на координатных осях на единичном расстоянии от начала координат ($\left| {\bar {x}} \right| + \left| {\bar {y}} \right| + \left| {\bar {z}} \right| = 1$). На рис. 1 изображен правильный октаэдр.

Рис. 1.

Правильный октаэдр.

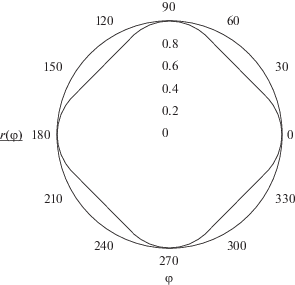
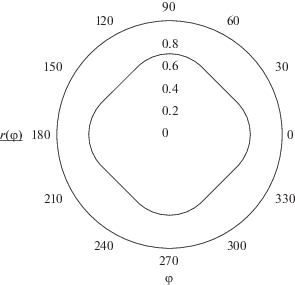
При конечных значениях параметра Тиле зерно представляет собой сферу, деформированную в направлении нормалей к граням октаэдра и пересекающую оси на единичном расстоянии от начала координат. На рис. 2 и 3 в качестве примера показаны при ψ = 3 сечения зерна в цилиндрических координатах при $\bar {z} = 0$ и $\bar {z} = 0.5$.

Рис. 2.

Сечение зерна при ψ = 3 и $\bar {z} = 0$.

Рис. 3.

Сечение зерна при ψ = 3 и $\bar {z} = 0.5~$.

При переходе к размерным переменным форма зерна получается путем растяжения безразмерного зерна до крайних точек зерна с координатами (±a, 0, 0), (0, ±b, 0) и (0, 0, ±c). При этом, в зависимости от соотношения параметров a, b и c, могут получаться различные тела – деформированные шары, диски, “сигары” и фигуры, похожие на эллипсоиды.

СТЕПЕНЬ ИСПОЛЬЗОВАНИЯ ЗЕРНА

Степень использования зерна в размерных переменных рассчитывается по формуле

${{\eta }} = \frac{1}{{k{{C}_{0}}V}}\int {kCdV} ,$

где интеграл берется по объему зерна. В безразмерных переменных интеграл преобразуется к виду

(15)

$\eta = \frac{1}{{\bar {V}}}\int {\bar {c}d\bar {V}} ,~$

где $\bar {V}$ – объем зерна в безразмерных переменных, а интеграл вычисляется по объему зерна в этих же переменных.

Из формулы (15) следует, что степень использования зерна зависит только от параметра Тиле.

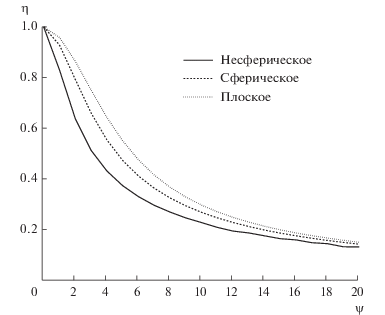
Поскольку аналитически вычислить интеграл (15) ввиду сложной поверхности зерна не представляется возможным, он был рассчитан численно с учетом выражения для $\bar {c}(\bar {x},\bar {y},\bar {z})$ (12) и формы зерна (14). На рис. 4 сплошной линией представлена полученная зависимость η(ψ).

Рис. 4.

Зависимость степени использования зерна от параметра Тиле для несферического, сферического и плоского зерен.

Асимптотическое поведение степени использования зерна при больших ψ можно получить, рассматривая “равностороннее” зерно с a = b = = c = R₀. Согласно (3), $L = \,\,~\frac{{{{R}_{0}}}}{{\sqrt 3 }}$, ${{\psi }} = \,\,~\frac{{{{R}_{0}}}}{{\sqrt 3 }}\sqrt {\frac{k}{D}} $. При больших ψ зерно имеет форму правильного тетраэдра с расстоянием от начала координат до вершин R₀. Можно показать, отношение V/S для этой фигуры составляет $\frac{{{{R}_{0}}}}{{3\sqrt 3 }}$. Степень использования зерна будет

${{\eta }} = \frac{1}{{\frac{V}{S}\sqrt {\frac{k}{D}} }} = \frac{1}{{\frac{{{{R}_{0}}}}{{3\sqrt 3 }}{\text{\;}}\sqrt {\frac{k}{D}} }} = \frac{3}{{{\psi }}}.$

Таким образом, асимптотическая зависимость степени использования зерна от параметра Тиле для несферического и сферического зерен совпадают. На рис. 4 пунктирной линией показана зависимости η(ψ) для сферического зерна.

Интересно сравнить также зависимости η(ψ) для несферического и плоского зерен. Если выбрать для плоского зерна в качестве характерного размера 3х₀, то зависимость η(ψ) будет выглядеть следующим образом

${{\eta }} = \frac{3}{{{\psi }}}{\text{th}}\left( {\frac{{{\psi }}}{3}} \right).$

Асимптотическое поведение η(ψ) при ψ → ∞ в этом случае для плоского зерна будет такое же, как для сферического. На рис. 4 верхняя штриховая линия соответствует плоскому зерну.

Кривые на рис. 4 дают представление о погрешностях определения степени использования несферического зерна, если ее рассчитывать на основе зависимостей для сферического или плоского зерен. В первом случае максимальное отклонение составляет 29% при ψ = 3.1, во втором – 49% при ψ = 4.1. Причем эти зависимости дают завышенное значение η.

Применение эквивалентного размера (2) для несферического зерна, исследованного в данной работе, не упрощает задачу, т.к. форма зерна и, соответственно, эквивалентный размер зависят от параметра Тиле. С практической точки зрения формы реальных зерен могут быть близкими к формам несферического зерна и поэтому полученные зависимости могут быть полезны для расчета степени их использования.

ЗАКЛЮЧЕНИЕ

В настоящей работе рассмотрена задача о трехмерном зерне катализатора с тремя характерными размерами a, b и с при наличии внутридиффузионного сопротивления и реакции первого порядка. На основе точного решения в декартовой системе координат предложены зависимости для расчета характерного размера зерна и степени его использования от параметра Тиле ψ. Особенностью решения является зависимость формы зерна от параметра Тиле. В безразмерных координатах при ψ → 0 поверхность зерна стремится к сфере единичного радиуса, а при ψ → ∞ принимает форму правильного октаэдра, вершины которого находятся на координатных осях на единичном расстоянии от начала координат. При конечных значениях параметра Тиле зерно представляет собой деформированную сферу, пересекающую оси на единичном расстоянии от начала координат. В размерных координатах в зависимости от соотношения параметров a, b и с зерно может принимать формы, похожие на эллипсоиды, диски или “сигары”. При больших значениях параметра Тиле зависимости η(ψ) для несферического и сферического зерен описываются одной зависимостью, равной 3/ψ. Найдена максимальная погрешность определения степени использования несферического зерна, если ее рассчитывать на основе зависимостей η(ψ) для сферического и плоского зерен.

Список литературы

Малиновская О.А., Бесков И.С., Слинько М.Г. Моделирование каталитических процессов на пористых зернах. Новосибирск: Наука, 1975. 266 с.
Арис Р. Анализ процессов в химических реакторах. Ленинград, Химия, Ленингр. отд-ние, 1967. 328 с. (Aris R. Introduction to the Analysis of Chemical Reactors, Prentice-Hall, Englewood Cliffs, N.J., 1965. 337 p.)
Aris R. // Chem. Eng. Sci. 1957. V. 6. P. 262.

Дополнительные материалы отсутствуют.

Инструменты

предыдущая статья выпуска содержание выпуска

Кинетика и катализ

Архивы выпусков Информация о журнале Отправить рукопись в журнал