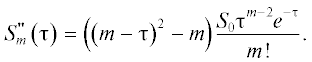Кинетика и катализ, 2021, T. 62, № 5, стр. 509-517
Идентификация механизмов линейных необратимых последовательных реакций
А. В. Луковенков a, *, В. И. Быков a, b, С. Д. Варфоломеев a, b, c
a ФГБУН Институт биохимической физики им. Н.М. Эмануэля РАН
119334 Москва, ул. Косыгина, 4, Россия
b ФГБОУ ВО Московский государственный университет им. М.В. Ломоносова (МГУ),
Институт физико-химических основ функционирования сетей нейронов и искусственного интеллекта
119192 Москва, Ломоносовский просп., 27, корп. 1, офисы Е801-Е804, А818, Россия
c ФГБОУ ВО Московский государственный университет им. М.В. Ломоносова (МГУ), Химический факультет, кафедра химической энзимологии
119192 Москва, ул. Колмогорова, 1, стр. 11б, Россия
* E-mail: luks.mipt@gmail.com
Поступила в редакцию 15.03.2021
После доработки 04.06.2021
Принята к публикации 04.06.2021
Аннотация
В работе показано, как анализ ограниченных кинетических данных (отдельных кинетических кривых или даже их частей) для системы последовательных реакций, рассмотренной при близких значениях констант скоростей отдельных стадий, позволяет получить представление о механизме реакции, в частности, о номере стадии, где находится вещество, кинетическая кривая которого построена. Предложенный авторами метод дает правдоподобные результаты при анализе известных кинетических кривых окисления углеводородов.
ВВЕДЕНИЕ
В химической кинетике, в том числе в биокинетике, особый интерес представляют методы исследования, позволяющие не только количественно описать протекающий процесс, но и выявить его качественные характеристики. В частности, анализ кинетических закономерностей может помочь оценить число стадий процесса и сделать разумные предположения о промежуточных продуктах, возникающих на этих стадиях. Современный этап развития этого направления начался с работ Манфреда Эйгена (M. Eigen) [1, 2].
К настоящему времени, в первую очередь благодаря развитию вычислительных методов квантовой механики и молекулярной динамики, становится возможным точно устанавливать структуру и роль промежуточных веществ в протекании цельного процесса (даже для сложных ферментативных реакций [3, 4]). Однако предварительные соображения о последовательности превращений и виде промежуточных субстратов нередко возникают из кинетических данных [5, 6], когда анализ экспериментально полученных кинетических кривых и знание исходных и конечных веществ для процесса помогают описать его целиком и правильно поставить задачи для дальнейшего исследования его отдельных стадий, например, методами квантовой химии.
В свою очередь, углубленный кинетический анализ может способствовать уточнению устоявшейся практики. Скажем, детальное отражение в кинетике механизма многостадийной реакции (полимеразной цепной реакции) дает возможность лучше управлять протеканием реального процесса [7].
Поэтому, несмотря на значительное число работ, в том числе обобщающего характера [8], интерес к поиску новых кинетических особенностей, позволяющих качественно охарактеризовать протекающий процесс, не ослабевает [9, 10].
В настоящей работе рассмотрен частный, но важный случай последовательной схемы превращений субстрата в продукт по линейному закону, минуя ряд промежуточных необратимых стадий. Анализ показывает, что при близости констант скорости реакции на каждой стадии изменение концентрации промежуточных субстратов описывается показательно-степенной функцией. При этом показатель степени однозначно определяется позицией соответствующего субстрата в цепи превращений. Это позволяет в отсутствие полной информации о соединениях-участниках процесса установить некоторые из них и указать их место в процессе.
Далее будем считать, что в реакторе идеального смешения проходит цепь последовательных реакций (стадий):
где Si (i = 0, …, n) – начальный и промежуточные субстраты с концентрациями Si, а P есть конечный продукт, концентрация которого P. Каждая стрелка в схеме есть реакция первого порядка с константой скорости ki. Тогда последовательности реакций соответствует система кинетических уравнений:(1)
$\left\{ \begin{gathered} \frac{{{\text{d}}{{S}_{0}}}}{{{\text{d}}t}} = - {{k}_{0}}{{S}_{0}} \hfill \\ \frac{{{\text{d}}{{S}_{1}}}}{{{\text{d}}t}} = {{k}_{0}}{{S}_{0}} - {{k}_{1}}{{S}_{1}} \hfill \\ \ldots \hfill \\ \frac{{{\text{d}}{{S}_{n}}}}{{{\text{d}}t}} = {{k}_{{n - 1}}}{{S}_{{n - 1}}} - {{k}_{n}}{{S}_{n}} \hfill \\ \frac{{{\text{d}}P}}{{{\text{d}}t}} = {{k}_{n}}{{S}_{n}}. \hfill \\ \end{gathered} \right.$Для реакций в живых системах кажется более правильным рассматривать каждую стрелку как ферментативное превращение по закону Михаэлиса–Ментен:
Таким образом, как в чисто химических, так и в части биохимических систем можно считать, что кинетика многостадийного процесса моделируется системой (1) из n + 1 обыкновенного линейного дифференциального уравнения, которую мы изучим при начальных условиях S0(0) = S и Si(0) = 0 при i = 1, …, n (в начале реакции был только первый субстрат и не было остальных). Последнее уравнение мы не учитываем, если останавливаем внимание на промежуточных субстратах, а не интересуемся специально образованием конечного продукта P.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ. РЕШЕНИЕ МОДЕЛЬНОЙ СИСТЕМЫ И ЕГО АНАЛИЗ
Совокупность системы (1) с вышеуказанными начальными условиями образует классическую задачу Коши. Для ее решения матрицу системы запишем в виде
(2)
$\left| {A - {{\lambda }}E} \right| = \left| {\begin{array}{*{20}{c}} { - {{k}_{0}} - {{\lambda }}}&0&0& \ldots &0&0 \\ {{{k}_{0}}}&{ - {{k}_{1}} - {{\lambda }}}&0& \ldots &0&0 \\ 0&{{{k}_{1}}}&{ - {{k}_{2}} - {{\lambda }}}& \ldots &0&0 \\ \ldots & \ldots & \ldots & \ldots & \ldots & \ldots \\ 0&0&0& \ldots &{{{k}_{{n - 1}}}}&{ - {{k}_{n}} - {{\lambda }}} \end{array}} \right| = {{\left( { - 1} \right)}^{{n + 1}}}\mathop \prod \limits_{i~{\text{ = 0}}}^n \left( {{{k}_{i}} + {{\lambda }}} \right) = 0.$Для случая, когда все собственные числа в уравнении (2) различны, существует общее решение, найденное, например, в работе [12] методами операционного исчисления. Притом в [12] рассмотрен как вариант, где изначально присутствует только субстрат (обозначаемый нами как S0), так и случай произвольного состава исходной смеси. Однако предложенное аналитическое решение весьма громоздко (что отмечается в работах других авторов, например, [13]). Делать на его основе качественные оценки поведения системы не представляется возможным.
Случай, когда среди значений ki есть одинаковые, приводит к тому, что число линейно независимых собственных векторов системы оказывается меньше числа уравнений в ней. Тогда приходится дополнять базис присоединенными векторами. Если не все константы скорости одинаковы, то упомянутые неудобства полного аналитического решения сохраняются. Но можно предположить, что все константы скорости отдельных стадий близки друг к другу (и, в идеале, равны: ki = k). Тогда, сделав замену τ = kt (т.е. изменив масштаб времени так, чтобы все константы скорости равнялись единице), перепишем систему в виде:
(3)
$\left\{ \begin{gathered} \frac{{{\text{d}}{{S}_{0}}}}{{{\text{d}}\tau }} = - {{S}_{0}} \hfill \\ \frac{{{\text{d}}{{S}_{1}}}}{{{\text{d}}\tau }} = {{S}_{0}} - {{S}_{1}} \hfill \\ \ldots \hfill \\ \frac{{{\text{d}}{{S}_{n}}}}{{{\text{d}}\tau }} = {{S}_{{n - 1}}} - {{S}_{n}} \hfill \\ \frac{{{\text{d}}P}}{{{\text{d}}\tau }} = {{S}_{n}}. \hfill \\ \end{gathered} \right.$Отбросим последнее уравнение и запишем характеристическое уравнение для оставшейся системы:
(4)
${{S}_{m}}\left( {{\tau }} \right) = \frac{{{{S}_{0}}{{{{\tau }}}^{m}}{{e}^{{ - {{\tau }}}}}}}{{m!}},\,\,\,\,m = 0,...,n.$Вычислив производную от (4) как
(5)
$S_{m}^{'}\left( {{\tau }} \right) = \left( {m - {{\tau }}} \right)\frac{{{{S}_{0}}{{{{\tau }}}^{{m - 1}}}{{e}^{{ - {{\tau }}}}}}}{{m!}},$получаем, что при переходе через τmax= m производная от Sm(τ) меняет знак с положительного на отрицательный, т.е. если все константы скорости равны, то в естественных единицах времени τ для m = 2, …, n момент τ = m соответствует максимуму концентрации m-го субстрата. Она равна
(6)
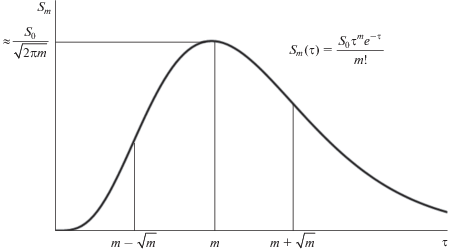
${{S}_{m}}\left( m \right) = \frac{{{{S}_{0}}{{m}^{m}}{{e}^{m}}}}{{m!}} \sim \frac{{{{S}_{0}}}}{{\sqrt {2{{\pi }}m} }} = {{\chi }}\left( m \right)$Приравнивая нулю получившееся в скобках квадратичное выражение, найдем, что точки перегиба графика имеют абсциссы τ1, 2 = m ± $\sqrt m .$ Примерный вид графика представлен на рис. 1.
Из формул τ1 = m – $\sqrt m $ для абсциссы первой (левой) точки перегиба графика и τmax = m для момента, когда концентрация продукта максимальна, получим, что у первого промежуточного субстрата перегиб происходит сразу (в начале координат). Для второго и третьего промежуточных субстратов график сначала обращен выпуклостью вниз, но первая точка перегиба лежит ближе к началу координат, нежели к точке максимума. Для четвертого субстрата первая точка перегиба находится ровно посередине между началом координат и максимумом: 4 – $\sqrt 4 $ = 2. У пятого и последующих субстратов перегиб расположен ближе к максимуму, чем к началу координат, причем чем больше номер субстрата в цепи, тем ближе точки максимума и перегиба. Эти соображения позволяют уже при беглом взгляде на кинетическую кривую оценить, какому субстрату она соответствует.
Для конечного продукта P скорость роста концентрации находится из закона сохранения массы, получаемого сложением всех уравнений системы (1), включая последнее:
(8)
$P\left( {{\tau }} \right) = {{S}_{0}}\left( {1 - {{e}^{{ - {{\tau }}}}}\mathop \sum \limits_{i = 0}^n \left( {\frac{{{{{{\tau }}}^{i}}}}{{i!}}} \right)} \right).$Рассматривая зависимость (8) при росте числа промежуточных стадий (n → ∞), заметим, что в этом случае n сумма ряда, который умножается в формуле на e–τ, стремится к eτ. Следовательно, при n → ∞ концентрация продукта в любой момент времени стремится к нулю. Это и очевидно — в бесконечной цепи промежуточных субстратов до конечного продукта дело никогда не дойдет.
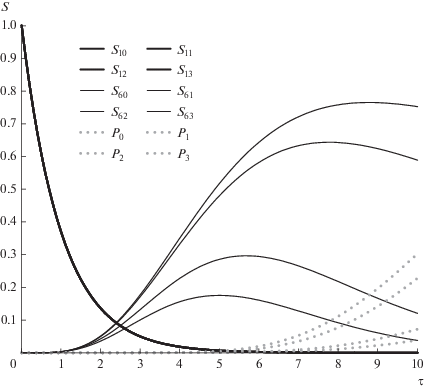
На рис. 2 представлены результаты численного расчета изменения концентраций субстратов и конечного продукта для n = 11 и S0 = 1 (13 веществ: от начального субстрата S0 через 11 промежуточных до продукта P) при условии равенства всех констант скорости. Расчеты сделаны в открытой математической среде SciLab 6.0.1. На рис. 3, где показаны графики зависимости концентраций промежуточных субстратов для той же системы (взятых через один, дабы графики не заслоняли друг друга), видно, что точки максимума промежуточных субстратов отсчитывают единицы времени: для первого промежуточного субстрата максимум лежит в точке τ = 1, для второго — в точке τ = 2 и т.д. Сами же максимумы лежат на кривой, приближающейся с ростом числа стадий к зависимости χ(τ) из формулы (6). Таким образом, рассматриваемая цепочка реакций есть своего рода химические часы, у которых максимумы концентрации каждого субстрата соответствуют определенным равноотстоящим моментам времени.
Рис. 2.
Изменение концентраций исходного (жирная черная линия), промежуточных (тонкие серые линии, показаны не все) субстратов и продукта (жирная серая линия) реакции для 13 стадий.
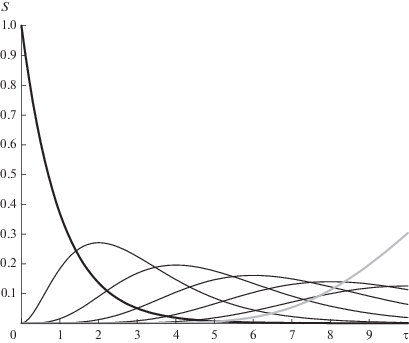
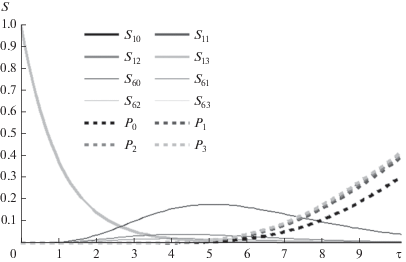
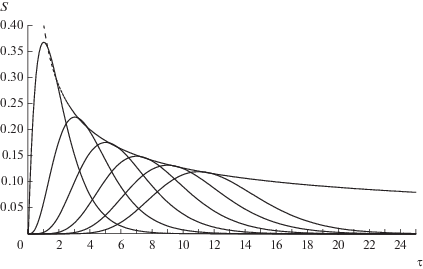
Рис. 3.
Концентрации промежуточных субстратов (S1, S3, S5, S7, S9, S11 и асимптотика их точек максимума).
Неудобство практического использования “часов” на базе последовательности кинетических кривых связано с тем, что с течением времени происходит уменьшение высоты пика концентрации соответствующего субстрата с одновременным расширением кривой – пик размывается, точное определение максимума для достаточно далеких от начала промежуточных субстратов затруднено. Размытие пика сопряжено со снижением его высоты, связанным с постоянством площади под графиком Sm(τ). Химический смысл этого в том, что в конце концов каждый промежуточный субстрат образуется из всего предыдущего и полностью израсходуется на синтез последующего.
В исследовании кинетики последовательных реакций интерес представляет не только вариант со стадиями равной скорости, но и случай, когда среди констант одинаковы все, кроме одной, которая значительно меньше, или, напротив, значительно больше других. В таком случае возможно и точное аналитическое решение, но численный анализ может проиллюстрировать возникающие эффекты более наглядно. На рис. 4 в упомянутую выше систему внесено изменение: шестая константа больше остальных, соответственно, в 5, 10 и 50 раз (случаи 1, 2 и 3, случай 0 – когда все константы равны). На рис. 5 та же шестая константа меньше в 2, 10 и 20 раз (случаи нумерованы аналогично). Как видно из рис. 4 и 5, на предыдущие стадии замедление последующих не влияет (кинетические кривые субстратов до шестого везде одинаковы). Максимальная концентрация субстрата, для которого константа скорости преобразования в следующий субстрат больше, уменьшается, а концентрация конечного продукта растет быстрее (см. рис. 4). При ускорении одной из стадий до бесконечности ситуация становится такой, как если бы эта стадия отсутствовала совсем.
Напротив, если один из субстратов (тот же шестой) расходуется медленнее, чем остальные, то его максимальная концентрация растет, а концентрация конечного продукта в соответствующие моменты времени оказывается меньше. На стадии, предшествующей медленной, такое замедление не влияет, как и в предыдущем случае. На рис. 5 показано поведение системы, в которой шестая реакция идет медленнее в 2, 10 и 20 раз (случаи 1, 2 и 3 соответственно; случай 0 отвечает варианту, когда все константы равны). Уменьшение до нуля константы скорости одной из стадий приведет к обрыву цепочки реакций на этой стадии, т.е. все последующие промежуточные субстраты и конечный продукт образовываться не будут, что тоже достаточно очевидно.
В изучаемой системе можно также изменять местоположение реакции, которая протекает быстрее или медленнее остальных (на рис. 4 и 5 это стадия S6 → S7). Можно увидеть, что в этом случае все стадии, предшествующие той, на которой скорость реакции отличается, сохранят свою кинетику неизменной, а все последующие стадии будут смещены во времени назад (при наличии медленной стадии) или вперед (при наличии быстрой). Соответственно, максимальная концентрация субстрата повышается, если скорость его расхода снижается (по сравнению с таковой в случае равенства констант), и, напротив, уменьшается, когда он расходуется быстрее прочих.
Качественный и численный анализ кинетической модели для исследованной схемы превращений показывает, что динамика системы (т.е. совокупность зависимостей от времени концентраций промежуточных субстратов) хорошо описывается набором степенно-экспоненциальных функций. При варьировании кинетических параметров ki решения уравнений химической кинетики на стадиях, предшествующих стадии, где параметр имеет иное значение, вовсе не претерпевают изменений, а на последующих стадиях (в т. ч. на кинетике образования продукта) это изменение сказывается. Экстремум кинетической кривой ускоренной или замедленной стадии смещается вдоль оси ординат (замедление стадии увеличивает максимальную концентрацию соответствующего субстрата, ускорение – уменьшает ее). Сдвиг точки экстремума происходит также вдоль оси времени: относительно стандартных экстремумов, определенных номером стадии, экстремум ускоренной стадии сдвигается влево, а замедленной – вправо. Эти наблюдения укладываются и в логику крайних состояний системы: бесконечно быстрая стадия приводит к кинетике с уменьшенным на единицу числом стадий, бесконечно медленная стадия означает окончательное прекращение всех последующих реакций, включая образование продукта.
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Полученные в работе аналитические и численные результаты можно использовать при исследовании конкретных химических и биохимических процессов. В частности, вышеприведенный анализ позволяет на базе одной хорошо построенной (по данным эксперимента) кинетической кривой оценивать порядковый номер в цепи соответствующего ей субстрата и предлагать вид кинетических кривых для всех предшествующих субстратов. Для этого подойдет следующий алгоритм.
1. Сначала с хорошей точностью (8–10 точек) построим кинетическую кривую расходования исходного субстрата S0.
2. Поскольку полученная кинетическая кривая — убывающая экспонента S0(t) = S0e–kt, перестроив ее в логарифмических координатах, найдем k.
3. Умножим на найденное k время достижения максимальной концентрации промежуточного продукта, для которого также построена кинетическая кривая, и округлим результат до ближайшего целого. Получим номер стадии, на которой образуется данный продукт в цепочке превращений.
Иногда в составе экспериментальных данных отсутствует кинетическая кривая расходования исходного субстрата. В этом случае выполнить п. 1 предыдущего алгоритма невозможно. Поможет точное построение начального участка кинетической кривой интересующего нас субстрата. Алгоритм при этом меняется.
1. Построим с хорошей точностью (8–10 точек) начальный участок кинетической кривой интересующего нас субстрата (здесь важно, чтобы на данном участке экпонента мало влияла на поведение графика в выбранных точках).
2. Перестроив вышеуказанную зависимость в двойных логарифмических координатах, найдем m (номер субстрата в цепи) как угловой коэффициент полученной прямой (значение надо округлить вверх до целого, т. к. влияние экспоненты стремится уменьшить искомый угловой коэффициент).
3. Поделим найденное m на время достижения максимальной концентрации промежуточного субстрата и получим константу скорости для последовательности реакций.
Применение нового алгоритма может затрудниться тем, что для субстратов, близких к началу последовательности превращений, влияние экспоненты начинает сказываться почти сразу, и уже на начальном участке форма кинетической кривой в двойных логарифмических координатах отличается от прямой линии. В этом случае может помочь надежное определение положения точки перегиба. Алгоритм здесь следующий.
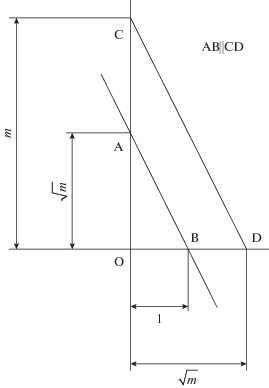
1. Определим длину отрезка оси абсцисс от начала координат до точки максимума (это значение m, но чему оно равно численно – неизвестно, поскольку не задан единичный отрезок).
2. Определим длину отрезка оси абсцисс от точки перегиба до точки максимума (это значение квадратного корня из m).
3. Далее геометрическим построением, используя пропорцию
найдем единичный отрезок как четвертый пропорциональный (см. рис. 6), а затем, сравнивая m с единичным отрезком, находим его числовое значение.4. Деля m на время достижения максимума концентрации, найдем константу скорости.
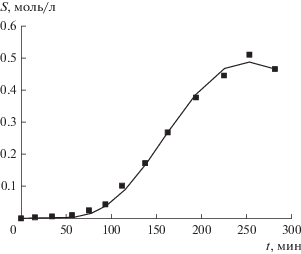
Еще один вариант алгоритма возможен, когда надежно удается определить только положение точки максимума, но не точки перегиба. Для иллюстрации этого варианта возьмем реальные данные о накоплении циклогексанона при окислении циклогексана, приведенные в [14] (с. 88, рис. 33 ). На рис. 7 отмечены экспериментальные точки и полученная по ним расчетная кривая. Алгоритм будет таким.
1. Определим возможно точнее момент достижения максимума концентрации субстрата (ось абсцисс).
2. Зададим разумный диапазон значений m положения интересующего нас субстрата в цепи последовательных превращений (в конкретном случае на рис. 7 использован диапазон 1–10).
3. Рассчитаем для каждого значения m по известному положению точки максимума значение константы скорости реакции k.
4. В уравнение (4) подставим значения k, m и моментов времени, для которых найдены экспериментально значения концентрации субстрата, и будем подбирать параметр S0 (используя, например, функцию подбора параметра в Microsoft Excel или LibreOffice Calc), минимизируя сумму квадратов отклонений расчетных значений от фактических.
5. Вычислив минимальные суммы квадратов отклонений для каждого m отдельно, выберем в качестве верного то, у которого эта сумма минимальна. В конкретном случае (накопление циклогексанона) это m = 7, т.е. циклогексанон является седьмым промежуточным субстратом в цепи окисления циклогексана. Вместе с найденным m определяются k и S0.
ЗАКЛЮЧЕНИЕ. ПЕРСПЕКТИВЫ ДАЛЬНЕЙШЕГО ИССЛЕДОВАНИЯ
Для дальнейшего исследования интерес представляет включение в систему обратимых стадий. В простейшем случае можно допустить, что все стадии процесса обратимы, причем константа kr скорости обратной реакции всюду одинакова и в известное число раз меньше (или больше) константы скорости прямой реакции. Для приложений к биохимии важной является и последовательность реакций, замыкающаяся в цикл (когда конечный продукт P есть одновременно исходный субстрат S0, как, например, в широко известном цикле Кребса). Анализ исходной модели в этих направлениях может послужить темой новой статьи.
Список литературы
Эйген М. Самоорганизация материи и эволюция биологических макромолекул. М.: Мир, 1973. 216 с.
Эйген М., Шустер П. Гиперцикл. Принципы самоорганизации макромолекул. М.: Мир, 1982. 270 с.
Варфоломеев С.Д., Коц Е.Д., Хренова М.Г., Лущекина С.В., Немухин А.В. // Докл. Акад. наук. 2017. Т. 474. № 4. С. 474.
Khrenova M.G., Kots E.D., Varfolomeev S.D., Lushchekina S.V., Nemukhin A.V. // J. Phys. Chem. 2017. V. 121. P. 9389.
Семенова Н.А., Ахадов Т.А., Петряйкин А.В., Сидорин С.С., Луковенков А.В., Варфоломеев С.Д. // Биохимия. 2012. № 77(4). С. 493.
Ублинский М.В., Семенова Н.А., Ахадов Т.А., Мельников И.А., Варфоломеев С.Д. // Изв. Акад. наук. Серия хим. 2015. № 2. С. 453.
Быков В.И., Луковенков А.В., Варфоломеев С.Д. // Докл. Акад. наук. 2017. Т. 474. № 3. С. 370.
Прямые и обратные задачи в химической кинетике. Под редакцией В.И. Быкова. Новосибирск: Наука. Сибирское отделение, 1993. 284 с.
Yablonsky G.S., Branco P.D., Marin G.B., Constales D. // Chem. Eng. Sci. 2019. № 196. P. 384.
Xi Y., Liu X., Constales D., Yablonsky G.S. // Entropy. 2020. № 22. P. 1160.
Gevertz J.L., Dunn S.M., Roth Ch.M. // Biotechnol. Bioeng. 2005. V. 92. № 3. P. 346.
Родигин Н.М., Родигина Э.Н. Последовательные химические реакции. Математический анализ и расчeт. М.: Издательство АН СССР, 1960. 138 с.
Малышев В.П., Турдукоджаева А.М., Кайкенов Д.А. // Докл. Нац. Акад. наук Респ. Казахстан, серия Математика. 2012. № 4. С. 5.
Березин И.В., Денисов Е.Т., Эмануэль Н.М. Окисление циклогексана. М.: Издательство Московского университета, 1962. 303 с.
Дополнительные материалы отсутствуют.
Инструменты
Кинетика и катализ