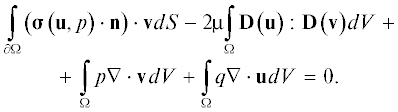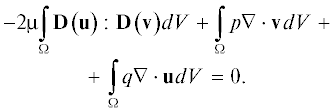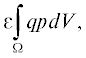Коллоидный журнал, 2019, T. 81, № 1, стр. 42-48

ВВЕДЕНИЕ

На аэрозольные частицы, находящиеся в среде с неоднородным распределением температуры, действуют термофоретические силы, которые вызывают их движение. Находясь на достаточно близком расстоянии друг от друга, частицы могут оказывать существенное влияние на процесс их взаимного движения. В аэрозольных системах, встречающихся на практике, наиболее вероятны сближения пар аэрозольных частиц [1]. Впервые влияние взаимодействия двух частиц на их термофоретическое движение исследовалось в работе [2]. В ней рассматривалось движение двух сферических частиц равного радиуса вдоль линии, проходящей через их центры, с учетом скачков температуры и изотермического скольжения газа на их поверхностях. Этой же задаче, но для частиц разных радиусов, посвящена работа [3]. Отметим, что в настоящее время получены более полные граничные условия, чем использованные в работах [2, 3]. Соответствующая задача с более общими граничными условиями, включающими линейные по числу Кнудсена эффекты, для частиц равных радиусов решена в работе [4]. Движение двух сферических аэрозольных частиц одинакового радиуса с учетом скачков температуры и изотермического скольжения газа на их поверхностях при произвольном направлении заданного вдали от частиц градиента температуры газа и с учетом их вращения рассмотрено в работе [5]. В ней использовался приближенный метод отражений. Точное же аналитическое решение этой задачи методом разделения переменных для крупных частиц, т.е. для частиц, размеры которых много больше средней длины свободного пробега молекул в газе, представлено в работе [6]. В ней же рассмотрено термофоретическое движение двух крупных аэрозольных частиц вдоль линии, проходящей через их центры, с учетом фазового перехода на их поверхности. Термофорез двух жидких крупных капель без учета фазового перехода на их поверхностях исследован в работе [7].

Из приведенного анализа видно, что к настоящему времени достаточно подробно рассмотрено термофоретическое движение двух частиц сферической формы. Вместе с тем, на практике форма частиц может быть произвольной. Поэтому представляет интерес исследование подходов, позволяющих вычислять скорости термофореза двух аэрозольных частиц произвольной формы. В настоящей работе предлагается подход, дающий возможность производить численный анализ подобных задач с помощью метода конечных элементов. При анализе мы ограничимся случаями, когда размеры частиц много больше средней длины свободного пробега молекул в газе, а число Рейнольдса ${\text{Re}} = \frac{{{\mathbf{U}}l}}{\nu }$ и тепловое число Пекле ${\text{Pe}} = \frac{{{\mathbf{U}}l}}{{\chi }}$ можно считать равными нулю. Здесь ${\mathbf{U}}$ – характерная скорость частиц, $l$ – их характерный размер, $\nu $ – кинематическая вязкость газа, ${\chi }$ – его температуропроводность. Движение частиц при этом считается обусловленным наличием заданного на большом расстоянии от частиц градиента температуры газа. Кроме того, будем полагать, что из некоторых дополнительных соображений, например из соображений симметрии, известно, что частицы движутся без вращения.

ПОСТАНОВКА ЗАДАЧИ

При указанных выше ограничениях распределения температур ${{T}_{1}},$ ${{T}_{2}},$ ${{T}_{{\text{e}}}}$ соответственно внутри первой и второй аэрозольных частиц и в их окрестности описываются [8, 9] уравнениями Лапласа

а распределение скоростей u и давления p газа в окрестности частиц – уравнениями Стокса где ${\mu }$ – коэффициент динамической вязкости газа. В системе отсчета, связанной с покоящимся на большом расстоянии от частиц газом, на поверхности первой частицы граничные условия имеют следующий вид [8, 9]:

Здесь ${{{\mathbf{n}}}_{{\text{i}}}}$ – нормаль, направленная от поверхности аэрозольной частицы в ее внутреннюю область, ${\mathbf{\tau }}$ – произвольный единичный тангенциальный вектор, проведенный из рассматриваемой точки поверхности, ${{\kappa }_{{\text{e}}}}$ – коэффициент теплопроводности газа, ${{\kappa }_{{{\text{i}}1}}}$ – коэффициент теплопроводности вещества первой частицы, ${{g}_{1}} = {{{{K}_{{{\text{ts}}1}}}} \mathord{\left/ {\vphantom {{{{K}_{{{\text{ts}}1}}}} {{{T}_{{01}}}}}} \right. \kern-0em} {{{T}_{{01}}}}}\quad{\text{,}}$ ${{K}_{{{\text{ts}}1}}}$ – коэффициент теплового скольжения газа на поверхности первой частицы, $\quad{{T}_{{01}}}$ – средняя температура газа на поверхности частицы,$\quad{{{\mathbf{U}}}_{{{\text{T}}1}}}$ – скорость термофореза первой частицы, которая определяется из условия равенства нулю силы, действующей на частицу со стороны газа. На поверхности второй частицы граничные условия аналогичны:

Здесь ${{\kappa }_{{{\text{i}}2}}}$ – коэффициент теплопроводности вещества второй частицы, ${{{\mathbf{U}}}_{{{\text{T}}2}}}$ – скорость термофореза второй частицы, ${{g}_{2}} = {{{{K}_{{{\text{ts}}2}}}} \mathord{\left/ {\vphantom {{{{K}_{{{\text{ts}}2}}}} {{{T}_{{02}}}{\text{,}}}}} \right. \kern-0em} {{{T}_{{02}}}{\text{,}}}}$ ${{K}_{{{\text{ts}}2}}}$ – коэффициент теплового скольжения газа на поверхности второй частицы, ${{T}_{{02}}}$ – средняя температура газа на поверхности второй частицы. Отметим, что при численных расчетах при равных ${{K}_{{{\text{ts}}1}}}$ и ${{K}_{{{\text{ts}}2}}}$ можно считать равными и величины ${{g}_{1}}$ и ${{g}_{2}},$ т.к. значения $\quad{{T}_{{01}}}$ и $\quad{{T}_{{02}}}$ мало отличаются друг от друга. В методе конечных элементов распределение той или иной величины всегда ищется в некоторой конечной области, и на границе этой области задаются те или иные граничные условия. В нашем случае будем полагать, что на этой границе задано распределение температур. Кроме того, будем полагать, что граница, проходящая в газе, находится от частицы настолько далеко, что с требуемой точностью можно считать, что газ вблизи этой границы неподвижен и его давление является постоянной величиной.

ОБЩАЯ СХЕМА РАСЧЕТА

В методе конечных элементов область, в которой ищется распределение той или иной величины, разбивается на множество подобластей. В результате получается расчетная сетка, на основе которой генерируется набор базисных функций, используемых для аппроксимации искомого распределения. При этом вследствие ошибок округления получаемое распределение флуктуирует около некоторого истинного распределения. При вычислении поверхностных интегралов от функций, содержащих эти распределения, влияние флуктуаций накапливается, и значения таких интегралов могут вычисляться со значительной погрешностью. Это приводит к тому, что даже при достаточно точном вычислении распределения скоростей течения газа рассчитываемые на его основе значения сил, действующих на аэрозольную частицу, могут получаться со значительной погрешностью. Поэтому в данной работе предлагается подход, позволяющий вычислять скорости установившего движения частиц без непосредственного вычисления действующих на них сил.

Представим скорости движения частиц в виде

Здесь ${{{\mathbf{U}}}_{{11}}}$ и ${{{\mathbf{U}}}_{{21}}}$ – соответственно составлющие скорости первой и второй частиц, обусловленные тепловым скольжением газа на поверхности первой частицы. То есть при вычислении этих скоростей вместо условий (6), (7) на поверхности первой частицы используются условия

а на поверхности второй частицы вместо (10), (11) условия

Аналогично ${{{\mathbf{U}}}_{{22}}}$ и ${{{\mathbf{U}}}_{{12}}}$ – соответственно составлющие скорости второй и первой частиц, обусловленные тепловым скольжением газа на поверхности второй частицы. При их вычиcлении вместо условий (6), (7) используются

а вместо (10), (11) условия

Рассмотрим схему расчета величин ${{{\mathbf{U}}}_{{11}}}$ и ${{{\mathbf{U}}}_{{21}}}$. После того как получены распределения температур, удалим подобласть, соответствующую внутренним областям первой частицы, и распределение скоростей в газе будем вычислять уже на основе вновь полученной расчетной сетки. Сам расчет проведем в системе отсчета, связанной с первой частицей. В этой системе отсчета граничные условия (12), (13) принимают вид

Их можно переписать в виде [10]

где ${\mathbf{n}}$ – внешний по отношению к расчетной области вектор нормали к ее границе. На внешней границе расчетной области условие неподвижности газа вблизи границы переходит в условие однородности распределения скорости газа. С учетом постоянства на указанной границе давления, которое при расчете распределения скоростей, не нарушая общности, можно положить равным нулю, это, в свою очередь, приводит к равенству нулю на этой границе компонент тензора вязких напряжений газа (описание тензора см. ниже). Именно это условие и будем использовать в качестве граничного для рассматриваемой границы. При этом мы можем полагать, что получаемая в результате расчетов скорость газа на этой границе равна по модулю и противоположна по направлению ${{{\mathbf{U}}}_{{11}}}$. В свою очередь где ${{{\mathbf{U}}}_{{2{\text{s}}}}}$ – скорость второй частицы относительно первой. Условия (14), (15) при этом переходят в условие равенства на поверхности второй частицы скорости газа скорости частицы ${{{\mathbf{U}}}_{{2{\text{s}}}}}$. Для численного расчета этой скорости будем рассматривать область второй частицы как область, заполненную неким газом, вязкость которого настолько велика, что он движется как единое целое, т.е. как твердая частица. Будем называть этот газ псевдогазом. При таком подходе уравнения (2), (3) применимы как в области газа, так и псевдогаза при условии, что ${\mu }$ – вязкость вещества в рассматриваемой точке, которая может находится как в газе, так и в псевдогазе. При численных расчетах мы просто будем задавать вязкость вещества в области псевдогаза много большей вязкости вещества в области газа. Условие равенства на границе второй частицы скоростей этой частицы и газа будет выполняться автоматически вследствие выполнения на этой границе уравнения непрерывности (3). Получаемая скорость псевдогаза в любой его точке и будет равна ${{{\mathbf{U}}}_{{2{\text{s}}}}}$. Так как течение газа является установившимся, то его импульс не изменяется, что соответствует равенству нулю действующей на вторую частицу силы со стороны газа. С учетом того, что течение газа также установившееся, а на внешних границах, отличных от поверхности первой частицы, заданы условия, которые не изменяют импульс газа, мы приходим к тому, что и первая частица этот импульс не изменяет, а, значит, общая сила взаимодействия первой частицы с газом равна нулю.

Расчет скоростей ${{{\mathbf{U}}}_{{22}}}$ и ${{{\mathbf{U}}}_{{12}}}$ проводится аналогично. Только теперь расчетная сетка будет получаться удалением подобласти, соответствующей внутренним областям второй частицы, расчет будет проводится в системе отсчета, связанной с этой частицей, а область, соотвествующая первой частице, будет рассматриваться как область, заполненная псевдогазом.

РАСЧЕТ СКОРОСТЕЙ ТЕРМОФОРЕЗА АЭРОЗОЛЬНЫХ ЧАСТИЦ С ИСПОЛЬЗОВАНИЕМ СЛАБОЙ ФОРМЫ ПОСТАНОВКИ ЗАДАЧИ

Перейдем теперь к описанию схемы расчета искомых распределений температуры и скоростей с помощью метода конечных элементов. Эта схема близка к описанной в работе [10], поэтому некоторые подробности, которые могут быть найдены в указанной работе будут опущены. В настоящее время имеется ряд компьютерных программ, позволяющих находить численное решение исходной системы дифференциальных уравнений методом конечных элементов по слабой форме представления этой системы. Естественно, что получаемые выражения желательно представить в форме, удобной для применения в используемой программе. В данной работе расчеты проводятся с использованием программы freefem++ [11]. В ней предполагается, что в выражении, описывающем постановку задачи в слабой форме, могут использоваться только производные первого порядка искомых функций от координат. Это связано с тем, что решение ищется в виде разложения в ряд по базисным функциям, которые принадлежат функциональному пространству Соболева первого порядка.

Рассмотрим сначала расчет распределения температуры. Для этого уравнения (1) запишем в виде

Здесь $T$ и ${{\kappa }_{{\text{p}}}}$ – соответственно температура и теплопроводность вещества в рассматриваемой точке, которая может находиться как в газе, так и в той или иной частице. Следуя традиционному подходу [12], умножим правую и левую части (21) на некоторую тестовую гладкую в каждой из подобластей функцию $w$ и применим формулу Грина для каждой из подобластей, полагая, что искомое распределение также описывается внутри каждой подобласти гладкой функцией. В результате, с учетом свойств базисных функций, используемых для экстраполяции искомого распределения, получаем [12]:

где V – объем рассматриваемой области ${\Omega }$, $\partial {\Omega }$ – граница рассматриваемой области, S – ее площадь. Как уже упоминалось выше, распределения искомых величин ищутся в виде разложений в ряд по базисным функциям с неизвестными коэффициентами. Тестовые функции используются для того, чтобы в результате их последовательной подстановки в итоговые выражения получить систему уравнений для расчета этих неизвестных коэффициентов. Согласно традиционному подходу [12], заданное на некоторых участках границы расчетной области распределение искомой величины учитывается непосредственно при формировании системы уравнений, а значение тестовой функции на этих участках полагается равными нулю. Этот подход используется и в программе freefem++ [11]. Поэтому на границах с заданными значениями температур функция w равна нулю, а, значит, подынтегральное выражение в правой части полученного выражения равно нулю. Следовательно, правая часть этого уравнения равна нулю, и итоговая слабая форма принимает вид [10]

Отметим, что использование функционального пространства Соболева для аппроксимации искомого решения автоматически обеспечивает непрерывность распределения температур и, следовательно, выполнение условий (4) и (8). Это, в свою очередь, совместно с (21) обеспечивает выполнение условий (5), (9).

Рассмотрим теперь расчет распределения скоростей. Для получения соответствующей слабой формы задачи о распределении скоростей перейдем от уравнения (2) к уравнению

которое при выполнении условия (3) ему эквивалентно [13]. Здесь ${\mathbf{\sigma }}\left( {{\mathbf{u}},p} \right)$ – тензор вязких напряжений [14]: где ${\mathbf{I}}$ – единичный тензор, а ${\mathbf{D}}\left( {\mathbf{u}} \right)$ – тензор скоростей деформаций,

Умножая уравнения (23) и (3) соответственно на векторную ${\mathbf{v}}$ и скалярную $q$ тестовые функции и интегрируя по рассматриваемой области, после ряда преобразований получаем [14]:

Задавая значения величины ${\mathbf{\sigma }}\left( {{\mathbf{u}},p} \right)$ на части границы расчетной области можно обеспечить единственность решения этого уравнения для поля скоростей, если на оставшейся части границы скорость задана однозначным образом [14]. Интегрирование по участкам, на которых задана скорость, не проводится, т.к. на таких участках, как сказано выше, значение тестовой функции полагается равным нулю. На остальных участках, как указано выше, равны нулю компоненты ${\mathbf{\sigma }}\left( {{\mathbf{u}},p} \right)$. Поэтому первое слагаемое в последней формуле можно опустить, и в результате получаем следующую итоговую слабую форму:

Напомним, что в этой формуле ${\mu }$, u, p, – соответственно, вязкость, скорость и давление газа или псевдогаза в рассматриваемой точке.

РАСЧЕТ СКОРОСТЕЙ ТЕРМОФОРЕЗА СФЕРИЧЕСКОЙ И СФЕРОИДАЛЬНОЙ ЧАСТИЦ

Применим разработанную схему расчета для вычисления скоростей термофореза частиц осесимметричной формы, движущихся вдоль их общей оси симметрии. В качестве конкретного примера рассмотрим движение сферической частицы, которая считалась первой, и сфероидальной, которая считалась второй, вдоль их общей оси симметрии. На большом расстоянии от частиц полагается заданным постоянный градиент ${{\left( {\nabla {{T}_{{\text{e}}}}} \right)}_{\infty }}$ температуры газа, направленный вдоль их оси симметрии. Так как в методе конечных элементов расчет всегда ведется в конечной области, мы будем полагать границы этой области достаточно удаленными от частиц и задание градиента температуры на бесконечности моделировать заданием соответствующего распределения температуры на этой границе. Если искомые распределения осесимметричны, как это имеет место в данном случае, требования к вычислительным ресурсам можно многократно снизить, перейдя к цилиндрическим координатам, и в результате трехмерную задачу свести к двумерной, в которой все распределения зависят только от полярного радиуса r и аппликаты z цилиндрической системы координат. Сведения, необходимые для перехода к цилиндрической системе координат, приведены в [12] и в руководстве к программе freefem++.

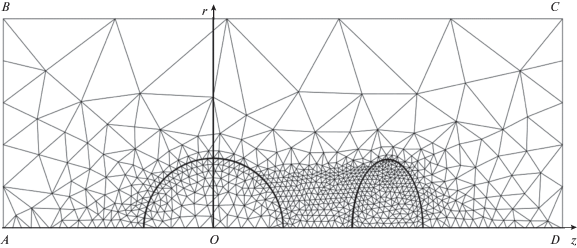
Рассмотрим теперь построение расчетной сетки и процедуру расчета с ее использованием. Для определенности будем полагать, что вторая частица имеет форму сплюснутого сфероида. Структура исходной расчетной области для этого случая показана на рис. 1. Для удобства отображения отдельных элементов соотношения их размеров отличаются от реально используемых. Обозначим через $a$ расстояние от центра второй частицы до ее поверхности вдоль оси $z$, а через $b$ расстояние от центра этой частицы до ее поверхности в направлении, перпендикулярном этой оси. Последнее расстояние бралось и в качестве радиуса первой частицы. При построении расчетной сетки расстояние $b$ было взято за единицу. При $a \leqslant b$ расстояния от центра частицы первой частицы до левой границы расчетной области, от центра второй частицы до правой границы и от оси 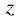до верхней границы полагались равными 25b, а в противном случае эти расстояния полагались равными 25a. Как показали результаты расчетов, дальнейшее увеличение размеров указанной области не приводило к заметному изменению получаемых результатов. Разбиение рассматриваемой области на подобласти производилось при помощи алгоритма Делоне–Вороного [16]. Программа freefem++ проводит такое разбиение автоматически по заданному числу точек на границах. Распределение температур на границе ABCD (рис. 1) расчетной области в газе полагалось равным $\quad{{T}_{{01}}} + z{{\left( {\nabla {{T}_{{\text{e}}}}} \right)}_{\infty }}.$ На границе расчетной области, соответствующей поверхности первой частицы, задается распределение скоростей, описываемое формулой (20), а на границе, соответствующей поверхности второй частицы, аналогичной формулой. Обратим внимание на то, что на границе AOD, совпадающей с осью симметрии, никаких условий в явном виде не задается. Фактически, как следует из вывода выражений (22), (24), это означает наличие неявных граничных условий, означающих непроницаемость этой границы для потоков тепла и течений газа. Вязкость псевдогаза полагалась в 10⁶ раз больше вязкости газа. При таком значении вязкости псевдогаза его скорость в различных точках в пределах той точности, с которой выдает результаты программа freefem++, получалась одинаковой. В результате расчетов находились величины ${{U}_{1}}$ и ${{U}_{2}}$:

Здесь индекс z обозначает проекцию соответствующего вектора на ось z, а ${{{\mathbf{U}}}_{{{\text{TP}}}}}$ – скорость термофореза твердой сферической аэрозольной частицы в неограниченной среде [15],

При расчетах использовались следующие критерии точности [10]:

Здесь ${{\Gamma }_{1}}$ и ${{\Gamma }_{2}}$ – границы, совпадающие с поверхностями соответственно первой и второй частиц, $S$ – длина границы, соответствующей поверхности частицы, ${{{\varepsilon }}_{1}}$ – относительная погрешность вычисления величин ${{{\mathbf{U}}}_{{11}}}$ и ${{{\mathbf{U}}}_{{21}}}$, а ${{{\varepsilon }}_{2}}$ – величин ${{{\mathbf{U}}}_{{22}}}$ и ${{{\mathbf{U}}}_{{12}}}$. Также для контроля точности на различных элементах границы расчетной области варьировалось число точек, на основе которых проводилось разбиение этой области на подобласти. В результате для исходной области число подобластей изменялось от 28 × 10³ до 56 × 10³. Максимально возможное число подобластей определяется размером доступной для расчета оперативной памяти, который в нашем случае составлял четыре гигабайта. Этого объема памяти достаточно для вычисления скоростей частиц с точностью до трех значащих цифр. Время одного расчета с использованием процессора Intel® Core® i3-210 достигало полутора минут. Для аппроксимации искомого распределения температуры использовались базисные функции на основе полиномов Лежандра третьего порядка. Суммарное число степеней свободы пространства конечных элементов для максимального числа подобластей в этом случае достигало 25 × 10⁴. Для аппроксимации поля скорости использовались полиномы Лежандра третьего порядка, а для поля давления – второго. Кроме того, как и в работе [10], к левой части слабой формы (23) добавлялось дополнительное стабилизационное слагаемое [12]

которое фактически является условием равенства нулю среднего значения давления. Здесь ε – малый положительный параметр. Для его подбора можно использовать следующий простой подход: если при уменьшении выбранного значения ε на несколько порядков значение вычисляемой на основе этого алгоритма скорости не изменяется, то выбранное значения ε можно использовать для расчета. В нашем случае это значение принималось равным 10^–10. Во всех случаях для решения получаемых систем уравнений с неизвестными коэффициентами в разложениях по базисным функциям использовался поддерживаемый freefem++ итерационный алгоритм UMFPACK [17].

В таблицах приведены полученные значения величин ${{U}_{1}}$ и ${{U}_{2}}$ для разных значений ${a \mathord{\left/ {\vphantom {a b}} \right. \kern-0em} b}.$ Результаты представлены с точностью, не превышающей ту, с которой получены их значения согласно указанным выше критериям точности. В табл. 1 отображены результаты расчетов величин ${{U}_{1}}$ и ${{U}_{2}}$ для двух сферических частиц. В пределах полученной точности представленные результаты совпадают с результатами работы [6], в которой эти скорости находились на основе аналитического подхода при ${{g}_{1}} = {{g}_{2}}$. Обратим внимание на то, что с увеличением расстояния между частицами величина ${{U}_{1}}$, как и следовало ожидать для этого случая, стремится к единице.

ВЫВОДЫ

Изложен подход, позволяющий применять метод конечных элементов для расчета скоростей термофореза двух твердых аэрозольных частиц произвольной формы с учетом их взаимного влияния друг на друга. Численное сравнение результатов, полученных на основе данного подхода, с результатами, полученными на основе известного аналитического решения для сферических частиц, свидетельствуют о его применимости для численного анализа термофоретического движения двух частиц, размеры которых много больше средней длины свободного пробега молекул в газе.