Коллоидный журнал, 2019, T. 81, № 2, стр. 256-262

1. ВВЕДЕНИЕ

Традиционно при описании диффузионных процессов предполагается, что перенос происходит в однородной среде с постоянным коэффициентом диффузии [1–3]. Однако, данное допущение далеко не всегда корректно, поскольку многие реальные среды локально неоднородны, вследствие чего коэффициент диффузии в них может зависеть от пространственных переменных. В качестве примеров отметим перенос в гетерогенных пористых средах [4], на случайных фракталах [5], в экосистемах [6] и в биологических клетках [7–9].

В настоящее время интенсивно развивается стохастический подход, в рамках которого с помощью уравнения Ланжевена выполнено большое количество аналитических и численных исследований броуновского переноса в бесконечной среде с переменным коэффициентом диффузии [10–13]. Однако на практике перенос протекает в неоднородных средах конечных размеров и его исследование представляет большое научно-практическое значение. Для описания переноса в таких средах может быть использовано уравнение Фоккера–Планка в одном из возможных представлений с соответствующими граничными условиями. В настоящее время для этого обычно используют одну из трех наиболее известных представлений: Ито, Стратоновича и Хангги–Климонтовича (обобщенное уравнение Фурье) [14–17]. Применимость последней формы представления для различных физических процессов переноса подробно обсуждена в работе [18].

Цель данной работы в рамках представления Хангги–Климонтовича выполнить математическое моделирование диффузионного переноса через композитную среду, состоящую из двух гетерогенных слоев, в которых коэффициенты диффузии различны и зависят от одной пространственной переменной. Подобная среда моделирует, в частности, композитные мембраны, применяющиеся в различных мембранных технологиях.

2. МОДЕЛЬ ПЕРЕНОСА ЧЕРЕЗ ДВУХСЛОЙНУЮ ГЕТЕРОГЕННУЮ СРЕДУ

Рассмотрим диффузию индивидуального вещества через двухслойную среду (мембрану) при конечных давлениях.

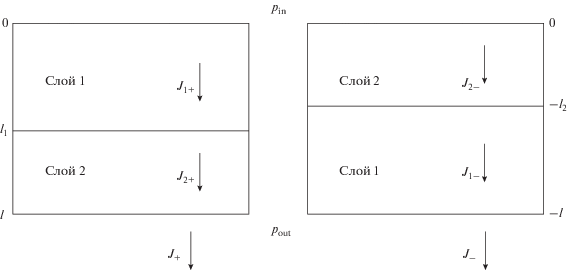
Пусть поверхность первого слоя ($i = 1$) контактирует с диффундирующим веществом (диффузантом) при давлении ${{p}_{{{\text{in}}}}}$, а поверхность второго слоя ($i = 2$) контактирует с пермеатом при давлении ${{p}_{{{\text{out}}}}}$ (рис. 1), причем ${{p}_{{{\text{in}}}}} > {{p}_{{{\text{out}}}}}.$

Будем предполагать, что диффузионный перенос в неоднородных мембранных слоях описывается уравнением Фоккера–Планка в представлении Хангги–Климонтовича

где ${{c}_{i}}$ и ${{D}_{i}}(x)$ – концентрация и коэффициент диффузии вещества в i-ом слое.

Будем считать, что диффузионный перенос внутри мембраны установился, тогда $\frac{{\partial {{c}_{1}}}}{{\partial t}} = 0.$ В этом случае диффузия через слои мембраны с учетом (1), (2) описывается выражениями вида

где ${{J}_{{1 + }}},{{J}_{{2 + }}}$ – диффузионные потоки через первый и второй слои.

Полагаем, что на внешней и внутренней границах среды установилось термодинамическое равновесие. В этом случае из равенства химических потенциалов при невысоких концентрациях на внешних границах мембраны следуют следующие соотношения:

где ${{c}_{1}}(0),\,\,{{c}_{2}}(l)$ – концентрации диффундирующего вещества на внешних границах первого и второго слоев соответственно, ${{S}_{1}},\,\,{{S}_{2}}$ – коэффициенты растворимости (Генри) диффундирующего вещества в 1-ом и 2-ом слоях соответственно.

Соответственно на внутренней границе слоев справедливо следующее соотношение:

В общем случае зависимость коэффициентов диффузии может быть записана в виде

где ${{f}_{1}}(x),{{f}_{2}}(x)$ – функции, моделирующие неоднородность соответствующего слоя в виде зависимости коэффициентов диффузии от пространственной переменной x, ${{D}_{{01}}},{{D}_{{02}}}$ – коэффициенты диффузии при x = 0.

В результате интегрирования выражений (3) с учетом (4)–(6) и условия неразрывности потока (т.е. ${{J}_{{1 + }}} = {{J}_{{2 + }}} = {{J}_{ + }}$) получим

где ${{l}_{i}}$ – толщина i-го слоя, $l = {{l}_{1}} + {{l}_{2}}$ – толщина мембраны, ${{F}_{{1 + }}} = \int_0^{{{l}_{1}}} {\frac{{dx}}{{{{f}_{1}}(x)}}} ,$ ${{F}_{{2 + }}} = \int_{{{l}_{1}}}^l {\frac{{dx}}{{{{f}_{2}}(x)}}} .$

Рассмотрим обратный перенос в композитной мембране (рис. 1). В этом случае второй слой (т.е. $i = 2$) мембраны находится в контакте с диффузантом при давлении ${{p}_{{{\text{in}}}}}$, а первый контактирует с пермеатом при давлении ${{p}_{{{\text{out}}}}}.$ Тогда диффузионные потоки через слои описываются выражениями вида

Так как на границах двухслойной мембраны термодинамическое равновесие устанавливается бесконечно быстро, из равенства химических потенциалов газа на внешних границах мембраны следует, что

а на внутренней границе

В результате интегрирования выражений (8) с учетом (9), (10) и условия неразрывности (${{J}_{{1 - }}} = {{J}_{{2 - }}} = {{J}_{ - }}$) получим

где ${{F}_{{2 - }}} = \int_0^{{{l}_{2}}} {\frac{{dx}}{{{{f}_{2}}(x)}}} ,$ ${{F}_{{1 - }}} = \int_{{{l}_{2}}}^l {\frac{{dx}}{{{{f}_{1}}(x)}}} .$

Исходя из определения ${{J}_{ + }} = \frac{{{{P}_{ + }}}}{l}({{p}_{{{\text{in}}}}} - {{p}_{{{\text{out}}}}})$ и ${{J}_{ - }} = \frac{{{{P}_{ - }}}}{l}({{p}_{{{\text{in}}}}} - {{p}_{{{\text{out}}}}})$ из (7) и (11) получим выражения для коэффициентов проницаемости двухслойной неоднородной мембраны при противоположных направлениях переноса –${{P}_{ + }},{{P}_{ - }}$ и произвольной зависимости коэффициентов диффузии от x

Рассмотрим ситуацию, когда оба слоя однородны. В этом случае коэффициенты диффузии пермеата в них не зависят от пространственной переменной, т.е. ${{f}_{1}}(x) = 1$ и ${{f}_{2}}(x) = 1,$ соответственно ${{D}_{1}}(x) = {{D}_{{10}}}$ и ${{D}_{2}}(x) = {{D}_{{20}}}.$ Тогда ${{F}_{{1 + }}} = {{l}_{1}},$ ${{F}_{{2 + }}} = {{l}_{2}}$ и ${{F}_{{1 - }}} = {{l}_{1}},$ ${{F}_{{2 - }}} = {{l}_{2}}.$ Подставляя эти значения в (7), (11) и (12), получим

где ${{P}_{{10}}} = {{D}_{{10}}}{{S}_{1}}$ и ${{P}_{{20}}} = {{D}_{{20}}}{{S}_{2}}$ – проницаемости соответствующих однородных слоев, ${{P}_{{ + 0}}}$ и ${{P}_{{ - 0}}}$ – проницаемости однородной композитной среды при противоположных направлениях переноса газа.

Таким образом, из (13), (14) следует, что в случае однородных слоев, когда коэффициенты диффузии в слоях постоянны, величина диффузионного потока через композитную среду не зависит от направления переноса.

Рассмотрим теперь случай, когда оба слоя неоднородны. Будем моделировать их неоднородность, предполагая, что зависимости обоих коэффициентoв диффузии от пространственной переменной х имеют вид

где ${{f}_{1}}(x) = \exp ({{{{a}_{1}}x} \mathord{\left/ {\vphantom {{{{a}_{1}}x} {{{l}_{1}}}}} \right. \kern-0em} {{{l}_{1}}}}),$ ${{f}_{2}}(x) = \exp ({{{{a}_{2}}x} \mathord{\left/ {\vphantom {{{{a}_{2}}x} {{{l}_{2}}}}} \right. \kern-0em} {{{l}_{2}}}}),$ ${{a}_{i}}$ – параметр, характеризующий степень структурной неоднородности i-го слоя.

Аналогичный вид зависимости использовался в [10] при исследовании аномальной диффузии в биологических клетках.

Заметим, что диффузионный поток через отдельный неоднородный i-ый слой толщиной ${{l}_{i}}$, когда толщина другого слоя была равна нулю, описывается следующим выражениями:

где ${{P}_{{{\text{eff1}}}}} = \frac{{{{D}_{{10}}}{{S}_{1}}{{a}_{1}}}}{{(1 - \exp ( - {{a}_{1}}))}},$ ${{P}_{{{\text{eff2}}}}} = \frac{{{{D}_{{20}}}{{S}_{2}}{{a}_{2}}}}{{(1 - \exp ( - {{a}_{2}}))}}$ – эффективные проницаемости соответствующих неоднородных мембранных слоев, ${{D}_{{{\text{eff}}i}}} = {{\left( {\int_0^{{{l}_{i}}} {\frac{1}{{{{D}_{i}}(x)}}} } \right)}^{{ - 1}}}$ = $ = \frac{{{{D}_{{i0}}}{{a}_{i}}}}{{(1 - \exp ( - {{a}_{i}}))}}$ – эффективный коэффициент диффузии в i-ом слое.

В случае двухслойной мембраны с учетом (15) следует, что

где $\quad{{L}_{{12}}} = \frac{{{{l}_{1}}}}{{{{l}_{2}}}} = {1 \mathord{\left/ {\vphantom {1 {{{L}_{{21}}}}}} \right. \kern-0em} {{{L}_{{21}}}}},$ ${{L}_{i}} = {l \mathord{\left/ {\vphantom {l {{{l}_{i}}}}} \right. \kern-0em} {{{l}_{i}}}}.$

Подставив (17) и (18), соответственно, в (7) и (11), получим

где $\frac{l}{{{{P}_{ + }}}} = \frac{{{{l}_{1}}}}{{{{P}_{{{\text{eff1}}}}}}} + \frac{{{{l}_{2}}}}{{{{P}_{{{\text{eff2}}}}}}}\exp \left( { - {{a}_{2}}\frac{{{{l}_{1}}}}{{{{l}_{2}}}}} \right),$ $\frac{l}{{{{P}_{ - }}}} = \frac{{{{l}_{2}}}}{{{{P}_{{{\text{eff2}}}}}}}$ + $ + \frac{{{{l}_{1}}}}{{{{P}_{{{\text{eff1}}}}}}}\exp \left( { - {{a}_{1}}\frac{{{{l}_{2}}}}{{{{l}_{1}}}}} \right),$ а ${{P}_{ + }}$ и ${{P}_{ - }}$ – проницаемости двухслойной неоднородной среды при противоположных направлениях переноса.

3. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

С помощью полученных соотношений (19), (20) проанализируем влияние эффекта неоднородности на газоперенос через двухслойную композитную мембрану.

Из (19), (20) следует, что проницаемость неоднородной двухслойной мембраны описывается более сложной зависимостью, чем традиционное соотношение для проницаемости однородной мембраны (14). Кроме того, из полученных соотношений следует, что величина потока газа через двухслойную неоднородную мембрану зависит от направления переноса (т.к. ${{J}_{ + }} \ne {{J}_{ - }}$), т.е. возникает эффект асимметрии переноса (ЭАП) [19–24].

Рассмотрим важные случаи, когда ${{l}_{1}} \to 0.$ Тогда из (19), (20) независимо от знака ${{a}_{2}}$ следует, что:

Как видно из (22), при малой толщине первого слоя и убывании коэффициента диффузии в этом слое по направлению переноса (${{a}_{1}} < 0$) различие в значениях проницаемости мембраны в зависимости от направления переноса может оказаться весьма существенным. Из (22) следует, что двухслойная мембрана при ${{l}_{1}} \to 0$ функционирует как “диффузионный диод” [25, 26], пропуская поток через мембрану, если первый слой контактирует с диффузантом, и практически непроницаема, если он контактирует с пермеатом.

Аналогично при ${{l}_{2}} \to 0$ из (19), (20) независимо от знака ${{a}_{1}}$ следует, что

Из (24) следует, что при ${{l}_{2}} \to 0$ и убывании коэффициента диффузии во втором слое по направлению переноса (${{a}_{2}} < 0$) двухслойная мембрана функционирует как “диффузионный диод”, если второй слой контактирует с диффузантом.

Отметим также, что ЭАП может возникать, если хотя бы один из слоев неоднороден. Так, если первый слой однороден (т.е. ${{a}_{1}} = 0$), из (19), (20) следует, что

Аналогично, если ${{a}_{2}} = 0$ из (19), (20) имеем

Заметим, что из анализа более общих формул (7) и (11) также следует, что ЭАП будет возникать при различных видах зависимости коэффициентов диффузии от x (т.е. от ${{f}_{1}}(x),{{f}_{2}}(x)$), и лишь в случае, когда оба слоя однородны, асимметрия не возникает и проницаемость среды описывается известным соотношением вида (14).

Исследуем количественно влияние неоднородности мембранных слоев на перенос газа через двухслойную непористую мембрану. Подобная ситуация реализуются в случае композитных и асимметричных мембран, в которых один из слоев (будем считать его первым слоем, $i = 1$) выполняет роль селективного слоя, а второй ($i = 2$) – роль подложки, имеющей более высокую проницаемость, чем селективный слой (т.е. ${{P}_{{02}}} \gg {{P}_{{01}}}$), и заметно большую толщину (т.е. ${{l}_{2}} \gg {{l}_{1}}$). С учетом сказанного при проведении численного анализа зависимости интенсивности асимметрии газопереноса в двухслойной мембране от параметров ${{a}_{1}},{{a}_{2}},$ характеризующих неоднородность мембранных слоев, были использованы следующие значения: ${{{{P}_{{10}}}} \mathord{\left/ {\vphantom {{{{P}_{{10}}}} {{{P}_{{20}}}}}} \right. \kern-0em} {{{P}_{{20}}}}} = 0.01,$ ${{{{l}_{2}}} \mathord{\left/ {\vphantom {{{{l}_{2}}} {{{l}_{1}}}}} \right. \kern-0em} {{{l}_{1}}}} = 100.$

Для количественного анализа влияния параметров гетерогенности на интенсивность ЭАП воспользуемся коэффициентом асимметрии. Заметим, что обычно в мембранных процессах для оценки интенсивности асимметрии переноса используется коэффициент асимметрии вида ${\eta } = \frac{{{{P}_{ + }}}}{{{{P}_{ - }}}}$ [19, 23–25].

Мы в данной работе для количественной оценки интенсивности эффекта асимметрии диффузии предлагаем использовать коэффициент интенсивности асимметрии вида

Удобство данного коэффициента состоит в том, что он, в отличие от ${\eta ,}$ изменяется в ограниченном диапазоне, $ - 1 \leqslant {\chi } \leqslant 1,$ причем значение ${\chi } = 0$ соответствует отсутствию асимметрии потока (т.к. ${{J}_{ + }} = {{J}_{ - }}$), а значения ${\chi } = \pm 1$ – режиму “диффузионного диода” (т.к. ${{J}_{ + }} = 0$ или ${{J}_{ - }} = 0$).

С помощью Mathcad 14 с использованием коэффициента асимметрии χ был выполнен численный анализ зависимости интенсивности ЭАП в двухслойной мембране от параметра ${{a}_{1}}$ селективного (первого) слоя с учетом формул (19), (20).

Анализ показал, что на интенсивность ЭАП заметно влияют значения параметров неоднородности слоев ${{a}_{2}},{{a}_{1}}.$

Были рассмотрены следующие ситуации при увеличении ${{a}_{1}}.$

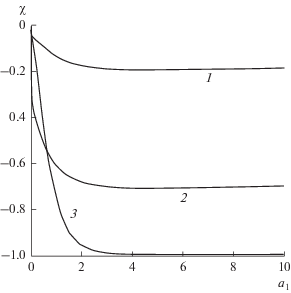
1. Коэффициенты диффузии в обоих слоях возрастают вдоль x при ${{a}_{2}} > 0,{{a}_{1}} > 0.$ Тогда при малых значениях ${{a}_{1}}$ эффект асимметрии усиливается независимо от величины $c = {{{{a}_{2}}} \mathord{\left/ {\vphantom {{{{a}_{2}}} {{{a}_{1}}}}} \right. \kern-0em} {{{a}_{1}}}}.$ Однако с ростом ${{a}_{1}}$ при $c \leqslant 1$ интенсивность асимметрии, достигнув максимального значения, начинает убывать, в то время как при $c > 1$ интенсивность ЭАП возрастает и ${\chi }$ достигает постоянного значения, в зависимости от величины c (рис. 2). Так, при значениях $c$ > 10 величина ${\chi }$ ≈ –1 (т.е. реализуется режим “диффузионного диода”). Кроме того, при любых c величина газового потока через двухслойную мембрану будет выше, если подложка, непосредственно контактирует с диффузантом (т.е. с более высоким давлением газа ${{p}_{{{\text{in}}}}}$).

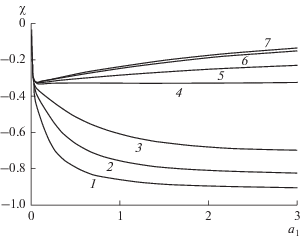
2. Коэффициент диффузии в селективном слое возрастает вдоль x при ${{a}_{1}} > 0$, а коэффициент диффузии в подложке убывает при ${{a}_{2}} < 0.$ Установлено, что при малых значениях ${{a}_{1}}$ и $\left| c \right| > 1$ интенсивность ЭПА сначала убывает (т.к. ${\chi } \to 0$), достигает минимального значения, а затем возрастает (т.к. ${\chi } \to - 1$), причем тем быстрее, чем больше $\left| c \right|$ (рис. 3). При $\left| c \right| < 1$ интенсивность ЭАП сначала убывает при малых значениях ${{a}_{1}}$, а затем, достигнув локального максимума, начинает медленно возрастать с увеличением ${{a}_{1}}.$

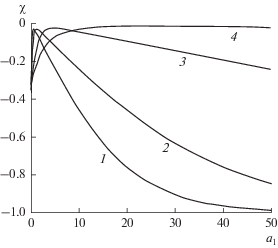
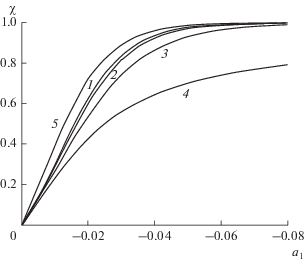
3. Коэффициент диффузии в селективном слое убывает вдоль x при ${{a}_{1}} < 0.$ Установлено, что интенсивность асимметрии переноса слабо зависит от величины и знака параметра c, при $\left| c \right|$ < 10, причем режим “диффузионного диода” (${\chi } \approx 1$) достигается при небольших значениях ${{a}_{1}}$ (рис. 4). С ростом $\left| c \right|$ интенсивность ЭАП заметно убывает при $c$ > 10, в то время как при $c$ < –10 она слабо растет. Больший поток в случае ${{a}_{1}} < 0$, в отличие от ранее рассмотренных, достигается, когда селективный слой контактирует с диффузантом.

Также установлено, что на интенсивность асимметрии переноса заметное влияние оказывает отношение толщин мембранных слоев ${{{{l}_{1}}} \mathord{\left/ {\vphantom {{{{l}_{1}}} {{{l}_{2}}}}} \right. \kern-0em} {{{l}_{2}}}}.$ Так, в случае ${{a}_{1}} > 0,{{a}_{2}} > 0$ с ростом отношения ${{{{l}_{1}}} \mathord{\left/ {\vphantom {{{{l}_{1}}} {{{l}_{2}}}}} \right. \kern-0em} {{{l}_{2}}}}$ наблюдается заметная асимметрия (рис. 5), соответствующая режиму “диффузионного диода”.

4. ЗАКЛЮЧЕНИЕ

В результате исследования одномерного диффузионного переноса через двухслойную непористую среду, состоящую из двух неоднородных слоев, получены выражения для диффузионного потока через нее при произвольной зависимости коэффициентов диффузии от пространственной переменной.

Получено уравнение для расчета проницаемости неоднородной двухслойной мембраны. Обнаружено, что величина проницаемости такой мембраны может зависеть от направления переноса.

Установлено, что эффект асимметрии переноса может возникать при условии неоднородности хотя бы одного из мембранных слоев.

Обнаружено, что при некоторых значениях параметров неоднородности мембраны перенос газа протекает в режиме “диффузионного диода”.

Установлено, что на интенсивность асимметрии переноса двухслойной мембраны заметно влияет отношение между толщинами мембранных слоев.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (грант № 17-08-01287_ а).