Коллоидный журнал, 2019, T. 81, № 3, стр. 382-400
Зародышеобразование в парах воды на поверхности с наноскопическими бороздами. 2. Особенности термодинамического поведения
С. В. Шевкунов *
Санкт-Петербургский политехнический университет Петра Великого
195251 Санкт-Петербург, ул. Политехническая, 29, Россия
* E-mail: shevk54@mail.ru
Поступила в редакцию 17.12.2018
После доработки 25.12.2018
Принята к публикации 27.12.2018
Аннотация
Методом Монте-Карло моделируется рост зародышей конденсированной фазы на поверхности кристалла йодистого серебра с нанесенными на нее параллельными наноскопическими бороздами различной глубины и профиля. Термодинамика роста исследована в терминах рассчитанных методом биканонического статистического ансамбля свободной энергии, энтропии, работы образования и энергии Гиббса реакций присоединения. Химический потенциал первых присоединяющихся к поверхности молекул воды понижается за счет борозд на 20kBT. Борозды на поверхности смещают начало зародышеобразования в область разреженного пара примерно на девять порядков, и повышают термодинамическую устойчивость зародышей, однако их действие в области средних значений плотности ослаблено и направлено в сторону торможения конденсации. Получены фундаментальные уравнения, представляющие собой обобщение уравнения Клапейрона–Клаузиуса на случай конденсированной фазы немакроскопических размеров. На основании указанных уравнений выявлены физические причины наблюдаемых в компьютерном моделировании закономерностей, проанализировано согласие численных результатов с универсальными соотношениями, вытекающими из уравнений.
1. ВВЕДЕНИЕ
Модифицирование рельефа поверхности является эффективным инструментом программирования ее поглощательной способности [1–8]. Действие рельефа наноскопических масштабов не сводится к простому увеличению эффективной площади поглощения, но способно изменять молекулярные механизмы сцепления с поверхностью. Рельеф со специальными характеристиками может обеспечивать избирательную способность поверхности в отношении различных материалов [9, 10], повышать или понижать поглощательную способность в заданных диапазонах плотности пара. Целенаправленное использование этих возможностей предполагает выявление универсальных закономерностей, сопровождающих взаимодействие рельефных поверхностей с парами различной плотности.
Поглощательная способность определяет активность поверхности в качестве стимулятора образования и роста зародышей конденсированной фазы. Вода в качестве жидкости, способной в естественной среде существовать как в форме пара, так и в форме конденсата, и одновременно обладающая уникальными структурными свойствами [11–13], занимает здесь особое место. Интерес к воде обусловлен необходимостью контролировать гидрофобность поверхностей различных приборов и механизмов, работающих в условиях переменной влажности и температуры. Гетерогенная нуклеация атмосферной влаги на поверхности кристаллических аэрозольных частиц остается основным способом воздействия на локальные атмосферные осадки и климат в целом [14, 15].
Серия компьютерных исследований выполнена для нуклеации паров воды на бездефектной поверхности кристаллического йодистого серебра (β-AgI) – наиболее активного из известных агентов нуклеации [16–31]. Менее изучено действие поверхностей с дефектами [26, 32–36]. Трещины и разломы наноскопической ширины могут образовываться в процессе формирования поверхности, а их характеристики могут контролироваться выбором режима приготовления [37–39]. Одним из способов формирования регулярного поверхностного микрорельефа является нанесение мелких царапин. Создание рисунка параллельных борозд наноскопического масштаба требует применения новейших технологий, относящихся к наногравировке [40, 41] и наноскопической литографии [42].
Зародышеобразование является промежуточным звеном перехода из газообразного в конденсированное состояние, при этом наблюдаемые в макроскопическом эксперименте величины являются некоторыми средними значениями. Достаточно медленные в молекулярных масштабах процессы в ансамбле зародышей могут быть описаны в терминах равновесных средних [43], вычисление которых возможно методами равновесной статистической термодинамики [44–50]. Наиболее информативной термодинамической характеристикой равновесного состояния является свободная энергия, которая определяет вероятности макроскопических событий и направление их развития. Через свободную энергию вычисляется работа образования, которая, в свою очередь, определяет устойчивость и скорость эволюции зародышей.
Свободная энергия, как и ее разновидность, энергия Гиббса, кроме внутренней энергии содержит энтропийное слагаемое. Наличие энтропийной составляющей является главным источником трудностей вычисления свободной энергии даже методами численного моделирования. Проблема состоит в том, что для энтропии не удается получить выражение в виде некоторого равновесного среднего, как это можно сделать для внутренней энергии и большинства других равновесных характеристик.
В настоящее время разработано несколько методов непрямого вычисления свободной энергии на молекулярном уровне. Наиболее известны метод возмущения (“free energy perturbation method”) [51–54] и метод термодинамического интегрирования [55–57]. В первом из них рассчитывается равновесное среднее экспоненты разности энергий двух состояний, а во втором вычисляется равновесное среднее производной энергии по параметру включения при различных его значениях, которое затем нужно по параметру включения численно проинтегрировать. В частном случае двух состояний, различающихся числом молекул, метод термодинамического возмущения получил название метода “внедренной частицы” (“particle insertion method”, метод Видома) и применяется для расчета химического потенциала [58, 59]. Несмотря на его внешнюю простоту, применение метода Видома к конденсированным средам затруднено медленной сходимостью вычисляемых средних, которая является следствием недостаточной представительности используемых случайных выборок. В том же частном случае двух состояний, различающихся одной молекулой, метод термодинамического интегрирования получил название метода “последовательных включений” [60]. В этом методе проблема медленной сходимости частично решается за счет многократного повторения расчетов для серии последовательно нарастающих значений параметра включения пробной частицы. В [61] разработан метод расчета разности в свободной энергии между состояниями, различающимися температурой, блужданием по температуре.
С начала восьмидесятых годов прошлого века расчеты этими методами применяются для вычисления свободной энергии сольватации и гидратации [62–68], адсорбции [69–72] и межмолекулярных связей в органических материалах [73–78], а также для определения точки равновесия фаз [79]. Свободную энергию сольватации и гидратации атомарных ионов в жидкостях рассчитывают в два этапа: сначала вычисляют свободную энергию образования в растворителе полости, которую должен занимать ион, и к ней добавляют свободную энергию “зарядки” этой полости [80–82]. Такой подход оправдан в частном случае простейшей модели ионов в форме жестких заряженных сфер. В общем случае произвольной формы и мягких взаимодействий четкие границы полости указать невозможно.
Уже первые расчеты этими методами применительно к конденсированным средам продемонстрировали необходимость генерировать много большие объемы случайной выборки, чем предполагалось [83]. Причиной является низкая частота посещений микросостояний, которые обладают сопоставимыми по величине статистическими весами в обоих термодинамических состояниях, для которых вычисляется разность свободной энергии. Частичное решение проблемы достигается применением метода “зонтичной выборки” (“umbrella sampling method”), идея которого, высказанная еще в конце семидесятых годов [84, 85], состоит в перераспределении частот посещения при случайном блуждании в пользу наиболее значимых микросостояний с компенсирующим переопределением усредняемой функции [86, 87]. Идея перераспределения статистических весов в генерируемой случайной выборке развита в методе “интегрированной выборки с закалкой” (“integrated tempering sampling”) [88–94]. В этом методе моделируется небольцмановское распределение, представляющее собой линейную комбинацию больцмановских распределений для нескольких близких значений температуры. Та же идея перераспределения статистических весов с целью повышения частоты преодоления энергетических барьеров в генерируемой случайной выборке заложена и в методе “гистограмм переопределяемых весов” (“histogram reweighting method”) [95–97] и в методе “смещающей силы” (“biasing force method”) [98–104], нацеленном на расчет потенциала средней силы.
Несмотря на свою популярность, разработанные методы позволили рассчитать только относительные значения – разницу в свободной энергии двух достаточно близких термодинамических состояний. При этом высокая трудоемкость вычисления этих разностей не позволяет повторить расчет многократно, чтобы выстроить цепочку от “нулевого” состояния и получить таким путем абсолютные значения свободной энергии и энтропии.
В представленной работе для расчета свободной энергии применен метод биканонического статистического ансамбля (БСА) [105–115]. Метод БСА позволяет вычислить абсолютные значения свободной энергии и энтропии, а также получить зависимости свободной энергии от количества частиц, составляющих систему. Именно зависимости от размеров системы определяют ее термодинамическую устойчивость и поэтому являются решающими при исследовании зародышеобразования. Вычисленные абсолютные значения свободной энергии дают возможность произвести сравнение термодинамического поведения системы в различных условиях, например, на гладкой и структурированной поверхностях, во внешних полях и без них. Разработанный самонастраивающийся алгоритм позволил с максимальной эффективностью использовать вычислительный ресурс компьютера. Снижение трудоемкости и максимальная автоматизация вычислений сделали возможным систематические расчеты абсолютных значений свободной энергии в широком диапазоне условий для зародышей размерами до нескольких тысяч молекул и более.
2. МОДЕЛЬ, МЕТОД И РАССЧИТЫВАЕМЫЕ ХАРАКТЕРИСТИКИ
2.1. Модель
Компьютерные расчеты равновесных термодинамических характеристик растущих зародышей конденсированной фазы воды на поверхности йодистого серебра (β-AgI) с нанесенными наноскопическими бороздами выполнены методом Монте-Карло. Моделирование произведено для той же молекулярной системы и в тех же условиях, которые представлены в предыдущей статье [116]. В плоскости адсорбции применялись периодические граничные условия. Размер ячейки периодичности составлял 95.19 × 54.96 Å (24 × 12 пар ионов в кристаллографическом слое, параллельном базовой грани) в расчетах для поверхности с бороздами и 79.33 × 91.60 Å (20 × 20 пар ионов) для поверхности без борозд. Параллельные прямые борозды бесконечной длины нанесены на поверхность базовой грани с катионами серебра в поверхностном слое. Расстояние между соседними бороздами составляет 95.19 Å, т.е. равно размеру ячейки периодичности. Выполнено моделирование поверхностей с двумя рисунками борозд. В первом случае борозды имели прямоугольный профиль глубиной в 6 кристаллографических слоев и шириной в 11 пар ионов, а во втором – профиль в виде ступенчатого, сужающегося книзу желоба такой же глубины и такой же ширины в его верхней части (см. рис. 2 в предыдущей статье [116]). Кроме того, во втором случае на поверхность между желобами в перпендикулярном к ним направлении нанесены тонкие прямые царапины глубиной в один кристаллографический слой путем удаления двух соседних цепочек положительных и отрицательных ионов.
Рис. 1.
Химический потенциал молекул воды в растущем из пара на базовой грани кристалла β-AgI зародыше конденсированной фазы при 260 K как функция количества молекул в пределах ячейки периодичности размером 95.194 × 54.960 Å: 1 – гладкая поверхность без дефектов, 2 – поверхность с параллельными наноскопическими бороздами прямоугольного профиля, как на рис. 1 предыдущей статьи [116], 3 – поверхность с наноскопическими бороздами сложного профиля, как на рис. 2 предыдущей статьи.
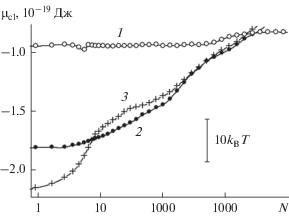
Рис. 2.
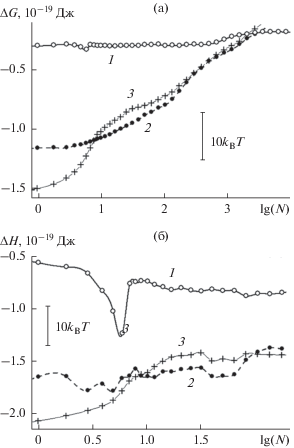
Энергия Гиббса, отнесенная к гипотетическому стандартному состоянию пара с давлением 1 атм (а), и энтальпия (б) реакции присоединения молекулы пара к зародышу конденсированной фазы на базовой грани кристалла β-AgI при 260 K. Нумерация кривых, относящихся к различным образом структурированным поверхностям, – как на рис. 1.
Для описания межмолекулярных взаимодействий применена та же модель [66–71], что и в предыдущей статье [116]. В явной форме учитывались взаимодействия молекул с ионами 12 кристаллографических слоев (6 слоев ионов Ag+ и 6 слоев ионов I–) вглубь подложки. В плоскости подложки взаимодействия рассчитывались методом ближайшего образа [117]. Все дальние электростатические взаимодействия между молекулами и молекул с ионами кристаллической решетки в плоскости подложки вычислялись двумерным методом Эвальда [22, 23, 26]. Кроме этого, методом Эвальда суммировались также и поляризационные взаимодействия молекул с ионами кристаллической решетки подложки и в форме поправок учитывались дисперсионные взаимодействия молекул с ионами кристаллической решетки за пределами ячейки периодичности [22, 23, 26].
2.2. Метод расчета
Расчеты равновесных термодинамических характеристик как функций размера зародышей конденсата выполнены методом Монте-Карло в БСА [105–115]. Метод БСА позволяет из первых принципов вычислить химический потенциал ${{{\mu }}_{{{\text{cl}}}}}$ в системе, состоящей из произвольного числа $N$ молекул. Метод БСА относится к разряду принципиально точных методов, не содержит приближений теорий сплошных сред и среднего поля. Расчет состоит в усреднении по случайной выборке из миллионов молекулярных конфигураций, которые генерируются на компьютере. Моделируется один из элементов статистического ансамбля, развивающегося по закону марковского случайного процесса. Переходные вероятности между конфигурациями разыгрываются с помощью датчика случайных чисел и определяются таким образом, чтобы их предельные значения представляли собой заданное равновесное распределение [118, 119].
В методе БСА моделируются два равновесных статистических ансамбля микросостояний с числами частиц $n = k,$ $n = k - 1.$ Случайные переходы между ними производятся с вероятностями большого канонического статистического ансамбля и заданным значением химического потенциала виртуального термостата ${\tilde {\mu },}$ который является входным параметром метода. Для этого кроме стандартных шагов по сдвигу и повороту молекул [117] совершаются попытки добавить в систему из термостата или удалить из системы в термостат одну случайным образом выбранную молекулу.
В пределе бесконечно большой случайной выборки рассчитываемое значение химического потенциала ${{{\mu }}_{{{\text{cl}}}}}$ не зависит от задаваемого значения ${\tilde {\mu },}$ однако минимизация статистической погрешности достигается в режиме ${\tilde {\mu }} = {{{\mu }}_{{{\text{cl}}}}}.$ Поскольку величина ${{{\mu }}_{{{\text{cl}}}}}$ заранее не известна, предварительная оценка оптимального значения ${\tilde {\mu }}$ производится численно, методом последовательных итераций отдельно для каждого значения $N.$ Химический потенциал ${{{\mu }}_{{{\text{cl}}}}}$ рассчитывается через отношение частот посещения состояний с $k$ и $k - 1$ молекулами [105–115]. Расчет равновесных характеристик каждого термодинамического состояния выполнялся усреднением по 15 млн марковских шагов, при этом первые 3 млн шагов использовались для термализации. Применялась процедура последовательного наращивания количества молекул в системе.
Метод БСА позволяет выполнить расчеты как для термодинамически устойчивых, так и неустойчивых равновесных состояний. В лабораторных условиях в макроскопических временных масштабах неустойчивые состояния под действием термических флуктуаций разрушаются – система скачкообразным образом переходит из одного устойчивого состояния в другое, минуя области неустойчивости, при этом количество молекул в зародыше может лавинообразно вырасти до макроскопических величин или, наоборот, зародыш может испариться. В методе БСА происходит стабилизация неустойчивых состояний – удается получить непрерывные зависимости термодинамических характеристик, без разрывов.
2.3. Рассчитываемые характеристики
Если метод БСА реализуется в условиях фиксированного давления $p$ (с использованием изотермо-изобарического статистического ансамбля [117–119]), численным суммированием рассчитанных значений химического потенциала вычисляется энергия Гиббса
Аналогично, суммированием результатов, полученных в условиях фиксированного объема, получается свободная энергия Гельмгольца
В случае достаточно больших $N$ зависимость химического потенциала от $k$ с ростом размеров системы становится все более гладкой, и для ее построения достаточно произвести расчет только в ограниченном количестве опорных точек ${{k}_{i}},i = 1,...,I.$ Вычисления химического потенциала выполнялись для нескольких десятков точек ${{k}_{i}},$ распределенных с увеличивающимся шагом, после чего производилась интерполяция результатов кубическими сплайнами во всех промежуточных точках, необходимых для расчета сумм (1) и (2).
В соответствии с общими принципами статистической механики свободная энергия $F(N,V,T)$ = = $ - {{k}_{{\text{B}}}}T\ln (Q(N,V,T))$ и все равновесные термодинамические характеристики выражаются через статистическую сумму системы $Q(N,V,T).$ В свою очередь, статистическая сумма частиц, подчиняющихся классической статистике, распадается в произведение конфигурационного интеграла $Z(N,V,T)$ и кинетической части: $Q(N,V,T)$ = $Z(N,V,T){{(Z_{{{\text{tr}}}}^{{{\text{kin}}}}Z_{{{\text{rot}}}}^{{{\text{kin}}}})}^{N}}$ [119], где $Z_{{{\text{tr}}}}^{{{\text{kin}}}} = {{\left( {\frac{h}{{\sqrt {2{\pi }{\kern 1pt} m{{k}_{{\text{B}}}}T} }}} \right)}^{{ - 3}}} = \frac{1}{{{{\Lambda }^{3}}}}$ – результат интегрирования по импульсам поступательного движения, а $Z_{{{\text{rot}}}}^{{{\text{kin}}}} = \frac{{{{{(2{{k}_{{\text{B}}}}T)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}{{{({{I}_{1}}{{I}_{2}}{{I}_{3}})}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{{{\pi }}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}{{{{h}^{3}}}}{\kern 1pt} $ – результат интегрирования по вращательным импульсам молекулы, ${{I}_{1}},{{I}_{2}},{{I}_{3}}$ – главные моменты инерции, $m$ – масса молекулы воды, $h$ – постоянная Планка, $\Lambda {\kern 1pt} $ – тепловая длина волны Де-Бройля. Конфигурационный интеграл $Z(N,V,T)$ содержит все зависящие от взаимодействий молекул вклады в статистическую сумму и не зависит от масс и моментов инерции частиц. Параметр симметрии молекул ${\chi }$ (для воды ${\chi } = {\text{2}}$) входит в $Z(N,V,T)$ в виде множителя ${{{\chi }}^{{ - N}}}$ и в выражения для химического потенциала молекул в виде универсального слагаемого $ - {{k}_{{\text{B}}}}T\ln \left( {\frac{{8{{{\pi }}^{2}}}}{{\chi }}} \right){\kern 1pt} .$
Химический потенциал зародыша конденсированной фазы представляет собой энергию Гиббса ${{G}_{{{\text{cl}}}}}(N,p,T)$ или свободную энергию Гельмгольца в расчете на одну молекулу:
(3)
$\begin{gathered} {{{\mu }}_{{{\text{cl}}}}}(N,p,T) = {{\left( {\frac{{\partial {{G}_{{{\text{cl}}}}}(N,p,T)}}{{\partial N}}} \right)}_{{p,T}}} = \\ = {{\left( {\frac{{\partial {{F}_{{{\text{cl}}}}}(N,V,T)}}{{\partial N}}} \right)}_{{V,T}}}. \\ \end{gathered} $Энергия Гиббса ${{G}_{{{\text{cl}}}}}(N,p,T)$ = ${{E}_{{{\text{cl}}}}} - T{{S}_{{{\text{cl}}}}} + p{{V}_{{{\text{cl}}}}}$ отличается от свободной энергии Гельмгольца ${{F}_{{{\text{cl}}}}}(N,V,T)$ = ${{E}_{{{\text{cl}}}}} - T{{S}_{{{\text{cl}}}}}$ конденсата объемным слагаемым $p{{V}_{{{\text{cl}}}}},$ в котором ${{V}_{{{\text{cl}}}}}$ – объем, который занимает конденсат в объеме V. Объемное слагаемое для конденсированной фазы, как правило, относительно мало, $p{{\text{v}}_{{{\text{cl}}}}} \ll {{k}_{{\text{B}}}}T,$ где удельный объем конденсированной фазы ${{\text{v}}_{{{\text{cl}}}}} = {{\left( {\frac{{\partial {{V}_{{{\text{cl}}}}}}}{{\partial N}}} \right)}_{{p,T}}}.$ Это позволяет для конденсированной фазы пренебречь разницей между энергией Гиббса и свободной энергией Гельмгольца, а также их зависимостью от давления и объема.
В терминах свободной энергии Гельмгольца химический потенциал молекул конденсата распадается на сумму конфигурационной и кинетической частей:
(4)
$\begin{gathered} {{{\mu }}_{{{\text{cl}}}}}(N,T) = \frac{{\partial {{F}_{{{\text{cl}}}}}(N,T)}}{{\partial N}} = - {{k}_{{\text{B}}}}T\frac{\partial }{{\partial N}}\ln \left( {Z(N,T)\text{v}_{{{\text{ref}}}}^{{ - N}}} \right) - \\ - \,\,{{k}_{{\text{B}}}}T\ln \left( {Z_{{{\text{tr}}}}^{{{\text{kin}}}}Z_{{{\text{rot}}}}^{{{\text{kin}}}}{{\text{v}}_{{{\text{ref}}}}}} \right) = {\mu }_{{{\text{cl}}}}^{{{\text{conf}}}}(N,T) + {\mu }_{{{\text{cl}}}}^{{{\text{kin}}}}(T), \\ \end{gathered} $Расчет кинетической части химического потенциала молекул конденсата сводится к простой подстановке соответствующих табличных значений молекулярных констант в формулу ${\mu }_{{{\text{cl}}}}^{{{\text{kin}}}}(T)$ = $ = - {{k}_{{\text{B}}}}T\ln \left( {Z_{{{\text{tr}}}}^{{{\text{kin}}}}Z_{{{\text{rot}}}}^{{{\text{kin}}}}{{\text{v}}_{{{\text{ref}}}}}} \right).$ Все трудности расчета химического потенциала сводятся к вычислению его конфигурационной части ${\mu }_{{{\text{cl}}}}^{{{\text{conf}}}}(N,T),$ которое выполняется численно методом БСА.
Как правило, в реальных лабораторных экспериментах по конденсации измеряются характеристики, связанные с переходом молекул из газообразной фазы в конденсат. Такие характеристики выражаются через разность химических потенциалов двух фаз. Поскольку химический потенциал молекул пара содержит кинетическую часть, совпадающую с кинетической частью молекул конденсата, а также и параметр симметрии молекул, во всех термодинамических величинах, выражающихся через разность химических потенциалов или свободных энергий пара и конденсата, например в работе образования или свободной энергии присоединения, кинетическая часть и параметр симметрии не содержатся. После взаимного сокращения одинаковых слагаемых эти величины выражаются через разность редуцированных конфигурационных частей химического потенциала пара ${{{\mu }}^{{\text{с }}}}(p,T) = {{{\mu }}^{{{\text{conf}}}}}(p,T)$ – ${{k}_{{\text{B}}}}T\ln \left( {\frac{{\chi }}{{{\text{8}}{{{\pi }}^{{\text{2}}}}}}} \right)$ и конденсата ${\mu }_{{{\text{cl}}}}^{{\text{c}}}(p,T),$ для которого действует аналогичная формула. Поэтому они не зависят ни от массы молекулы, ни от ее момента инерции, ни от ее симметрии, а возможные неточности в экспериментальном определении этих характеристик молекул не влияют на результаты расчетов методом БСА.
Для пересчета значений химического потенциала молекул пара ${\mu }$ в давление $p$ применяются формулы идеального газа жестких ротаторов, в которых конфигурационная часть химического потенциала имеет вид ${{{\mu }}^{{{\text{conf}}}}}(p,T)$ = = $ - {{k}_{{\text{B}}}}T\ln \left( {\frac{{{\text{8}}{{{\pi }}^{{\text{2}}}}}}{{\chi }}\frac{{{{k}_{{\text{B}}}}T}}{p}\text{v}_{{{\text{ref}}}}^{{ - {\text{1}}}}} \right){\kern 1pt} $ [119], а давление выражается через редуцированную конфигурационную часть, не содержащую параметра симметрии молекулы:
Таким образом, масса молекулы, ее момент инерции и симметрия не влияют ни на разностные термодинамические характеристики, ни на расчет соответствующих им значений давления пара.3. РЕЗУЛЬТАТЫ КОМПЬЮТЕРНЫХ ВЫЧИСЛЕНИЙ
3.1. Химический потенциал
На рис. 1 представлены результаты сравнительных расчетов химического потенциала молекул воды, адсорбированных кристаллом йодистого серебра, на поверхностях трех типов: гладкой поверхности базовой грани (кривая 1), на той же поверхности с нанесенными на нее параллельными наноскопическими бороздами прямоугольного профиля глубиной в 12 кристаллографических слоев (кривая 2) и бороздами такой же глубины в виде желоба с дополнительными царапинами глубиной в один кристаллографический слой, нанесенными в перпендикулярном направлении (кривая 3). Сопоставление демонстрирует чрезвычайно сильное влияние рельефа поверхности на термодинамику растущего конденсата. Различие особенно велико на начальной стадии поглощения и постепенно нивелируется с ростом поверхностной плотности молекул.
Химический потенциал включает энергетическую и энтропийную составляющие,
(6)
${{{\mu }}_{{{\text{cl}}}}}(N,T) = {{e}_{{{\text{cl}}}}} - T{{s}_{{{\text{cl}}}}} + p{{\text{v}}_{{{\text{cl}}}}} \approx {{e}_{{{\text{cl}}}}} - T{{s}_{{{\text{cl}}}}},$Наличие в химическом потенциале (1) энтропийной составляющей делает устойчивость термодинамического состояния зависимым не только от его низкой энергии, но еще и от достаточно высокой энтропии. Более высокими значениями энтропии обладают состояния, охватывающие бóльшие объемы конфигурационного пространства. Таким состояниям отвечают более “мягкие” межмолекулярные связи. Баланс вкладов “жестких” и “мягких” связей зависит от величины температуры $T$, входящей множителем в энтропийное слагаемое $T{{s}_{{{\text{cl}}}}},$ и при повышении T статистический вес “мягких” связей растет.
Результаты моделирования показывают, что за счет наноскопических борозд прямоугольного профиля химический потенциал первых захватываемых поверхностью молекул понижается на огромную в молекулярных масштабах величину – примерно на 20kBT (кривая 2), а на поверхности с более сложным рисунком борозд – примерно на 30kBT (кривая 3). В первом случае вероятность отрыва молекул уменьшается примерно на девять, а во втором случае на четырнадцать порядков величины. В первом приближении, при прочих равных условиях во столько же раз падает плотность пара, достаточная для инициирования начала адсорбции.
Из анализа компьютерных изображений, приведенных в предыдущей статье [116], следует, что разница между кривыми 2 и 3 на их начальных участках обеспечена за счет более прочного удержания молекул в благоприятных для присоединения точках тонких царапин. Ограниченная вместимость этих мест определяет относительно небольшой диапазон давлений, в котором поверхность с тонкими царапинами демонстрирует свою повышенную поглощательную способность.
Из приведенных данных видно, что наличие наноскопических борозд существенно смещает начало адсорбционного процесса в сторону низких давлений, однако с накоплением молекул эффект ослабевает: после увеличения поверхностной плотности на порядок величины (точка N = 10 на рис. 1) химические потенциалы на обеих поверхностях с бороздами (кривые 2 и 3) выравниваются, а после увеличения плотности еще на порядок (точка N = 100 на рис. 1) эффект борозд в химическом потенциале уменьшается до 12kBT, что, тем не менее, в вероятности отрыва молекул от конденсата составляет внушительную величину, измеряемую примерно пятью порядками.
Локальный минимум на кривой 1 в точке, отвечающей шести молекулам в расчете на ячейку периодичности, отражает формирование устойчивого шестизвенного цикла. Наличие столь выраженного минимума следует отнести к артефактам периодических граничных условий, благодаря которым молекулы оказываются распределенными по поверхности более равномерно, чем в отсутствие периодических граничных условий. В этих условиях преимущество получают конфигурации, в которых синхронно, одновременно во всех ячейках периодичности формируются кластеры одного и того же наиболее устойчивого размера. В отсутствие периодических граничных условий указанный минимум был бы “смазан”. В то же время, наличие такого минимума указывает на повышенную устойчивость шестизвенных циклов. Аналогичный минимум на кривых 2 и 3 не наблюдается, так как в поле борозд условия, способствующие формированию гексагональных структур, отсутствуют. Из данных, полученных в предыдущей статье [116] для корреляционных функций, следует, что поле борозд действует на молекулярные кластеры разрушительным образом, разрывая водородные связи и разделяя молекулы. Представленные термодинамические расчеты подтверждают этот эффект.
3.2. Свободная энергия реакций присоединения
Энергия Гиббса (свободная энергия) реакции присоединения молекул пара к зародышу конденсированной фазы равна изменению энергии Гиббса $G(N,p,T)$ объединенной системы “конденсат + пар” в результате переноса одной молекулы из пара в конденсат:
где ${\mu }(p,T)$ – химический потенциал молекул пара, для которого, как правило, применяется формула идеального газа жестких ротаторов: ${\mu }(p,T) = - {{k}_{{\text{B}}}}T{\kern 1pt} {\kern 1pt} {\kern 1pt} \ln \left( {\frac{{8{{{\pi }}^{2}}}}{{\chi }}\,\,\frac{{{{k}_{{\text{B}}}}T}}{p}Z_{{{\text{tr}}}}^{{{\text{kin}}}}Z_{{{\text{rot}}}}^{{{\text{kin}}}}} \right).$ Энтальпия реакции присоединения рассчитывается как $\Delta H(N,T)$ = $[{{e}_{{{\text{cl}}}}} + p{{\text{v}}_{{{\text{cl}}}}}] - [({6 \mathord{\left/ {\vphantom {6 2}} \right. \kern-0em} 2}){{k}_{{\text{B}}}}T + p{{\text{v}}_{0}}]$ ≈ ≈ $\Delta U - {{k}_{{\text{B}}}}T,$ где $\Delta U$ = $U(N,T) - U(N - 1,T)$ = = ${{e}_{{{\text{cl}}}}} - ({6 \mathord{\left/ {\vphantom {6 2}} \right. \kern-0em} 2}){{k}_{{\text{B}}}}T$ – потенциальная часть энергии присоединения, ${{\text{v}}_{0}} = {{{{k}_{{\text{B}}}}T} \mathord{\left/ {\vphantom {{{{k}_{{\text{B}}}}T} p}} \right. \kern-0em} p}$ – удельный объем, приходящийся на одну молекулу в парах воды.Количественные результаты для $\Delta G(N,p,T)$ принято представлять в расчете на “стандартное” давление ${{p}_{0}}$ = 1 атм. Водяной пар при таком давлении и температуре 260 K в газообразном состоянии не существует, однако данное состояние используется как виртуальное для стандартизации представления данных. Пересчет к любому другому давлению $p$ реального состояния пара может быть осуществлен по формуле $\Delta G(N,p,T)$ = = $\Delta G(N,{{p}_{0}},T) - {{k}_{{\text{B}}}}T\ln ({p \mathord{\left/ {\vphantom {p {{{p}_{0}}}}} \right. \kern-0em} {{{p}_{0}}}}).$ Переход к другому значению давления приводит к смещению кривой, отражающей зависимость (2) от N, вдоль вертикальной оси без изменения ее формы. Аналогичный пересчет можно провести для остальных, связанных со свободной энергией, величин, например, для энтропии реакции присоединения $\Delta \,S(N,p,T)$ = $\Delta \,S(N,{{p}_{0}},T) + {{k}_{{\text{B}}}}\ln ({p \mathord{\left/ {\vphantom {p {{{p}_{0}}}}} \right. \kern-0em} {{{p}_{0}}}}),$ где $S(N,p,T)$ = ${{(H(N,T) - G(N,p,T))} \mathord{\left/ {\vphantom {{(H(N,T) - G(N,p,T))} T}} \right. \kern-0em} T}$ – энтропия, $H(N,T)$ – энтальпия, а $G(N,p,T)$ – энергия Гиббса объединенной системы.
При расчете величины (7) достаточно в правой части учесть только конфигурационные компоненты химических потенциалов, так как кинетические части $ - {{k}_{{\text{B}}}}T\ln \left( {\frac{{8{{{\pi }}^{2}}}}{{\chi }}Z_{{{\text{tr}}}}^{{{\text{kin}}}}Z_{{{\text{rot}}}}^{{{\text{kin}}}}} \right)$ в обоих химических потенциалах взаимно сокращаются. Поэтому ни массы, ни моменты инерции, ни симметрия молекул не влияют на величину свободной энергии реакции присоединения. Из (7) видно, что в изобарических условиях кривая $\Delta G(N,p,T)$ должна повторять форму кривой ${{{\mu }}_{{{\text{cl}}}}}(N,T)$ с некоторым сдвигом по оси ординат, зависящим от давления пара $p$.
Чтобы сопоставить вариации энергетической и энтропийной компонент в свободной энергии, на рис. 2 представлена зависимость энергии Гиббса $\Delta G(N,p,T),$ а также в наиболее интересном, начальном сегменте размеров зависимость энтальпии $\Delta H(N,T)$ реакции присоединения от количества адсорбированных молекул $N$ в пределах ячейки периодичности. Для гладкой поверхности локальный минимум на зависимости энтальпии (кривая 1 на рис. 2б) более чем на порядок величины глубже, чем на зависимости энергии Гиббса (кривая 1 на рис. 2а). В энергии Гиббса энергетическая выгодность шестизвенного цикла в значительной степени компенсируется его энтропийной невыгодностью. Относительно низкая энтропия шестизвенного кольца обусловлена повышенной жесткостью такой конструкции. Вариации энтропии существенно сглажены вариациями энергии. Этот эффект наблюдается и в случае поверхностей с нанобороздами: кривые энтальпии (рис. 2б) гораздо сильнее структурированы, чем кривые энергии Гиббса (рис. 2а). “Зигзаги” на кривых энтальпии обусловлены последовательным захватом молекул пара различными участками изрезанной поверхности, в которых энергетическая и энтропийная составляющие представлены в различных пропорциях. При этом если начальные участки кривых 2 и 3 на рис. 2б сильно различаются по форме, то после заполнения мелких царапин, при $\lg (N) > 1$ в ходе этих кривых наблюдается выраженная синхронность, отражающая сходство поверхностного рельефа. При этом на поверхностях с бороздами энергия молекул ниже примерно на 10kBT.
3.3. Энтропия
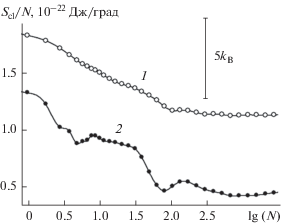
Поскольку энергия Гиббса (свободная энергия) ${{G}_{{{\text{cl}}}}}(N,T)$ = ${{E}_{{{\text{cl}}}}}(N,T) - T{{S}_{{{\text{cl}}}}}(N,T) + p{{\text{v}}_{{{\text{cl}}}}}$ конденсата в пренебрежении малым слагаемым $p{{\text{v}}_{{{\text{cl}}}}}$ отличается от его внутренней энергии ${{E}_{{{\text{cl}}}}}(N,T)$ отрицательным энтропийным слагаемым $ - T{{S}_{{{\text{cl}}}}},$ свободная энергия всегда меньше внутренней энергии. Как свидетельствуют зависимости, представленные на рис. 3, с ростом $N$ растут как свободная, так и внутренняя энергия. Разница между ними (энтропийная компонента) на поверхности по мере заполнения борозд уменьшается в расчете на одну молекулу примерно с 8kBT до 2kBT.
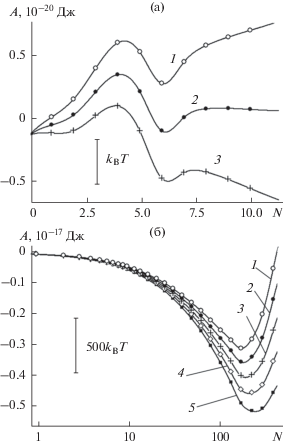
Рис. 3.
Удельная (в расчете на одну молекулу) свободная энергия (1) и внутренняя энергия ${{E}_{{{\text{cl}}}}} = {{U}_{{{\text{cl}}}}} + {{K}_{{{\text{cl}}}}}$ (с учетом потенциальной ${{U}_{{{\text{cl}}}}}$ и кинетической ${{K}_{{{\text{cl}}}}}$ частей) (2) зародыша конденсированной фазы воды, растущего из пара при 260 K на базовой грани кристалла β-AgI с наноскопическими бороздами прямоугольного профиля.
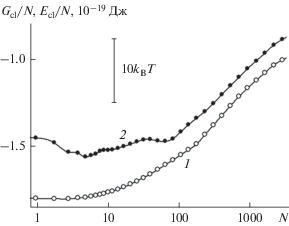
Энтропийная компонента играет в устойчивости системы существенную роль. Игнорирование энтропийной компоненты привело бы к завышению величины свободной энергии не менее чем на 2NkBT. При этом завышение только на 2kBT сопровождается погрешностью в статистическом весе состояния примерно на один порядок величины. Из данных, представленных на рис. 3 видно, что термические флуктуации приводят к радикальному перераспределению между вероятностями различных молекулярных конфигураций, причем с увеличением количества молекул эффект экспоненциально резко усиливается.
Энтропия зародыша рассчитывается через разность внутренней энергии и свободной энергии: ${{S}_{{{\text{cl}}}}} = {{(U(N,T) - {{F}_{{{\text{cl}}}}}(N,T)} \mathord{\left/ {\vphantom {{(U(N,T) - {{F}_{{{\text{cl}}}}}(N,T)} T}} \right. \kern-0em} T}.$ Удельная энтропия понижается с ростом конденсата как на поверхностях без борозд, так и с бороздами, рис. 4. При этом борозды приводят к формированию более жестких молекулярных конструкций, о чем свидетельствует меньшая энтропия. Наблюдается существенное, примерно двукратное различие. Кривая 3 на ее начальном участке проходит ниже кривой 2, что указывает на еще более жесткие конструкции, образующиеся при заполнении узких царапин.
Рис. 4.
Удельная (в расчете на одну молекулу) энтропия зародыша конденсированной фазы воды, растущего из пара при 260 K на базовой грани кристалла β-AgI. Нумерация кривых – как на рис. 1.
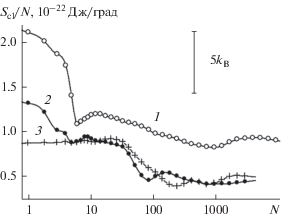
На кривой 1 рис. 4 отчетливо виден локальный минимум в точке N = 6, отвечающий повышенной жесткости шестизвенных циклов. Падение удельной энтропии превышает здесь 5kB. Отсутствие аналогичного минимума на кривых 2 и 3 подтверждает разрушительное действие борозд в отношении циклических молекулярных структур. Поскольку последние являются основным элементом мономолекулярной пленки, такая пленка в условиях борозд не образуется. Вместо этого конденсат формируется в виде несвязанных между собой фрагментов сначала на стенках борозд, а затем распространяется на их дно [116].
3.4. Термодинамическая устойчивость
Термодинамическая устойчивость является необходимым требованием, чтобы соответствующее состояние было возможно наблюдать в реальном лабораторном эксперименте. Устойчивость или неустойчивость зародыша конденсированной фазы определяется формой кривой работы его образования из пара.
Равновесная работа образования зародыша конденсата как функция количества адсорбированных молекул $N,$
на гладкой поверхности на стадии многослойной пленки и на поверхностях с бороздами представляет собой вогнутую кривую, $\frac{{{{\partial }^{2}}A(N,p,T)}}{{\partial {{N}^{2}}}} > 0,$ свидетельствующую о термодинамической устойчивости зародыша, рис. 5. Термодинамическая устойчивость означает, что зародыш в условиях термических флуктуаций не испаряется и не растет до макроскопических размеров. Его размер совершает флуктуационные колебания около равновесного значения ${{N}_{{\text{s}}}},$ отвечающего минимуму работы образования и зависящего от давления пара над поверхностью. При варьировании давления пара устойчивый размер обратимым образом увеличивается с ростом давления и уменьшается с его падением. Этот характер зависимости размера от давления следуют из полученного ранее [120–123] термодинамического тождества(9)
${{\left( {\frac{{\partial {{N}_{{{\kern 1pt} {\text{s}}}}}}}{{\partial p}}} \right)}_{T}} = \frac{{{{k}_{{\text{B}}}}T}}{p}{{\left( {\frac{{{{\partial }^{2}}{{G}_{{{\text{cl}}}}}(N,T)}}{{\partial {\kern 1pt} {{N}^{2}}}}\begin{array}{*{20}{c}} | \\ | \\ | \end{array}\begin{array}{*{20}{c}} {} \\ {} \\ {_{{N = {{N}_{{\text{s}}}}}}} \end{array}} \right)}^{{ - 1}}},$Рис. 5.
Равновесная работа образования зародыша конденсированной фазы воды из пара при 260 K на базовой грани кристалла β-AgI , отнесенная к фрагменту в пределах ячейки периодичности: (а) на поверхностях различного рельефа, нумерация кривых – как на рис. 1, давление пара 370.7 Па; (б) на поверхности без дефектов (1–3) и с наноскопическими бороздами прямоугольного профиля (4–6) в области низких значений давления пара: 4.87 (1, 4), 9.74 (2, 5), 19.5 Па (3, 6).
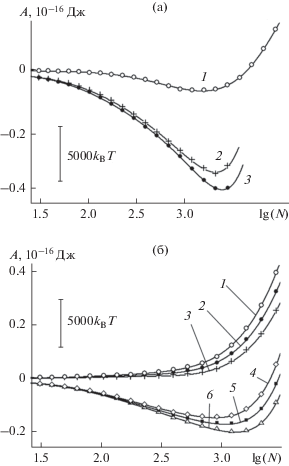
На рис. 1 видно, что на поверхностях с бороздами химический потенциал растет с $N$ гораздо быстрее, чем на гладкой поверхности – борозды усиливают устойчивость зародыша. В том же можно убедиться, сравнивая на рис. 5 форму кривой 1 с формой кривых 2, 3. Минимум работы образования в случае поверхностей с бороздами при прочих равных условиях является более глубоким и узким. Разница в глубине в расчете на одну молекулу составляет примерно kBT.
На рис. 5а представлены зависимости, как они выглядят в условиях относительно большой поверхностной плотности молекул – в несколько раз больше той, которая отвечает мономолекулярной пленке. В этих условиях положения минимумов кривой 1 и кривых 2, 3 почти совпадают – равновесный размер ${{N}_{{\text{s}}}}$ на поверхностях с бороздами такой же, как и на поверхности без борозд. Влияние борозд на величину ${{N}_{{\text{s}}}}$ усиливается с уменьшением поверхностной плотности молекул. В субмономолекулярной области наличие поверхностных борозд влечет увеличение ${{N}_{{\text{s}}}}$ на порядок величины и более. Этот случай изображен на рис. 5б: с понижением давления пара более чем на порядок величины минимум на кривых 2, 3 почти остался на старом месте, в то время как минимум на кривой 1 сместился в сторону малых размеров так сильно, что вышел за границу ${{N}_{{\text{s}}}} = 1$ и исчез как таковой. В области таких давлений пара на поверхности без борозд адсорбированных молекул практически нет, в то время как на поверхности с бороздами адсорбированные молекулы устойчиво удерживаются с плотностью, в несколько раз превышающей плотность мономолекулярной пленки. В области низких давлений пара поверхностные борозды кардинально усиливают адсорбционную способность поверхности: поверхность с бороздами может покрываться толстой полимолекулярной пленкой воды, тогда как гладкая поверхность остается практически полностью свободной от молекул. Такая картина характерна для диапазона низких давлений пара порядка 10–2–101 Па.
В области экстремально низких давлений и поверхностных плотностей адсорбированных молекул форма кривой работы образования зародыша конденсата кардинально зависит от наличия на поверхности наноскопических борозд. Если на гладкой поверхности образование шестизвенных молекулярных циклов проявляет себя в виде дополнительного характерного минимума в области $N = 6$ и максимума левее него (рис. 6а), то на кривых, полученных для поверхности с бороздами, даже при гораздо более низких давлениях пара минимума в этой области размеров нет (рис. 6б). Нет здесь и максимумов, отвечающих неустойчивости – наноборозды устраняют неустойчивость, связанную с кластеризацией.
Рис. 6.
То же, что на рис. 5, на начальной стадии зародышеобразования на поверхности без дефектов (а) и с наноскопическими бороздами прямоугольного профиля (б). В первом случае (а) давление пара: 1 – 27.6, 2 – 32.8, 3 – 39.0 Па; во втором случае (б) давление пара: 1 – 0.001, 2 – 0.002, 3 – 0.004, 4 – 0.008, 5 – 0.016 Па.
Минимум на зависимостях работы образования зародыша конденсата в области средних давлений пара имеет глубину в расчете на одну ячейку периодичности, равную примерно 103kBT, или в расчете на одну молекулу несколько kBT, рис. 6б. Относительно большая глубина этого минимума свидетельствует о высокой термодинамической устойчивости равновесного состояния: отрыв или присоединение к зародышу дополнительной молекулы сопровождается изменением вероятности соответствующего состояния более чем на порядок.
Наглядным индикатором термодинамической устойчивости является работа образования зародыша из пара, находящегося с ним в равновесии,
В отличие от (8), работе ${{A}^{{{\text{eq}}}}}(N,T)$ не соответствует какое-то единственное значение давления. Каждому значению $N$ в (10) отвечает свое давление пара p, при котором он находится в равновесии (устойчивом или неустойчивом) с конденсатом на поверхности кристалла. Это значение $p$ является точкой экстремума (минимума или максимума) функции (8).
По своему смыслу величина ${{A}^{{{\text{eq}}}}}(N,T)$ равна высоте соответствующего максимума или глубине соответствующего минимума работы образования (8). Можно показать [124], что в области убывания функции ${{A}^{{{\text{eq}}}}}(N,T)$ $\left( {\frac{{\partial {\kern 1pt} {{A}^{{{\text{eq}}}}}(N,T)}}{{\partial N}} < 0} \right)$ кривая $A(N,p,T)$ вогнута $\left( {\frac{{{{\partial }^{2}}A(N,p,T)}}{{\partial {{N}^{2}}}} > 0} \right)$ и работа $A(N,p,T)$ может иметь только минимум, означающий термодинамическую устойчивость зародыша. Наоборот, растущая функция ${{A}^{{{\text{eq}}}}}(N,T)$ указывает на его неустойчивость. Из данных, представленных на рис. 7, следует, что ${{A}^{{{\text{eq}}}}}(N,T)$ является убывающей функцией, и зародыш устойчив. Борозды на поверхности усиливают устойчивость (кривая 2 имеет более сильный наклон, чем кривая 1).
Рис. 7.
Работа образования зародыша конденсированной фазы воды на поверхности базовой грани кристалла β-AgI из пара, находящегося в материальном равновесии с зародышем, отнесенная к фрагменту в пределах ячейки периодичности размером 95.194 × 54.960 Å при 260 K: 1 – гладкая поверхность без дефектов, 2 – поверхность с параллельными наноскопическими бороздами прямоугольного профиля.
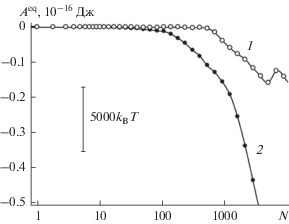
На кривой 1, отвечающей поверхности без борозд, выделяются отдельные сегменты с относительно постоянным наклоном. Сегментация зависимости ${{A}^{{{\text{eq}}}}}(N,T)$ объясняется послойным ростом зародыша. На кривой 2 следы сегментации отсутствуют, так как борозды действуют на слоистую структуру разрушительно. На поверхности с бороздами падение ${{A}^{{{\text{eq}}}}}(N,T)$ с ростом $N$ начинается раньше, чем на гладкой поверхности, – при меньшей поверхностной плотности молекул. Очевидно, для стабилизации зародыша на гладкой поверхности необходимо накопление достаточного количества связей между соседними молекулами, в то время как на поверхности с бороздами стабилизации способствует сильно неоднородное поле борозд.
3.5. Адсорбционная кривая
Представленные зависимости термодинамических характеристик объясняют ход адсорбционных кривых и механизм влияния на них наноскопических борозд. В отличие от термодинамических характеристик адсорбционные кривые наиболее доступны для прямых измерений в лабораторных исследованиях.
Адсорбционная кривая ${{N}_{{\text{s}}}}(p)$ – равновесное количество молекул, удерживаемых на поглощающей поверхности, как функция давления пара над ней рассчитывалась численным обращением вычисленной методом БСА зависимости ${{{\mu }}_{{{\text{cl}}}}}(N,T){\text{:}}$
Для рассчитанных значений ${{{\mu }}_{{{\text{cl}}}}}$ с учетом условия материального равновесия ${{{\mu }}_{{{\text{cl}}}}} = {\mu }(p,T)$ обращением функциональной зависимости (4) вычислялись соответствующие им значения давления
Из полученных таким образом в табличной форме зависимостей (11) и (12) исключался промежуточный параметр ${{{\mu }}_{{{\text{cl}}}}}$, чтобы получить зависимость ${{N}_{{\text{s}}}}(p)$.
Как видно на рис. 8а, наличие борозд приводит к сильному сдвигу начала поглощения молекул в область низких давлений. Если на гладкой поверхности формирование и рост зародыша с увеличением плотности пара происходит относительно резко (кривая 1), то на поверхности с нанобороздами он сильно растягивается в сторону низких давлений (кривая 2). В естественной среде, даже в условиях “сухой” в обыденном смысле атмосферы поверхность с наноскопическими бороздами всегда адсорбирует существенное количество влаги. При этом количество удерживаемой воды определяется поверхностной плотностью борозд.
Рис. 8.
Адсорбционные кривые. Равновесное количество молекул пара в пределах ячейки периодичности размером 95.194 × 54.960 Å на поверхности базовой грани кристалла β-AgI при 260 K (а) и то же на начальной стадии зародышеобразования (б): 1 – гладкая поверхность без дефектов, 2 – поверхность с параллельными наноскопическими бороздами прямоугольного профиля, 3 – поверхность с наноскопическими бороздами сложного профиля.
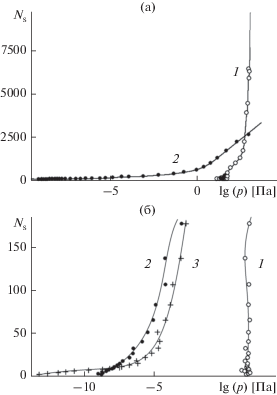
Борозды способствуют накоплению молекул воды на начальной стадии адсорбции и в то же время сдерживают переход микроконденсации в лавинообразный режим на ее заключительной стадии. Об этом свидетельствует более слабый наклон кривой 2 по сравнению с кривой 1 в области средних давлений (p > 102 Па). Таким образом, стабилизирующее действие борозд не ограничивается только областью низких давлений: если в области низких давлений борозды сдерживают испарение молекул с поверхности, то в области средних давлений они, наоборот, препятствуют росту конденсата. Молекулярный механизм сдерживания обусловлен здесь нарушением упорядоченной слоисто-гексагональной структуры зародыша. Зародыш в поле борозд становится более “рыхлым”, в нем не происходит разделение на объемные и поверхностные составляющие. В отсутствие таковых зависимость свободной энергии от размера зародыша не обретает характерную форму выпуклой кривой, и, как следствие, зависимости работы образования не имеют максимумов, которые свидетельствовали бы о термодинамической неустойчивости.
На рис. 8б представлены начальные участки адсорбционных кривых, в области низкой поверхностной плотности молекул – в субмономолекулярном режиме адсорбции, когда на поверхности наблюдаются отдельные молекулы и их небольшие кластеры. В представленном масштабе отчетливо видно, что нанесение наноскопических борозд на поверхность (кривая 2) сдвигает начало адсорбции по давлению не менее чем на 9 порядков величины, а добавление сверхтонких царапин шириной в один кристаллографический слой (кривая 3) усиливает сдвиг еще на 5 порядков. При этом в случае гладкой поверхности (кривая 1) адсорбционная кривая представляет собой почти вертикальную линию с небольшим отрицательным наклоном, свидетельствующим о состоянии, близком к неустойчивому, в то время как для поверхностей с нанобороздами (кривые 2, 3) зависимости сохраняют положительный наклон, свидетельствующий об устойчивости. Во всем рассчитанном диапазоне, за исключением области сверхнизких давлений (p < 10–10), кривая 3, отвечающая поверхности с дополнительными сверхтонкими царапинами, проходит на рис. 8б ниже кривой 2, отвечающей поверхности, не содержащей последних. Относительное положение этих кривых свидетельствует о немонотонной зависимости поглощательной способности поверхности от характеристик ее рельефа: усложнение рельефа приводит к безусловному усилению поглощения сильно разреженного пара и к обратному эффекту для пара более высокой плотности.
Полученные данные позволяют с высокой степенью уверенности предположить, что для каждого конкретного значения плотности пара существует свой оптимальный рисунок борозд, обеспечивающий максимальную адсорбционную активность поверхности. В этой многофакторной зависимости усматривается общее правило: поверхности с более сложным рельефом и высокой плотностью борозд наиболее активны в условиях сильно разреженного пара. Наоборот, гладкие поверхности или с редкими бороздами эффективны в парах высокой плотности.
3.6. Влияние температуры
Оценить влияние термических флуктуаций на термодинамическое поведение зародышей можно из сравнения зависимостей, полученных при различной температуре. На рис. 9 представлены зависимости удельной, в расчете на одну молекулу, энтропии зародышей конденсата на поверхности с бороздами. Кривая 1, полученная при более высокой температуре, более гладкая, чем кривая 2, хотя и на ней повторяются следы изгибов, отражающих неравномерное заполнение молекулами элементов рельефа. Кривая 1, полученная при температуре выше точки кипения воды, проходит выше соответствующей кривой 2, полученной при температуре ниже точки замерзания. Разница нарастает примерно с 3kB в начале кривых до 5kB в их конце. Повышение энтропии при нагревании происходит вследствие заполнения состояний с более высокой энтропией – более широких, но менее глубоких локальных минимумов на энергетической поверхности и развивается с темпом примерно в 1kB на каждые двадцать градусов.
Рис. 9.
То же, что на рис. 4, для поверхности с параллельными наноскопическими бороздами прямоугольного профиля при различных значениях температуры пара: 1 – 400, 2 – 260 K. Вертикальный отрезок указывает масштаб в единицах тепловой энергии при 260 K.
Из общего термодинамического тождества $\frac{{\partial S}}{{\partial T}} = - \frac{{{{\partial }^{2}}F}}{{\partial {{T}^{2}}}}$ видно, что темп изменения энтропии с нагреванием определяется нелинейной зависимостью свободной энергии от температуры и, с учетом связи последней со статистической суммой Q, $F = - {{k}_{{\text{B}}}}T\ln (Q),$ является компактной характеристикой рельефа энергетической поверхности в конфигурационном пространстве системы. Скорость роста энтропии с температурой служит мерой неустойчивости молекулярной конструкции к термическим флуктуациям. Из рис. 9 следует, что с ростом конденсата его устойчивость к термическим флуктуациям снижается: молекулярные кластеры на поверхности оказываются более устойчивыми, чем многослойная молекулярная пленка. В первом случае молекулы, в целом, оказываются ближе к поверхности. Это наблюдение находится в согласии с предыдущими свидетельствами стабилизирующего действия поверхности с бороздами.
Зависимость работы образования из пара, находящегося в равновесии с зародышем, рассчитанная при повышенной температуре (кривая 1 на рис. 10) смещена в сторону высоких давлений относительно кривой 2, полученной для низкой температуры, на 2–3 порядка величины, при этом форма кривой принципиально не изменилась. После повышения температуры с одновременным увеличением давления пара конденсат на поверхности ведет себя так же, как при исходной низкой температуре, хотя такие вариации температуры сопровождаются качественными изменениями состояния объемной фазы от твердокристаллического к газообразному.
Рис. 10.
То же, что на рис. 7, как функция давления пара над поверхностью с параллельными наноскопическими бороздами прямоугольного профиля при различных значениях температуры пара: 1 – 400, 2 – 260 K. Вертикальный отрезок указывает масштаб в единицах тепловой энергии при 260 K.
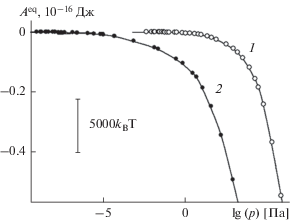
Отрицательный наклон кривой 1, свидетельствующий о термодинамической устойчивости системы, несколько больше, чем кривой 2. Следует, однако, учитывать, что устойчивость к термическим флуктуациям определяется не абсолютными значениями работы, а их относительными величинами, выраженными в единицах kBT. Если сравнивать зависимости на рис. 10 с учетом этого обстоятельства, следует заключить, что повышение температуры привело к незначительному понижению устойчивости системы.
3.7. Фундаментальные соотношения
Состояние равновесия макроскопической конденсированной фазы с паром характеризуется температурой $T$ и соответствующим ей давлением p. Зависимость равновесного давления от температуры подчиняется уравнению Клапейрона–Клаузиуса [125]
(13)
$\frac{{\partial p}}{{\partial T}} = \frac{{\lambda }}{{T({{\text{v}}_{{\text{g}}}} - {{\text{v}}_{{\text{l}}}})}},$Для описания термодинамического состояния конденсированной фазы немакроскопических размеров, требуется на одну переменную больше, чем для макроскопических фаз. Эта переменная, равновесное количество молекул ${{N}_{{\text{s}}}}$ в конденсированной системе, представляет собой дополнительную термодинамическую степень свободы. В соответствии с этим, для равновесного состояния конденсированной фазы немакроскопических размеров вместо зависимости равновесного давления от температуры $p = p(T)$ действует зависимость между тремя переменными $p = p({{N}_{{\text{s}}}},T),$ для которой вместо одного уравнения (13) зависимость положения точки равновесия от термодинамических условий характеризуется тремя производными: ${{\left( {\frac{{\partial p}}{{\partial T}}} \right)}_{{{{N}_{{\text{s}}}}}}},$ ${{\left( {\frac{{\partial {{N}_{{\text{s}}}}}}{{\partial T}}} \right)}_{p}}$ и ${{\left( {\frac{{\partial {{N}_{{\text{s}}}}}}{{\partial p}}} \right)}_{T}}.$ Первое из трех уравнений для этих производных в случае немакроскопической жидкой фазы имеет формально тот же вид, что и уравнение (13), с той лишь разницей, что входящие в его правую часть параметры ${\lambda }$ и ${{\text{v}}_{{\text{l}}}}$ должны быть отнесены к микрокапле равновесного размера, ${\lambda } \to {\lambda }({{N}_{{\text{s}}}},p,T),$ ${{\text{v}}_{{\text{l}}}} \to {{\text{v}}_{{{\text{cl}}}}}{\text{:}}$
(14)
${{\left( {\frac{{\partial p}}{{\partial T}}} \right)}_{{{{N}_{{\text{s}}}}}}} = \frac{{{\lambda }({{N}_{{\text{s}}}},p,T)}}{{T({{\text{v}}_{{\text{g}}}} - {{\text{v}}_{{{\text{cl}}}}})}}.$Чтобы получить выражение для ${{\left( {\frac{{\partial {{N}_{{\text{s}}}}}}{{\partial T}}} \right)}_{p}},$ применим известную теорему о производной функции $N(T),$ заданной в неявной форме $\Phi (N,T) = 0,$ для $\Phi (N,T) \equiv {\mu }_{{{\text{cl}}}}^{{\text{c}}}(N,T) - {{{\mu }}^{{\text{c}}}}(p,T)$ [126]:
(15)
$\frac{{\partial N}}{{\partial T}} = - {{\frac{{\partial \Phi (N,T)}}{{\partial T}}} \mathord{\left/ {\vphantom {{\frac{{\partial \Phi (N,T)}}{{\partial T}}} {\frac{{\partial \Phi (N,T)}}{{\partial N}}}}} \right. \kern-0em} {\frac{{\partial \Phi (N,T)}}{{\partial N}}}}.$Условие равенства редуцированных конфигурационных частей химических потенциалов конденсата и пара $\Phi (N,T) \equiv {\mu }_{{{\text{cl}}}}^{{\text{c}}}(N,T) - {{{\mu }}^{{\text{c}}}}(p,T) = 0$ отвечает материальному равновесию между ними, $N = {{N}_{{\text{s}}}}.$
Числитель в правой части (15) с учетом (5) имеет вид
(16)
$\begin{gathered} \frac{{\partial \Phi (N,T)}}{{\partial T}} = \frac{{\partial {\mu }_{{{\text{cl}}}}^{{\text{c}}}(N,T)}}{{\partial T}} + {{k}_{{\text{B}}}}\left( {\ln \left( {\frac{{{{k}_{{\text{B}}}}T}}{p}\text{v}_{{{\text{ref}}}}^{{ - {\text{1}}}}} \right) + 1} \right) = \\ = \frac{{\partial {{{\mu }}_{{{\text{cl}}}}}(N,T)}}{{\partial T}} + {{k}_{{\text{B}}}}\left( {\ln \left( {\frac{{8{{{\pi }}^{2}}}}{{\chi }}Z_{{{\text{tr}}}}^{{{\text{kin}}}}Z_{{{\text{rot}}}}^{{{\text{kin}}}}\frac{{{{k}_{{\text{B}}}}T}}{p}} \right) + 4} \right), \\ \end{gathered} $(17)
$\frac{{\partial \Phi (N,T)}}{{\partial N}} = \frac{{\partial {\mu }_{{{\text{cl}}}}^{{\text{c}}}(N,T)}}{{\partial N}} = \frac{{\partial {{{\mu }}_{{{\text{cl}}}}}(N,T)}}{{\partial N}}.$Последнее равенство в (17) справедливо в силу того, что разница между химическим потенциалом и его конфигурационной частью от $N$ не зависит. Подстановка производных (16) и (17) в (15) с учетом (3) позволяет получить явное выражение для темпа температурного смещения равновесного размера через энергию Гиббса (свободную энергию):
(18)
$\begin{gathered} {{\left( {\frac{{\partial {{N}_{{\text{s}}}}}}{{\partial T}}} \right)}_{p}} = - \left( {\frac{{{{\partial }^{2}}{{G}_{{{\text{cl}}}}}(N,T)}}{{\partial N\partial T}}{{{\begin{array}{*{20}{c}} | \\ | \\ | \end{array}}}_{{N = {{N}_{{\text{s}}}}}}}} \right. + \\ + \left. {{{k}_{{\text{B}}}}\left( {\ln \left( {\frac{{8{{{\pi }}^{2}}}}{{\chi }}Z_{{{\text{tr}}}}^{{{\text{kin}}}}Z_{{{\text{rot}}}}^{{{\text{kin}}}}\frac{{{{k}_{{\text{B}}}}T}}{p}} \right) + 4} \right)} \right)\,\left( {\frac{{{{\partial }^{2}}{{G}_{{{\text{cl}}}}}(N,T)}}{{\partial {{N}^{2}}}}} \right)\begin{array}{*{20}{c}} | \\ | \\ | \end{array}_{{N = {{N}_{{\text{s}}}}}}^{{ - 1}}. \\ \end{gathered} $Хотя χ, $Z_{{{\text{tr}}}}^{{{\text{kin}}}}$ и $Z_{{{\text{rot}}}}^{{{\text{kin}}}}$ присутствуют в правой части (18), из предпоследних выражений в (16) и (17) видно, что ${{\left( {\frac{{\partial {{N}_{{\text{s}}}}}}{{\partial T}}} \right)}_{p}}$ от массы, момента инерции и симметрии молекулы не зависит – вклады, содержащие χ, $Z_{{{\text{tr}}}}^{{{\text{kin}}}}$ и $Z_{{{\text{rot}}}}^{{{\text{kin}}}},$ в правой части (18) взаимно компенсируются.
Для количественно анализа ${{\left( {\frac{{\partial {{N}_{{\text{s}}}}}}{{\partial T}}} \right)}_{p}}$ вернемся к исходной форме записи (15). Перепишем ее с учетом ${\mu }_{{{\text{cl}}}}^{{\text{c}}}(N,T) - {{{\mu }}^{{\text{c}}}}(p,T)$ = ${{{\mu }}_{{{\text{cl}}}}}(N,T) - {\mu }(p,T),$ независимости кинетической части химического потенциала от $N$: $\frac{{\partial {\mu }_{{{\text{cl}}}}^{{\text{c}}}(N,T)}}{{\partial N}} = \frac{{\partial {{{\mu }}_{{{\text{cl}}}}}(N,T)}}{{\partial N}},$ а также общего термодинамического выражения химического потенциала ${\mu } = {{\left( {\frac{{\partial G}}{{\partial N}}} \right)}_{{p,T}}}$ через энергию Гиббса $G$ в виде
(19)
$\begin{gathered} {{\left( {\frac{{\partial {{N}_{{\text{s}}}}}}{{\partial T}}} \right)}_{p}} = - {{\frac{{\partial \Phi (N,T)}}{{\partial T}}{{{\begin{array}{*{20}{c}} | \\ | \\ | \end{array}}}_{{N = {{N}_{{\text{s}}}}}}}} \mathord{\left/ {\vphantom {{\frac{{\partial \Phi (N,T)}}{{\partial T}}{{{\begin{array}{*{20}{c}} | \\ | \\ | \end{array}}}_{{N = {{N}_{{\text{s}}}}}}}} {\frac{{\partial \Phi (N,T)}}{{\partial N}}{{{\begin{array}{*{20}{c}} | \\ | \\ | \end{array}}}_{{N = {{N}_{{\text{s}}}}}}}}}} \right. \kern-0em} {\frac{{\partial \Phi (N,T)}}{{\partial N}}{{{\begin{array}{*{20}{c}} | \\ | \\ | \end{array}}}_{{N = {{N}_{{\text{s}}}}}}}}} = \\ = \frac{\partial }{{\partial T}}{{\left( {{\kern 1pt} {\mu }(p,T) - {{{\mu }}_{{{\text{cl}}}}}({{N}_{{\text{s}}}},T)} \right)} \mathord{\left/ {\vphantom {{\left( {{\kern 1pt} {\mu }(p,T) - {{{\mu }}_{{{\text{cl}}}}}({{N}_{{\text{s}}}},T)} \right)} {\frac{{\partial {\mu }_{{{\text{cl}}}}^{{\text{c}}}(N,T)}}{{\partial N}}}}} \right. \kern-0em} {\frac{{\partial {\mu }_{{{\text{cl}}}}^{{\text{c}}}(N,T)}}{{\partial N}}}}{{\begin{array}{*{20}{c}} | \\ | \end{array}}_{{N = {{N}_{{\text{s}}}}}}} = \\ = \left( {\frac{{{{\partial }^{2}}{{G}_{{\text{v}}}}({{N}_{{\text{v}}}},p,T)}}{{\partial {{N}_{{\text{v}}}}\partial T}}} \right. - \\ - \,\,{{\left. {\frac{{{{\partial }^{2}}{{G}_{{{\text{cl}}}}}(N,T)}}{{\partial N\partial T}}{{{\begin{array}{*{20}{c}} | \\ | \end{array}}}_{{N = {{N}_{{\text{s}}}}}}}} \right)} \mathord{\left/ {\vphantom {{\left. {\frac{{{{\partial }^{2}}{{G}_{{{\text{cl}}}}}(N,T)}}{{\partial N\partial T}}{{{\begin{array}{*{20}{c}} | \\ | \end{array}}}_{{N = {{N}_{{\text{s}}}}}}}} \right)} {\frac{{{{\partial }^{2}}{{G}_{{{\text{cl}}}}}(N,T)}}{{\partial {{N}^{2}}}}}}} \right. \kern-0em} {\frac{{{{\partial }^{2}}{{G}_{{{\text{cl}}}}}(N,T)}}{{\partial {{N}^{2}}}}}}{{\begin{array}{*{20}{c}} | \\ | \end{array}}_{{N = {{N}_{{\text{s}}}}}}}, \\ \end{gathered} $(20)
$\begin{gathered} {{\left( {\frac{{\partial {{N}_{{\text{s}}}}}}{{\partial T}}} \right)}_{p}} = - \left( {\frac{{\partial {{S}_{{\text{v}}}}({{N}_{{\text{v}}}},p,T)}}{{\partial {{N}_{{\text{v}}}}}}{{ - }^{{^{{^{{^{{}}}}}}}}}} \right. \\ - \,\,{{\left. {\frac{{\partial {{S}_{{{\text{cl}}}}}(N,T)}}{{\partial N}}{{{\begin{array}{*{20}{c}} | \\ | \end{array}}}_{{N = {{N}_{{\text{s}}}}}}}} \right)} \mathord{\left/ {\vphantom {{\left. {\frac{{\partial {{S}_{{{\text{cl}}}}}(N,T)}}{{\partial N}}{{{\begin{array}{*{20}{c}} | \\ | \end{array}}}_{{N = {{N}_{{\text{s}}}}}}}} \right)} {\frac{{{{\partial }^{2}}{{G}_{{{\text{cl}}}}}(N,T)}}{{\partial {{N}^{2}}}}}}} \right. \kern-0em} {\frac{{{{\partial }^{2}}{{G}_{{{\text{cl}}}}}(N,T)}}{{\partial {{N}^{2}}}}}}{{\begin{array}{*{20}{c}} | \\ | \end{array}}_{{N = {{N}_{{\text{s}}}}}}} = \\ = - {{\left( {{{s}_{{\text{v}}}}(p,T) - {{s}_{{{\text{cl}}}}}({{N}_{{\text{s}}}},T)} \right)} \mathord{\left/ {\vphantom {{\left( {{{s}_{{\text{v}}}}(p,T) - {{s}_{{{\text{cl}}}}}({{N}_{{\text{s}}}},T)} \right)} {\frac{{{{\partial }^{2}}{{G}_{{{\text{cl}}}}}(N,T)}}{{\partial {{N}^{2}}}}}}} \right. \kern-0em} {\frac{{{{\partial }^{2}}{{G}_{{{\text{cl}}}}}(N,T)}}{{\partial {{N}^{2}}}}}}{{\begin{array}{*{20}{c}} | \\ | \end{array}}_{{N = {{N}_{{\text{s}}}}}}} = \\ = - {{\frac{{{\lambda }({{N}_{{\text{s}}}},p,T)}}{T}} \mathord{\left/ {\vphantom {{\frac{{{\lambda }({{N}_{{\text{s}}}},p,T)}}{T}} {\frac{{{{\partial }^{2}}{{G}_{{{\text{cl}}}}}(N,T)}}{{\partial {{N}^{2}}}}}}} \right. \kern-0em} {\frac{{{{\partial }^{2}}{{G}_{{{\text{cl}}}}}(N,T)}}{{\partial {{N}^{2}}}}}}{{\begin{array}{*{20}{c}} | \\ | \end{array}}_{{N = {{N}_{{\text{s}}}}}}}, \\ \end{gathered} $Система уравнений (9), (14) и (20) является обобщением уравнения Клапейрона–Клаузиу-са (13) на случай немакроскопической жидкой фазы и представляет собой универсальные термодинамические соотношения, определяющие положение поверхности равновесия в трехмерном пространстве переменных N, $p$ и T.
3.8. Равновесный размер: универсальные соотношения и результаты моделирования
Поскольку энтропия конденсата всегда ниже энтропии пара, ${{s}_{{{\text{cl}}}}}({{N}_{{\text{s}}}},T) < {{s}_{{\text{v}}}}(p,T),$ а теплота испарения всегда положительна, ${\lambda }({{N}_{{\text{s}}}},p,T) > 0,$ числитель (20) всегда отрицателен, и направление изменения равновесного размера зародыша ${{N}_{{\text{s}}}}$ с вариациями температуры определяется знаком знаменателя (20), $\frac{{{{\partial }^{2}}{{G}_{{{\text{cl}}}}}(N,T)}}{{\partial {{N}^{2}}}}{{\begin{array}{*{20}{c}} | \\ | \end{array}}_{{N = {{N}_{{\text{s}}}}}}}.$ Работа образования (8) отличается от ${{G}_{{{\text{cl}}}}}(N,T)$ линейным по $N$ слагаемым. Поэтому их вторые производные совпадают: $\frac{{{{\partial }^{2}}{{G}_{{{\text{cl}}}}}(N,T)}}{{\partial {{N}^{2}}}}$ = $\frac{{{{\partial }^{2}}A(N,p,T)}}{{\partial {{N}^{2}}}}.$ В точке равновесия фаз кривая работы образования имеет либо минимум, либо максимум. Если это минимум $\left( {\frac{{{{\partial }^{2}}A(N,p,T)}}{{\partial {{N}^{2}}}}{{{\begin{array}{*{20}{c}} | \\ | \end{array}}}_{{N = {{N}_{{\text{s}}}}}}} > 0} \right)$, выражение (20) отрицательно, и с ростом температуры равновесный размер уменьшается. Наоборот, если в точке равновесия сформировался максимум, $\frac{{{{\partial }^{2}}A(N,p,T)}}{{\partial {{N}^{2}}}}{{\begin{array}{*{20}{c}} | \\ | \end{array}}_{{N = {{N}_{{\text{s}}}}}}}$ < 0, представляющий собой барьер росту зародыша, с повышением температуры он сдвинется в сторону бо'льших размеров.
Таким образом, в условиях фиксированного давления с повышением температуры устойчивый равновесный размер всегда уменьшается, а барьер свободной энергии, если он образуется, смешается к большим размерам. Темп смещения определяется абсолютными значениями числителя и знаменателя (20). Чем меньше по абсолютной величине в точке экстремума производная $\frac{{{{\partial }^{2}}A(N,p,T)}}{{\partial {{N}^{2}}}},$ тем шире соответствующий максимум или минимум работы образования и тем чувствительнее величина равновесного размера зародыша к вариациям температуры. Узкий минимум, означающий высокую устойчивость зародыша к термическим флуктуациям, означает и слабую чувствительность его размера к вариациям температуры. Повышенная термодинамическая устойчивость зародышей на поверхностях с бороздами означает более глубокие минимумы на кривой работы образования и высокие значения $\frac{{{{\partial }^{2}}{{G}_{{{\text{cl}}}}}(N,T)}}{{\partial {{N}^{2}}}}{{\begin{array}{*{20}{c}} | \\ | \end{array}}_{{N = {{N}_{{\text{s}}}}}}},$ которые, в свою очередь, согласно (20), влекут ослабление зависимости равновесного размера зародышей от температуры.
Темп смещения равновесного размера зависит также от абсолютной величины числителя (20). Чем больше по абсолютной величине теплота испарения, тем выше чувствительность равновесного размера зародыша к вариациям температуры. Из того же выражения видно, что изменение степени упорядоченности при конденсации, количественной мерой которого является изменение энтропии, непосредственно влияет на чувствительность размера зародыша к вариациям температуры. Чем выше степень упорядоченности конденсированной фазы по сравнению с газообразной, тем сильнее зависимость равновесного размера зародыша от температуры. В частности, следует ожидать ослабление зависимости равновесного размера от температуры при приближении к критической точке.
Общие соотношения для производных в точках экстремумов работы образования (9), (20) содержат прямые указания на фундаментальные факторы, определяющие форму кривых работы образования, без чего невозможно понимание физики явления. Темп смещения экстремумов при вариациях температуры и давления определяется зависимостью энергии Гиббса от размера, а также теплотой испарения, которые, принципиально, могут быть рассчитаны численно методом БСА и подставлены в формулы (9), (20). Однако этот путь менее рационален, чем прямой расчет зависимостей работы образования, поскольку предполагает вычисление производных, что сопряжено с дополнительными погрешностями численной аппроксимации. В данном исследовании численный расчет производился для зависимостей работы образования, а проверка согласия численных результатов с общими соотношениями для точек экстремумов выполнена на качественном уровне.
На рис. 11 представлены рассчитанные методом БСА пары кривых работы образования, 1, 4, 2, 5 и 3, 6. Кривые в каждой паре получены для различных значений температуры, но одного и того же давления. Кривые в различных парах отличаются величиной давления. В полном соответствии с полученными выше уравнениями с повышением температуры при постоянном давлении устойчивый размер (положение минимума) смещается в сторону меньших размеров, а при повышении давления пара при фиксированной температуре – в сторону больших размеров.
Рис. 11.
То же, что на рис. 5, на поверхности с наноскопическими бороздами прямоугольного профиля для двух значений температуры, 400 (1–3) и 260 K (4–6). Давление пара над поверхностью: 27.6 (1, 4), 77.9 (2, 5), 220.4 Па (3, 6). Вертикальный отрезок указывает масштаб в единицах тепловой энергии при 260 K.
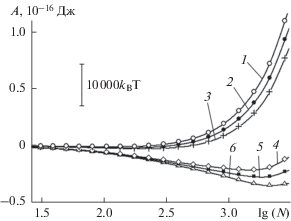
Смещение величины равновесного размера для каждого значения давления имеет своим результатом смещение всей адсорбционной кривой. С увеличением давления растет равновесный размер ${{N}_{{\text{s}}}}$ и вместе с ним в знаменателе (20) быстро уменьшается, приближаясь к своему макроскопическому пределу, равному нулю, производная $\frac{{{{\partial }^{2}}{{G}_{{{\text{cl}}}}}(N,T)}}{{\partial {{N}^{2}}}}{{\begin{array}{*{20}{c}} | \\ | \end{array}}_{{N = {{N}_{{\text{s}}}}}}}$ – минимум на зависимости работы образования становится более широким, что должно приводить к росту ${{\left( {\frac{{\partial {{N}_{{\text{s}}}}}}{{\partial T}}} \right)}_{p}}.$ Одновременно с ростом давления примерно по логарифмическому закону падает удельная энтропия пара, а энтропия конденсата почти не изменяется. Это приводит к уменьшению по абсолютной величине числителя (20) и работает в сторону падения ${{\left( {\frac{{\partial {{N}_{{\text{s}}}}}}{{\partial T}}} \right)}_{p}}.$ Направление результирующего изменения температурного смещения определяется соотношением между темпами, с которыми изменяются числитель и знаменатель. Как правило, при приближении к насыщающему давлению рост равновесного размера зародыша идет ускоренными темпами, становясь лавинообразным, в то время как относительно медленное, по логарифмическому закону уменьшение с ростом давления энтропии пара в числителе (20) рано или поздно отстает от уменьшения знаменателя. Результатом является быстрый рост ${{\left( {\frac{{\partial {{N}_{{\text{s}}}}}}{{\partial T}}} \right)}_{p}}$ для достаточно больших Ns.
Именно такой характер зависимостей воспроизводится в численных расчетах. Две адсорбционные кривые, полученные для поверхности с наноскопическими бороздами при различных температурах методом БСА, выглядят почти параллельными, со сдвигом высокотемпературной кривой в сторону высоких давлений (рис. 12). Из-за резкого увеличения наклона при приближении к насыщающему давлению расстояние между кривыми, отсчитанное по вертикали, с ростом давления быстро увеличивается, что является прямым свидетельством роста ${{\left( {\frac{{\partial {{N}_{{\text{s}}}}}}{{\partial T}}} \right)}_{p}}$ по абсолютной величине, при этом, в полном согласии с (20), направление сдвига соответствует ее отрицательному знаку.
Рис. 12.
То же, что на рис. 8, для поверхности с параллельными наноскопическими бороздами прямоугольного профиля при различных значениях температуры пара: 1 – 400, 2 – 260 K. Стрелками указаны величины давления насыщенного пара над плоской поверхностью жидкой воды и переохлажденной жидкой воды.
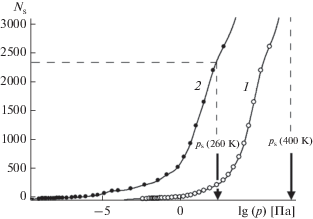
Следует отметить, что, несмотря на относительно большую разницу в температуре, разделяющую кристаллическое и газообразное состояния воды при нормальных условиях, обе кривые в логарифмическом масштабе давлений имеют практически одну и ту же форму.
4. ЗАКЛЮЧЕНИЕ
Компьютерное моделирование демонстрирует существенное, примерно на 20kBT понижение химического потенциала первых адсорбированных молекул пара за счет нанесенных на поверхность наноскопических борозд, а добавление сверхтонких царапин понижает его еще на 10kBT. Результатом является смещение начала зародышеобразования в область разреженного пара на порядки величины по его плотности, при этом адсорбционная кривая сильно вытягивается в сторону низких давлений.
В поле наноборозд происходит разрушение гексагональной структуры, характерной для кластеров и пятен мономолекулярной пленки на начальной стадии адсорбции пара. Результатом является сглаживание зависимости работы образования адсорбированного материала и повышение термодинамической устойчивости на ранней стадии зародышеобразования. Наноборозды способствуют устойчивости зародышей и на последующих стадиях, сдерживая переход в лавинообразный рост.
Для анализа физических факторов, влияющих на формирование температурной зависимости состояния равновесия зародыша конденсированной фазы с паром, получена система фундаментальных уравнений, являющаяся обобщением уравнения Клапейрона–Клаузиуса на конденсированные фазы немакроскопических размеров. Найдено явное выражение для темпа изменения равновесного размера зародыша с температурой через энергию Гиббса и удельную теплоту парообразования. Полученные универсальные соотношения находятся в принципиальном согласии с результатами численного моделирования и на поверхностях с нанобороздами предсказывают ослабление зависимости адсорбционной кривой от температуры.
Полученные результаты доказывают, что нанесение наноборозд на поверхность является эффективным способом программирования ее адсорбционных свойств и активности в качестве агента гетерогенной нуклеации паров воды. Эффективность данного инструмента особенно высока в условиях разреженных паров и ослабляется по мере приближения к насыщающему давлению.
По всей видимости, наблюдаемые для паров воды закономерности справедливы и для широкого круга веществ с полярными молекулами, а явление повышенной адсорбционной способности поверхности с нанобороздами может быть использовано при конструировании чувствительных газоанализаторов и тонких фильтров очистки. Полученные общие сведения о влиянии рельефа поверхности на ее поглощательную способность могут быть полезными и при изучении работы органов обоняния животных.
Работа выполнена при поддержке Министерства образования и науки РФ (проект № 3.4808.2017/6.7) и Российского фонда фундаментальных исследований (проект № 18-03-00011-a).
Список литературы
Кугатов П.В., Баширов И.И., Жирнов Б.С. // Коллоид. журн. 2015. Т. 77. С. 464.
Смагин А.В. // Коллоид. журн. 2016. Т. 78. С. 380.
Назаров В.Г., Столяров В.П. // Коллоид. журн. 2016. Т. 78. С. 59.
Школин А.В., Фомкин А.А. // Коллоид. журн. 2017. Т. 79. С. 661.
Yamauchi Y.U., Блонская И.В., Апель П.Ю. // Коллоид. журн. 2017. Т. 79. С. 668.
Фомкин А.А., Меньшиков И.Е., Прибылов А.А., Гурьянов В.В., Школин А.В., Зайцев Д.С., Твардовский А.В. // Коллоид. журн. 2017. Т. 79. С. 96.
Сизова А.А., Сизов В.В., Бродская Е.Н. // Коллоид. журн. 2018. Т. 80. С. 458.
Ma X., Li L., Chen R., Wang C., Zhou K., Li H. // Appl. Surf. Sci. 2018. V. 459. P. 657.
Matin A., Baig U., Gondal M. A., Akhtar S., Zubair S.M. // Appl. Surf. Sci. 2018. V. 462. P. 95.
Saengkaew J., Le D., Samart C., Sawada H., Nishida M., Chanlek N., Kongparakul S., Kiatkamjornwong S. // Appl. Surf. Sci. 2018. V. 462. P. 164.
Волошин В.П., Маленков Г.Г., Наберухин Ю.И. // Журн. cтрукт. химии. 2013. Т. 54 (S2). С. 239.
Маленков Г.Г. // Журн. cтрукт. химии. 2016. Т. 57. С. 831.
Маленков Г.Г. // Журн. cтрукт. химии. 2017. Т. 58. С. 166.
Баханова Р.А., Киселев В.И., Куку Е.И., Ким Н.С., Школкин А.В. // Физика облаков и активные воздействия. Труды Украинского регионального научно-исследовательского гидрометеорологического института. Под ред. Бахановой Р.А, Осокиной И.Н. М.: Гидрометеоиздат, 1991. Вып. 242. С. 102.
Водопьянов М.Я., Пермяков Г.Н., Чурбанов Е.В. // Труды Всесоюзной конференции “Активные воздействия на гидрометеорологические процессы”, Нальчик, 22–25 октября 1991 г. СПб.: Гидрометеоиздат, Т. 2. С. 166.
Шевкунов С.В. // ЖЭТФ. 1995. Т. 108. С. 1373.
Шевкунов С.В. // Докл. АН. 2005. Т. 402. С. 41.
Шевкунов С.В. // Коллоид. журн. 2005. Т. 67. С. 548.
Шевкунов С.В. // Журн. общей химии. 2005. Т. 75. С. 1709.
Шевкунов С.В. // Электрохимия. 2006. Т. 42. С. 10.
Шевкунов С.В. // Журн. физ. химии. 2006. Т. 80. С. 884.
Шевкунов С.В. // Коллоид. журн. 2006. Т. 68. С. 391.
Шевкунов С. В. // Коллоид. журн. 2006. Т. 68. С. 691.
Шевкунов С.В. // Коллоид. журн. 2007. Т. 69. С. 390.
Шевкунов С.В. // Коллоид. журн. 2007. Т. 69. С. 409.
Шевкунов С.В. // ЖЭТФ. 2008. Т. 134. С. 1130.
Шевкунов С.В. // Докл. АН. 2011. Т. 438. С. 752.
Шевкунов С.В. // Коллоид. журн. 2012. Т. 74. С. 612.
Шевкунов С.В. // Коллоид. журн. 2012. Т. 74. С. 634.
Шевкунов С.В. // Коллоид. журн. 2014. Т. 76. С. 243.
Шевкунов С.В. // Коллоид. журн. 2014. Т. 76. С. 263.
Шевкунов С.В. // Коллоид. журн. 2006. Т. 68. С. 405.
Шевкунов С. В. // Теплофизика выс. температур 2015. Т. 53. С. 270.
Шевкунов С.В. // Коллоид. журн. 2017. Т. 79. С. 644.
Шевкунов С.В. // Коллоид. журн. 2018. Т. 80. С. 224.
Шевкунов С.В. // Журн. структ. химии. 2018. Т. 59. С. 618.
Kopani M., Mikula M., Kosnac D., Vojtek P., Gregus J., Vavrinsky E., Jergel M., Pincik E. // Appl. Surf. Sci. 2018. V. 461. P. 44.
Li Y., Zhang D., Han M., He J., Wang Y., Wang K., Wang Y. // Appl. Surf. Sci. 2018. V. 458. P. 119.
Hutli E., Nedeljkovic M., Bonyár A. // Appl. Surf. Sci. 2018. V. 458. P. 293.
Irmer B., Blick R.H., Simmel F., Gödel W., Lorenz H., Kotthaus J.P. // Appl. Phys. Lett. 1998. V. 73. P. 2051.
Cortes Rosa J., Wendel M., Lorenz H., Kotthaus J.P., Thomas M., Kroemer H. // Appl. Phys. Lett. 1998. V. 73. P. 2684.
Попова Л.М., Введение в нанотехнологию. СПб.: Изд-во Санкт-Петербургского технологического университета растительных полимеров, 2013.
Hill T.L. Thermodynamics of Small Systems, Parts I & II. New York: Dover, 2013.
Зубарев Д.Н. Неравновесная статистическая термодинамика. М.: Мир, 1971.
Kashchiev D. Nucleation: Basic Theory with Applications. Oxford: Butterworth-Heinemann, 2000.
Wyslouzil B.E., Wolk J. // J. Chem. Phys. 2016. V. 145. 211 702.
Filipponi A., Giammatteo P. // J. Chem. Phys. 2016. V. 145. 211 913.
Plankova B., Vins V., Hruby J. // J. Chem. Phys. 2017. V. 147. 164 702.
Amaya A.J., Wyslouzil B.E. // J. Chem. Phys. 2018. V. 148. 084501.
Галимзянов Б.Н., Мокшин А.В. // Коллоид. журн. 2017. Т. 79. С. 16.
Zwanzig R.W. // J. Chem. Phys. 1954. V. 22. P. 1420.
Henderson D., Barker J.A. // Phys. Rev. A. 1970. V. 1. P. 1266.
Luzhkov V.B. // J. Chem. Phys. 2010. V. 132. 194104.
Vaikuntanathan S., Jarzynski C. // J. Chem. Phys. 2011. V. 134. 054107.
Miyata T., Ikuta Y., Hirata F. // J. Chem. Phys. 2010. V. 133. 044114.
Harvey J.-P., Gheribi A.E., Chartrand P. // J. Chem. Phys. 2011. V. 135. 084502.
Moustafa S.G., Schultz A.J., Kofke D.A. // J. Chem. Phys. 2013. V. 139. 084105.
Widom B. // J. Chem. Phys. 1963. V. 39. P. 2808.
Malasics A., Boda D. // J. Chem. Phys. 2010. V. 132. 244103.
Mirzaeinia A., Feyzi F., Hashemianzadeh S.M. // J. Chem. Phys. 2017. V. 147. 214503.
Lyubartsev A.P., Martsinovski A.A., Shevkunov S.V., Vorontsov-Velyaminov P.N. // J. Chem. Phys. 1992. V. 96. P. 1776.
Warshel A. // J. Phys. Chem. 1982. V. 86. P. 2218.
Bash P.A., Singh U.C., Langridge R., Kollman P.A. // Science. 1987. V. 236. P. 564.
Carlson H.A., Nguyen T.B., Orozco M., Jorgensen W.L. // J. Comput. Chem. 1993. V. 14. P. 1240.
Chipot C., Millot C., Maigret B., Kollman P.A. // J. Chem. Phys. 1994. V. 101. P. 7953.
Pohorille A., Benjamin I. // J. Chem. Phys. 1991. V. 94. P. 5599.
Шевкунов С.В. // Журн. общей химии. 2002. Т. 72. С. 735.
Шевкунов С.В. // Журн. общей химии. 2004. Т. 74. С. 1585.
Шевкунов С.В. // ЖЭТФ. 2009. Т. 136. С. 282.
Шевкунов С.В. // Докл. АН. 2010. Т. 433. С. 761.
Pohorille A., Benjamin I. // J. Chem. Phys. 1991. V. 94. P. 5599.
Leung K., Rempe S.B., von Lilienfeld O.A. // J. Chem. Phys. 2009. V. 130. 204507.
Bash P.A., Singh U.C., Brown F.K., Langridge R., Kollman P.A. // Science. 1987. V. 235. P. 574.
Merz K.M., Kollman P.A. // J. Am. Chem. Soc. 1989. V. 111. P. 5649.
Hirono S., Kollman P.A. // J. Mol. Biol. 1990. V. 212. P. 197.
Cummins P.L., Ramnarayan K., Singh U.C., Gready J.E. // J. Am. Chem. Soc. 1991. V. 113. P. 8247.
Reddy M.R., Viswanadhan V.N., Weinstein J.N. // Proc. Natl. Acad. Sci. U.S.A. 1991. V. 88. P. 10287.
Miyamoto S., Kollman P.A. // Proc. Natl. Acad. Sci. U.S.A. 1993. V. 90. P. 8402.
Ustinov E. // J. Chem. Phys. 2017. V. 146. 034110.
Asthagiri D., Pratt L.R., Kress J.D. // Phys. Rev. E. 2003. V. 68. 041505.
Sabo D., Varma S., Martin M.G., Rempe S.B. // J. Phys. Chem. B. 2008. V. 112. P. 867.
Duignan T.T., Baer M.D., Schenter G.K., Mundy C.J. // J. Chem. Phys. 2017. V. 147. 161716.
Perlman D.A., Kollman P.A. // J. Chem. Phys. 1989. V. 91. P. 7831.
Torrie G.M., Valleau J.P. // J. Comput. Phys. 1977. V. 23. P. 187.
Bennett C.H. // J. Comput. Phys. 1976. V. 22. P. 245.
Christ C.D., van Gunsteren W.F. // J. Chem. Phys. 2008. V. 128. 174112.
Tan T.B., Schultz A.J., Kofke D.A. // J. Chem. Phys. 2010. V. 132. 214103.
Gao Y.Q. // J. Chem. Phys. 2008. V. 128. 064105.
Yang L., Shao Q., Gao Y.Q. // J. Chem. Phys. 2009. V. 130. 124111.
Gao Y.Q. // J. Chem. Phys. 2008. V. 128. 134111.
Gao Y.Q., Yang L., Fan Y., Shao Q. // Int. Rev. Phys. Chem. 2008. V. 27. P. 201.
Yang L., Gao Y.Q. // J. Chem. Phys. 2009. V. 131. 214109.
Yang M., Yang L., Gao Y., Hu H. // J. Chem. Phys. 2014. V. 141. 044108.
Xie L., Shen L., Chen Z.-N., Yang M. // J. Chem. Phys. 2017. V. 146. 024103.
Ferrenberg A.M., Swendsen R.H. // Phys. Rev. Lett. 1988. V. 61. P. 2635.
Ferrenberg A.M., Swendsen R.H. // Phys. Rev. Lett. 1989. V. 63. P. 1195.
Lindahl V., Lidmar J., Hess B. // J. Chem. Phys. 2014. V. 141. 044110.
Шевкунов С.В. // Письма в ЖЭТФ. 2002. Т. 76. С. 828.
Шевкунов С.В. // Коллоид. журн. 2004. Т. 66. С. 263.
Шевкунов С.В. // Коллоид. журн. 2004. Т. 66. С. 554.
Шевкунов С.В. // Коллоид. журн. 2004. Т. 66. С. 566.
Шевкунов С.В. // Химия высоких энергий. 2005. Т. 39. С. 405.
Шевкунов С.В. // Журн. вычисл. математики и мат. физики. 2005. Т. 45. С. 2283.
Cao L., Stoltz G., Lelièvre T., Marinica M.-C., Athènes M. // J. Chem. Phys. 2014. V. 140. 104108.
Шевкунов С.В. // Коллоид. журн. 2005. Т. 67. С. 561.
Шевкунов С.В. // Коллоид. журн. 2009. Т. 71. С. 404.
Шевкунов С.В. // Журн. физ. химии. 2011. Т. 85. С. 1702.
Шевкунов С.В. // Коллоид. журн. 2015. Т. 77. С. 384.
Шевкунов С.В. // Коллоид. журн. 2016. Т. 78. С. 124.
Шевкунов С.В. // ЖЭТФ. 2009. Т. 135. С. 510
Shevkunov S.V., Lukyanov S.I., Leyssale J.-M., Millot C. // Chem. Phys. 2005. V. 310. P. 97.
Lukyanov S.I., Zidi Z.S., Shevkunov S.V. // Chem. Phys. 2007. V. 332. P. 188.
Lukyanov S.I., Zidi Z.S., Shevkunov S.V. // Fluid Phase Equilib. 2005. V. 233. P. 34.
Шевкунов С.В. // Электрохимия. 2014. Т. 50. С. 1260.
Shevkunov S.V., Singh J.K. // J. Mol. Liq. 2018. V. 264. P. 150.
Шевкунов С.В. // Коллоид. журн. 2019. Т. 81. С. 367.
Замалин В.М., Норман Г.Э., Филинов В.С. Метод Монте-Карло в статистической термодинамике. М.: Наука, 1977.
Киттель Ч. Статистическая термодинамика. М.: Наука, 1977.
Хилл Т. Статистическая механика. М.: ИЛ, 1960.
Шевкунов С.В. // Коллоид. журн. 2011. Т. 73. С. 267.
Шевкунов С.В. // Коллоид. журн. 2011. Т. 73. С. 123.
Шевкунов С.В. // Коллоид. журн. 2014. Т. 76. С. 533.
Шевкунов С.В. // Коллоид. журн. 2016. Т. 78. С. 509.
Шевкунов С.В. // Коллоид. журн. 2018. Т. 80. С. 241.
Румер Ю.Б., Рывкин М.Ш. Термодинамика, статистическая физика и кинетика. М: Наука, 1972. С. 90.
Фихтенгольц Г.М., Курс дифференциального и интегрального исчисления. Т. 1. Издание седьмое. М.: Наука, 1979. С. 451.
Дополнительные материалы отсутствуют.
Инструменты
Коллоидный журнал


