Коллоидный журнал, 2019, T. 81, № 5, стр. 584-589
Об информативности высших моментов в хроматографии
А. В. Ларин *
Институт физической химии и электрохимии им. А.Н. Фрумкина РАН
119071 Москва,
Ленинский проспект, 31, Россия
* E-mail: larin@phyche.ac.ru
Поступила в редакцию 18.02.2019
После доработки 01.03.2019
Принята к публикации 11.03.2019
Аннотация
На основе модели слоя равновесной адсорбции получены аналитические решения для обычных, нормированных и высших (третьего и четвертого порядка) центральных моментов. Решения представляют собой одночленные дроби и включают в себя длину слоя адсорбента, скорость подвижной фазы, эффективную кинетическую константу и константу Генри. Для третьего и четвертого моментов получены выражения для входного сигнала прямоугольной формы, проведен их анализ. Показано, что вычисление высших моментов при решении обратной задачи хроматографии не дает новой информации о кинетических или каких-то других свойствах слоя адсорбента.
ВВЕДЕНИЕ
Обратную задачу феноменологической теории линейной хроматографии можно определить как вычисление эффективного коэффициента массопереноса (кинетической константы) и адсорбционной константы Генри. Для высокоэффективной хроматографии решение обратной задачи получено в рамках теории тарелок [1]. Позднее для решения обратной задачи линейной хроматографии был предложен метод моментов [2], который до этого широко использовался и используется сейчас в математической статистике. В [2] были получены аналитические решения для центра тяжести и второго центрального момента, из которых вычисляется эффективная кинетическая константа и адсорбционная константа Генри. Детальный анализ этих решений представлен в [3].
Уже в [2] были получены аналитические решения для высших центральных моментов, вплоть до пятого. Утверждалось, что высшие моменты могут дать дополнительную информацию о свойствах слоя адсорбента, находящегося в динамических условиях конвективного массопереноса веществ в потоке инертной подвижной фазы. В дальнейшем, предположение о том, что высшие моменты дают дополнительную информацию в хроматографическом исследовании, были продолжены. В [4] говорится о том, что третий и четвертый центральный моменты необходимы для детального изучения свойств несимметричных кривых элюирования. Проведенные в [4] теоретические и экспериментальные исследования фактически не доказали полезность высших моментов. В других экспериментальных исследованиях, например, в [5], методом обращенно-фазовой жидкостной хроматографии были изучены несимметричные кривые элюирования двух пептидов. Далее были рассчитаны третий и четвертый центральный моменты и на этой основе проведено неинформативное обсуждение причин несимметричности кривых элюирования.
Экспериментальные и теоретические исследования высших моментов продолжаются и в настоящее время. В [6] предполагают, что поскольку третий момент характеризует симметрию кривой элюирования, то это является туннелем, через который можно получить дополнительную информацию о процессах массопереноса. В [7, 8] подчеркивается, что первые два момента не могут характеризовать кривую элюирования полностью, а более высокие моменты необходимы для количественного описания важных кинетических процессов в слое адсорбента.
Другие авторы в своих работах также предполагали использование высших моментов в анализе экспериментальных данных. В [9] изучены первые три центральных момента, а в [10] оперируют с первыми четырьмя центральными моментами. Интересно, что позднее те же авторы разошлись в своих оценках возможности использования высших моментов. В [11] метод моментов был применен к анализу кривых элюирования, полученных на колонках с обращенными фазами и различающихся степенью симметрии. При этом были использованы только первые два момента. В то же время в [12] при изучении массопереноса веществ через насадочные колонки цилиндрической формы использовали все те же четыре центральных момента.
Отметим, что сами аналитические выражения для моментов, анализируемые в [2, 4–12], представляют собой суммы рациональных дробей и явно не являются корректными решениями, что и проанализировано в [3]. Кроме того, в представленных работах отсутствуют решения для вклада в величину третьего и четвертого моментов начальных условий, а именно формы входного сигнала. Не приведены полностью решения для обычных моментов. Представляется актуальным более детально, на основе достоверной теоретической модели рассмотреть свойства высших моментов в хроматографии.
Целью работы явилось получение новых аналитических решений для третьего и четвертого центральных моментов в хроматографии, оценка вклада входного сигнала в эти моменты и анализ их информативности.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
В теории тарелок [1] для решения прямой задачи хроматографии применяется уравнение, которое в модели слоя равновесной адсорбции записывается в виде
(1)
${{c}_{n}}{{\left( t \right)} \mathord{\left/ {\vphantom {{\left( t \right)} {{{c}_{0}}}}} \right. \kern-0em} {{{c}_{0}}}} = {\text{exp}}{{\left( { - bt} \right){{{\left( {bt} \right)}}^{{n\, - \,1}}}} \mathord{\left/ {\vphantom {{\left( { - bt} \right){{{\left( {bt} \right)}}^{{n\, - \,1}}}} {\left( {n - 1} \right)}}} \right. \kern-0em} {\left( {n - 1} \right)}}!,$В теории тарелок уравнение (1) используется как промежуточное для получения симметричной кривой Гаусса при допущении
$n \to \infty .$ В модели слоя равновесной адсорбции уравнение (1) обосновано в [13] на основе численных решений для натуральных n. Позднее уравнение (1) было распространено на область действительных 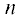 [14, 15], когда факториал действительного числа определяется через гамма-функцию Эйлера.
[14, 15], когда факториал действительного числа определяется через гамма-функцию Эйлера.
Обычные моменты вычисляются по уравнению
где $k$ – порядок обычного момента, $c\left( t \right)$ – экспериментальная или теоретическая кривая элюирования.В математике известно равенство $\int_0^\infty {{{e}^{{ - t}}}} {{t}^{n}}dt = n!,$ полученное интегрированием по частям. Используя тот же прием интегрирования по частям, для уравнений (1) и (2) имеем решение
(3)
${{m}_{k}} = {{\left( {n + k - 1} \right)!} \mathord{\left/ {\vphantom {{\left( {n + k - 1} \right)!} {{{b}^{{k\, + \,1}}}\left( {n - 1} \right)!.}}} \right. \kern-0em} {{{b}^{{k\, + \,1}}}\left( {n - 1} \right)!.}}$На основании уравнения (3), публикуемого впервые, запишем аналитические решения для обычных моментов:
(4)
$\begin{gathered} {{m}_{0}} = {{\left( {n - 1} \right)!} \mathord{\left/ {\vphantom {{\left( {n - 1} \right)!} {b\left( {n - 1} \right)!}}} \right. \kern-0em} {b\left( {n - 1} \right)!}} = {1 \mathord{\left/ {\vphantom {1 b}} \right. \kern-0em} b}, \\ {{m}_{1}} = {{n!} \mathord{\left/ {\vphantom {{n!} {{{b}^{2}}}}} \right. \kern-0em} {{{b}^{2}}}}\left( {n - 1} \right)! = {n \mathord{\left/ {\vphantom {n {{{b}^{2}}}}} \right. \kern-0em} {{{b}^{2}}}}, \\ {{m}_{2}} = {{\left( {n + 1} \right)!} \mathord{\left/ {\vphantom {{\left( {n + 1} \right)!} {{{b}^{3}}}}} \right. \kern-0em} {{{b}^{3}}}}\left( {n - 1} \right)! = {{n\left( {n + 1} \right)} \mathord{\left/ {\vphantom {{n\left( {n + 1} \right)} {{{b}^{3}}}}} \right. \kern-0em} {{{b}^{3}}}}, \\ {{m}_{3}} = {{\left( {n + 2} \right)!} \mathord{\left/ {\vphantom {{\left( {n + 2} \right)!} {{{b}^{4}}}}} \right. \kern-0em} {{{b}^{4}}}}\left( {n - 1} \right)! = n{{\left( {n + 1} \right)\left( {n + 2} \right)} \mathord{\left/ {\vphantom {{\left( {n + 1} \right)\left( {n + 2} \right)} {{{b}^{4}}}}} \right. \kern-0em} {{{b}^{4}}}}, \\ {{m}_{4}} = {{\left( {n + 3} \right)!} \mathord{\left/ {\vphantom {{\left( {n + 3} \right)!} {{{b}^{5}}\left( {n - 1} \right)!}}} \right. \kern-0em} {{{b}^{5}}\left( {n - 1} \right)!}} = \\ = n\left( {n + 1} \right)\left( {n + 2} \right){{\left( {n + 3} \right)} \mathord{\left/ {\vphantom {{\left( {n + 3} \right)} {{{b}^{5}}.}}} \right. \kern-0em} {{{b}^{5}}.}} \\ \end{gathered} $Центр тяжести ${{t}_{{\text{c}}}},$ который в литературе обычно называется первым моментом, был вычислен в [16] как отношение первых двух моментов (4):
(5)
${{t}_{{\text{c}}}} = {{{{m}_{1}}} \mathord{\left/ {\vphantom {{{{m}_{1}}} {{{m}_{0}}}}} \right. \kern-0em} {{{m}_{0}}}} = {{\left( {{n \mathord{\left/ {\vphantom {n {{{b}^{2}}}}} \right. \kern-0em} {{{b}^{2}}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{n \mathord{\left/ {\vphantom {n {{{b}^{2}}}}} \right. \kern-0em} {{{b}^{2}}}}} \right)} {\left( {{1 \mathord{\left/ {\vphantom {1 b}} \right. \kern-0em} b}} \right)}}} \right. \kern-0em} {\left( {{1 \mathord{\left/ {\vphantom {1 b}} \right. \kern-0em} b}} \right)}} = {n \mathord{\left/ {\vphantom {n b}} \right. \kern-0em} b}.$(6)
$\begin{gathered} {{\vartheta }_{1}} = {n \mathord{\left/ {\vphantom {n b}} \right. \kern-0em} b},\,\,\,\,{{\vartheta }_{2}} = n{{\left( {n + 1} \right)} \mathord{\left/ {\vphantom {{\left( {n + 1} \right)} {{{b}^{2}}}}} \right. \kern-0em} {{{b}^{2}}}}, \\ {{\vartheta }_{3}} = n\left( {n + 1} \right){{\left( {n + 2} \right)} \mathord{\left/ {\vphantom {{\left( {n + 2} \right)} {{{b}^{3}}}}} \right. \kern-0em} {{{b}^{3}}}}, \\ {{\vartheta }_{4}} = n\left( {n + 1} \right)\left( {n + 2} \right){{\left( {n + 3} \right)} \mathord{\left/ {\vphantom {{\left( {n + 3} \right)} {{{b}^{4}}}}} \right. \kern-0em} {{{b}^{4}}}}. \\ \end{gathered} $Второй центральный момент был вычислен в [17] по уравнению
(7)
${{{\mu }}_{2}} = {{\vartheta }_{2}} - \vartheta _{1}^{2} = n{{\left( {n + 1} \right)} \mathord{\left/ {\vphantom {{\left( {n + 1} \right)} {{{b}^{2}}}}} \right. \kern-0em} {{{b}^{2}}}} - {{({n \mathord{\left/ {\vphantom {n b}} \right. \kern-0em} b})}^{2}} = {n \mathord{\left/ {\vphantom {n {{{b}^{2}}}}} \right. \kern-0em} {{{b}^{2}}}}.$(8)
${{{\mu }}_{3}} = {{2n} \mathord{\left/ {\vphantom {{2n} {{{b}^{3}}}}} \right. \kern-0em} {{{b}^{3}}}}.$(9)
${{{\mu }}_{4}} = 3n{{\left( {n + 2} \right)} \mathord{\left/ {\vphantom {{\left( {n + 2} \right)} {{{b}^{4}}}}} \right. \kern-0em} {{{b}^{4}}}}.$(10)
$\begin{gathered} {{c}_{0}}\left( t \right) = {{c}_{{\text{f}}}} = {\text{const}}\,\,{\text{п р и }}\,\,0 \leqslant t \leqslant {{T}_{{\text{f}}}}, \\ {{c}_{0}}\left( t \right) = 0\,\,\,\,{\text{п р и }}\,\,\,\,t \geqslant {{T}_{{\text{f}}}}, \\ \end{gathered} $Для начальных условий (10) по уравнению (2) были рассчитаны начальные моменты и из них определены нормированные моменты:
(11)
$\begin{gathered} \vartheta _{1}^{0} = {{{{T}_{{\text{f}}}}} \mathord{\left/ {\vphantom {{{{T}_{{\text{f}}}}} 2}} \right. \kern-0em} 2},\,\,\,\,\vartheta _{2}^{0} = {{T_{{\text{f}}}^{2}} \mathord{\left/ {\vphantom {{T_{{\text{f}}}^{2}} 3}} \right. \kern-0em} 3}, \\ \vartheta _{3}^{0} = {{T_{{\text{f}}}^{3}} \mathord{\left/ {\vphantom {{T_{{\text{f}}}^{3}} 4}} \right. \kern-0em} 4},\,\,\,\,\vartheta _{4}^{0} = {{T_{{\text{f}}}^{4}} \mathord{\left/ {\vphantom {{T_{{\text{f}}}^{4}} 5}} \right. \kern-0em} 5}. \\ \end{gathered} $ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ
Численный эксперимент проводили на основе теории слоя равновесной адсорбции [18]. При численном моделировании элюат вводили прямоугольным импульсом, отметим этот ввод “1”. Другим изученным входным импульсом был мгновенный, который задается δ-функцией Дирака. Отметим этот ввод как “2”. Длительность ввода пробы ${{T}_{{\text{f}}}}$ составляла 2 с. При мгновенном вводе количество вещества выбиралось равным его количеству, вводимому в виде прямоугольника.
Численное моделирование проводили при условиях, когда объемная скорость подвижной фазы $w$ = 0.926 см3/с, масса слоя равновесной адсорбции ${{m}_{{\text{e}}}}$ = 0.152 г, величина удельного удерживаемого объема ${{V}_{{{\text{Rm}}}}}$ = 6.7 см3/г. Выбранные для моделирования значения указанных параметров соответствуют используемым при исследовании фронтальной динамики адсорбции изотопов аргона на активированном угле из потока гелия. Такие же значения параметров использовались в [19] для моделирования влияния начального сигнала в виде произвольного треугольника на характеристики кривых элюирования.
Кривые элюирования при относительной длине слоя адсорбента $n = 2$ приведены на рис. 1. Отметим, что рассчитанные концентрации для кривой 2 на рис. 1 представлялись в виде табличных данных с интервалом по времени, равным 0.01 с. Для кривой 1 (рис. 1) интервал по времени составлял 0.1 с. Выбранные интервалы времени обеспечивали высокую точность последующего вычисления начальных моментов. Из начальных моментов рассчитывались нормированные и высшие моменты, значения которых приведены в табл. 1.
Рис. 1.
Кривые элюирования, смоделированные для условий, когда входной сигнал задан прямоугольником (1) и функцией Дирака (2) (мгновенный ввод). Относительная длина слоя адсорбента $n$ = 2.
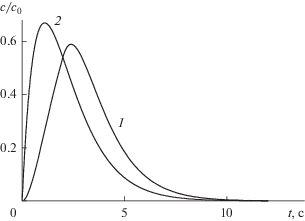
Таблица 1.
Значения нормированных и центральных моментов, вычисленные для двух видов входного сигнала
| Тип входного сигнала | ${{\vartheta }_{1}},$ с | ${{\vartheta }_{2}},$ с2 | ${{\vartheta }_{3}},$ с3 | ${{\vartheta }_{4}},$ с4 | ${{\mu }_{2}},$ с2 | ${{\mu }_{3}},$ с3 | ${{\mu }_{4}},$ с4 |
|---|---|---|---|---|---|---|---|
| Прямоугольный сигнал (1) | 3.20 | 12.99 | 64.49 | 382.08 | 2.75 | 5.32 | 40.14 |
| Функция Дирака (2) | 2.20 | 7.26 | 31.92 | 175.44 | 2.42 | 5.32 | 35.00 |
| Разница значений моментов для случаев 1 и 2 | 1.0 | – | – | – | 0.33 | 0 | 5.14 |
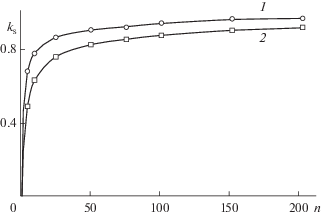
Для изучения зависимости симметрии кривых элюирования от относительной длины слоя адсорбента было проведено численное моделирование этих кривых согласно уравнению (1) в интервале 5 $ \leqslant n \leqslant $ 200 при $b$ = 0.9 с–1. Степень симметрии кривых элюирования определяли через коэффициент их симметрии ${{k}_{{\text{s}}}}$. Этот коэффициент равен отношению отрезков (на фиксированной относительной высоте кривой элюирования $l$), измеряемых от передней границы до абсциссы максимума кривой и от абсциссы максимума до задней границы кривой элюирования. Вычисления проведены для значений $l$ = 0.1 и 0.5. Полученные зависимости приведены на рис. 2. Отметим, что и при других значениях константы $b$ зависимости, приведенные на рис. 2, не изменяются.
ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ
В [3] отмечалось, что все утверждения о том, что высшие моменты, начиная с момента третьего порядка, могут дать дополнительную информацию об элюировании веществ в хроматографических колонках, до настоящего времени разумного объяснения не получили. Рассмотрим полученные решения для третьего и четвертого моментов.
Сравним уравнения моментов, полученные выше на основе модели слоя равновесной адсорбции, с уравнениями, представленными в литературе. Уравнения моментов, особенно, высших порядков, содержат большое количество слагаемых [2, 4–10, 12]. Каждое слагаемое представляет собой произведение и отношение физико-химических констант и опытных величин, т.е. является рациональной (алгебраической) дробью. В модели слоя равновесной адсорбции моменты описываются одним слагаемым, которое представляется отношением простых выражений $n$ к константе $b$ с изменяющейся степенью: для высших моментов это уравнения (8) и (9).
Используя полученные уравнения и числовые значения величин скорости подвижной фазы, эффективной кинетической константы и константы Генри, которые применялись при численном моделировании кривых элюирования, можно сравнить результаты расчета по указанным уравнениям с результатами, полученными в численном эксперименте.
В табл. 1 приведены значения нормированных моментов и высших моментов, рассчитанные из кривой элюирования, которая была определена методом численного эксперимента для условий мгновенного ввода (кривая 2 на рис. 1). Полагая, что первый нормированный момент численно равен выражению для центра тяжести или первому моменту, можно провести сравнение моментов, полученных по результатам численного эксперимента и аналитических решений. Все значения моментов, представленные в табл. 1, точно совпадают со значениями моментов, вычисленными из уравнений (5), (7), (8) и (9).
Небольшое отличие наблюдается для нормированного и центрального моментов четвертого порядка. Для этих моментов расчет по уравнениям (6) и (9) дает значения, отличающиеся от значений, вычисленных из смоделированной кривой на величину, не превышающую 0.3%. Эта ошибка может быть вызвана недостаточно точным выбором интервала интегрирования, что особенно сказывается на вычислениях моментов высших порядков [4].
Проведенное сравнение показывает высокую точность численного эксперимента, проведенного в соответствии с положениями модели слоя равновесной адсорбции [18]. С другой стороны, обнаруженное совпадение значений моментов, рассчитанных различными способами, свидетельствует о корректности уравнений, полученных выше. Еще раз отметим, что эти уравнения включают в себя только переменные $n$ и b. Это позволяет утверждать, что высшие моменты определяются только этими переменными, для вычисления которых требуются два момента: центр тяжести кривой элюирования или первый момент и второй центральный момент.
Оценим решения для вкладов входного сигнала в изменение значений моментов высшего порядка. Для центра тяжести, который может быть определен в табл. 1 через первый нормированный момент, разница значений этого момента, рассчитанная с учетом входного прямоугольного сигнала и при условии мгновенного ввода, задаваемого функцией Дирака, составляет 1 с (табл. 1). Это значение соответствует известному уравнению ${{{{T}_{{\text{f}}}}} \mathord{\left/ {\vphantom {{{{T}_{{\text{f}}}}} 2}} \right. \kern-0em} 2}$ [20] и доказывает соблюдение принципа аддитивности вкладов в первый момент входного сигнала и процессов, происходящих непосредственно в слое адсорбента. Такое же соответствие наблюдается и для второго момента, когда та же разница равна 0.33 с2, что совпадает с решением ${{T_{{\text{f}}}^{2}} \mathord{\left/ {\vphantom {{T_{{\text{f}}}^{2}} {12}}} \right. \kern-0em} {12}}$ [20].
Для центрального момента третьего порядка обнаружено, что вклад входного прямоугольного сигнала в изменение величины этого момента является нулевым – уравнение (12). Это и наблюдается в полученных результатах (табл. 1), когда разница рассчитанных для прямоугольного и мгновенного ввода вещества значений ${{{\mu }}_{3}}$ равна нулю.
Для центрального момента четвертого порядка не наблюдается соответствия полученного уравнения (12) результатам численного эксперимента. Разница между моментами, вычисленными из кривых элюирования для случаев прямоугольного входного импульса и при мгновенном вводе вещества, составляет 5.14 с4, что сильно отличается от значения, рассчитанного по уравнению (12). Расчеты для других значений ${{T}_{{\text{f}}}}$ также показали несовпадение этих величин. Можно предположить, что для четвертого центрального момента правило аддитивности вкладов в этот момент входного сигнала и процессов, происходящих непосредственно в слое адсорбента, не соблюдается.
Из полученных результатов следует, что даже по формальному принципу решения для уравнений моментов, представленные в [2, 4–10, 12] и других многочисленных работах различных авторов, нельзя назвать удобными для анализа экспериментальных данных. Эти решения не только менее удобны по сравнению решениями в виде уравнений (5), (7), (8) и (9), полученными с использованием модели слоя равновесной адсорбции, но и могут приводить к существенным ошибкам при анализе получаемых данных.
Метод моментов, используемый в математической статистике, действительно, оперирует с высшими центральными моментами, каждый из которых по-своему характеризует кривую распределения. Но, в отличие от конкретных статистик, в которых число переменных фиксировано, например в социологических исследованиях, в хроматографии реализуются процессы с функциональным изменением одной из важнейших характеристик процесса – относительной длины слоя адсорбента. Поэтому моменты высшего порядка не могут давать дополнительную информацию о динамических процессах, происходящих в хроматографической колонке.
Ранее было рассмотрено изменение симметрии кривой элюирования в зависимости от относительной длины слоя адсорбента [21]. Эти вычисления повторены в настоящей работе в более широком интервале изменения $n$ для двух разных по отношению к максимуму значениях высоты кривой элюирования (рис. 2).
Из результатов, представленных на рис. 2, следует, что такая важная характеристика как симметрия кривой элюирования, связанная с третьим центральным моментом, имеет функциональную зависимость от относительной длины слоя адсорбента $n$. При этом получаемые зависимости совпадают друг с другом при любых значениях константы $b$ и легко могут быть линеаризованы [22]. Это еще раз свидетельствует о том, что высшие моменты не дают дополнительной информации о динамических и кинетических свойствах хроматографического процесса.
ЗАКЛЮЧЕНИЕ
На основании модели слоя равновесной адсорбции получены аналитические решения для высших центральных моментов третьего и четвертого порядка. Высшие моменты описываются одним слагаемым в виде алгебраической дроби, которая представляет собой отношение простых выражений относительной длины слоя адсорбента $n$ к константе $b$ с изменяющейся степенью. Таким образом, высшие моменты определяются теми же величинами, что и центр тяжести (первый момент) и второй центральный момент. Это означает, что высшие моменты не могут дать дополнительную информацию о динамических и кинетических процессах, происходящих в хроматографической колонке.
Об этом же свидетельствует обнаруженная устойчивость зависимости коэффициента симметрии от относительной длины слоя адсорбента. Полученные результаты уточняют возможности решения обратной задачи хроматографии на основе метода моментов, позволяющего определять адсорбционную и кинетическую константу хроматографической системы.
Список литературы
Martin A.J.P., Synge R.L.M. // Biochem. J. 1941. V. 35. P. 1358.
Kucera E. // J. Chromatogr. 1965. V. 19. P. 237.
Ларин А.В. // Коллоид. журн. 2019. Т. 81. С. 185.
Vidal-Madjar C., Guiochon G. // J. Chromatogr. 1977. V. 142. P. 61.
Choi D.Y., Row K.H. // Biotechnol. Bioprocess Eng. 2004. V. 9. P. 495.
Gao H., Stevenson P.G., Gritti F., Guiochon G. // J. Chromatogr. 2012. V. 1222. P. 81.
Gao H., Wu X., Lin B. // J. Chromatogr. Sci. 2010. V. 48. P. 478.
Gao H., Wu X., Lin B. // J. Chromatogr. Sci. 2010. V. 48. P. 742.
Miyabe K. // Trends Anal. Chem. 2016. V. 81. P. 79.
Qamar Sh., Seidel-Morgenstern A. // Trends Anal. Chem. 2016. V. 81. P. 87.
Miyabe K. // J. Chromatogr. 2018. V. 1567. P. 155.
Qamar Sh., Uche D.U., Khan F.U., Seidel-Morgenstern A. // J. Chromatogr. 2017. V. 1496. P. 96.
Ларин А.В. // Изв. АН СССР. Cер. хим. 1984. С. 1212.
Ларин А.В. // Инж.-физ. журн. 2011. Т. 84. С. 1175.
Ларин А.В. // Изв. АН. Сер. хим. 2011. С. 367.
Ларин А.В. // Коллоид. журн. 2011. Т. 73. С. 858.
Ларин А.В. // Коллоид. журн. 2012. Т. 74. С. 430.
Ларин А.В. // Изв. АН СССP. Cер. хим. 1983. С. 236.
Ларин А.В. // Коллоид. журн. 2018. Т. 80. С. 411.
Sternberg J.C. // In Advances in Chromatography. V. 2. Ed. by Giddings J.C., Keller R.A. New York: Marcel Dekker, 1966. P. 205.
Губкина М.Л., Ларин А.В., Шеховцова Л.Г. // Изв. АН СССР. Сер. хим. 1985. С. 513.
Ларин А.В. // Неопубликованные результаты.
Дополнительные материалы отсутствуют.
Инструменты
Коллоидный журнал