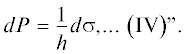Коллоидный журнал, 2019, T. 81, № 6, стр. 767-773

ВВЕДЕНИЕ

Термодинамика тонких пленок знаменательна, прежде всего, тем, что выходит за рамки гиббсовской теории капиллярности, составляющей основу современной термодинамики поверхностных явлений. Это новый раздел термодинамики, сформировавшийся ближе к середине 20 в. и освященный брендом расклинивающего давления. Открытие последнего и его последующие исследования школой Дерягина подробно описаны в монографии [1], а термодинамическая интерпретация расклинивающего давления – в обзоре [2]. Дерягин [3] дал определение расклинивающего давления Π как (формула Дерягина)

где ${{p}^{\alpha }}$– внешнее давление на пленку, а ${{p}^{\beta }}$ – давление в равновесной материнской объемной фазе β тонкой пленки. Фаза β может находиться в равновесии с пленкой при контакте с ее торцом, но реальное присутствие фазы β не обязательно (${{p}^{\beta }}$ может быть расчетным значением давления для фазы β при тех же значениях температуры и химических потенциалов, какие есть в пленке). Благодаря формуле Дерягина, где фигурируют лишь фазовые давления, расклинивающее давление легко вошло в термодинамику фазовых равновесий [4–9].

В традиционной теории капиллярности есть похожая и не менее знаменитая разность давлений: капиллярное давление Лапласа

где σ – поверхностное натяжение и R – радиус межфазной разделяющей поверхности. Есть даже случаи, когда разности давлений в формулах Дерягина и Лапласа совпадают (например, для сидящего на плоской поверхности пузырька), однако их судьба в термодинамике разная. При решении задач теории капиллярности редко капиллярное давление рассматривается как отдельный параметр и с особым обозначением вводится в термодинамические формулы. Обычно фазовые давления рассматриваются как отдельные переменные, и это правильно, поскольку они могут меняться независимо. Очевидно, та же ситуация и в случае разности давлений в формуле Дерягина, но здесь, наоборот, расклинивающее давление считается основной переменной и буквально “царит” во всех формулах теории. В данном сообщении мы хотели бы обратить внимание на то, что расклинивающее давление – сложносоставная величина и его изменение за счет только ${{p}^{\alpha }}$ или только ${{p}^{\beta }}$ – это разные вещи.

В историческом плане пионером термодинамики тонких пленок следует считать А.Н. Фрумкина. О его близости к термодинамике говорит и факт перевода им (вместе с П.А. Ребиндером) на русский язык “Термодинамики” Планка еще в 1919 г., и то, что уже в 1938 г. он пользуется понятием химического потенциала (называя его термодинамическим потенциалом или просто потенциалом) [10, 11] – главной величиной всей термодинамики Гиббса. Тогда термин “расклинивающее давление” еще не вошел в обиход, и А.Н. Фрумкин (под впечатлением опытов Б.В. Дерягина и M.M. Кусакова [12] по исследованию равновесной толщины пленки h как функции внешнего давления P) ставил задачей установить связь между P и поверхностным натяжением “слоя под пузырьком” σ. Приведем рассуждения А.Н. Фрумкина дословно [10]. “Так как ${v}dP = - d\mu $ (I – А.Р.), где μ – потенциал слоя, V – молекулярный объем вещества слоя (пренебрегая зависимостью последнего от P), и $sd\sigma = - d\mu $(II), то ${v}dP = sd\sigma $ (III) и

Уравнение Фрумкина IV фигурирует в его статье [10] под номером (1). Мы же отдадим первый номер модификации IV

связанной с тем обстоятельством, что вариация расклинивающего давления в опытах Б.В. Дерягина достигалась именно изменением P.

А теперь посмотрим внимательно на цитируемый текст. Читатель, знакомый с термодинамикой, должен заметить, что из четырех формул верна только формула II, в которой угадывается уравнение адсорбции Гиббса при условии, что адсорбируется лишь один компонент. Главная ошибка заключена в формуле I. По идее это уравнение Гиббса–Дюгема, но тогда должен быть плюс, а не минус. Кроме того, уравнение Гиббса–Дюгема относится к объемной фазе и неприложимо к тонкой пленке. Дальше – больше. Если по ходу вывода устранить ошибку в знаке, получится минус в формуле (1). Но это рушит всю концепцию работы [10]: она уже не объясняет опыты Б.В. Дерягина, а, наоборот, противоречит им. Формула же (1), результат какой-то нелепой ошибки типа описки, после цитирования Б.В. Дерягиным [13] работы [11] (правда, в несколько другом плане) начинает свой путь по литературе под именем уравнения Фрумкина. В этом контексте самое удивительное, что оно все-таки оказалось правильным при определенных условиях. Автору самому приходилось выводить уравнение Фрумкина несколько раз [2, 8, 9, 14], каждый раз комплиментарно ссылаясь на работу [10] и нарушая свое же железное правило – при цитировании смотреть первоисточник. Хорош! – скажет читатель – всю жизнь цитировал А.Н. Фрумкина, а теперь решил с ним разобраться. Но, как говорится, лучше поздно, чем никогда. Посмотрим, какие существуют подходы к выводу соотношений типа уравнения Фрумкина.

МЕТОД ПОВЕРХНОСТНОГО СЛОЯ КОНЕЧНОЙ ТОЛЩИНЫ

Поскольку сама тонкая пленка имеет конечную толщину, казалось, что более естественно рассматривать ее на основе метода поверхностного слоя конечной толщины, т.е. как составную часть реального поверхностного слоя [4–9]. При этом толщина поверхностного слоя и толщина тонкой пленки – совершенно разные вещи (первая – неопределенна, вторая – весьма конкретна). Неопределенность толщины поверхностного слоя связана с формулировкой самого метода. В строгой трактовке [16–19] толщина поверхностного слоя задается введением двух разделяющих поверхностей, но избытки берутся только с внешних сторон: в пространстве между разделяющими поверхностями находится то, что там реально есть. Чем больше разделяющие поверхности удаляются друг от друга, двигаясь каждая в глубину прилегающей объемной фазы, тем меньше внешние избытки. Положение, когда ими можно пренебречь, – чисто практическая условность (например, избытки должны быть такими, что и погрешность измерений). Поэтому толщина поверхностного слоя определяется по-разному для каждой методики. Статистическая механика определяет законы асимптотического описания поверхностных слоев (при стремлении расстояний к бесконечности), но на практике мы пользуемся конечными расстояниями и размерами (например, объемами макроскопических фаз). Поэтому термодинамические уравнения для поверхностного слоя конечной толщины часто имеют тот же вид, что и уравнения для двухфазной системы в целом (включая поверхностный слой).

В работах [4–9] тонкая пленка на границе фаз рассматривалась в масштабе всей межфазной неоднородной области, включая поверхностные слои прилегающих к пленке фаз. В качестве последних могли быть и твердые тела, сближением которых исследовалось расклинивающее давление пленки. Термодинамика твердых поверхностей еще не была развита, и для твердых тел использовались фундаментальные уравнения жидких фаз. Важно было другое – что каждое такое тело было непроницаемым и нерастворимым по отношению к пленке. При этом было строго показано, что в формулах типа уравнения Фрумкина должна стоять толщина только собственно жидкой прослойки за вычетом толщин поверхностных зон всех прилегающих фаз. В качестве примера приведем формулу из [8, c. 295] со своим номером

где γ – натяжение пленки (с вкладом от всей межфазной неоднородности, т.е. по существу межфазное натяжение поверхности, куда входит и пленка), а $\tau {\kern 1pt} '$ – толщина собственно жидкой прослойки (т.е. тонкой пленки), T – температура, P – давление в материнской фазе пленки. Таким образом, особенностью формулы (XIII.109) является то обстоятельство, что в левой части (в величине γ) учитываются вклады от поверхностных слоев прилегающих к пленке тел, а в правой части они, наоборот, исключаются.

Конечно, метод слоя конечной толщины включает в себя и элементы гиббсовского подхода там, где дело касается поверхностного натяжения. Без этой величины не обойтись, но ведь она требует истинной (геометрической) поверхности, а не слоя. С другой стороны, для изучения многокомпонентных поверхностных слоев требуется такое общепринятое в химии понятие как состав. Набор гиббсовских адсорбций вряд ли для этого подойдет. Тут необходим набор реальных мольных долей компонентов поверхностного слоя, и метод слоя конечной толщины отлично с ними справляется. Эти проблемы решаются и для тонких пленок: ведь любая из них – это тоже слой конечной толщины. Однако по мере развития термодинамики тонких пленок метод Гиббса проникал в нее во все большей степени. Можно сказать, что если метод слоя конечной толщины способствовал практическим приложениям теории, то метод Гиббса чаще поднимал принципиальные вопросы. И в них-то хорошим индикатором может служить уравнение Фрумкина. Ниже мы рассмотрим разновидности метода Гиббса, связанные с использованием разного числа разделяющих поверхностей.

МЕТОД ГИББСА С ОДНОЙ РАЗДЕЛЯЮЩЕЙ ПОВЕРХНОСТЬЮ

Это самый простой подход: тонкая пленка рассматривается лишь как составная часть межфазной переходной области, а все выводы делаются на основе термодинамики поверхностных явлений. При этом неважно, является ли пленка смачивающей или адсорбционной, для термодинамики это без разницы, и всегда можно опираться на уравнение адсорбции Гиббса. В данной работе будем считать, что одна из фаз – твердая (пусть это будет фаза γ в контакте с фазой α, индекс β сбережем для материнской фазы пленки). Тогда работает обобщенное уравнение адсорбции Гиббса [15] (еще более общие уравнения для твердых поверхностей можно найти в [14])

где ${{\sigma }^{{\alpha \gamma }}}$ – термодинамическое поверхностное натяжение межфазной поверхности αγ, $\bar {s}$ – избыток энтропии на единицу поверхности, T – температура, $\hat {\gamma }$ – тензор механического поверхностного натяжения, $\hat {1}$ – единичный тензор (символ Кронекера), ${{\hat {e}}^{\sigma }}$ – тензор поверхностной деформации (двоеточие означает бискалярное произведение тензоров), ${{\Gamma }_{i}}$ и μ_i – адсорбция и химический потенциал компонента i. Особо отметим, что химический потенциал самого твердого тела (величина тензорная) не входит в правую часть (2) (он был использован при выводе второго слагаемого).

Для жидкостей механическое и термодинамическое определения поверхностного натяжения дают один и тот же результат, тензоры в круглых скобках совпадают, и второе слагаемое в правой части (2) исчезает. С другой стороны, второе слагаемое элиминируется и в случае абсолютно твердого тела, поскольку оно не способно к деформации, $d{{\hat {e}}^{\sigma }}$ = 0. Таким образом, традиционная форма уравнения адсорбции Гиббса восстанавливается не только для жидкости, но и для твердого тела, если оно не способно к деформации. Считая фазу γ недеформируемой и нерастворимой (с четкой граничной поверхностью), запишем (2) в виде

Следуя Гиббсу, уравнение (3) нужно рассматривать совместно с уравнениями Гиббса–Дюгема для объемных фаз. В нашем случае тонкой пленки имеются два таких уравнения: для прилегающей к твердой поверхности с пленкой фазы α

и для материнской фазы пленки β

где p – давление, ${{s}_{{v}}}$ – объемная плотность энтропии и ${{c}_{i}}$ – концентрация компонента i.

Если пленка и ее материнская фаза состоят только из одного вещества (пусть это будет компонент 1) и оно не входит в фазу α, то из (5) получаем

Подстановка (6) в (3) дает

Хотя адсорбция может быть любого знака, для массивной смачивающей пленки она, конечно, положительна, и, считая, что плотность пленки соответствует плотности ее материнской фазы, можно принять

где ${{h}_{1}}$ – толщина пленки первого компонента. Тогда из (7) находим

Из (4) следует, что при постоянстве температуры и химических потенциалов давление ${{p}^{\alpha }}$ также постоянно. Но тогда, согласно формуле Дерягина, $d\Pi = - d{{p}^{{\beta }}},$ и (9) можно переписать как

Допустим теперь, что компонент 1 входит и в фазу α. Тогда (9) остается в силе, но закрепление температуры и остальных химических потенциалов (например, путем контакта с атмосферой, куда не входит компонент 1) уже не приводит к постоянству давления ${{p}^{\alpha }}.$ Уравнения (4) и (5) принимают вид

откуда следует, что оба давления изменяются одновременно при условии

Если, например, фаза α – газ, а фаза β – жидкость вдали от критической точки, то изменение ${{p}^{\alpha }}$ будет малым по сравнению с изменением ${{p}^{{\beta }}}.$ Тогда не только (9), но и практически (10) сохранит работоспособность. Но в общем случае давления ${{p}^{\alpha }}$ и ${{p}^{{\beta }}}$ работают раздельно, и зависимость между ними может быть довольно сложной. Хорошим примером может служить недавняя работа [20], где фаза α была внутри сидячего пузырька в условиях переменного давления ${{p}^{{\beta }}}.$ В таких задачах даже и в голову не приходит вводить расклинивающее давление.

До сих пор мы полагали, что пленка однокомпонентна. Рассмотрим теперь случай, когда компонентов несколько. Приписав им индекс k и выделив их в отдельную сумму, запишем (3) как

В многокомпонентной фазе β дифференциал химического потенциала компонента k дается выражением

где ${{s}_{k}}$ и ${{{v}}_{k}}$ – парциальные (в расчете на молекулу или моль) энтропия и объем компонента k, набор мольных долей ${{x}_{k}}$ характеризует состав фазы β. При фиксированных температуре и составе фазы β в правой части (15) остается лишь второе слагаемое. В этих условиях подстановка (15) в (14) дает

Теперь, казалось бы, применяя соотношение типа (8) к каждому компоненту, наберем в сумме по k полную толщину пленки из толщин прослоек отдельных компонентов. Но ситуация осложняется тем, что метод Гиббса имеет дело не с реальными массами, а их избытками. Адсорбция сразу нескольких компонентов – процесс состязательный, и если какие-то вещества адсорбируются положительно, то другие – отрицательно. Переход здесь к толщинам прослоек реальных компонентов пленки проблематичен.

МЕТОД ГИББСА С ДВУМЯ РАЗДЕЛЯЮЩИМИ ПОВЕРХНОСТЯМИ

Чтобы внедрить расклинивающее давление в термодинамику фазовых равновесий, необходим метод двух разделяющих поверхностей [7–9]. С внешних сторон избытки берутся как обычно, но в пространстве между поверхностями, где находится пленка, избытки берутся по отношению к ее материнской фазе. Кроме того, поскольку пленка тонкая, избытки (например, адсорбции по разным сторонам пленки) не являются независимыми и должны рассматриваться совместно. Таким образом, у нас пространство разбито теперь не на две, а на три фазы, толщина пленки определяется как расстояние между двумя разделяющими поверхностями с раздельными поверхностными натяжениями ${{\sigma }^{\alpha }}$ (между фазами α и β) и ${{\sigma }^{\gamma }}$ (на границе твердого тела с фазой β), как показано на рис. 1.

После взятия всех избытков и перехода от абсолютных к относительным адсорбциям путем подстановки уравнений Гиббса–Дюгема для объемных фаз, уравнение адсорбции Гиббса принимает вид [2]

Фундаментальное уравнение (17) сформулировано исключительно в терминах метода двух разделяющих поверхностей. Здесь ${{\Gamma }_{{i(j)}}}$ – суммарная для обеих разделяющих поверхностей адсорбция компонента i по отношению к компоненту j (выбранному компоненту пленки), численно равная такой величине адсорбции, которая соответствует нулевой адсорбции компонента j; член ${{\bar {S}}_{{(j)}}}$ имеет аналогичную интерпретацию. Особо нужно сказать о величине ${{H}_{{(j)}}}.$ Переход к относительной адсорбции и расстоянию${{H}_{{(j)}}}$ между разделяющими поверхностями означает и термодинамическое определение толщины тонкой пленки. Из уравнения (17) следует важное соотношение [8, 9]

которое позволяет вычислять поверхностные натяжения тонкой пленки из изотермы расклинивающего давления.

Если теперь сопоставить методы Гиббса с одной и двумя разделяющими поверхностями, то для поверхностного натяжения единственной разделяющей поверхности, рассмотренной в предыдущем разделе, получим выражение [8, 9]

Подстановка (19) в (17) дает

Из уравнения (20) следует

что явно перекликается с выражением (10). Однако, в отличие от (10), соотношение (21) является точным для недеформируемых твердых тел и несжимаемых жидкостей.

Заметим, что уравнения (20) и (21) уже включают три разделяющих поверхности: одну для поверхностного натяжения и две для границ пленки. Чем больше мы использовали разделяющих поверхностей, тем четче и элегантней становилась формулировка термодинамики тонких пленок. Примечательно, что сама термодинамика дает определение толщины пленки. У Гиббса это связано с процедурой перехода к относительным адсорбциям, но это общая операция совместного решения уравнения адсорбции Гиббса и уравнений Гиббса–Дюгема для объемных фаз. Суть в том, что эти уравнения содержат общие химические потенциалы, два из которых можно исключить и тем самым определить толщину тонкой пленки, которая, подобно относительным адсорбциям, является инвариантом и не зависит от положения разделяющих поверхностей.

Глядя на уравнение (21), можно также высказать следующее полезное замечание. Здесь j – это номер как раз того компонента, химический потенциал которого исключен и, следовательно, не может быть закреплен. Из уравнения Гиббса–Дюгема следует, что, если температура и химические потенциалы фазы закреплены, то давление этой фазы также меняться не может. Если же закрепление хотя бы одного из химических потенциалов невозможно, этим гарантируется возможность изменения давления фазы (нужно лишь, чтобы компонент, о химическом потенциале которого идет речь, присутствовал в данной фазе). Мы можем теперь сказать, что если компонент j – вещество, присутствующее в тонкой пленке, то в уравнении (21) выход на расклинивающее давление происходит через давление ${{p}^{{\beta }}}$ в материнской фазе пленки. Если же компонент j отсутствует в пленке и наличествует только в фазе α, то выход на расклинивающее давление в уравнении (21) осуществляется через внешнее давление ${{p}^{\alpha }}.$

МЕТОД ПОЛЯ ТЯЖЕСТИ

Автор с удивлением узнал, что есть и такой метод вывода уравнения Фрумкина, правда, для простейшего случая свободной пленки. Он реализуется в разделе “Равновесие пленок в поле тяжести” монографии [1, с. 42–44]. Но сначала – обескураживающая термодинамическая ошибка. Цитируем текст: “… химические потенциалы ${{\mu }_{i}}$ всех компонентов удовлетворяют условию

где ${{m}_{i}}$– масса моля i-го компонента; g – ускорение силы тяжести; ${{C}_{i}}$– некоторая константа. При этом, однако, из уравнения Гиббса

применимого для пленки, средние слои которой обладают свойствами объемной фазы, следует, что разность поверхностных натяжений $d{{\sigma }_{{13}}}$ способна уравновесить только ту часть веса участка пленки, которая заключена в адсорбционных поверхностных слоях”.

Поясним. Бывают химические потенциалы и, при наличии внешних полей, полные химические потенциалы. То, что стоит в левой части (II.21), – полный химический потенциал при наличии гравитационного поля. Хотя обычно полный химический потенциал разбивают на части, как это показано в (II.21) сочетанием химической и гравитационной частей, физический смысл имеет только полный химический потенциал целиком. Поэтому при переходе к случаю полей, все химические потенциалы в термодинамических соотношениях заменяются полными химическими потенциалами. Например, в системе с электрическими полями химические потенциалы заменяются электрохимическими потенциалами. Оперировать только с химическим потенциалом заряженных частиц некорректно. Точно так же нельзя оперировать только с химическим потенциалом вещества, если оно в гравитационном поле. Очевидно, при наличии гравитационного поля в уравнение адсорбции Гиббса входят полные химические потенциалы. Туда надо подставлять всю левую часть выражения (II.21), а не только ${{\mu }_{i}},$ как это сделано в (II.22). Соотношение (II.22) ошибочно, как и все, что из него следует (мы цитировали лишь частично).

Данный ляпсус не задел вывода уравнения Фрумкина, который в данном случае очень прост. Влияние гравитации на поверхностное натяжение установил еще сам Гиббс. Его формула (614) имеет вид [21, c. 280]

где z – высота (заменяется на H в [1]). Для пленки нужно лишь заменить σ на натяжение пленки ${{\sigma }_{0}}$ и Γ – на разность плотностей пленки ρ и среды ${{\rho }_{1}}$, домноженную на “эффективную” толщину пленки h:

С расклинивающим давлением еще проще. Согласно формуле Дерягина оно определяется как разность давлений, но ведь для каждого давления существуют барометрические формулы. Это сразу дает

Из (II.27) и (II.33) следует “известное соотношение [22, 10, 8 ]” (номера ссылок изменены в соответствии с нашим списком литературы)

что совпадает с уравнением Фрумкина (1). В качестве единственного комментария к нему прибавлена фраза “Безоговорочно соотношение (II.34) верно для однокомпонентной пленки [12]” (номер ссылки изменен). Поскольку самого уравнения Фрумкина в работе [12] нет (а есть только ссылка [11]) и поскольку А.Н. Фрумкин пытался вывести уравнение именно для однокомпонентной пленки, можно заключить, что в [1] подтверждается безоговорочность результата А.Н. Фрумкина. К указанным ссылкам добавим, что уравнение Фрумкина в работе Л.М. Щербакова [22] автору найти не удалось.

Завершая работу, автор казнится тем, что пришлось критиковать замечательных ученых, о которых хранится самая добрая память. Утешает то, что для маститых, а тем более, великих мастеров (лидеров мировой электрохимической и коллоидной науки) случайные ошибки уже не имеют значения. Но и от настоящих ошибок не застрахован никто, даже великие. Ошибки М.В. Ломоносова и Д.И. Менделеева – можно сказать, неисчерпаемая тема. Дольше всех считался безгрешным Гиббс, но публикация [23] и этому положила конец (здесь самое место автору покаяться и в собственных ошибках, они случались!). Что же делать? Давайте примем, что исправление ошибок – нормальный путь развития науки. Ведь это не мы вносим или нам вносят исправления, это истина пробивает себе дорогу. На то она и истина.