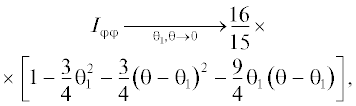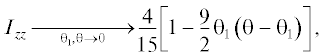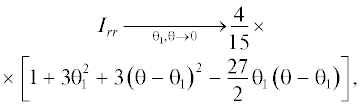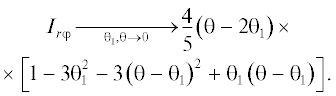Коллоидный журнал, 2020, T. 82, № 4, стр. 393-399

В нашем предыдущем исследовании [1] были получены общие формулы для тензора давления Ирвинга–Кирквуда [2] (см. Приложение 1) в пустой клиновидной щели многокомпонентного твердого тела с дисперсионными взаимодействиями. Соответствующий парный потенциал имеет вид

где ${{A}_{{ij}}}$ – константа взаимодействия компонентов i и j, R – расстояние между взаимодействующими молекулами. В этом сообщении мы дополним полученные результаты более детальным анализом угловой зависимости компонент тензора давления в пустой клиновидной щели, исправив некоторые неточности.

Чтобы облегчить читателю знакомство с новыми результатами, напомним основные моменты предыдущей работы. Представим клиновидную полость в виде двугранного угла, грани которого считаем плоскими и бесконечными. Для такой системы наиболее удобны цилиндрические координаты r, φ, z с осью z на ребре двугранного угла (рис. 1).

Очевидно, что в силу симметрии системы тензор давления, как и все другие локальные свойства, не может зависеть от z. Из этого также следует, что ${{p}_{{z\varphi }}} = {{p}_{{\varphi {\kern 1pt} z}}} = 0$ и ${{p}_{{rz}}} = {{p}_{{zr}}} = 0$. Остаются четыре составляющих тензора давления: три диагональных, ${{p}_{{rr}}},$ ${{p}_{{\varphi \varphi }}}$ и ${{p}_{{zz}}}$, и одна недиагональная (сдвиговая) ${{p}_{{r\varphi }}} = {{p}_{{\varphi {\kern 1pt} r}}}.$ В данном случае давление ${{p}_{{\varphi \varphi }}} \equiv {{p}_{\operatorname{N} }}$ действует по нормали к стенкам полости, составляющие же ${{p}_{{rr}}}$ и ${{p}_{{zz}}}$ играют роль тангенциальных давлений. Все они зависят от положения внутри полости, но при его изменении должны удовлетворять условию механического равновесия

которое в данном случае эквивалентно трем скалярным уравнениям

Пропуская данный в [1] подробный вывод компонент тензора давления, приведем почти окончательный результат

где а составляющие тензора $\hat {\kappa }(\varphi )$ даются выражениями

В выражение для постоянной $C \equiv \pi \sum\nolimits_{i,j} {{{A}_{{ij}}}{{\rho }_{i}}{{\rho }_{j}}} $ входят парциальные плотности компонентов ${{\rho }_{i}}$, суммирование проводится по всем компонентам твердого тела. Диагональные составляющие тензорного интеграла (7) удовлетворяют условию

а потому и для диагональных составляющих тензора давления можно записать

Очевидно, что локальная зависимость тензора давления характеризуется расстоянием r₀ до ребра клина и одной угловой переменной, например, θ₁, поскольку θ₂ = θ – θ₁. Интегралы (7) легко берутся, но приводят к громоздким выражениям из тригонометрических функций. Их явный вид дан в Приложении 2. Но убедиться, что полученные выражения удовлетворяют условиям механического равновесия (3)–(5), можно и не обращаясь к явным аналитическим выражениям для интегралов. Для этого введем переменную $\psi \equiv \varphi - {{\theta }_{1}},$ с помощью которой составляющие тензорного интеграла (7) примут вид

Теперь, пользуясь выражениями (6) и (11)–(14), легко убедиться в том, что уравнения (3) и (4) выполняются, если принять во внимание тождество ∂/∂φ ≡ –∂/∂θ₁. Последнее вытекает из выбора направления орта e_φ (рис. 1) и определения углов ${{\theta }_{1}}$ и ${{\theta }_{2}}$. Условие (5) следует из симметрии системы.

Очевидно, что локальная угловая зависимость тензора давления в клиновидной щели сосредоточена в интегралах (11)–(14) как функциях угла θ₁. На рис. 2 приведены эти интегралы как двумерные функции θ и θ₁. Видно, что при больших значениях угла раствора клина все функции обращаются в нуль при любых значениях θ₁ в силу исчезновения щели и превращения системы в плоский поверхностный слой твердого тела в вакууме с нулевым значением давления. Все диагональные компоненты тензорного интеграла (рис. 2а, 2б, 2в) при фиксированном значении угла раствора являются симметричными функциями относительно серединного сечения щели при ${{\theta }_{1}} = {\theta \mathord{\left/ {\vphantom {\theta 2}} \right. \kern-0em} 2}$, где они принимают минимальные значения. Недиагональная компонента (рис. 2г) равна нулю на данном сечении и меняет знак при пересечении этой плоскости, являясь антисимметричной функцией относительно серединного сечения. Как объяснено в работе [1], это не означает изменения знака реальной сдвиговой компоненты давления на противоположных стенках щели и связано лишь с выбором направления орта полярного угла локальной системы координат (рис. 1).

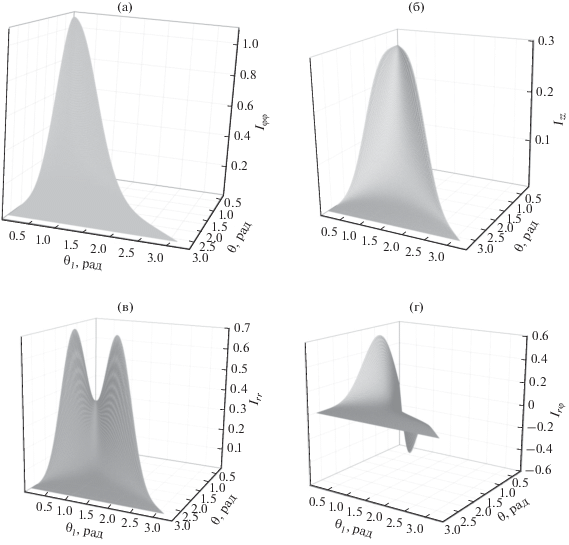
Интеграл I_φφ при небольших значениях угла раствора описывает отклонения нормального давления от постоянного значения в плоской щели. Для заданного значения угла θ₁ этот интеграл монотонно уменьшается с ростом угла раствора. Аналогично ведет себя интеграл I_zz (рис. 2б), хотя его значения заметно меньше значений I_φφ. Отсюда следует, что аналог тангенциального давления в плоской щели I_zz менее чувствителен к отклонению ее стенок от параллельности по сравнению с нормальным давлением. Гораздо более сложным поведением отличается второй аналог тангенциального давления I_rr (рис. 2в), характеризуемый немонотонной зависимостью от угла раствора щели при заданном локальном положении рассматриваемой точки.

В области малых значений переменных можно получить простые аналитические зависимости интегралов, разлагая точные выражения из Приложения 2 в степенные ряды. Получим следующие выражения:

Приведенные выражения удовлетворяют условиям равновесия (3)–(5). Следует отметить, что в отличие от локальной переменной θ₁ зависимость интегралов $\hat {I}(\theta ,{{\theta }_{1}})$ от угла раствора θ не характеризует эту зависимость компонент тензора давления, поскольку согласно формуле (6) помимо интегралов нужно учитывать еще множитель sin^–3θ перед ними. Это затрудняет анализ поведения компонент тензора давления при малых значениях угла раствора и сравнения их с компонентами давления в плоской щели [3–5]. Более удобным для этой цели оказывается другой набор локальных переменных, в котором вместо расстояния до ребра ${{r}_{0}}$ рассматривают локальную ширину H, определяемую длиной отрезка (между стенками полости) прямой, перпендикулярной плоскости-биссектрисе двугранного угла и проходящей через расчетную точку ${\mathbf{r}}({{r}_{0}},{{\theta }_{1}})$ (рис. 3).

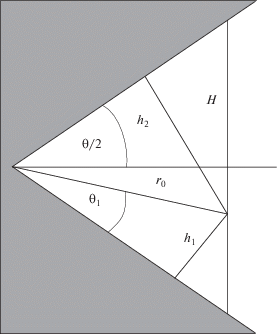
Согласно геометрии

Подставляя это выражение в формулу (6), получим новую формулу для тензора давления в пустой клиновидной щели

Видно, что характерная для тонких пленок обратная кубическая зависимость от поперечного размера сохраняется и для клиновидной полости. Теперь угловая зависимость компонент тензора давления будет описываться следующими тензорными интегралами:

Их численные значения отличаются от значений интегралов $\hat {I}(\theta ,{{\theta }_{1}})$ на множитель

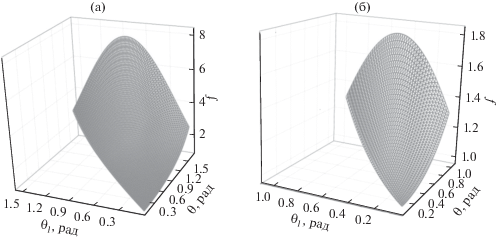
Очевидно, что функция (22) будет стремиться к бесконечности при приближении угла раствора к развернутому углу. Однако для сравнения с плоской пленкой достаточно изучить поведение этой функции при значениях углов, ограниченных величиной прямого угла. На рис. 4 приведены угловые зависимости данной функции для случаев θ < π/2 и θ < π/6. Видно, что функция симметрична, всюду больше единицы и при θ₁ = θ/2 принимает максимальные значения. В случае угла раствора π/6 максимальное значение примерно равно 1.8.

Учитывая поведение функции f, можно убедиться, что интегралы$\hat {F}(\theta ,{{\theta }_{1}})$ будут качественно отличаться от интегралов $\hat {I}(\theta ,{{\theta }_{1}})$ (рис. 2) и их численные значения окажутся больше. Компоненты этого интеграла при θ ≤ π приведены на рис. 5.

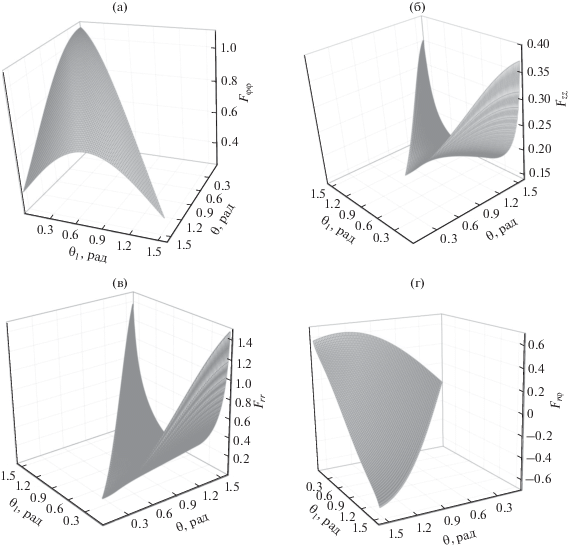
Интеграл F_φφ (рис. 5а) при небольших значениях угла раствора описывает отклонения нормального давления от постоянного значения в плоской щели. Будучи симметричной функцией локальной переменной θ₁, на серединном сечении он принимает максимальные значения. При малых значениях угла раствора зависимость от θ₁ является довольно слабой, что согласуется с постоянством этой компоненты в плоской щели. Для заданного значения угла θ₁ интеграл F_φφ монотонно уменьшается с ростом угла раствора. В отличие от функции F_φφ аналоги тангенциальных компонент тензора F_zz (рис. 5б) и F_rr (рис. 5в) принимают максимальные значения на стенках щели. При малых значениях угла раствора их значения близки друг другу, что согласуется с фактом тождества тангенциальных компонент в плоской щели. Однако с увеличением угла раствора предельные значения двух компонент начинают заметно различаться, так что F_rr > F_zz. Очевидно, что недиагональная компонента является слабо немонотонной функцией угла раствора клина. Как и интеграл I_rφ, F_rφ является антисимметричной функцией локальной переменной θ₁, хотя соответствующая компонента тензора давления остается симметричной функцией, которая обращается в нуль на серединном сечении клина.

Поскольку при анализе этих функций особый интерес представляет область малых углов, полезно найти аналитические выражения для этой области. В пределе малых значений угла раствора функция f может быть представлена следующим образом:

Имея предельные значения интегралов (15)–(18) и функции f (23), можно найти приближенные формулы для компонент тензора давления в пределе слабых отклонений стенок щели от параллельности. Для удобства сравнения с известными результатами для плоских щелей [3–5] запишем выражения для тензора давления в терминах расстояний рассматриваемой точки до стенок щели h₁ и h₂, показанных на рис. 1 и 3. С учетом равенств h_i = r₀sin θ_i ≅ r₀θ_i (i = 1, 2) приближенные выражения для компонент тензора давления принимают следующий вид:

По своей точности формулы (24)–(27) должны соответственно заменить формулы (26)–(29) в [1], при выводе которых не был учтен вклад функции f. Из формул (24)–(27) видно, что аналог нормального давления в клиновидной щели (p_φφ) для данного значения локальной ширины меньше нормального давления в плоской щели, а аналоги тангенциальных компонент (p_zz, p_rr), наоборот, больше, чем тангенциальные компоненты в плоской щели.