Коллоидный журнал, 2020, T. 82, № 4, стр. 432-439
Осаждение аэрозольных наночастиц в сеточных диффузионных батареях
В. А. Кирш 1, 2, *, А. А. Кирш 2
1 Институт физической химии и электрохимии им. А.Н. Фрумкина РАН
119071 Москва, Ленинский просп., 31, Россия
2 Национальный исследовательский центр “Курчатовский институт”
123182 Москва, пл. Академика Курчатова, 1, Россия
* E-mail: va_kirsch@mail.ru
Поступила в редакцию 20.12.2019
После доработки 29.01.2020
Принята к публикации 07.02.2020
Аннотация
Рассмотрено осаждение аэрозольных наночастиц в диффузионных батареях, состоящих из модельных сеток, ориентированных перпендикулярно стоксову потоку. Рассчитаны коэффициенты захвата частиц в зависимости от параметров сеток и диффузионного числа Пекле. Показано, что проскок наночастиц через плотные сетки при больших числах Пекле не зависит от расстояния между сетками и совпадает с проскоком, рассчитанным по эмпирической формуле, используемой для сеточных диффузионных батарей.
1. ВВЕДЕНИЕ
Для экспресс-анализа размера взвешенных в газе наночастиц используется поточный диффузионный метод, основанный на измерении коэффициента проскока частиц $P = {n \mathord{\left/ {\vphantom {n {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}}$ через набор сеток, называемых диффузионными батареями (ДБ). Здесь ${{n}^{{}}}$ – концентрация частиц на выходе, ${{n}_{0}}$ – на входе. По величине проскока ${n \mathord{\left/ {\vphantom {n {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}}$ определяют коэффициент диффузии частиц $D$, который связан с радиусом сферических частиц ${{r}_{{\text{p}}}}$ формулой Эйнштейна–Милликена–Каннингема [1]
(1)
$D = {{{{k}_{{\text{B}}}}T\left( {1 + A{{\lambda } \mathord{\left/ {\vphantom {{\lambda } {{{r}_{{\text{p}}}}}}} \right. \kern-0em} {{{r}_{{\text{p}}}}}} + B{{e}^{{ - {{b{{r}_{{\text{p}}}}} \mathord{\left/ {\vphantom {{b{{r}_{{\text{p}}}}} {\lambda }}} \right. \kern-0em} {\lambda }}}}}{{\lambda } \mathord{\left/ {\vphantom {{\lambda } {{{r}_{{\text{p}}}}}}} \right. \kern-0em} {{{r}_{{\text{p}}}}}}} \right)} \mathord{\left/ {\vphantom {{{{k}_{{\text{B}}}}T\left( {1 + A{{\lambda } \mathord{\left/ {\vphantom {{\lambda } {{{r}_{{\text{p}}}}}}} \right. \kern-0em} {{{r}_{{\text{p}}}}}} + B{{e}^{{ - {{b{{r}_{{\text{p}}}}} \mathord{\left/ {\vphantom {{b{{r}_{{\text{p}}}}} {\lambda }}} \right. \kern-0em} {\lambda }}}}}{{\lambda } \mathord{\left/ {\vphantom {{\lambda } {{{r}_{{\text{p}}}}}}} \right. \kern-0em} {{{r}_{{\text{p}}}}}}} \right)} {6{\pi \mu }{{r}_{{\text{p}}}}}}} \right. \kern-0em} {6{\pi \mu }{{r}_{{\text{p}}}}}},$Интерес к диффузионному методу возрос после того, как было показано [2], что при логнормальном распределении размеров частиц зависимости проскока частиц с разной степенью полидисперсности и с одинаковым средним геометрическим размером от параметра, включающего скорость течения аэрозоля и размеры ДБ, пересекаются в узком интервале значений, ${n \mathord{\left/ {\vphantom {n {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}}$ = 0.36–0.37, причем величина проскока, соответствующая этой точке, очень слабо зависит от среднего размера частиц. В [2] это было показано на примере щелевых ДБ (для плоскопараллельного канала). Впоследствии результат работы [2] был подтвержден численным методом для ДБ, состоящих из слоев цилиндрических волокон, расположенных перпендикулярно потоку [3–5]. Использование в качестве ДБ слоя волокон оказалось возможным благодаря экспериментальному подтверждению [6] полученной ранее аналитической связи коэффициента диффузии с безразмерным коэффициентом проскока P монодисперсных наночастиц при заданной входной скорости потока $U$ перед слоем параллельных волокон
где $a$ – радиус волокна, $l = {\alpha \mathord{\left/ {\vphantom {\alpha {\pi {{a}^{2}}}}} \right. \kern-0em} {\pi {{a}^{2}}}}$ – длина волокон в единице объема фильтра, $\alpha $ – плотность упаковки волокон, $H$ – толщина слоя волокон, $\eta $ – коэффициент захвата – доля частиц, осаждающихся на волокне из набегающего потока, в данном случае равный [7, 8](3)
${{\eta }_{0}} = 2.892{{k}^{{ - {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}{\text{P}}{{{\text{e}}}^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}} = 1.244{{F}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}{\text{P}}{{{\text{e}}}^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}},$(5)
$k = \left( {\frac{1}{2} - \ln 2t + \frac{1}{3}{{t}^{2}} - \frac{1}{{18}}{{t}^{4}} + \frac{4}{{135}}{{t}^{6}} - \frac{{53}}{{2700}}{{t}^{8}} + ...} \right),$В обзоре [11] указывалось на перспективность использования в качестве ДБ упорядоченной волокнистой структуры, но на практике широкое распространение получили ДБ из непараллельных волокон. В [12] в качестве ДБ был предложен слой волокон, который состоял из близко расположенных рядов параллельных волокон, повернутых друг относительно друга на произвольный угол (веерная модель). В недавней работе [5] авторы уточнили метод определения полидисперсности измеряемых частиц c помощью веерной модели.
Проскок наночастиц через “веерную” ДБ описывается формулой (2), но с другим коэффициентом захвата, не зависящим от $\alpha $,
(6)
${{{\eta }}^{{\text{f}}}} = 2.7{\text{P}}{{{\text{e}}}^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}.$Наиболее широкое распространение веерная модель получила после того, как Ченг и Йех предложили в качестве ДБ применять плотные сетки [14]. Свои результаты авторы аппроксимировали следующей формулой:
(7)
${n \mathord{\left/ {\vphantom {n {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}} = \exp \left[ { - 2alH{{{{{\eta }}^{{\text{f}}}}} \mathord{\left/ {\vphantom {{{{{\eta }}^{{\text{f}}}}} {\left( {1 - {\alpha }} \right)}}} \right. \kern-0em} {\left( {1 - {\alpha }} \right)}}} \right],$(8)
${{\eta }_{s}} = {{2.7{\text{P}}{{{\text{e}}}^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}} \mathord{\left/ {\vphantom {{2.7{\text{P}}{{{\text{e}}}^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}} {(1 - \alpha )}}} \right. \kern-0em} {(1 - \alpha )}}.$В плетеных сетках параллельные волокна расположены довольно плотно. Отношение диаметра волокна к расстоянию между осями соседних параллельных волокон составляет примерно $b$ = = 0.3–0.4, и в столь плотных системах волокон плотность упаковки должна заметно влиять на осаждение частиц. Ранее гидродинамическое сопротивление и диффузионное осаждение частиц в отдельных сетках рассматривалось в [18, 20], причем особое внимание уделялось случаю осаждения частиц при Ре < 1, для которого в [19] была развита теория. Были рассмотрены сетки типа pressure welded screen (DIN 4192, ISO 4783/3) [21], представляющие собой пары сдвоенных под прямым углом рядов параллельных волокон. В [22] было показано, что рассчитанное гидродинамическое сопротивление этих сеток почти не отличается от измеренных значений сопротивления плетеных сеток.
В случае высокопористых волокнистых фильтров учет плотности упаковки имеет второстепенное значение, но для плотных сеточных ДБ он оказывается существенным. В данном сообщении мы численно исследуем диффузионное осаждение наночастиц из трехмерного стоксова потока в ДБ, состоящей из сеток с разной плотностью упаковки, проверим постоянство коэффициента захвата при сближении сеток и то, насколько обоснованно используется веерная модель в диффузионном методе.
2. МЕТОД РАСЧЕТА
Поля скоростей и концентрации находились из численного решения стационарных уравнений Стокса [23]
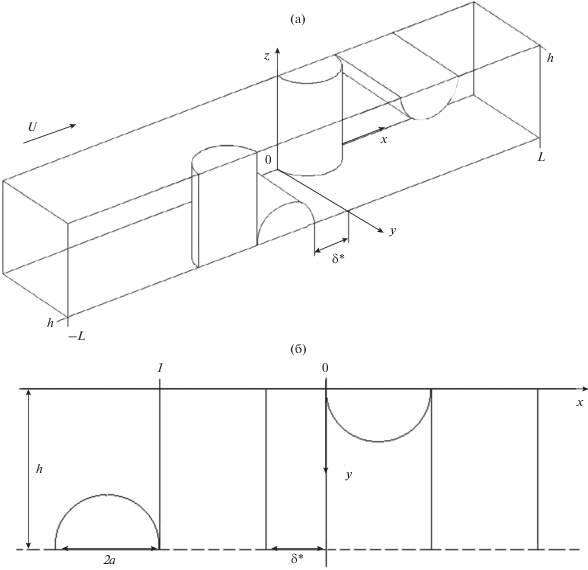
и конвективной диффузии [24] описывающих соответственно течение вязкой несжимаемой жидкости при малых числах Рейнольдса $\operatorname{Re} = {{2aU} \mathord{\left/ {\vphantom {{2aU} \nu }} \right. \kern-0em} \nu } \ll 1$, где $\nu $ – кинематическая вязкость газа, и перенос взвешенных броуновских частиц в конвективном потоке. Расчетная ячейка показана на рис. 1. В уравнениях (9) и (10) ${\mathbf{u}}$ – вектор скорости потока, $p$ – давление. Здесь все переменные приведены к безразмерному виду с использованием характерных масштабов длины и скорости – радиуса волокна $a$ и скорости набегающего потока $U$. В качестве граничных условий на поверхности волокон ставились условия прилипания ${\mathbf{u}} = 0$ и поглощения частиц $n = 0$. На входной границе при $x = - L$ ставились условия невозмущенной скорости ${\mathbf{u}} = 1$ и однородной концентрации $n = 1$, при $x = L$ – условия отсутствия вязких напряжений, нулевого давления $p = 0$ и выравнивания концентрации. На боковых, верхней и нижней гранях ячейки ставились условия симметрии для компонент скорости и концентрации.Рис. 1.
Расчетная ячейка длины 2$L$ в задаче об обтекании пакета модельных сеток поперечным потоком: (а) изометрия, (б) поперечное xy–сечение ячейки в плоскости $z$ = 0. $\delta {\text{*}}$ – зазор между сетками, $h$ – высота ячейки – половина расстояния между осями соседних волокон в рядах параллельных волокон, образующих сетки. Стрелкой указано направление потока.
Метод численного решения задачи изложен в [18]. Безразмерная сила сопротивления единицы длины волокна была найдена интегрированием по поверхности цилиндра проекции локального потока импульса на направление потока жидкости
где поток импульса равен ${\mathbf{T}} = \left( { - p{\text{I}} + \sigma {\kern 1pt} '} \right){\mathbf{n}}$ [23], $\sigma {\kern 1pt} '$ – тензор вязких напряжений, ${\text{I}}$ – единичный тензор, ${\mathbf{n}}$ – вектор внешней нормали к поверхности, $dS$ − элемент поверхности.Рассчитав поле концентрации, находим коэффициент проскока частиц через модельную сетку, который для любых значений ${\text{Pe}}$ и $b$ связан с коэффициентами захвата частиц волокнами, образующими модельную сетку, следующим соотношением:
где $i$ − число рядов волокон, $\eta _{j}^{{}}$ − коэффициент захвата частиц волокном (j – номер ряда), рассчитываемый по формуле(13)
${{\eta }_{j}} = \frac{{2a}}{{h{\text{Pe}}}}\int\limits_S {\left( {{{\partial n} \mathord{\left/ {\vphantom {{\partial n} {\partial N}}} \right. \kern-0em} {\partial N}}} \right)} dS.$Как показывают расчеты, при больших ${\text{Pe}}$ коэффициент захвата для всех сеток в ДБ практически одинаков, и проскок частиц через батарею из большого числа сеток в этом случае равен $P = \exp \,{\kern 1pt} \left( { - 2alH\,\bar {\eta }} \right)$. Учитывая, что плотность упаковки модельной сетки равна $\alpha = {{\pi a} \mathord{\left/ {\vphantom {{\pi a} {4h}}} \right. \kern-0em} {4h}}$, получим $l = {\alpha \mathord{\left/ {\vphantom {\alpha {\pi {{a}^{2}}}}} \right. \kern-0em} {\pi {{a}^{2}}}} = {1 \mathord{\left/ {\vphantom {1 {4h}}} \right. \kern-0em} {4h}}a$. Толщина слоя из сомкнутых $N$ рядов волокон равна $H = N2а$, и, следовательно, $2alH = {{Na} \mathord{\left/ {\vphantom {{Na} h}} \right. \kern-0em} h}$, т.е. $P = \exp \left( { - bN\bar {\eta }} \right)$, откуда средний коэффициент захвата наночастиц волокном в ДБ равен
Средний коэффициент захвата волокном в слое из $N$ рядов волокон может быть также найден с учетом (12), если рассчитана безразмерная концентрация за ним, усредненная по площади поперечного сечения расчетной ячейки,(15)
$\bar {\eta } = \frac{{ - \ln \left( {1 - b\sum\limits_{j = 1}^i {{{\eta }_{j}}} } \right)}}{{bN}}.$(16)
${{\bar {\eta }}_{s}} = \frac{{ - \ln [1 - b\left( {{{\eta }_{1}} + {{\eta }_{2}}} \right)]}}{{2b}}.$Вычисленные по (16) и (14) значения коэффициентов захвата одиночных сеток и пакетов из восьми сеток с разными $b$ сравним далее с рассчитанными по формулам (3) и (8).
3. РЕЗУЛЬТАТЫ РАСЧЕТОВ И ВЫВОДЫ
Осаждение частиц в отдельном ряду волокон
Прежде, чем приступить к рассмотрению осаждения в системах волокон с трехмерным течением, было проверено, до каких значений $b$ применима формула (3) для диффузионного коэффициента захвата точечных частиц в отдельном ряду параллельных волокон. Эта формула была получена при $b \ll 1$ в приближении тонкого граничного диффузионного слоя на волокне на основе решения параболического уравнения конвективной диффузии (без учета члена, учитывающего т.н. продольную диффузию) [7]. Входящая в (3) безразмерная сила сопротивления потоку волокна в ряду параллельных волокон (11) была найдена с помощью численного решения задачи о стоксовом поле течения в ряду волокон при $\operatorname{Re} $ $ \ll $ 1. Были определены границы применимости известных формул для сил сопротивления волокон в разреженном и плотном рядах, а для промежуточного интервала $0.5 \leqslant b \leqslant 0.7$ получена следующая аппроксимационная формула:
(17)
${{F}_{2}} = \left[ {1 - A\exp \left( { - B\xi } \right)} \right]{\kern 1pt} {{F}_{1}} + \left[ {1 - C\exp \left( { - {E \mathord{\left/ {\vphantom {E \xi }} \right. \kern-0em} \xi }} \right)} \right]{\kern 1pt} {{F}_{3}},$(18)
${{F}_{3}} = \frac{{9\pi }}{{2\sqrt 2 }}{{\left( {1 - b} \right)}^{{{{ - 5} \mathord{\left/ {\vphantom {{ - 5} 2}} \right. \kern-0em} 2}}}}.$(19)
$F = {{F}_{1}},\,\,\,\,b \leqslant 0.5;\,\,{{F}_{2}},\,\,0.5 \leqslant b \leqslant 0.7;\,\,\,\,{{F}_{3}},\,\,b \geqslant 0.7.$На рис. 2 приводится сравнение рассчитанных коэффициентов захвата η для рядов с $b$ = 0.1−0.6 (кривая 1) со значениями η, вычисленными по (3) (кривая 3) и по формуле Натансона–Стечкиной [28] (кривая 2),
(20)
${{\eta }_{0}} = 2.892{{k}^{{ - {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}{\text{P}}{{{\text{e}}}^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}} + 0.624{\text{P}}{{{\text{e}}}^{{ - 1}}}.$Рис. 2.
Коэффициенты захвата волокном η0 в ряду волокон: 1 – результаты прямого численного моделирования, 2 – расчет по формуле Натансона с поправкой Стечкиной (20), 3 − расчет по формуле Натансона (3); ${\text{Pe}}$ = 10 (а); 100 (б); 1000 (в).
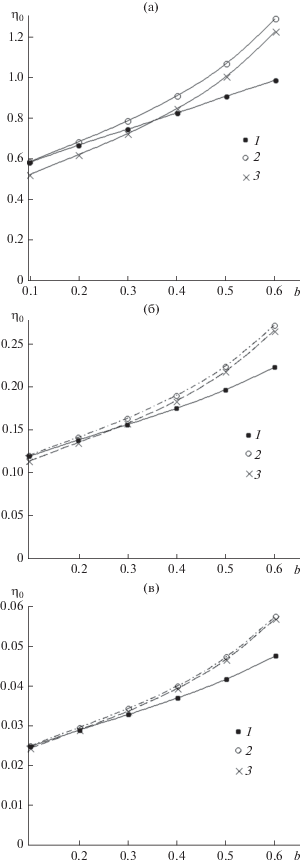
Рисунок 2 демонстрирует, что в плотных рядах волокон с $b$ > 0.5 осаждение частиц заметно меньше, чем следует из расчетов по аналитическим формулам при всех значениях Ре, и что при больших Ре удовлетворительное согласие коэффициентов захвата наблюдается для рядов с $b$ < 0.3. Отметим хорошее согласие коэффициента захвата, найденного прямым моделированием, с коэффициентом захвата, вычисленным по (20), для ряда с $b$ = 0.1 при небольшом значении числа Пекле (${\text{Pe}}$ = 10), когда величина поправки в (20) существенно влияет на η. Полученные результаты для двумерного поля течения в ряду сравним с данными для сеток.
Осаждение частиц в отдельной сетке
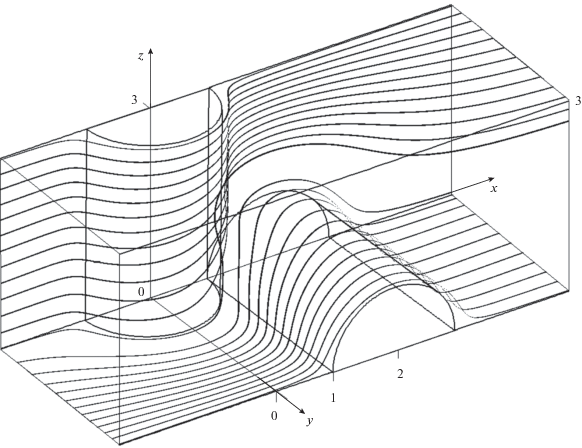
Пример рассчитанного трехмерного поля течения вблизи поверхности волокон в сетке с $b$ = 1/3 показан на рис. 3. Здесь представлены линии тока в перпендикулярных плоскостях, прилегающих к плоскостям симметрии; видно, что бóльшая часть волокон в каждом ряду обтекается почти плоскопараллельным потоком. Следовательно, функциональные зависимости осаждения частиц в сетке и в ряду от размера частиц и волокон при одинаковой скорости не должны существенно различаться.
Рис. 3.
Линии тока вблизи перекрестия волокон при обтекании модельной сетки. Входные координаты: {$y$ = 0.01, 0.5, 1, 1.5, 2, 2.5, 2.99, $z$ = 0.01} и {$y$ = 2.99, $z$ = 0.01 …. 2.99}; $b$ = 1/3.
Результаты расчета сил сопротивления и проскока частиц через одну сетку с разными значениями $b$ представлены в табл. 1. Они свидетельствуют о том, что силы сопротивления F1 и F2, действующие на волокна в первом и втором ряду, равны и для всех значений $b$ превышают силу в отдельном ряду F0. В то же время полученные прямым моделированием средние коэффициенты захвата сетки ${{{\bar {\eta }}}_{{\text{s}}}}$ при больших и промежуточных числах Пекле близки к значениям ${{\eta }_{0}}$ для изолированного ряда волокон, рассчитанным по (3).
Таблица 1.
Результаты расчета безразмерных коэффициентов захвата $\eta $ и сил сопротивления волокон $F$ в одной сетке при разных значениях ${\text{Pe}}$; ${{{\bar {\eta }}}_{{\text{s}}}}$ − расчет по (16), ${{\eta }_{0}}$ − по (3), ${{{\eta }}_{{\text{s}}}}$ − по (8); индекс 1 − первый по потоку ряд волокон, 2 − второй ряд
| ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-0em} h}$ = 0.5, ${{F}_{1}}$ = 65.343, ${{F}_{2}}$ = 65.339, ${{F}_{0}}$ = 52.85 | ||||||
|---|---|---|---|---|---|---|
| ${\text{Pe}}$ | $P$ | ${{\eta }_{1}}$ | ${{\eta }_{2}}$ | ${{{\bar {\eta }}}_{{\text{s}}}}$ | ${{\eta }_{0}}$ | ${{{\eta }}_{{\text{s}}}}$ |
| 10 | 0.34141 | 0.8366 | 0.4806 | 1.0747 | 1.0085 | 0.9579 |
| 100 | 0.8167 | 0.1934 | 0.1733 | 0.2025 | 0.2173 | 0.2064 |
| 1000 | 0.9571 | 0.0432 | 0.0426 | 0.0439 | 0.0468 | 0.0445 |
| ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-0em} h}$ = 0.4, ${{F}_{1}}$ = 39.503, ${{F}_{2}}$ = 39.503, ${{F}_{0}}$ = 31.74 | ||||||
| ${\text{Pe}}$ | $P$ | ${{\eta }_{1}}$ | ${{\eta }_{2}}$ | ${{{\bar {\eta }}}_{{\text{s}}}}$ | ${{\eta }_{0}}$ | ${{{\eta }}_{{\text{s}}}}$ |
| 10 | 0.4903 | 0.7571 | 0.5171 | 0.8909 | 0.8501 | 0.8467 |
| 100 | 0.8689 | 0.1714 | 0.1565 | 0.1757 | 0.1833 | 0.1827 |
| 1000 | 0.9699 | 0.0378 | 0.0374 | 0.0382 | 0.0395 | 0.0394 |
| ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-0em} h}$ = 1/3, ${{F}_{1}}$ = 28.7829, ${{F}_{2}}$ = 28.7844, ${{F}_{0}}$ = 23.202 | ||||||
| ${\text{Pe}}$ | $P$ | ${{\eta }_{1}}$ | ${{\eta }_{2}}$ | ${{{\bar {\eta }}}_{{\text{s}}}}$ | ${{\eta }_{0}}$ | ${{{\eta }}_{{\text{s}}}}$ |
| 10 | 0.5872 | 0.7102 | 0.5282 | 0.7986 | 0.7706 | 0.7879 |
| 100 | 0.8984 | 0.1586 | 0.1462 | 0.1607 | 0.1651 | 0.1697 |
| 1000 | 0.9769 | 0.0348 | 0.0344 | 0.0347 | 0.0356 | 0.0366 |
| ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-0em} h}$ = 0.2, ${{F}_{1}}$ = 15.034, ${{F}_{2}}$ = 15.034, ${{F}_{0}}$ = 12.603 | ||||||
| ${\text{Pe}}$ | $P$ | ${{\eta }_{1}}$ | ${{\eta }_{2}}$ | ${{{\bar {\eta }}}_{{\text{s}}}}$ | ${{\eta }_{0}}$ | ${{{\eta }}_{{\text{s}}}}$ |
| 10 | 0.7689 | 0.6256 | 0.5298 | 0.6569 | 0.6248 | 0.6688 |
| 100 | 0.9474 | 0.1359 | 0.1276 | 0.1354 | 0.1347 | 0.1480 |
| 1000 | 0.9884 | 0.0292 | 0.0288 | 0.0291 | 0.0290 | 0.0320 |
| ${a \mathord{\left/ {\vphantom {a h}} \right. \kern-0em} h}$ = 0.1, ${{F}_{1}}$ = 8.4877, ${{F}_{2}}$ = 8.4889, ${{F}_{0}}$ = 7.54 | ||||||
| ${\text{Pe}}$ | $P$ | ${{\eta }_{1}}$ | ${{\eta }_{2}}$ | ${{{\bar {\eta }}}_{{\text{s}}}}$ | ${{\eta }_{0}}$ | ${{{\eta }}_{{\text{s}}}}$ |
| 10 | 0.8923 | 0.5614 | 0.5161 | 0.5700 | 0.5271 | 0.6313 |
| 100 | 0.9768 | 0.1180 | 0.1136 | 0.1171 | 0.1147 | 0.1360 |
| 1000 | 0.9950 | 0.02495 | 0.0247 | 0.0249 | 0.0245 | 0.0293 |
Однако формулу (3) нельзя использовать для расчета проскока через плотные сетки, так как силы сопротивления ряда и сетки заметно различаются. Отметим, также, что при Ре < 100 осаждение на первый слой волокон больше, чем на второй, что является следствием влияния диффузионного следа, причем коэффициент захвата первого слоя равен коэффициенту захвата, рассчитанному по (16).
Из табл. 1 также следует, что рассчитанные средние коэффициенты захвата для плотных сеток удовлетворительно совпадают со значениями ${{{\eta }}_{{\text{S}}}}$, рассчитанными по эмпирической формуле (8) при плотности упаковки $\alpha = {{\pi b} \mathord{\left/ {\vphantom {{\pi b} 4}} \right. \kern-0em} 4}$. Для рыхлых сеток с большим шагом формула (8) неприменима.
Проскок частиц через восемь последовательно установленных сеток
Учитывая, что в ДБ соседние сетки взаимно ориентированы под произвольными углами, мы также нарушили упорядоченность расположения сеток и уменьшили влияние диффузионного следа от перекрестий волокон в соседних сетках. С этой целью четные сетки были сдвинуты относительно нечетных (в направлении потока по оси $X$) по осям $z$ и $y$ в своих плоскостях на величину $h$ – половину расстояния между волокнами в ряду, как показано на рис. 1a и 1б. Расчеты показали, что входного эффекта в пакете сеток не было (сопротивление сеток при их сближении не увеличивалось), а разброс значений сил сопротивления, рассчитанных для каждого ряда в сетке, составлял менее одного процента.
В табл. 2 приведены результаты расчета проскоков наночастиц через сетки и коэффициентов захвата при трех значениях числа Пекле в зависимости от расстояния между соседними сетками, $X = 2 + \delta $, где $\delta $ – зазор между сетками. Из этой таблицы следует, что осаждение в сетках практически не изменяется при их сближении, за исключением случая при ${\text{Pe}}$ = 10. При необходимости измерения $D$ в этом диапазоне ${\text{Pe}}$ между сетками можно устанавливать кольцевые прокладки.
Таблица 2.
Средние коэффициенты захвата ${{{\bar {\eta }}}_{{\text{s}}}}$ пакетом из восьми сеток (расчет по формуле 14) при разном безразмерном (в единицах $a$) расстоянии между сетками $X = 2 + \delta $ (см. рис. 1)
| $b$ | $\delta $ | ${\text{Pe}} = 10$ | ${\text{Pe}} = 100$ | ${\text{Pe}} = 1000$ | |||
|---|---|---|---|---|---|---|---|
| $P$ | ${{{\bar {\eta }}}_{{\text{s}}}}$ | $P$ | ${{{\bar {\eta }}}_{{\text{s}}}}$ | $P$ | ${{{\bar {\eta }}}_{{\text{s}}}}$ | ||
| 1/2 | 8 | 2.389 × 10−4 | 1.0424 | 0.1734 | 0.2190 | 0.7056 | 0.0436 |
| 2 | 1.446 × 10−4 | 1.1052 | 0.1688 | 0.2224 | 0.6960 | 0.0453 | |
| 0.1 | 4.854 × 10−5 | 1.2416 | 0.1833 | 0.2121 | 0.7173 | 0.0415 | |
| 1 сетка | 0.34141 | 1.0747 | 0.8167 | 0.2025 | 0.9571 | 0.0439 | |
| 1/3 | 8 | 0.0128 | 0.8172 | 0.4146 | 0.1651 | 0.8358 | 0.0336 |
| 2 | 0.0101 | 0.8616 | 0.4214 | 0.1620 | 0.8327 | 0.0343 | |
| 1 | 0.00590 | 0.9624 | 0.4301 | 0.1582 | 0.8427 | 0.0321 | |
| 0.1 | 0.00547 | 0.9766 | 0.4325 | 0.1572 | 0.8308 | 0.0348 | |
| 1 сетка | 0.5872 | 0.7986 | 0.8984 | 0.1607 | 0.9770 | 0.0347 | |
4. ЗАКЛЮЧЕНИЕ
Из результатов расчетов следует, что, поскольку гидродинамическое сопротивление стоксову потоку при $\operatorname{Re} $ $ \ll $ 1 рассмотренных модельных сеток и плетеных сеток, используемых в ДБ, практически совпадает [22], и коэффициенты захвата для плотных сеток и веерной модели также очень близки, то при вычислении коэффициента диффузии наночастиц по измеренным значениям проскока через ДБ из плотных сеток можно пользоваться эмпирической формулой (8) в широком диапазоне чисел Пекле, при Ре > 10, подставляя в число Пекле значение скорости невозмущенного течения $U$. Кроме того, при больших числах Пекле, ${\text{Pe}}$ > 1000, коэффициент проскока можно оценить также по аналитической формуле для изолированного ряда (3), используя соответствующее значение силы, рассчитаннoе по (17). В последнем случае достаточно знать просвет сетки и диаметр проволочки, не проводя измерений истинной плотности упаковки в единице объема сеточной ДБ.
В заключение отметим, что сеточный диффузионный метод может быть использован и для определения коэффициента диффузии субмикронных частиц [14, 15]. Однако при учете собственного размера субмикронных частиц эффект скольжения газа на волокнах обычно не учитывается, поскольку число Кнудсена ${\text{Kn}} = {\lambda \mathord{\left/ {\vphantom {\lambda a}} \right. \kern-0em} a}$ для толстых волокон в сетках мало (${\text{Kn}}$ $ \ll $ 1). Но для таких волокон мал и параметр зацепления $R = {{{{r}_{p}}} \mathord{\left/ {\vphantom {{{{r}_{p}}} a}} \right. \kern-0em} a} \ll 1$, и поэтому, сколь бы большим волокно не было, скольжение газа на волокне влияет на осаждение, так как поправка к коэффициенту захвата за счет зацепления, учитывающая скольжение газа, равна (1 + ${{{\text{Kn}}} \mathord{\left/ {\vphantom {{{\text{Kn}}} R}} \right. \kern-0em} R}$) [29, 13 ]. Не учитывая влияние скольжения газа на зацепление частиц и специфику диффузионного осаждения при малых ${\text{Pe}}$ [19], авторы иногда предлагают свои подгоночные коэффициенты в отдельных членах в формуле для суммарного коэффициента захвата в веерной модели [30]. Отметим также необходимость учета полноты укрупнения наночастиц до и после ДБ в пересыщенных парах разных жидкостей. Вопрос о детектировании укрупненных наночастиц, доля которых зависит от их размера и концентрации, рассмотрен в [31].
Список литературы
Fuchs N.A. The Mechanics of Aerosols. New York: Pergamon Press, 1964.
Fuchs N.A., Stechkina I.B., Starosselskii V.I. // Br. J. Appl. Phys. 1962. V. 13. P. 280.
Lee K.W., Connick P.A., Gieseke J.A. // J. Aerosol Sci. 1981. V. 12. P. 385.
Кирш А.А., Загнитько A.В., Чечуев П.В. // Журн. физ. химии. 1981. Т. 55. С. 3034.
Стечкина И.Б., Кирш A.A. // Коллоид. журн. 2013. Т. 75. С. 538.
Кирш A.A.,Фукс Н.A. // Коллоид. журн. 1968. Т. 30. С. 836.
Натансон Г.JI. // Докл. АН СССР. 1957. Т. 112. С. 100.
Фукс Н.А., Стечкина И.Б. // Докл. АН СССР. 1962. Т. 147. С. 1144.
Kuwabara S. // J. Phys. Soc. Jpn. 1959. V. 14. P. 527.
Miyagi T. // J. Phys. Soc. Jpn. 1958. V. 13. P. 493.
Фукс Н.А., Сутугин А.Г. // Высокодисперсные аэрозоли. Итоги науки. Серия “Физическая химия”. М.: Изд-во ВИНИТИ, 1969.
Kirsch A.A., Stechkina I.B. // Proc. 7th International Conference on Condensation and Ice Nuclei. Prague: Academia, 1969, P. 284.
Kirsch A.A., Stechkina I.B. // Fundamentals of Aerosol Science / Ed. by Shaw D.T. New York: Wiley–Interscience, 1978. P. 165.
Cheng Y.S., Yeh H.C. // J. Aerosol Sci. 1980. V. 11. P. 313.
Cheng Y.S., Yeh H.C., Brinsko K.J. // Aerosol Sci. Technol. 1985. V. 4. P. 165.
Scheibel H.G., Porstendorfer J. // J. Aerosol Sci. 1984. V. 15. P. 673.
Heim M., Mullins B.J., Wild M., Meyer J., Casper G. // Aerosol Sci. Technol. 2005. V. 39. P. 782.
Kirsch V.A., Kirsch A.A. // Aerosols – Science and Technology / Ed. by Agranovski I. Weinheim: Wiley–VCH, 2010. P. 283.
Черняков А.Л., Кирш А.А., Ролдугин В.И., Стечкина И.Б. // Коллоид. журн. 2000. Т. 62. С. 547.
Кирш В.А., Кирш A.A. // Коллоид. журн. 2010. Т. 72. С. 468.
Purchas D.B. // Handbook of Filter Media. Oxford: Elsevier Advanced Technology, 1996.
Кирш В.А. // Коллоид. журн. 2006. Т. 68. С. 17.
Ландау Л.Д., Лифшиц И.М. Теоретическая физика. Т. 6. Гидродинамика. Издание 4-е, М.: Наука, 1988.
Левич В.Г. Физико-химическая гидродинамика. М.: ГИФМЛ, 1959.
Keller J.B. // J. Fluid Mech. 1964. V. 18. P. 94.
Sangani A.S., Acrivos A. // Int. J. Multiphase Flow. 1982. V. 8. P. 193.
Wang C.Y. // Fluid Dynamics Res. 2001. V. 29. P. 65.
Стечкина И.Б. // Докл. АН СССР. 1966. Т. 167. С. 1327.
Натансон Г.JI. // Коллоид. журн. 1962. Т. 24. С. 52.
Cena L.G., Ku B.K., Peters T. // Aerosol Sci. Technol. 2012. V. 46. P. 214.
Кирш А.А., Хмелевский В.О., Будыка А.К., Кирш В.А. // Теор. основы хим. технологии. 2011. Т. 55. С. 702.
Дополнительные материалы отсутствуют.
Инструменты
Коллоидный журнал


