Коллоидный журнал, 2020, T. 82, № 5, стр. 618-629

1. ВВЕДЕНИЕ

Коалесценцией называют процесс слияния частиц или пузырьков с формированием более крупной дочерней частицы (пузырька). Обычно данный термин используется применительно к слиянию капель, тогда как процесс образования единой стабильной структуры (агломерата) из двух и более твердых частиц называют спеканием или коагуляцией. Первоначально термин “спекание” имел исключительно техническое звучание и отвечал завершающему этапу технологии порошковой металлургии, которому предшествуют получение порошков, их смешивание и прессование. Четкое разграничение между коалесценцией и спеканием отсутствует, хотя вполне очевидно, что в порошковой металлургии спекание осуществляется при некоторой температуре $T$, меньшей температуры плавления объемной фазы $T_{{\text{m}}}^{{\left( \infty \right)}}$.

В 40-х гг. 20-го столетия стало понятным, что процессы коалесценции и спекания представляют интерес не только с прикладной, но и научной точки зрения, и начало научному изучению спекания было положено Зауэрвальдом [1]. Вскоре Френкель [2] разработал первую физическую теорию спекания, и идеи Френкеля, по крайней мере, четверть века определяли деятельность всех тех, кто занимался изучением этого процесса [3–5]. На его теорию часто ссылались и в более поздних статьях и монографиях [6–8]. Примечательно также, что в монографии Гегузина [4], наряду с исключительно высокой оценкой Френкеля как физика-теоретика, имеются и некоторые критические соображения по поводу его теории [2]. В частности, в строении твердых тел и жидкостей Френкель видел гораздо больше сходства, чем различия [9]. Соответственно теория Френкеля [2] сводит процесс спекания к вязкому течению твердых тел. Однако ниже будет показано, что как исходная теория [2], так и ее уточненный вариант, предложенный в данной работе, достаточно адекватно описывают не кинетику спекания, а кинетику коалесценции как макроскопических, так и наноразмерных капель. Что же касается закономерностей и механизмов спекания, то они, в соответствии с нашими результатами, не сводятся к механизму вязкого течения. Следует также отметить, что за исключением недавней статьи Морачевского [10] остались практически не замеченными две имеющие отношение к данной работе юбилейных даты: столетие со дня рождения Гегузина (2018 г.), автора известной монографии [5], посвященной спеканию макро- и микрочастиц, и 125-летие со дня рождения Френкеля (2019 г.), который впервые подошел к изучению явлений коалесценции и спекания как физик-теоретик.

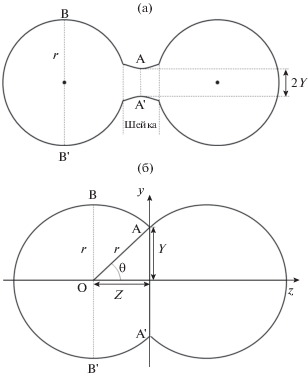
Хотя в литературе обсуждались различные механизмы коалесценции и спекания, начиная с 60-х гг. под влиянием известной и часто цитируемой работы [11] в центре внимания оказался механизм поверхностной диффузии, индуцированной капиллярностью (ПДИК). В частности, молекулярно-динамические (МД) результаты [12, 13] по кинетике коалесценции и спекания сравнивались только с теоретическими оценками, основывающимися на концепции ПДИК. Суть этой концепции сводится к тому, что в перешейке, соединяющем две спекаемые частицы (рис. 1a), т.е. под вогнутым мениском, капиллярное давление ${{P}_{{\text{c}}}}$ отрицательно. В результате разность химических потенциалов $\Delta \mu = {v}{{P}_{{\text{c}}}}$ под мениском перешейка (точки A и A' на рис. 1а) и под удаленной от него поверхностью (включая точки B и B') также отрицательна (здесь ${v}$ – удельный объем материала частицы). Согласно [11], именно отрицательный химический потенциал в области перешейка выступает в роли движущей силы поверхностной диффузии атомов (молекул) в сторону перешейка.

В соответствии с концепцией ПДИК, текущее время коалесценции/спекания $t$ связано с радиусом шейки $Y\left( t \right)$ и начальным радиусом частицы ${{r}_{0}}$ следующей зависимостью:

где $R$ – универсальная газовая постоянная, ${\Omega }$ – молярный объем, $D$ – коэффициент поверхностной диффузии, $W$ – толщина диффузионной зоны, $\sigma $ – поверхностное натяжение на границе жидкости или твердого тела с паром, $C$ – числовая постоянная. Согласно (1), механизму поверхностной диффузии должно отвечать следующее соотношение для $Y\left( t \right)$: Кроме того, учитывая, что характерному времени коалесценции/спекания $\tau $ будет отвечать некоторое определенное максимальное значение величины ${Y \mathord{\left/ {\vphantom {Y {{{r}_{0}}}}} \right. \kern-0em} {{{r}_{0}}}}$, заключаем, что механизм поверхностной диффузии должен проявляться в пропорциональности между $\tau $ и $r_{0}^{4}$:

Вполне естественно, что, начиная с 90-х годов, в связи с развитием нанотехнологий большой интерес стал проявляться к коалесценции нанокапель и спеканию твердых наночастиц. Помимо порошковой металлургии с использованием наночастиц в качестве еще одного примера практического применения можно отметить печать наноструктурированных деталей с использованием коалесценции, индуцированной наносекундными лазерными импульсами [14]. Вместе с тем, в 90-е годы возможности экспериментального исследования спекания твердых наночастиц были ограниченными. Что же касается коалесценции нанокапель, то этот процесс является гораздо более быстрым, и, очевидно, кинетика коалесценции на наномасштабах экспериментально не исследовалась вплоть до настоящего времени. В связи с этим, имеющиеся сравнительно недавние экспериментальные данные, включая [16, 17], относятся только к спеканию твердых наночастиц, а первые интересные результаты [12] как по коалесценции, так и по спеканию на наномасштабах были получены для наночастиц Au с использованием МД-моделирования. Примечательно также, что наночастицы Au по-прежнему остаются основным объектом при изучении коалесценции и спекания как в компьютерных [14, 15], так и в лабораторных [16, 17] экспериментах, в которых использовалась просвечивающая электронная микроскопия (ПЭМ). Как уже отмечалось выше, неоднократно предпринимались попытки сравнения результатов лабораторных и компьютерных экспериментов [12, 15–17] с имеющимися теоретическими моделями и, прежде всего, с предсказаниями, основывающимися на концепции ПДИК [11]. В частности, в [12] было установлено, что оба степенных закона, (2) и (3), не выполняются даже приближенно. Вместе с тем, в [13] также на основе МД-моделирования для наночастиц Au был сделан противоположный вывод.

Альтернативные, т.е. не основывающиеся на концепции ПДИК теоретические подходы к коалесценции и спеканию на наномасштабах [18–21] также сводятся к распространению на наносистемы предложенных ранее макроскопических моделей. Однако правомерность такого распространения в полной мере не обоснована. Примечательно также, что в публикациях по коалесценции и спеканию на наномасштабах эти два явления четко не дифференцируются. В наших недавних работах [22, 23], посвященных МД-моделированию этих явлений, было предложено относить к коалесценции случай, когда температура $T$ системы из двух частиц превышает температуру плавления ${{T}_{{\text{m}}}}$ каждой из них, а к спеканию – случай, когда $T < {{T}_{{\text{m}}}}$.

Учитывая отмеченное выше, основной целью данной работы являлось выяснение закономерностей и механизмов коалесценции нанокапель и спекания твердых наночастиц с использованием МД-моделирования указанных процессов. Кинетика коалесценции, позволяющая судить и о механизме данного процесса, изучалась также с использованием теоретического подхода, отвечающего уточнению теории Френкеля [2] и ее распространению на наномасштабы. В качестве основных объектов исследования выступали наноразмерные частицы Au, для которых имеются как МД-результаты других авторов [12, 13, 15], так и некоторые недавние надежные экспериментальные данные [16, 17].

2. ТЕОРИЯ КОАЛЕСЦЕНЦИИ КАПЕЛЬ: РАЗВИТИЕ ПОДХОДА ФРЕНКЕЛЯ [2]

Как уже отмечалось во введении, по своему замыслу работа Френкеля [2] была посвящена, прежде всего, развитию концепции вязкого течения кристаллических твердых тел, которые, в соответствии с его воззрениями, принципиально не отличаются от жидкостей. Согласно [2], процесс спекания происходит в две стадии. На первой из них имеет место увеличение поверхности соприкосновения соседних частиц; на второй – закрытие остаточных, не соприкасающихся друг с другом пор. Первую стадию Френкель интерпретировал как вязкое течение, т.е. фактически развитая в [2] теория относится к начальной стадии коалесценции двух сферических капель жидкости.

Френкель исходил из предположения, что в начальный момент времени капли контактируют в одной точке, а через некоторое время $t$ соприкасаются друг с другом по кругу радиуса $r\sin \theta $, отвечающего максимальным в этом сечении значениям $X$ и $Y$ координат ($x$ и $y$ соответственно, см. рис. 1б). Ось $z$ на рисунке совпадает с осью симметрии системы из двух капель. Следуя Френкелю, мы также будем полагать, что поверхности обеих капель сохраняет сферическую форму, хотя текущее значение радиуса сфер $r\left( t \right)$ изменяется в процессе коалесценции. Если исходить из вполне резонного для нелетучей жидкости допущения, что общий объем $V$ системы из двух нелетучих капель не меняется в процессе коалесценции, то конечный радиус дочерней капли ${{r}_{{\text{f}}}}\left( \tau \right)$ будет связан с радиусом исходных капель ${{r}_{0}}$ соотношением ${{r}_{{\text{f}}}} = 1.26{{r}_{0}}$.

В [2] Френкель ограничился рассмотрением малых значений угла $\theta $ (рис. 1б), т.е. начальной стадии коалесценции. Приравнивая изотермическую работу поверхностного натяжения работе диссипативных сил, он получил следующую формулу для площади соприкосновения сфер:

где $\eta $ – коэффициент динамической (сдвиговой) вязкости. Полагая в (4) $r = {{r}_{{\text{f}}}} = {{Y}_{{{\text{max}}}}} = 1.26$, где ${{Y}_{{{\text{max}}}}}$ – максимальное значение $Y$, отвечающее характерному времени коалесценции $\tau $, приходим к выводу о пропорциональности между $\tau $ и ${{r}_{0}}$: где коэффициент пропорциональности $3.3\left( {{\eta \mathord{\left/ {\vphantom {\eta \sigma }} \right. \kern-0em} \sigma }} \right)$ определяется отношением коэффициента вязкости жидкости η к ее поверхностному натяжению σ. Следует только отметить, что при выводе исходного соотношения (4) Френкель допустил небольшую ошибку. Если ее исправить, то множитель π в (4) исчезает, и вместо (5) получим соотношение с числовым множителем, равным единице: что, впрочем, не затрагивает вывода о пропорциональности между τ и ${{r}_{0}}$. Со ссылкой на [2] эта формула приводится в [6] и [7], хотя в работе [2] она не фигурирует. Вместе с тем, сам Френкель, обсуждая соотношение (4), отмечал, что время полного спекания должно иметь порядок $\left( {{\eta \mathord{\left/ {\vphantom {\eta \sigma }} \right. \kern-0em} \sigma }} \right){{r}_{0}}$.

Однако применение даже формулы (6) с уточненным значением числового множителя для нахождения характерного времени коалесценции τ является не вполне корректным, поскольку в своей теории Френкель исходил из допущения о малости угла θ, когда можно положить $\sin \theta \cong \theta $ и $r \cong {{r}_{0}} = {\text{const}}$. Учитывая это, в данной работе подход Френкеля был распространен на произвольные значения $0 < \theta \leqslant {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$. При этом мы исходили из той же геометрической модели сливающихся капель (рис. 1б). В соответствии с этой моделью,

В дальнейшем учтем, что параметры $r$ и $\theta $ взаимосвязаны, и взаимосвязь между ними можно установить из условия $V = {\text{const}}$. С использованием формулы для объема шарового сегмента находим, что где $h = r - Z$. В свою очередь, площадь поверхности $S$ тела, показанного на рис. 1б, можно оценить по формуле а из условия ${{{\text{d}}V} \mathord{\left/ {\vphantom {{{\text{d}}V} {{\text{d}}t}}} \right. \kern-0em} {{\text{d}}t}} = 0$ получим следующую взаимосвязь между производными ${{{\text{d}}r} \mathord{\left/ {\vphantom {{{\text{d}}r} {{\text{d}}t}}} \right. \kern-0em} {{\text{d}}t}}$ и ${{{\text{d}}\theta } \mathord{\left/ {\vphantom {{{\text{d}}\theta } {{\text{d}}t}}} \right. \kern-0em} {{\text{d}}t}}$: Следуя [2], будем исходить из того, что изотермическая работа диссипативных сил (сил внутреннего трения) за единицу времени ${{A}_{{{\text{diss}}}}}$ совершается за счет убыли свободной поверхностной энергии сливающихся капель, т.е. из равенства между ${{A}_{{{\text{diss}}}}}$ и работой сил поверхностного натяжения ${{A}_{{{\text{surf}}}}} = - \sigma \left( {{{{\text{d}}S} \mathord{\left/ {\vphantom {{{\text{d}}S} {{\text{d}}t}}} \right. \kern-0em} {{\text{d}}t}}} \right)$ за единицу времени. В свою очередь, производная ${{{\text{d}}S} \mathord{\left/ {\vphantom {{{\text{d}}S} {{\text{d}}t}}} \right. \kern-0em} {{\text{d}}t}}$ выражается через производные ${{{\text{d}}\theta } \mathord{\left/ {\vphantom {{{\text{d}}\theta } {{\text{d}}t}}} \right. \kern-0em} {{\text{d}}t}}$ и ${{{\text{d}}r} \mathord{\left/ {\vphantom {{{\text{d}}r} {{\text{d}}t}}} \right. \kern-0em} {{\text{d}}t}}$: Текущий радиус $r\left( t \right)$ каждой из сливающихся капель изменяется в сравнительно небольшом интервале, от ${{r}_{0}}$ до ${{r}_{{\text{f}}}} = 1.26{{r}_{0}}$. Соответственно, как следует из (7), второе слагаемое в правой части (8) пренебрежимо мало при малых θ, составляет не более 1% при $\theta = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$ и увеличивается до нескольких процентов лишь при приближении θ к своему максимальному значению $\theta = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$. Учитывая это, вторым слагаемым в правой части (8) пренебрегаем и полагаем соответственно, что ${{A}_{{{\text{surf}}}}} = 4\pi {{r}^{2}}\sigma \sin \theta \left( {{{{\text{d}}\theta } \mathord{\left/ {\vphantom {{{\text{d}}\theta } {{\text{d}}t}}} \right. \kern-0em} {{\text{d}}t}}} \right)$. В свою очередь, ${{A}_{{{\text{diss}}}}}$ можно выразить через усредненную работу диссипативных сил в расчете на единицу объема за единицу времени где ${{{\bar {v}}}_{{ij}}}$ – средние значения компонент симметричной части градиента скорости. Следуя Френкелю, мы используем здесь декартовы координаты ${{x}_{i}} = ~x,y,z$, хотя, разумеется, учитываем в дальнейшем симметрию рассматриваемой системы относительно оси $z$. На этой оси, т.е. при $x = y = 0$, ${{{v}}_{x}} = {{{v}}_{y}} = 0$, и соответственно градиенты компонент скорости ${{{v}}_{x}}$ и ${{{v}}_{y}}$ в направлении оси $z$ отсутствуют. Максимальные же (по модулю) значения этих компонент градиента скорости достигаются на поверхности перешейка, в частности в точках A и A′ (рис. 1б) с координатами (0, $Y$, $Z$) и (0, $ - Y$, $Z$). При $Z = 0$, т.е. в точках B и B′ на рис. 1б значение $\left| {{{{v}}_{y}}} \right| = {{{\text{d}}r} \mathord{\left/ {\vphantom {{{\text{d}}r} {{\text{d}}t}}} \right. \kern-0em} {{\text{d}}t}}$ пренебрежимо мало по сравнению со значениями $\left| {{{{v}}_{y}}} \right|$ в точках A и A′, а для компоненты скорости ${{{v}}_{y}}$ в точке A имеем С учетом (7), вторым слагаемым в правой части (10) можно пренебречь, т.е. положить, что В свою очередь, средние значения компонент ${{\partial {{{v}}_{x}}} \mathord{\left/ {\vphantom {{\partial {{{v}}_{x}}} {\partial z}}} \right. \kern-0em} {\partial z}}$ и ${{\partial {{{v}}_{y}}} \mathord{\left/ {\vphantom {{\partial {{{v}}_{y}}} {\partial z}}} \right. \kern-0em} {\partial z}}$ градиента скорости можно оценить следующим образом: Далее, в допущении, что круговое сечение перешейка, отвечающее $z = Z$ и перпендикулярное оси $z$, приближается к началу координат, т.е. к точке O, сохраняя свою исходную ориентацию, приходим к выводу, что компоненты градиента скорости ${{\partial {{{v}}_{z}}} \mathord{\left/ {\vphantom {{\partial {{{v}}_{z}}} {\partial x}}} \right. \kern-0em} {\partial x}}$ и ${{\partial {{{v}}_{z}}} \mathord{\left/ {\vphantom {{\partial {{{v}}_{z}}} {\partial y}}} \right. \kern-0em} {\partial y}}$ приблизительно равны нулю. Наконец, равенство ${{\partial {{{v}}_{y}}} \mathord{\left/ {\vphantom {{\partial {{{v}}_{y}}} {\partial x}}} \right. \kern-0em} {\partial x}} = {{\partial {{{v}}_{x}}} \mathord{\left/ {\vphantom {{\partial {{{v}}_{x}}} {\partial y}}} \right. \kern-0em} {\partial y}} = 0$ следует из допущения о симметрии системы из двух сливающихся капель относительно оси $z$, т.е. из допущения об отсутствии круговых потоков относительно этой оси. Таким образом, в правой части выражения (9) остаются только квадраты средних значений компонент градиента скорости ${{\partial {{{v}}_{x}}} \mathord{\left/ {\vphantom {{\partial {{{v}}_{x}}} {\partial z}}} \right. \kern-0em} {\partial z}}$ и ${{\partial {{{v}}_{y}}} \mathord{\left/ {\vphantom {{\partial {{{v}}_{y}}} {\partial z}}} \right. \kern-0em} {\partial z}}$. Окончательно для ${{A}_{{{\text{diss}}}}}$ находим Приравнивая ${{A}_{{{\text{diss}}}}}$ и ${{A}_{{{\text{surf}}}}}$, получим дифференциальное уравнение В принципе, в правой части (14) можно было бы выразить текущий радиус капель $r\left( t \right)$ через $\theta \left( t \right)$, предварительно решив дифференциальное уравнение вытекающее из (7). Однако во избежание громоздких выкладок можно учесть, что $r$ изменяется в сравнительно небольших пределах, от ${{r}_{0}}$ до ${{r}_{{\text{f}}}} = 1.26{{r}_{0}}$. Соответственно в правой части (14) положим $r = \left\langle r \right\rangle = {{\left( {{{r}_{0}} + {{r}_{{\text{f}}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{r}_{0}} + {{r}_{{\text{f}}}}} \right)} 2}} \right. \kern-0em} 2} = 1.13{{r}_{0}}$. Тогда (14) сводится к дифференциальному уравнению с разделяющимися переменными.

При решении уравнения (15) учтем, что, вопреки мнению Френкеля, первой быстрой стадией коалесценции является не вязкое течение, а формирование контакта между частицами, и эта стадия не соответствует механизму вязкого течения. Иными словами, механизм вязкого течения можно привлекать для описания лишь второй стадии коалесценции, отвечающей $t > {{t}_{0}}$, где ${{t}_{0}}$ – время формирования контакта (перешейка) некоторого малого, но конечного диаметра $d \ll {{r}_{0}}$. Соответственно в (15) интегрирование по $\theta $ следует производить не от $\theta = 0$, как это делалось в [2], а от некоторого малого угла ${{\theta }_{0}}$, определяемого из условия

Таким образом, решение дифференциального уравнения (15) можно записать в виде Наконец, полагая, что продолжительность всего процесса коалесценции много больше времени формирования контакта ($\tau \gg {{t}_{0}}$), окончательно находим: где в качестве параметра $d$, отвечающего минимальному по площади контакту, можно взять значение эффективного атомного/молекулярного диаметра.

3. СРАВНЕНИЕ ТЕОРЕТИЧЕСКИХ ОЦЕНОК ХАРАКТЕРНОГО ВРЕМЕНИ КОАЛЕСЦЕНЦИИ С РЕЗУЛЬТАТАМИ ЛАБОРАТОРНЫХ И КОМПЬЮТЕРНЫХ ЭКСПЕРИМЕНТОВ

Согласно [4], еще в 40-х годах сам Френкель предпринимал попытку экспериментальной проверки своей теории [2]. Две твердых бусинки выдерживались при высокой температуре, а затем охлаждались. Циклы нагрева–охлаждения повторялись при все более высокой температуре, и, наконец, при некоторой температуре имела место коалесценция. По мнению Гегузина [4], у этих опытов имелся ряд недостатков: 1) бусинки были малы, и изменение их формы обнаруживать трудно, 2) они не были идеально сферическими, 3) сила тяжести искажала форму размягченных бусинок, 4) 5–10 полученных экспериментальных точек недостаточно для достоверных выводов. Сам Гегузин осуществил опыты, в которых кусочки смолы в виде сфер диаметром 5 см помещали в жидкость с примерно той же плотностью для имитации невесомости и соответственно для обеспечения сферической формы капель, в которые превращались эти кусочки смолы с повышением температуры. Коалесценция регистрировалась с помощью скоростной киносъемки. Некоторые последовательные кадры из этого фильма, взятые из [4], представлены на рис. 2а.

К сожалению, детали экспериментов в [4] не указаны. В частности не указано, какая именно смола использовалась. В данной работе мы предприняли попытку оценить время коалесценции двух капель эпоксидной смолы того же размера с использованием как нашей формулы (17), так и формулы (6), отвечающей теории Френкеля [2] с исправленным значением числового множителя. Для неотвержденных эпоксидных смол имеются экспериментальные данные по их вязкости и поверхностному натяжению. Так, согласно ГОСТу 10 587-84 (изм. № 1), вязкость эпоксидно-диановых смол составляет 5–20 Па с, что на 4 порядка больше вязкости воды. Примем соответственно, что $\eta = 10~$ Па с. Согласно [24], поверхностное натяжение $\sigma $ эпоксидных смол составляет 35–40 мДж/м², и мы положим далее, что $\sigma \approx $ 40 мДж/м². Следует только учесть, что в данном случае в формулы (6) и (17) следует подставлять не значение поверхностного натяжения эпоксидной смолы $\sigma $, а межфазное натяжение ${{\sigma }_{{12}}}$ на границе эпоксидной смолы с окружающим ее раствором. Очевидно, в [4] применялся водный раствор какой-либо соли с поверхностным натяжением $\sigma {\kern 1pt} '$, приблизительно равным поверхностному натяжению воды 72 мДж/м² [25] при $T = $ 293 К. Тогда, по правилу Антонова, ${{\sigma }_{{12}}} \cong \left| {\sigma - \sigma {\text{'}}} \right| \cong $ 30 мДж/м². Эффективный диаметр молекул смолы, фигурирующий в формуле (17), можно положить равным 1 нм. Соответственно по формуле Френкеля (6) находим, что $\tau = $ 8.3 с, а при использовании нашей формулы (17) получим на порядок большее значение $\tau = $ 80 с, которое хорошо согласуется с экспериментальным результатом Гегузина $\tau \approx $ 1 мин.

В работе [7], посвященной МД-моделированию спекания наночастиц Si, формула (6) приводится без какой-либо попытки ее применения к наноразмерным объектам. Очевидно, в [22, 23] мы впервые предприняли такого рода попытку, сопоставляя наши результаты МД-моделирования коалесценции нанокапель Au с результатами расчетов по формуле (6). Ниже наши МД-результаты сравниваются с результатами расчетов $\tau $ как по формуле (6), так и по формуле (17). МД-моделирование коалесценции нанокапель и спекания твердых наночастиц Au осуществлялось нами с использованием известной программы LAMMPS и метода погруженного атома с параметризацией [26].

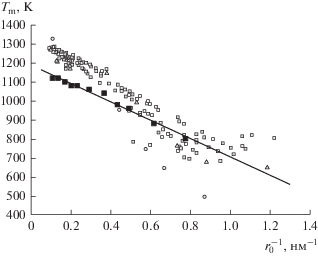
В [22, 23] мы предложили различать коалесценцию нанокапель и спекание твердых наночастиц, исходя из их температуры плавления ${{T}_{{\text{m}}}}$. Соответственно случай, когда $T \geqslant {{T}_{{\text{m}}}}$, будем относить к коалесценции капель, а ситуацию, когда $T < {{T}_{{\text{m}}}}$, – к спеканию твердых наночастиц. При этом необходимо учесть, что температура плавления наночастиц ${{T}_{{\text{m}}}}$ зависит от их размера. Соответственно моделированию процессов коалесценции и спекания предшествовало исследование размерной зависимости температуры плавления наночастиц. С этой целью начальные конфигурации в виде сферических фрагментов ГЦК-решетки Au релаксировали при различных фиксированных значениях температуры, и температура ${{T}_{{\text{m}}}}$, отвечающая скачку потенциальной (когезионной) составляющей внутренней энергии частицы, интерпретировалась как равновесная температура плавления наночастиц данного размера. Разумеется, определяемая таким способом температура плавления отвечает разрушению кристаллической упорядоченности в наночастице. Найденная по результатам МД-экспериментов зависимость ${{T}_{{\text{m}}}}$ от обратного радиуса частиц $r_{0}^{{ - 1}}$ представлена на рис. 3. Выбор обратного радиуса $r_{0}^{{ - 1}}$ в качестве аргумента обусловлен тем, что в некотором приближении ${{T}_{{\text{m}}}}$ уменьшается с ростом $r_{0}^{{ - 1}}$ по линейному закону, что подтверждается имеющимися экспериментальными данными, также представленными на рис. 3, и согласуется с известной формулой Томсона, детально обсуждавшейся нами ранее в работе [30].

В связи с использованием понятия температуры плавления применительно к наночастицам необходимо отметить следующее. В общем случае, как было показано Русановым [31], для наноразмерных объектов понятия термодинамической фазы, фазового перехода и, следовательно, температуры фазового перехода становятся физически неадекватными. Однако в соответствии с нашими МД-результатами и результатами лабораторных экспериментов [27–29], представленными на рис. 3, мезоскопические металлические наночастицы, содержащие от нескольких сотен до нескольких сотен тысяч атомов, демонстрируют вполне воспроизводимый переход между твердым (кристаллическим) и жидкоподобным состояниями при вполне определенной температуре ${{T}_{{\text{m}}}}$, интерпретируемой как температура плавления (см. также [32, 33]), хотя в некоторых случаях, обсуждение которых выходит за рамки данной работы, такой переход может быть размытым, т.е. происходит в некотором малом температурном интервале.

Как это ни удивительно, но кадры из фильма, отснятого Гегузиным (рис. 2а), относящиеся к коалесценции крупных капель смолы, очень схожи с нашими МД-конфигурациями, демонстрирующими коалесценцию нанокапель Au и показанными на рис. 2б, хотя некоторые различия все же имеются. В частности, МД-конфигурация, отвечающая $t = $ 0.06 нс, характеризуется более вытянутым перешейком и соответственно несколько большим отклонением от геометрической модели, представленный на рис. 1б.

Результаты расчетов по формулам (6) и (17), а также наши МД-результаты представлены на рис. 4а. Значение вязкости $\eta = $ 5.6 × 10^–3 Па с расплава Au при $T = $ 1500 К, необходимое для оценок по формулам (6) и (17), взято из работы [34], а значения поверхностного натяжения $\sigma = $ 1.170 Н/м при температуре плавления Au (1300 К) и его температурной производной ${{{\text{d}}\sigma } \mathord{\left/ {\vphantom {{{\text{d}}\sigma } {{\text{d}}T}}} \right. \kern-0em} {{\text{d}}T}}$, необходимые для оценки σ при $T = $ 1500 К, – из обзора [35]. Как и следовало ожидать, характерные времена коалесценции макроскопических и наноразмерных капель различаются на много порядков величины. Следует также отметить, что формула (17) лучше согласуется с МД-результатами, хотя различие в коэффициентах наклона соответствующих зависимостей 2 и 3 является существенным.

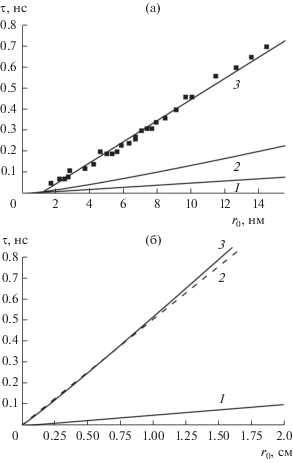
Рисунок 4а показывает также, что нелинейность зависимости 2, предсказываемая формулой (17), практически не заметна. Более заметное отклонение от линейности при малых ${{r}_{0}}$ (${{r}_{0}} \leqslant $ 4 нм) демонстрируют МД-результаты, представленные точками на рис. 4а. Экстраполяция МД-результатов для нанокапель Au к ${{r}_{0}}$ порядка 1 см (рис. 4б) приводит к тому, что МД-зависимость 3 на этом рисунке гораздо лучше согласуется с зависимостью 2, рассчитанной по формуле (17) и показанной штриховой линией. Кроме того, при ${{r}_{0}}$ порядка 1 см нелинейность зависимости (17) становится более заметной, чем на наномасштабах, но все же остается незначительной.

4. О МЕХАНИЗМАХ СПЕКАНИЯ ТВЕРДЫХ НАНОЧАСТИЦ

Спекание твердых наночастиц Au ($T < {{T}_{{\text{m}}}}$) также моделировалось нами с использованием программы LAMMPS. В случае спекания нахождение вида зависимости $\tau \left( {{{r}_{0}}} \right)$ затруднительно, поскольку этот процесс является гораздо более медленным и не завершается формированием дочерней сферической частицы.

На рис. 5 представлена МД-конфигурация дочерней наночастицы Au, полученной спеканием при $T = ~$ 700 К двух сферических наночастиц Au с ГЦК-структурой, содержащих по 3043 атома каждая. Конфигурация, показанная на рис. 5, отвечает одинаковой исходной кристаллографической ориентации (100) обеих наночастиц. Начальная стадия этого процесса сопровождается небольшими поворотами частиц относительно друг друга, завершающимися формированием двухзеренной структуры, подобной структурам, наблюдавшимся экспериментально с помощью ПЭМ [16, 17]. Рисунок с нашей МД-конфигурацией и ПЭМ-изображения, полученные авторами работ [16] и [17], представлены с их разрешения в нашей недавней работе [22]. Отжиг МД-конфигурации, показанной на рис. 5, на протяжении доступного для моделирования времени (100 нс) также не привел к формированию наноразмерного монокристалла.

Однако при более высокой температуре $T = {{T}_{{\text{m}}}} - $ 60 К = 920 К и одинаковой кристаллографической ориентации исходных наночастиц монокристаллическая структура дочерней частицы формировалась за характерное время, меньшее 1 нс. Если же исходные кристаллографические ориентации различались на 45°, то при $T = {{T}_{{\text{m}}}} - $ 60 К двухзеренная структура сохраняла свою стабильность, но при более высокой температуре $T = {{T}_{{\text{m}}}} - $ 20 К = 960 К она также переходила в монокристаллическую. Таким образом, эффект исчезновения межзеренной границы, наблюдавшейся экспериментально в работах [16, 17], существенно зависит от температуры. Согласно данным работы [16] он имеет место даже при достаточно низкой температуре $T = $ 700 К, но реализуется за время порядка 10 с, которое заведомо недоступно для воспроизведения в компьютерном МД-эксперименте.

Несколько неожиданными оказались МД-результаты, отвечающие низкотемпературному спеканию ($T = $ 700 К) более крупных сферических наночастиц Au, состоящих каждая из 10 053 атомов и одинаково ориентированных в направлении (100), совпадающем с направлением оси $z$, проходящей через центры исходных частиц. В этом случае какой-либо выраженный переходный слой (граница зерен) в области перешейка не наблюдался, т.е. при контакте частиц сразу формировался наноразмерный монокристалл гантелеобразной формы (рис. 6). Однако кристаллографические плоскости в области перешейка оказались изогнутыми. Очевидно, в данном случае был бы уместнее термин “кристаллографические поверхности”, не используемый в классической кристаллографии. Примечательно также, что в наших МД-экспериментах наблюдались небольшие колебания спекаемых частиц данного размера, отвечающие их поворотам относительно друг друга со смещением в разные стороны центров масс частиц от исходного направления, т.е. от оси $z$. Как видно на рис. 6, полупериод таких колебаний составляет примерно 0.02 нс. Примечательно, что небольшие повороты наблюдались экспериментально и при спекании микрочастиц [5].

5. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

При теоретическом рассмотрении наночастиц и наносистем часто впадают в две крайности: 1) некритично применяют понятия и концепции макроскопической физики, включая классическую термодинамику, к наноразмерным объектам, 2) полностью отрицают применимость понятий и концепций термодинамики к наночастицам и наносистемам. В данной работе на примере явлений коалесценции и спекания было показано, что существуют как закономерности, общие для макро-, микро- и наночастиц, так и специфические закономерности, проявляющиеся только на наномасштабах. В частности, теория коалесценции капель, отвечающая развитию подхода Френкеля [2], основывающегося на гидродинамике и линейной неравновесной термодинамике, достаточно адекватно описывает коалесценцию как очень крупных капель смолы, так и нанокапель золота радиусом порядка 1 нм. Отсюда можно сделать вывод, что при таких размерах еще можно пользоваться макроскопическими значениями коэффициента вязкости и поверхностного натяжения для описания диссипации энергии при коалесценции. В наших МД-экспериментах в качестве объектов исследования выступали наночастицы размером не менее 6 нм. Для таких частиц интерпретация результатов МД-экспериментов как коалесценции капель и спекания твердых частиц становится, на наш взгляд, вполне правомерной.

Разумеется, теоретический подход к коалесценции, рассмотренный в разделе 2, связан с рядом упрощающих допущений. Вместе с тем, удалось отказаться от допущений Френкеля, не совместимых с применением его теории к завершающей стадии коалесценции. Однако даже применительно к мезоскопическим наночастицам возникает вопрос о правомерности подстановки в формулы (6) и (17) макроскопического значения ${{\sigma }^{{\left( \infty \right)}}}$ поверхностного натяжения $\sigma $. Для оценки характерного значения радиуса частиц ${{r}^{{\left( {{\text{ch}}} \right)}}}$, ниже которого необходимо учитывать размерную зависимость поверхностного натяжения, воспользуемся линейной формулой $\sigma = Kr$, предсказанной для малых $r$ Русановым еще в 60-х годах [36]. Здесь $K$ – коэффициент пропорциональности, зависящий от температуры и давления. Характерный радиус ${{r}^{{\left( {{\text{ch}}} \right)}}}$ можно оценить из условия

Что же касается параметра $K$, то для наночастиц металлов в твердом и жидком состояниях он оценивался Витолем [37] по экспериментальным данным о скорости испарения наночастиц. Как было показано в нашей работе [38], оценки Витоля являются достаточно грубыми, но, тем не менее, степень их точности вполне достаточна для оценки порядка величины ${{r}^{{\left( {{\text{ch}}} \right)}}}$. Согласно [37], для нанокапель Au ${{K}_{{\text{L}}}}~$ = 30 × 10¹⁰ мДж/м³, а для твердых наночастиц ${{K}_{{{\text{S\;}}}}}$ = 40 × 10¹⁰ мДж/м³. Соответственно, воспользовавшись экспериментальными значениями $\sigma _{{\text{L}}}^{{\left( \infty \right)}}$ = 1170 мДж/м², $\sigma _{{\text{S}}}^{{\left( \infty \right)}}$ = = 1363 мДж/м² [35] поверхностного натяжения золота в расплавленном и твердом состояниях, находим: $r_{{\text{L}}}^{{\left( {{\text{ch}}} \right)}}~$ = 3.9 нм, $r_{{\text{S}}}^{{\left( {{\text{ch}}} \right)}}~$ = 3.4 нм. Этим величинам соответствуют следующие значения характерного числа атомов ${{N}^{{\left( {{\text{ch}}} \right)}}}$, содержащихся в частице: $N_{{\text{L}}}^{{\left( {{\text{ch}}} \right)}} \cong $ 4000, $N_{{\text{S}}}^{{\left( {{\text{ch}}} \right)}} \cong $ 3000. Таким образом, при $N > {\text{\;}}$ 3000–4000 размерную зависимость поверхностного натяжения можно не учитывать. Очевидно, неравенство $r \geqslant {{r}^{{\left( {{\text{ch}}} \right)}}}$ можно рассматривать и как условие применимости, в некотором приближении, макроскопического значения коэффициента вязкости $\eta $. Действительно, равенство $\sigma = {{\sigma }^{{\left( \infty \right)}}}$ означает, что значения локальных термодинамических и кинетических параметров в центральной области частицы не должны заметно отличаться от значений тех же параметров в соответствующей объемной фазе.

Наши теоретические оценки $\tau $ и МД-результаты подтверждают сделанный в [12] вывод о том, что коалесценция нанокапель происходит в две стадии: 1) быстрая стадия формирования контакта между ними (характерное время порядка 0.01 нс), 2) более медленная стадия приобретения дочерней каплей сферической формы (характерное время от долей нс до 1 нс). Подтвержден и сделанный в [12] вывод о том, что коалесценция нанокапель Au не описывается механизмом ПДИК [11]. Вместе с тем, авторы работы [12] не сделали определенного вывода о механизмах коалесценции и спекания на наномасштабах.

По нашему мнению, механизм первой стадии коалесценции нанокапель отвечает взаимодействию между ближайшими атомами (молекулами) двух сближающихся капель. Природа этого взаимодействия может быть различной, поскольку она определяется природой химической связи в веществе капель. МД-результаты подтвердили также принятое в разделе 2 допущение, что продолжительность первой стадии коалесценции (формирование контакта между каплями) ${{t}_{0}}$ много меньше характерного времени коалесценции $\tau $ (${{t}_{0}} \ll \tau $). Что же касается второй стадии, то сопоставление результатов расчетов по формуле (17) с экспериментальными данными для макроскопических капель смолы и с нашими МД-результатами для нанокапель Au позволяет сделать следующий вывод: основная и наиболее продолжительная стадия коалесценции как макроскопических, так и наноразмерных капель происходит по механизму вязких течений в сливающихся каплях. Эти течения являются следствием тенденции к уменьшению свободной поверхностной энергии и соответственно площади поверхности дочерней капли. Соотношение (9), записанное с учетом линейной взаимосвязи между тензором вязкости и градиентом скорости, отвечает использованию модели ньютоновской жидкости. Тем не менее, теория, развитая в данной работе, адекватно описывает коалесценцию капель эпоксидной смолы, т.е. достаточно вязкой жидкости.

МД-результаты, представленные в данной работе, подтверждают адекватность дифференциации между коалесценцией и спеканием на наномасштабах с учетом соотношения между температурой процесса $T$ и температурой плавления частиц ${{T}_{{\text{m}}}}$, относя к коалесценции нанокапель ситуацию, когда $T > {{T}_{{\text{m}}}}$, а к спеканию твердых частиц – случай, когда $T < {{T}_{{\text{m}}}}$. Промежуточная ситуация ($T = {{T}_{{\text{m}}}}$) требует отдельного рассмотрения. Однако нами было установлено, что, по крайней мере, при ${\Delta }T = \left| {T - {{T}_{{\text{m}}}}} \right| \geqslant $ 20 К закономерности и механизмы указанных выше процессов принципиально различаются. Действительно, начальная стадия спекания кристаллических частиц ($T < {{T}_{{\text{m}}}}$) связана с взаимной подстройкой их кристаллографических ориентаций. Как и для микрочастиц [5], протекание этой стадии зависит от их исходной взаимной ориентации. Взаимные малые вращения спекаемых частиц относительно друг друга, в том числе в виде затухающих вращательных колебаний, наблюдались при формировании контакта как в наших МД-экспериментах на наночастицах, так и в лабораторных экспериментах на микроскопических крупинках [5]. В некоторых случаях в наших МД-экспериментах по спеканию кристаллических наночастиц Au уже на первой стадии процесса образовывался наноразмерный монокристалл вытянутой (гантелеобразной) формы, сохраняющий свою стабильность на протяжении всего времени, доступного для МД-моделирования. В других же случаях, например при спекании наночастиц Au, содержащих каждая по 3043 атома, на первой стадии формировалась двухзеренная структура с различными кристаллографическими ориентациями зерен и соответственно с некоторым переходным слоем между ними, т.е. границей зерен. В этом случае вторая стадия спекания отвечала релаксации двухзеренной структуры, т.е. ее переходу в монокристаллическую. При значениях температуры $T$, близких к ${{T}_{{\text{m}}}}$, такой процесс релаксации наблюдался и в наших МД-экспериментах. Но при $T \ll {{T}_{{\text{m}}}}$, например при $T = $ 700 К, такого рода релаксацию, время которой составляет порядка 10 с, можно наблюдать лишь в лабораторных экспериментах [16, 17]. Таким образом, структурные превращения в спекаемых наночастицах отчасти носят вероятностный характер, что согласуется с мнением Русанова о динамичности структуры наноразмерных объектов [31].

Следует также отметить, что как теоретические оценки, так и наши МД-результаты, представленные выше, относятся к коалесценции капель и спеканию частиц, не находящихся на какой-либо твердой поверхности. Закономерности коалесценции капель, сливающихся на подложке [39], и спекания частиц или островковых пленок на твердой поверхности [40] могут существенно отличаться от поведения свободных капель и твердых частиц. Одно из интересных, на наш взгляд, явлений – явление смачивания в твердом состоянии (СТС) – можно рассматривать как предельный случай спекания, когда одна из частиц имеет микронный или субмикронный размер, а радиус другой частицы стремится к бесконечности. В экспериментальных работах [41, 42] было показано, что микрочастицы Cu размером порядка 10 мкм растекаются по поверхности поликристаллической меди подобно каплям жидкости, но очень медленно. Согласно [42] характерное время СТС для таких частиц составляет примерно 3 ч при условии, что их температура на 30 K ниже макроскопического значения температуры плавления меди. Очевидно, в наших работах [43, 44] впервые была выдвинута и обоснована гипотеза о том, что явление СТС должно быть еще более характерно для наночастиц на твердой поверхности. При этом как в работе [42], так и в нашей работе [44] было показано, что концепция ПДИК [11] адекватно описывает кинетику СТC и для микро-, и наночастиц. Таким образом, в некоторых случаях доминирующие механизмы коалесценции и спекания, а также более сложных связанных с ними явлений, включая СТС, могут отличаться от механизмов, рассмотренных в данной работе.

6. ЗАКЛЮЧЕНИЕ

Френкель, положивший своей работой [2] начало теоретическим подходам к коалесценции и спеканию, был виртуозным мастером элементарных, но физически адекватных оценок. Что же касается Гегузина, то его научному наследию присущи как талант популяризатора науки, так и глубокие физически адекватные подходы к теоретическому рассмотрению технологических процессов, включая спекание. В данной работе мы детально проанализировали и уточнили предложенную Френкелем теорию коалесценции капель и впервые применили ее к прогнозированию кинетики коалесценции нанокапель. С использованием теоретических оценок, наших МД-результатов и экспериментальных данных, полученных ранее Гегузиным, было установлено, что основной механизм коалесценции как макроскопических, так и наноразмерных капель отвечает вязким течениям в дочерней капле, индуцированным уменьшением площади ее поверхности. В свою очередь, уменьшение площади поверхности объясняется тенденцией к уменьшению свободной поверхностной энергии при слиянии капель. Вместе с тем, было установлено, что часто упоминаемый в научной литературе механизм ПДИК не вносит заметного вклада ни в коалесценцию нанокапель, ни в спекание твердых кристаллических наночастиц.

С использованием МД-результатов было показано, что механизм спекания наночастиц существенно отличается от механизма коалесценции нанокапель, т.е. не сводится к вязким течениям и связанной с ними диссипацией энергии. Было, в частности, установлено, что спекание наноразмерных частиц происходит либо в одну, либо в две стадии, На первой из них происходит припекание, т.е. формируется контакт между частицами, и при одинаковой кристаллографической ориентации исходных частиц может образоваться стабильный наноразмерный монокристалл гантелеобразной формы. В других же случаях спекание связано с формированием двухзеренной структуры, где зерна, различающиеся кристаллографическими ориентациями, разделены некоторым переходным слоем (границей зерен). Вторая стадия отвечает релаксации двухзеренной структуры, т.е. ее переходу в наноразмерный монокристалл. Поверхностная диффузия атомов в сторону перешейка также наблюдалась нами в МД-экспериментах, но как в случае коалесценции нанокапель, так и в случае спекания двух свободных сферических наночастиц механизм ПДИК не является определяющим.