Коллоидный журнал, 2020, T. 82, № 6, стр. 661-667

Вычисление химического потенциала молекулы на основе радиальных функций распределения

Н. А. Волков^1, *, Е. В. Гоноровская¹, А. К. Щёкин¹, П. Н. Воронцов-Вельяминов¹

¹ Санкт-Петербургский государственный университет
199034 Санкт-Петербург, Университетская набережная, д. 7/9, Россия

Поступила в редакцию 29.05.2020
После доработки 09.06.2020
Принята к публикации 11.06.2020

DOI: 10.31857/S0023291220060191

Аннотация

Работа посвящена применению метода Хилла для расчета химического потенциала молекулы в однокомпонентной однородной молекулярной системе в рамках компьютерного моделирования. Данный метод основан на двойном интегрировании молекулярных радиальных функций распределения, зависящих от дополнительного параметра, который регулирует силу взаимодействия между частицами. Результаты вычисления химического потенциала молекулы аргона методом Хилла сравниваются с результатами, полученными нами при помощи двух других методов расчета химического потенциала: метода вставки пробной частицы Видома и метода расширенного ансамбля с использованием алгоритма Ванга–Ландау.

ВВЕДЕНИЕ

Для вычисления химического потенциала при помощи молекулярного моделирования обычно используются хорошо апробированные специализированные методы, например, метод Видома [1], метод термодинамического интегрирования [2], метод расширенного ансамбля [3] и т.д. В книге Хилла [4] по статистической механике описан метод вычисления химического потенциала однокомпонентной жидкости или газа, основанный на двойном интегрировании радиальных функций распределения, зависящих от дополнительного параметра, который регулирует силу взаимодействия между частицами. По-видимому, этот метод тесно связан с работой Кирквуда [5], опубликованной в 1935 году. Помимо монографии Хилла, подробное описание метода изложено в книге Маккварри по статистической механике [6], а окончательная формула для химического потенциала приведена в книге Аллена и Тилдесли [7], посвященной компьютерному моделированию. Отметим также, что метод Хилла может рассматриваться как частный случай метода термодинамического интегрирования, широко применяемого в молекулярном моделировании для вычисления разности свободных энергий.

Одно из преимуществ метода, описанного Хиллом, заключается в том, что радиальные функции распределения молекул, на основе которых вычисляется химический потенциал, могут быть стандартным образом получены при помощи молекулярного моделирования в рамках как метода Монте-Карло, так и метода молекулярной динамики. Целью нашей работы является разработка вычислительной процедуры, реализующей метод Хилла, и ее апробация на системе, состоящей из молекул аргона. При этом результаты расчетов сравниваются с результатами, полученными нами при помощи как метода Видома, так и комбинированного подхода, включающего в себя метод расширенного ансамбля, алгоритм Ванга–Ландау и метод молекулярной динамики.

1. МОДЕЛИ И МЕТОДЫ

1.1. Метод Хилла

Рассмотрим метод вычисления химического потенциала однокомпонентной молекулярной системы в объемной фазе, следуя книге Хилла [4]. Будем рассматривать классическую систему, состоящую из $N$ одинаковых молекул, находящуюся в объеме $V$ при температуре T. Гамильтониан такой системы имеет вид

(1)

${{H}_{N}} = \sum\limits_{i = 1}^N \frac{{{\mathbf{p}}_{i}^{2}}}{{2m}} + U({{{\mathbf{r}}}_{1}},...,{{{\mathbf{r}}}_{N}}).$

Здесь векторы ${{{\mathbf{p}}}_{1}},{{{\mathbf{p}}}_{2}},...,{{{\mathbf{p}}}_{N}}$ – импульсы молекул, $m$ – масса молекулы, $U({{{\mathbf{r}}}_{1}},...,{{{\mathbf{r}}}_{N}})$ есть полная потенциальная энергия взаимодействия молекул жидкости, положения которых задаются радиус-векторами ${{{\mathbf{r}}}_{1}},...,{{{\mathbf{r}}}_{N}}.$

Статистическая сумма $Q$ канонического ансамбля для рассматриваемой системы имеет вид

(2)

$Q = \frac{1}{{{{{\left( {2\pi \hbar } \right)}}^{{3N}}}N!}}\int ...\int {{e}^{{{{ - {{H}_{N}}} \mathord{\left/ {\vphantom {{ - {{H}_{N}}} {kT}}} \right. \kern-0em} {kT}}}}}d{{{\mathbf{p}}}_{1}}...d{{{\mathbf{p}}}_{N}}d{{{\mathbf{r}}}_{1}}...d{{{\mathbf{r}}}_{N}}.$

Произведя интегрирование по импульсам, получаем $Q = {Z \mathord{\left/ {\vphantom {Z {N!{{\Lambda }^{{3N}}}}}} \right. \kern-0em} {N!{{\Lambda }^{{3N}}}}},$ где $\Lambda = {{2\pi \hbar } \mathord{\left/ {\vphantom {{2\pi \hbar } {\sqrt {2\pi mkT} }}} \right. \kern-0em} {\sqrt {2\pi mkT} }}$ – длина волны де Бройля, $Z = \int ...\int_V {{e}^{{{{ - U} \mathord{\left/ {\vphantom {{ - U} {kT}}} \right. \kern-0em} {kT}}}}}d{{{\mathbf{r}}}_{1}}...d{{{\mathbf{r}}}_{N}}$ – конфигурационный интеграл. По статистической сумме $Q$ находим свободную энергию $F = - kT\ln Q$ в виде

(3)

$F = - kT\ln \frac{Z}{{N!{{\Lambda }^{{3N}}}}}.$

Представим химический потенциал $\mu $ молекул в системе как

(4)

$\mu = F(N) - F(N - 1) \approx {{\left( {\frac{{\partial F}}{{\partial N}}} \right)}_{{V,T}}}.$

Используя выражение (3), химический потенциал можно записать как

(5)

$\mu = - kT\ln \frac{{{{Z}_{N}}}}{{V{{Z}_{{N - 1}}}}} - kT\ln \frac{V}{{N{{\Lambda }^{3}}}},$

где ${{Z}_{N}}$ – конфигурационный интеграл системы $N$ частиц.

Введем параметр включения взаимодействия $\xi \in [0,1]$ для первой молекулы (назовем ее “особенной”). Параметр ξ определяет степень взаимодействия “особенной” молекулы с остальными молекулами, на него умножается соответствующий межмолекулярный потенциал взаимодействия. Тогда потенциальную энергию взаимодействия можно записать в виде суммы двух вкладов: энергии взаимодействия первой молекулы со всеми остальными и энергии взаимодействия оставшихся $N - 1$ молекул друг с другом,

(6)

$U({{{\mathbf{r}}}_{1}},...,{{{\mathbf{r}}}_{N}},\xi ) = \sum\limits_{j = 2}^N \xi u({{{\mathbf{r}}}_{{1j}}}) + {{U}_{{N - 1}}},$

где

(7)

${{U}_{{N - 1}}} = \sum\limits_{2 \leqslant i < j \leqslant N} u({{{\mathbf{r}}}_{{ij}}}),$

$u({{{\mathbf{r}}}_{{ij}}})$ – потенциал взаимодействия между молекулами с номерами $i$ и $j$, зависящий от расстояния ${{{\mathbf{r}}}_{{ij}}} = {{{\mathbf{r}}}_{j}} - {{{\mathbf{r}}}_{i}}$ между этими молекулами. Если $\xi = 1,$ то имеем систему из $N$ молекул с полностью включенными взаимодействиями $U({{{\mathbf{r}}}_{1}}...{{{\mathbf{r}}}_{N}},1) = {{U}_{N}}.$ Если же $\xi = 0,$ то выбранная молекула не взаимодействует ни с одной из остальных $N - 1$ молекул (хотя взаимодействие между остальными $N - 1$ молекулами полностью включено) и $U({{{\mathbf{r}}}_{1}}...{{{\mathbf{r}}}_{N}},0) = {{U}_{{N - 1}}}.$

Отношение конфигурационных интегралов в выражении (5) можно выразить через параметр включения взаимодействия. Имеем

(8)

${{Z}_{N}}(\xi = 1) = {{Z}_{N}} = Z,$

(9)

$\begin{gathered} {{Z}_{N}}(\xi = 0) = \int ...\int\limits_V {{{e}^{{{{ - {{U}_{{N - 1}}}} \mathord{\left/ {\vphantom {{ - {{U}_{{N - 1}}}} {kT}}} \right. \kern-0em} {kT}}}}}} d{{{\mathbf{r}}}_{1}}...d{{{\mathbf{r}}}_{N}} = \\ = V\int ...\int\limits_V {{{e}^{{{{ - {{U}_{{N - 1}}}} \mathord{\left/ {\vphantom {{ - {{U}_{{N - 1}}}} {kT}}} \right. \kern-0em} {kT}}}}}} d{{{\mathbf{r}}}_{2}}...d{{{\mathbf{r}}}_{N}} = V{{Z}_{{N - 1}}}. \\ \end{gathered} $

Поэтому можно написать

(10)

$\ln \frac{{{{Z}_{N}}}}{{V{{Z}_{{N - 1}}}}} = \ln \frac{{{{Z}_{N}}(\xi = 1)}}{{{{Z}_{N}}(\xi = 0)}} = \int\limits_0^1 {\frac{{\partial \ln Z(\xi )}}{{\partial \xi }}d\xi } {\text{,}}$

где

(11)

$Z(\xi ) = \int ...\int\limits_V {{{e}^{{{{ - U({{{\mathbf{r}}}_{1}}...{{{\mathbf{r}}}_{N}},\xi )} \mathord{\left/ {\vphantom {{ - U({{{\mathbf{r}}}_{1}}...{{{\mathbf{r}}}_{N}},\xi )} {kT}}} \right. \kern-0em} {kT}}}}}d{{{\mathbf{r}}}_{1}}...d{{{\mathbf{r}}}_{N}}} .$

Согласно (11) и (6)

(12)

$\frac{{\partial Z(\xi )}}{{\partial \xi }} = - \frac{1}{{kT}}\int ...\int\limits_V {{{e}^{{{{ - U({{{\mathbf{r}}}_{1}}...{{{\mathbf{r}}}_{N}},\xi )} \mathord{\left/ {\vphantom {{ - U({{{\mathbf{r}}}_{1}}...{{{\mathbf{r}}}_{N}},\xi )} {kT}}} \right. \kern-0em} {kT}}}}}} \sum\limits_{j = 2}^N u({{{\mathbf{r}}}_{{1j}}})d{{{\mathbf{r}}}_{1}}...d{{{\mathbf{r}}}_{N}}.$

Все $N - 1$ слагаемых в (12) равны по величине, и, следовательно,

(13)

$\frac{{\partial \ln Z(\xi )}}{{\partial \xi }} = - \frac{1}{{NkT}}\int \int\limits_V {u({{{\mathbf{r}}}_{{12}}}){{\rho }^{{(2)}}}({{{\mathbf{r}}}_{1}},{{{\mathbf{r}}}_{2}},\xi )d{{{\mathbf{r}}}_{1}}d{{{\mathbf{r}}}_{2}},} $

где ${{\rho }^{{(2)}}}({{{\mathbf{r}}}_{1}},{{{\mathbf{r}}}_{2}})$ – двухчастичная функция распределения

(14)

${{\rho }^{{(2)}}}({{{\mathbf{r}}}_{1}},{{{\mathbf{r}}}_{2}},\xi ) = \frac{{N!}}{{(N - 2)!}}\frac{{\int ...\int\limits_V {{{e}^{{{{ - U({{{\mathbf{r}}}_{1}}...{{{\mathbf{r}}}_{N}},\xi )} \mathord{\left/ {\vphantom {{ - U({{{\mathbf{r}}}_{1}}...{{{\mathbf{r}}}_{N}},\xi )} {kT}}} \right. \kern-0em} {kT}}}}}} d{{{\mathbf{r}}}_{3}}...d{{{\mathbf{r}}}_{N}}}}{{Z(\xi )}},$

которая дает плотность вероятности события, что одна частица будет найдена в элементе объема $d{{{\mathbf{r}}}_{1}}$ около координаты, задаваемой радиус-вектором ${{{\mathbf{r}}}_{1}}$, а вторая – в элементе $d{{{\mathbf{r}}}_{2}}$ около ${{{\mathbf{r}}}_{2}}.$

Используя связь между двухчастичной функцией распределения и радиальной функцией распределения для случая однородной жидкости или газа

(15)

${{\rho }^{{(2)}}}({{{\mathbf{r}}}_{1}},{{{\mathbf{r}}}_{2}},\xi ) = {{\rho }^{2}}g(r,\xi ),$

где $\rho = {N \mathord{\left/ {\vphantom {N V}} \right. \kern-0em} V},$ а r – расстояние между частицами 1 и 2, перепишем (13) в случае жидкости или газа как

(16)

$\frac{{\partial \ln Z(\xi )}}{{\partial \xi }} = - \frac{N}{{VkT}}\int\limits_0^\infty {u(r)g(r,\xi )4\pi {{r}^{2}}dr} .$

Комбинируя (5), (10) и (13), получаем финальное выражение для химического потенциала в методе Хилла:

(17)

$\mu = kT\ln \frac{{N{{\Lambda }^{3}}}}{V} + \frac{N}{V}\int\limits_0^1 {\int\limits_0^\infty {u(r)g(r,\xi )4\pi {{r}^{2}}drd\xi } } .$

Видим, что для практического вычисления химического потенциала с использованием формулы (17) необходимо получить набор радиальных функций распределения “обычных” частиц относительно “особенной” частицы при различных значениях параметра включения взаимодействий $\xi $, что может быть сделано при помощи методов молекулярного моделирования, таких как метод молекулярной динамики и метод Монте-Карло.

Отметим, что метод Хилла также может рассматриваться как частный случай метода термодинамического интегрирования для молекулярной системы в объемной фазе. Приведем финальную формулу этого метода для вычисления разности свободных энергий двух состояний системы, различающихся значением параметра $\xi $ [2]:

(18)

$F(\xi = 1) - F(\xi = 0) = \int\limits_0^1 {d\xi {{{\left\langle {\frac{{\partial U(\xi )}}{{\partial \xi }}} \right\rangle }}_{\xi }}} .$

Для случая, рассмотренного выше, разность $F(\xi = 1) - F(\xi = 0)$ и есть избыточный химический потенциал молекулы. Частная производная, стоящая под интегралом в (18), вычисляется аналитически (см. формулу (6)). Таким образом, под интегралом в формуле (18) будет стоять $\left\langle {\sum\nolimits_{j = 2}^N u({{r}_{{1j}}})} \right\rangle $, т.е. средняя энергия взаимодействия первой молекулы со всеми остальными молекулами, которая может быть выражена стандартным образом через интеграл по $r$ от $g(r,\xi )$ как $\frac{N}{V}\int_0^\infty u(r)g(r,\xi ){\kern 1pt} 4\pi {{r}^{2}}dr.$ Следовательно, из формулы (18) в методе термодинамического интегрирования следует формула (17) для химического потенциала в методе Хилла.

1.2. Метод Видома

Эффективным и сравнительно простым в реализации в рамках молекулярного моделирования является метод вычисления химического потенциала при помощи вставки пробной частицы, предложенный Видомом [1]. Следуя [2], рассмотрим систему из $N$ взаимодействующих частиц. Как и в предыдущем разделе, потенциальная энергия системы равна сумме энергий парных взаимодействий, ${{U}_{N}} = \sum\nolimits_{1 \leqslant i < j \leqslant N} {u({{{\mathbf{r}}}_{{ij}}})} ,$ и химический потенциал $\mu $ выражается через конфигурационный интеграл соотношением (5), которое удобно переписать в виде

(19а)

$\begin{gathered} \mu = - kT\ln \frac{V}{{N{{\Lambda }^{3}}}} - kT\ln \frac{{{{Z}_{{N + 1}}}}}{{V{{Z}_{N}}}} = \\ = kT\ln \frac{{N{{\Lambda }^{3}}}}{V} - kT\ln \frac{{\int ...\int\limits_V {{{e}^{{{{ - {{U}_{{N + 1}}}} \mathord{\left/ {\vphantom {{ - {{U}_{{N + 1}}}} {kT}}} \right. \kern-0em} {kT}}}}}d{{{\mathbf{r}}}_{1}}...d{{{\mathbf{r}}}_{{N + 1}}}} }}{{V\int ...\int\limits_V {{{e}^{{{{ - {{U}_{N}}} \mathord{\left/ {\vphantom {{ - {{U}_{N}}} {kT}}} \right. \kern-0em} {kT}}}}}d{{{\mathbf{r}}}_{1}}...d{{{\mathbf{r}}}_{N}}} }}. \\ \end{gathered} $

Перепишем (19a) в виде суммы

(19б)

$\mu = {{\mu }_{{{\text{id}}}}} + {{\mu }_{{{\text{ex}}}}},$

где ${{\mu }_{{{\text{id}}}}} = kT\ln \frac{{N{{\Lambda }^{3}}}}{V}$ – химический потенциал идеального газа и μ_ex – избыточный химический потенциал. Введем разность $\Delta {{U}_{{N + 1}}} \equiv {{U}_{{N + 1}}} - {{U}_{N}}$ потенциальных энергий системы из $N + 1$ частицы и системы из $N$ частиц (очевидно, это энергия взаимодействия (N + 1)-ой частицы с остальными). Тогда с учетом (19а) можно записать избыточный химический потенциал как

(20)

${{\mu }_{{{\text{ex}}}}} = - kT\ln \frac{{\int\limits_V {d{{{\vec {r}}}_{{N + 1}}}} {{{\left\langle {{{e}^{{ - {{\Delta {{U}_{{N + 1}}}} \mathord{\left/ {\vphantom {{\Delta {{U}_{{N + 1}}}} {kT}}} \right. \kern-0em} {kT}}}}}} \right\rangle }}_{N}}}}{V},$

где ${{\left\langle {{{e}^{{ - {{\Delta {{U}_{{N + 1}}}} \mathord{\left/ {\vphantom {{\Delta {{U}_{{N + 1}}}} {kT}}} \right. \kern-0em} {kT}}}}}} \right\rangle }_{N}}$ обозначает усреднение функции ${{e}^{{ - {{\Delta {{U}_{{N + 1}}}} \mathord{\left/ {\vphantom {{\Delta {{U}_{{N + 1}}}} {kT}}} \right. \kern-0em} {kT}}}}}$ в каноническом ансамбле по конфигурационному пространству системы из $N$ частиц.

Процедура вычисления μ_ex выглядит следующим образом: в процессе моделирования системы при помощи стандартного метода Монте-Карло в каноническом ансамбле [8] раз в несколько шагов генерируется случайная координата (N + 1)-ой частицы и вычисляется значение ${{e}^{{ - {{\Delta {{U}_{{N + 1}}}} \mathord{\left/ {\vphantom {{\Delta {{U}_{{N + 1}}}} {kT}}} \right. \kern-0em} {kT}}}}}.$ Усредняя последнюю величину по всем генерируемым пробным положениям частицы, получаем среднее значение больцмановского фактора, связанного со вставкой дополнительной частицы в систему.

1.3. Метод расширенного ансамбля

Метод расширенного ансамбля [3] – это универсальный и эффективный метод Монте-Карло, позволяющий вычислять разность свободных энергий (и, разумеется, химический потенциал). Метод основан на построении статистического ансамбля в виде набора стандартных (например, канонических) ансамблей, так называемых подансамблей. Подансамбли различаются значениями макропараметра, который носит название параметра расширения. Наибольшее и наименьшее значения параметра расширения соответствуют состояниям системы, разность свободных энергий которых требуется вычислить. В процессе моделирования производятся шаги Монте-Карло двух типов: шаг внутри текущего подансамбля по стандартным правилам и переход из одного подансамбля в другой. Вероятности перехода из одного подансамбля в другой модифицируются при помощи так называемых балансировочных параметров с целью повышения эффективности вычислений. Зная балансировочные параметры и вероятности посещения подансамблей, можно получить разность свободных энергий между последними.

Задача расчета химического потенциала тесно связана с вычислением свободной энергии, поскольку химический потенциал представляет собой изменение свободной энергии, возникающее при добавлении дополнительной частицы в систему при фиксированных объеме и температуре.

Следуя работе [9], рассмотрим систему из $N + 1$ частиц, где N частиц являются “обычными”, а одна частица – “особенной”. Для “особенной” частицы вводится параметр включения взаимодействия ${{\xi }_{m}}$ (дискретный аналог континуального параметра $\xi $ в методе Хилла), который принимает дискретные значения, распределенные между 0 и 1, и регулирует силу взаимодействия “особенной” частицы с “обычными”. В нашем случае параметр включения взаимодействия играет роль параметра расширения, т.е. подансамбли различаются значением параметра ${{\xi }_{m}}.$ Пусть $m$ пробегает значения от 0 до M, тогда расширенный ансамбль будет состоять из $M + 1$ подансамблей. C учетом введенных ранее обозначений запишем статсумму $m$-го подансамбля, сразу проведя интегрирование по импульсу (N + 1)-ой частицы:

(21)

$\begin{gathered} {{Q}_{m}} = \frac{1}{{{{{\left( {2\pi \hbar } \right)}}^{{3N}}}\left( {N + 1} \right)!{{\Lambda }^{3}}}} \times \\ \times \,\,\int ...\int {{{e}^{{ - {{({{H}_{N}} + {{\xi }_{m}}\Delta {{U}_{{N + 1}}})} \mathord{\left/ {\vphantom {{({{H}_{N}} + {{\xi }_{m}}\Delta {{U}_{{N + 1}}})} {kT}}} \right. \kern-0em} {kT}}}}}} d{{{\mathbf{p}}}_{1}}...d{{{\mathbf{p}}}_{N}}d{{{\mathbf{r}}}_{1}}...d{{{\mathbf{r}}}_{{N + 1}}}. \\ \end{gathered} $

Статистическая сумма расширенного ансамбля может быть определена как

(22)

$\begin{gathered} Q = \sum\limits_{m = 0}^M {{e}^{{{{\eta }_{m}}}}}{{Q}_{m}} = \frac{1}{{{{{\left( {2\pi \hbar } \right)}}^{{3N}}}\left( {N + 1} \right)!{{\Lambda }^{3}}}} \times \\ \times \,\,\sum\limits_{m = 0}^M \int ...\int {{{e}^{{ - {{({{H}_{N}} + {{\xi }_{m}}\Delta {{U}_{{N + 1}}})} \mathord{\left/ {\vphantom {{({{H}_{N}} + {{\xi }_{m}}\Delta {{U}_{{N + 1}}})} {kT}}} \right. \kern-0em} {kT}} + {{\eta }_{m}}}}}} d{{{\mathbf{p}}}_{1}}...d{{{\mathbf{p}}}_{N}}d{{{\mathbf{r}}}_{1}}...d{{{\mathbf{r}}}_{{N + 1}}}, \\ \end{gathered} $

где величины ${{\eta }_{m}}$ – это балансировочные параметры, выбрав значения которых оптимальным образом, можно добиться достаточно равномерного посещения всех подансамблей, включая “крайние” подансамбли с номерами 0 и 1, разность свободных энергий которых и требуется найти.

Нулевой подансамбль с ${{\xi }_{0}} = 0$ соответствует системе с $N + 1$ частицами, одна из которых не взаимодействует с остальными $N$ частицами. Статистическая сумма нулевого подансамбля соотносится со статистической суммой $Q(N)$ системы из $N$ частиц как

(23)

$\begin{gathered} {{Q}_{0}} = \frac{1}{{{{{\left( {2\pi \hbar } \right)}}^{{3N}}}\left( {N + 1} \right)!{{\Lambda }^{3}}}} \times \\ \times \,\,\sum\limits_{m = 0}^M \int ...\int {{{e}^{{ - {{{{H}_{N}}} \mathord{\left/ {\vphantom {{{{H}_{N}}} {kT}}} \right. \kern-0em} {kT}}}}}} d{{{\mathbf{p}}}_{1}}...d{{{\mathbf{p}}}_{N}}d{{{\mathbf{r}}}_{1}}...d{{{\mathbf{r}}}_{{N + 1}}} = \frac{{Q(N)V}}{{\left( {N + 1} \right){{\Lambda }^{3}}}}. \\ \end{gathered} $

M-й ансамбль с ${{\xi }_{M}} = 1$ соответствует системе с $(N + 1)$-ой обычной частицей, его статистическая сумма равна

(24)

${{Q}_{M}} \equiv Q(N + 1).$

В расширенном каноническом ансамбле производятся два типа шагов: перемещение частиц согласно стандартному алгоритму Метрополиса [8] и выбор подансамбля. Вероятность выбора подансамбля ${{p}_{m}}$ удовлетворяет условию

(25)

$\begin{gathered} \frac{{{{p}_{M}}}}{{{{p}_{0}}}} = \frac{{{{Q}_{M}}}}{{{{Q}_{0}}}}{{e}^{{{{\eta }_{M}} - {{\eta }_{0}}}}} = \frac{{(N + 1)Q(N + 1){{\Lambda }^{3}}}}{{Q(N)V}}{{e}^{{{{\eta }_{M}} - {{\eta }_{0}}}}} = \\ = \frac{{(N + 1){{\Lambda }^{3}}}}{V}{{e}^{{ - {{(F(N + 1) - F(N))} \mathord{\left/ {\vphantom {{(F(N + 1) - F(N))} {kT}}} \right. \kern-0em} {kT}} + {{\eta }_{M}} - {{\eta }_{0}}}}}{\text{.}} \\ \end{gathered} $

С учетом (25) получаем следующее выражение для химического потенциала:

(26)

$\mu = kT\left( { - \ln \frac{{{{p}_{M}}}}{{{{p}_{0}}}} + {{\eta }_{M}} - {{\eta }_{0}} + \ln \frac{{\left( {N + 1} \right){{\Lambda }^{3}}}}{V}} \right).$

Согласно (19б) и (26) избыточный химический потенциал μ_ex равен

(27)

${{\mu }_{{{\text{ex}}}}} = kT\left( { - \ln \frac{{{{p}_{M}}}}{{{{p}_{0}}}} + {{\eta }_{M}} - {{\eta }_{0}}} \right).$

Как уже было сказано, оптимальный подбор балансировочных параметров ${{\eta }_{m}}$ играет важную роль при проведении расчетов методом расширенного ансамбля. Алгоритм Ванга–Ландау, предложенный в работе [10], позволяет автоматизировать настройку балансировочных параметров в рамках итерационной процедуры, проводимой в процессе моделирования [11].

2. ДЕТАЛИ МОДЕЛИРОВАНИЯ И РЕЗУЛЬТАТЫ РАСЧЕТОВ

В качестве исследуемой системы была выбрана система, состоящая из молекул аргона, взаимодействия между которыми традиционно описываются потенциалом Леннард-Джонса [12]:

(28)

$u\left( r \right) = 4\varepsilon \left[ {{{{\left( {\frac{\sigma }{r}} \right)}}^{{12}}} - {{{\left( {\frac{\sigma }{r}} \right)}}^{6}}} \right].$

Значения параметров потенциала Леннард-Джонса были выбраны аналогично работе [9]: $\sigma = 3.41$ Å, $\varepsilon = 0.9939$ кДж/моль. Моделирование всеми рассмотренными методами проводилось в каноническом ансамбле при температуре T = = 239.6 K и числе частиц N = 1000 (из которых 999 были “обычными” частицами, а одна – “особенной”). Использовалась кубическая ячейка с периодическими граничными условиями. Ребро ячейки имело следующие значения длины L: 67.28, 44.84, 40.92 и 39.55 Å. Рассмотренные термодинамические параметры соответствуют газовой фазе.

При моделировании с использованием методов Хилла и Видома использовался как стандартный потенциал Леннард-Джонса, так и его модифицированный вариант: на расстояниях между молекулами, меньших ${{r}_{0}} = 0.7\sigma $, потенциал Леннард-Джонса был заменен параболической зависимостью $f\left( r \right) = a{{r}^{2}} + b$, где параметры a и b удовлетворяют системе уравнений

(29)

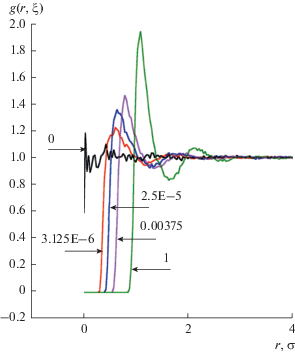
$\left\{ \begin{gathered} u\left( {{{r}_{0}}} \right) = f\left( {{{r}_{0}}} \right) \hfill \\ u{\kern 1pt} '\left( {{{r}_{0}}} \right) = f{\kern 1pt} '\left( {{{r}_{0}}} \right), \hfill \\ \end{gathered} \right.$

$u{\kern 1pt} '\left( {{{r}_{0}}} \right)$ – значение производной от потенциала Леннард-Джонса в точке ${{r}_{0}}$, а $f{\kern 1pt} '\left( {{{r}_{0}}} \right)$ – значение производной от параболы в этой же точке. Решая систему (29), получаем следующие значения параметров: $a = - 3330.5,$ $b = 1886.9.$

На рис. 1 представлены радиальные функции распределения “обычных” молекул аргона относительно “особенной” молекулы для пяти значений параметра $\xi $, полученные в рамках расчетов по методу Хилла. При полном включении взаимодействия “особенной” молекулы с остальными молекулами (что соответствует $\xi = 1$) наблюдается обычная радиальная функция распределения для молекулы аргона в объемной фазе при заданной плотности. При уменьшении параметра $\xi $ взаимодействие между “особой” молекулой и остальными $(N - 1)$ молекулами постепенно ослабевает, и радиальная функция распределения начинает стремиться к единице во всем диапазоне значений r, как и должно быть для молекулы, не взаимодействующей с окружением.

Рис. 1.

Радиальные функции распределения g(r, ξ) “обычных” молекул аргона относительно “особенной” молекулы для системы, моделируемой с потенциалом Леннард-Джонса в ячейке с длиной ребра L = 40.92 Å, при ξ = 1, 0.00375, 2.5E-5, 3.125E-6, 0.

Мы проверили, что радиальные функции распределения для систем, в которых молекулы аргона взаимодействуют со стандартным и модифицированным потенциалами Леннард-Джонса, практически совпадают. Это дает возможность использовать при расчетах по методу Хилла модифицированный потенциал взаимодействия. Преимущество такого подхода состоит в том, что при стремлении параметра $\xi $ к 0 “особенная” частица в системе, моделируемой с модифицированным потенциалом Леннард-Джонса, быстрее “превращается” в частицу идеального газа, чем в случае стандартного потенциала Леннард-Джонса. Таким образом, нет необходимости рассматривать слишком малые значения параметра $\xi .$

В расчетах по методу Хилла радиальные функции распределения g(r, ξ) вычислялись при 14 различных значениях параметра $\xi $, для большинства расчетов был выбран следующий набор значений: 0.00025, 0.00075, 0.00325, 0.00775, 0.015, 0.03, 0.05, 0.07, 0.09, 0.15, 0.3, 0.5, 0.7, 0.9.

Для расчета химического потенциала методами Хилла и Видома нами были написаны собственные компьютерные программы; расчеты методом расширенного ансамбля проводились с помощью программного пакета MDynaMix v.5.2.8 [13], в котором реализован метод расширенного ансамбля с автоматической настройкой балансировочных параметров [11] при помощи алгоритма Ванга–Ландау.

При расчетах методом молекулярной динамики с использованием расширенного по числу частиц ансамбля для контроля температуры использовался термостат Нозе [14]. Шаг по времени составлял 2 фс. Леннард-джонсовские взаимодействия обрезались на расстояниях, больших половины длины ребра ячейки моделирования. Такой большой радиус обрезания в методе расширенного ансамбля был выбран для того, чтобы привести в соответствие расчеты разными методами, поскольку при использовании методов Хилла и Видома учитывались взаимодействия всех частиц в ячейке моделирования и их ближайших образов, т.е. радиус обрезания не вводился. Расширенный ансамбль в наших расчетах состоял из 35 подансамблей. Попытка перехода между подансамблями совершалась один раз в 10 шагов. Для настройки балансировочных параметров было совершено 12 итераций в рамках алгоритма Ванга–Ландау. После завершения настройки балансировочных параметров их значения оставались неизменными до конца моделирования.

В табл. 1 представлены результаты вычисления нами избыточного химического потенциала. Результаты, полученные с помощью метода Хилла для модифицированного и стандартного потенциалов Леннард-Джонса, сравнивались со значениями избыточного химического потенциала, полученными по методу Видома, а также с результатами метода расширенного ансамбля. Расчет по методу Хилла включал от 35 до 55 млн шагов для получения каждой из радиальных функций распределения. Расчет методом Видома состоял из 20 млн. шагов, расчет методом расширенного ансамбля – из 8–20 млн. шагов. В методе Хилла и Видома отбрасывались первые 200 тыс. шагов, в методе расширенного ансамбля – первые 100 тыс. шагов.

Таблица 1.

Избыточный химический потенциал μ_ex, полученный при помощи методов Хилла, Видома и расширенного ансамбля для стандартного и модифицированного потенциала Леннард-Джонса. L – длина ребра ячейки моделирования

L, Å	μ_ex, кДж/моль
L, Å	метод расширенного ансамбля	метод Видома для стандартного потенциала Леннард-Джонса	метод Видома для модифицированного потенциала Леннард-Джонса	метод Хилла для стандартного потенциала Леннард-Джонса	метод Хилла для модифицированного потенциала Леннард-Джонса
67.28	0.546 ± 0.143	–0.596	–0.576		–0.622
44.84	0.725 ± 0.131	–0.831	–0.803	–0.843	–0.816
40.92	0.289 ± 0.082	0.104	0.095	0.061	0.076
39.55	1.093 ± 0.097	0.869	0.900		0.806

По приведенным в табл. 1 данным можно сделать вывод, что значения избыточного химического потенциала, полученные с использованием стандартного и модифицированного потенциалов Леннард-Джонса методами Видома и Хилла, в целом, согласуются между собой. Результаты метода расширенного ансамбля согласуются с результатами метода Видома в пределах погрешности при большинстве рассмотренных концентраций. Различия в результатах, полученных методами Видома, Хилла и расширенного ансамбля, могут быть связаны с разными использованными процедурами обрезания леннард-джонсовских взаимодействий, с недостаточно подробным разбиением интервала интегрирования по параметру ξ в методе Хилла и со статистическими погрешностями.

ЗАКЛЮЧЕНИЕ

В работе приведен обзор трех методов вычисления химического потенциала, в том или ином виде использующих вставку дополнительной молекулы в систему – методов Хилла, Видома и расширенного ансамбля с использованием алгоритма Ванга–Ландау. Предложена и опробована на системе, состоящей из молекул аргона, вычислительная процедура, реализующая метод Хилла. Для реализации методов Хилла и Видома нами были написаны собственные программы. Для расчетов по методу расширенного ансамбля использовался программный пакет MDynaMix v.5.2.8.

Результаты, полученные с использованием метода Хилла, сравнивались с результатами, полученными при помощи методов Видома и расширенного ансамбля. Значения избыточного химического потенциала, в целом, согласуются между собой, тем не менее, желательно проведение дополнительных расчетов при других значениях плотности и температуры. Также необходимо дополнительное исследование по поиску оптимального разбиения интервала интегрирования по параметру ξ включения взаимодействий для повышения эффективности вычислений.

Привлекательной стороной использования метода Хилла в рамках молекулярного моделирования является то, что необходимые для вычисления химического потенциала радиальные функции распределения могут быть получены при помощи как метода Монте-Карло, так и метода молекулярной динамики, в том числе и с помощью существующих в настоящее время многочисленных программных пакетов без необходимости их модификации. Радиальные функции распределения для разных значений параметра ξ могут быть рассчитаны независимо друг от друга. К примеру, вычисления для разных значений ξ могут быть выполнены на разных ядрах одного и того же процессора без необходимости взаимодействия и синхронизации между этими процессами, что дает хорошие возможности для эффективных параллельных вычислений.

Полагаем, что метод Хилла может быть применен для нахождения химического потенциала молекулы, состоящей из нескольких атомов, например молекулы воды, путем перехода к огрубленной модели с центральным межмолекулярным потенциалом взаимодействия [15]. Отметим также, что метод Хилла может быть расширен на многокомпонентные системы и использоваться для расчета химического потенциала молекулы в смеси.

Список литературы

Widom B. // J. Chem. Phys. 1963. V. 39 P. 2802.
Frenkel D., Smit B. Understanding Molecular Simulation: From Algorithms to Applications. 2nd Ed. Orlando, FL, USA: Academic Press Inc., 2002.
Lyubartsev A.P., Martsinovskii A.A., Shevkunov S.V., Vorontsov-Velyaminov P.N. // J. Chem. Phys. 1992. V. 96. P. 1776.
Хилл Т. Статистическая механика. Принципы и избранные приложения. М.: Издательство иностранной литературы, 1960.
Kirkwood J. // J. Chem Phys. 1935. V. 3. P. 300.
McQuarrie D.A. Statistical Mechanics. New York: Harper and Row, 1976.
Allen M.P., Tildesley D.J. Computer Simulation of Liquids. 2nd Ed. Oxford: Oxford University Press, 2017.
Metropolis N., Rosenbluth A.W., Rosenbluth M.N., Teller A.N., Teller E. // J. Chem. Phys. 1953. V. 21. P. 1087.
Lyubartsev A.P., Laaksonen A., Vorontsov-Velyaminov P.N. // Mol. Simulat. 1996. V. 18. P. 43.
Wang F., Landau D.P. // Phys. Rev. Lett. 2001. V. 86. P. 2050.
Jämbeck J.P.M., Mocci F., Lyubartsev A.P., Laaksonen A. // J. Comput. Chem. 2013. V. 34. P. 187.
Lennard-Jones J.E. // Proc. R. Soc. Lond. A. 1924. V. 106. P. 463.
Lyubartsev A.P., Laaksonen A. // Comp. Phys. Commun. 2000. V. 128. P. 565.
Nosé S. // J. Chem. Phys. 1984. V. 81. P. 511.
Volkov N.A., Shchekin A.K. // Book of Abstracts of XXII International Conference on Chemical Thermodynamics in Russia, St. Petersburg, Petropolis PH. Ltd, 2019. P. 165. ISBN: 978-5-9676-1076-9.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Коллоидный журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал