1. На главную
  2. Электронные версии
  3. Коллоидный журнал
  4. T. 83, № 1, 2021

Коллоидный журнал, 2021, T. 83, № 1, стр. 51-56

Порог перколяции в полимерных нанокомпозитах

В. И. Иржак *

Институт проблем химической физики РАН
142420 Московская область, Черноголовка, Россия

* E-mail: irzhak@icp.ac.ru

Поступила в редакцию 30.06.2020
После доработки 04.08.2020
Принята к публикации 12.08.2020

Полный текст (PDF)

Аннотация

Проанализированы два подхода к расчету величины порога перколяции в полимерных нанокомпозитах – теория исключенного объема и модель, предложенная Ли и Кимом. Показано, что первый подход позволяет получать ориентировочную оценку порога, а второй приводит к простым формулам, которыми можно пользоваться, но с существенными поправками. Во-первых, необходимо учитывать результат решения задачи об узлах на решетке, во-вторых, более корректно усреднять ориентацию анизодиаметричных наночастиц. Проанализирована роль межфазных слоев.

ВВЕДЕНИЕ

Широкое использование полимерных нанокомпозитов (НК), стартовавшее в последней четверти прошлого века, привлекло внимание к проблеме порога перколяции [1–6].

Характерной особенностью НК является резкое изменение свойств в узком диапазоне концентраций наночастиц (НЧ). Рост вязкости трактуется как образование упругой сетки [7]. Формирование сетки проявляется также в механических, электрофизических и других свойствах композитов [8–13]. Для этих свойств формирование сетки формулируется как перколяция, или протекание.

Теория перколяции [14, 15] основана на идее, что при увеличении объемной концентрации φ НЧ объединяются в постоянно увеличивающиеся кластеры и, когда достигается определенное значение φс, образуют бесконечную структуру – перколяционный кластер. Значение φс называется порогом перколяции.

Все кластеры имеют фрактальную структуру. “Путешествие” по связям, соединяющим НЧ в конечном кластере (φ < φс), неизбежно приводит к терминальным ветвям (“хвостам”). Перколяционный кластер (φ ≥ φс) соединяет противоположные границы образца, хотя число “хвостов” в его структуре может быть большим. Порог перколяции определяется соотношениями11 (1):

(1)
$\sigma \propto \left\{ \begin{gathered} 0,\,\,\,\,\varphi < {{\varphi }_{{\text{c}}}} \hfill \\ {{\left( {\varphi - {{\varphi }_{{\text{c}}}}} \right)}^{\beta }},\,\,\,\,\varphi \geqslant {{\varphi }_{{\text{c}}}}. \hfill \\ \end{gathered} \right.$

Вводится также представление о корреляционной длине (характерном размере) конечного кластера ξ:

$\xi \propto {{\left( {{{\varphi }_{{\text{с}}}} - \varphi } \right)}^{{ - \nu }}},\,\,\,\,\varphi < {{\varphi }_{{\text{c}}}}.$

Значения критических показателей β и ν сильно варьируют в зависимости от типа конкретной системы, хотя теоретически для трехмерной системы β = 2. Фрактальная размерность перколяционного кластера Df меньше евклидовой размерности пространства D: Df= D – β/ν.

Существует множество подходов к объяснению перколяционного поведения НК, основанных, главным образом, на вычислительных моделях [16–19], но ни одной из них не удалось объяснить все различные экспериментальные результаты, поскольку в таких системах играют роль многие факторы, в частности межфазное взаимодействие [20–22].

ФОРМИРОВАНИЕ ПЕРКОЛЯЦИОННОЙ СЕТКИ

Как сказано выше, при достижении критической концентрации φс свойства НК изменяются кардинальным образом, что обусловлено возникновением перколяционного кластера (рис. 1) контактирующих друг с другом НЧ.

Рис. 1.

Схематическое изображение НК с перколяционными кластерами, образованными сферическими и стержнеобразными НЧ [17].

Для сферических частиц установлена не зависящая от типа решетки величина порога перколяции φс ≅ 0.16 с точностью порядка 10% [15]. В случае анизодиаметричных НЧ, таких как нанотрубки и графен, дело обстоит не так просто. Сложность связана с тем, что возможны различные варианты взаимных контактов и ориентации НЧ. В целях ее преодоления предложена теория исключенного объема [1–3].

Основная идея этого подхода заключается в том, что порог перколяции связан не с истинным объемом самого объекта, а с его исключенным объемом. Так, если Nc является критической концентрацией числа объектов в системе, V – объем одного из таких объектов, а 〈Ve〉 – соответствующий исключенный объем, то свойство инвариантности величины NcV, установленное для перколяции как образование сетки, больше не действительно, но инвариант (то есть нечувствительный к структуре решетки параметр) равен Nc〈Ve〉.

В качестве НЧ в работе [23] рассматривается цилиндр, концы которого представляют собой полусферы, что позволяет в пределе получать сферу или стержень. Объем такой частицы V определен уравнением (2)

(2)
$V = \frac{4}{3}\pi {{r}^{3}} + \pi {{r}^{2}}l,$
(3)
$\left\langle {{{V}_{{\text{e}}}}} \right\rangle = \left[ {8\left( {{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}} \right)\pi {{r}^{3}} + 8\pi l{{r}^{2}}} \right] + 4{{l}^{2}}r{{\left\langle {{\text{sin}}\gamma } \right\rangle }_{\mu }}.$

Здесь l – длина, r – радиус цилиндра, 〈sin γ〉μ – среднее значение для случая, когда диапазон углов ориентации лежит в пределах телесного угла γ вокруг оси z. Вводится понятие аспектного отношения χ = l/2r.

Первый член в формуле (3) – исключенный объем, окружающий НЧ, а второй был предложен [24] для характеристики влияния распределения ориентаций на исключенный объем при условии l $ \gg $ r. Для исключенного объема системы объектов авторы [3] получили нижнюю оценку 1.4 путем моделирования системы бесконечно тонких цилиндров и верхнюю границу 2.8 для случая χ = = l/2r → 1. Таким образом, φс находится в пределах

(4)
$1 - \exp \left( {\frac{{ - 1.4V}}{{\left\langle {{{V}_{{\text{e}}}}} \right\rangle }}} \right) \leqslant {{\varphi }_{{\text{c}}}} \leqslant 1 - \exp \left( {\frac{{ - 2.8V}}{{\left\langle {{{V}_{{\text{e}}}}} \right\rangle }}} \right).$

В работе [3] получена связь величины порога перколяции с ориентацией цилиндрических частиц (табл. 1).

Таблица 1.  

Зависимость порога перколяции от угла ориентации НЧ [3]

γ, град sin γ φc, об. %
  0 0 16.05 ≤ φc ≤ 20.53
30 0.5 1.00 ≤ φc ≤ 1.99
60 0.866 0.75 ≤ φc ≤ 1.49
90 1 0.58 ≤ φc ≤ 1.15

Заметим, этот подход должен учитывать, что для достижения порога перколяции достаточно иметь относительно небольшую долю, порядка 30%, контактирующих элементов [15].

Идеология исключенного объема, выражаемая уравнением (4), определяет “геометрические” пределы порога перколяции. Истинные значения φс могут отличаться от них достаточно сильно. В частности, это связано с наличием в НК межфазных слоев, “прокладок” матрицы между НЧ.

РОЛЬ МЕЖЧАСТИЧНЫХ СЛОЕВ

Толщина слоя δ между частицами вносит относительно малый вклад в эффективные свойства композитов, содержащих микрочастицы, но поскольку δ может быть сравнима с размером НЧ, ее потенциальное влияние в НК существенно. В частности, перколяция может иметь место при объемных долях ниже теоретических пороговых значений из-за возможности передачи внешнего воздействия через последовательность НЧ–прослойка–НЧ, другими словами, “псевдоперколяционный” контакт [23].

Естественно, в этом случае величина φс будет зависеть от свойств среды и различна для физически разных способов испытаний. Так, “реологический” порог перколяции в НК углеродные нанотрубки (УНТ)/полиметилметакрилат составляет 0.12 мас. %, тогда как по данным об электропроводности он равен 0.39 мас. % [6]. Этот факт, как считают авторы, обусловлен крайне низкой проводимостью полимерной матрицы, с одной стороны, и участием нанотрубок в образовании макромолекулярной сетки зацеплений, с другой.

Электропроводность в полимерных НК осуществляется посредством туннельного эффекта: хотя соседние НЧ напрямую не связаны, проводимость может реализовываться посредством прыжков электронов между ними [25]. Вероятность процесса электронного туннелирования р определяет формула

(5)
$р = {{р}_{0}}{\text{exp(}}{{ - 2\delta } \mathord{\left/ {\vphantom {{ - 2\delta } \varepsilon }} \right. \kern-0em} \varepsilon }{\text{)}}.$

Здесь р0 – константа, ε – характерная длина туннелирования, обычно величина порядка нескольких нм.

При этом критические значения δ отвечают соотношениям δс/l ∝ χ–2 для стержней и δс/D ∝ χ–1 для дисков [25]. В случае дисков χ = D/t, т.е. это отношение диаметра диска к его толщине.

Если перколяционный механизм электропроводности более или менее ясен, то объяснить псевдоперколяционный эффект применительно к механическим свойствам гораздо труднее. Как показало микромеханическое моделирование композита “параллельные стержни в матрице”, с увеличением модуля упругости межфазного слоя толщиной около 15 нм наблюдается рост как трансверсального, так и продольного модулей. При этом механический перколяционный эффект проявлялся даже при умеренной жесткости межфазного слоя [23].

Порог электрической перколяции является нижним пределом порога жесткости. Действительно, когда проводящий путь сформирован, составляющие его УНТ еще лабильны и не могут нести нагрузку. Только ту концентрацию, которая обеспечивает достаточно сильные взаимодействия между УНТ для образования жесткой связи, можно рассматривать как порог перколяции. Согласно [26] “механический” φс = 8.2/χ, “электрический” – 5.8/χ.

В работе [27] приведены следующие данные: “реологический” порог перколяции в случае двумерных НЧ (дисков) равен 1.27/χ, “механический” 1.6/χ. Последнее соотношение практически совпадает с критической концентрацией перекрытия для дисков, полученной из простых соображений концепции исключенного объема: φс = π/2χ [24].

АНАЛИТИЧЕСКАЯ ТЕОРИЯ ПЕРКОЛЯЦИИ

Различные теоретические подходы, такие как предложенные в [18, 23, 28–37], логически и математически довольно сложны, хотя лежащая в их основе модель проста: это формирование сетки. Однако согласно принципу бритвы Оккама “не следует множить сущее без необходимости”. Поэтому рассмотрим простую модель.

Простейший аналитический подход к вычислению порогового значения перколяции предложили Ли и Ким [38].

Суть их модели сводится к следующему. Весь объем системы делится на кубические элементы с длиной ребра L. Каждый куб содержит одну проводящую НЧ. Общее число кубических элементов равно общему количеству НЧ. Объемная доля наполнителя φ равна:

(6)
$\varphi = \frac{{{{V}_{{{\text{NP}}}}}}}{{{{L}^{3}}}},$
где VNP объем НЧ.

Если L равно сумме геометрического размера частицы (например, диаметра шара D) и толщины слоя δ матрицы, который обеспечивает туннельную передачу заряда, то весь объем станет проводящим. Согласно [38] это порог перколяции:

(7)
${{\varphi }_{{\text{c}}}} = \frac{{{{V}_{{{\text{NP}}}}}}}{{{{{\left( {D + \delta } \right)}}^{3}}}}.$

Порог перколяции φc3 для трехмерных проводящих сферических НЧ равен [38, 39]:

(8)
${{\varphi }_{{{\text{c}}3}}} = \frac{{\pi {{D}^{3}}}}{{6{{{\left( {D + \delta } \right)}}^{3}}}} \to \frac{\pi }{6} \cong 0.523$
при D $ \gg $ δ.

Двумерные НЧ, содержащиеся в полимерных НК, моделировали тонкими круглыми пластинками толщиной t и диаметром D, диспергированными в матрице [18, 19]. Если дробь D/t = χ, представляющая собой аспектное отношение, больше 1, необходимо учитывать ориентацию НЧ.

Порог перколяции φс2 в случае двумерных НЧ определится как

(9)
${{\varphi }_{{{\text{с}}2}}} = \frac{{\pi {{D}^{2}}t}}{{4{{{\left( {\left\langle {{\text{co}}{{{\text{s}}}^{2}}\gamma } \right\rangle \left( {D + \delta } \right)} \right)}}^{3}}}} \to \frac{{27\pi }}{{4\chi }} = \frac{{21.2}}{\chi },$
где γ – угол между направлениями ориентации НЧ и образца, угловые скобки обозначают усреднение; в трехмерном пространстве для случайного распределения ориентации $\left\langle {{\text{co}}{{{\text{s}}}^{2}}\gamma } \right\rangle $ = 1/3.

Итак, φc2 обратно пропорционально аспектному отношению χ.

Одномерные НЧ, содержащиеся в полимерных НК, моделировали тонкими стержнями с толщиной d и длиной l, χ = l/d [40]. Порог перколяции, φc1, определяется как

(10)
${{\varphi }_{{{\text{c}}1}}} = \frac{{\pi {{d}^{2}}l}}{{4{{{\left( {\left\langle {{\text{co}}{{{\text{s}}}^{2}}\gamma } \right\rangle \left( {l + \delta } \right)} \right)}}^{3}}}} \to \frac{{27\pi }}{{4{{\chi }^{2}}}}.$

Однако в [1] высказано мнение, что φc1 ∝ χ–1 при χ ≤ 15, в случае бóльших значений аспектного отношения φc1 ∝ χ–2.

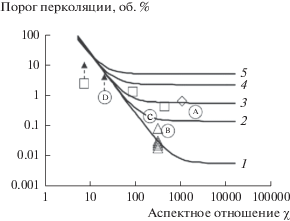
Естественно, порог перколяции зависит от конкретных размерных характеристик НЧ и их распределения (степени диспергирования) в матрице НК. Повышение степени диспергирования НЧ в полимерной матрице может снизить значение порога перколяции. На рис. 2 представлены данные [41] по влиянию степени диспергирования и аспектного отношения χ частиц на величину φc1. Авторы этой работы рассмотрели поведение цилиндрических НЧ, используя модифицированные (с учетом агрегации) формулы (8) и (10): предполагалось, что агрегированные НЧ образуют сферические клубки. Это приближение является упрощением экспериментально наблюдаемых агломератов и не учитывает факты изогнутости УНТ и наличия их трехмерной сетки. Однако ранее такую модель успешно применяли для изучения влияния сферических включений на упругие свойства композитов, армированных УНТ [8, 42].

Рис. 2.

Связь значений порога перколяции с параметрами χ и ε. Кривые – расчет по (11) при ε = 0.01 (1), 0.05 (2), 0.1 (3), 0.2 (4) и 0.4 (5) [41]; точки – экспериментальные данные для многослойных УНТ в эпоксидной матрице: A, B, C, D [41]; ◻ [43]; ◇ [44]; △ [45].

Итак, если объемная доля ε цилиндрических частиц наполнителя включена в сферические агломераты, то

(11)
${{\varphi }_{{\text{c}}}} = {\text{\;}}0.523\varepsilon + \left( {1 - \varepsilon } \right)\frac{{21.2}}{{{{\chi }^{2}}}}.$

Как видно, с ростом χ значения φc выходят на плато, и только агрегация становится решающим фактором. Чем меньше степень агрегации ε, то есть чем выше дисперсность НЧ, тем ниже порог перколяции. В то же время значение φc нечувствительно к размеру агрегатов при χ < 10. Представленные на рис. 2 экспериментальные данные по электропроводности НК на постоянном ([41, 44]) и переменном ([43, 45]) токе, относятся к НЧ, различающимся как аспектным отношением, так и способом смешивания с полимером, следствием чего является разная степень их агрегирования.

В работе [46] (см. также [47, 48]) приведены многочисленные данные по порогу перколяции для полимерных НК, содержащих УНТ (χ порядка 1000) в качестве наполнителя. Они показывают, что, в отличие от других полимеров, в случае эпоксидных матриц значение φс, как правило, находится в интервале 10–3–10–1 мас. %. Если исходить из модели, то по формуле (10) φс одиночных УНТ должна быть порядка 10–5, что согласуется с предельными значениями (объемная концентрация многослойных УНТ приблизительно вдвое выше массовой, а в случае однослойных УНТ они близки).

КОРРЕКЦИЯ МОДЕЛИ [49]

На взгляд авторов [41], экспериментальные результаты согласуются с расчетными. Однако если сравнить то, что дает теория, с данными компьютерного моделирования, увидим, что предложенная модель дает завышенные значения φс. Как уже было сказано, для композита, содержащего случайно расположенные частицы наполнителя сферической формы и близкого размера, значение φс приблизительно равно 0.16 [15]. В то же время формула (8) дает величину 0.523.

Дело в том, что модель требует, по существу, чтобы для перколяции все элементарные объемы стали проводящими. Между тем, для реализации эффекта перколяции достаточно иметь относительно небольшую долю таких элементарных объемов. Так, в рамках задачи узлов22 на кубической решетке эта доля равна примерно 0.31 [15]. Учитывая это обстоятельство, получаем: 0.523 × × 0.31 = 0.162, т.е. совпадение с данными компьютерного моделирования. Следовательно, каждое рассчитанное в соответствии с моделью значение порога перколяции должно быть умножено на 0.31.

С учетом приведенной выше поправки

(9а)
${{\varphi }_{{{\text{с}}2}}} = {\text{\;}}\frac{{6.57}}{\chi },$
(10а)
${{\varphi }_{{{\text{c}}1}}} = \frac{{6.57}}{{{{\chi }^{2}}}}.$

Это означает, что расчетные данные, приведенные на рис. 2, завышены, а УНТ агрегированы в большей степени, чем это следует из рисунка.

Кроме того, метод усреднения вызывает сомнения. В работе [28], на которую ссылаются авторы, проведено усреднение по углам ориентации НЧ, отсюда коэффициент 1/3. Но логичнее было бы получить среднее значение порога перколяции, имея в виду прямую зависимость последнего от угла ориентации НЧ γ [3, 50, 51], т.е. φc1 = f (lγ), а φc2 = f (Dγ). Поэтому метод усреднения должен учитывать это обстоятельство. Например, таким образом:

(12)
${{\varphi }_{{{\text{c}}1\gamma }}} = \frac{{\pi {{d}^{2}}l}}{{4{{{\left( {{{l}_{{\gamma ~}}} + \delta } \right)}}^{3}}}} \to \frac{\pi }{{4{{\chi }^{2}}}}\frac{1}{{{\text{co}}{{{\text{s}}}^{3}}\gamma }},$
где ${{{{l}_{\gamma }}} \mathord{\left/ {\vphantom {{{{l}_{\gamma }}} l}} \right. \kern-0em} l}$ = cos γ, т.е.
(13)
${{\varphi }_{{{\text{c1}}\gamma }}}{\text{co}}{{{\text{s}}}^{3}}\gamma = \frac{\pi }{{4{{\chi }^{2}}}}.$
Соответственно

(14)
${{\varphi }_{{{\text{c}}1}}} = \left\langle {{{\varphi }_{{{\text{c}}1\gamma }}}{\text{co}}{{{\text{s}}}^{3}}\gamma } \right\rangle = B\frac{\pi }{{4{{\chi }^{2}}}}.$

Аналогичное соотношение получается для дисков:

(15)
${{\varphi }_{{{\text{c}}2}}} = \left\langle {{{\varphi }_{{{\text{c}}2\gamma }}}{\text{co}}{{{\text{s}}}^{3}}\gamma } \right\rangle = B\frac{\pi }{{4\chi }},$
где $\cos \gamma $ = ${{{{D}_{\gamma }}} \mathord{\left/ {\vphantom {{{{D}_{\gamma }}} D}} \right. \kern-0em} D}.$

В свете сказанного выше формула (11) примет вид

(11а)
${{\varphi }_{{\text{c}}}} = {\text{\;}}0.162\varepsilon + \left( {1 - \varepsilon } \right)B\frac{\pi }{{4{{\chi }^{2}}}}.$
Вычислить коэффициент B можно, опираясь на данные зависимости φc1 = f$({{l}_{\gamma }})$. Например, в работе [3] получена связь величины порога перколяции со степенью ориентации цилиндрических частиц $\cos \gamma $ (табл. 1).

Пользуясь этими данными, получаем:

(16)
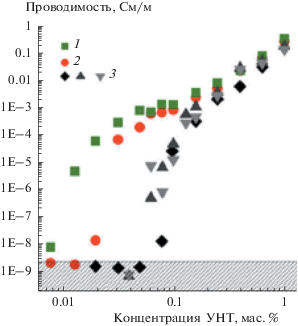
$\begin{gathered} {{\varphi }_{{{\text{c}}1}}} = \left\langle {{{\varphi }_{{{\text{c}}1\gamma }}}{\text{co}}{{{\text{s}}}^{3}}\gamma } \right\rangle = \\ = \frac{{\sum\limits_\gamma {{{\varphi }_{{{\text{c}}1\gamma }}}{\text{co}}{{{\text{s}}}^{3}}\gamma } }}{{\sum\limits_\gamma {{\text{co}}{{{\text{s}}}^{3}}\gamma } }} = \frac{{4\frac{\pi }{{4{{\chi }^{2}}}}}}{{1.774}} = 2.25\frac{\pi }{{4{{\chi }^{2}}}}. \\ \end{gathered} $
По-видимому, угловая зависимость φс может объяснить результаты экспериментов [47, 52] по влиянию скорости сдвига на порог перколяции (рис. 3). Как показано в табл. 1, высокой степени ориентации $(\gamma = 0)$ соответствует большая величина φс. Снижение степени ориентации ведет к существенному уменьшению порога перколяции. Если бы интенсивность перемешивания уменьшала агрегацию и это определяло результаты эксперимента, то эффект был бы обратным: чем выше интенсивность перемешивания, тем ниже порог перколяции.

Рис. 3.

Проводимость НК многослойные УНТ/эпоксидная смола как функция массовой доли УНТ для образцов, полученных при различной скорости перемешивания дисперсии до отверждения в течение 5 мин при 80°C: 50 (1), 500 (2) и 2000 об./мин (3). Данные [47].

Теоретическое исследование влияния степени ориентации УНТ на электропроводность с использованием моделирования методом Монте-Карло было проведено в работе [51]. Оказалось, что минимальное удельное сопротивление имело место при невысокой, а не идеальной степени ориентации УНТ в их однослойных и многослойных пленках.

ЗАКЛЮЧЕНИЕ

Сравнение различных подходов к проблеме порога перколяции показывает следующее. Компьютерные модели убедительно решают частные задачи, не всегда поддающиеся обобщению. Идея об исключенном объеме дает возможность получать ориентировочную оценку φс. Простую модель Ли и Кима [38] можно использовать для расчета величины порога перколяции полимерных НК, но с существенными поправками [49]: во-первых, необходимо учитывать множитель 0.31 [15], во-вторых, более корректно усреднять ориентацию анизодиаметричных НЧ. Как следствие, уравнение (11а) приводит к более низким значениям порога перколяции, чем получаемые из (11), но в пределах одного десятичного порядка. При этом надо подчеркнуть, что уравнение (13) и аналогичное уравнение для дисков являются инвариантами, не зависящими от угла ориентации.

Список литературы

  1. Balberg I., Anderson C.H., Alexander S., Wagner N. // Phys. Rev. B. 1984. V. 30. P. 3933.

  2. Balberg I. // Philosoph. Mag. B. 1987. V. 56. P. 991.

  3. Celzard A., McRae E., Deleuze C., Dufort M., Furdin G., Marêché J.F. // Phys. Rev. B. 1996. V. 53. P. 6209.

  4. Pukánszky B. // Compos. 1990. V. 21. P. 255.

  5. Youngs I.J. // J. Phys. D. 2003. V. 36. P. 738.

  6. Du F., Scogna R.C., Zhou W., Brand S., Fischer J.E., Winey K. // Macromolecules. 2004. V. 37. P. 9048.

  7. Hobbie E.K., Fry D.J. // J. Chem. Phys. 2007. V. 126. 124907.

  8. Kozlov G.V., Dolbin I.V. // J. Appl. Mech. Techn. Phys. 2018. V. 59. P. 765.

  9. Козлов Г.В., Долбин И.В. // Изв. вузов. Физика. 2018. Т. 61. № 5. С. 151.

  10. Martin-Gallego M., Bernal M.M., Hernandez M., Verdejo R., Lopez-Manchado M.A. // Eur. Polym. J. 2013. V. 49. P. 1347.

  11. Shi B., Dong L., Li M., Liu B., Kim K., Xu X., Zhou J., Liu J. // Appl. Phys. Lett. 2018. V. 113. 041902.

  12. Marsden A.J., Papageorgiou D.G., Vallés C., Liscio A., Palermo V., Bissett M.A., Young R.J., Kinloch I.A. // 2D Mater. 2018. V. 5. 032003.

  13. Wang S., Liang R., Wang B., Zhang C. // Carbon. 2009. V. 47. P. 53.

  14. Stauffer D., Aharony A. Introduction to Percolation Theory. London: Taylor and Francis, 1994.

  15. Эфрос А.Л. Физика и геометрия беспорядка. М.: Наука, 1982.

  16. Spanos P., Elsbernd P., Ward B., Koenck T. // Philos. Trans. R. Soc. A. 2013. V. 371. 20120494.

  17. Rahaman M., Aldalbahi A., Govindasami P., Khanam N.P., Bhandari S., Feng P., Altalhi T. // Polymers. 2017. V. 9. P. 527.

  18. Ni X., Hui C., Su N., Jiang W., Liu F. // Nanotechnology. 2018. V. 29. 075401.

  19. Ni X., Hui C., Su N., Cutler R., Liu F. // Nanotechnology. 2019. V. 30. 185302.

  20. Yan K.Y., Xue Q.Z., Zheng Q.B., Hao L.Z. // Nanotechnology. 2007. V. 18. 255705.

  21. Wang Y., Yang C., Pei Q.-X., Zhang Y. // ACS Appl. Mater. Interfaces. 2016. V. 8. P. 8272.

  22. Deng H., Wu F., Chen L., Xu Z.W., Liu L.S., Yang C.Y., Mai W., Cheng B.W. // J. Appl. Polym. Sci. 2014. V. 131. 41164.

  23. Baxter S.C., Robinson C.T. // Compos. Sci. Technol. 2011. V. 71. P. 1273.

  24. Onsager L. // Ann. N.Y. Acad. Sci. 1949. V. 51. P. 627.

  25. Ambrosetti G., Grimaldi C., Balberg I., Maeder T., Danani A., Ryser P. // Phys. Rev. B. 2010. V. 81. 155434.

  26. Chen Y., Pan F., Guo Z., Liu B., Zhang J. // J. Mech. Phys. Solids. 2015. V. 84. P. 395.

  27. Plummer C.J.G., Rodlert M., Bucaille J.-L., Grünbauer H.J.M., Månson J.-A.E. // Polymer. 2005. V. 46. P. 6543.

  28. Nadiv R., Fernandes R.M.F., Ochbaum G., Dai J., Buzaglo M., Varenik M., Regev O. // Polymer. 2018. V. 153. P. 52.

  29. Kale S., Karimi P., Sabet F.A., Jasiuk I., Ostoja-Starzewski M. //. J. Appl. Phys. 2018. V. 123. 085104.

  30. Gharehnazifam Z., Baniassadi M., Abrinia K., Karimpour M., Baghani M. // Int. J. Appl. Mech. 2016. V. 08. 1650055.

  31. Soto M., Esteva M., Martínez-Romero O., Baez J., Elías-Zúñiga A. // Materials. 2015. V. 8. P. 6697.

  32. Chen Y., Pan F., Wang S., Liu B., Zhang J. // Compos. Struct. 2015. V. 124. P. 292.

  33. Mutlay İ., Tudoran L.B. // Fuller. Nanotub. Carbon Nanostr. 2014. V. 22. P. 413.

  34. Lu W., Chou T.-W., Thostenson E.T. // Appl. Phys. Lett. 2010. V. 96. 223106.

  35. Seidel G.D., Lagoudas D.C. // J. Compos. Mater. 2009. V. 43. P. 917.

  36. Balberg I. // J. Phys. D. 2009. V. 42. 064003.

  37. White S.I., DiDonna B.A., Mu M., Lubensky T.C., Winey K.I. // Phys. Rev. B. 2009. V. 79. 024301.

  38. Li J., Kim J.-K. // Compos. Sci. Technol. 2007. V. 67. P. 2114.

  39. Zhang B., Yu Y., Liu Y., Huang Z-D., He Y., Kim J-K. // Nanoscale. 2013. V. 5. P. 2100.

  40. Li J., Ma P.C., Sze C.W., Kai T.C., Tang B.Z., Kim J.K. // Proc. 16th Int. Conf. on Composite Materials. CM-16. Kyoto, Japan. 2007. http://hdl.handle.net/1783.1/50129.

  41. Li J., Ma P.C., Chow W.S., To C.K., Tang B.Z., Kim J.-K. // Adv. Funct. Mater. 2007. V. 17. P. 3207.

  42. Shi D.-L., Feng X.-Q., Huang Y.Y., Hwang K.-C., Gao H. // J. Eng. Mater. Technol. 2004. V. 126. P. 250.

  43. Kim Y.J., Shin T.S., Choi H.D., Kwon J.H., Chung Y.C., Yoon H.G. // Carbon. 2005. V. 43. P. 23.

  44. Allaoui A., Bai S., Cheng H.M., Bai J.B. // Compos. Sci. Technol. 2002. V. 62. P. 1993.

  45. Bai J.B., Allaoui A. // Compos.: Part A. 2003. V. 34. P. 689.

  46. Combessis A., Bayon L., Flandin L. // Appl. Phys. Lett. 2013. V. 102. 011907.

  47. Bauhofer W., Kovacs J.Z. // Compos. Sci. Technol. 2009. V. 69. P. 1486.

  48. Spitalsky Z., Tasis D., Papagelis K., Galiotis C. // Prog. Polym. Sci. 2010. V. 35. P. 357.

  49. Иржак В.И. // Журн. физ. химии. 2020. Т. 94. С. 1228.

  50. Du F., Fischer J.E., Winey K.I. // Phys. Rev. B. 2005. V. 72. 121 404.

  51. Behnam A., Guo J., Ural A. // J. Appl. Phys. 2007. V. 102. 044313.

  52. Kovacs J.Z., Velagala B.S., Schulte K., Bauhofer W. // Compos. Sci. Technol. 2007. V. 67. P. 922.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Коллоидный журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал