Коллоидный журнал, 2021, T. 83, № 1, стр. 86-97

Нелинейный магнитный отклик вязкоупругого ферроколлоида: приближение эффективного поля

В. В. Русаков^1, 2, *, Ю. Л. Райхер¹

¹ Институт механики сплошных сред Уральского отделения РАН
614068 Пермь, ул. Академика Королева, 1, Россия

² Пермский национальный исследовательский политехнический университет
614000 Пермь, Комсомольский просп., 29А, Россия

^* E-mail: vvr@icmm.ru

Поступила в редакцию 24.08.2020
После доработки 01.09.2020
Принята к публикации 03.09.2020

DOI: 10.31857/S0023291221010110

Полный текст (PDF)

Аннотация

Рассмотрено зондирование вязкоупругого ферроколлоида слабым переменным магнитным полем, вызывающим вращательные качания наночастиц. Для описания реологии дисперсионной среды использована феноменологическая схема Джефриса; коллоидные частицы предполагаются магнитожесткими. На основе уравнений Ланжевена, описывающих броуновское вращательное движение, выведена система уравнений, определяющих динамическую намагниченность и кинетику ориентации коллоидного ансамбля. Решение задачи получено методом эффективного поля, найдены: линейная и кубическая динамические магнитные восприимчивости, а также ориентационный отклик системы. Показано, что в спектрах откликов всех порядков – от линейного до кубического – эффекты механического запаздывания (релаксация напряжений) приводят к появлению специфических особенностей: с ростом упругости среды изменятся и положение и высота главного максимума. Предложены соотношения, устанавливающие связь реологических параметров используемой модели Джефриса со структурными характеристиками полимерного раствора: числом мономеров в макромолекуле, размером блоба, концентрацией узлов физической сетки.

1. ВВЕДЕНИЕ

Использование малых магнитных частиц, возбуждаемых внешним переменным полем, является высокочувствительным методом как микро- или нанореологического анализа [1–4], так и дистанционного мониторинга перемещения/распределения этих частиц при лекарственной терапии [5–7] или проведении магнитно-резонансной томографии. Отметим, что в обоих указанных выше случаях внешнее воздействие (амплитуда поля) поддерживается на невысоком уровне, чтобы возникающая диссипация не сказывалась ни на свойствах частиц, ни на свойствах окружающей их среды. В этом отношении рассматриваемые ситуации отличаются от случая магнитной гипертермии, где определяющим фактором является генерация избыточного тепла.

Простейший способ наблюдения отклика частиц на приложенное поле – это измерение линейной магнитной восприимчивости, однако с точки зрения точности он не является ни единственным, ни оптимальным. Так, использование нелинейного магнитного отклика, пусть и относительно слабого, имеет ряд важных преимуществ и не создает больших технических трудностей. Например, по измерениям нелинейной восприимчивости удается находить и визуализировать распределение наночастиц в живой ткани [8–10]. В тех многочисленных случаях, когда среда с измеряемой микрореологией имеет достаточную степень прозрачности, способом определения этих ее свойств может стать регистрация динамического двулучепреломления, индуцированного вынужденным вращением анизометричных частиц-зондов. Успешность этого способа для жидкостей с простой (ньютоновской) реологией была убедительно доказана некоторое время назад [11–13].

Магнитный отклик ансамбля идентичных однодоменных частиц, взвешенных в жидкой среде, формируется при совместном влиянии двух факторов: 1) приложенного поля ${\mathbf{H}},$ выстраивающего магнитные моменты вдоль своего направления, и 2) броуновской вращательной диффузии частиц, препятствующей такой ориентации. В этих условиях, если допустимо пренебречь межчастичным взаимодействием, равновесная кривая намагничивания системы ${\mathbf{M}}\left( {\mathbf{H}} \right)$ описывается законом Ланжевена независимо от того, какова реология среды. Вязкоупругость среды проявляется, однако, при динамическом зондировании, когда угол поворота частицы под действием переменного поля определяется совместным действием эффектов мгновенной упругости и вязкого запаздывания. Именно такая ситуация рассмотрена в настоящей работе.

2. МОДЕЛЬ

Теоретическое описание ориентационного движения наночастицы, погруженной в вязкоупругую среду, строится на основе модели Джефриса [14, 15]. Этот выбор обусловлен простотой и надежностью указанной реологической схемы: она позволяет корректным образом, не сталкиваясь с артефактами, присущими вязкоупругой модели Максвелла, произвести переход от макроскопической к стохастической (броуновской) динамике частицы [16, 17]. В модели Джефриса (см. рис. 1) вязкоупругая среда представляется как “гибрид” двух жидкостей: ньютоновской и максвелловской; поэтому три феноменологических параметра, характеризующие ее, имеют ясный качественный смысл.

Рис. 1.

Схема механического взаимодействия частицы с вязкоупругой матрицей, описываемой моделью Джефриса.

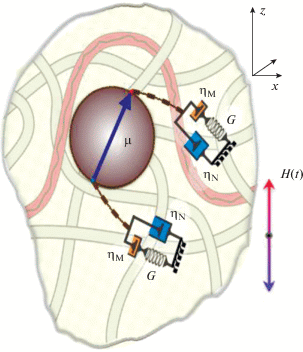
Коэффициент вязкости ${{\eta }_{{\text{N}}}}$ принято относить к низкомолекулярной (ньютоновской) компоненте жидкости Джефриса, а коэффициент ${{\eta }_{{\text{M}}}}$ – к ее высокомолекулярной (максвелловской) компоненте. Из естественного условия ${{\eta }_{{\text{N}}}} \ll {{\eta }_{{\text{M}}}}$ следует, что реакция частицы на внешнее воздействие является комбинацией быстрой и медленной составляющих с сильно различающимися временами реакции. Модуль упругости $G$ (см. рис. 1) характеризует упругость полимерной сетки зацеплений, за необратимую деформацию которой отвечает коэффициент “максвелловской” вязкости ${{\eta }_{{\text{M}}}}.$

3. УРАВНЕНИЯ ЛАНЖЕВЕНА И ФОККЕРА–ПЛАНКА

Система уравнений, описывающих ориентационное движение броуновской частицы в жидкости Джефриса без учета инерции, имеет вид [17, 18]:

(1)

$\begin{gathered} {\mathbf{\dot {e}}} = \left( {{\mathbf{\Omega }} \times {\mathbf{e}}} \right), \\ {\mathbf{\Omega }} = \frac{1}{{{{\zeta }_{N}}}}\left[ { - {\mathbf{\hat {L}}}E + {\mathbf{Q}} + {{{\mathbf{y}}}_{{\text{N}}}}\left( t \right)} \right],\,\,\,\,{\mathbf{\hat {L}}} = \left( {{\mathbf{e}} \times \frac{\partial }{{\partial e}}} \right), \\ \left( {1 + {{\tau }_{{\text{M}}}}\frac{\partial }{{\partial t}}} \right)Q = - {{\zeta }_{{\text{M}}}}{\mathbf{\Omega }} + {{{\mathbf{y}}}_{{\text{N}}}}\left( t \right),\,\,\,\,{{\tau }_{{\text{M}}}} = {{{{\zeta }_{{\text{M}}}}} \mathord{\left/ {\vphantom {{{{\zeta }_{{\text{M}}}}} K}} \right. \kern-0em} K}. \\ \end{gathered} $

Здесь ${\mathbf{e}}$ – единичный вектор ориентации частицы, ${\mathbf{\Omega }}$ – угловая скорость, $E$ – энергия взаимодействия частицы с полем, а ${\mathbf{\hat {L}}}$ – оператор бесконечного малого поворота, и использовано стандартное обозначение для векторного произведения. Коэффициенты реакции среды задаются стандартными для микрореологии выражениями [19]:

${{\zeta }_{\alpha }} = 6{{\eta }_{\alpha }}V,\,\,\,\,K = 6GV,\,\,\,\,\alpha = {\text{N}},{\text{M}},$

где $G$ – динамический модуль упругости, ${{\eta }_{\alpha }}$ – ньютоновская $\left( {\alpha = {\text{N}}} \right)$ или максвелловская $\left( {\alpha = {\text{M}}} \right)$ вязкость, $V$ – гидродинамический объем частицы. Случайные силы, моделирующие тепловой шум системы, в соответствии с флуктуационно-диссипативной теоремой определяются следующими корреляционными соотношениями [17, 18]:

(2)

$\left\langle {{{y}_{{i\alpha }}}\left( t \right){{y}_{{j\beta }}}\left( {t + \tau } \right)} \right\rangle = 2T{{\zeta }_{\alpha }}{{\delta }_{{\alpha \beta }}}{{\delta }_{{ij}}}\delta \left( \tau \right),$

здесь и далее температура $T$ измеряется в энергетических единицах $\left( {{{k}_{{\text{B}}}} = 1} \right).$

В системе уравнений (1) величина ${\mathbf{Q}}$ имеет смысл момента сил, действующих на частицу со стороны динамической квазисетки, среднее время жизни узла (зацепления) в которой составляет ${{\tau }_{{\text{M}}}}.$ Таким образом, фазовая переменная ${\mathbf{Q}}$ моделирует запаздывающую реакцию среды.

В рассматриваемой модели, схематически показанной на рис. 1, механизмы запаздывающего и обычного вязкого трения, обусловленного диссипативным взаимодействием частицы с низкомолекулярной компонентой среды, работают параллельно. Поэтому гель (равновесную сетку в хорошем растворителе) можно рассматривать как предельный случай модели Джефриса при ${{\tau }_{{\text{M}}}} \to \infty .$ В указанном пределе уравнение для запаздывающего момента сил трения редуцируется до ${\mathbf{\dot {Q}}} = - K{\mathbf{\Omega }},$ т.е. реакция высокомолекулярной компоненты среды становится чисто упругой. Для такой редуцированной системы в случае плоского вращения частицы уравнения (1) упрощаются и дают одномерную модель Кельвина; броуновское движение частицы в такой ситуации рассмотрено в работе [20].

Системе стохастических уравнений (1) соответствует кинетическое уравнение типа Фоккера–Планка (УФП) для ориентационной функции распределения $W\left( {{\mathbf{e}},{\mathbf{Q}},t} \right),$ получаемое стандартным способом (см., например, [18, 21]):

$\begin{gathered} \frac{\partial }{{\partial t}}W = \left[ {\frac{1}{{{{\zeta }_{{\text{N}}}}}}\left( {{\mathbf{\hat {L}}} - \frac{\partial }{{\partial {\mathbf{Q}}}}} \right)W\left( {{\mathbf{\hat {L}}} - \frac{\partial }{{\partial {\mathbf{Q}}}}} \right) + \frac{1}{{{{\zeta }_{{\text{M}}}}}}\frac{\partial }{{\partial {\mathbf{Q}}}}W\frac{\partial }{{\partial {\mathbf{Q}}}}} \right] \times \\ \times \,\,\left[ {E\left( {\mathbf{e}} \right) + \frac{1}{2}K{{Q}^{2}} + T{\text{ln}}W} \right]. \\ \end{gathered} $

Здесь и далее мы используем фазовую переменную ${\mathbf{Q}}$ в безразмерной форме, т.е. производим в исходной системе уравнений (1) замену ${\mathbf{Q}} \to K{\mathbf{Q}}.$ Из структуры УФП следует, что его стационарным (равновесным) решением является обобщенное распределение Больцмана

(3)

${{W}_{0}}\left( {{\mathbf{e}},{\mathbf{Q}}} \right)\sim {\text{exp}}\left[ { - \frac{1}{T}\left( {E\left( {\mathbf{e}} \right) + \frac{1}{2}K{{Q}^{2}}} \right)} \right].$

Из формулы (3) видно, что равновесное состояние системы в отсутствие поля $\left( {E = 0} \right)$ изотропно, а в постоянном внешнем поле $\left( {E \ne 0} \right)$ фазовые переменные ${\mathbf{e}}$ и ${\mathbf{Q}}$ статистически независимы.

Мы предполагаем, что модельная наночастица ферромагнетика обладает достаточной магнитной жесткостью, так что ее магнитный дипольный момент ${\mathbf{\mu }}$ закреплен (вморожен) в теле частицы, и поэтому энергия его взаимодействия с полем имеет стандартный вид ориентационного потенциала Зеемана:

(4)

$E\left( {{\mathbf{e}},{\mathbf{h}}} \right) = - {\mathbf{\mu H}} = - \mu H\left( {{\mathbf{eh}}} \right),\,\,\,\,{\mathbf{h}} = \left( {0,0,1} \right).$

Для расчета отклика системы на зондирующее поле $H\left( t \right)$ усредним стохастические уравнения (1) по статистическому ансамблю. После подстановки явного вида потенциала взаимодействия частиц с полем система (1) принимает форму

(5)

$\begin{gathered} {\mathbf{\dot {e}}} = {{\gamma }_{{\text{H}}}}\left( {{\mathbf{e}} \times \left( {{\mathbf{h}} \times {\mathbf{e}}} \right)} \right) + {{\gamma }_{{\text{N}}}}\left( {{\mathbf{Q}} \times {\mathbf{e}}} \right) + \left( {{\mathbf{u}} \times {\mathbf{e}}} \right), \\ {\mathbf{u}} = {{{{{\mathbf{y}}}_{{\text{N}}}}\left( t \right)} \mathord{\left/ {\vphantom {{{{{\mathbf{y}}}_{{\text{N}}}}\left( t \right)} {{{\zeta }_{{\text{N}}}}}}} \right. \kern-0em} {{{\zeta }_{{\text{N}}}}}},\,\,\,\,{\mathbf{\dot {Q}}} + {\tilde {\gamma }}{\mathbf{Q}} = - {{\gamma }_{{\text{H}}}}\left( {{\mathbf{e}} \times {\mathbf{h}}} \right) + {\mathbf{\tilde {u}}}, \\ {\mathbf{\tilde {u}}} = {{{{{\mathbf{y}}}_{{\text{M}}}}\left( t \right)} \mathord{\left/ {\vphantom {{{{{\mathbf{y}}}_{{\text{M}}}}\left( t \right)} {{{\zeta }_{{\text{M}}}}}}} \right. \kern-0em} {{{\zeta }_{{\text{M}}}}}} - {\mathbf{u}},\,\,\,\,{{\gamma }_{{\text{H}}}} = {{\mu H} \mathord{\left/ {\vphantom {{\mu H} {{{\zeta }_{{\text{N}}}}}}} \right. \kern-0em} {{{\zeta }_{{\text{N}}}}}}, \\ {{\gamma }_{\alpha }} = {K \mathord{\left/ {\vphantom {K {{{\zeta }_{\alpha }}}}} \right. \kern-0em} {{{\zeta }_{\alpha }}}},\,\,\,\,\tilde {\gamma } = {{\gamma }_{{\text{N}}}} + {{\gamma }_{{\text{M}}}} = {{\gamma }_{{\text{N}}}}\left( {1 + {1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0em} q}} \right), \\ q = {{{{\eta }_{{\text{M}}}}} \mathord{\left/ {\vphantom {{{{\eta }_{{\text{M}}}}} {{{\eta }_{{\text{N}}}}}}} \right. \kern-0em} {{{\eta }_{{\text{N}}}}}}. \\ \end{gathered} $

Корреляционные функции случайных сил, входящих в эту систему, определяются соотношением (2).

4. РАВНОВЕСНОЕ СОСТОЯНИЕ

Равновесная функция распределения (3) после подстановки потенциала Зеемана принимает вид

(6)

$\begin{gathered} {{W}_{0}}\left( {{\mathbf{e}},{\mathbf{Q}}} \right) = \frac{1}{Z}\left[ {\xi \left( {{\mathbf{eh}}} \right) - \frac{{{{Q}^{2}}}}{{2\tilde {T}}}} \right],\,\,\,\,Z = {{Z}_{\xi }}{{Z}_{Q}}, \\ {{Z}_{\xi }} = 2\pi \int\limits_{ - 1}^1 {dx~{\text{exp}}\left( {\xi x} \right)} = 4\pi {\text{sh}}\xi {\text{\;}}, \\ {{Z}_{Q}} = \int {d{\mathbf{Q}}{\text{exp}}\left( {{{ - {{Q}^{2}}} \mathord{\left/ {\vphantom {{ - {{Q}^{2}}} {2\tilde {T}}}} \right. \kern-0em} {2\tilde {T}}}} \right)} = {{\left( {2\pi \tilde {T}} \right)}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}, \\ \end{gathered} $

где последний интеграл берется по всем значениям модуля и направлениям вектора ${\mathbf{Q}}.$ В (6) использованы обозначения для безразмерной величины поля $\xi = {{\mu H} \mathord{\left/ {\vphantom {{\mu H} T}} \right. \kern-0em} T}$ и безразмерной температуры $\tilde {T} = {T \mathord{\left/ {\vphantom {T K}} \right. \kern-0em} K}.$ В слабом поле $\left( {\xi \ll 1} \right)$ равновесные статистические моменты ориентационной функции выражаются соотношениями

(7)

$\begin{gathered} {{\left\langle {{{{\left( {{\mathbf{eh}}} \right)}}^{{\left( n \right)}}}} \right\rangle }_{0}} \equiv {{\left\langle {e_{z}^{{\left( n \right)}}} \right\rangle }_{0}} \cong \\ \cong \left\{ \begin{gathered} \frac{\xi }{{2k + 3}}\left[ {1 - \frac{{{{\xi }^{2}}}}{{3\left( {2k + 5} \right)}}} \right],\,\,\,\,~n = 2k + 1 \hfill \\ \frac{1}{{2k + 1}}\left[ {1 + \frac{{2{{\xi }^{2}}}}{{3\left( {2k + 3} \right)}}} \right],\,\,\,\,n = 2k.~ \hfill \\ \end{gathered} \right. \\ \end{gathered} $

Из вида функций (3) и (6) следует, что распределение фазовой переменной ${\mathbf{Q}}$ остается изотропным даже при наличии постоянного поля, в силу чего все нечетные равновесные статистические моменты этой величины обращаются в нуль, а четные моменты можно представить в виде

$\begin{gathered} {{\left\langle {{{Q}^{{2n}}}} \right\rangle }_{0}} = Z_{Q}^{{ - 1}}\int {{{d}^{3}}{\mathbf{Q}}{\text{\;}}{{Q}^{{2n}}}} {\text{exp}}\left( {{{ - {{Q}^{2}}} \mathord{\left/ {\vphantom {{ - {{Q}^{2}}} {2\tilde {T}}}} \right. \kern-0em} {2\tilde {T}}}} \right) = \\ = {{\left( {\tilde {T}} \right)}^{n}}\left( {2n + 1} \right)!!,\,\,\,\,{{\left\langle {Q_{x}^{{2n}}} \right\rangle }_{0}} = {{\left\langle {Q_{y}^{{2n}}} \right\rangle }_{0}} = \\ = {{\left\langle {Q_{z}^{{2n}}} \right\rangle }_{0}} = {{\left( {\tilde {T}} \right)}^{n}}\left( {2n - 1} \right)!!. \\ \end{gathered} $

В ансамбле идентичных и не взаимодействующих друг с другом наночастиц намагниченность определяется их числовой концентрацией $\nu $ и величиной проекции совокупного магнитного момента единицы объема на направление приложенного поля. В настоящей работе мы рассматриваем отклик системы на слабое зондирующее поле $\left( {\xi \ll 1} \right)$ и учитываем только главный нелинейный вклад:

(8)

$M = \nu \left\langle {{\mathbf{\mu h}}} \right\rangle = \nu \mu \left\langle {{{e}_{z}}} \right\rangle = {{\chi }^{{(1)}}}H + {{\chi }^{{(3)}}}{{H}^{3}},$

здесь ${{{\chi }}^{{\left( 1 \right)}}}$ и ${{{\chi }}^{{\left( 3 \right)}}}{\text{\;}}$ – линейная и кубическая восприимчивости ферроколлоида соответственно. Их статические значения находятся с помощью распределения (6):

(9)

$\chi _{0}^{{(1)}} = \frac{{\nu {{\mu }^{2}}}}{{3T}},\,\,\,\,\chi _{0}^{{(3)}} = - \frac{{\nu {{\mu }^{4}}}}{{45{{T}^{3}}}}.$

В том случае, когда наночастицы обладают анизометрией формы, их ориентация полем придает коллоиду оптическую анизотропию. Причиной эффекта является разница между диэлектрическими проницаемостями материалов частиц и среды [22]. Оптическая анизотропия системы наблюдается в виде двойного лучепреломления (ДЛП) и характеризуется разностью ${\Delta }n = {{n}_{{\text{e}}}} - {{n}_{{\text{o}}}}$ показателей преломления необыкновенного и обыкновенного лучей, то есть световых волн, поляризованных соответственно параллельно и перпендикулярно направлению ${\mathbf{h}}$ приложенного поля. В приближении малых возмущений величина ${\Delta }n$ рассматриваемой системы пропорциональна квадрупольному параметру ориентационного порядка частиц. Для статического случая из (3) имеем

(10)

${\Delta }n \propto {{\left\langle {e_{z}^{2}} \right\rangle }_{0}} - \frac{1}{3} = \frac{2}{{45}}{{\xi }^{2}} = \frac{2}{{45}}\frac{{{{\mu }^{2}}}}{{{{T}^{2}}}}{{H}^{2}}.$

5. НЕРАВНОВЕСНОЕ РАСПРЕДЕЛЕНИЕ В ПРИБЛИЖЕНИИ СРЕДНЕГО ПОЛЯ

Уравнения динамики наблюдаемых величин находятся по стандартной процедуре [21] усреднением системы уравнений Ланжевена (1) с неравновесной функцией распределения $W\left( {{\mathbf{e}},{\mathbf{Q}},t} \right).$ Нетрудно видеть, что при этом получается бесконечная цепочка уравнений, которая связывает между собой статистические моменты нарастающего порядка. В работах [23, 24] был найден полный функциональный базис для функции распределения $W,$ что позволило построить удобный алгоритм точного расчета получающихся статистических моментов. Тем самым была решена бесконечная цепочка уравнений и полностью определена линейная динамическая восприимчивость ${{\chi }^{{(1)}}}\left( \omega \right).$

К сожалению, функциональный базис [23, 24] пригоден только для расчета ориентационных средних первого порядка по амплитуде приложенного поля, выполнить аналитический расчет функций $\left\langle {e_{z}^{2}} \right\rangle \left( t \right)$ и $\left\langle {e_{z}^{3}} \right\rangle \left( t \right)$ не удается. В настоящей работе для определения указанных величин мы используем упрощенный подход – так называемое приближение эффективного поля [25, 26], которое позволяет достаточно легко замкнуть систему уравнений для моментов неравновесной функции распределения $W\left( {{\mathbf{e}},{\mathbf{Q}},t} \right).$ Основываясь на нашем опыте сопоставления точного и приближенного расчетов линейной динамической восприимчивости [23, 24], мы предполагаем, что полученные методом эффективного поля аппроксимации нелинейных восприимчивостей будут не слишком сильно отличаться от точных характеристик изучаемой системы.

Процедура метода эффективного поля предполагает разложение неравновесной функции распределения по минимально достаточному числу базисных функций, которые мы представим в системе координат, где ось Oz параллельна направлению приложенного поля, см. (4). Из анализа уравнений (1) следует, что для учета вязкоупругости в такой функциональный базис, наряду с фазовыми переменными ${{e}_{z}}$ и $e_{z}^{2},$ нужно включить функции первого порядка по величине момента сил запаздывающего трения ${{P}_{z}} = {{\left( {{\mathbf{Q}} \times {\mathbf{e}}} \right)}_{z}}$ и ${{e}_{z}}{{P}_{z}}.$

С помощью указанного набора функций приближенное решение УФП (5) представим в виде

(11)

$\begin{gathered} W\left( {{\mathbf{e}},{\mathbf{Q}},t} \right) = {{W}_{0}}\left( {{\mathbf{e}},{\mathbf{Q}}} \right) \times \\ \times \,\,\left[ {1 + a(t){{e}_{z}} + b(t){{P}_{z}} + c(t)\left( {e_{z}^{2} - \frac{1}{3}} \right) + f(t){\kern 1pt} {{e}_{z}}{{P}_{z}}} \right]. \\ \end{gathered} $

Используемые здесь базисные функции удовлетворяют условию нормировки $\left\langle 1 \right\rangle = {{\left\langle 1 \right\rangle }_{0}}$ и при этом взаимно ортогональны: $\left\langle {{{e}_{z}}\left( {e_{z}^{2} - \frac{1}{3}} \right)} \right\rangle = \left\langle {{{e}_{z}}{{P}_{z}}} \right\rangle = 0.$ Связь между зависящими от времени коэффициентами $a,$ $b,$ $c,$ $f$ и неравновесными средними значениями базисных функций находим, усредняя последние с распределением (11). Это приводит к соотношениям

(12)

$\begin{gathered} \left\langle {{{e}_{z}}} \right\rangle = a{{\left\langle {e_{z}^{2}} \right\rangle }_{0}} = \frac{1}{3}a,\,\,\,\,\left\langle {{{P}_{z}}} \right\rangle = b{{\left\langle {P_{z}^{2}} \right\rangle }_{0}} = \frac{2}{3}b\tilde {T}, \\ \left\langle {e_{z}^{2} - \frac{1}{3}} \right\rangle = c{{\left\langle {{{{\left( {e_{z}^{2} - \frac{1}{3}} \right)}}^{2}}} \right\rangle }_{0}} = \frac{4}{{45}}c, \\ ~\left\langle {{{e}_{z}}{{P}_{z}}} \right\rangle = f{{\left\langle {{{{\left( {{{e}_{z}}{{P}_{z}}} \right)}}^{2}}} \right\rangle }_{0}} = \frac{2}{{15}}f\tilde {T}. \\ \end{gathered} $

6. СИСТЕМА МОМЕНТНЫХ УРАВНЕНИЙ

Рассмотрим, в первую очередь, уравнение для среднего (наблюдаемого) вектора магнитного момента. Формальное усреднение первого уравнения системы (5) дает

$\frac{\partial }{{\partial t}}\left\langle {\mathbf{e}} \right\rangle = {{\gamma }_{{\text{H}}}}\left\langle {\left( {{\mathbf{e}} \times \left( {{\mathbf{h}} \times {\mathbf{e}}} \right)} \right)} \right\rangle + {{\gamma }_{{\text{N}}}}\left\langle {\left( {{\mathbf{Q}} \times {\mathbf{e}}} \right)} \right\rangle + \left\langle {\left( {{\mathbf{u}} \times {\mathbf{e}}} \right)} \right\rangle .$

Для вычисления последнего слагаемого в правой части, определяющего вклад вращательной диффузии, воспользуемся следующим способом [17, 21, 27]. Так как в искомое выражение входит случайная функция, результат определяется только сингулярной, т.е. пропорциональной случайной силе частью решения уравнения (5):

(13)

$\delta {\mathbf{e}}(t) = \hat {I}\left( {{\mathbf{u}}{\kern 1pt} '\, \times {\mathbf{e}}{\kern 1pt} '} \right) \equiv \mathop {\lim }\limits_{\varepsilon \to 0} \int\limits_{t - \varepsilon }^t {dt{\kern 1pt} '\left( {{\mathbf{u}}\left( {t{\kern 1pt} '} \right) \times {\mathbf{e}}\left( {t{\kern 1pt} '} \right)} \right){\kern 1pt} } .$

Эта формула выражает принцип причинности, согласно которому состояние физической системы в данный момент времени зависит только от предшествующих воздействий. После усреднения слагаемого со случайной силой с помощью определения (13) и использования корреляционных соотношений (2) уравнение движения для проекции вектора $\left\langle {\mathbf{e}} \right\rangle $ принимает вид

(14)

$\begin{gathered} \left( {\frac{\partial }{{\partial t}} + {{\gamma }_{{\text{D}}}}} \right)\left\langle {{{e}_{z}}} \right\rangle = {{\gamma }_{{\text{H}}}}\left[ {\frac{2}{3} - \left\langle {e_{z}^{2} - \frac{1}{3}} \right\rangle } \right] + {{\gamma }_{{\text{N}}}}\left\langle {{{P}_{z}}} \right\rangle , \\ {{\gamma }_{{\text{D}}}} = \frac{1}{{{{\tau }_{{\text{D}}}}}}, \\ \end{gathered} $

где в правой части возникла вторая базисная функция – параметр ориентационного порядка. Здесь ${{\tau }_{{\text{D}}}} = {{{{\zeta }_{{\text{N}}}}} \mathord{\left/ {\vphantom {{{{\zeta }_{{\text{N}}}}} {2T}}} \right. \kern-0em} {2T}}$ – известное дебаевское время броуновской вращательной диффузии сферической частицы в ньютоновой жидкости с вязкостью ${{\eta }_{{\text{N}}}}.$

Уравнение для статистического момента $\left\langle {{{P}_{z}},} \right\rangle $ следующее из системы (5), принимает вид

(15)

$\begin{gathered} \frac{\partial }{{\partial t}}\left\langle {{{P}_{z}}} \right\rangle = \left\langle {{{{\left( {{\mathbf{\dot {Q}}} \times {\mathbf{e}}} \right)}}_{z}} + {{{\left( {{\mathbf{Q}} \times {\mathbf{\dot {e}}}} \right)}}_{z}}} \right\rangle = \\ = {{\gamma }_{{\text{H}}}}\left[ {\left\langle {{{{\left( {{\mathbf{Q}} \times \left( {{\mathbf{e}} \times \left( {{\mathbf{h}} \times {\mathbf{e}}} \right)} \right)} \right)}}_{z}}} \right\rangle - \left\langle {{{{\left( {{\mathbf{e}} \times \left( {{\mathbf{h}} \times {\mathbf{e}}} \right)} \right)}}_{z}}} \right\rangle } \right] + \\ + \,\,~{{\gamma }_{{\text{N}}}}\left\langle {{{{\left( {{\mathbf{Q}} \times \left( {{\mathbf{Q}} \times {\mathbf{e}}} \right)} \right)}}_{z}}} \right\rangle + \left\langle {{{{\left( {{\mathbf{\tilde {u}}} \times {\mathbf{e}}} \right)}}_{z}}} \right\rangle + \left\langle {{{{\left( {{\mathbf{Q}} \times \left( {{\mathbf{u}} \times {\mathbf{e}}} \right)} \right)}}_{z}}} \right\rangle . \\ \end{gathered} $

Найдем сначала его диффузионную часть, определяемую действием случайных сил:

$\begin{gathered} \left\langle {{{{\left( {{\mathbf{\tilde {u}}} \times {\mathbf{e}}} \right)}}_{z}} + {{{\left( {{\mathbf{Q}} \times \left( {{\mathbf{u}} \times {\mathbf{e}}} \right)} \right)}}_{z}}} \right\rangle = \\ = \hat {I}\left\langle {2{{{\left[ {{\mathbf{u}}{\kern 1pt} '\left( {{\mathbf{\tilde {u}e}}{\kern 1pt} '} \right) - {\mathbf{e}}{\kern 1pt} '\left( {{\mathbf{\tilde {u}u}}} \right)} \right]}}_{z}} + } \right. \\ \left. { + \,\,{{{\left( {{\mathbf{Q}} \times \left[ {{\mathbf{u}}{\kern 1pt} '\left( {{\mathbf{ue}}{\kern 1pt} '} \right) - {\mathbf{e}}{\kern 1pt} '\left( {{\mathbf{uu}}{\kern 1pt} '} \right)} \right]} \right)}}_{z}}} \right\rangle = {{\gamma }_{{\text{D}}}}\left[ {2\left\langle {{{e}_{z}}} \right\rangle - \left\langle {{{P}_{z}}} \right\rangle } \right]. \\ \end{gathered} $

Здесь использована процедура (12) вычисления сингулярной части величин, усредняемых вместе со случайной силой, и учтено соотношение $\hat {\delta }Q\left( t \right) = \hat {I}\left( {{\mathbf{\tilde {u}}}{\kern 1pt} '} \right)$ = $\mathop {\lim }\limits_{\varepsilon \to 0} \int_{t - \varepsilon }^t {dt{\kern 1pt} '{\mathbf{\tilde {u}}}\left( {t{\kern 1pt} '} \right)} .$

Вычисление квадратичного по ${\mathbf{Q}}$ момента с распределением (11) дает

(16)

$\begin{gathered} \left\langle {{{{\left( {{\mathbf{Q}} \times \left( {{\mathbf{Q}} \times {\mathbf{e}}} \right)} \right)}}_{z}}} \right\rangle = a{{\left\langle {{{e}_{z}}\left[ {{{Q}_{z}}\left( {{\mathbf{eQ}}} \right) - {{e}_{z}}{{{\mathbf{Q}}}^{2}}} \right]} \right\rangle }_{0}} = \\ = a{{\left\langle {e_{z}^{2}\left( {Q_{z}^{2} - {{Q}^{2}}} \right)} \right\rangle }_{0}} = - \frac{2}{3}a\tilde {T} = - 2\tilde {T}\left\langle {{{e}_{z}}} \right\rangle , \\ \end{gathered} $

и это позволяет замкнуть систему моментных уравнений по переменной ${\mathbf{Q}}.$ Действительно, с учетом соотношения (16) уравнение (14) преобразуется к форме, содержащей только средние от базисных функций приближения эффективного поля (11):

(17)

$\begin{gathered} \left( {\frac{\partial }{{\partial t}} + {{\gamma }_{{\text{D}}}} + \tilde {\gamma }} \right)\left\langle {{{P}_{z}}} \right\rangle = \\ = {{\gamma }_{{\text{H}}}}\left( { - \frac{2}{3} + \left\langle {e_{z}^{2} - \frac{1}{3}} \right\rangle - \left\langle {{{e}_{z}}{{P}_{z}}} \right\rangle } \right) + {{\gamma }_{{\text{D}}}}\left\langle {{{e}_{z}}} \right\rangle . \\ \end{gathered} $

Аналогичным способом получаются динамические уравнения и для моментов $\left\langle {e_{z}^{2} - \frac{1}{3}} \right\rangle $ и $\left\langle {{{e}_{z}}{{P}_{z}}} \right\rangle .$

В итоге полная замкнутая система моментных уравнений имеет вид

(18)

$\begin{gathered} \left( {1 + \frac{\partial }{{\partial t}}} \right)\left\langle {{{e}_{z}}} \right\rangle = \frac{1}{3}\xi \left( t \right)\left[ {1 - \frac{3}{2}\left\langle {e_{z}^{2} - \frac{1}{3}} \right\rangle } \right] + \beta \left\langle {{{P}_{z}}} \right\rangle , \\ \left( {1 + \tilde {\beta } + \frac{\partial }{{\partial t}}} \right)\left\langle {{{P}_{z}}} \right\rangle = - \frac{1}{3}\xi \left( t \right) \times \\ \times \,\,\left[ {1 - \frac{3}{2}\left\langle {e_{z}^{2} - \frac{1}{3}} \right\rangle + \frac{3}{2}\left\langle {{{e}_{z}}{{P}_{z}}} \right\rangle } \right] + \left\langle {{{e}_{z}}} \right\rangle ,\,\,\,\,\left( {3 + \frac{\partial }{{\partial t}}} \right)\left\langle {e_{z}^{2} - } \right. \\ \left. { - \,\,\frac{1}{3}} \right\rangle = \frac{2}{5}\xi \left( t \right)\left\langle {{{e}_{z}}} \right\rangle + 2\beta \left\langle {{{e}_{z}}{{P}_{z}}} \right\rangle ,\,\,\,\,\left( {3 + \tilde {\beta } + \frac{\partial }{{\partial t}}} \right)\left\langle {{{e}_{z}}{{P}_{z}}} \right\rangle = \\ = \frac{1}{5}\xi \left( t \right)\left[ { - \left\langle {{{e}_{z}}} \right\rangle + \frac{3}{2}\left\langle {{{P}_{z}}} \right\rangle } \right] + \frac{3}{2}\left\langle {e_{z}^{2} - \frac{1}{3}} \right\rangle , \\ \beta = {K \mathord{\left/ {\vphantom {K {2T}}} \right. \kern-0em} {2T}},\,\,\,\,\tilde {\beta } = \beta \left( {{{1 + 1} \mathord{\left/ {\vphantom {{1 + 1} q}} \right. \kern-0em} q}} \right). \\ \end{gathered} $

Здесь введено безразмерное время, измеряемое в единицах дебаевского времени ${{\tau }_{{\text{D}}}}.$ Решение системы (18) в статическом пределе (${\partial \mathord{\left/ {\vphantom {\partial {\partial t}}} \right. \kern-0em} {\partial t}} = 0$) дается формулами (9) и (10).

7. ДИНАМИЧЕСКИЕ ВОСПРИИМЧИВОСТИ

Найдем первые три гармоники отклика системы на зондирующее поле

$\xi \left( t \right) = {{\xi }_{0}}\cos \omega t = \frac{1}{2}{{\xi }_{0}}\left[ {{\text{exp}}\left( { - i\omega t} \right) + {\text{к}}.{\text{c}}.} \right].$

Искомые функции будем искать в виде разложений по малому параметру, которым здесь является амплитуда ${{\xi }_{0}}$ переменного поля. Так, например, усредненную проекцию магнитного момента представим в виде

(19)

$\begin{gathered} \left\langle {{{e}_{z}}} \right\rangle = \frac{1}{2}{{\xi }_{0}}\left[ {A_{\omega }^{{\left( 1 \right)}}{\text{exp}}\left( { - i\omega t} \right) + {\text{к}}.{\text{c}}.} \right] + \\ + \,\,\frac{1}{8}\xi _{0}^{3}\left[ {A_{{3\omega }}^{{\left( 3 \right)}}{\text{exp}}\left( { - 3i\omega t} \right) + {\text{к}}.{\text{c}}.} \right], \\ \end{gathered} $

аналогичную форму будет иметь и момент $\left\langle {{{P}_{z}}} \right\rangle .$ Из системы (18) следует, что параметр ориентации $\left\langle {e_{z}^{2} - \frac{1}{3}} \right\rangle $ и момент $\left\langle {{{e}_{z}}{{P}_{z}}} \right\rangle $ появляются во втором порядке по $\xi .$ Таким образом, эти величины будут содержать постоянную составляющую и гармонику $2\omega .$ Подстановка таких выражений в систему дифференциальных уравнений (18) сводит ее к алгебраической задаче, решение которой в первом порядке малости по параметру разложения приводит к известному из работы [24] результату

(20)

$\begin{gathered} \tilde {\chi }_{\omega }^{{(1)}}\left( \omega \right) = \frac{{\chi _{\omega }^{{(1)}}}}{{\chi _{0}^{{(1)}}}} = \frac{1}{{1 - ix\left( {1{\text{\;}} + {\text{\;}}\frac{\beta }{{{{1 + \beta } \mathord{\left/ {\vphantom {{1 + \beta } {q - ix}}} \right. \kern-0em} {q - ix}}}}} \right)}}, \\ x \equiv \omega {{\tau }_{{\text{D}}}}, \\ \end{gathered} $

здесь статическая восприимчивость определена формулой (9) и восстановлена размерность времени.

Используя выражение (19) и аналогичное ему первое приближение для момента $\left\langle {{{P}_{z}}} \right\rangle ,$ из системы (18) получим алгебраическую систему для определения комплексных амплитуд вторых гармоник параметра ориентационного порядка и момента $\left\langle {{{e}_{z}}{{P}_{z}}} \right\rangle .$ Решение этой задачи имеет вид

(21)

$\begin{gathered} \tilde {\chi }_{{2\omega }}^{{(2)}} \equiv \frac{{\left\langle {e_{z}^{2} - \frac{1}{3}} \right\rangle _{{2\omega }}^{{(2)}}}}{{\left\langle {e_{z}^{2} - \frac{1}{3}} \right\rangle _{0}^{{(2)}}}} = \\ = \tilde {\chi }_{\omega }^{{(1)}}\frac{{1 + \frac{{i\beta x}}{{2\left( {1 + \frac{\beta }{q} - ix} \right)\left( {1 + \frac{\beta }{{3q}} - {{2ix} \mathord{\left/ {\vphantom {{2ix} 3}} \right. \kern-0em} 3}} \right)}}}}{{1 - \frac{{2ix}}{3}\left( {1 + \frac{{{\beta \mathord{\left/ {\vphantom {\beta 3}} \right. \kern-0em} 3}}}{{1 + {\text{\;}}\frac{\beta }{{3q}} - {{~2ix} \mathord{\left/ {\vphantom {{~2ix} 3}} \right. \kern-0em} 3}}}} \right)}}{\kern 1pt} , \\ \tilde {s}_{{2\omega }}^{{(2)}} \equiv \frac{{\left\langle {P_{z}^{2}} \right\rangle _{{2\omega }}^{{(2)}}}}{{\left\langle {e_{z}^{2} - \frac{1}{3}} \right\rangle _{0}^{{(2)}}}} = ix\tilde {\chi }_{\omega }^{{(1)}}\frac{{\frac{1}{{3 - 2ix~}} + \frac{{{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0em} 4}}}{{1 + {\beta \mathord{\left/ {\vphantom {\beta {q - ix}}} \right. \kern-0em} {q - ix}}}}}}{{1 + \frac{\beta }{{3q}} - \frac{{2ix}}{3}\left( {1 + {\text{\;}}\frac{{{\beta \mathord{\left/ {\vphantom {\beta 3}} \right. \kern-0em} 3}}}{{{{1 - 2ix} \mathord{\left/ {\vphantom {{1 - 2ix} 3}} \right. \kern-0em} 3}}}} \right)}}. \\ \end{gathered} $

Отметим, что динамическая магнитная восприимчивость во втором порядке обращается в нуль по соображениям симметрии, см. (19).

Используя формулы (21), из уравнений (18) получаем алгебраическую систему для определения амплитуды динамической магнитной восприимчивости на частоте $3\omega {\kern 1pt} .$ Решая ее, находим после стандартных вычислений:

(22)

$\tilde {\chi }_{{3\omega }}^{{(3)}} \equiv \frac{{\left\langle {{{e}_{z}}} \right\rangle _{{3\omega }}^{{(3)}}}}{{\left\langle {{{e}_{z}}} \right\rangle _{0}^{{(3)}}}} = \frac{{\tilde {\chi }_{{2\omega }}^{{(2)}} + ~\frac{{\beta \tilde {s}_{{2\omega }}^{{(2)}}}}{{{{1 + \beta } \mathord{\left/ {\vphantom {{1 + \beta } q}} \right. \kern-0em} q} - 3ix}}}}{{1 - 3ix\left( {1 + ~\frac{\beta }{{{{1 + \beta } \mathord{\left/ {\vphantom {{1 + \beta } q}} \right. \kern-0em} q} - 3ix}}} \right)}}.$

Соотношения (20)–(22) позволяют проанализировать частотную зависимость магнитной восприимчивости на исходной частоте сигнала и на утроенной частоте, а также зависимость сигнала ДЛП на удвоенной частоте. Как и следовало ожидать, в предельном случае простой вязкой жидкости ($\beta \to 0$), т.е. в отсутствие вязкоупругости, эти формулы сводятся к соответствующим выражениям, полученным ранее, см., например, [26].

Характерной особенностью изучаемой модели является появление в спектрах коллоидов с развитой упругостью ($q \gg \beta \gg 1$) низкочастотной моды релаксации. В этом случае линейную динамическую восприимчивость (20) можно представить в виде суммы двух основных релаксационных мод, “медленной” (slow) и “быстрой” (fast),

(23)

$\begin{gathered} \tilde {\chi }_{\omega }^{{(1)}} \cong \frac{1}{{1 - i\beta \omega {{\tau }_{{\text{D}}}}}} + \frac{1}{\beta }\frac{1}{{1 - {{i\omega {{\tau }_{{\text{D}}}}} \mathord{\left/ {\vphantom {{i\omega {{\tau }_{{\text{D}}}}} \beta }} \right. \kern-0em} \beta }}} = \\ = \frac{1}{{1 - i\omega {{\tau }_{{\text{s}}}}}} + \frac{1}{\beta }\frac{1}{{1 - i\omega {{\tau }_{{\text{f}}}}}}, \\ \end{gathered} $

и ввести, тем самым, два характерных времени:

(24)

${{\tau }_{{\text{s}}}} = \beta {{\tau }_{{\text{D}}}} = \frac{{{{\zeta }_{{\text{N}}}}K}}{{4{{T}^{2}}}} = {{\left( {\frac{{3V}}{T}} \right)}^{2}}{{\eta }_{{\text{N}}}}G,\,\,\,\,{{\tau }_{{\text{f}}}} = \frac{{{{\tau }_{{\text{D}}}}}}{\beta } = \frac{{{{\eta }_{{\text{N}}}}}}{G}.$

Видно, что в рассматриваемом пределе максвелловская вязкость вовсе не входит в выражения для времен релаксации. Отметим также, что при любых значениях параметров модели Джефриса среднеквадратичное значение времен (24) всегда равно дебаевскому времени: $\sqrt {{{\tau }_{{\text{s}}}}{{\tau }_{{\text{f}}}}} = {{\tau }_{{\text{D}}}}.$

Формула (23) описывает линейную восприимчивость в области значений параметра упругости $q \gg \beta \gg 1,$ где происходит переход от режима быстрой диффузии наночастицы, определяемой вязкостью ${{\eta }_{{\text{N}}}}$ низкомолекулярного растворителя, к режиму медленной диффузии, обусловленной вязкоупругостью высокомолекулярной компоненты. В размерной форме условие $q \gg \beta $ принимает вид ${{\tau }_{{\text{M}}}} \gg {{\tau }_{{\text{D}}}},$ что всегда выполняется для субмикронных частиц в вязкоупругих системах. В работе [23] было показано, что, несмотря на малость амплитуды высокочастотной компоненты восприимчивости, именно она дает наибольший вклад в мощность электромагнитного излучения, поглощаемую системой. На наш взгляд, экспериментальное подтверждение этого эффекта может служить достоверной проверкой применимости изучаемой модели. С теоретической точки зрения аргумент, подтверждающий наличие высокочастотной компоненты восприимчивости, вполне очевиден, поскольку в атермическом пределе ($T \to 0$) в спектре упругой системы с трением всегда имеется такая мода.

Интересно отметить зависимость характерных времен релаксации от размера зонда. Так, согласно (24) время медленной релаксации ${{\tau }_{{\text{s}}}}$ пропорционально квадрату объема частицы-зонда, тогда как быстрое время ${{\tau }_{{\text{f}}}}$ целиком определяется только реологическими параметрами среды.

В режиме развитой упругости ($q \gg \beta \gg 1$) выражение для комплексной амплитуды второй гармоники отклика приводится к виду

(25)

$\begin{gathered} \tilde {\chi }_{{2\omega }}^{{(2)}} \cong \frac{{{{1 + i\omega {{\tau }_{{\text{s}}}}} \mathord{\left/ {\vphantom {{1 + i\omega {{\tau }_{{\text{s}}}}} 2}} \right. \kern-0em} 2}}}{{\left( {1 - i\omega {{\tau }_{{\text{s}}}}} \right)\left( {{{1 - 2i\omega {{\tau }_{{\text{s}}}}} \mathord{\left/ {\vphantom {{1 - 2i\omega {{\tau }_{{\text{s}}}}} 9}} \right. \kern-0em} 9}} \right)}} + \\ + \,\,\frac{3}{{{{\beta }^{2}}}}\frac{{{{1 + 3} \mathord{\left/ {\vphantom {{1 + 3} {i\omega {{\tau }_{{\text{f}}}}}}} \right. \kern-0em} {i\omega {{\tau }_{{\text{f}}}}}}}}{{\left( {1 - i\omega {{\tau }_{{\text{f}}}}} \right)\left( {1 - 2i\omega {{\tau }_{{\text{f}}}}} \right)}}. \\ \end{gathered} $

Это асимптотическое выражение ясно указывает на смещение частотного спектра ДЛП в область низких частот по мере увеличения упругости системы. Следует отметить и тот факт, что высокочастотная компонента этого отклика убывает с ростом параметра упругости по квадратичному закону.

Отмеченные выше особенности имеют место и в спектре кубической восприимчивости, аппроксимационная формула для которой в пределе $q \gg \beta \gg 1$ есть

(26)

$\begin{gathered} \tilde {\chi }_{{3\omega }}^{{(3)}} \cong \frac{{1 + \left( {{{19} \mathord{\left/ {\vphantom {{19} {12}}} \right. \kern-0em} {12}}} \right)i\omega {{\tau }_{{\text{s}}}}}}{{\left( {1 - i\omega {{\tau }_{{\text{s}}}}} \right)\left( {1 - 3i\omega {{\tau }_{{\text{s}}}}} \right)\left( {{{1 - 2i\omega {{\tau }_{{\text{s}}}}} \mathord{\left/ {\vphantom {{1 - 2i\omega {{\tau }_{{\text{s}}}}} 9}} \right. \kern-0em} 9}} \right)}} + \\ + \,\,\frac{3}{{{{\beta }^{3}}}}\frac{{1 + {7 \mathord{\left/ {\vphantom {7 6}} \right. \kern-0em} 6}i\omega {{\tau }_{{\text{f}}}}}}{{\left( {1 - i\omega {{\tau }_{{\text{f}}}}} \right)\left( {1 - 3i\omega {{\tau }_{{\text{f}}}}} \right)\left( {1 - 2i\omega {{\tau }_{{\text{f}}}}} \right)}}. \\ \end{gathered} $

На рис. 2а–2в показаны графики действительных (штриховые линии) и мнимых (сплошные линии) частей восприимчивостей: линейной, квадратичной и кубической; все они нормированы на соответствующие статические значения. Расчет проводился по формулам (20)–(22), а числовые значения параметров вычислялись по схеме

(27)

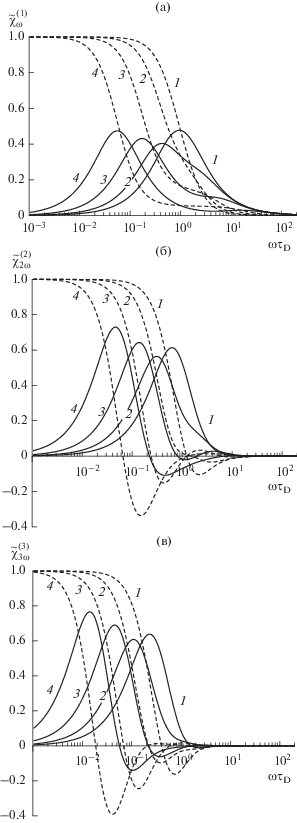
$\begin{gathered} \beta = {{\beta }_{0}}w,\,\,\,\,{{\beta }_{0}} = 1,\,\,\,\,q = {{q}_{0}}{{w}^{{{5 \mathord{\left/ {\vphantom {5 4}} \right. \kern-0em} 4}}}},\,\,\,\,{{q}_{0}} = 1000, \\ w = \left( {{\phi \mathord{\left/ {\vphantom {\phi {{{\phi }_{0}}}}} \right. \kern-0em} {{{\phi }_{0}}}}} \right) = 0.1,{\text{\;}}1,{\text{\;}}4,{\text{\;}}16, \\ \end{gathered} $

здесь $\phi $ – объемная доля полимера в растворе, а ${{\phi }_{0}}$ – некоторое нормирующее ее значение; указанные зависимости параметров $\beta $ и $q$ от $\phi $ пояснены ниже в формулах (33).

Рис. 2.

Частотные зависимости мнимой (сплошные линии) и действительной (штрихи) компонент динамических магнитных восприимчивостей ферроколлоида Джефриса: линейной (а), квадратичной (б), кубической (в); параметр упругости $\beta $ равен 0.1 (1), 1 (2), 4 (3) и 16 (4) при ${{q}_{0}} = {{10}^{3}},$ см. формулу (27).

8. ДИНАМИЧЕСКОЕ ДВУЛУЧЕПРЕЛОМЛЕНИЕ

Динамический ориентационный эффект (квадратичная восприимчивость $\chi _{{2\omega }}^{{(2)}}$) в ферроколлоиде хотя и обусловлен откликом наночастиц на приложенное поле, не может быть зафиксирован в магнитных измерениях, поскольку имеет квадрупольный, а не дипольный характер. Однако этот эффект можно прямо наблюдать в поляризационно-оптических измерениях, если только в ферроколлоиде присутствуют анизометричные частицы. Действительно, в указанной ситуации $\chi _{{2\omega }}^{{(2)}}$ является единственным источником оптической анизотропии, так как в отсутствие внешнего поля ферроколлоид оптически изотропен.

Рассмотрим появление оптической анизотропии в таком ферроколлоиде, принимая, что взвешенные в среде Джефриса наночастицы обладают некоторой степенью анизометрии, например, напоминают по форме вытянутые эллипсоиды вращения (сфероиды). Это предположение очень часто оправдывается на практике и обычно приписывается наличию в дисперсиях магнитных наночастиц их ассоциатов в виде коротких (2–3 частицы) цепочек. Тогда – ввиду того что диэлектрические проницаемости материала частиц и жидкой среды различны – ориентация частиц полем приводит к индуцированному ДЛП. Динамической переменной, ответственной за этот эффект, является тензор ориентации ансамбля частиц. Поскольку в настоящей модели магнитные моменты ${\mathbf{\mu }}$ считаются “вмороженными”, положим, что в каждой анизометричной частице вектор ${\mathbf{\mu }}$ направлен вдоль главной оси сфероида, к этому должна приводить магнитостатическая анизотропия формы. В этом случае степень ориентационного упорядочения ансамбля частиц удобно характеризовать параметром

(28)

${{S}_{{ik}}} = \frac{3}{2}\left( {\left\langle {{{e}_{i}}{{e}_{k}}} \right\rangle - \frac{1}{3}{{\delta }_{{ik}}}} \right).$

В изотропной системе все диагональные компоненты этого бесследового тензора обращаются в нуль, а в случае полной ориентации частиц его диагональная компонента в направлении поля равна единице.

Индуцированная оптическая анизотропия – разность показателей преломления необыкновенного и обыкновенного лучей – в ансамбле частиц при условии, что объемная концентрация последних не слишком велика, а характерный размер частиц меньше, чем длина волны $\lambda $ падающего света, выражается соотношением

(29)

$\Delta n = {{n}_{{\text{e}}}} - {{n}_{{\text{o}}}} = {{n}_{0}}A{{\phi }_{{\text{p}}}}{{S}_{{ik}}}{{h}_{i}}{{h}_{k}},$

где ${{n}_{0}}$ – коэффициент преломления среды в изотропном (при $H = 0$) состоянии, $A$ – коэффициент, зависящий от формы и относительной диэлектрической проницаемости частицы на частоте падающего света, ${{\phi }_{{\text{p}}}}$ – объемное содержание частиц в коллоиде (оно предполагается малым), ${\mathbf{h}} = \left( {0,0,1} \right)$ – единичный вектор приложенного магнитного поля.

Используя решение второго порядка системы уравнений (18) в поле $\xi \left( t \right) = \xi \cos \omega t$ для определения главной компоненты ориентационного тензора (28), имеем

(30)

$\begin{gathered} {{S}_{{ik}}}{{h}_{i}}{{h}_{k}} = {{S}_{{zz}}}\left( t \right) = \frac{1}{{30}}\xi _{0}^{2} \times \\ \times \,\,\left[ {P\left( \omega \right) + {\text{Re}}\left( {\tilde {\chi }_{{2\omega }}^{{(2)}}} \right)\cos 2\omega t + {\text{Im}}\left( {\tilde {\chi }_{{2\omega }}^{{(2)}}} \right){\text{sin}}2\omega t} \right] = \\ = \frac{1}{{30}}\xi _{0}^{2}\left[ {P\left( \omega \right) + \left| {\tilde {\chi }_{{2\omega }}^{{(2)}}} \right|{\text{cos}}\left( {2\omega t - \delta } \right)} \right], \\ \end{gathered} $

где

$\begin{gathered} \left| {\tilde {\chi }_{{2\omega }}^{{(2)}}} \right| = \sqrt {{{{\left[ {{\text{Re}}\left( {\tilde {\chi }_{{2\omega }}^{{(2)}}} \right)} \right]}}^{2}} + {{{\left[ {{\text{Im}}\left( {\tilde {\chi }_{{2\omega }}^{{(2)}}} \right)} \right]}}^{2}}} , \\ \delta = {\text{arctg}}\left[ {{{{\text{Im}}\left( {\tilde {\chi }_{{2\omega }}^{{(2)}}} \right)} \mathord{\left/ {\vphantom {{{\text{Im}}\left( {\tilde {\chi }_{{2\omega }}^{{(2)}}} \right)} {{\text{Re}}\left( {\tilde {\chi }_{{2\omega }}^{{(2)}}} \right)}}} \right. \kern-0em} {{\text{Re}}\left( {\tilde {\chi }_{{2\omega }}^{{(2)}}} \right)}}} \right]. \\ \end{gathered} $

В статическом случае ($\omega = 0$) величина ${{S}_{{zz}}}$ дается формулой (10).

Как и должно быть, ориентационный отклик содержит два вклада: не зависящую от времени функцию $P\left( \omega \right)$ и вторую гармонику основной частоты. Постоянная составляющая параметра ориентационного порядка – она находится из той же системы уравнений, что и зависимости (21), – имеет вид

(31)

$\begin{gathered} P\left( x \right) = \frac{{{{{\left( {1{\text{\;}} + {\beta \mathord{\left/ {\vphantom {\beta q}} \right. \kern-0em} q}} \right)}}^{2}} + {{x}^{2}}\left[ {1 - \frac{{{{\beta }^{2}}\left( {{{1 + 1} \mathord{\left/ {\vphantom {{1 + 1} {3q}}} \right. \kern-0em} {3q}}} \right)}}{{2\left( {{{1 + \beta } \mathord{\left/ {\vphantom {{1 + \beta } {3q}}} \right. \kern-0em} {3q}}} \right)}}} \right]}}{{{{{\left( {1 + {\beta \mathord{\left/ {\vphantom {\beta q}} \right. \kern-0em} q} - {{x}^{2}}} \right)}}^{2}} + {{x}^{2}}{{{\left( {2 + \tilde {\beta }} \right)}}^{2}}}}, \\ x \equiv \omega {{\tau }_{{\text{D}}}}. \\ \end{gathered} $

Подстановка (30) в (29) приводит к соотношению, которое описывает оптическую анизотропию вязкоупругого ферроколлоида в использованном приближении:

(32)

$\begin{gathered} \Delta n = \frac{1}{{30}}{{n}_{0}}A{{\phi }_{{\text{p}}}}\xi _{0}^{2} \times \\ \times \,\,\left[ {P\left( {\omega {{\tau }_{{\text{D}}}}} \right) + \left| {\tilde {\chi }_{{2\omega }}^{{(2)}}\left( {\omega {{\tau }_{{\text{D}}}}} \right)} \right|{\text{cos}}\left( {2\omega t - \delta } \right)} \right], \\ \end{gathered} $

где зависящие от частоты коэффициенты задаются формулами (21) и (31).

Рисунок 3 показывает частотные зависимости этих функций для тех же наборов параметров вязкоупругости $\beta $ и $q,$ что и на рис. 2.

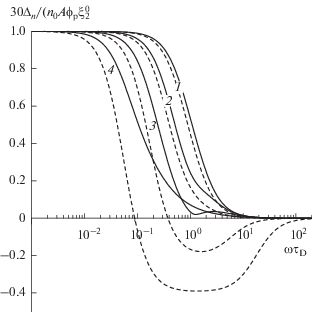
Рис. 3.

Частотные зависимости статической (штрихи) и динамической (сплошные линии) компонент оптической анизотропии (32) ферроколлоида Джефриса; параметр упругости $\beta $ равен 0.1 (1), 1 (2), 4 (3) и 16 (4) при ${{q}_{0}} = {{10}^{3}},$ см. формулу (27). Каждая штриховая линия всегда лежит левее сплошной, соответствующей тому же значению $\beta $.

9. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Из проведенного анализа следует, что в изучаемой модели частотные спектры всех динамических откликов определяются в основном величиной безразмерного параметра упругости $\beta = {K \mathord{\left/ {\vphantom {K {2T}}} \right. \kern-0em} {2T}}.$ Системы со слабо выраженной упругостью подобны обычным ньютоновским жидкостям. Рост упругости существенно изменяет спектры откликов: их основная компонента смещается в низкочастотную область, а высокочастотное “крыло” сдвигается по частоте вправо и при этом быстро уменьшается.

Связь параметров модели Джефриса со свойствами полимера

Рассмотрим, для примера, в качестве среды-носителя полуразбавленный раствор линейного полимера в хорошем растворителе. Скейлинговая теория растворов полимеров [28] позволяет связать реологические параметры изучаемой модели с основными физическими характеристиками такой среды – объемной долей полимера $\phi $ и числом звеньев макромолекулы $N.$ Согласно этой теории, каждая макромолекула в растворе представляет собой цепочку блобов – участков, состоящих из $g$ звеньев (мономеров размера $a$), взаимодействующих только между собой. Размер блоба $\rho \sim a{{g}^{{{3 \mathord{\left/ {\vphantom {3 5}} \right. \kern-0em} 5}}}}\sim a{{\phi }^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 4}} \right. \kern-0em} 4}}}}$ определяет по порядку величины среднее расстояние между фрагментами макромолекул в растворе.

В полуразбавленном растворе конформация макромолекул слабо зависит от концентрации растворителя. В этих условиях число звеньев между зацеплениями ${{N}_{{\text{a}}}}\sim g{{N}_{{\text{e}}}}$ не должно зависеть от объемной концентрации полимера [28]. Поскольку упругость такому раствору придает сетка мгновенных зацеплений составляющих ее гауссовых цепочек, содержащих ${{N}_{{\text{e}}}}$ блобов, то энтропийный модуль упругости системы по порядку величины составляет

$G\sim \frac{T}{{{{\rho }^{3}}{{N}_{{\text{e}}}}}}\sim \frac{{gT}}{{{{\rho }^{3}}{{N}_{{\text{a}}}}}}\sim \frac{\phi }{{{{a}^{3}}{{N}_{{\text{a}}}}}}T.$

Тепловое движение макромолекулы в полуразбавленном растворе описывается как одномерная диффузия цепочки блобов в трубке зацеплений, имеющей диаметр $d~\sim \rho N_{{\text{e}}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}$ и длину $L~\sim \left( {{N \mathord{\left/ {\vphantom {N {g{{N}_{{\text{e}}}}}}} \right. \kern-0em} {g{{N}_{{\text{e}}}}}}} \right)d.$ Коэффициент диффузии оценивается по формуле Эйнштейна, в которой коэффициент трения пропорционален числу блобов, составляющих цепочку, и вязкости растворителя ${{{\eta }}_{{\text{S}}}},$ что дает

${{D}_{{\text{t}}}}\sim \frac{T}{{\rho {{\eta }_{{\text{S}}}}\left( {{N \mathord{\left/ {\vphantom {N g}} \right. \kern-0em} g}} \right)}}\sim \frac{T}{{a{{\eta }_{{\text{S}}}}N}}{{\phi }^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}.$

Время выползания макромолекулы из трубки зацеплений или, иначе, время жизни узлов квазисетки определяется соотношением

$\tau \sim \frac{{{{L}^{2}}}}{{{{D}_{{\text{t}}}}}}\sim \frac{{{{\eta }_{{\text{S}}}}}}{{T{{N}_{{\text{e}}}}}}{{\left( {\frac{{\rho N}}{g}} \right)}^{3}}\sim \left( {\frac{{{{a}^{3}}{{\eta }_{{\text{S}}}}}}{T}} \right)\frac{{{{N}^{3}}}}{{{{N}_{{\text{a}}}}}}{{\phi }^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}},$

а обусловленная таким механизмом запаздывания вязкость есть

${{\eta }_{{\text{M}}}}\sim \tau G\sim {{\eta }_{{\text{S}}}}\frac{{{{N}^{3}}}}{{{{g}^{3}}N_{{\text{e}}}^{2}}}\sim {{\eta }_{{\text{S}}}}\frac{{{{N}^{3}}}}{{N_{{\text{a}}}^{2}}}{{\phi }^{{{5 \mathord{\left/ {\vphantom {5 4}} \right. \kern-0em} 4}}}}.$

Используя приведенные выше соотношения, безразмерные реологические параметры среды Джефриса, моделирующей полуразбавленный раствор полимера, можно представить в виде

(33)

$\begin{gathered} \beta = \frac{K}{{2T}} = \frac{{3GV}}{T}\sim \left( {\frac{V}{{{{a}^{3}}{{N}_{{\text{a}}}}}}} \right)\phi ,\,\,\,\,q = \frac{{{{{\eta }}_{{\text{M}}}}}}{{{{{\eta }}_{{\text{N}}}}}}\sim \frac{{{{N}^{3}}}}{{N_{{\text{a}}}^{2}}}{{\phi }^{{{5 \mathord{\left/ {\vphantom {5 4}} \right. \kern-0em} 4}}}}, \\ \frac{\beta }{q} = \frac{{{{\tau }_{{\text{D}}}}}}{{{{\tau }_{{\text{M}}}}}}\sim \frac{V}{{{{a}^{3}}}}\left( {\frac{{{{N}_{{\text{a}}}}}}{{{{N}^{3}}}}} \right){{\phi }^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 4}} \right. \kern-0em} 4}}}} \ll 1, \\ \end{gathered} $

здесь $V$ – объем магнитной наночастицы.

Эти формулы устанавливают, что по мере роста объемной доли полимера параметры модели Джефриса $\beta $ и $q$ увеличиваются, но при этом всегда выполняется соотношение ${\beta \mathord{\left/ {\vphantom {\beta q}} \right. \kern-0em} q} \ll 1.$ Отметим также, что в то время как максвелловская вязкость ${{{\eta }}_{{\text{M}}}}$ быстро растет с длиной макромолекул, параметр упругости практически не чувствителен к этой характеристике.

Подставляя $\beta $ из формул (33) в выражения (24) для “медленного” и “быстрого” времен релаксации, имеем

(34)

$\begin{gathered} {{\tau }_{{\text{s}}}}\sim \frac{V}{{{{a}^{3}}{{N}_{{\text{a}}}}}}\phi {{\tau }_{{\text{D}}}}\sim \frac{{3{{\eta }_{{\text{N}}}}{{V}^{2}}}}{{{{a}^{3}}{{N}_{{\text{a}}}}T}}\phi ,\,\,\,\,{{\tau }_{{\text{f}}}}\sim \frac{{{{a}^{3}}{{N}_{{\text{a}}}}}}{{\phi V}}{{\tau }_{{\text{D}}}}\sim \\ \sim \frac{{3{{{\eta }}_{{\text{N}}}}{{a}^{3}}{{N}_{{\text{a}}}}}}{{\phi T}}, \\ \end{gathered} $

Оценки (34) показывают, что оба эффективных времени имеют диффузионное происхождение и сильно зависят от концентрации полимера в растворе. Медленное время ${{\tau }_{{\text{s}}}}$ увеличивается c $\phi $ и квадратично возрастает с увеличением размера частицы-зонда. Очевидно, что чем крупнее частица, тем больше затруднений она встречает при вращательной диффузии, связанной с преодолением сопротивления квазисетки.

Уменьшение быстрого времени ${{\tau }_{{\text{f}}}}$ с ростом концентрации полимера обусловлено, скорее всего, тем, что с увеличением плотности системы амплитуда вращательных движений частицы, не деформирующих квазисетку, уменьшается. В самом деле, с ростом $\phi $ угловые перемещения, при которых частица взаимодействует только с растворителем – ньютоновской жидкостью с вязкостью ${{\eta }_{{\text{N}}}},$ – становятся все более ограниченными.

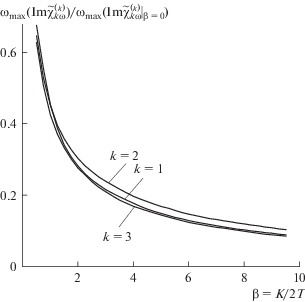
Иллюстрацией этих выводов может служить рис. 2a, где приведены частотные спектры действительной и мнимой частей линейной восприимчивости $\tilde {\chi }_{\omega }^{{(1)}}$ для нескольких значений объемной доли полимера, которую мы характеризуем параметром $w,$ см. формулы (27). Видно, что с увеличением плотности системы (с ростом параметра упругости $\beta $) возрастает роль частотной дисперсии, связанной с медленным эффективным временем ${{\tau }_{{\text{s}}}}.$ Обусловленный ею (главный) пик спектра поглощения ${\text{Im}}\tilde {\chi }_{\omega }^{{(1)}}$ смещается в низкочастотную область, как показано на рис. 4. Там же приведены зависимости от $\beta $ частот главных максимумов высших гармоник восприимчивости, см. кривые на рис. 2б и 2в. Видно что, в нормированном виде все кривые оказываются весьма близкими. Вопрос о том, сохранится ли это сходство в точном решении задачи, однако, открыт; напомним, что здесь мы используем упрощенную модель – метод эффективного поля. Тем не менее, можно с уверенностью говорить о том, что в качественном отношении снижение частоты максимального поглощения – установленный факт.

Рис. 4.

Зависимости частот главных максимумов мнимых частей динамических восприимчивостей (показаны на рис. 2) от параметра упругости.

В ферроколлоидах с развитой упругостью ($\beta \gg 1$) на правом крыле линии поглощения ${\text{Im}}\tilde {\chi }_{\omega }^{{(1)}}$ проявляется локальный максимум, обусловленный быстрой релаксацией с временем ${{\tau }_{{\text{f}}}}.$ Однако его высота с увеличением упругости системы убывает (последовательность кривых 1–4 на рис. 2a); как показывает второе слагаемое в правой части формулы (20), это происходит по закону $ \propto {1 \mathord{\left/ {\vphantom {1 \beta }} \right. \kern-0em} \beta }{\text{.}}$ Влияние высокочастотной моды релаксации уменьшается также и с ростом порядка рассматриваемой гармоники. Действительно, согласно асимптотическим формулам (22) и (23), высокочастотные вклады в восприимчивости высших порядков убывают как $ \propto {1 \mathord{\left/ {\vphantom {1 {{{\beta }^{2}}}}} \right. \kern-0em} {{{\beta }^{2}}}}$ и $ \propto {1 \mathord{\left/ {\vphantom {1 {{{\beta }^{3}}}}} \right. \kern-0em} {{{\beta }^{3}}}}$ для ${\text{Im}}\tilde {\chi }_{{2\omega }}^{{(2)}}$ и ${\text{Im}}\tilde {\chi }_{{3\omega }}^{{(3)}}$ соответственно.

Сопоставление с экспериментом

Выявление эффектов вязкоупругости требует весьма точных измерений, что чрезвычайно трудоемко. Однако анализ опубликованных данных позволяет обнаружить в них доводы в пользу некоторых из представленных выше предсказаний. Так, в экспериментальных работах [3, 4] с помощью магнитожестких нанозондов изучались реологические свойства водных растворов полиэтиленгликоля и желатина. Были получены спектры линейной восприимчивости в широком интервале частот: от единиц Гц до нескольких сотен кГц. В этих работах было обнаружено быстрое смещение спектров в низкочастотную область по мере увеличения концентрации и длины макромолекул [3], а также плотности сшивок [4].

Рассмотрение графиков рис. 2 указывает на еще одну общую тенденцию: высота главного максимума мнимых частей всех восприимчивостей – ${\text{Im}}{{\chi }_{\omega }},$ ${\text{Im}}{{\chi }_{{2\omega }}},$ ${\text{Im}}{{\chi }_{{3\omega }}}$ – с ростом $\beta $ ведет себя немонотонно: сначала уменьшается, а затем растет. Аналогичное поведение характерно и для вещественных компонент восприимчивостей – ${\text{Re}}{{\chi }_{{2\omega }}}$ и ${\text{Re}}{{\chi }_{{3\omega }}}$ (см. рис. 2б и 2в); у этих функций немонотонная зависимость от $\beta $ присуща глубине минимума, локализованного в отрицательной области. Указанное свойство отсутствует только у ${\text{Re}}{{\chi }_{\omega }},$ поскольку эта функция неотрицательна.

В работе [29] найдено именно такое поведение мнимой части линейной динамической магнитной восприимчивости (вещественная часть не приведена). Функция ${\text{Im}}{{\chi }_{\omega }}\left( \omega \right)$ измерялась для наносуспензий CoFe₂O₄ (магнитожесткий феррит), частицы которых были покрыты полиэтиленгликолем. Вязкоупругую среду, окружающую частицы, создавали, добавляя в раствор бычий сывороточный альбумин (БСА). Полиэтиленгликоль связывает молекулы БСА и, тем самым, формирует на частице биополимерную “корону”. Таким образом, частица феррита кобальта, поворотные осцилляции которой возбуждаются зондирующим магнитным полем, совершает движение внутри вязкоупругой короны, размер и плотность которой растут с увеличением концентрации БСА.

ВЫВОДЫ

Рассмотрен отклик вязкоупругого ферроколлоида на слабое переменное (зондирующее) магнитное поле. Ферроколлоид моделируется как ансамбль невзаимодействующих магнитожестких наночастиц, взвешенных в неньютоновской жидкости, имеющей реологию среды Джефриса. На основе уравнений Ланжевена, описывающих вращательное броуновское движение наночастицы, получена система моментных уравнений, определяющих средние (наблюдаемые) характеристики системы: динамическую намагниченность и кинетику ориентации. Система моментных уравнений решена в приближении эффективного поля. Частотные спектры всех изученных откликов – от линейного до кубического – представлены в аналитическом виде. Показано, что эффекты механического запаздывания (релаксация напряжений), обусловленные вязкоупругостью среды-носителя коллоидных частиц, приводят к появлению специфических особенностей в спектрах всех порядков. В частности, рост упругости среды приводит к смещению главного максимума в низкочастотную область и к немонотонному изменению высоты этого пика. В предположении, что жидкость Джефриса представляет собой полуразбавленный раствор гибкоцепного полимера, найдена связь реологических параметров этой феноменологической модели со структурными характеристиками раствора: числом мономеров в макромолекуле, размером блоба, числом зацеплений физической сетки.

Список литературы

Wilhelm C., Browaeys J., Ponton A., Bacri J.-C. // Phys. Rev. E. 2003. V. 67. Art. no. 011504.
Chevry L., Sampathkumar N.K., Cebers A., Berret J.-F. // Phys. Rev. E. 2013. V. 88. Art. no. 062306.
Reoben E., Roeder L., Teusch S., Effertz M., Dieters U.K., Schmidt A.M. // Colloid Polymer Sci. 2014. V. 292. P. 2013.
Hess M., Roeben E., Rochels P., Zylla M., Webers S., Wende H., Schmidt A.M. // Phys. Chem. Chem. Phys. 2019. V. 21. P. 26525.
Nikitin P.I., Vetoshko P.M., Ksenevich T.I. // J. Magn. Magn. Mater. 2007. V. 311. P. 455.
Nikitin M.P., Torno M., Chen H., Rosengart A. // J. A-ppl. Phys. 2008. V. 103. Art. no. 07A304.
Nikitin M.P., Orlov A.V., Sokolov I.L., Minakov A.A., Nikitin P.I., Ding J., Bader S.D., Rozhkova E.A., Novosad V. // 2018. Nanoscale. V. 10. P. 11642.
Gleich B., Weizenecker J. // Nature. 2005. V. 435. P. 1214.
Weizenecker J., Gleich B., Rahmer J., Dahnke H., Borgert J. // Phys. Med. Biol. 2009. V. 54. P. L1.
Panagiotopoulos N., Duschka R., Ahlborg M., Dringout G., Debbeler C., Graeser M., Keathner C., Lüdtke-Buzug K., Medimagh H., Steizner J., Buzug T., Barkhausen J., Vogt F.M., Haegele J. // Int. J. Nanomedicine. 2015. V. 10. P. 3097.
Dumas J., Bacri J.-C. // J. Phys. Lett. – Paris. 1980. V. 41. P. 279.
Bacri J.-C., Dumas J., Gorse D., Perzynski R., Salin D. // J. Phys. Lett. – Paris. 1985. V. 46. P. 1199.
Wilhelm C., Gazeau F., Roger J., Pons J.N., Salis M.F., Perzynski R., Bacri J.-C. // Phys. Rev. E. 2002. V. 65. Art. no. 031404.
Malkin A.Ya., Isayev A.I. Rheology: Concepts, Methods, Applications. Toronto: ChemTech Publ., 2005.
Oswald P. Rheophysics: The Deformation and Flow of Matter. Cambridge: Cambridge University Press, 2009.
Райхер Ю.Л., Русаков В.В. // Журн. эксперим. теор. физики. 2010. Т. 138. С. 998.
Rusakov V.V., Raikher Yu.L., Perzynski R. // Math. Model. Nat. Phenom. 2015. V. 10. № 4. P. 1.
Rusakov V.V., Raikher Yu.L., Perzynski R. // Soft Matter. 2013. V. 9. P. 10857.
Gardel M.L., Valentine M.T., Weitz D.A. // Microscale Diagnostic Techniques. Ed. by Breuer K. Heidelberg: Springer-Verlag, 2005. P. 1.
Raikher Yu.L., Rusakov V.V., Coffey W.T., Kalmykov Yu.P. // Phys. Rev. E. 2001. V. 63. Art. no. 031402.
Coffey W.T., Kalmykov Yu.P. The Langevin Equation. 3^rd ed. Singapore: World Scientific, 2012.
Борн М., Вольф Э. Основы оптики. 2 изд. М.: Наука, 1973.
Русаков В.В., Райхер Ю.Л. // Коллоид. журн. 2017. Т. 79. С. 212.
Русаков В.В., Райхер Ю.Л. // Коллоид. журн. 2020. Т. 82. С. 204.
Raikher Yu.L., Shliomis M.I. // Relaxation Phenomena in Condensed Matter. Ed. by Coffey W. Adv. Chem. Phys. Ser. N.Y.: Wiley, 1994. V. 87. P. 595.
Raikher Yu.L., Stepanov V.I. // Adv. Chem. Phys. Ser. N.Y.: Wiley, 2004. V. 129. P. 419.
Климонтович Ю.Л. Статистическая теория открытых систем. М.: Янус-К, 1999.
Гросберг А.Ю., Хохлов А.Р. Полимеры и биополимеры с точки зрения физики. Долгопрудный: Издательский дом “Интеллект”, 2010.
Bohórquez A.C., Yang C., Bejleri D., Rinaldi C. // J. Colloid Interface Sci. 2017. V. 506. P. 393.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Коллоидный журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал