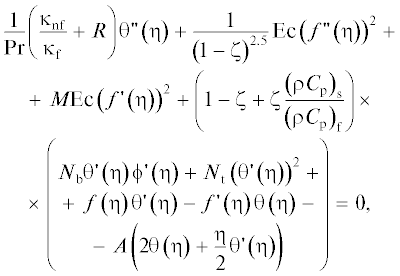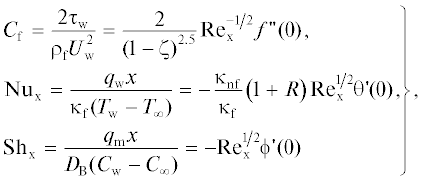Коллоидный журнал, 2021, T. 83, № 4, стр. 466-478

1. ВВЕДЕНИЕ

Суспензия наноразмерных частиц металлов, оксидов, углеродных нанотрубок или карбидов в некоторой базовой жидкости, такой как этиленгликоль, масло или вода, называется наножидкостью. Наножидкости обладают свойством усиливать процесс теплопередачи, который имеет множество применений в машиностроении и промышленных технологиях. Идея повышения теплопроводности жидкостей путем диспергирования в них твердых наноразмерных частиц была впервые предложена в работе Чоя и др. [1]. Позже в работе [2] был проведен подробный теоретический анализ инерции, броуновской диффузии, диффузиофореза, термофореза и эффекта Магнуса для наножидкостей. Исследование естественной конвекции наножидкостей было продолжено в работах [3] и [4] для случаев горизонтальных концентрических колец и неглубокой полости соответственно. Авторы объяснили влияние числа Рэлея в сочетании с теплопроводностью и объемной долей твердой фазы в наножидкости на характеристики теплопередачи. Впоследствии Хамад [5] учел влияние внешнего магнитного поля на течение и теплопередачу при естественной конвекции наножидкостей, а затем в работе [6] был исследован эффект нестационарности в случае смешанной конвекции. Термофорез и броуновское движение играют важную роль в изучении течения и температуры наножидкостей. Влияние этих явлений, связанных с выделением тепла, на течение наножидкости вблизи растягивающегося листа обсуждалось также в работе [7]. Позже многие авторы [8–10] расширили исследование течения наножидкостей, включив в него эффект излучения. В работе [11] был рассмотрен плоский канал с одной пористой стенкой и проанализировано магнитогидродинамическое (МГД) течение наножидкости в нем. Решение было получено методом Галеркина, после чего авторы [11] пришли к выводу, что использование наножидкости на основе наночастиц меди и этиленгликоля дает максимальную скорость среди всех рассмотренных наножидкостей для различных моделей теплопроводности и динамической вязкости. После этого авторы [12] расширили свое исследование [10], рассмотрев течение с точкой торможения жидкости в пористой среде над растягивающимся/сжимающимся листом. В работе [13] было проведено сравнительное изучение зависящего от времени течения различных наножидкостей вдоль вертикальной проницаемой растягивающейся поверхности. Авторы с помощью численного счета показали, что среди всех рассмотренных наножидкостей поверхностное трение было максимальным для наножидкости CuO–вода и минимальным для наножидкости Al₂O₃–вода. Гадам и Моради [14] модифицировали упомянутую работу [12], учтя эффекты смешанной конвекции. Позже Хан и Азам [15] использовали наножидкость Карро и объяснили зависящий от времени механизм тепломассопереноса в потоке с помощью модели Буонджорно [2]. В дополнение к этому авторы работы [16] сделали попытку объяснить явление конвективного охлаждения наножидкостями на основе воды и частиц Al₂O₃, TiO₂ и CuO. Недавно в статье [17] были применены дробные производные Капуто и Капуто–Фабрицио для анализа химической реакции и ньютоновских эффектов нагрева в МГД-потоке наножидкости. В нашей предыдущей работе [18] было исследовано влияние источника/поглотителя тепла на смешанное конвективное МГД-течение с точкой торможения вдоль вертикального растягивающегося листа.

Целью данной работы является анализ зависящего от времени МГД-течения наножидкостей CuO, Al₂O₃, TiO₂−вода по проницаемой вертикально растягивающейся поверхности с учетом процессов тепло- и массообмена. При сравнительном изучении этих наножидкостей кроме растяжения поверхности учитывается влияние вязкой диссипации, излучения, смешанной конвекции и других явлений.

2. МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧИ

Рассмотрим нестационарное двумерное смешанно-конвективное ламинарное МГД-течение вязкой несжимаемой наножидкости вдоль растягивающейся поверхности. Предполагается, что поверхность проницаема вследствие ее пористости. Поверхность берется вдоль оси x, ось y нормальна к ней, а внешнее зависящее от времени магнитное поле напряженности B прикладывается в направлении оси y. Компоненты скорости в направлениях x и y равны u и v соответственно. Потоки жидкости, тепла и массы считаются установившимися в течение времени $t < 0.$ С использованием приведенных выше предположений уравнения неразрывности, импульса, энергии и конвективной диффузии задаются следующим образом (см. [7, 9, 15]):

где ${{({{\beta }_{{\text{t}}}}{\text{)}}}_{{{\text{nf}}}}}$ и ${{({{\beta }_{{\text{c}}}}{\text{)}}}_{{{\text{nf}}}}}$ являются коэффициентами теплового и концентрационного расширения соответственно, ${{\mu }_{{{\text{nf}}}}}$ и ${{\rho }_{{{\text{nf}}}}}$ – вязкость и плотность наножидкости, ${{K}_{{\text{p}}}}$ – проницаемость пористой среды, $B = {{{{B}_{0}}} \mathord{\left/ {\vphantom {{{{B}_{0}}} {\sqrt {1 - ct} }}} \right. \kern-0em} {\sqrt {1 - ct} }}$ – внешнее магнитное поле, $g$ – ускорение свободного падения, $\sigma $ – электропроводность, ${{\kappa }_{{{\text{nf}}}}}$ – эффективная теплопроводность, ${{(\rho {{C}_{{\text{p}}}}{\text{)}}}_{{{\text{nf}}}}}$ – теплоемкость, $T$ и $C$ – температура и концентрация наножидкости соответственно, ${{D}_{{\text{B}}}}$ и ${{D}_{{\text{T}}}}$ – броуновский и термодиффузионный коэффициенты, $\tau = {{{{{(\rho {{C}_{{\text{p}}}}{\text{)}}}}_{{\text{s}}}}} \mathord{\left/ {\vphantom {{{{{(\rho {{C}_{{\text{p}}}}{\text{)}}}}_{{\text{s}}}}} {{{{(\rho {{C}_{{\text{p}}}}{\text{)}}}}_{{\text{f}}}}}}} \right. \kern-0em} {{{{(\rho {{C}_{{\text{p}}}}{\text{)}}}}_{{\text{f}}}}}}$ – отношение эффективной теплоемкости материала наночастиц к эффективной теплоемкости жидкой среды, ${{T}_{\infty }}$ и ${{C}_{\infty }}$ представляют температуру и концентрацию наножидкости вдали от проницаемой поверхности соответственно.

Параметры наножидкости задаются следующими формулами (см. [19]):

где объемная доля твердой фазы в наножидкости обозначена как ζ, и для обычных ньютоновских жидкостей ее значение лежит в диапазоне от 0 до 0.2. Характеристики жидкой и твердой фаз обозначаются нижними индексами “f” и “s” соответственно. В табл. 1 приведены теплофизические свойства наножидкостей (см. [3, 4, 6]). В настоящем исследовании аппроксимация для κ_nf ограничена сферическими наночастицами.

Граничные условия для физической задачи имеют вид (см. [6, 13]):

где $u = {{U}_{{\text{w}}}}\left( {x,t} \right)$ есть скорость растяжения поверхности а ${{{v}}_{{\text{w}}}}\left( t \right)$ – скорость массопереноса (фильтрации) через растягивающуюся поверхность, ${{C}_{{\text{w}}}}\left( {x,t} \right)$ и ${{T}_{{\text{w}}}}\left( {x,t} \right)$ – поверхностные концентрация и температура соответственно. Здесь a и c – положительные константы, имеющие размерность обратного времени и $1 - ct > 0.$ Постоянные b и d имеют размерности температура/длина и концентрация/длина соответственно.

В диффузионном приближении Росселанда излучательный тепловой поток задается формулой ${{q}_{{\text{r}}}} = - \frac{4}{3}\frac{{{{\sigma }_{{\text{s}}}}}}{{k{\text{*}}}}\frac{{\partial {{T}^{4}}}}{{\partial y}},$ где $k{\text{*}}$ и ${{\sigma }_{{\text{s}}}}$ являются средним коэффициентом поглощения Росселанда и постоянной Стефана–Больцмана соответственно. Здесь градиент температуры в потоке считается достаточно малым, так что ${{T}^{4}}$ выражается как линейная функция T, т.е. ${{T}^{4}} \cong 4T_{\infty }^{3}T - 3T_{\infty }^{4}.$ Следовательно, градиент излучательного теплового потока становится равным $\frac{{\partial {{q}_{{\text{r}}}}}}{{\partial y}} = - \frac{{16{{\sigma }_{{\text{s}}}}T_{\infty }^{3}}}{{3k{\text{*}}}}\frac{{{{\partial }^{2}}T}}{{\partial {{y}^{2}}}}.$ Поэтому уравнение энергии (3) сводится к следующему:

3. МЕТОД РЕШЕНИЯ И ЕГО ВАЛИДАЦИЯ

Чтобы получить решение уравнений (1), (2), (4) и (7) с граничными условиями (6), будем использовать следующее преобразование Ли (см. [6, 13]):

При этом уравнение неразрывности автоматически удовлетворяется, а уравнения импульса, энергии и конвективной диффузии приобретают следующий вид:

где производные по $\eta $ обозначены штрихами, Pr – число Прандтля, R – параметр излучения, A – параметр нестационарности, K – параметр проницаемости, M – магнитный параметр, ${\text{Ri}}$ – число Ричардсона (см. [10]), ${\text{Ec}}$ – число Эккерта, ${\text{Le}}$ – число Льюиса, ${{N}_{{\text{t}}}}$ – термофоретический параметр, ${{N}_{{\text{b}}}}$ – параметр броуновского движения, $\xi $ – отношение концентрационной и термической плавучестей, υ_f – кинематическая вязкость. Для уточнения физической значимости числа Льюиса можно воспользоваться ссылками [7, 9, 15].

Соответствующие граничные условия сводятся к виду

где ${{f}_{{\text{w}}}}$ – безразмерный параметр, характеризующий скорость фильтрации.

Локальный поверхностный коэффициент трения, числа Нуссельта и Шервуда даются выражениями

где напряжение сдвига на стенке ${{\tau }_{{\text{w}}}},$ тепловой поток ${{q}_{{\text{w}}}}$ и поток массы ${{q}_{{\text{m}}}}$ равны соответственно а ${\text{R}}{{{\text{e}}}_{{\text{x}}}}\left( { = \frac{{{{U}_{{\text{w}}}}x}}{{{{\upsilon }_{{\text{f}}}}}}} \right)$ представляет собой локальное число Рейнольдса.

Уравнения (9)–(11) являются сильно нелинейными связанными дифференциальными уравнениями с граничными условиями (12). Для численного решения этих уравнений используется метод Рунге–Кутты четвертого порядка в сочетании с методом стрельбы. Для этого дифференциальные уравнения более высокого порядка с помощью метода декомпозиции сводятся к системе дифференциальных уравнений первого порядка:

При этом соответствующие граничные условия приобретают вид где Для решения этих уравнений требуются значения ${{f}_{1}},$ ${{f}_{2}},$ ${{f}_{3}},$ ${{f}_{4}},$ ${{f}_{5}},$ ${{f}_{6}}$ и ${{f}_{7}}$ при $\eta = 0.$ Так как в рассматриваемой задаче ${{f}_{3}},$ ${{f}_{5}}$ и ${{f}_{7}}$ не известны при $\eta = 0,$ то, согласно методу стрельбы, первоначальные приближения для ${{f}_{3}},$ ${{f}_{5}}$ и ${{f}_{7}}$ принимаются равными ${{s}_{1}},$ ${{s}_{2}}$ и ${{s}_{3}}$ соответственно. Пошаговое интегрирование осуществляется с помощью программного обеспечения MATLAB. Для валидации вычислительного метода локальные значения числа Нуссельта для наножидкостей (при значении $ - \theta {\kern 1pt} {\text{'}}(0)$ для чистой воды) сравнивались с данными Грубки и Боббы [20], Исхака и др. [21], Мадхи [6] и Фрейдонимехра и др. [13]. Из табл. 2 следует, что полученные нами результаты находятся в хорошем согласии с ранее опубликованными данными.

4. РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

В этом разделе поведение скорости, температуры и концентрации наножидкостей на пористой растягивающейся поверхности в зависимости от различных физических параметров представлено на рис. 1–23. Полученные численно значения коэффициента поверхностного трения, числа Нуссельта и числа Шервуда для исследованных наножидкостей в зависимости от выбранных параметров представлены в табл. 3–5.

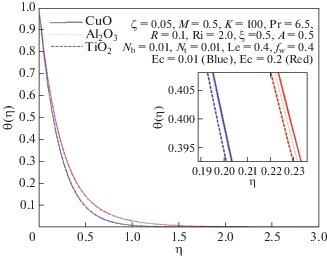
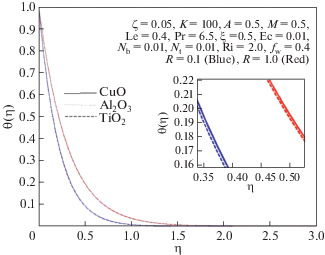
На рис. 1, 2 и 3 показано влияние параметра нестационарности на скорость, температуру и концентрацию наножидкости. Увеличение параметра нестационарности уменьшает скорость растяжения поверхности, что приводит к падению скорости жидкости, температуры и концентрации. Эти эффекты вызывают уменьшение коэффициента поверхностного трения и увеличение чисел Нуссельта и Шервуда.

Рисунки 4 и 5 показывают, что скорость и температура наножидкости повышаются из-за тепла, генерируемого вязкой диссипацией. Рост числа Эккерта увеличивает скорость переноса энергии в наножидкость, что и приводит к росту ее скорости и температуры. Как следствие, растет коэффициент поверхностного трения, в то время как число Нуссельта уменьшается.

Повышение параметра проницаемости увеличивает скорость жидкости, поскольку имеет место обратное влияние этого параметра на температуру и концентрацию, как это видно на рис. 6, 7 и 8. Физическая причина, стоящая за этим явлением, заключается в том, что увеличение параметра проницаемости соответствует увеличению пористости, что приводит к возрастанию потока жидкости, в результате скорость увеличивается, а температура и концентрация наножидкости уменьшаются. Увеличение скорости вызывает большее поверхностное трение, уменьшение температуры и концентрации наножидкости, повышает разность температур и концентраций вблизи поверхности и ядре потока, поэтому скорость тепломассопереноса на поверхности увеличивается. Это приводит к увеличению коэффициента поверхностного трения, числа Нуссельта и числа Шервуда.

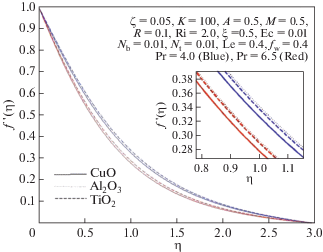
На рис. 9 и 10 показано, что увеличение числа Прандтля приводит к падению скорости и температуры жидкости, за счет чего уменьшается поверхностное трение, а число Нуссельта увеличивается, что согласуется с данными, приведенными в табл. 3 и 4 (см. ниже). При увеличении числа Прандтля проводимость жидкости падает, а вязкость увеличивается. Это приводит к падению скорости и температуры жидкости вблизи фильтрующей поверхности. Благодаря снижению скорости поверхностное трение уменьшается, а вследствие роста перепада температуры увеличивается число Нуссельта.

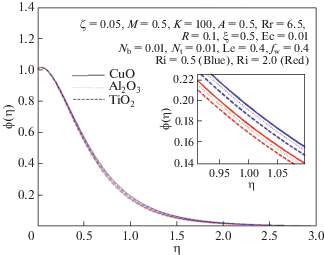
Рисунки 11, 12 и 13 показывают, что большее число Ричардсона приводит к большей скорости наножидкости и понижает ее температуру и концентрацию вблизи поверхности. Это происходит потому, что с увеличением числа Ричардсона уменьшается вязкость. В результате увеличивается скорость жидкости и из-за меньшего сопротивления потоку температура и концентрация снижаются. Увеличивающаяся скорость вызывает большее поверхностное трение, а рост разности температур и концентраций приводит к увеличению числа Нуссельта и числа Шервуда.

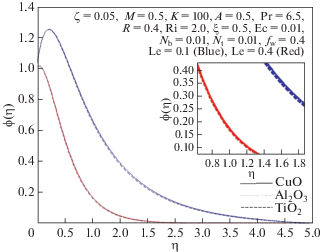
Увеличение числа Льюиса вызывает повышение температуры наножидкости и снижает ее концентрацию, что видно на рис. 14 и 15. Большему числу Льюиса соответствуют меньший коэффициент броуновской диффузии и больший коэффициент термодиффузии, что и приводит к указанным эффектам. Разница температур уменьшается из-за повышения температуры вблизи поверхности, и из-за этого уменьшается число Нуссельта. В то же время бóльшая разность концентраций оказывает обратное влияние на число Шервуда – оно возрастает.

Из рис. 16 и 17 следует, что скорость и температура жидкости возрастают при увеличении параметра излучения, что соответствует большему количеству излучаемого тепла, потребляемого водной фазой наножидкости на нагреваемой поверхности. В результате увеличиваются скорость и температура текущей жидкости, что приводит к увеличению коэффициента поверхностного трения и соответственно уменьшению числа Нуссельта.

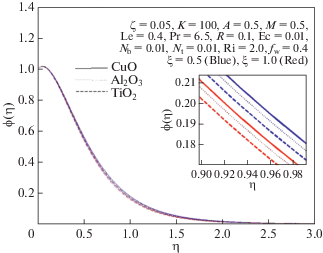
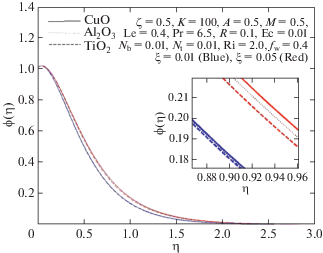
На рис. 18, 19 и 20 показано, что скорость жидкости увеличивается, а ее температура и концентрация вблизи поверхности уменьшаются с ростом отношения концентрационной и термической плавучестей. Эти эффекты дают более высокие значения коэффициента поверхностного трения, чисел Нуссельта и Шервуда.

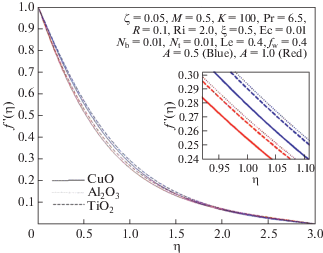
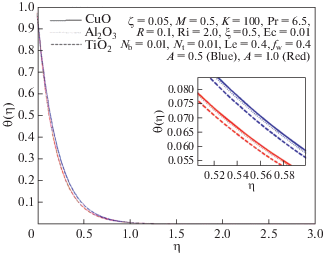
На рис. 21, 22 и 23 показано, что при увеличении объемной доли твердой фазы в наножидкости вблизи фильтрующей поверхности температура и концентрация повышаются, а скорость уменьшается в случае наножидкости CuO–вода и увеличивается для наножидкостей Al₂O₃–вода и TiO₂–вода. За счет увеличения объемной доли твердой фазы число Нуссельта уменьшается, а число Шервуда увеличивается. С физической точки зрения это объясняется тем, что теплопроводность наножидкости возрастает.

Таблица 1 показывает, что наночастицы Al₂O₃ имеет минимальную плотность, а CuO – максимальную. Вследствие этого различия в плотности наночастиц, как следует из приведенных выше рисунков, скорость максимальна для наножидкости Al₂O₃–вода и минимальна для наножидкости CuO–вода. Аналогично, CuO и TiO₂ имеют максимальную и минимальную теплопроводность соответственно. Поэтому температура наножидкости CuO–вода максимальна, а наножидкости TiO₂–вода – минимальна, как это видно на рис. 22.

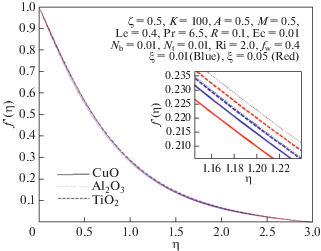
Согласно данным табл. 3, коэффициент поверхностного трения $f{\kern 1pt} ''(0)$ растет за счет увеличения параметра проницаемости, параметра излучения, числа Ричардсона, отношения концентрационной и термической плавучестей и числа Эккерта и уменьшается с увеличением числа Льюиса, числа Прандтля и параметра нестационарности. Также следует отметить, что выбор наночастиц Al₂O₃ приводит к максимальному значению коэффициента поверхностного трения, в то время как выбор наночастиц CuO дает минимальное его значение. Это объясняется тем, что, как отмечалось выше, CuO и Al₂O₃ имеют соответственно максимальное и минимальное значение плотности среди рассматриваемых типов наночастиц.

Из табл. 4 следует, что из-за увеличения параметра нестационарности, параметра проницаемости, числа Прандтля, числа Ричардсона и отношения концентрационной и термической плавучестей число Нуссельта $ - \theta {\kern 1pt} '(0)$ увеличивается, в то время как оно уменьшается с увеличением числа Эккерта, параметра излучения, объемной доли твердой фазы в наножидкости и числа Льюиса. Также видно, что число Нуссельта является максимальным для наножидкости TiO₂–вода и минимальным для наножидкости CuO–вода. Это происходит потому, что TiO₂ имеет наименьшую теплопроводность, а CuO – наибольшую из всех рассмотренных нами веществ.

Таблица 5 показывает, что увеличение параметра нестационарности, параметра проницаемости, параметра излучения, числа Ричардсона, отношения концентрационной и термической плавучестей, числа Эккерта или числа Льюиса приводит к увеличению числа Шервуда $ - \phi {\kern 1pt} '(0).$

5. ЗАКЛЮЧЕНИЕ

Проведено сравнительное исследование нестационарного магнитогидродинамического течения наножидкостей на водной основе, содержащих частицы CuO, Al₂O₃ или TiO₂, около проницаемой вертикально растягивающейся поверхности. Исследовано влияние различных физических параметров на скорость наножидкости, температуру, концентрацию, коэффициент поверхностного трения, число Нуссельта и число Шервуда. На основании полученных результатов можно сделать следующие основные выводы, перечисленные ниже.

– Наножидкость CuO–вода имеет минимальные скорость и локальный коэффициент поверхностного трения, в то время как наножидкость Al₂O₃–вода имеет максимальные значения этих параметров.

– Скорость жидкости и локальный коэффициент поверхностного трения могут быть уменьшены путем увеличения числа Льюиса, числа Прандтля или параметра нестационарности.

– Скорость теплопередачи может быть увеличена за счет использования наножидкости TiO₂–вода вместо наножидкостей CuO–вода или Al₂O₃–вода.

– Температура жидкости может быть понижена путем увеличения числа Ричардсона и параметра проницаемости или отношения концентрационной и термической плавучестей.

– Число Шервуда является максимальным для наножидкости Al₂O₃–вода и минимальным для наножидкости CuO–вода.