Коллоидный журнал, 2021, T. 83, № 4, стр. 484-495
Молекулярно-термодинамическая модель солюбилизации в прямых сферических мицеллах неионных ПАВ
А. К. Щёкин 1, *, Н. А. Волков 1, И. Н. Кольцов 2, Н. Ю. Третьяков 3, С. С. Волкова 3, Е. А. Турнаева 3
1 Санкт-Петербургский государственный университет
199034 Санкт-Петербург, Университетская набережная, 7–9, Россия
2 ООО “ГАЗПРОМНЕФТЬ – Технологические Партнерства”
625048 Тюмень, ул. 50 лет Октября, 14, Россия
3 Тюменский государственный университет
625003 Тюмень, ул. Володарского, 6, Россия
* E-mail: akshch@list.ru
Поступила в редакцию 20.02.2021
После доработки 01.03.2021
Принята к публикации 05.03.2021
Аннотация
Построена термодинамическая модель работы образования молекулярного агрегата из молекул неионного ПАВ и солюбилизата в растворе углеводород–ПАВ–вода как функции температуры, концентраций ПАВ и углеводорода в растворе, чисел агрегации ПАВ и углеводорода в агрегате. Модель зависит от структурных параметров и физических характеристик молекул ПАВ и солюбилизата. Исследованы предсказания модели относительно минимума и седловой точки работы агрегации, построены распределения относительных концентраций агрегатов по числам агрегации ПАВ и солюбилизата при разных концентрациях мономеров ПАВ и углеводорода в растворе. Сделаны численные оценки долей ПАВ и солюбилизата в агрегатах по отношению к равновесным концентрациям мономеров ПАВ и солюбилизата, найдены средние числа агрегации ПАВ и солюбилизата в агрегатах. Показана возможность колоссального накопления молекул солюбилизата в молекулярных агрегатах. Рассмотрены агрегация и солюбилизация при равновесных концентрациях ПАВ существенно меньших, чем критическая концентрация мицеллообразования в чистом растворе ПАВ. Установлено, что предельные концентрации неионного ПАВ и солюбилизата, соответствующие формированию устойчивых наноэмульсий, лежат в достаточно узких интервалах, попасть в которые при их случайном поиске в лабораторных экспериментах маловероятно.
ВВЕДЕНИЕ
Накапливание малорастворимых в водных средах углеводородов при их добавлении в водные растворы поверхностно-активного вещества (ПАВ) в мицеллах из молекул ПАВ (явление солюбилизации в мицеллярном растворе) может приводить к формированию устойчивых или неустойчивых прямых микроэмульсий [1–6]. Установление связи между структурой и физико-химическими свойствами молекул ПАВ и углеводородов и их агрегационным поведением по-прежнему остается актуальной проблемой коллоидной науки и построенных на ней технологий создания микроэмульсий [2, 6]. Несмотря на активное развитие исследований в этом направлении за последние десятилетия, разработка аналитической прогностической молекулярно-термодинамической модели для дисперсных систем из самоорганизующихся мицелл в присутствии захваченных молекул гидрофобного солюбилизата остается первоочередной задачей, без решения которой нельзя построить термодинамику и кинетику прямых нано- и микроэмульсий. Известные термодинамические модели мицеллярных систем исходят из модели Танфорда [7]. Главная задача такой модели [5–16] состоит в нахождении минимальной работы образования неионных мицелл в зависимости от чисел агрегации молекул ПАВ в мицелле и молекул солюбилизата в мицеллярном ядре. Эта минимальная работа определяет совокупное равновесное распределение агрегатов по числам агрегации ПАВ и солюбилизата.
Конкретной задачей нашей работы является расширение капельной модели для сферических мицелл [5, 15–17] таким образом, чтобы включить в нее зависимость минимальной работы агрегации и других термодинамических характеристик агрегации ПАВ в присутствии солюбилизата от количества молекул солюбилизата в сферическом мицеллярном ядре. Эта зависимость должна присутствовать через размер мицеллярного ядра, гидрофобный вклад за счет включенных молекул солюбилизата, влияния концентраций ПАВ и углеводорода, через поверхностное натяжение на границе ядро мицеллы–раствор и вклад свободной энергии двойного электрического слоя мицеллярной короны. В зависимости от физических параметров ПАВ и солюбилизата, их концентраций в растворе модель должна описывать стабильные и квазистабильные состояния соответствующей наноэмульсии и кинетику установления ее равновесия или распада.
1. ВКЛАДЫ В РАБОТУ АГРЕГАЦИИ ПРИ СОЛЮБИЛИЗАЦИИ В ПРЯМЫХ СФЕРИЧЕСКИХ МИЦЕЛЛАХ
Рассмотрим мицеллярный раствор неионного ПАВ в полярном растворителе (воде) при брутто-концентрации ПАВ ниже и выше критической концентрации мицеллообразования (ККМ). Нас будут интересовать равновесные состояния такой системы в присутствии некоторого количества молекул такого неполярного углеводорода как гептан или декан. Будем считать, что добавляемый неполярный углеводород плохо растворим в воде, но может солюбилизироваться в молекулярных агрегатах рассматриваемого ПАВ. В дальнейшем для краткости будем называть неполярный углеводород солюбилизатом.
Обозначим через ${{n}_{{\text{C}}}}$ число атомов углерода в углеводородной цепи молекулы ПАВ. Концевая метильная группа CH3 имеет характерный объем ${{\upsilon }_{0}},$ а метиленовые группы CH2 – характерный объем $\upsilon .$ При абсолютной температуре $Т = 293$ K раствора имеем: ${{\upsilon }_{0}} = 54.3$ Å3 и $\upsilon = 26.9$ Å3 [8]. Будем ниже приближенно полагать ${{{{\upsilon }_{{\text{0}}}}} \mathord{\left/ {\vphantom {{{{\upsilon }_{{\text{0}}}}} \upsilon }} \right. \kern-0em} \upsilon } \approx 2.$
В капельной модели сферического молекулярного агрегата считается, что полное число углеводородных сегментов всех молекул ПАВ и солюбилизата, вошедших в молекулярный агрегат, упаковывается компактно (без пустот) внутри сферического ядра агрегата (ядра мицеллы). Через ${{n}_{1}}$ обозначим число молекул ПАВ в агрегате, а через ${{n}_{2}}$ – число молекул солюбилизата в ядре агрегата. Эти числа будем в дальнейшем называть числами агрегации.
Объем ядра молекулярного агрегата радиуса $r$ положим равным
(1)
$\frac{{4\pi {{r}^{3}}}}{3} = \upsilon \left( {{{n}_{{\text{C}}}} + 1} \right){{n}_{1}} + {{\upsilon }_{2}}{{n}_{2}},$(2)
${{\upsilon }_{0}} + \upsilon \left( {{{n}_{{\text{C}}}} - 1} \right) \approx \upsilon \left( {{{n}_{{\text{C}}}} + 1} \right)$Вводя обозначения
(3)
$\lambda \equiv {{\left[ {\frac{{3\upsilon \left( {{{n}_{{\text{C}}}} + 1} \right)}}{{4\pi }}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}},\,\,\,\,\alpha \equiv \frac{{{{\upsilon }_{2}}}}{{\upsilon \left( {{{n}_{{\text{C}}}} + 1} \right)}},$(4)
$r = \lambda {{\left( {{{n}_{1}} + \alpha {{n}_{2}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}},$Ключевой величиной, описывающей термодинамику и кинетику агрегации, а также различные квазиравновесные состояния дисперсных систем, служит минимальная работа образования молекулярного агрегата. Для краткости в дальнейшем будем называть ее работой агрегации. При фиксированной температуре в растворе, содержащем ПАВ и солюбилизат, работа агрегации будет функцией чисел агрегации ${{n}_{1}}$ и ${{n}_{2}},$ а также химических потенциалов ПАВ и солюбилизата в растворе.
Обозначим безразмерную работу агрегации, выраженную в тепловых единицах ${{k}_{{\text{B}}}}T,$ где ${{k}_{{\text{B}}}}$ – постоянная Больцмана, как W. Рассмотрим различные термодинамические вклады в работу агрегации W. В общем случае можно представить $W\left( {{{n}_{1}},{{n}_{2}}} \right)$ в виде
где ${{W}_{{\text{h}}}}$ – гидрофобный вклад, учитывающий выигрыш свободной энергии при переносе углеводородного хвоста молекулы ПАВ и молекулы солюбилизата из водного раствора в ядро агрегата, ${{W}_{{\text{s}}}}$ – поверхностный вклад, учитывающий наличие поверхностного натяжения агрегата, ${{W}_{{{\text{el}}}}}$ – электрический вклад, который учитывает электрические взаимодействия полярных головных групп молекул ПАВ на поверхности агрегата, ${{W}_{{{\text{conc}}}}}$ – концентрационный вклад, обусловленный различием концентраций ПАВ и солюбилизата в агрегате и в растворе.Найдем явные термодинамические выражения для указанных вкладов. Начнем с гидрофобного вклада ${{W}_{{\text{h}}}}$ в работу W, даваемого первым слагаемым в правой части (5). Для выраженной в единицах ${{k}_{{\text{B}}}}T$ работы ${{w}_{1}}$ переноса (через плоскую поверхность) из раствора в объемную углеводородную фазу всей гидрофобной части отдельной молекулы ПАВ, содержащей ${{n}_{{\text{C}}}}$ углеводородных групп, имеем эмпирическое выражение
где ${{B}_{1}}$ – положительная и безразмерная величина. Аналогично, для выраженной в единицах ${{k}_{{\text{B}}}}T$ работы ${{w}_{2}}$ переноса (через плоскую поверхность) из раствора в объемную углеводородную фазу одной молекулы солюбилизата, запишемПоложительность величин ${{B}_{1}}$ и ${{B}_{2}}$ (т.е. отрицательность правых частей (6) и (7)) означает гидрофобность углеводородных групп молекул ПАВ и солюбилизата. Для разбавленного раствора величины ${{B}_{1}}$ и ${{B}_{2}}$ не зависят от концентраций ПАВ и солюбилизата в растворе, но, строго говоря, могут зависеть от концентраций углеводородных частей молекул ПАВ и солюбилизата в ядре агрегата. Если молекула солюбилизата также состоит из метильных групп CH3 и метиленовых групп CH2, то величины ${{B}_{1}}$ и ${{B}_{2}}$ можно считать постоянными. Известно [8], что константа ${{B}_{1}}$ равна примерно $1.4$ при 20°С. Отличие работы переноса одного-двух ближайших к полярной группе сегментов углеводородной цепи и работы переноса концевой метильной группы от работы $ - {{B}_{1}}$ практически не сказывается при ${{n}_{{\text{C}}}} \gg 1$ на применимости линейного по ${{n}_{{\text{C}}}}$ выражения (6). То, что в принятой нами модели молекулярного агрегата углеводородное ядро не является в действительности бесконечной объемной фазой, а окружено поверхностью радиуса r, будет учтено несколько ниже.
Полный вклад ${{W}_{{\text{h}}}}$ в безразмерную работу $W$ определяется суммированием и интегрированием по ${{n}_{1}}$ и ${{n}_{2}}$ выражений (5) и (7). В итоге получаем
Отрицательность величины ${{W}_{{\text{h}}}}$ способствует образованию молекулярных агрегатов в растворе.При упаковке в сферическое углеводородное ядро молекулярного агрегата гидрофобная часть молекулы ПАВ и молекула солюбилизата претерпевают определенную деформацию, и их конформация в среднем будет отличаться от конформации в растворе. Отличие конформаций порождает положительный вклад в работу образования молекулярного агрегата. Назовем его деформационным и обозначим через ${{W}_{{{\text{def}}}}}.$ Вклад ${{W}_{{{\text{def}}}}}$ для молекулы ПАВ описан в литературе [6, 8, 11–13] и обычно выступает как небольшая поправка к гидрофобному вкладу ${{W}_{{\text{h}}}}.$ В присутствии солюбилизата роль вклада ${{W}_{{{\text{def}}}}}$ с ростом числа агрегации ${{n}_{2}}$ должна уменьшаться. На этом основании вклад ${{W}_{{{\text{def}}}}}$ далее учитывать не будем.
Как уже отмечалось выше, углеводородное ядро не является в действительности бесконечной объемной фазой с плоской межфазной поверхностью. Сферическое искривление последней приводит к появлению лапласовой разности давлений и соответствующему поверхностному вкладу ${{W}_{{\text{s}}}},$ представленному вторым слагаемым в правой части (5). Этот вклад, выраженный в единицах ${{k}_{{\text{B}}}}T,$ можно записать в виде
где ${{\gamma }_{0}}$ – поверхностное натяжение на границе между углеводородным ядром и раствором, которое будем считать постоянным и равным своему значению для плоской поверхности. То, что поверхностное натяжение ядра агрегата в присутствии полярных групп молекул ПАВ отличается от ${{\gamma }_{0}}$ и зависит от чисел агрегации, в дальнейшем автоматически учитывается через электрический вклад ${{W}_{{{\text{el}}}}}$ от взаимодействия полярных групп.С учетом (4) перепишем (9) как
(10)
${{W}_{{\text{s}}}} = \frac{{4\pi {{\gamma }_{0}}{{\lambda }^{2}}}}{{{{k}_{{\text{B}}}}T}}{{\left( {{{n}_{1}} + \alpha {{n}_{2}}} \right)}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}.$Найдем теперь явное выражение для электрического вклада ${{W}_{{{\text{el}}}}}$ от взаимодействия полярных групп молекул ПАВ. Насильственное сближение этих групп для малых агрегатов в процессе перехода углеводородных хвостов внутрь ядра молекулярного агрегата приводит к их взаимодействию, наиболее типичным видом которого является взаимное электростатическое отталкивание диполей. Рассмотрим случай, когда электростатическая компонента достаточно хорошо характеризует все взаимодействие полярных групп. Поскольку образование молекулярных агрегатов в растворе происходит при постоянстве температуры и внешнего давления, то ${{W}_{{{\text{el}}}}}$ представляет собой электрическую энергию Гиббса конденсатора, образуемого гидрофильными частями молекул ПАВ в молекулярном агрегате. При предполагаемой в капельной модели молекулярного агрегата сферической симметрии конденсатора (обкладки этого конденсатора формируются зарядами в диполях молекул ПАВ, выступающими радиально из ядра агрегата) имеем (в единицах ${{k}_{{\text{B}}}}T$ измерения энергии) следующее электростатическое выражение для ${{W}_{{{\text{el}}}}}$ [5, 15, 16]:
(11)
${{W}_{{{\text{el}}}}} = \frac{{{{{\left( {ze{{n}_{1}}} \right)}}^{2}}\delta }}{{8\pi {{k}_{{\text{B}}}}T{{\varepsilon }_{0}}\varepsilon \left( {r + \Delta l} \right)\left( {r + \Delta l + \delta } \right)}}.$Предполагая, что при ${{n}_{{\text{C}}}} \gg 1,$ ${{n}_{1}} \gg 1$ и ${{n}_{2}} \gg 1$ справедливы неравенства $r \gg \delta $ и $r \gg \Delta l,$ получим из (11):
(12)
${{W}_{{{\text{el}}}}} \approx \frac{{{{{\left( {ze{{n}_{1}}} \right)}}^{2}}\delta }}{{8\pi {{k}_{{\text{B}}}}T{{\varepsilon }_{0}}\varepsilon {{r}^{2}}}}.$(13)
${{W}_{{{\text{el}}}}} = \frac{{{{{\left( {ze} \right)}}^{2}}\delta n_{1}^{2}}}{{8\pi {{k}_{{\text{B}}}}T{{\varepsilon }_{0}}\varepsilon {{\lambda }^{2}}{{{\left( {{{n}_{1}} + \alpha {{n}_{2}}} \right)}}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}}}.$При очень близком расположении гидрофильных частей молекул ПАВ возможны, помимо электрических сил, еще и более мощные силы непосредственного отталкивания полярных групп при их контакте. Такая картина типична для случая, когда упаковка молекул в мицеллах диктуется размером полярных групп [8, 11]. Мы же концентрируем внимание на случае, когда упаковка определяется углеводородными цепями, а полярные группы участвуют в образовании мицелл лишь дальнодействующими электрическими силами отталкивания.
Рассмотрим теперь концентрационный вклад ${{W}_{{{\text{conc}}}}},$ который происходит от различия концентраций молекул ПАВ и солюбилизата в ядре агрегата и растворе. Поскольку искривление поверхности агрегата уже учтено во вкладе ${{W}_{{\text{s}}}},$ а взаимодействие полярных групп на поверхности ядра – во вкладе ${{W}_{{{\text{el}}}}},$ то для определения вклада ${{W}_{{{\text{conc}}}}}$ рассмотрим только разности химических потенциалов гидрофобных частей молекул ПАВ и молекул солюбилизата в углеводородной фазе и растворе.
Для разности химических потенциалов ${{\mu }_{{1n}}} - {{\mu }_{1}}$ углеводородных частей молекул ПАВ в углеводородной фазе (соответствующей ядру агрегата, но без учета искривления его поверхности) с концентрацией ${{c}_{1}}_{n}$ и в растворе с концентрацией ${{c}_{1}}$ можем написать
(14)
${{\mu }_{{1n}}} - {{\mu }_{1}} = {{k}_{{\text{B}}}}T{{w}_{1}} + {{k}_{{\text{B}}}}T\ln \left( {{{{{c}_{{1n}}}} \mathord{\left/ {\vphantom {{{{c}_{{1n}}}} {{{c}_{1}}}}} \right. \kern-0em} {{{c}_{1}}}}} \right).$(15)
${{\mu }_{{2n}}} - {{\mu }_{2}} = {{k}_{{\text{B}}}}T{{w}_{2}} + {{k}_{{\text{B}}}}T\ln \left( {{{{{c}_{{2n}}}} \mathord{\left/ {\vphantom {{{{c}_{{2n}}}} {{{c}_{2}}}}} \right. \kern-0em} {{{c}_{2}}}}} \right).$(16)
${{W}_{{{\text{conc}}}}} = - {{n}_{1}}\ln \frac{{{{c}_{1}}}}{{{{c}_{{1n}}}}} - {{n}_{2}}\ln \frac{{{{c}_{2}}}}{{{{c}_{{2n}}}}}.$(17)
${{c}_{{1n}}} \approx {{3{{n}_{1}}} \mathord{\left/ {\vphantom {{3{{n}_{1}}} {4\pi {{r}^{3}}}}} \right. \kern-0em} {4\pi {{r}^{3}}}},\,\,\,\,{{c}_{{2n}}} \approx {{3{{n}_{2}}} \mathord{\left/ {\vphantom {{3{{n}_{2}}} {4\pi {{r}^{3}}}}} \right. \kern-0em} {4\pi {{r}^{3}}}}.$(18)
${{c}_{{1n}}} \approx \frac{{3{{n}_{1}}}}{{4\pi {{\lambda }^{3}}}}{{\left( {{{n}_{1}} + \alpha {{n}_{2}}} \right)}^{{ - 1}}},\,\,\,\,{{c}_{{2n}}} \approx \frac{3}{{4\pi {{\lambda }^{3}}}}\frac{{{{n}_{2}}}}{{{{n}_{1}} + \alpha {{n}_{2}}}}.$Подставляя (17) и (18) в (16), находим окончательное выражение для концентрационного вклада ${{W}_{{{\text{conc}}}}}$ в работу агрегации W:
(19)
$\begin{gathered} {{W}_{{{\text{conc}}}}} = - {{n}_{1}}\ln \left( {\frac{{4\pi {{\lambda }^{3}}{{c}_{1}}}}{3}\frac{{{{n}_{1}} + \alpha {{n}_{2}}}}{{{{n}_{1}}}}} \right) - \\ - \,\,{{n}_{2}}\ln \left( {\frac{{4\pi {{\lambda }^{3}}{{c}_{2}}}}{3}\frac{{{{n}_{1}} + \alpha {{n}_{2}}}}{{{{n}_{2}}}}} \right). \\ \end{gathered} $Из (19) следует, что при $\frac{{4\pi {{\lambda }^{3}}{{c}_{1}}}}{3}\frac{{{{n}_{1}} + \alpha {{n}_{2}}}}{{{{n}_{1}}}} > 1$ и $\frac{{4\pi {{\lambda }^{3}}{{c}_{2}}}}{3}\frac{{{{n}_{1}} + \alpha {{n}_{2}}}}{{{{n}_{2}}}} > 1$ имеем ${{W}_{{{\text{conc}}}}} > 0,$ а в остальных случаях знак ${{W}_{{{\text{conc}}}}}$ может быть как положительным, так и отрицательным. Таким образом, концентрационный вклад ${{W}_{{{\text{conc}}}}}$ может как способствовать, так и препятствовать образованию молекулярных агрегатов в растворе.
Подведем промежуточный итог. С учетом соотношений (5), (8), (10), (13) и (19) выражение для безразмерной работы агрегации $W$ при солюбилизации растворенного углеводорода в молекулярных агрегатах ПАВ как функции числа агрегации ${{n}_{1}}$ ПАВ и числа агрегации ${{n}_{2}}$ солюбилизата, концентрации ${{c}_{1}}$ мономеров ПАВ и концентрации ${{c}_{2}}$ мономеров углеводорода в растворе может быть представленo в виде
(20)
$\begin{gathered} W \equiv W\left( {{{n}_{1}},{{n}_{2}},{{c}_{1}},{{c}_{2}}} \right) = - {{n}_{{\text{C}}}}{{B}_{1}}{{n}_{1}} - {{B}_{2}}{{n}_{2}} + \frac{{4\pi {{\gamma }_{0}}{{\lambda }^{2}}}}{{{{k}_{{\text{B}}}}T}} \times \\ \times \,\,{{\left( {{{n}_{1}} + \alpha {{n}_{2}}} \right)}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}} - {{n}_{1}}\ln \left( {\frac{{4\pi {{\lambda }^{3}}{{c}_{1}}}}{3}\frac{{{{n}_{1}} + \alpha {{n}_{2}}}}{{{{n}_{1}}}}} \right) - \\ - \,\,{{n}_{2}}\ln \left( {\frac{{4\pi {{\lambda }^{3}}{{c}_{2}}}}{3}\frac{{{{n}_{1}} + \alpha {{n}_{2}}}}{{{{n}_{2}}}}} \right) + \frac{{\delta {{{\left( {ze} \right)}}^{2}}n_{1}^{2}}}{{8\pi {{k}_{{\text{B}}}}T{{\varepsilon }_{0}}\varepsilon {{\lambda }^{2}}{{{\left( {{{n}_{1}} + \alpha {{n}_{2}}} \right)}}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}}}. \\ \end{gathered} $(21)
$\begin{gathered} {{W}_{{\text{M}}}}\left( {{{n}_{1}},{{c}_{1}}} \right) = - {{n}_{{\text{C}}}}{{B}_{1}}{{n}_{1}} + \frac{{4\pi {{\gamma }_{0}}{{\lambda }^{2}}}}{{{{k}_{{\text{B}}}}T}}n_{1}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}} - \\ - \,\,{{n}_{1}}\ln \left( {\frac{{4\pi {{\lambda }^{3}}{{c}_{1}}}}{3}} \right) + \frac{{\delta {{{\left( {ze} \right)}}^{2}}n_{1}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}}}{{8\pi {{\varepsilon }_{0}}\varepsilon {{k}_{{\text{B}}}}T{{\lambda }^{2}}}} \\ \end{gathered} $(22)
$\begin{gathered} {{W}_{{\text{D}}}}\left( {{{n}_{2}},{{c}_{2}}} \right) = - \left[ {{{B}_{2}} + \ln \left( {{{\upsilon }_{2}}{{c}_{2}}} \right)} \right]{{n}_{2}} + \\ + \,\,\frac{{4\pi {{\gamma }_{0}}}}{{{{k}_{{\text{B}}}}T}}{{\left( {\frac{{3{{\upsilon }_{2}}}}{{4\pi }}} \right)}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}n_{2}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}} \\ \end{gathered} $2. ПРОИЗВОДЯЩИЕ СВОЙСТВА РАБОТЫ АГРЕГАЦИИ
Работа агрегации $W$ молекулярного агрегата с солюбилизатом связана с химическими потенциалами ПАВ ${{\mu }_{{1\left\{ n \right\}}}}$ и солюбилизата ${{\mu }_{{2\left\{ n \right\}}}}$ в ядре агрегата соотношениями
(23)
$\begin{gathered} {{k}_{{\text{B}}}}T{{\partial W} \mathord{\left/ {\vphantom {{\partial W} {\partial {{n}_{1}}}}} \right. \kern-0em} {\partial {{n}_{1}}}} = {{\mu }_{{1\left\{ n \right\}}}} - {{\mu }_{1}}, \\ {{k}_{{\text{B}}}}T{{\partial W} \mathord{\left/ {\vphantom {{\partial W} {\partial {{n}_{2}}}}} \right. \kern-0em} {\partial {{n}_{2}}}} = {{\mu }_{{2\left\{ n \right\}}}} - {{\mu }_{2}}. \\ \end{gathered} $(24)
$\begin{gathered} - {{n}_{{\text{C}}}}{{B}_{1}} + \frac{{8\pi {{\gamma }_{0}}{{\lambda }^{2}}}}{{3{{k}_{{\text{B}}}}T{{{\left( {{{n}_{1}} + \alpha {{n}_{2}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}}} - \ln \left( {\frac{{4\pi {{\lambda }^{3}}{{c}_{1}}}}{3}\frac{{{{n}_{1}} + \alpha {{n}_{2}}}}{{{{n}_{1}}}}} \right) + \\ + \,\,\frac{{\left( {\alpha - 1} \right){{n}_{1}}{{n}_{2}}}}{{{{n}_{1}}\left( {{{n}_{1}} + \alpha {{n}_{2}}} \right)}} + {{\left. {\frac{{\delta {{{\left( {ze} \right)}}^{2}}{{n}_{1}}}}{{12\pi {{\varepsilon }_{0}}\varepsilon {{k}_{{\text{B}}}}T{{\lambda }^{2}}}}\frac{{2{{n}_{1}} + 3\alpha {{n}_{2}}}}{{{{{\left( {{{n}_{1}} + \alpha {{n}_{2}}} \right)}}^{{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3}}}}}}} \right|}_{{{{n}_{{1{\text{e}}}}},{{n}_{{2{\text{e}}}}}}}} = 0, \\ \end{gathered} $(25)
$\begin{gathered} - {{B}_{2}} + \frac{{8\pi {{\gamma }_{0}}{{\lambda }^{2}}\alpha }}{{3{{k}_{{\text{B}}}}T{{{\left( {{{n}_{1}} + \alpha {{n}_{2}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}}} - \ln \left( {\frac{{4\pi {{\lambda }^{3}}{{c}_{2}}}}{3}\frac{{{{n}_{1}} + \alpha {{n}_{2}}}}{{{{n}_{2}}}}} \right) - \\ - \,\,\frac{{\left( {\alpha - 1} \right){{n}_{1}}}}{{{{n}_{1}} + \alpha {{n}_{2}}}} - {{\left. {\frac{{\delta {{{\left( {ze} \right)}}^{2}}\alpha n_{1}^{2}}}{{12\pi {{k}_{{\text{B}}}}T{{\varepsilon }_{0}}\varepsilon {{\lambda }^{2}}{{{\left( {{{n}_{1}} + \alpha {{n}_{2}}} \right)}}^{{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3}}}}}}} \right|}_{{{{n}_{{1{\text{e}}}}},{{n}_{{2{\text{e}}}}}}}}. \\ \end{gathered} $Для понимания полной картины агрегации в присутствии ПАВ и солюбилизата в растворе полезно сначала рассмотреть, что показывает предложенная модель работы агрегации $W$ в предельных случаях. В частности, в пределе при ${{n}_{2}} \to 0$ мы переходим к растворам ПАВ, в которых выше ККМ должно происходить образование мицелл. Соотношение (25) при ${{n}_{2}} \to 0$ исчезает, а соотношение (24) становится квадратным уравнением на точки максимума $n_{{1{\text{c}}}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}$ и минимума $n_{{1{\text{s}}}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}$ работы агрегации ${{W}_{{\text{M}}}}\left( {{{n}_{1}},{{c}_{1}}} \right){\text{:}}$
(26)
$\begin{gathered} \frac{{\delta {{{\left( {ze} \right)}}^{2}}}}{{6\pi {{\varepsilon }_{0}}\varepsilon {{k}_{{\text{B}}}}T{{\lambda }^{2}}}}n_{1}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}} - \left[ {{{n}_{{\text{C}}}}{{B}_{1}} + \ln \left( {\frac{{4\pi {{\lambda }^{3}}{{c}_{1}}}}{3}} \right)} \right]n_{1}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}} + \\ + \,\,{{\left. {\frac{{8\pi {{\gamma }_{0}}{{\lambda }^{2}}}}{{3{{k}_{{\text{B}}}}T}}} \right|}_{{{{n}_{{1{\text{c}}}}},{{n}_{{1{\text{s}}}}}}}} = 0. \\ \end{gathered} $Решения этого уравнения имеют вид
(27)
$\begin{gathered} n_{{1{\text{s}}}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}} = \frac{{3\pi {{\varepsilon }_{0}}\varepsilon {{k}_{{\text{B}}}}T{{\lambda }^{2}}}}{{\delta {{{\left( {ze} \right)}}^{2}}}}\left\{ {{{n}_{{\text{C}}}}{{B}_{1}} + \ln \left( {\frac{{4\pi {{\lambda }^{3}}{{c}_{1}}}}{3}} \right) + } \right. \\ \left. { + \,\,\sqrt {{{{\left( {{{n}_{{\text{C}}}}{{B}_{1}} + \ln \left( {\frac{{4\pi {{\lambda }^{3}}{{c}_{1}}}}{3}} \right)} \right)}}^{2}} - \frac{{16\delta {{{\left( {ze} \right)}}^{2}}{{\gamma }_{0}}}}{{9{{\varepsilon }_{0}}\varepsilon {{{\left( {{{k}_{{\text{B}}}}T} \right)}}^{2}}}}} } \right\}, \\ \end{gathered} $(28)
$\begin{gathered} n_{{1{\text{c}}}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}} = \frac{{3\pi {{\varepsilon }_{0}}\varepsilon {{k}_{{\text{B}}}}T{{\lambda }^{2}}}}{{\delta {{{\left( {ze} \right)}}^{2}}}}\left\{ {{{n}_{{\text{C}}}}{{B}_{1}} + \ln \left( {\frac{{4\pi {{\lambda }^{3}}{{c}_{1}}}}{3}} \right) - } \right. \\ \left. { - \,\,\sqrt {{{{\left( {{{n}_{{\text{C}}}}{{B}_{1}} + \ln \left( {\frac{{4\pi {{\lambda }^{3}}{{c}_{1}}}}{3}} \right)} \right)}}^{2}} - \frac{{16\delta {{{\left( {ze} \right)}}^{2}}{{\gamma }_{0}}}}{{9{{\varepsilon }_{0}}\varepsilon {{{\left( {{{k}_{{\text{B}}}}T} \right)}}^{2}}}}} } \right\}, \\ \end{gathered} $(29)
${{с}_{{10}}} = \frac{1}{{\upsilon \left( {{{n}_{{\text{C}}}} + 1} \right)}}{{e}^{{ - {{n}_{{\text{C}}}}{{B}_{1}} + \frac{{4ze}}{{3{{k}_{{\text{B}}}}T}}\sqrt {\frac{{\delta {{\gamma }_{0}}}}{{{{\varepsilon }_{0}}\varepsilon }}} }}}$(30)
$n_{{10}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}} = \frac{{3\pi {{\varepsilon }_{0}}\varepsilon {{k}_{{\text{B}}}}T{{\lambda }^{2}}}}{{\delta {{{\left( {ze} \right)}}^{2}}}}\left[ {{{n}_{{\text{C}}}}{{B}_{1}} + \ln \left( {\frac{{4\pi {{\lambda }^{3}}{{c}_{{10}}}}}{3}} \right)} \right],$Так как из (27) и (28) имеем ${{\partial n_{{1{\text{s}}}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}} \mathord{\left/ {\vphantom {{\partial n_{{1{\text{s}}}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}} {\partial {{c}_{1}}}}} \right. \kern-0em} {\partial {{c}_{1}}}} > 0,$ ${{\partial n_{{1{\text{c}}}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}} \mathord{\left/ {\vphantom {{\partial n_{{1{\text{c}}}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}} {\partial {{c}_{1}}}}} \right. \kern-0em} {\partial {{c}_{1}}}} < 0,$ то с ростом концентрации ${{c}_{1}}$ мономеров ПАВ максимум работы сдвигается влево, а минимум работы – вправо относительно точки ${{n}_{0}}$ на оси чисел агрегации. Благодаря вытекающему из (21) неравенству ${{\partial {{W}_{{\text{M}}}}\left( {{{n}_{1}},{{c}_{1}}} \right)} \mathord{\left/ {\vphantom {{\partial {{W}_{{\text{M}}}}\left( {{{n}_{1}},{{c}_{1}}} \right)} \partial }} \right. \kern-0em} \partial }{{с}_{1}} = - {{{{n}_{1}}} \mathord{\left/ {\vphantom {{{{n}_{1}}} {{{c}_{1}}}}} \right. \kern-0em} {{{c}_{1}}}} < 0,$ максимум и минимум работы становятся меньше с ростом концентрации ${{c}_{1}},$ но минимум углубляется быстрее. Очевидно, что концентрация ${{c}_{{10}}}$ играет роль предвестника ККМ. Так как при ККМ наблюдается заметная доля ПАВ в устойчивых агрегатах, числа агрегации которых должны соответствовать области достаточно глубокой потенциальной ямы работы ${{W}_{{\text{M}}}}\left( {{{n}_{1}},{{c}_{1}}} \right),$ то ${{c}_{{10}}}$ всегда несколько меньше концентрации мономеров при ККМ. Описанная выше картина соответствует результатам [5, 15, 16].
Чтобы найти ККМ, учтем теперь, что работа агрегации ${{W}_{{\text{M}}}}\left( {{{n}_{1}},{{c}_{1}}} \right)$ определяет вид кривой распределения агрегатов по числам агрегации при равновесии в мицеллярном растворе [5]. Обозначим равновесную концентрацию молекулярных агрегатов ПАВ в единице объема раствора как $c_{{{{n}_{1}}}}^{{\left( {\text{e}} \right)}}.$ Эта концентрация связана с работой ${{W}_{{\text{M}}}}\left( {{{n}_{1}},{{c}_{1}}} \right)$ соотношением [5]
(31)
$c_{{{{n}_{1}}}}^{{\left( {\text{e}} \right)}} = {{c}_{1}}{{e}^{{ - {{W}_{{\text{M}}}}\left( {{{n}_{1}} - 1,{{c}_{1}}} \right)}}}\,\,\,\,\left( {{{n}_{1}} = 1,2,...} \right)$Доля ПАВ в молекулярных агрегатах (степень мицеллизации ${{\alpha }_{{\text{M}}}}$) может быть определена как
(32)
${{\alpha }_{{\text{M}}}}\left( {{{с}_{1}}} \right) = \frac{{\sum\limits_{{{n}_{1}} = {{n}_{{1{\text{c}}}}}}^\infty {{{n}_{1}}c_{{{{n}_{1}}}}^{{\left( {\text{e}} \right)}}\left( {{{с}_{1}}} \right)} }}{{\sum\limits_{{{n}_{1}} = 1}^\infty {{{n}_{1}}c_{{{{n}_{1}}}}^{{\left( {\text{e}} \right)}}\left( {{{с}_{1}}} \right)} }},$(34)
$n_{{2{\text{c}}}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}} = \frac{{8\pi {{\gamma }_{0}}}}{{3{{k}_{{\text{B}}}}T\left[ {{{B}_{2}} + \ln \left( {{{\upsilon }_{2}}{{c}_{2}}} \right)} \right]}}{{\left( {\frac{{3{{\upsilon }_{2}}}}{{4\pi }}} \right)}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}.$Очевидно, что этот максимум существует (т.е. $0 < n_{{2{\text{c}}}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}} < \infty $), если выполнено условие ${{c}_{2}} > {{c}_{{20}}},$ где
Таким образом, рассматриваемая модель для работы агрегации солюбилизата в полярном растворителе в отсутствие ПАВ предсказывает существование конечного активационного барьера у работы ${{W}_{{\text{D}}}}\left( {{{n}_{2}},{{c}_{2}}} \right),$ необходимой для расслоения раствора при концентрации мономеров солюбилизата ${{c}_{2}} > {{с}_{{20}}}$ в растворе ПАВ. Ниже концентрации ${{c}_{2}} = {{с}_{{20}}}$ раствор устойчив.
Вернемся теперь к анализу полной картины агрегации при совместном присутствии ПАВ и солюбилизата в растворе. Проведенное рассмотрение предельных одномерных случаев показывает, что в присутствии ПАВ и солюбилизата в растворе равновесные корни уравнений (24) и (25) могут соответствовать минимуму (устойчивому агрегату) и седловой точке (агрегату в неустойчивом критическом равновесии) на поверхности работы агрегации $W\left( {{{n}_{1}},{{n}_{2}},{{c}_{1}},{{c}_{2}}} \right).$ Условие минимума $W\left( {{{n}_{1}},{{n}_{2}},{{c}_{1}},{{c}_{2}}} \right)$ записывается как
(36)
$\begin{gathered} {{\left. {{{{{\partial }^{2}}W} \mathord{\left/ {\vphantom {{{{\partial }^{2}}W} {\partial n_{1}^{2}}}} \right. \kern-0em} {\partial n_{1}^{2}}}} \right|}_{{{{n}_{{1{\text{s}}}}},{{n}_{{2{\text{s}}}}}}}} > 0, \\ {{\left. {{{{{\partial }^{2}}W} \mathord{\left/ {\vphantom {{{{\partial }^{2}}W} {\partial n_{1}^{2}}}} \right. \kern-0em} {\partial n_{1}^{2}}}{{{{\partial }^{2}}W} \mathord{\left/ {\vphantom {{{{\partial }^{2}}W} {\partial n_{2}^{2}}}} \right. \kern-0em} {\partial n_{2}^{2}}} - {{{\left( {{{{{\partial }^{2}}W} \mathord{\left/ {\vphantom {{{{\partial }^{2}}W} {\partial {{n}_{1}}\partial {{n}_{2}}}}} \right. \kern-0em} {\partial {{n}_{1}}\partial {{n}_{2}}}}} \right)}}^{2}}} \right|}_{{{{n}_{{1{\text{s}}}}},{{n}_{{2{\text{s}}}}}}}} > 0, \\ \end{gathered} $(37)
${{\left. {{{{{\partial }^{2}}W} \mathord{\left/ {\vphantom {{{{\partial }^{2}}W} {\partial n_{1}^{2}}}} \right. \kern-0em} {\partial n_{1}^{2}}}{{{{\partial }^{2}}W} \mathord{\left/ {\vphantom {{{{\partial }^{2}}W} {\partial n_{2}^{2}}}} \right. \kern-0em} {\partial n_{2}^{2}}} - {{{\left( {{{{{\partial }^{2}}W} \mathord{\left/ {\vphantom {{{{\partial }^{2}}W} {\partial {{n}_{1}}\partial {{n}_{2}}}}} \right. \kern-0em} {\partial {{n}_{1}}\partial {{n}_{2}}}}} \right)}}^{2}}} \right|}_{{{{n}_{{1{\text{c}}}}},{{n}_{{2{\text{c}}}}}}}} < 0,$Если возможно состояние агрегативного (дисперсного) равновесия для раствора при заданных концентрациях ${{c}_{1}}$ и ${{c}_{2}}$ молекул ПАВ и углеводорода, то должно реализоваться термодинамически устойчивое распределение агрегатов по числам агрегации ${{n}_{1}}$ и ${{n}_{2}}.$ По аналогии с (31) обозначим равновесную концентрацию молекулярных агрегатов с числами агрегации ${{n}_{1}}$ и ${{n}_{2}}$ в единице объема раствора как $c_{{{{n}_{1}}{{n}_{2}}}}^{{\left( {\text{e}} \right)}}.$ Очевидно, что совокупность концентраций $c_{{{{n}_{1}}{{n}_{2}}}}^{{\left( {\text{e}} \right)}}$ формирует функцию распределения агрегатов ${{c}^{{\left( {\text{e}} \right)}}}\left( {{{n}_{1}},{{n}_{2}}} \right)$ по числам агрегации ${{n}_{1}}$ и ${{n}_{2}}$ при агрегативном равновесии в мицеллярном растворе.
Концентрация $c_{{{{n}_{1}}{{n}_{2}}}}^{{\left( {\text{e}} \right)}}$ связана с работой $W\left( {{{n}_{1}},{{n}_{2}},{{c}_{1}},{{c}_{2}}} \right)$ соотношением
(38)
$c_{{{{n}_{1}}{{n}_{2}}}}^{{\left( {\text{e}} \right)}} = A{{e}^{{ - W\left( {{{n}_{1}},{{n}_{2}},{{c}_{1}},{{c}_{2}}} \right)}}}\,\,\,\,({{n}_{1}} = 1,2,...;\,\,{{n}_{2}} = 1,2,...),$Заметим, что полное число ${{N}_{{{\text{agg}}}}}$ устойчивых агрегатов в единице объема раствора равно
(40)
${{N}_{{{\text{agg}}}}} = \sum\limits_{{{n}_{2}} = 0}^\infty {\sum\limits_{{{n}_{1}} = {{n}_{{1{\text{c}}}}}}^\infty {c_{{{{n}_{1}}{{n}_{2}}}}^{{\left( {\text{e}} \right)}}} } .$(41)
$\tilde {c}_{{{{n}_{1}}{{n}_{2}}}}^{{\left( {\text{e}} \right)}} = \frac{{{{e}^{{ - W\left( {{{n}_{1}},{{n}_{2}},{{c}_{1}},{{c}_{2}}} \right)}}}}}{{\sum\limits_{{{n}_{2}} = 0}^\infty {\sum\limits_{{{n}_{1}} = {{n}_{{1{\text{c}}}}}}^\infty {{{e}^{{ - W\left( {{{n}_{1}},{{n}_{2}},{{c}_{1}},{{c}_{2}}} \right)}}}} } }}.$3. ЧИСЛЕННЫЕ ОЦЕНКИ
Для численных оценок возьмем следующие значения исходных параметров для раствора, ПАВ и солюбилизата:
(44)
$\begin{gathered} \upsilon = {\text{26}}{\text{.9}} \times {\text{1}}{{{\text{0}}}^{{ - 30}}}\,\,{{{\text{м}}}^{{\text{3}}}},\,\,\,\,{{B}_{1}} = 1.4,\,\,\,\,{{n}_{{\text{C}}}} = 12, \\ \lambda = 5.0 \times {{10}^{{ - 10}}}\,\,{\text{м}},\,\,\,\,{{\gamma }_{0}} = 40\,\,{{{\text{мН}}} \mathord{\left/ {\vphantom {{{\text{мН}}} {\text{м}}}} \right. \kern-0em} {\text{м}}},\,\,\,\,\varepsilon = 40, \\ \delta = 3 \times {{10}^{{ - 10}}}\,\,{\text{м}},\,\,\,\,z = 1,\,\,\,\,T = 293\,\,K, \\ {{\upsilon }_{2}} = {\text{3}}{\text{.2}} \times {\text{1}}{{{\text{0}}}^{{ - 28}}}\,\,{{{\text{м}}}^{{\text{3}}}},\,\,\,\,{{B}_{2}} = 14. \\ \end{gathered} $(45)
$\begin{gathered} {{с}_{{10}}} = 3.393 \times {{10}^{{24}}}\,\,{{{\text{м}}}^{{ - {\text{3}}}}},\,\,\,\,{{n}_{{10}}} = 35.63, \\ {{с}_{{1{\text{ККМ}}}}} = 1.28{{c}_{{10}}},\,\,\,\,{{с}_{{20}}} = 2.81 \times {{10}^{{21}}}\,\,{{{\text{м}}}^{{ - {\text{3}}}}}. \\ \end{gathered} $Проведенные с помощью (20), (41) и (44), (45) результаты расчета работы агрегации $W\left( {{{n}_{1}},{{n}_{2}},{{c}_{1}},{{c}_{2}}} \right)$ и $\tilde {c}_{{{{n}_{1}}{{n}_{2}}}}^{{\left( {\text{e}} \right)}}$ как функций чисел агрегации ${{n}_{1}}$ и ${{n}_{2}}$ при различных равновесных концентрациях мономеров ПАВ и мономеров солюбилизата в водном растворе представлены ниже на рис. 1–4. К каждому рисунку по формулам (24), (25) и (42), (43) были найдены равновесные числа агрегации ${{n}_{{1{\text{e}}}}},$ ${{n}_{{2{\text{e}}}}}$(отвечающие особым точкам работы агрегации и распределения по числам агрегации) и относительные доли ${{\alpha }_{{{\text{sur}}}}}$ и ${{\alpha }_{{{\text{sol}}}}}$ молекул ПАВ и солюбилизата в агрегатах. Прокомментируем рис. 1–4 последовательно.
Рис. 1.
(а) Работа агрегации $W$ молекулярных агрегатов при ${{с}_{1}} = 1.5{{с}_{{10}}}$ = ${\text{3}}{\text{.59}} \times {{10}^{{24}}}$ м–3, ${{с}_{2}} = {{10}^{{ - 5}}}{{с}_{{10}}}$ = $2.{\text{39}} \times {{10}^{{19}}}$ м–3 (${{{{с}_{2}}} \mathord{\left/ {\vphantom {{{{с}_{2}}} {{{с}_{{20}}}}}} \right. \kern-0em} {{{с}_{{20}}}}} = 0.008$); (б) распределение относительных концентраций $\tilde {c}_{{{{n}_{1}}{{n}_{2}}}}^{{\left( {\text{e}} \right)}}$ молекулярных агрегатов, соответствующее работе на рис. 1а.

Рис. 2.
(а) Работа агрегации $W$ молекулярных агрегатов при ${{с}_{1}} = 1.5{{с}_{{10}}}$ = ${\text{3}}{\text{.59}} \times {{10}^{{24}}}$ м–3, ${{с}_{2}} = 7 \times {{10}^{{ - 5}}}{{с}_{{10}}}$ = $1.7 \times {{10}^{{20}}}$ м–3 (${{{{с}_{2}}} \mathord{\left/ {\vphantom {{{{с}_{2}}} {{{с}_{{20}}} = 0.06}}} \right. \kern-0em} {{{с}_{{20}}} = 0.06}}$); (б) относительная концентрация $\tilde {c}_{{{{n}_{1}}{{n}_{2}}}}^{{\left( {\text{e}} \right)}}$ молекулярных агрегатов, соответствующая работе на рис. 2а.

Рис. 3.
(а) Работа агрегации $W$ молекулярных агрегатов при ${{с}_{1}} = 1.5{{с}_{{10}}}$ = ${\text{3}}{\text{.59}} \times {{10}^{{24}}}$ м–3, ${{с}_{2}} = 2 \times {{10}^{{ - 4}}}{{с}_{{10}}}$ = $4.8 \times {{10}^{{20}}}$ м–3 (${{{{с}_{2}}} \mathord{\left/ {\vphantom {{{{с}_{2}}} {{{с}_{{20}}} = 0.17}}} \right. \kern-0em} {{{с}_{{20}}} = 0.17}}$); (б) относительная концентрация $\tilde {c}_{{{{n}_{1}}{{n}_{2}}}}^{{\left( {\text{e}} \right)}}$ молекулярных агрегатов, соответствующая работе на рис. 3а.
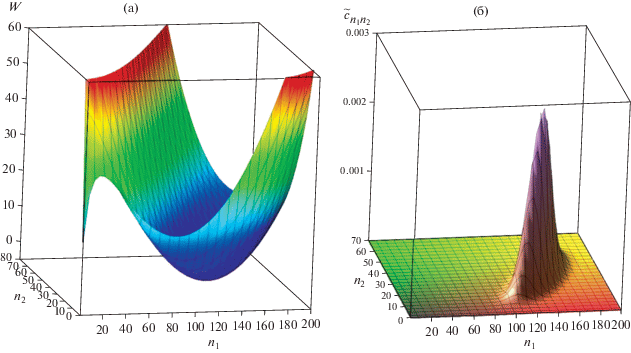
Рис. 4.
(а) Работа агрегации $W$ молекулярных агрегатов при ${{с}_{1}} = 0.8{{с}_{{10}}}$ = ${\text{1}}{\text{.91}} \times {{10}^{{24}}}$ м–3, ${{с}_{2}} = 6.38 \times {{10}^{{ - 4}}}{{с}_{{10}}}$ = $1.53 \times {{10}^{{21}}}$ м–3 (${{{{с}_{2}}} \mathord{\left/ {\vphantom {{{{с}_{2}}} {{{с}_{{20}}} = 0.54}}} \right. \kern-0em} {{{с}_{{20}}} = 0.54}}$); (б) относительная концентрация $\tilde {c}_{{{{n}_{1}}{{n}_{2}}}}^{{\left( {\text{e}} \right)}}$ молекулярных агрегатов, соответствующая работе на рис. 4а.

Рисунки 1–3 относятся к фиксированной концентрации ${{с}_{1}} = 1.5{{с}_{{10}}}$ мономеров ПАВ, которая немного ниже концентрации мономеров ${{с}_{{1{\text{ККМ}}}}} = 1.625{{c}_{{10}}}$ (найденной с помощью (33) и (32)) для чистого раствора ПАВ. При концентрации солюбилизата ${{с}_{2}} = {{10}^{{ - 5}}}{{с}_{{10}}},$ взятой при построении рис. 1а и 1б, видим, что у работы агрегации $W$ имеется седловая точка при ${{n}_{{1{\text{c}}}}} \approx 15$ и ${{n}_{{2{\text{c}}}}} = 0$ и минимум при ${{n}_{{1{\text{s}}}}} \approx 84$ и ${{n}_{{2{\text{s}}}}} \approx 1$ (находим из (24) и (25)). На рис. 1б минимуму работы агрегации соответствует максимум распределения концентраций $\tilde {c}_{{{{n}_{1}}{{n}_{2}}}}^{{\left( {\text{e}} \right)}}.$ Заметно выражен еще один пик распределения, который лежит в окрестности мономеров ПАВ. Соответствующие доля ПАВ и доля солюбилизата в устойчивых молекулярных агрегатах равны ${{\alpha }_{{{\text{sur}}}}} = 9 \times {{10}^{{ - 5}}}$ и ${{\alpha }_{{{\text{sol}}}}} = 0.35.$ Из вида распределения на рис. 1б следует, что сначала образуется достаточно много устойчивых мицелл с числами агрегации ${{n}_{1}}$ от 40 до 140, которые захватывают молекулы солюбилизата. Число агрегации ${{n}_{2}}$ в этих мицеллах лежит в интервале от 0 до 5.
При концентрации солюбилизата c2 = 7 × $ \times \,\,{{10}^{{ - 5}}}{{с}_{{10}}},$ взятой при построении рис. 2а и 2б, видим, что у работы агрегации $W$ имеется седловая точка при ${{n}_{{1{\text{c}}}}} \approx 15$ и ${{n}_{{2{\text{c}}}}} = 0$ и минимум при ${{n}_{{1{\text{s}}}}} \approx 95$ и ${{n}_{{2{\text{s}}}}} \approx 5.$ То, что седловая точка практически не сместилась по сравнению с рис. 1а, означает с учетом вида рис. 2б, что сначала образуется мицеллы чистого ПАВ. Минимуму работы агрегации соответствует заметный максимум распределения концентраций $\tilde {c}_{{{{n}_{1}}{{n}_{2}}}}^{{\left( {\text{e}} \right)}},$ в то время как пик распределения в окрестности мономеров ПАВ становится менее выраженным. Соответствующие доли ПАВ и солюбилизата в устойчивых молекулярных агрегатах равны ${{\alpha }_{{{\text{sur}}}}} = 0.05$ и ${{\alpha }_{{{\text{sol}}}}} = 68$ (т.е., число молекул солюбилизата в агрегатах уже на 2 порядка превышает концентрацию этих молекул в растворе). В растворе присутствует много не очень крупных мицелл с числами агрегации ${{n}_{1}}$ от 50 до 140 и числами молекул солюбилизата ${{n}_{2}}$ от 0 до 15.
При дальнейшем росте концентрации ${{с}_{2}}$ минимум работы агрегации становится глубже и смещается в область бóльших значений чисел агрегации ${{n}_{1}}$ и ${{n}_{2}}.$ Это хорошо видно на рис. 3а при ${{с}_{2}} = 2 \times {{10}^{{ - 4}}}{{с}_{{10}}}.$ Корни системы уравнений (24) и (25) имеют следующие значения: для седловой точки ${{n}_{{1{\text{c}}}}} \approx 14,$ ${{n}_{{2{\text{c}}}}} = 0$ и для минимума ${{n}_{{1{\text{s}}}}} \approx 136,$ ${{n}_{{2{\text{s}}}}} \approx 29.$ Происходит сильное накопление ПАВ и вещества солюбилизата в мицеллах: ${{\alpha }_{{{\text{sur}}}}} = 1.1 \times {{10}^{5}},$ ${{\alpha }_{{{\text{sol}}}}} = 1.8 \times {{10}^{8}}.$ Мицеллы будут заметно больше, с числами агрегации ${{n}_{1}}$ от 80 до 180 и числами агрегации ${{n}_{2}}$ от 5 до 55. При взятом масштабе на рис. 3б пик распределения видится изолированным при ${{n}_{2}} > 10,$ однако, согласно рис. 3а, сначала образуются мицеллы чистого ПАВ при ${{n}_{2}} = 0,$ которые затем “скатываются” к минимуму работы при ${{n}_{{1{\text{s}}}}} \approx 136,$ ${{n}_{{2{\text{s}}}}} \approx 29.$ При дальнейшем увеличении концентрации солюбилизата ${{с}_{2}}$ минимум работы агрегации уходит в отрицательную область, хотя раствор остается равновесным.
Заметим, что при выбранном для расчетов, результаты которых были представлены на рис. 1–3 и в комментариях к этим рисункам, значении концентрации мономеров ПАВ ${{с}_{1}} = 1.5{{с}_{{10}}}$ с ростом концентрации ${{с}_{2}}$ достаточно быстро возрастала и равновесная брутто-концентрация ПАВ. Можно ожидать, что при меньших равновесных концентрациях мономеров ПАВ указанная тенденция будет выражена слабее.
На рис. 4а и 4б представлено поведение работы агрегации $W$ агрегатов из молекул ПАВ и солюбилизата и распределения относительных концентраций агрегатов $\tilde {c}_{{{{n}_{1}}{{n}_{2}}}}^{{\left( {\text{e}} \right)}}$ как функций чисел агрегации ${{n}_{1}}$ и ${{n}_{2}}$ при концентрации мономеров ПАВ ${{с}_{1}} = 0.8{{с}_{{10}}},$ что в 2 раза ниже концентрации ${{с}_{{1{\text{ККМ}}}}}$ в чистом водном растворе ПАВ. При концентрации ${{с}_{2}} = 6.38 \times {{10}^{{ - 4}}}{{с}_{{10}}}$ корни системы уравнений (24) и (25) имеют следующие значения: для седловой точки работы агрегации ${{n}_{{1{\text{c}}}}} \approx 36,$ ${{n}_{{2{\text{c}}}}} \approx 3$ и для минимума работы ${{n}_{{1{\text{s}}}}} \approx 374,$ ${{n}_{{2{\text{s}}}}} \approx 430.$ Видим, что в среднем число молекул солюбилизата уже превышает число молекул ПАВ в агрегате, и такие агрегаты становятся ближе к капле эмульсии. Агрегаты будут большими, с числами агрегации ${{n}_{1}}$ от 270 до 470 и числами агрегации ${{n}_{2}}$ от 200 до 700. Значения ${{\alpha }_{{{\text{sur}}}}} = 391$ и ${{\alpha }_{{{\text{sol}}}}} = 5.7 \times {{10}^{5}}$ для рассматриваемых концентраций ${{c}_{1}}$ и ${{c}_{2}}$ означают, что происходит существенное накопление ПАВ и вещества солюбилизата в агрегатах, однако доля ПАВ в агрегатах становится меньше. Это подтверждает сделанное выше предположение, что при уменьшении равновесной концентрации мономеров ПАВ дальнейший рост равновесной брутто-концентрация ПАВ с ростом концентрации ${{с}_{2}}$ замедляется. Заметим, однако, что с уменьшением концентрации мономеров ПАВ возрастает активационный барьер для перехода от мономеров к устойчивым мицеллам. Этот барьер равен значению работы агрегации в седловой точке и определяет время установления мицеллярного равновесия и другие кинетические характеристики релаксации мицеллярных растворов [22–24]. Чем больше этот барьер, тем дольше устанавливается равновесие в дисперсных системах. При приближении равновесной концентрации молекул солюбилизата к значению ${{c}_{{20}}}$ система теряет термодинамическую устойчивость.
ЗАКЛЮЧЕНИЕ
В данном сообщении обосновано новое термодинамическое соотношение (20) для работы образования молекулярного агрегата из молекул неионного ПАВ и молекул солюбилизата в тройном растворе углеводород–ПАВ–вода. Это соотношение учитывает гидрофобное взаимодействие углеводородных групп в ядре агрегата, сферическое искривление ядра и возникающую разницу давлений, электростатическое взаимодействие полярных групп молекул неионного ПАВ, разницу химических потенциалов молекул ПАВ и солюбилизата в водном растворе и в агрегате. Записанная для работы агрегации формула определяет ее как функцию температуры, концентраций ПАВ и углеводорода в растворе, чисел агрегации ПАВ и углеводорода в агрегате и параметрически зависит от строения и физических характеристик молекул ПАВ и углеводорода.
Найдены соотношения (24) и (25) для чисел агрегации в седловой точке и точке минимума работы агрегации, определяющих прямой и обратный активационный барьеры при образовании устойчивых агрегатов. Записано соотношение (41) для распределения относительных концентраций агрегатов по числам агрегации ПАВ и солюбилизата при разных концентрациях мономеров ПАВ и углеводорода в растворе.
На примере водного раствора неионного ПАВ c числом атомов C в углеводородном радикале равным 12 и декана как солюбилизата рассчитаны примеры двумерных поверхностей работы агрегации и распределения при разных равновесных концентрациях солюбилизата и равновесных концентрациях мономеров ПАВ существенно меньших, чем концентрация, соответствующая ККМ в чистом растворе ПАВ (рис. 1–4). Сделанные с помощью формул (24) и (25) и формул (42) и (43) оценки чисел агрегации и долей ПАВ и солюбилизата в агрегатах по отношению к равновесным концентрациям мономеров ПАВ и солюбилизата показывают возможность колоссального накопления солюбилизата в молекулярных агрегатах и переход при относительно низких концентрациях ПАВ к прямым микроэмульсиям. При этом в рассмотренных примерах формирование микроэмульсии начинается с образования практически чистых мицелл ПАВ и последующего захвата мономеров солюбилизата.
Показано, что предельные концентрации неионного ПАВ и солюбилизата, соответствующие формированию устойчивых нано- и микроэмульсий, лежат в достаточно узких интервалах, попасть в которые при случайном поиске в лабораторных экспериментах маловероятно.
Список литературы
Dynamics of Surfactant Self-Assemblies: Micelles, Microemulsions, Vesicles and Lyotropic Phases. Surfactant Science Series. V. 125 / Ed. by Zana R. Boca Raton: CRC Press, 2005.
Schramm L.L. Emulsions, Foams, and Suspensions. Fundamentals and Applications. Weinheim, Wiley-VCH Verlag GmbH & Co. KGaA, 2005.
Surfactants and Interfacial Phenomena / Ed. by Rosen M.J., Kunjappu J.T. Hoboken, New Jersey: Wiley, 2012.
Micelles: Structural Biochemistry, Formation and Functions & Usage / Ed. by Bradburn D., Bittinger T. New York: Nova Science Publ., 2014.
Русанов А.И., Щёкин А.К. Мицеллообразование в растворах поверхностно-активных веществ. 2-е изд. СПб.: Лань, 2016.
Self-Assembly: From Surfactants to Nanoparticles / Ed. by Nagarajan R. Hoboken: Wiley, 2019.
Tanford C. The Hydrophobic Effect: Formation of Micelles and Biological Membranes. 2nd ed. N.Y.: Wiley, 1980.
Nagarajan R., Ruckenstein E. // Equations of State for Fluids and Fluid Mixtures. Ed. by Sengers J.V., Kayser R.F., Peters C.J., White H.J. Experimental Thermodynamics. V. 5. P. 589. Amsterdam: Elsevier, 2000.
Puvvada S., Blankschtein D. // J. Chem. Phys. 1990. V. 92. P. 3710.
Kralchevsky P.A., Danov K.D., Anachkov S.E. // Colloid J. 2014. V. 76. P. 255.
Danov K.D., Kralchevsky P.A., Stoyanov S.D., Cook J.L., Stott I.P., Pelan E.G. // Adv. Colloid Interface Sci. 2018. V. 256. P. 1.
Danov K.D., Kralchevsky P.A., Stoyanov S.D., Cook J.L., Stott I.P. // J. Colloid Interface Sci. 2019. V. 547. P. 245.
Danov K.D., Kralchevsky P.A., Stoyanov S.D., Cook J.L., Stott I.P. // J. Colloid Interface Sci. 2019. V. 551. P. 227.
Danov K.D., Kralchevsky P.A., Stoyanov S.D., Cook J.L., Stott I.P. // J. Colloid Interface Sci. 2021. V. 581. Part A. P. 262.
Русанов А.И., Гринин А.П., Куни Ф.М., Щекин А.К. // Журн. общей химии. 2002. Т. 72. С. 651.
Русанов А.И., Куни Ф.М., Гринин А.П., Щекин А.К. // Коллоид. журн. 2002. Т. 64. С. 670.
Русанов А.И. // Коллоид. журн. 2021. Т. 83. С. 98.
Щёкин А.К., Шабаев И.В. // Коллоид. журн. 2010. Т. 72. С. 424.
Reiss H. // J. Chem. Phys. 1950. V. 18. P. 840.
Мелихов А.А., Курасов В.Б., Джикаев Ю.Ш., Куни Ф.М. // Журн. техн. физики. 1991. Т. 61. № 1. С. 27.
Wilemski G., Wyslouzil B.E. // J. Chem. Phys. 1995. V. 103. P. 1127.
Куни Ф.М., Русанов А.И., Щёкин А.К., Гринин А.П. // Журн. физ. химии. 2005. Т. 79. С. 967.
Shchekin A.K., Kuni F.M., Grinin A.P., Rusanov A.I. // Nucleation Theory and Application. Ed. by Schmelzer J.W.P. N.Y.: Wiley, 2005. Ch. 9. P. 312.
Щёкин А.К., Аджемян Л.Ц., Бабинцев И.А., Волков Н.А. // Коллоид. журн. 2018. Т. 80. С. 115.
Дополнительные материалы отсутствуют.
Инструменты
Коллоидный журнал


