Коллоидный журнал, 2021, T. 83, № 5, стр. 499-504

ВВЕДЕНИЕ

Теоретическое исследование поверхностных сил началось с суммирования парного потенциала дисперсионных взаимодействий между молекулами сорта p и q

где R – расстояние между молекулами и A – постоянная. Таким путем Гамакер [1] рассчитал силу взаимодействия F между двумя шарами, между шаром и полубесконечным твердым телом с плоской поверхностью и между двумя плоскопараллельными поверхностями (на единицу поверхности S).

Последняя сила, пожалуй, – наиболее известный результат классической коллоидной науки

и постоянная $C \equiv {{\pi {{c}_{1}}{{c}_{2}}{{A}_{{12}}}} \mathord{\left/ {\vphantom {{\pi {{c}_{1}}{{c}_{2}}{{A}_{{12}}}} 6}} \right. \kern-0em} 6}$ теперь носит имя Гамакера (с – молекулярная плотность взаимодействующих тел 1 и 2, H – расстояние между поверхностями). Дерягин [2] назвал величину Π расклинивающим давлением с общим определением где p – давление на поверхностях взаимодействующих тел, а p^α – давление в материнской фазе пленки, находящейся с ней в равновесии (в случае вакуума p^α = 0 и Π = p < 0). Наличие расклинивающего давления отличает тонкие пленки от толстых, и его изучение является одним из центральных направлений коллоидной науки [3].

Во многих задачах с участием поверхностных сил важным является не только сила взаимодействия наночастиц как целых, но и распределение сил в самих частицах. Это распределение задается полем тензора напряжений $\hat {E}$ (шляпка – символ тензора), вычисление которого также стало задачей коллоидной науки. Вычисления такого рода можно осуществлять методом статистической механики с помощью тензора напряжений Ирвинга–Кирквуда [4]

Здесь $\hat {E}({\mathbf{r}})$ – значение тензора напряжений в точке r; k – постоянная Больцмана; T – температура; ${{\rho }_{p}}({\mathbf{r}})$ – одночастичная функция распределения (локальная плотность) частиц сорта p; $\hat {1}$ – единичный тензор; R – вектор, соединяющий две взаимодействующие частицы с расстоянием R между ними и проходящий через точку r (запись ${\mathbf{R}} \times {\mathbf{R}}$ символизирует прямое векторное произведение, являющееся тензором); $\Phi _{{pq}}^{'}(R)$ – производная от потенциала парного взаимодействия (1) частиц сортов p и q (т.е. сила взаимодействия этих частиц); $\rho _{{pq}}^{{(2)}}({\mathbf{r}} - \eta \,{\mathbf{R}},\,\;{\mathbf{r}} - \eta \,{\mathbf{R}} + \,{\mathbf{R}})$ – двухчастичная функция распределения для частиц, находящихся одновременно в точках ${{{\mathbf{r}}}_{1}} = {\mathbf{r}} - \eta \,{\mathbf{R}}$ и ${{{\mathbf{r}}}_{2}} = {\mathbf{r}} - \eta \,{\mathbf{R}} + \,{\mathbf{R}}$ по разные стороны от единичной площадки с координатой r (что регулируется вспомогательной переменной η). При работе с жидкостями обычно используют не тензор напряжений, а тензор давления $\hat {p}({\mathbf{r}}),$ который только знаком отличается от тензора напряжений:

Первым применением тензора давления Ирвинга–Кирквуда в коллоидной науке был расчет тензора давления и расклинивающего давления в плоской тонкой жидкой пленке [5]. Разработанный там алгоритм расчета многократно использовался в дальнейшем для описания поверхностных сил в телах различной конфигурации (см. обзор [6]). Важен был переход (уже в 21 веке) к телам ограниченных размеров и, в частности, к клиновидным пленкам, позволивший сформулировать термодинамику трещин [7]. Нужно отметить, что оперировать с тензором напряжений Ирвинга–Кирквуда непросто, и подобных работ в мировой литературе чрезвычайно мало. Можно сказать, что это направление стало брендом петербургской термодинамической школы.

Одним из примеров твердых тел, для которых исследование распределения механических напряжений особенно важно, являются пористые адсорбенты. Первые расчеты с применением тензора напряжений Ирвинга–Кирквуда были проведены в работах [8, 9] для плоских (щелевидных), цилиндрических и сферических пор. В частности, для парного потенциала ${{\Phi }_{{ij}}}(R) = - A_{{ij}}^{{({{\lambda }})}}{{R}^{{ - {{\lambda }}}}}$ (λ = 6 для дисперсионных сил без запаздывания, и λ = 7 для дисперсионных сил с запаздыванием) в рамках асимптотической теории были получены выражения для нормального давления в центре (где оно изотропно) сферической полости радиуса a

и цилиндрической полости такого же радиуса где давление p, молекулярные плотности ρ_i и гиббсовские адсорбции ${{\Gamma }_{i}}$ относятся к макроскопической системе (при а → ∞), фаза α лежит внутри полости, фаза β – снаружи, и суммирование производится по всем компонентам, c_λ равно π для четных λ и 2 для нечетных.

Полученные в [8, 9] результаты вновь использовались при создании теории сорбострикции [10] – механохимического явления деформации пористого тела в процессе адсорбции. Однако формула (6) характеризует только пустой центр полости. Для широкого представления нужен полный расчет на основе формулы (4), что мы и сделаем в этом сообщении. Чтобы можно было использовать в расчетах интегрирование, мы должны принять, что объект не является монокристаллом (иначе замена суммирования по кристаллическим плоскостям интегрированием давало бы существенную ошибку). Но число компонентов ограничивать не будем.

ПРОЦЕДУРА РАСЧЕТА

Будем рассматривать пустые сферическую и цилиндрическую полости в твердом теле как классические поры с искривленными поверхностями, чтобы выделить вклад от кривизны в тензор напряжений. Примерами адсорбентов со сферическими порами являются цеолиты, а цилиндрические поры характерны для различных силикатных и углеродных адсорбентов.

СФЕРИЧЕСКАЯ ПОЛОСТЬ

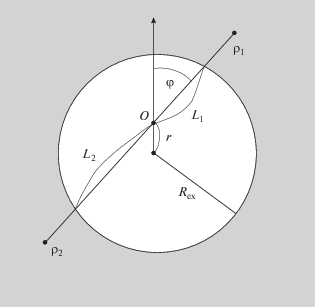
Начнем со сферической полости, сечение которой изображено схематически на рис. 1. Радиус полости равен ${{R}_{{\operatorname{ex} }}}$. Расчетная точка O лежит внутри полости, но не в ее центре. Поместим начало сферической системы координат в рассматриваемую точку O, расстояние которой до центра сечения равно r. Величина r изменяется от 0 до R_ex. Из пары взаимодействующих молекул одна находится в точке 1 и указана вектором ${{{\mathbf{r}}}_{1}},$ а другая – в точке 2 с вектором ${{{\mathbf{r}}}_{2}}$. Кроме того, если рассматривать точку 1 только в верхней части пространства по отношению к элементарной площадке в расчетной точке, а точку 2 – в нижней его части, то множитель ½ перед интегралом следует опустить. Тензор напряжений Ирвинга–Кирквуда в пустой поре принимает вид

Расстояние R между взаимодействующими точками теперь равно r₁ + r₂.

Перейдем далее от переменных R, η, определенных выше при описании формулы (4), к r₁ и r₂:

где D – якобиан. Тогда тензорное произведение под интегралом ${\mathbf{R}} \times {\mathbf{R}}$ преобразуется в ${{\left( {\frac{{{{r}_{1}} + {{r}_{2}}}}{{{{r}_{1}}}}} \right)}^{2}}{{{\mathbf{r}}}_{1}} \times {{{\mathbf{r}}}_{1}}$. В сферических координатах составляющие вектора r₁ равны и тензор ${{{\mathbf{r}}}_{1}} \times {{{\mathbf{r}}}_{1}}$ равен $r_{1}^{2}\hat {\kappa }(\varphi ,\vartheta )$, где введен новый тензор, зависящий только от угловых координат ϑ и φ. В силу симметрии задачи в тензоре ${{\hat {\kappa }}}({{\varphi }},\vartheta )$нужно будет учитывать только диагональные компоненты

При этом κ_rr соответствует нормальной компоненте, а κ_φφ и κ_ϑϑ – тангенциальной в тензоре напряжения.

Условие, чтобы прямая, соединяющая молекулы 1 и 2, проходила через рассматриваемую точку, накладывает ограничения на пределы интегрирования выбранных переменных. Для переменных r₁ и r₂ − это величины L_k (k = 1, 2), которые определяют расстояния от точки O (начала координат) до пересечения линии, проходящей через точки 1 и 2, с ограничивающей полость сферой (рис. 1). Для заданного угла ϑ их величину находим из соответствующих треугольников, а именно

Угловые переменные φ и ϑ меняются в интервалах $0 < {{\varphi }} < 2{{\pi }},$ $0 < \vartheta < {{{\pi }} \mathord{\left/ {\vphantom {{{\pi }} 2}} \right. \kern-0em} 2}$. Перейдя к новым переменным и подставив под интеграл в правой части производную потенциала (1)

тензор напряжения в этих переменных запишем в следующем виде:

где учтена симметрия системы относительно угла φ.

Пренебрегая корреляциями, заменим двухчастичную функцию произведением соответствующих плотностей компонентов твердой фазы β. Это означает, что следует накладывать какое-то ограничение на расстояние рассматриваемой точки до поверхности. После этого несложно провести интегрирование по φ, r₁ и r₂. Поскольку от угла φ зависят только компоненты тензора $\hat {\kappa }({{\varphi }},\vartheta )$, то, проведя интегрирование по этому углу, получим множитель π и новый тензор ${{\hat {\kappa }}_{1}}(\vartheta )$:

В силу симметрии ${{\kappa }_{{1rr}}}$ соответствует нормальной компоненте тензора напряжений E_N, а обе компоненты ${{\kappa }_{{1\vartheta \vartheta }}}$ и ${{\kappa }_{{1{{\varphi \varphi }}}}}$ − тангенциальной компоненте E_T.

Далее легко выполнить интегрирование по r₁ и r₂, в результате которого получим следующее выражение для тензора напряжения:

Вводя постоянный множитель C, равный

и подставив в интеграл выражения (12) для L₁ и L₂, запишем для $\hat {E}(r)$ следующее выражение:

Интегралы в (18) для компонент тензора напряжений вычисляются аналитически и дают следующие формулы:

Полученные выражения удовлетворяют условию механического равновесия

Вводя переменную x = r/R_ex, можем представить тензор напряжений в виде

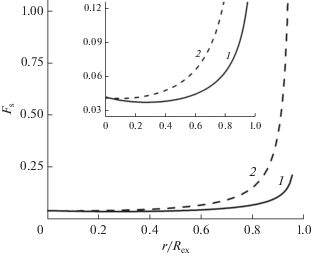
Функции ${{F}_{{{\text{sN}}}}}(x)$ и ${{F}_{{{\text{sT}}}}}(x)$ показаны на рис. 2, где видно, что в ближайшей к центру окрестности зависимость компонент тензора довольно слабая от x. При этом согласно формулам (23) и (24) тангенциальная составляющая отклоняется от значения в центре несколько сильнее, чем нормальная. Наименьшим вкладом оказывается квадратичный с тем же знаком, что и у главного члена разложения. На вкладке рис. 2 видно, что тангенциальная компонента является почти монотонной функцией, а нормальная компонента слабо меняется в области r < 0.8R_ex, демонстрируя незначительный широкий минимум при r ≈ 0.4R_ex. Такое поведение нормальной компоненты оправдывает использованное в [10] приближение с заменой локального нормального напряжения в сферической поре его значением в центре. В другой проблемной области – вблизи поверхности – не происходит взаимной компенсации расходящихся вкладов, и можно наблюдать сравнительно слабую расходимость нормального напряжения по сравнению с тангенциальным (рис. 2).

Следует помнить, что формулы (19) и (20) применимы в любой точке полости за исключением точек r = 0 и r = R_ex. Однако предельное поведение в центральной области можно получить, раскладывая в ряд по степеням малого параметра r/R_ex окончательные выражения в уравнениях (19) и (20). В результате взаимной компенсации вкладов от двух слагаемых имеем в пределе следующие конечные выражения:

и главный член разложения обратно пропорционален кубу радиуса полости и одинаков для обеих компонент тензора в соответствии с симметрией системы. Кроме того, он согласуется с результатом асимптотического подхода при λ = 6 для вклада второго слагаемого в правой части уравнения (6). Ограничения формулы (19) по сравнению с формулой (6) состоят в том, что она относится только к пустой полости, в то время как (6) описывает поведение локального давления в полости, заполненной флюидной фазой α. Но в отличие от результатов, полученных в [8, 9], результаты данного расчета применимы во всей полости, а не только в ее центральной области.

ЦИЛИНДРИЧЕСКАЯ ПОЛОСТЬ

Рассмотрим теперь бесконечную цилиндрическую пору, схема сечения которой перпендикулярно оси z представлена на рис. 3. Процедура расчета аналогична проделанной выше со сферической полостью, поэтому опишем только те моменты, которые присущи цилиндрической поре. В качестве исходного выражения тензора напряжений будет использоваться формула (8).

Поместим начало цилиндрической системы координат в точку O. Полярная ось направлена вдоль линии, соединяющей центр сечения и точку O. Отрезки ρ₁ и ρ₂ представляют собой проекции соответствующих векторов на координатную плоскость и равны расстояниям рассматриваемых точек до оси z. Не следует их смешивать с одночастичными плотностями компонентов ${{\rho }}_{p}^{{{\beta }}}$.

Заменим переменные R и η на r₁(ρ₁, z_1, φ) и ρ₂:

где D – якобиан. Тогда тензорное произведение под интегралом ${\mathbf{R}} \times {\mathbf{R}}$ преобразуется в ${{\left( {\frac{{{{{{\rho }}}_{1}} + {{{{\rho }}}_{2}}}}{{{{{{\rho }}}_{1}}}}} \right)}^{2}}{{{\mathbf{r}}}_{1}} \times {{{\mathbf{r}}}_{1}}$. В цилиндрических координатах составляющие вектора r₁ равны

Подынтегральное выражение в формуле (8) с учетом уравнения (13) представляется следующим образом:

Как и ранее, заменим двухчастичную функцию произведением соответствующих плотностей компонентов твердой фазы β и выполним интегрирование по z₁. Это приведет подынтегральное выражение к следующему виду:

где диагональные компоненты тензора $\hat {\kappa }({{\varphi }}),$ равны

Компонента ${{\kappa }_{{{{\rho \rho }}}}}$ соответствует нормальной компоненте тензора напряжения E_N, а две другие – двум тангенциальным: ${{\kappa }_{{{{\varphi \varphi }}}}}$ − E_T1, ${{\kappa }_{{zz}}}$ − E_T2. В цилиндрической поре в отличие от сферической появляются две различные тангенциальные компоненты.

Чтобы провести интегрирование по ρ₁ и ρ₂, нужно учесть пределы их изменения, определенные уравнениями, аналогичными (12), где следует заменить угол ϑ на угол φ, который изменяется от −π/2 до π/2. В результате интегрирования получим окончательное выражение для тензора напряжения

где C определено уравнением (17). В отличие от уравнения (18) для сферической полости дальнейшее интегрирование (30) в элементарных функциях невозможно, поскольку все интегралы представляют собой комбинации полных эллиптических функций первого (K(x)) и второго (E(x)) рода (x = r/R_ex < 1). Записав тензор напряжений с введением интегрального тензора ${{\hat {F}}_{{\text{с}}}}(x)$ как для его компонентов получим следующие выражения:

C использованием определений эллиптических интегралов можно убедиться, что полученный тензор напряжений удовлетворяет условию механического равновесия, которое для этой системы имеет вид

Результаты численного интегрирования для всех трех компонентов интегрального тензора ${{\hat {F}}_{{\text{с}}}}(x)$ представлены на рис. 4.

Как и в сферической полости, локальная зависимость тензора напряжения слабо проявляется вплоть до расстояний 0.7R_ex−0.8R_ex от оси, а затем функции начинают быстро расти при приближении к твердой поверхности. При этом вблизи оси значения нормальной E_ρρ = E_N и тангенциальной E_φφ = E_T1 компонент практически совпадают. Согласно соотношениям (28) вторая тангенциальная компонента ${{E}_{{zz}}} = ({{E}_{{{{\rho \rho }}}}} + {{E}_{{{{\varphi \varphi }}}}}{\text{)/5}}\;{\text{ = }}\;{{E}_{{{\text{T2}}}}}$. Если сопоставить кривые на рис. 2 и 3, то видно, что по сравнению со сферической полостью значения компонентов тензора давления в цилиндрической поре заметно меньше. В этом можно убедиться, исследуя предельные зависимости компонентов при r $ \ll $ R_ex. Раскладывая в ряд по степеням r/R_ex подынтегральные функции, получим следующие предельные соотношения:

На оси цилиндрической полости при r = 0 в силу симметрии значения нормальной компоненты и первой тангенциальной совпадают. Отличной от них будет вторая тангенциальная компонента, характеризующая напряжения вдоль оси z. Полученные предельные значения, как и в сферической системе, обратно пропорциональны кубу радиуса полости, но их значения примерно в 1.36 раз меньше, чем в сферической полости. Главный член разложения (34) для нормальной компоненты тензора напряжений совпадает с соответствующим вкладом в формуле (7), полученной на основе асимптотического принципа для λ = 6.

ЗАКЛЮЧЕНИЕ

Одним из главных среди полученных результатов является вывод о том, что в обеих порах, сферической и бесконечной цилиндрической, компоненты тензора напряжения удовлетворяют условиям механического равновесия. Кроме того, показано, что предельное поведение тензора напряжений в условиях малой кривизны ограничивающих твердых поверхностей совпадает с результатами асимптотического подхода для рассматриваемого их вклада в случае ван-дер-ваальсовских сил.