Коллоидный журнал, 2021, T. 83, № 5, стр. 505-511

ВВЕДЕНИЕ

В предыдущей статье [1] мы исследовали поведение локального тензора напряжений в пустой сферической щели и оценивали вклад ее кривизны в расклинивающее давление. Продолжая изучение влияния искривления ограничивающих щель твердых поверхностей на поведение тензора напряжений, рассмотрим цилиндрическую щель, как еще один пример классического случая искривленных щелей, рассмотренных в [2] при анализе сорбострикционных явлений на основе асимптотического принципа. Рассмотрение будем проводить на основе дисперсионных взаимодействий с парным потенциалом между молекулами сорта p и q

где R – расстояние между молекулами и A – постоянная. Одним из первых эти силы использовал Гамакер [3] для определения силы взаимодействия между двумя шарами, между шаром и полубесконечным твердым телом с плоской поверхностью и между двумя плоскопараллельными поверхностями (на единицу поверхности S). Введение понятия расклинивающего давления Дерягиным [4, 5] было самым существенным дальнейшим развитием в этой области.

Во многих задачах с участием поверхностных сил важным является не только сила взаимодействия наночастиц как целых, но и распределение сил в самих частицах. Это распределение задается полем тензора напряжений $\hat {E}$ (шляпка – символ тензора), вычисление которого также стало задачей коллоидной науки. Успехи в определении локальных сил в различных системах, включая тонкие пленки и тела ограниченных размеров, были получены на основе асимптотического принципа [6]. Вычисления такого рода можно осуществлять методом статистической механики с помощью тензора напряжений Ирвинга–Кирквуда [7]

Здесь $\hat {E}({\mathbf{r}})$ – значение тензора напряжений в точке r; k – постоянная Больцмана; T – температура; ${{\rho }_{p}}({\mathbf{r}})$ – одночастичная функция распределения (локальная плотность) частиц сорта p; $\hat {1}$ – единичный тензор; R – вектор, соединяющий две взаимодействующие частицы с расстоянием R между ними и проходящий через точку r (запись ${\mathbf{R}} \times {\mathbf{R}}$ символизирует прямое векторное произведение, являющееся тензором); $\Phi _{{pq}}^{'}(R)$ – производная от потенциала парного взаимодействия (1) частиц сортов p и q (т.е. сила взаимодействия этих частиц); $\rho _{{pq}}^{{(2)}}({\mathbf{r}} - \eta \,{\mathbf{R}},\,\;{\mathbf{r}} - \eta \,{\mathbf{R}} + \,{\mathbf{R}})$ – двухчастичная функция распределения для частиц, находящихся одновременно в точках ${{{\mathbf{r}}}_{1}} = {\mathbf{r}} - \eta \,{\mathbf{R}}$ и ${{{\mathbf{r}}}_{2}} = {\mathbf{r}} - \eta \,{\mathbf{R}} + \,{\mathbf{R}}$ по разные стороны от единичной площадки с координатой r (что регулируется вспомогательной переменной η).

Первым применением тензора напряжений Ирвинга–Кирквуда в коллоидной науке был расчет тензора давления и расклинивающего давления в плоской тонкой жидкой пленке [8]. Разработанный там алгоритм расчета многократно использовался в дальнейшем для описания поверхностных сил в телах различной конфигурации (см. обзор [9]). Важен был переход (уже в 21 веке) к телам ограниченных размеров и, в частности, к клиновидным пленкам, позволивший сформулировать термодинамику трещин [10] в дополнение к усовершенствованию теории разрушения твердых тел вообще [11].

Для широкого представления нужен полный расчет на основе формулы (2), что мы и сделаем в этом сообщении на примере пустой цилиндрической щели. Чтобы можно было использовать в расчетах интегрирование, мы должны принять, что объект не является монокристаллом (иначе замена суммирования по кристаллическим плоскостям интегрированием давало бы существенную ошибку). Но число компонентов ограничивать не будем.

ПРОЦЕДУРА РАСЧЕТА

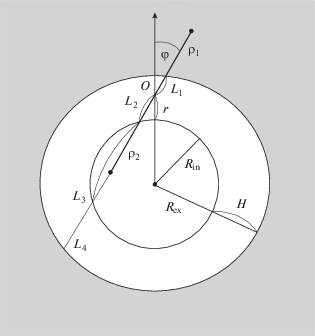
Будем рассматривать бесконечную пустую цилиндрическую щель между твердыми телами (внешняя фаза β и внутренняя фаза γ ) как еще один пример классической поры с искривленными поверхностями, чтобы выделить вклад от кривизны в расклинивающее давление и сравнить его со случаем ранее рассмотренной сферической щели. Схема сечения щели перпендикулярно оси z представлена на рис. 1.

Щель заключена между радиусами ${{R}_{{\operatorname{ex} }}}$ и ${{R}_{{\operatorname{in} }}}$ и имеет ширину $H = $ ${{R}_{{\operatorname{ex} }}}$– ${{R}_{{\operatorname{in} }}}$. Расчетная точка O лежит внутри полости, но не в ее центре. Поместим начало цилиндрической системы координат в рассматриваемую точку O, расстояние которой до центра сечения равно r. Величина r изменяется от R_in до R_ex. В цилиндрической системе координат положение рассматриваемых точек задается величинами ρ, φ и z. Полярная ось, от которой отсчитывается полярный угол φ, направлена вдоль линии, соединяющей центр сечения и точку O. Отрезки ρ₁ и ρ₂ представляют собой проекции соответствующих векторов на координатную плоскость и равны расстояниям рассматриваемых точек до оси z. Не следует их смешивать в дальнейшем с одночастичными плотностями компонентов ${{\rho }}_{p}^{{{\beta }}}$. Кроме того, если рассматривать точку 1 только в верхней части пространства по отношению к элементарной площадке в расчетной точке, а точку 2 – в нижней его части, то множитель 1/2 перед интегралом следует опустить. Тензор напряжений Ирвинга–Кирквуда в пустой поре принимает вид

С учетом симметрии системы в тензоре напряжений отличными от нуля будут только диагональные компоненты, а именно, нормальная ${{E}_{{\rho \rho }}} \equiv {{E}_{\operatorname{N} }}$ и две тангенциальные – ${{E}_{{\varphi \varphi }}} \equiv {{E}_{{{\text{T}}1}}}$ и ${{E}_{{zz}}} \equiv {{E}_{{{\text{T2}}}}}$, которые должны удовлетворять следующим условиям механического равновесия:

Последнее – очевидное следствие бесконечности щели в направлении оси z.

Займемся непосредственным расчетом выражения (3), в котором заменим переменные R и η на r₁(ρ₁, z_1, φ) и ρ₂:

где D – якобиан. Условие, чтобы прямая, соединяющая молекулы 1 и 2, проходила через расчетную точку, накладывает ограничения на пределы интегрирования ${{L}_{k}}$ выбранных переменных, а именно (рис. 1),

Тензорное произведение под интегралом ${\mathbf{R}} \times {\mathbf{R}}$ преобразуется в ${{\left( {{\text{(}}{{{{\rho }}}_{1}} + {{{{{{\rho }}}_{2}})} \mathord{\left/ {\vphantom {{{{{{\rho }}}_{2}})} {{{{{\rho }}}_{1}}}}} \right. \kern-0em} {{{{{\rho }}}_{1}}}}} \right)}^{2}}{{{\mathbf{r}}}_{1}} \times {{{\mathbf{r}}}_{1}}$, и составляющие вектора r₁ в цилиндрических координатах равны

Учитывая, что

подынтегральное выражение в формуле (3) представляется следующим образом:

Далее, как и в случае сферической щели, разделим тензор напряжения на две части:

из которых первая соответствует вкладу взаимодействий молекул внешней фазы с молекулами внутреннего цилиндра, а вторая − вкладу взаимодействий молекул внешней фазы друг с другом. Для дальнейших преобразований заменим двухчастичную функцию ${{\rho }}_{{pq}}^{{(2)}}({{{\mathbf{r}}}_{1}},{{{\mathbf{r}}}_{2}}){\kern 1pt} $ произведением частичных плотностей твердых фаз ${{\rho }}_{p}^{{{\beta }}}{{\rho }}_{q}^{{{\gamma }}}$ или ${{\rho }}_{p}^{{{\beta }}}{{\rho }}_{q}^{{{\beta }}}$, пренебрегая молекулярными корреляциями. Теперь можно провести интегрирование по z₁, принимая во внимание (10), что приведет к появлению перед интегралом множителя 15π/8 и под интегралом останется функция в которой диагональные компоненты тензора $\hat {\kappa }({{\varphi }})\;$ равны

Компонента ${{\kappa }_{{{{\rho \rho }}}}}$ соответствует нормальной компоненте тензора напряжения E_N, а две другие – двум тангенциальным: ${{\kappa }_{{{{\varphi \varphi }}}}}$ − E_T1, ${{\kappa }_{{zz}}}$ − E_T2. Как было отмечено выше, в цилиндрической поре в отличие от сферической появляются две различные тангенциальные компоненты.

ВКЛАД ВЗАИМОДЕЙСТВИЙ МОЛЕКУЛ ФАЗ β И γ

С учетом пределов изменения переменных ${{{{\rho }}}_{1}}$ и ${{{{\rho }}}_{2}}$ (7) и (8) получим следующие формулы для вкладов в тензор напряжений:

Интегрирование (16) по ${{{{\rho }}}_{1}}$ и ${{{{\rho }}}_{2}}$ легко выполняется. Рассмотрим сначала тензор ${{\hat {E}}_{{`1}}}(r)$, для которого после интегрирования получим следующее уравнение:

Очевидно, что такие внешние параметры щели как R_in и H наряду с локальной переменной r будут определять локальную зависимость тензора напряжения. Введем относительные переменные для ширины щели x = H/R_in и расстояния от внутренней поверхности y = r/R_in. После подстановки в (17) выражений (7) и (8) и ряда преобразований получим окончательную формулу для ${{\hat {E}}_{1}}(r)$ в терминах новых переменных

где введены постоянный множитель и интегральный тензор

Компоненты этого тензора выражаются посредством совокупности эллиптических интегралов, которые наиболее просто вычисляются численно.

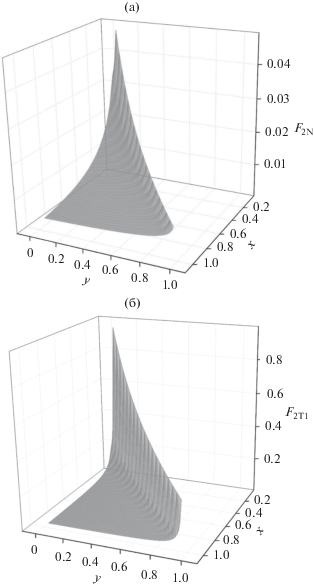
На рис. 2 показаны нормальная и первая тангенциальная компоненты тензора ${{\hat {F}}_{1}}$, пространственное поведение которых совершенно аналогично полученному ранее для аналогичного тензора в сферической щели.

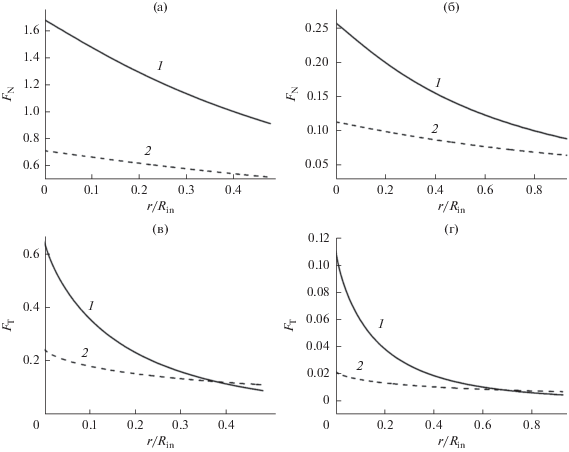
Следует заметить, что значения второй тангенциальной компоненты заметно меньше, чем первой. Как и следовало ожидать, значения компонент в цилиндрической щели заметно меньше, чем в соответствующей сферической, особенно, в области узких щелей. Это отчетливо демонстрирует рис. 2в, где приведена разность для нормальных компонент интегральных тензоров двух щелей. Это различие видно и при рассмотрении сечений поверхностей на рис. 3 для отдельных значений ширины щели. Все компоненты в цилиндрической щели (кривые 2) являются более пологими функциями расстояниями r от внутренней границы щели. Для нормальных компонент разность значений для тензоров в сферической и цилиндрической щелях сохраняется на всем протяжении щели, уменьшаясь при приближении к внешней границе щели. Для тангенциальных компонент вблизи внутренней поверхности соотношение такое же, как и для нормальных. Однако при движении к внешней границе функции быстро сближаются, а вблизи самой границы разность значений даже меняет знак.

Так же как и в сферической щели, на основании анализа формул (18) и (20) можно оценить предельное поведение компонент тензора напряжений при R_in $ \gg $ r. Раскладывая подынтегральное выражение в ряд по степеням x и y, с точностью до первой степени получим следующие предельные функции для компонент тензора напряжений:

С точностью до главных вкладов полученные выражения удовлетворяют условию механического равновесия (4). Если перейти к среднему радиусу кривизны, который для цилиндрической симметрии равен 2R_in, данные выражения совпадут с соответствующими соотношениями для сферической щели. Для такого сравнения в цилиндрической щели следует взять среднее значение двух тангенциальных компонент. Это означает, что в случае слабо искривленных поверхностей вклад от кривизны поверхности в первом приближении будет описываться соотношениями, полученными для сферической щели.

ВКЛАД ВЗАИМОДЕЙСТВИЙ МОЛЕКУЛ ФАЗЫ β

Оценим теперь вклад в тензор напряжений от взаимодействия друг с другом молекул внешней твердой фазы ${{\hat {E}}_{2}}$, который запишется с использованием пределов интегрирования следующим образом:

Проделаем те же преобразования с этим интегралом, что и при анализе ${{\hat {E}}_{1}}$. Вводя интегральный тензор ${{\hat {F}}_{2}}$, запишем окончательное выражение для этого вклада в тензор напряжений

где и

Интегралы в (25) выражаются через полные эллиптические интегралы первого (K) и второго (E) рода, а именно,

где $k \equiv \frac{{1 + y}}{{1 + x}}$. Можно убедиться, что компоненты этого вклада удовлетворяют условию равновесия (4), учитывая тождества операций $\frac{\partial }{{\partial r}} = \frac{\partial }{{\partial y}} = \frac{\partial }{{\partial k}}$. На рис. 4 показаны нормальная и первая тангенциальная компоненты этого тензора. Обе функции демонстрируют существенный рост при приближении к внешней границе щели. При этом в отличие от первого вклада значения первой тангенциальной компоненты в несколько раз превосходят значения нормальной компоненты, хотя обе почти на два порядка меньше по сравнению с соответствующими величинами, учитывающими взаимодействие двух твердых тел, ограничивающих щель. Как и в случае сферической щели, при анализе влияния кривизны на поведение тензора напряжений этим вкладом можно пренебречь.

РАСКЛИНИВАЮЩЕЕ ДАВЛЕНИЕ

Для определения расклинивающего давления в условиях искривленной щели выберем, во-первых, поверхность внутреннего цилиндра, то есть, положим r = 0. Во-вторых, будем рассматривать только первый вклад в тензор напряжений с учетом приведенных выше оценок второго слагаемого (4). Тогда расклинивающее давление Π_cyl в пустой щели будет равно

По сравнению с аналогичным определением расклинивающего давления в сферической щели [1]

как и следовало ожидать, абсолютное значение расклинивающего давления в цилиндрической щели будет несколько меньше, чем в сферической. На рис. 5 приведены относительные значения расклинивающего давления в плоскопараллельной, сферической и цилиндрической щелях, а именно, ${{F}_{\Pi }} = \left| {{{\Pi }_{{{\text{pore}}}}}} \right|{{R_{{{\text{in}}}}^{3}} \mathord{\left/ {\vphantom {{R_{{{\text{in}}}}^{3}} C}} \right. \kern-0em} C}$. Видно, что абсолютные значения расклинивающего давления тем больше по сравнению с плоскопараллельной щелью, чем больше искривление щели.

ЗАКЛЮЧЕНИЕ

Сравнение со случаем сферической щели приводит к выводу, что чем больше искривление цилиндрической щели, тем больше вклад твердых поверхностей в компоненты тензора напряжений и, следовательно, в расклинивающее давление. Показано, что в условиях малой кривизны результаты для двух щелей совпадают при использовании среднего радиуса кривизны.