Коллоидный журнал, 2022, T. 84, № 1, стр. 114-124

ВВЕДЕНИЕ

Ключевой характеристикой термодинамической и кинетической теории мицеллообразования является минимальная работа образования агрегатов из молекул поверхностно-активного вещества (ПАВ). С работой образования связано равновесное распределение агрегатов по числам агрегации молекул ПАВ при заданных значениях объемной концентрации мономеров ПАВ в растворе и температуры. В термодинамике мицеллообразования равновесное распределение определяет степень мицеллизации, среднее число агрегации и дисперсию чисел агрегации мицелл [1–6]. В кинетической теории это распределение играет роль начального или граничного условия и определяет кинетические коэффициенты, связанные со скоростью испускания мономеров ПАВ при молекулярном механизме мицеллярной релаксации [6–11] или скоростью распада при механизме слияния–распада мицелл [6, 8, 12].

Именно по появлению при увеличении концентрации мономеров ПАВ разнесенных максимума и минимума работы образования агрегатов можно судить о достижении критической концентрации мицеллообразования (ККМ), то есть такой брутто-концентрации ПАВ, при которой заметная его доля оказывается в мицеллах и можно говорить о мицеллярном растворе.

Поэтому первым шагом на пути к построению термодинамической и кинетической теории мицеллообразования прямых мицелл является нахождение минимальной работы образования сферического молекулярного агрегата ПАВ как аналитической функции числа агрегации и концентрации мономеров ПАВ в растворе. Первый подход к решению этой задачи, предложенный в [1–5, 13–17], опирается на минимизацию термодинамического потенциала Гиббса раствора, закон действующих масс и молекулярно-термодинамическое моделирование различных вкладов в работу образования в расчете на одну молекулу ПАВ в мицелле. Второй подход состоит в рассмотрении капельной модели работы агрегации [6, 18–20] в духе представлений теории нуклеации.

Как известно [1–6], самосборка прямой мицеллы ПАВ в полярных растворителях обусловлена гидрофобным эффектом для неполярных “хвостов” молекул ПАВ, при этом размер мицелл стабилизируется за счет электростатических отталкиваний в двойном электрическом слое в короне мицеллы и эффекта исключенной поверхности на границе ядро–корона. Менее определенным является механизм самосборки обратных мицелл. Так как сольвофобный эффект при растворении ПАВ в неполярном растворителе мал, то сборка “мокрых” обратных мицелл из ПАВ, углеводородов и воды обычно считается вызванной электростатическим притяжением диполей или ионов головных групп молекул ПАВ, противоионов и диполей молекул воды в ядре мицеллы. За счет чего происходит стабилизация обратных мицелл – остается дискуссионным вопросом. Еще более противоречивая картина возникает при рассмотрении основных факторов, обуславливающих образование “сухих” обратных мицелл в неполярных растворителях в отсутствие молекул воды. Рукенштейн и Нагараджан впервые в [21], а затем в [2] обобщили и расширили модель для прямых мицелл на случай формирования обратных мицелл ПАВ в неводных и в неполярных растворах. При этом они предположили, что присутствие даже малого количества молекул воды в растворах ПАВ в неполярном растворителе, которые могли бы накапливаться в ядрах обратных мицелл, является необходимым условием существования ККМ, и в случае отсутствия воды ККМ для “сухих” обратных мицелл не существует. Это предположение было поддержано и авторами ряда других работ [22–25], в которых главный вклад в формирование обратных мицелл ПАВ в неполярных растворителях, по крайней мере, в случае ионных ПАВ возникает вследствие сильных электростатических взаимодействий в ядре в присутствии молекул воды. В последнее десятилетие появились экспериментальные работы и работы по молекулярно-динамическому моделированию обратных мицелл, как ионных, так и неионных, где показано, что ККМ и сухие обратные неионные и ионные мицеллы в неполярных растворах реально существуют [26–29]. К этому выводу приводят и наши собственные результаты молекулярного моделирования обратных мицелл С₁₂Е₄ в гептане [30]. Как показано в [31], наличие полярных добавок, которые могут быть солюбилизированы в ядрах обратных мицелл, снижает ККМ и увеличивает размер обратных мицелл.

Таким образом, объяснение механизма агрегации ПАВ в неполярном растворителе в отсутствие воды, предсказание ККМ и характерных чисел агрегации сухих обратных мицелл остается актуальной проблемой. В данном сообщении рассматривается вывод выражения для минимальной работы мицеллообразования в случае прямых и обратных сферических мицелл на основе расширенной капельной модели мицелл. Эта модель будет построена с учетом вкладов, обусловленных гидрофобным эффектом при образовании ядра прямой мицеллы и электростатическим взаимодействием при образовании ядра обратной мицеллы, эффектами изменения конформации углеводородных хвостов и полярных головных групп, влиянием поверхностного натяжения на границе между ядром мицеллы и раствором. Показано, что важную роль в стабилизации как прямых, так и обратных мицелл играет уравнение состояния молекулярных групп на поверхности ядра мицеллы.

1. ОБЩЕЕ ВЫРАЖЕНИЕ ДЛЯ РАБОТЫ АГРЕГАЦИИ ПРЯМОЙ И ОБРАТНОЙ НЕИОННОЙ МИЦЕЛЛЫ

Пусть единица объема раствора включает ${{c}_{{{\text{sol}}}}}$ молекул растворителя и ${{c}_{{1t}}}$ молекул ПАВ. В равновесии молекулы ПАВ распределены между мономерами с объемной концентрацией ${{c}_{1}}$ и молекулярными агрегатами с объемными концентрациями ${{c}_{n}}$, где $n > 1$ – число агрегации молекул ПАВ в агрегате. При наличии агрегатов величина брутто-концентрации ПАВ ${{c}_{{1t}}}$ может быть представлена в виде

Пусть величина $W\left( n \right)$ представляет собой деленную на ${{k}_{{\text{B}}}}T$ (${{k}_{{\text{B}}}}$ – постоянная Больцмана, $Т$ – абсолютная температура раствора) разность термодинамического потенциала Гиббса агрегата с числом агрегации $n$ и потенциала Гиббса $\left( {n - \operatorname{l} } \right){{\mu }_{1}}$ для $n - 1$ мономера ПАВ при равновесной концентрации мономеров ПАВ $c_{{\text{1}}}^{{\left( {\text{e}} \right)}}$ в растворе. Это разность описывает изменение термодинамического потенциала Гиббса совокупности из $n$ молекул ПАВ в результате обратимого образования агрегата в растворе при заданных значениях давления и температуры за счет присоединения $n - \operatorname{l} $ мономеров ПАВ к некоторому зафиксированному мономеру ПАВ, с которого это образование начиналось. Как известно [32], такое изменение равно минимальной работе образования агрегата (работе агрегации). При $n = \operatorname{l} $ имеем $W\left( {n = 1} \right) = 0$, что естественно, так как агрегат из одной молекулы ПАВ уже есть в растворе (более подробно об этом пределе в теории нуклеации и мицеллообразования сказано в [6, 8, 33, 34]). Можно показать [12], что выражение для равновесной объемной концентрации агрегатов $c_{n}^{{\left( {\text{e}} \right)}}$ в растворе имеет вид где $W\left( {n,{{c}_{1}}} \right)$ – выраженная в тепловых единицах ${{k}_{{\text{B}}}}T$ работа агрегации мицеллы с числом агрегации $n$ при некоторой выбранной объемной концентрации ${{c}_{1}}$. Выражение (2) применимо для прямых и обратных мицелл и совпадает с использовавшимся ранее в теории нуклеации и мицеллообразования [6, 12, 33].

Полное число ${{N}_{{{\text{agg}}}}}$ устойчивых агрегатов в единице объема раствора равно

Удобно определить нормированное на полное число ${{N}_{{{\text{agg}}}}}$ распределение агрегатов $\tilde {c}_{n}^{{\left( {\text{e}} \right)}}$ как

Важной дополнительной характеристикой будет степень мицеллизации $\alpha \equiv \frac{1}{{{{c}_{{1t}}}}}\sum\nolimits_{n = 2}^\infty {nc_{n}^{{\left( {\text{e}} \right)}}\left( {c_{{\text{1}}}^{{\left( {\text{e}} \right)}}} \right)} $ – доля молекул ПАВ в агрегатах по отношению к брутто-концентрации ${{c}_{{1t}}}$ ПАВ. С учетом (1) и (2) имеем

Работа агрегации $W\left( {n,{{c}_{1}}} \right)$ молекулярного агрегата связана с химическим потенциалом мономеров ПАВ ${{\mu }_{{1n}}}$ в ядре агрегата и химическим потенциалом ${{\mu }_{1}}\left( {{{c}_{1}}} \right)$ мономеров в растворе термодинамическим соотношением

Для агрегата, который находится в химическом равновесии с раствором при значении ${{\mu }_{1}} = {{\mu }_{{1n}}},$ в правой части в (6) будет стоять нуль. Соответствующие корни уравнения ${{\partial W} \mathord{\left/ {\vphantom {{\partial W} {\partial n}}} \right. \kern-0em} {\partial n}} = 0$ определяют максимумы и минимумы работы агрегации.

Соотношение (2) предполагает, что работа агрегации $W$ зависит от концентрации ${{с}_{1}}$ как $\ln {\kern 1pt} {{с}_{1}}$. Это соответствует идеальной смеси мономеров и агрегатов в растворе. Дальнейшие шаги на пути к количественной теории мицеллообразования требуют явного термодинамического определения работы $W$ как функции числа агрегации n.

В [1–5, 13–17] были предложены молекулярно-термодинамические модели различных вкладов в величину ${{W\left( {n,{{c}_{1}}} \right)} \mathord{\left/ {\vphantom {{W\left( {n,{{c}_{1}}} \right)} n}} \right. \kern-0em} n}$ как для прямых, так и для обратных мицелл. С учетом этих результатов и представлений капельной модели сферической мицеллы [6, 18, 19] мы в данном сообщении попробуем построить термодинамическое выражение в духе теории нуклеации для полной работы агрегации $W\left( {n,{{c}_{1}}} \right)$ как функции чисел агрегации n.

Согласно представлениям термодинамики нуклеации и капельной модели [6, 18, 19] выражение для работы $W = W\left( {n,{{c}_{1}}} \right)$ изотермического образования молекулярного агрегата из молекул ПАВ может быть представлено в виде

где $\mu _{1}^{\alpha }$ – химический потенциал молекул ПАВ внутри агрегата, но при плоской поверхности ядра агрегата, искривление поверхности ядра агрегата учитывается слагаемым $\gamma A\left( n \right)$, $A\left( n \right)$ – площадь поверхности ядра агрегата, $\gamma $ – межфазное натяжение на границе между ядром и раствором (для прямых и обратных мицелл в общем случае разное), ${{W}_{{{\text{dl}}}}}$ – электрический вклад в работу агрегации, обусловленный возможным существованием двойного электрического слоя на поверхности ядра в случае прямых мицелл.

Представим разность химических потенциалов $\mu _{1}^{\alpha }\left( n \right) - {{\mu }_{1}}$ в виде [6, 18, 19]

где ${{w}_{1}}$ – работа переноса (через плоскую поверхность) из раствора ПАВ в объемную, соответствующую ядру мицеллы, фазу той части отдельной молекулы ПАВ, которая будет образовывать это ядро. В случае прямой мицеллы речь идет о содержащем ${{n}_{{\text{C}}}}$ неполярных углеводородных групп гидрофобном хвосте молекулы ПАВ. В случае обратной мицеллы имеем в виду полярные группы головной части молекулы ПАВ. Величину ${{c}_{{1n}}}$ прокомментируем чуть ниже.

Для прямой мицеллы работа ${{w}_{1}}$ включает при ${{n}_{{\text{C}}}} \gg 1$ так называемый гидрофобный вклад

где $B$ – положительная (что и означает гидрофобность углеводородных групп) безразмерная величина, зависящая только от температуры. Для обратной мицеллы аналогичный вклад должен возникать вследствие электростатических взаимодействий связанных зарядов, входящих в состав полярных групп. Обозначим этот вклад как ${{w}_{{{\text{el}}}}}{\text{:}}$где ${{B}_{{{\text{el}}}}}$ – положительная безразмерная величина, зависящая не только от температуры, но и от числа агрегации $n$. Как показали численные оценки для решеточной модели “сухой” обратной мицеллы [35] и молекулярно-динамическое моделирование обратных мицелл С₁₂Е₄ в гептане [30], ${{B}_{{{\text{el}}}}} \gg 1$ и имеет тенденцию выхода на постоянное значение при $n \gg 1.$

Следует теперь учесть положительный вклад в разность $\mu _{1}^{\alpha }\left( n \right) - {{\mu }_{1}}$, который возникает из-за того, что образующая корону часть молекулы ПАВ с площадью сечения ${{a}_{0}}$ должна быть на поверхности ядра мицеллы, доступная площадь которой ограничена при заданном числе агрегации $n$ величиной $A\left( n \right) - n{{a}_{0}}.$ Появление такого вклада в свободную энергию мицеллы ранее подробно обсуждалось в [1, 2]. Здесь же поступим следующим образом. Без учета привязки к поверхности и эффекта исключенной площади в приближении однородности фазы ядра мицеллы можно записать ${{k}_{{\text{B}}}}T\ln \left( {{{{{c}_{{1n}}}} \mathord{\left/ {\vphantom {{{{c}_{{1n}}}} {{{c}_{1}}}}} \right. \kern-0em} {{{c}_{1}}}}} \right)$ как

где – равновесная объемная концентрация в фазе ядра мицеллы объемом $V\left( n \right)$. Учтем теперь, что вместо $V\left( n \right)$ под знаком логарифма должна присутствовать величина $V\left( n \right)\frac{{A\left( n \right) - n{{a}_{0}}}}{{A\left( n \right)}}$, т.е.

Второе слагаемое в квадратных скобках в правой части (13) положительно и требует выполнения неравенства ${{n{{a}_{0}}} \mathord{\left/ {\vphantom {{n{{a}_{0}}} A}} \right. \kern-0em} A} < 1$.

Далее будем нижним индексом ${\text{d}}$ помечать величины, относящиеся к прямым мицеллам, и нижним индексом ${\text{in}}$ – величины, относящиеся к обратным мицеллам. Подставляя (9), (10) и (13) в (8), получаем

для прямых мицелл и – для обратных мицелл.

2. РАБОТА ОБРАЗОВАНИЯ И КОНФОРМАЦИОННЫЕ ВКЛАДЫ

Помимо ${{w}_{{\text{h}}}}$ или ${{w}_{{{\text{el}}}}}$ в работу переноса следует включить вклады, связанные с изменением конформации молекул ПАВ при переносе их в мицеллу [1–5]. Обсудим ниже эти вклады подробнее. Конформационный вклад в свободную энергию мицеллы определяется уменьшением числа доступных состояний молекулы ПАВ, обладающей протяженными головной и хвостовой частями, при включении ее в мицеллу – уменьшением энтропии из-за влияния соседних молекул. Такое ограничение числа состояний имеет разную природу для короны мицеллы и ее ядра, поэтому можно говорить о сумме соответствующих конформационных вкладов в работу образования мицеллы. Для обратных мицелл углеводородные хвосты, образующие корону мицеллы, как мы наблюдали в молекулярно-динамическом моделировании для молекул C₁₂E₄ в гептане [30], двигаются относительно свободно.

Как изображено на рис. 1, по сравнению со случаем идеальной свободной цепи движение некоторого выбранного хвоста ограничивается эффективной силой $\vec {f}$, действующей со стороны ближайших соседних хвостов. Ось $x$ будем считать направленной по нормали к поверхности мицеллы так же, как и силу $\vec {f}$.

При заданном расстоянии между концами цепи $\vec {R}$ число возможных конформаций $W(\vec {R})$ определяет энтропию ${{S}_{{{\text{conf}}}}}(\vec {R})$ соотношением Больцмана

Очевидно, $W(\vec {R}) = CP(\vec {R})$, где $P(\vec {R})$ – плотность вероятности того, что конец цепи имеет координату $\vec {R}$, $C$ – коэффициент пропорциональности. Таким образом,

В гауссовом приближении [26]

где $l$ – длина всей цепи, ${{l}_{{{\text{sg}}}}}$ – эффективная длина сегмента цепи. Тогда

Усреднение этого выражения для свободной идеальной цепи производится с помощью вытекающих из (18) соотношений

Учет действия эффективной внешней силы проведем по Флори [36]. Пусть в результате действия внешней силы возникло “утолщение” мицеллярной короны в $b$ раз: $\left\langle {R_{x}^{2}} \right\rangle = {{b}^{2}}\left\langle {R_{{x0}}^{2}} \right\rangle \equiv \frac{{{{D}^{2}}}}{3}$, где введена эффективная толщина короны $D$, в терминах которой параметр растяжения $b$ выражается в виде

Строго говоря, параметр растяжения $b$ должен зависеть от числа агрегации $n$. Из условия несжимаемости мономера для составляющих $x$ и $y$ имеем [36]

Для усредненного изменения энтропии $\left\langle {\Delta {{S}_{{{\text{conf}}}}}} \right\rangle $ под действием эффективной внешней силы получаем

откуда с учетом (20) имеем

Таким образом, искомый конформационный вклад от короны мицеллы $w_{{{\text{conf}}}}^{{{\text{cr}}}} = - T\left\langle {\Delta {{S}_{{{\text{conf}}}}}} \right\rangle $ в свободную энергию мицеллы в расчете на одну молекулу ПАВ равен

При расчете конформационного вклада от ядра прямой мицеллы в работах [5, 37] была принята следующая модель. Головные группы молекул ПАВ считались закрепленными на поверхности ядра мицеллы с радиальной координатой $R = 0$ (в центре мицеллы $R = r$, где $r$– радиус ядра мицеллы), свободный конец цепи находился внутри мицеллы при $R = {{R}_{0}}$. Цепи рассматривались как непрерывные нити длиной $l = {{l}_{{{\text{sg}}}}}{{N}_{{{\text{sg}}}}},$ где ${{N}_{{{\text{sg}}}}}$ – эффективное число сегментов. Форма цепи описывалась функцией $R(k)$, где $k$ – номер сегмента, а $R(k)$ – его радиальное расстояние от поверхности мицеллы; $0 \leqslant k \leqslant {{N}_{{{\text{sg}}}}}.$ По определению, на поверхности мицеллы $R(0) = 0$, а для внутреннего конца цепи $R({{N}_{{{\text{sg}}}}}){\text{ }} = {{R}_{0}}.$ Локальное растяжение цепи в радиальном направлении характеризовалось функцией $E({{R}_{0}},R) = {{dR} \mathord{\left/ {\vphantom {{dR} {dk}}} \right. \kern-0em} {dk}}$ ($0 < {{R}_{0}} \leqslant r$), обратная величина, ${1 \mathord{\left/ {\vphantom {1 {E({{R}_{0}},R)}}} \right. \kern-0em} {E({{R}_{0}},R)}} = {{dk} \mathord{\left/ {\vphantom {{dk} {dR}}} \right. \kern-0em} {dR}}$, определяла количество сегментов (данной молекулы) на единицу длины в радиальном направлении.

Для получения конформационного вклада соотношение (19) применялось к каждому фрагменту углеводородного хвоста мономера внутри ядра мицеллы. Для фрагмента, концы которого разнесены на $\Delta R$ и содержат $\Delta k$ сегментов, формула (19) с заменами $R \to \Delta R,\,\,l \to {{l}_{{{\text{sg}}}}}\Delta k$ дает $\Delta {{S}_{{{\text{conf}}}}}{\text{ = }} - \frac{3}{2}\frac{{{{{(\Delta R)}}^{2}}}}{{\Delta kl_{{{\text{sg}}}}^{2}}}$, или, для бесконечно малого фрагмента,

Для усреднения этого выражения по всем цепям (всем молекулам ПАВ, входящим в мицеллу) вводилась величина $G({{R}_{0}})d{{R}_{0}}$ – среднее число молекул, у которых хвосты лежат в интервале $d{{R}_{0}}.$ Полный конформационный вклад в свободную энергию ${{F}_{{{\text{conf}}}}}$ получался интегрированием выражения (26) с функцией $G({{R}_{0}}){\text{:}}$

Здесь интегрирование по $R$ эквивалентно суммированию вкладов от всех сегментов данной молекулы, а интегрирование по ${{R}_{0}}$ – суммированию по всем молекулам ПАВ. Функции $G({{R}_{0}})$ и $E({{R}_{0}},R)$ были найдены в [5] из условия максимума полной энтропии при условии постоянства плотности сегментов внутри ядра мицеллы. В результате было получено следующее выражение для конформационного вклада в свободную энергию ядра мицеллы на одну молекулу:

При постоянной плотности сегментов в ядре $r(n) \sim {{n}^{{1/3}}}$, поэтому $w_{{{\text{conf}}}}^{{{\text{nu}}}} \sim {{n}^{{2/3}}}$. Такая же зависимость конформационного вклада от числа агрегации имеет место при отличной от сферической геометрии ядра [5]. В этом случае изменяется лишь численный коэффициент в (28).

Число конформаций в ядре обратной мицеллы, по-видимому, значительно меньше, чем в ядре прямой мицеллы. Это связано с тем, что ядро прямых мицелл формируется в результате гидрофобного эффекта со стороны полярного растворителя, и число конформаций внутри ядра ограничивается объемом ядра при постоянной средней плотности сегментов. В случае же обратных мицелл ядро формируется за счет кулоновских взаимодействий внутри ядра, что резко уменьшает число допустимых конформаций. Это приводит к значительному уменьшению энтропии при переносе головной части мономера внутрь ядра. Однако эта величина не зависит от параметров мицеллы и лишь переопределяет постоянную составляющую в $w_{{{\text{conf}}}}^{{{\text{nu}}}},$ что приводит к линейному положительному вкладу в работу образования обратной мицеллы.

3. РАБОТА ОБРАЗОВАНИЯ МИЦЕЛЛЫ И УРАВНЕНИЕ СОСТОЯНИЯ ЧАСТЕЙ МОЛЕКУЛЫ ПАВ НА ПОВЕРХНОСТИ ЯДРА МИЦЕЛЛЫ

Еще более точное, чем (14) или (15), представление для разности химических потенциалов $\mu _{1}^{\alpha }\left( n \right) - {{\mu }_{1}}$ в (7) можно получить из уравнения состояния для системы жестких дисков с исключенной поверхностью. С этой целью возьмем двумерное уравнение состояния теории масштабируемых частиц [38, 39], которое в наших обозначениях имеет вид

где ${{\rho \equiv n} \mathord{\left/ {\vphantom {{\rho \equiv n} A}} \right. \kern-0em} A}$ – поверхностная плотность полярных групп в случае прямой мицеллы или углеводородных хвостов в случае обратной мицеллы, $\Pi $ – двумерное давление. Как известно, это уравнение является двумерным аналогом известного уравнения Карнахана–Старлинга для жестких шаров. Как отмечалось в [39], уравнение (29), несмотря на его аналитическую простоту, хорошо применимо при всех значениях плотности ${n \mathord{\left/ {\vphantom {n A}} \right. \kern-0em} A}$. Нас интересует вклад $\Delta \mu _{1}^{\alpha }\left( \rho \right)$ в $\mu _{1}^{\alpha }\left( n \right) - {{\mu }_{1}}$, который возникает от разности давления $\Pi $ и вклада ${{k}_{{\text{B}}}}T{n \mathord{\left/ {\vphantom {n A}} \right. \kern-0em} A}$ в приближении идеального газа. Интегрируя соотношение Гиббса–Дюгема с учетом (29), находим

Подставляя (30) в (8), учитывая (9), (10), (25) (28) и (30), получаем

для прямых мицелл и – для обратных мицелл. Обращаем внимание, что вторые слагаемые в квадратных скобках в (14), (15) и (31), (32) совпадают. Заметим, что можно использовать и более точные, чем (29), двумерные уравнения состояния [40–42].

В итоге, с учетом (7) и (31), (32) приходим к следующим выражениям для работы ${{W}_{{\text{d}}}}$ образования прямой мицеллы и работы ${{W}_{{{\text{in}}}}}$ образования обратной мицеллы произвольной формы:

В случае сферической мицеллы радиус ядра мицеллы в капельной модели связан с числом агрегации $n$ как [6, 18, 19]

Для прямой мицеллы

где $\upsilon $ – объем метиленовой группы CH₂. Для обратной мицеллы где ${{\upsilon }_{{\text{p}}}}$ – объем полярной части молекулы ПАВ. Площадь ядра $A\left( n \right) = 4\pi {{r}^{2}},$ и соответственно

Если в ${{W}_{{{\text{dl}}}}}$ для прямых мицелл учитывать вклад диполей полярных головных групп молекул ПАВ, то имеем [6, 18, 19]

где $ze$ – электрический заряд в диполе отдельной гидрофильной части молекулы ПАВ (e – элементарный заряд), $\delta $ – длина диполя гидрофильной части, т.е. толщина конденсатора, $\varepsilon $ – эффективная диэлектрическая проницаемость среды, в которой находится конденсатор, ${{\varepsilon }_{0}}$ – электрическая постоянная.

С учетом (35)–(40) перепишем выражения (33) и (34) для ${{W}_{{\text{d}}}}$ и ${{W}_{{{\text{in}}}}}$ в случае сферических мицелл в виде

4. ЧИСЛЕННЫЕ ОЦЕНКИ

Для численных оценок в качестве молекулы ПАВ возьмем молекулу C₁₂E₄, в качестве полярного растворителя – воду, в качестве неполярного растворителя – гептан. На рис. 2а и 2б изображена молекула C₁₂E₄ и указаны ее характерные размеры. Заметим, что длина ее углеводородного хвоста согласно [2] равна l = l(CH₃) + 11l(CH₂) = 1.67 нм, где $l\,({\text{C}}{{{\text{H}}}_{{\text{3}}}}) = 0.280\,$ нм, $l\,({\text{C}}{{{\text{H}}}_{{\text{2}}}}) = 0.1265$ нм. Видим, что данные [2] и данные, полученные нами путем анализа структуры молекулы C12E4 [43], несколько различаются. Поперечные размеры двух групп СН₂ совпадают с поперечными размерами группы E на рис. 2б.

Возьмем следующие значения параметров системы и учтем (36), (37):

$T = 293\,\,K,$ $\upsilon = {\text{26}}{\text{.9}} \times {\text{1}}{{{\text{0}}}^{{ - 30}}}$ м³ [2], ${{v}_{{\text{p}}}} = {\text{63}} \times {\text{4}} \times {\text{1}}{{{\text{0}}}^{{ - 30}}} = 252 \times {\text{1}}{{{\text{0}}}^{{ - 30}}}$ м³ [2], $B = 1.4$ [2], ${{B}_{{{\text{el}}}}} = 20$ [30], ${{n}_{{\text{C}}}} = 12$, ${{\lambda }_{{\text{d}}}} = 4.4 \times {{10}^{{ - 10}}}$ м,

${{\lambda }_{{{\text{in}}}}} = 3.9 \times {{10}^{{ - 10}}}$ м, γd = 40 мН/м [5], ${{\gamma }_{{{\text{in}}}}} = 30$ мН/м, ${{a}_{{0{\text{d}}}}} = 21 \times {{10}^{{ - 20}}}$ м2 [2], ${{a}_{{0{\text{in}}}}} = 21 \times {{10}^{{ - 20}}}$ м2 [2],

Для эффективной длины гидрофобного сегмента примем значение ${{l}_{{{\text{sg}}}}} = 0.46\,\,$ нм [45]. Тогда эффективное число сегментов ${{N}_{{{\text{sg}}}}} = {l \mathord{\left/ {\vphantom {l {{{l}_{{{\text{sg}}}}}}}} \right. \kern-0em} {{{l}_{{{\text{sg}}}}}}} \approx 4.$ Максимальное значение ${{D}_{{\max }}} = l,$ поэтому согласно (21) $b_{{\max }}^{2} = {{N}_{{{\text{sg}}}}} \approx 4,$ откуда ${{b}_{{\max }}} \approx 2,$ и из (25) находим

На рис. 3а показана зависимость работы ${{W}_{{\text{d}}}}\left( {n,{{c}_{1}}} \right)$ образования прямой мицеллы в водном растворе от равновесной концентрации ${{c}_{1}}$ мономеров ПАВ в растворе и числа агрегации n. Расчет был сделан по формуле (41) с учетом (43), где мы положили $n = n - 1$, чтобы обеспечить ${{W}_{{\text{d}}}}\left( {n = 1} \right) = 0.$

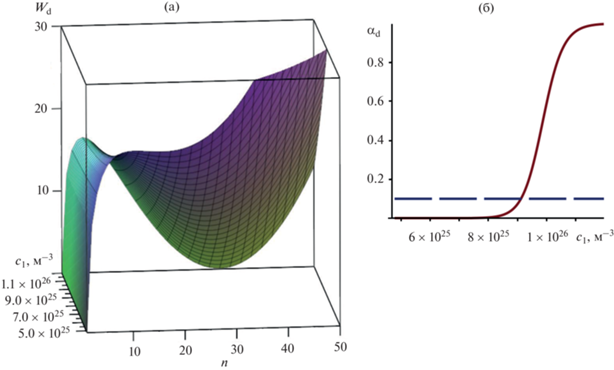
На рис. 3б изображена степень мицеллизации ${{\alpha }_{{\text{d}}}}\left( {{{c}_{1}}} \right)$ молекул ПАВ в прямых мицеллах в водном растворе ПАВ, рассчитанная по формулам (5) и (41). На рис. 3б горизонтальной линией показано значение степени мицеллизации ${{\alpha }_{{{\text{ККМ}}}}} = 0.1,$ при котором достигается ККМ в водном растворе.

Из рис. 3а следует, что при выбранных значениях параметров работа ${{W}_{{\text{d}}}}\left( {n,{{c}_{1}}} \right)$ агрегации прямой мицеллы как функция числа агрегации $n$ имеет точку перегиба, отвечающую корню уравнения ${{{{\partial }^{2}}{{W}_{{\text{d}}}}\left( {n,{{c}_{1}}} \right)} \mathord{\left/ {\vphantom {{{{\partial }^{2}}{{W}_{{\text{d}}}}\left( {n,{{c}_{1}}} \right)} {\partial {{n}^{2}}}}} \right. \kern-0em} {\partial {{n}^{2}}}} = 0.$ Именно наличие точки перегиба приводит с ростом концентрации мономеров ПАВ ${{c}_{1}}$ к появлению максимума работы ${{W}_{{\text{d}}}}\left( {n,{{c}_{1}}} \right)$ левее и минимума работы ${{W}_{{\text{d}}}}\left( {n,{{c}_{1}}} \right)$ правее точки перегиба на рис. 3а. Числа агрегации для максимума и минимума работы агрегации отвечают корням уравнения (6) с учетом выражения (41). С ростом концентрации ${{c}_{1}}$ высота максимума работы агрегации медленно убывает, а сам максимум сдвигается в сторону меньших чисел агрегации. При этом минимум работы агрегации сдвигается в сторону больших чисел агрегации, а его глубина быстро растет. Накопление числа агрегатов в области минимума работы агрегации ${{W}_{{\text{d}}}}\left( {n,{{c}_{1}}} \right)$ (потенциальной ямы для образования прямых мицелл) с увеличением ${{c}_{1}}$ приводит к достижению ККМ и быстрому росту степени мицеллизации при ${{c}_{1}} > {{\left. {{{c}_{1}}} \right|}_{{{\text{ККМ}}}}}$ на рис. 3б. Результаты расчета очень чувствительны к выбору параметров υ, ${{a}_{{0{\text{d}}}}}$ и учету или отбрасыванию вклада ${{W}_{{{\text{dl}}}}}.$ Учет конформационных вкладов слабо влияет на положение точки перегиба, но заметно изменяет значение ККМ.

На рис. 4а показана зависимость работы образования ${{W}_{{{\text{in}}}}}\left( {n,{{c}_{1}}} \right)$ обратной мицеллы в гептане от равновесной концентрации ${{c}_{1}}$ мономеров ПАВ в растворе и числа агрегации $n$. Расчет был сделан по формуле (42) с учетом (43) и (44). Мы положили $n = n - 1$ в (42), чтобы обеспечить ${{W}_{{{\text{in}}}}}\left( {n = 1} \right) = 0$. На рис. 4б изображена степень мицеллизации ${{\alpha }_{{{\text{in}}}}}\left( {{{c}_{1}}} \right)$ молекул ПАВ в прямых мицеллах в водном растворе ПАВ, рассчитанная по формулам (5) и (42). На рис. 4б горизонтальной линией показано значение степени мицеллизации ${{\alpha }_{{{\text{ККМ}}}}} = 0.1,$ при котором достигается ККМ в гептане.

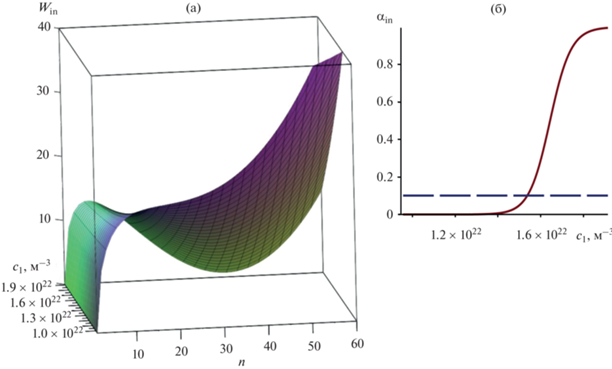
На рис. 4а видно, что при выбранных значениях параметров работа агрегации ${{W}_{{{\text{in}}}}}\left( {n,{{c}_{1}}} \right)$ сухой обратной мицеллы как функция числа агрегации $n$ так же, как и работа ${{W}_{{\text{d}}}}\left( {n,{{c}_{1}}} \right)$, имеет точку перегиба, отвечающую в данном случае корню уравнения ${{{{\partial }^{2}}{{W}_{{{\text{in}}}}}\left( {n,{{c}_{1}}} \right)} \mathord{\left/ {\vphantom {{{{\partial }^{2}}{{W}_{{{\text{in}}}}}\left( {n,{{c}_{1}}} \right)} {\partial {{n}^{2}}}}} \right. \kern-0em} {\partial {{n}^{2}}}} = 0$. Соответственно с ростом концентрации мономеров ПАВ ${{c}_{1}}$ в неполярном растворителе появляется максимум работы ${{W}_{{{\text{in}}}}}\left( {n,{{c}_{1}}} \right)$ левее и минимум работы ${{W}_{{{\text{in}}}}}\left( {n,{{c}_{1}}} \right)$ правее точки перегиба на рис. 4а. Числа агрегации для максимума и минимума работы агрегации ${{W}_{{{\text{in}}}}}\left( {n,{{c}_{1}}} \right)$ отвечают корням уравнения (6) с учетом выражения (42). С ростом концентрации ${{c}_{1}}$ высота максимума работы агрегации ${{W}_{{{\text{in}}}}}\left( {n,{{c}_{1}}} \right)$ медленно убывает, а сам максимум сдвигается в сторону меньших чисел агрегации. При этом минимум работы агрегации ${{W}_{{{\text{in}}}}}\left( {n,{{c}_{1}}} \right)$ сдвигается в сторону больших чисел агрегации, а его глубина быстро растет. Как следствие накопления числа обратных мицелл в области минимума работы ${{W}_{{{\text{in}}}}}\left( {n,{{c}_{1}}} \right)$ (потенциальной ямы для образования обратных мицелл) на рис. 4б закономерно возникает ККМ для сухих обратных мицелл. При ${{c}_{1}} > {{\left. {{{c}_{1}}} \right|}_{{{\text{ККМ}}}}}$ степень мицеллизации на рис. 4б демонстрирует характерный быстрый рост. Результаты расчета очень чувствительны к выбору параметров ${{a}_{{0{\text{in}}}}}$ и ${{v}_{{\text{p}}}}.$ Учет конформационного вклада слабо влияет на положение точки перегиба, но значительно влияет на значение ККМ в случае обратных мицелл.

ЗАКЛЮЧЕНИЕ

В данном сообщении обоснованы новые выражения для зависимости работы агрегации прямых и обратных мицелл, определяемые формулами (33), (34) и (41), (42). Показано, что важную роль в стабилизации как прямых, так и обратных мицелл играет уравнение состояния молекулярных групп на поверхности ядра мицеллы. Учтенные вклады в работу агрегации позволяют объяснить механизм агрегации ПАВ в неполярном растворителе в отсутствие воды, убедиться в существовании ККМ и оценить средние числа агрегации сухих обратных мицелл при разных брутто-концентрациях ПАВ.