Коллоидный журнал, 2022, T. 84, № 2, стр. 127-140
О теоретических посылках к классификации режимов электродиспергирования жидкости
А. И. Григорьев 1, *, С. О. Ширяева 1
1 Ярославский государственный университет им. П.Г. Демидова
150000 Ярославль, ул. Советская, 14, Россия
* E-mail: grigorai@mail.ru
Поступила в редакцию 05.07.2021
После доработки 25.10.2021
Принята к публикации 08.11.2021
- EDN: WUFRSJ
- DOI: 10.31857/S0023291222020045
Аннотация
Предлагается чисто теоретический подход к построению классификации наблюдаемых режимов электродиспергирования с торца капилляра, по которому жидкость подается в разрядную систему, в отличие от феноменологических классификаций, предлагавшихся ранее. Классификацию предлагается провести путем разделения диспергируемых жидкостей по физико-химическим свойствам, а также по степени симметрии азимутальных волн на поверхности струи, выбрасываемой из мениска, и закономерностям отрыва капель непосредственно от мениска. Показано, что при диспергировании маловязкой весьма электропроводной жидкости мениском эмитируются сильно заряженные капли, неустойчивые по отношению к собственному заряду, распадающиеся на еще более мелкие. Жидкости с низкой электропроводностью эмитируют заряженные капли, но с незначительным зарядом, устойчивые по отношению к собственному заряду, либо заряженные струи жидкости, распадающиеся на устойчивые капли.
ВВЕДЕНИЕ
Исследование электрических разрядов с жидких менисков на торце капилляра, по которому жидкость подается в разрядную систему, приводящих к диспергированию жидкости, начавшееся в начале прошлого века, инициировало интенсивное развитие капиллярного электродиспергирования [1–6]. В настоящее время капиллярное электродиспергирование жидкости широко используется как в различных разделах академической науки, так и в технике и технологии. С ним приходится сталкиваться при распылении инсектицидов, горюче-смазочных материалов, лаков и красок [7, 8], в ионных коллоидных реактивных двигателях при тонкой регулировке орбит космических кораблей [9, 10]. Оно используется в каплеструйной печати [11] и для создания потоков монодисперсных капель в термоядерном синтезе [12]. Его мы встречаем при создании ионно-кластерно-капельных пучков в жидкостной масс-спектрометрии и жидкометаллических источниках ионов [13, 14], а также в ускорителях макрочастиц [15, 16] и в жидкометаллической эпитаксии и литографии [17] и т.д. и т.п.
В связи с многообразием приложений в ходе проведения исследований были выделены около двух десятков различных режимов электродиспергирования в зависимости от: объемного расхода жидкости, прикладываемого к разрядному промежутку напряжения, геометрии установки, физико-химических свойств диспергируемых жидкостей. Диспергирование в разных режимах различалось размерами и зарядами образующихся при этом капель и скоростью их производства. Возникла потребность в их классификации, которая и была реализована в [18–22] на основе чистой феноменологии.
Кроме экспериментальных подходов к классификации режимов электродиспергирования жидких струй предпринимались и теоретические подходы. В [23] предложено проводить классификацию на основе сравнения характерных времен релаксации заряда, вязкости и выравнивания давления в объеме диспергируемых жидкостей. В [24] осуществлена подобная попытка с введением дополнительных технологических характерных времен, но предложенная классификация опиралась на экспериментальные данные [18–22]. В [25] изложена теоретически-феноменологическая модификация классификации [24], углубленная в теорию дробления струй с различной азимутальной симметрией.
В настоящей работе предполагается провести чисто теоретическую классификацию возможных режимов электродиспергирования жидкости с вершины мениска на торце капилляра, по которому жидкость подается в разрядную систему. Следует иметь в виду, что капли жидкости могут отрываться непосредственно с торца капилляра или с вершины мениска, а также могут образовываться при распаде струй, выбрасываемых мениском. В обоих случаях образующиеся капли могут быть как устойчивыми, так и неустойчивыми по отношению к суперпозиции собственного и индуцированного внешним электростатическим полем электрических зарядов.
Классификацию будем проводить, исходя из идеи, высказанной в [23]: сравнения характерных времен, оставив в неизменности характерные времена релаксации заряда, выравнивания давления в капле и заменив характерное время релаксации вязкости на характерное время развития неустойчивости в струе вязкой жидкости, т.к. оно более соответствует основной идее диспергирования – отрыву капли от струи. Технологические времена, зависящие от вида и строения используемых разрядных устройств, вносящих элемент неопределенности, предлагается убрать из рассмотрения.
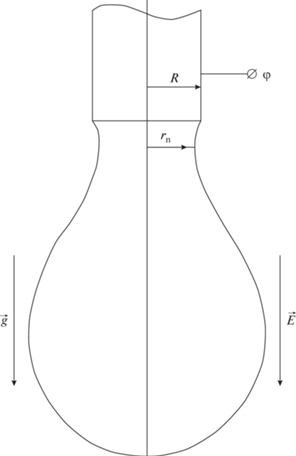
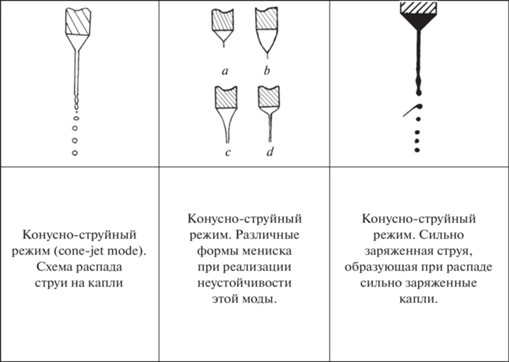
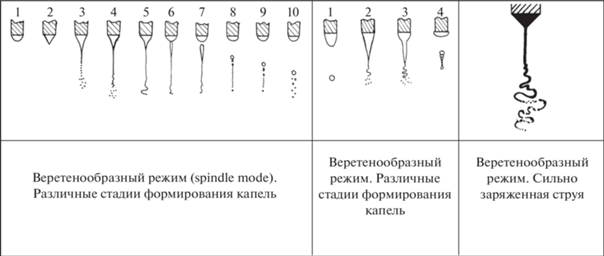
Следует отметить, что различные установки для электродиспергирования, на которых обнаруживаются “новые” режимы, различаются между собой. В итоге, распределение электрического поля в пространстве между электродами в разрядном промежутке и азимутальная симметрия поля у них различные, вот и появляются “новые” режимы, связанные с вибрациями и колебаниями мениска жидкости на торце капилляра, и соответственно меняется феноменология. Например, в [20] вводятся “режим осциллирующей струи (oscillating jet)” и “режим прецессирующей струи (precession jet)”, см. рис. 1. В этой связи предлагается ограничить классификацию режимами диспергирования, получаемыми на установках с идеализированным осесимметричным распределением электрического поля в пространстве, в противном случае систематизацию режимов нужно будет проводить для каждой установки в отдельности.
Рис. 1.
Режимы, представляющиеся надуманными, обусловленными особенностями конкретной установки для электродиспергирования.
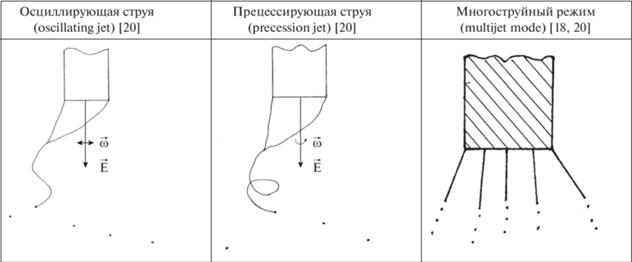
И еще одно нововведение. Режимы, получаемые изменением технологических параметров, например объемного расхода жидкости через капилляр или прикладываемой к разрядному промежутку разности потенциалов, предлагается не выделять в отдельные режимы. В частности, это касается мультиструйного (multijet) режима, описанного в [18–20], в который трансформируется конусно-короткоструйный (cone shot jet) режим при снижении объемного расхода жидкости или при увеличении подаваемой разности потенциалов. При этом отчетливо выраженный полусфероидальный мениск жидкости на торце капилляра практически исчезает, а на срезе капилляра, на плоской поверхности жидкости под влиянием давления электрического поля реализуется неустойчивость цилиндрических волн, пропорциональных функциям Бесселя различных порядков. В итоге, по периметру капилляра образуется конечное количество (в зависимости от порядка функции Бесселя и номера ее корня [26]) мелких эмиссионных выступов, из которых вырываются тоненькие струйки (см. рис. 1).
Начать классификацию следует с режимов образования капель прямо на торце капилляра или вершине мениска, а потом перейти к режимам, связанным с дроблением струй, которые целесообразно разделить по степени азимутальной симметрии мод капиллярных волн, бегущих по струе.
Говоря об азимутальной симметрии, будем иметь в виду, что решения задачи об устойчивости струи, удовлетворяющие необходимым уравнениям и граничным условиям для электростатического $\Phi \left( {{\mathbf{r}},t} \right)$ и гидродинамического $\psi \left( {{\mathbf{r}},t} \right)$ потенциалов, а также для функции тока $f\left( {{\mathbf{r}},t} \right)$, записываются в виде волн, бегущих вдоль оси симметрии невозмущенной струи:
(1)
$\begin{gathered} \Phi \left( {{\mathbf{r}},t} \right) \sim \exp (ist)\exp (ikz + im\varphi ){{K}_{m}}\left( {kr} \right), \\ \psi \left( {{\mathbf{r}},t} \right) \sim \exp (ist)\exp (ikz + im\varphi ){{I}_{m}}\left( {kr} \right), \\ f\left( {{\mathbf{r}},t} \right) \sim \exp (ist)\exp (ikz + im\varphi ){{K}_{m}}\left( {kr} \right). \\ \end{gathered} $1. РАЗДЕЛЕНИЕ ЖИДКОСТЕЙ ПО ИХ ФИЗИКО-ХИМИЧЕСКИМ СВОЙСТВАМ
Очевидно, что на процесс диспергирования должны оказывать влияние радиус капилляра $r$, коэффициент поверхностного натяжения жидкости $\sigma $, ее кинематическая вязкость ${{\nu }_{c}}$, массовая плотность жидкости $\rho $ и удельная электропроводность $\chi $. Если ввести безразмерные переменные, в которых $\sigma = \rho = r = 1$, остаются в явном виде только вязкость и электропроводность жидкости, а в неявном – их зависимости от $r$, $\sigma $, $\rho $.
Есть еще один параметр, не упомянутый выше: ускорение свободного падения ${\mathbf{g}}$. Это вектор, направленный вниз. Сила тяжести капли вместе с силой ее электростатического взаимодействия с внешним электрическим полем в разрядной системе отрывает каплю.
Определение характерных времен. Согласно сказанному выше, проблему классификации по физико-химическим свойствам диспергируемой жидкости в безразмерных переменных, в которых $\sigma = \rho = r = 1$, можно свести к изменению двух параметров: характерного безразмерного времени релаксации заряда и характерного безразмерного времени отрыва капли от струи (величины, обратной безразмерному инкременту неустойчивости струи).
Характерное время электрической релаксации ${{\tau }_{\chi }}$ [27, с. 27]:
Чтобы получить это выражение в безразмерном виде в указанных выше безразмерных переменных, нужно разделить полученное выражение на характерный безразмерный масштаб времени $\sqrt {\frac{\sigma }{{\rho {{r}^{3}}}}} ,$ который легко выводится из соображений теории размерностей. Оставляя за безразмерными величинами прежние обозначения, получим: Для пресной воды, с которой проводилось большинство экспериментов, χ = 10–3 Ом–1 м–1 [27, с. 531]. Плотность $\rho $, диэлектрическую проницаемость $\varepsilon $ коэффициент поверхностного натяжения $\sigma $ для воды возьмем стандартными для нормальной температуры, в итоге по (2) получим:Характерное время отрыва капли от струи. Маловязкая жидкость. Будем исходить из задачи об устойчивости цилиндрической струи вязкой несжимаемой жидкости по отношению к осесимметричным капиллярным волнам, решение которой приведено в [28, с. 626]. Жидкость будем считать электропроводной, а струю заряженной, с зарядом $\mu $ на единице длины струи. Решая задачу введением гидродинамического потенциала и функции тока по аналогии с тем, как это делалось в [28], получим дисперсионное уравнение задачи. В указанных безразмерных переменных, в асимптотике длинных капиллярных волн, для случая маловязкой жидкости (l 2 ≡ (s/νck2) $ \gg $ 1) это дисперсионное уравнение можно записать в виде
(3)
$\begin{gathered} {{s}^{2}} + 3\nu {{k}^{2}}s - G\left( k \right)\left( {1 - {{k}^{2}} - w~\left( {1 - H\left( k \right)} \right)} \right) = 0, \\ G\left( k \right) \equiv k\frac{{{{I}_{1}}\left( k \right)}}{{{{I}_{0}}\left( k \right)}},\,\,\,\,H\left( k \right) \equiv k\frac{{{{K}_{1}}\left( k \right)}}{{{{K}_{0}}\left( k \right)}},\,\,\,\,w \equiv \frac{{{{\mu }^{2}}}}{{\pi r\sigma }}. \\ \end{gathered} $(4)
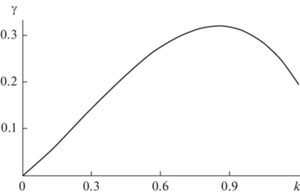
$\begin{gathered} {{s}_{{1,2}}} = - \frac{3}{2}{{\nu }_{c}}{{k}^{2}} \pm \\ \pm \,\,\sqrt {\frac{9}{4}\nu _{c}^{2}{{k}^{4}} + G\left( k \right)\left( {1 - {{k}^{2}} - w~\left( {1 - ~H\left( k \right)} \right)} \right){\kern 1pt} } . \\ \end{gathered} $На рис. 2 приведена качественная зависимость безразмерного инкремента неустойчивости капиллярных волн на струе от безразмерного волнового числа, рассчитанная по (4) для $w = 1$ и безразмерного коэффициента кинематической вязкости жидкости 0.125 (это значение соответствует воде). Положение максимума полученной зависимости находится в численных расчетах: величина безразмерного инкремента ${{\gamma }_{m}} \approx 0.31$ при ${{k}_{m}} \approx 0.84$. В итоге, характерное время отрыва капли маловязкой жидкости от струи равно
Как показано в [30] величина безразмерной вязкости капли (струи) зависит от характерного линейного размера объекта, в нашем случае радиуса. Так, капля воды сантиметрового радиуса ведет себя как маловязкая, а микрометрового радиуса – уже как сильновязкая.Рис. 2.
Зависимость безразмерного инкремента неустойчивости осесимметричной капиллярной волны на струе от безразмерного волнового числа, рассчитанная для безразмерного коэффициента кинематической вязкости жидкости $\nu = 0.125$.
Сильновязкая жидкость. Значительная вязкость жидкости приводит к снижению частоты периодических движений жидкости и их инкрементов неустойчивости и к увеличению декрементов затухания. Когда струя вязкая и можно полагать ${{l}^{2}} \approx {{k}^{2}}$ или, что то же самое, k2$ \gg $ s/νc, асимптотическое выражение дисперсионного уравнения (3) имеет вид
(5)
${{s}^{2}} + 4{{\nu }_{c}}{{k}^{2}}s - G\left( k \right)\left( {1 - {{k}^{2}} - w~\left( {1 - H\left( k \right)} \right)} \right) = 0,$(6)
$\begin{gathered} {{s}_{{1,2}}} = - 2{{\nu }_{c}}{{k}^{2}} \pm \\ \pm \,\,\sqrt {4\nu _{c}^{2}{{k}^{4}} + G\left( k \right)\left( {1 - {{k}^{2}} - w~\left( {1 - ~H\left( k \right)} \right)} \right){\kern 1pt} } . \\ \end{gathered} $Рис. 3.
Зависимости безразмерных инкрементов неустойчивости осесимметричных капиллярных волн на струе от безразмерного волнового числа, рассчитанные при безразмерных коэффициентах кинематической вязкости жидкости $\nu = 1.25;\;12.5;\;125$ (сверху вниз).
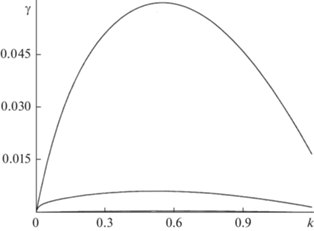
Положение максимума зависимости безразмерного инкремента от безразмерного волнового числа характеризуется значениями γm ≈ 0.06 при ${{k}_{m}} \approx 0.55,{{\gamma }_{m}} \approx 0.0063$ при ${{k}_{m}} \approx 0.52,$ ${{\gamma }_{m}} \approx 0.00062$ при ${{k}_{m}} \approx 0.5$, полученными при $w = 1$ и указанных значениях νc. Отметим, что величина νc = 100 соответствует глицерину. Из (5) следует, что рост вязкости приводит к снижению инкремента неустойчивости и увеличению характерного времени отрыва капли от струи, которое при значениях νc = 1.25, 12.5, 125 составит соответственно τd = = 1/γm ≈ 16.7, 164, 1613.
В приведенном примере величина безразмерного коэффициента кинематической вязкости изменялась в диапазоне от 0.125 до 125, т.е. на четыре порядка. Этот пример может относиться как к струям разной толщины одной жидкости, так и к струям одинаковой толщины, но с различными значениями размерного коэффициента кинематической вязкости. Это обстоятельство необходимо принимать во внимание.
Сказанное выше касается чистых жидкостей, когда же речь идет об их смесях, часто использующихся в электродиспергировании, чтобы добиться конкретных значений какого-либо физико-химического показателя [1–5, 8–11, 18–23], то диапазон возможного изменения безразмерной вязкости может быть еще шире. К сожалению, ситуация усугубляется еще и тем, экспериментаторы, как правило, не контролируют весь набор физико-химических свойств, важных для феномена электродиспергирования, а следят за изменением какого-либо одного свойства (например, вязкости или электропроводности) при изменении концентрации компонентов смеси, оставляя другие без внимания, хотя они также при этом изменяются.
Вернемся теперь к классификации режимов электродиспергирования, и на поле безразмерных параметров – характерного безразмерного времени релаксации заряда и характерного безразмерного времени отрыва капли от струи – определим место основных режимов электродиспергирования, ограничившись для начала осесимметричной ситуацией.
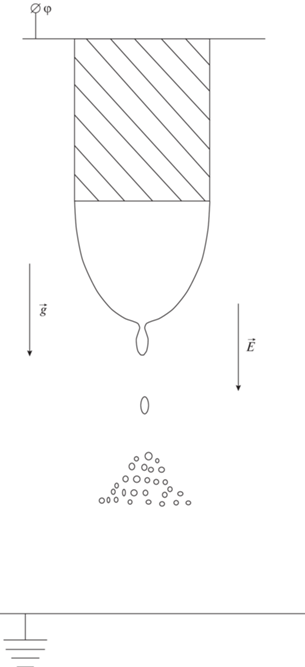
Капельные режимы. Капельные режимы: капельный (dripping mode), микрокапельный (microdripping mode), каплеструйный (dripping mode with emission of jet), капельный с длинной перетяжкой (dripping mode with long neck) и т.п., – появляются первыми по мере увеличения электрической силы, действующей на каплю, если к ориентированному вертикально капилляру кроме силы тяжести приложить еще электрическое поле. Капля будет отрываться от капилляра под действием двух однонаправленных сил: силы тяжести и электрической силы; примем для определенности, что капля заряжена положительно, см. рис. 4 (противоэлектрод считаем достаточно удаленным).
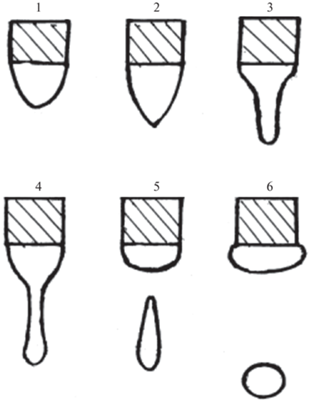
Следует отметить, что капельные режимы были обнаружены одними из первых, уже в работах Зелени, Инглиша, Дрозина [1–4], позднее эти режимы были детально исследованы [31, 32] и классифицированы [18–22, 25], а в [33] построена их исчерпывающая теория. На рис. 5 скопирован из [32] рисунок постадийного отрыва капли от капилляра.
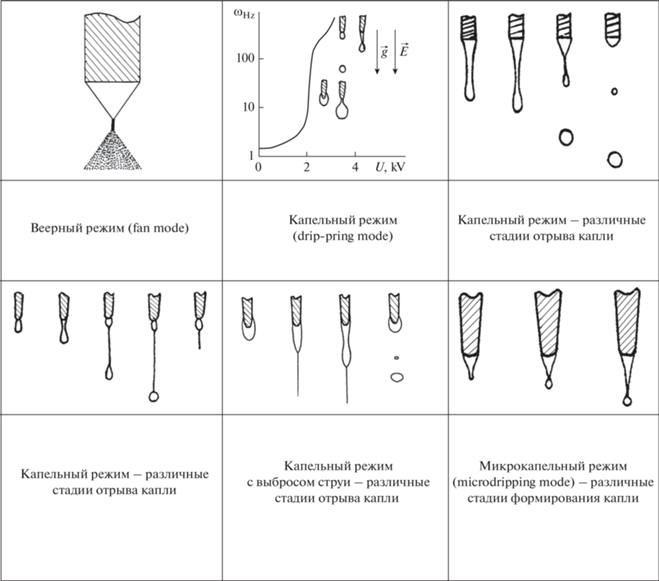
На рис. 6 приведены некоторые капельные режимы, выделяемые в [1, 2, 18–22].
Схематическое изображение “веерного” режима (fan mode) приведено на рис. 5. Он наблюдался в [1–5, 34, 35] (в [1–5] этот режим назывался “щеточным” (brush), и лишь в [34, 35] его поименовали “веерным”, что лучше соответствует феноменологии). В этом режиме мениск эмитирует изначально сильно заряженные капли, неустойчивые по отношению к собственному заряду и распадающиеся на более мелкие. Неустойчивая капля теряет при распаде согласно экспериментальным исследованиям [36] $23 \pm 5$% собственного заряда и $5 \pm 5$% массы (обращает на себя внимание тот факт, что обнаруженное в [36] изменение массы капли лежит в пределах точности измерений). Дочерние капельки также неустойчивы по отношению к собственному заряду и распадаются по тому же закону. В силу большого заряда на дочерних капельках у их поверхности загорается самоподдерживающийся за счет фотоионизации коронный разряд, а у вершины мениска появляется “веерное” свечение [34, 35, 37]. В “веерном” режиме продуцируется большое количество весьма мелких полидисперсных заряженных капелек, поскольку исходно значительный заряд на дочерних капельках снимается коронным разрядом.
В терминах характерных времен на плоскости безразмерных параметров – характерного безразмерного времени релаксации заряда и характерного безразмерного времени отрыва капли от струи – режим “веерного” свечения займет левую верхнюю часть плоскости. Эту область можно выделить аналитически, будучи выписана в размерном виде, она ограничена неравенствами
(7)
$\begin{gathered} \frac{\varepsilon }{\chi }\sqrt {\frac{\sigma }{{\rho {{R}^{3}}}}} \ll \left[ { - \frac{3}{2}{{\nu }_{c}}{{k}^{2}} + } \right. \\ {{\left. { + \,\,\sqrt {\frac{9}{4}\nu _{c}^{2}{{k}^{4}} + G\left( k \right)\left( {1 - {{k}^{2}} - w~\left( {1 - H\left( k \right)} \right)} \right)} } \right]}^{{ - 1}}} \ll 1. \\ \end{gathered} $Кроме (7), необходимо также выполнение дополнительного требования: потенциал $\varphi $, прикладываемый к капилляру (струе), должен обеспечивать отрывающейся капле заряд, превышающий рэлеевский предел [38]:
(8)
$\frac{{{{\varphi }^{2}}r}}{{16\pi \sigma }} \geqslant 1 \Rightarrow \varphi \geqslant \sqrt {\frac{{16\pi \sigma }}{r}} .$Поскольку капля отрывается от мениска под действием двух сил, то первоначальное разделение режимов должно проходить по принципу: какая из сил преобладает, а затем по физико-химическим свойствам, т.к. в зависимости от них меняется и феноменологическая картина диспергирования.
В веерном режиме от мениска на торце капилляра отрывается сильно заряженная (выше рэлеевского предела) капля, когда выполняются условия (7), (8). Если же эти условия не выполняются, то отрывающаяся от мениска капля устойчива по отношению к собственному заряду, и реализуются режимы, следующие за веерным режимом на рис. 6. Хотя если отклонение критерия Рэлея для эмитированной капли невелико, то капля, двигаясь относительно газовой среды, будет испаряться и достигнет рэлеевского предела на некотором расстоянии от мениска. Такая капля распадется по указанному выше закону (см. [36]), как это показано в экспериментах [47], причем этот процесс может повторяться (см. фотографии в [47]).
В гравитационно-капельном режиме преобладает сила гравитации. Наличие электричества (капилляр поддерживается при некотором небольшом потенциале) обеспечивает появление на капле незначительного заряда. По мере увеличения потенциала на капилляре заряд на капле увеличивается, а размер отрывающихся капель уменьшается [32, 33].
Следует также отметить, что от диаметра капилляра, по которому подается жидкость, зависит и феноменология явления отрыва капель. Если капилляр тонкий, то отрыв капли радиуса $r$ c массовой плотностью $\rho $ под действием силы тяжести происходит непосредственно с торца капилляра радиусом ${{r}_{0}}$, а лапласовская сила на кромке капилляра, удерживающая каплю, определяет максимальный вес капли:
Отсюда легко находится радиус отрывающейся капли
(9)
$r = \sqrt[3]{{\frac{{3{{r}_{0}}\sigma }}{{2\rho g}}}} \equiv \sqrt[3]{{\frac{{3{{r}_{0}}{{\alpha }^{2}}}}{4}}},$Если к силе тяжести капли добавить электрическую силу, то радиус отрывающейся капли уменьшится по сравнению со значением, задаваемым (9).
Если капилляр толстый, то самое тонкое место (перетяжка) обычно располагается ниже среза капилляра, как это показано на рис. 4, и удерживающая сила $2\pi {{r}_{п}}\sigma $ определяется радиусом перетяжки ${{r}_{п}}$, который меньше радиуса капилляра. В [1, 2, 32], приведены рисунки постадийного отрыва капли от толстого капилляра, позволяющие в деталях рассмотреть, как осуществляется отрыв капли (см. рис. 5 и 6).
При электродиспергировании в микрокапельном режиме, когда вклад силы тяжести в баланс сил в перетяжке незначителен (пренебрежимо мал), на торце капилляра формируется мениск жидкости размерами порядка толщины капилляра, и отрыв капель идет за счет электрической силы, отрывающей заряженную вершину мениска (см. рис. 6 и 7).
Теоретический расчет размеров и зарядов эмитируемых капель. Теоретический расчет основывается на принципе Онзагера наименьшей скорости рассеяния энергии в неравновесном процессе [40, 41]. Процедура аналогична использованной ранее [34, 42–44].
Будем рассчитывать радиусы $r$ и заряды $q$ капель, эмитированных жидким мениском на торце капилляра, принимая, что на капилляр подан потенциал $\varphi $. Будем также полагать, что характерное время релаксации электрического заряда ${{\tau }_{\chi }}$ много меньше характерного времени отрыва капли от мениска ${{\tau }_{d}}$. Противоэлектрод будем считать достаточно удаленным от мениска так, чтобы электрическое поле в окрестности отрывающейся капельки определялось потенциалом $\varphi $. Для последующего качественного анализа поле в окрестности отрывающейся капли примем совпадающим с полем у поверхности сильно вытянутого сфероида с эксцентриситетом $e = \sqrt {1 - {{{\left[ {\frac{{{{r}_{0}}}}{{\left( {0.5L + {{r}_{0}}} \right)}}} \right]}}^{2}}} $, где $L$ – длина капилляра с мениском жидкости на его вершине.
Заряд Q на модельном сфероиде (на капилляре с жидким мениском) определится потенциалом $\varphi $ и электроемкостью сфероида. Тогда электрический потенциал в месте отрыва капли от мениска $f\left( \nu \right)$ будет иметь вид [45, с. 41]
Из рис. 4 и общефизических соображений следует, что бóльшая часть заряда сосредоточена на той части отрывающейся капли, которая имеет положительную среднюю кривизну. После разрыва перетяжки, связывающей отрывающуюся каплю с мениском на торце капилляра, за время порядка времени гидродинамической релаксации ${{\tau }_{с}} = \frac{r}{c}$, где $с$ – скорость звука в жидкости, оторвавшаяся капля примет в электрическом поле разрядной системы форму, близкую к вытянутому по полю сфероиду с эксцентриситетом ${{е}_{0}}$ [48].
Для качественного анализа примем, что форма вершины отрывающейся капли в момент разрыва перетяжки – полусфера с радиусом ${{r}_{p}} = r{{(1 - е_{0}^{2})}^{{\frac{2}{3}}}}$, равным среднему радиусу кривизны сфероида с эксцентриситетом ${{е}_{0}}$. Тогда электроемкость отрывающейся капли (в предположении, что заряд накапливается только на полусферической вершине) будет равна $\frac{{{{r}_{p}}}}{2}$. В итоге для емкости отрывающейся капли ${{С}_{{\text{к}}}}$ получим:
(10)
$\begin{gathered} \Delta F \equiv 4\pi {{r}^{2}}\sigma A\left( {{{е}_{0}}} \right) + \frac{{{{q}^{2}}}}{{2r}}{{B}_{0}}\left( {{{е}_{0}}} \right) - \\ - \,\,q\left[ {\varphi \left( \nu \right) - \varphi } \right] + \frac{{2\pi {{r}^{3}}\rho {{U}^{2}}}}{3}, \\ A\left( {{{е}_{0}}} \right) = \frac{1}{2}\left( {{{{\left( {1 - e_{0}^{2}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} + \frac{{{\text{arcsin}}{{e}_{0}}}}{{{{e}_{0}}}}} \right)\frac{1}{{{{{\left( {1 - e_{0}^{2}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0em} 6}}}}}}, \\ \end{gathered} $Первое слагаемое в (10) описывает изменение свободной поверхностной энергии при эмиссии одной капли; второе слагаемое определяет собственную электростатическую энергию появившейся заряженной капли, третье слагаемое – изменение энергии электростатического взаимодействия эмитированной капельки с мениском, а последнее слагаемое – кинетическую энергию эмитированной капли.
Примем, что отрыв капли от вершины мениска происходит с вершины выступа, вырастающего на мениске при развитии в нем неустойчивости капиллярных волн. При этом под действием кулоновского взаимодействия заряда вершины выступа и заряда мениска вершина выступа вместе с находящимся на ней зарядом отрывается, как только кулоновская сила отталкивания между зарядами превысит силу поверхностного натяжения $2\pi {{r}_{п}}\sigma $, удерживающую вершину выступа.
Примем для качественного анализа, что форма вершины выступа – сфероид с меньшей полуосью ${{b}_{0}}$, и учтем, что величина напряженности поля E, создаваемого зарядом модельного сфероида в месте отрыва маленькой капельки, равна [45, с. 40]
(11)
$E\left( \nu \right) \equiv \frac{{Q{{{\left( {1 - e_{0}^{2}} \right)}}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}}}{{R_{*}^{2}\left( {{{\nu }^{2}} - e_{0}^{2}} \right)}}.$(12)
$\begin{gathered} 2\pi \alpha \sigma r{{\left( {1 - e_{0}^{2}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0em} 6}}}} = \\ = \left( {\frac{{{{Q}^{2}}{{{\left( {1 - e_{0}^{2}} \right)}}^{{{7 \mathord{\left/ {\vphantom {7 6}} \right. \kern-0em} 6}}}}}}{{r_{0}^{3}\left( {{{\nu }^{2}} - e_{{}}^{2}} \right)}}\frac{{\left( {B\left( e \right) - Н\left( e \right)} \right)}}{{{{B}_{0}}\left( {{{e}_{0}}} \right)}} + \frac{4}{3}U\sqrt {2\sigma \rho {{r}^{3}}} } \right), \\ B\left( е \right) = \left( {\frac{1}{e}{{{\left( {1 - e_{{}}^{2}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}\arcsin e} \right),\,\,\,\,\alpha \equiv \frac{{{{r}_{п}}}}{{r{{{(1 - e_{0}^{2})}}^{{{1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0em} 6}}}}}}, \\ \end{gathered} $Выражение (12) представляет собой уравнение для определения параметра $\nu $, характеризующего расстояние между центрами капель в момент разрыва перетяжки.
В безразмерном виде, когда вводятся безразмерный радиус капли $X \equiv \frac{r}{R}$, безразмерный заряд $Y \equiv \frac{q}{Q}$ и безразмерное изменение энергии ${{\Delta \Phi }} \equiv \frac{{\Delta F}}{{4\pi \sigma r_{0}^{2}}}$, (10) и (12) принимают следующий вид:
(10а)
$\begin{gathered} \Delta {{\Phi }} = A\left( {{{e}_{0}}} \right){{X}^{2}} + 2{{W}^{2}}{{Y}^{2}}{{X}^{{ - 1}}}{{В}_{0}}\left( {{{е}_{0}}} \right) - \\ - \,\,4P\left( e \right){{W}^{2}}Y + \frac{1}{6}{{\delta }^{2}}{{X}^{3}} = 0, \\ \alpha = N\left( {{{e}_{0}}} \right){{W}^{2}} + G\left( {{{e}_{0}}} \right){{X}^{{\frac{1}{2}}}}\delta , \\ P\left( е \right) \equiv \left[ {В\left( е \right) - Н\left( е \right)} \right]{{(1 - e_{{}}^{2})}^{{{1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0em} 6}}}}, \\ K \equiv {{\left( {\frac{{{{U}_{0}}}}{U}} \right)}^{2}},\,\,\,\,{{\delta }^{2}} \equiv \frac{{\rho {{U}^{2}}{{r}_{0}}}}{\sigma }, \\ N\left( {e,\nu } \right) \equiv 8\frac{{P\left( е \right)(1 - e_{{}}^{2})}}{{B\left( {{{e}_{0}}} \right)({{\nu }^{2}} - {{e}^{2}}){{{(1 - e_{0}^{2})}}^{{\frac{1}{6}}}}}}, \\ \end{gathered} $(12а)
$G\left( {{{e}_{0}}} \right) \equiv \frac{{4{{{(1 - e_{0}^{2})}}^{{\frac{{ - 1}}{6}}}}}}{{3\pi \sqrt 2 }},\,\,\,\,{{\Theta }^{2}} \equiv \frac{{{{Q}^{2}}}}{{16\pi \sigma R_{*}^{3}}},$Потребуем, чтобы в силу принципа наименьшего рассеяния энергии в неравновесных процессах Онзагера [41] изменение энергии при эмиссии капли было экстремальным и выполнялись условия
(13)
$\frac{{\partial \left( {\Delta F} \right)}}{{\partial r}} = 0,\,\,\,\,\frac{{\partial \left( {\Delta F} \right)}}{{\partial q}} = 0.$Условия экстремальности (13) в безразмерном виде запишутся как
(13а)
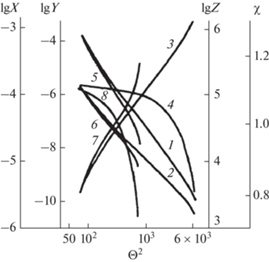
$XA\left( {{{e}_{0}}} \right) - {{Y}^{2}}{{X}^{{ - 2}}}{{В}_{0}}\left( {{{е}_{0}}} \right){{\Theta }^{2}} + 0.25{{\delta }^{2}}{{X}^{2}} = 0,$Рис. 8.
Пример расчета по (12а), (13а) и (13б) безразмерных размеров $X$ (кривые 1, 5), зарядов $Y$ (2, 6), удельных зарядов $Z$ (3, 7) и параметра электростатической устойчивости эмиттированной капли $\Xi $ (4, 8). Расчеты проведены для двух значений параметра ${{\delta }^{2}}$: ${{\delta }^{2}} = {{10}^{{ - 5}}}$ (кривые 1–4) и ${{\delta }^{2}} = {{10}^{{ - 4}}}$ (кривые 5–8).
Упомянутый критерий имеет вид [48]
(14)
$\begin{gathered} \Xi \equiv (1 + 2.07{{e}^{2}})W + 4.64(1 + 6.6{{e}^{2}}){{w}_{d}} + \\ + \,\,3\sqrt {W{{w}_{d}}} (1 + 0.476{{e}^{2}}) \geqslant 1, \\ {{e}^{2}} = \frac{{9{{w}_{d}}}}{{(1 - W)}},\,\,\,W \equiv \frac{{{{q}^{2}}}}{{16\pi \sigma {{r}^{3}}}},\,\,\,\,{{w}_{d}} \equiv \frac{{E_{0}^{2}r}}{{16\pi \sigma }}. \\ \end{gathered} $При $\Xi < 1$ капли устойчивы по отношению к комбинации собственного и индуцированного внешним полем зарядов, а при $\Xi \geqslant 1$ они неустойчивы и распадаются на несколько сотен более мелких.
В (14) ${{E}_{0}}$ – квазиоднородная напряженность внешнего электростатического поля в месте нахождения капли (в пределах объема, занимаемого каплей, внешнее электростатическое поле можно приближенно для качественных расчетов считать однородным).
На рис. 8 видно, что с увеличением ${{\Theta }^{2}}$ безразмерные размер и заряд капли быстро уменьшаются, а удельный заряд увеличивается; при малых значениях ${{\Theta }^{2}}$ параметр $\Xi $ для эмитированных капель оказывается больше единицы, и, следовательно, эмитированные капли неустойчивы по отношению к суперпозиции собственного и индуцированного зарядов. Сам собой напрашивается вопрос: почему только при малых значениях $\Theta $? Это происходит потому, что при малых значениях ${{\Theta }^{2}}$ основной вклад в параметр устойчивости $\Xi $ вносит собственный заряд капли, когда все дочерние капельки неустойчивы [49]. Вклад индуцированного заряда при этом, по-видимому, играет пассивирующую роль и незначителен.
Обратим внимание на тот факт, что диапазон изменения параметра ${{\Theta }^{2}}$ на рис. 8 весьма широк. Это сделано для того, чтобы охватить весь диапазон электростатических напряжений электродиспергирования жидкости, использованных в разнообразных приложениях феномена [11, 13, 14, 50, 51].
Общий вывод из приведенных рассуждений и расчетов заключается в том, что в зависимости от величины внешнего поля эмитируемые капли могут быть как неустойчивыми по отношению к заряду, так и устойчивыми. В области неустойчивости мы получаем веерное свечение, а в области устойчивости выброшенных капель вариации физико-химических свойств рабочей жидкости объясняют все разнообразие капельных режимов (см. рис. 6).
Сначала истолкуем появление струй в “капельном” режиме (см. режимы со струйками на рис. 6). Струйки выбрасываются в “капельном” режиме (см., например, в [18] “каплеструйный” режим или dripping-jet mode), когда электрическое давление на вершину мениска превышает лапласовскую силу, ее удерживающую, но безразмерная вязкость жидкости в образовавшейся струе тормозит разрыв струи на капельки (см. рис. 3 и комментарий к нему). Струя будет удлиняться до тех пор, пока медленно развивающаяся “перетяжечная” неустойчивость в ней не завершится разрывом струйки.
Струйные режимы. Струи образуются, когда гравитационные и электрические силы, действующие на вершину мениска, и гидродинамическое давление в капилляре превысят лапласовскую силу, удерживающую вершину мениска, но характерное время разрыва перетяжки, связывающей вершину мениска с его основанием, весьма велико из-за вязкости жидкости. Иначе говоря, когда произведение скорости элемента жидкости в мениске ${{U}_{0}}$ на характерное время разрыва перетяжки ${{\tau }_{d}}$ много больше единицы: τdU0$ \gg $ 1.
Цилиндрическая струя неустойчива уже в капиллярном смысле: ее свободная поверхностная энергия больше, чем свободная энергия совокупности капель, на которые струя может распасться [28]. Наличие внешнего электрического поля усложняет ситуацию: кроме разрыва струи на капли при $m = 0$ появляется еще возможность закручивания струи при $m = 1$ и выбрасывания дочерних струек при $m \geqslant 2$, что соответствует неустойчивости ее первых трех азимутальных мод.
На рис. 9 приведены примеры осесимметричных струйных режимов с $m = 0$. Эти режимы более-менее изучены экспериментально, а их теория проста [33]: основой образования капель в таких режимах является осесимметричная “перетяжечная” неустойчивость. В этих режимах выделяются “капельный” и “микрокапельный” режимы, реализующиеся при преобладающем влиянии гравитационной (капельный режим) или электростатической (микрокапельный режим) силы, отрывающей каплю [32, 33]. Остальные выделяемые экспериментаторами капельные режимы являются феноменологическими вариациями упомянутых двух режимов, имеющими место при различных геометриях установки для электродиспергирования и разных физико-химических свойствах диспергируемых жидкостей. В рамках развития неустойчивости азимутальной моды с $m = 0$ можно истолковать режимы: “прерывистый конусно-струйный” (intermittent cone-jet mode) [18] и “конусно-короткоструйный” (cone-short jet mode) [18].
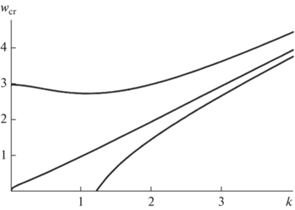
На рис. 10 приведены примеры неосесимметричных струйных режимов с $m = 1$. Главным в этих режимах является изгиб струи, а будет ли при этом струя распадаться на капли или нет, зависит от величины заряда, приходящегося на единицу длины струи, и физико-химических свойств жидкости. Дело в том, что изгибная азимутальная мода ($m = 1$) теряет устойчивость при сколь угодно малом заряде на струе, а осесимметричная мода с $m = 0$, – начиная с некого порогового значения заряда, величина которого зависит от скорости движения струи относительно среды и волнового числа (см., например, рис. 11). На этом рисунке изображен график зависимости критического зарядового параметра ${{w}_{{{\text{cr}}}}}$ от безразмерного волнового числа $k$ для первых трех азимутальных мод заряженной струи, движущейся относительно газообразной среды при фиксированном значении параметра Вебера ${\text{We = }}\frac{{{{\rho }_{{{\text{ex}}}}}{{U}^{2}}{{r}_{0}}}}{\sigma }$, равном 0.5. Видно, что, например, при $k = 0.5$ с увеличением заряда, приходящегося на единицу длины струи, первой становится неустойчивой азимутальная мода с $m = 1$, а осесимметричная мода с $m = 0$ для той же длины волны будет устойчива. Зрительно это будет выглядеть как изгибающаяся струя. С увеличением волнового числа, например, при $k = 2$ и ${\text{We}} = 0.5$, первой теряет устойчивость осесимметричная мода с $m = 0$ и только затем становится неустойчивой изгибная мода с $m = 1$. Визуально это будет восприниматься как изгибающаяся струя, с торца которой отрываются капли. Следует также отметить, что распаду струи при $m = 1$ будет способствовать и центробежная сила, действующая на свободный конец струи. В рамках развития изгибной неустойчивости могут быть описаны режимы: “веретенообразный” (spindle mode) [18], “многоверетенный” (multispindle) [20], режим с “нерегулярно ветвящимся мениском” (ramified meniscus) [20].
Рис. 11.
Критические кривые потери устойчивости первых трех азимутальных мод при We = 0.5 [52]. Снизу вверх: $m = 0,\;1,\;2$.
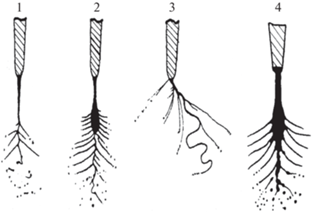
На рис. 12 приведены примеры нескольких неосесимметричных струйных режимов с $m \geqslant 2$. Они называются режимами “ветвящихся струй”, или в оригинале [18, 19] – “fan configuration” или “ramified jet’’. Про эти режимы можно сказать, что экспериментально они плохо изучены, поскольку реализуются при очень высоких значениях заряда, приходящегося на единицу длины струи. Значения напряженности электростатического поля у поверхности струи оказываются близкими к пробойному в смысле зажигания коронного разряда, который при возникновении искажает всю феноменологию явления электродиспергирования. Экспериментальных данных не хватает даже для того, чтобы определить, относятся ли схемы на рис. 12 к одному режиму или к разным. Во всяком случае, в [53] приведена фотография струи, которая в сильном поле претерпевает электростатическую неустойчивость и выбрасывает струйку, которая в свою очередь распадающиеся на капельки. Однако визуально картина распада отличается от всех приведенных на рис. 12, а схемы 1 и 3 на приведенном выше рисунке визуально отличаются от второй и четвертой (считая слева). Видно, что объемный расход жидкости при диспергировании в режимах 2 и 4 меньше скорости ее поступления в мениск, и в итоге жидкость накапливается на конце струи, образуя утолщение. Размер капелек, образующихся на конечной стадии, в любом случае весьма мал. Теоретический подход к изучению режимов “ветвящихся струй” приведен в [54].
Рис. 12.
Визуальные примеры режимов “ветвящихся струй” (ramified jet) – осенесимметричных струйных режимов с высокими значениями азимутальных чисел: $m \geqslant 2$, как они наблюдались в [18, 19]. Внутреннего разделения между режимами, приведенными на рисунке, пока не проведено ввиду слабой их изученности. Можно предположить, что изображения, отмеченные цифрами 1 и 3, и изображения, помеченные цифрами 2 и 4, относятся к различным значениям $m$.
Следует отметить, что имеют место и переходы между режимами. Их можно назвать непредсказуемыми, неожиданными, и происходят они с нарушением симметрии. Так, в работе [18, Fig. 16] показано что переход от микрокапельного режима к конусно-струйному (cone-jet mode) происходит при повышении прикладываемого напряжения, как и переход от капельного режима к веретенному [18, Fig. 17]. Впрочем, такие переходы укладываются в теорию дробления струй.
ЗАКЛЮЧЕНИЕ
Предлагается чисто теоретический подход к классификации режимов электродиспергирования жидкости. Электродиспергирование может идти с отрывом капель непосредственно с мениска на торце капилляра, по которому жидкость подается в разрядную систему, или через промежуточную стадию выброса мениском струи жидкости, распадающейся на отдельные капли. На поверхности выброшенных струй может реализоваться неустойчивость трех различных азимутальных мод. При учете физико-химических свойств жидкостей все сказанное выше обеспечивает многообразие феноменологически наблюдаемых режимов электродиспергирования жидкости.
Список литературы
Zeleny J. // Proc. Cambridge Philos. Soc. 1914. V. 18. Pt. 1. P. 71.
Zeleny J. // Phys. Rev. 1917. V. 10. P. 1.
English W.H. // Phys. Rev. 1948. V. 74. P. 179.
Drozin V.G. // J. Colloid Sci. 1955. P. 158.
Бураев Т.К., Пашин М.М. // Электричество. 1971. № 5. С. 70.
Macky W.A. // Proc. Roy. Soc. London. 1931. V. A133. P. 565.
Jones A.R., Thong K.C. // J. Phys. D: Appl. Phys. 1971. V. 4. P. 1159.
Schultze V.K. // Z. Angew. Physik. 1961. V. 13. № 1. P. 11.
Perel J., Yahiku A.Y., Mahoney J.F. et al. // J. Spacecraft. 1973. V. 8. P. 702.
Bartoli C., von Rohden M., Thompson S.P. et al. // Vacuum. 1984. V. 34. P. 43.
Bailey A.G. // Phys. Bull. 1984. V. 35. 146.
Woosley J.P., Turnbull R.J., Kim K. // J. Appl. Phys. 1988. V. 64. P. 4278.
Fenn J.B., Mann M., Meng C.K. et al. // Science. 1989. V. 246. P. 64.
Габович М.Д. // УФН. 1983. Т. 140. С. 137.
Kim Y.E., Rabinowitz M., Chulck G.S., Rice R.A. // Modern Phys. Lett. B. 1991. V. 5. P. 427.
Манзон Б.М. // УФН. 1981. Т. 134. С. 611.
Jeynes C. // Vacuum. 1989. V. 39. P. 1047.
Cloupeau M., Prunet-Foch B. // J. Electrostatics. 1990. V. 25. P. 165.
Cloupeau M., Prunet-Foch B. // J. Aerosol Sci. 1994. V. 25. P. 1021.
Jaworek A., Krupa A. // J. Aerosol Sci. 1999. V. 30. P. 873.
Verdoold S., Agostinho L.L.F., Yurteri C.U., Marijennisen J.S.W. // J. Aerosol Sci. 2014. V. 67. P. 87.
Park I., Kim S.B., Hong W.S., Kim S.S. // J. Aerosol Sci. 2015. V. 89. P. 26.
Pfeifer R.J. // Phys. Fluids. 1973. V. 16. P. 454.
Shiryaeva S.O., Grigor’ev A.I. // J. Electrostatics. 1995. V. 34. P. 51.
Григорьев А.И., Ширяева С.О. // Электронная обработка материалов. 2018. Т. 54. № 2. С. 23.
Григорьев А.И. / ЖТФ. 2007. Т. 77. № 2. С. 31.
Стреттон Дж.А. Теория электромагнетизма. М.: ОГИЗ Гостехиздат, 1948.
Левич В.Г. Физико-химическая гидродинамика. М.: Физматгиз, 1959.
Абрамовиц М., Стиган И. Справочник по специальным функциям. М.: Наука, 1979.
Григорьев А.И. // ЖТФ. 2001. Т. 71. № 10. С. 1.
Raghupathy B., Sample S.B. // Rev. Sci. Instrum. 1970. V. 71. P. 645.
Sample S.B., Raghupathy B. // J. Colloid Interface Sci. 1972. V. 41. P. 185.
Zemskov A.A., Shiryaeva S.O., Grigor’ev A.I. // J. Colloid Interface Sci. 1993. V. 158. P. 54.
Войцеховский Б.В., Войцеховский Б.Б. // Письма в ЖЭТФ. 1976. Т. 23. С. 37.
Войцеховский Б.Б. // ДАН СССР. 1982. Т. 262. С. 84.
Schweizer J.W., Hanson D.N. // J. Colloid Interface Sci. 1971. V. 35. P. 417.
Григорьев А.И., Синкевич О.А. // ЖТФ. 1984. Т. 54. С. 1276.
Rayleigh (Strutt J.W.) // Phil. Mag. 1882. V. 14. P. 184.
Ландау Л.Д., Лифшиц Е.М. Гидродинамика. М.: Наука, 1986.
Базаров И.П., Геворкян Э.В., Николаев П.Н. Неравновесная термодинамика и физическая кинетика. М.: Изд. МГУ, 1989.
Базаров И.П. Термодинамика. М.: Высшая школа, 1991. 376 с.
Grigor’ev A.I., Shiryaeva S.O. // J. Phys. D.: Appl. Phys. 1990. V. 23. P. 1361.
Grigor’ev A.I., Shiryaeva S.O., Verbitskii S.S. // J. Colloid Interface Sci. 1991. V. 146. P. 137.
Grigor’ev A.I., Shiryaeva S.O. // J. Aerosol Sci. 1994. V. 25. P. 1079.
Ландау Л.Д., Лифшиц Е.М. Электродинамика сплошных сред. М.: Наука, 1982.
O’Konski C.J., Thacher H.C. // J. Phys. Chem. 1953. V. 57. P. 955.
Vonnegut B., Newbauer R.L. // J. Colloid Sci. 1952. V. 7. P. 616.
Григорьев А.И., Ширяева С.О., Белавина Е.И. // ЖТФ. 1989 Т. 59. № 6. С. 27.
Григорьев А.И., Ширяева С.О. // ЖТФ. 1991. Т. 61. № 3. С. 19.
Фукс Н.А. // Успехи химии. 1976. Т. 45. С. 2274.
Bailey A.G. // Atomization and Spray Technology. 1986. V. 2. P. 95.
Shiryaeva S.O., Grigor’ev A.I., Brusnitsina A.O. // Surf. Eng. Appl. Electrochem. 2021. V. 57. P. 190.
Kim O.V., Dunn P.F. // Langmuir. 2010. V. 26. P. 15807.
Григорьев А.И., Ширяева С.О. // Изв. РАН. МЖГ. 2021. № 3. С. 48.
Дополнительные материалы отсутствуют.
Инструменты
Коллоидный журнал