Коллоидный журнал, 2022, T. 84, № 2, стр. 141-163
Капиллярные волны и дипольное электромагнитное излучение, создаваемое нелинейными осцилляциями незаряженной капли во внешнем однородном электростатическом поле
А. И. Григорьев 1, *, Н. Ю. Колбнева 2, С. О. Ширяева 2
1 Институт проблем механики им. А.Ю. Ишлинского
119526 Москва, пр-кт Вернадского, д. 101, к. 1, Россия
2 Ярославский государственный университет им. П.Г. Демидова
150000 Ярославль, ул. Советская дом 14, Россия
* E-mail: grigorai@mail.ru
Поступила в редакцию 08.12.2021
После доработки 04.03.2022
Принята к публикации 06.03.2022
- EDN: RKRRGV
- DOI: 10.31857/S0023291222020057
Аннотация
В аналитических расчетах второго порядка малости по безразмерной амплитуде $\varepsilon $ осцилляций незаряженной электропроводной капли во внешнем электростатическом поле найдено аналитическое выражение для интенсивности ее дипольного электромагнитного излучения, связанного с осцилляциями, позволяющее исследовать зависимость интенсивности излучения от физических параметров задачи. Такая задача представляет интерес в связи с проблемой радиолокационного зондирования таких метеорологических объектов как облака, туманы и смерчи. Исследована временная эволюция интенсивности электромагнитного излучения и ее компонент: величины индуцированного заряда и дипольного момента, капли. Во втором порядке малости по квадрату отношения характерного линейного размера капли к длине излучаемой волны оценена интенсивность дипольного излучения. Она оказалась на величину $ \sim {\kern 1pt} \varepsilon $ больше интенсивности, получаемой в линейных по $\varepsilon $ расчетах. Однако, квадратичная по $\varepsilon $ поправка к интенсивности излучения от капли реализуется в другом интервале частот, что влияет на спектр электромагнитного излучения.
ВВЕДЕНИЕ
В нижеследующем рассмотрении в аналитических асимптотических расчетах второго порядка малости по безразмерной амплитуде осцилляций рассчитывается интенсивность дипольного электромагнитного излучения незаряженной электропроводной капли, совершающей нелинейные осцилляции конечной амплитуды во внешнем электростатическом поле.
Хорошо известно, что на поверхности незаряженной электропроводной капли, помещенной во внешнее электростатическое поле, появляются индуцированные полем заряды противоположных знаков: отрицательные на стороне капли, обращенной к полю, и положительные на противоположной [1]. В капле жидкости всегда существуют капиллярные волны, связанные с тепловым движением молекул [2], приводящие к искажению равновесной в электростатическом поле формы капли, которая будет примерно сфероидальной [3, 4]. Капиллярные волны, отличаются от обычных гравитационных только тем, что имеют существенно меньшие длины и реализуются не под действием силы тяжести, а под влиянием сил поверхностного натяжения (капиллярных сил). Амплитуда тепловых капиллярных волн (реализующихся в капле) весьма мала: $ \sim {\kern 1pt} \sqrt {{{\kappa T} \mathord{\left/ {\vphantom {{\kappa T} \sigma }} \right. \kern-0em} \sigma }} $, где $\kappa $ – постоянная Больцмана, $T$ – абсолютная температура, $\sigma $ – коэффициент поверхностного натяжения [2]. Для всех жидкостей, включая жидкие металлы, их амплитуда не превышает $0.1\,\,{\text{нм}}$. Но для нижеследующего рассмотрения важно, что индуцированные в капле внешним электростатическим полем заряды, двигаясь ускоренно вместе с поверхностью осциллирующей капли, будут излучать электромагнитные волны [1, 5–7].
Теория излучения электромагнитных волн при ускоренном движении электрических зарядов хорошо развита [8, 9]. Полное электромагнитное излучение системы ускоренно движущихся зарядов набольших расстояниях от излучающей системы согласно мультипольным представлениям [8, 9] можно представить в виде суммы дипольной, квадрупольной и магнитно-дипольной компонент. Эти компоненты значительно различаются по интенсивности. Так, для капли воды, осциллирующей во внешнем однородном электростатическом поле, интенсивность дипольного излучения от капли примерно в ${{10}^{{14}}}$ раз превышает интенсивность квадрупольного излучения, а также магнитно-дипольного [10].
В теории электромагнитного излучения вводится малый параметр $\delta $ – квадрат отношения характерного линейного размера системы к длине излучаемой волны [8, 9]. Именно по нему и ведется разделение всего излучения на мультипольные компоненты.
Для осциллирующей капли проводящей жидкости, имеющей индуцированные заряды, следует использовать еще один малый параметр: $\varepsilon $ – отношение амплитуды осцилляций к радиусу капли.
Проблема существования самого факта наличия электромагнитного излучения от осциллирующей капли в грозовом облаке была впервые поставлена в [5] в связи с изучением электромагнитных помех от конвективных облаков и их дистанционного электромагнитного зондирования [11–13]. В [5] же был предложен способ оценивания его интенсивности на модели осциллирующей и излучающей заряженной капли идеальной жидкости, исходя из решения электрогидродинамической задачи об осцилляциях заряженной капли и закона сохранения энергии.
В [14] была рассмотрена задача о расчете интенсивности дипольной компоненты полного излучения от осциллирующей заряженной капли в электростатическом поле, а в [15] решена задача о расчете интенсивности квадрупольной компоненты полного излучения. В настоящей работе, в рамках асимптотического аналитического подхода, на модели капли идеальной несжимаемой электропроводной жидкости во втором порядке малости будет проведена качественная оценка интенсивности дипольной компоненты полного излучения от незаряженной капли, осциллирующей в электростатическом поле грозового облака.
ОСНОВНАЯ ЧАСТЬ
1. Постановка задачи. Пусть дана незаряженная осциллирующая капля идеальной, несжимаемой, идеально проводящей жидкости с плотностью $\rho $, в однородном электростатическом поле напряженностью ${{\vec {E}}_{0}}$. Предположим, что окружающая для капли среда может моделироваться вакуумом, а ее объем равновелик объему сферы радиуса $R$. Равновесная форма капли в электростатическом поле в линейном приближении по амплитуде стационарной деформации может считаться сфероидальной [16]. Такой сфероидальной каплей будем моделировать каплю в грозовом облаке.
Численные величины размеров капель и напряженностей внутриоблачных электрических полей, необходимых для проведения качественных оценок, будем брать согласно [17, 18].
Все расчеты задачи будем проводить в сферической системе координат $\left( {r,\theta ,\varphi } \right)$ с началом в центре масс капли в безразмерных переменных, в которых $R = \rho = \sigma = {{\left[ {4\pi {{\varepsilon }_{0}}} \right]}^{{ - 1}}} = 1$ (ε0 – электрическая постоянная). Остальные величины задачи будут выражены в долях своих характерных значений: $\left[ {{{E}_{0}}} \right] = {{\left[ {4\pi {{\varepsilon }_{0}}} \right]}^{{ - \frac{1}{2}}}}{{R}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{{\sigma }^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$, $\left[ t \right] = {{R}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}{{\rho }^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{{\sigma }^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$, $\left[ V \right] = {{R}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{{\rho }^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{{\sigma }^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$, $\left[ r \right] = R$, $\left[ P \right] = {{R}^{{ - 1}}}\sigma $.
Равновесный эксцентриситет капли (отношение межфокусного расстояния сфероидальной капли к длине ее большой оси) в указанных безразмерных переменных определится выражением ${{e}^{2}} \approx \frac{{9E_{0}^{2}}}{{16\pi }}$, т.е. ${{e}^{2}} \sim E_{0}^{2}$ [16]. Уравнение образующей равновесной сфероидальной поверхности капли запишется в виде:
(1)
$r\left( \theta \right) \approx 1 + \frac{1}{3}{{e}^{2}}{{P}_{2}}\left( \mu \right) + O({{e}^{4}}),\,\,\,\,\mu \equiv \cos \theta ,$Строго говоря, в квадратичном приближении по $\varepsilon $ имеет место отклонение равновесной формы от сфероидальности, пропорциональное третьему полиному Лежандра ${{P}_{3}}\left( {\cos \theta } \right) \equiv \frac{1}{2}\left( {5{{{\cos }}^{3}}\theta - 3\cos \theta } \right)$ [16]. Но, во-первых, амплитуда такого отклонения весьма мала (меньше на порядок по сравнению с поправкой, пропорциональной второму полиному Лежандра), а, во-вторых, выгода использования сфероидальной формы в аналитических расчетах очевидна: для такой формы имеются готовые аналитические решения для распределения электрического потенциала в окрестности капли в разных ситуациях [20–22].
Следует отметить, что квадратичная по $\varepsilon $ поправка к асимптотически точному решению первого порядка по $\varepsilon $ имеет место в другом интервале частот, по сравнению с решением первого порядка. Хотя такая поправка будет не совсем корректна (в соответствии со сказанным в предыдущем абзаце), ее следует учесть уже хотя бы потому, что в общей интенсивности излучения она будет в ${{10}^{{13}}}$ раз превышать интенсивность квадрупольного и магнитно-дипольного излучений [10].
Пусть в начальный момент времени $t = 0$ равновесная сфероидальная форма капли с эксцентриситетом $e$ претерпевает виртуальное осесимметричное возмущение $\xi \left( \theta \right)$ фиксированной амплитуды. Отношение $\max \left| {\xi \left( \theta \right)} \right|$ к радиусу $R$ (в размерном виде) будем использовать в качестве малого параметра: $\varepsilon \equiv \left( {\frac{{\max \left| {\xi \left( \theta \right)} \right|}}{R}} \right)$.
Т.к. начальное возмущение равновесной поверхности капли осесимметрично очевидно, что такая симметрия сохранится и при $t > 0$, а уравнение ее образующей в сферической системе координат с началом в центре масс капли в безразмерных переменных будет иметь вид:
(2)
$\begin{gathered} r\left( {\theta ,t} \right) = r\left( \theta \right) + \xi \left( {\theta ,t} \right) = 1 + {{e}^{2}}h\left( \theta \right) + \xi \left( {\theta ,t} \right), \\ h\left( \theta \right) \equiv \frac{1}{3}{{P}_{2}}\left( \mu \right),\,\,\,\,\left| \xi \right| \ll 1. \\ \end{gathered} $Математическая формулировка задачи об электромагнитном излучении незаряженной капли во внешнем электростатическом поле имеет вид:
(5)
$r \to \infty {\kern 1pt} :\,\,\,\,\vec {E}\left( {\vec {r},t} \right) \to {{\vec {E}}_{0}} \equiv {{E}_{0}}{{\vec {e}}_{z}},\,\,\,\,\vec {E} = - \nabla \Phi ,$(6)
$\begin{gathered} r = r\left( \theta \right) + \xi \left( {\theta ,t} \right){\kern 1pt} {\kern 1pt} :\,\,\,\,\frac{{\partial \xi \left( {\theta ,t} \right)}}{{\partial t}} = \frac{{\partial \psi \left( {\vec {r},t} \right)}}{{\partial r}} - \\ - \,\,\frac{1}{{{{r}^{2}}}}\frac{{\partial \psi \left( {\vec {r},t} \right)}}{{\partial \theta }}\left( {\frac{{\partial r\left( \theta \right)}}{{\partial \theta }} + \frac{{\partial \xi \left( {\theta ,t} \right)}}{{\partial \theta }}} \right), \\ \end{gathered} $(7)
$\Delta P - \frac{{\partial \psi }}{{\partial t}} - \frac{1}{2}{{(\nabla \psi )}^{2}} + {{P}_{E}} = {{P}_{\sigma }},$Для замыкания выписанной системы введем интегральные условия: неизменности полного объема (следствие несжимаемости жидкости), неподвижности центра масс, а также условие незаряженности капли.
(9)
$\mathop \smallint \limits_V {{r}^{2}}dr\sin \theta d\theta d\varphi = \frac{4}{3}\pi ,\,\,\,\,\mathop \smallint \limits_V \vec {r}{{r}^{2}}dr\sin \theta d\theta d\varphi = 0,$(10)
$\begin{gathered} V = \left[ {0 \leqslant r \leqslant r\left( \theta \right) + \xi \left( {\theta ,t} \right),\,\,0 \leqslant \theta \leqslant \pi ,\,\,0 \leqslant \varphi \leqslant 2\pi } \right], \\ \frac{1}{{4\pi }}\oint\limits_S {\left( {\vec {n},\vec {E}} \right)dS = 0} , \\ S = \left[ {r = r\left( \theta \right) + \xi \left( {\theta ,t} \right),\,\,0 \leqslant \theta \leqslant \pi ,\,\,0 \leqslant \varphi \leqslant 2\pi } \right], \\ \end{gathered} $Начальные условия в общем случае задаются в виде начальной деформации равновесной сфероидальной формы капли и равенства нулю начальной скорости движения поверхности
(11)
$\begin{gathered} t = 0{\kern 1pt} {\kern 1pt} :\,\,\,\,\xi \left( \theta \right) = {{\xi }_{0}}{{P}_{0}}\left( \mu \right) + {{\xi }_{1}}{{P}_{1}}\left( \mu \right) + \\ + \,\,\varepsilon \mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } {{h}_{j}}{{P}_{j}}\left( \mu \right),\,\,\,\,\mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } {{h}_{j}} = 1,\,\,\,\,\frac{{\partial \xi \left( \theta \right)}}{{\partial t}} = 0, \\ \end{gathered} $В выражениях (6)–(11) введены обозначения: $\Delta P$ – перепад постоянных давлений внутри капли и вне капли в состоянии равновесия, $\vec {E}$ – вектор напряженности электрического поля, ${{P}_{E}} = \frac{{{{{\vec {E}}}^{2}}}}{{8\pi }}$ – давление электрического поля, ${{P}_{\sigma }} = {\text{div}}\vec {n}$ – капиллярное давление (можно отметить, что ${{P}_{\sigma }}$, согласно [23], стр. 334 – лапласовское давление, определяемое как произведение коэффициента поверхностного натяжения на удвоенную среднюю кривизну поверхности жидкости в данной точке, которая определяется как дивергенция $\vec {n}$ [24, стр. 179]), $\vec {n}$ – единичный вектор внешней нормали к поверхности жидкости, описываемой выражением (2), ${{h}_{j}}$ – коэффициенты, определяющие парциальный вклад $j$-ой колебательной моды в суммарное начальное возмущение, ${{\xi }_{0}}$ и ${{\xi }_{1}}$ – константы (амплитуды нулевой и первой мод осцилляций), равные нулю в расчетах первого порядка, и определяемые в расчетах второго порядка малости по $\varepsilon $ из условий постоянства объема и неподвижности центра масс в начальный момент времени и с точностью до слагаемых $ \sim {\kern 1pt} \varepsilon {{e}^{2}}$ и $ \sim {\kern 1pt} {{\varepsilon }^{2}}$, равные:
(12)
$\begin{gathered} {{\xi }_{0}} \approx - \mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } \left[ {{{\varepsilon }^{2}}\frac{{h_{j}^{2}}}{{\left( {2j + 1} \right)}} + \varepsilon {{e}^{2}}\frac{2}{{15}}{{h}_{j}}{{\delta }_{{j,2}}}} \right] + O({{\varepsilon }^{3}}), \\ {{\xi }_{1}} \approx - \mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } \left[ {{{\varepsilon }^{2}}\frac{{9j{{h}_{{j{\kern 1pt} - {\kern 1pt} 1}}}{{h}_{j}}}}{{\left( {2j - 1} \right)\left( {2j + 1} \right)}} + \varepsilon {{e}^{2}}\frac{9}{{35}}{{h}_{j}}{{\delta }_{{j,3}}}} \right] + O({{\varepsilon }^{3}}), \\ \end{gathered} $Отметим, что в сформулированной задаче имеются два малых параметра: квадрат эксцентриситета капли ${{e}^{2}}$ и безразмерная амплитуда $\varepsilon \equiv \left( {\frac{{\max \left| {\xi \left( \theta \right)} \right|}}{R}} \right)$. Согласно [25, 26] свободно падающие осциллирующие капли дождя совершают сфероидальные осцилляции с амплитудой до шестидесяти процентов величины от радиуса. Иными словами, целесообразно рассмотреть ситуацию, когда малые параметры ${{e}^{2}}$ и $\varepsilon $ имеют один порядок величины ${{e}^{2}} \sim \varepsilon $. Это несколько упростит громоздкие вычисления, но сузит область применимости полученных результатов, что для проводимой качественной оценки представляется несущественным. Ограничивая рассмотрение поставленной задачи квадратичным приближением, нижеследующие расчеты проведем с сохранением слагаемых $ \sim {\kern 1pt} {{\varepsilon }^{2}}$ и $ \sim {\kern 1pt} {{e}^{2}}\varepsilon $. Для определенности положим ${{e}^{2}} \sim \varepsilon $, сводя в таком случае задачу к одному малому параметру $\varepsilon $.
Основанием для принятия предположения, сделанного в предыдущем абзаце, является то, что напряженность внутриоблачного электростатического поля, как правило, мала [18], стр. 440, табл. 1 . Но напряженность электростатического поля определяет величину эксцентриситета капель, которые малы в свою очередь. Таким образом, квадрат эксцентриситета ${{e}^{2}}$ может быть сравним по величине с безразмерной амплитудой мод осцилляций облачной капли $\varepsilon $, обдуваемой восходящим потоком воздуха.
Учитывая, что отклонение равновесной сфероидальной формы капли от сферической связано с наличием электрического поля, примем ${{E}_{0}} \sim e$. Таким образом, в дальнейших расчетах электрического потенциала в окрестности возмущенного заряженного сфероида во внешнем поле и величины индуцированного заряда на возмущенной поверхности капли потребуем учесть слагаемые порядка $ \sim {\kern 1pt} {{\varepsilon }^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}$. Эти слагаемые связанны с нелинейным взаимодействием возбужденных колебательных мод, как со стационарной деформацией капли $ \sim {\kern 1pt} {{E}_{0}}{{e}^{2}}\varepsilon \sim {{e}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}\varepsilon \sim {{\varepsilon }^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}$, так и между собой, а также со стационарной деформацией капли $ \sim {\kern 1pt} {{E}_{0}}{{\varepsilon }^{2}} \sim {{e}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{{\varepsilon }^{2}} \sim {{\varepsilon }^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}$.
Введем формальные параметры ${{\beta }_{E}}$ и ${{\beta }_{e}}$ в соответствии со следующими выражениями: ${{E}_{0}} \equiv {{\beta }_{E}}{{\varepsilon }^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$, ${{e}^{2}} \equiv {{\beta }_{e}}\varepsilon $, чтобы иметь возможность в конечных выражениях разделить вклады от ${{E}_{0}}$ и ${{e}^{2}}$. В окончательном результате, чтобы избавиться от формальных обозначений, положим ${{\beta }_{E}} = {{\beta }_{e}} = 1$.
2. Асимптотические разложения искомых величин. Будем решать задачу с точностью до ${{\varepsilon }^{2}}$ методом многих временны́х масштабов [19]. Искомые функции $\xi \left( {\theta ,t} \right)$, $\psi \left( {\vec {r},t} \right)$, $\Phi \left( {\vec {r},t} \right)$ представим в виде рядов по степеням $\varepsilon $ и будем считать зависящими не просто от времени $t$, а от разных его масштабов, определенных как ${{T}_{m}} \equiv {{\varepsilon }^{m}}t$, где $m$ целое число: $m = 0;1;2$:
(13)
$\begin{gathered} \xi \left( {\theta ,t} \right) = \mathop \sum \limits_{m{\kern 1pt} = {\kern 1pt} 1}^\infty {{\varepsilon }^{m}}{{\xi }^{{\left( m \right)}}}\left( {\theta ,{{T}_{0}},{{T}_{1}}} \right), \\ \psi \left( {\vec {r},t} \right) = \mathop \sum \limits_{m{\kern 1pt} = {\kern 1pt} 1}^\infty {{\varepsilon }^{m}}{{\psi }^{{\left( m \right)}}}\left( {r,\theta ,{{T}_{0}},{{T}_{1}}} \right), \\ \Phi \left( {\vec {r},t} \right) = {{\Phi }^{{\left( {{\text{eq}}} \right)}}}\left( {r,\theta } \right) + {{\varepsilon }^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}{{\Phi }^{{\left( {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} \right)}}}\left( {r,\theta ,{{T}_{0}}} \right) + \\ + \,\,{{\varepsilon }^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}{{\Phi }^{{\left( {{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}} \right)}}}\left( {r,\theta ,{{T}_{0}}} \right) + O({{\varepsilon }^{{{7 \mathord{\left/ {\vphantom {7 2}} \right. \kern-0em} 2}}}}). \\ \end{gathered} $(14)
$\begin{gathered} {{\Phi }^{{\left( {{\text{eq}}} \right)}}}\left( {r,\theta } \right) = {{\varepsilon }^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{{\beta }_{E}}r\left[ {\frac{1}{{{{r}^{3}}}} - 1} \right]{{P}_{1}}\left( \mu \right) + \\ + \,\,{{\varepsilon }^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}{{\beta }_{E}}{{\beta }_{e}}\frac{2}{5}\frac{1}{{{{r}^{2}}}}\left[ {{{P}_{1}}\left( \mu \right) + \frac{3}{2}\frac{1}{{{{r}^{2}}}}{{P}_{3}}\left( \mu \right)} \right]. \\ \end{gathered} $Производные по времени будем вычислять, имея в виду полный набор различных его масштабов, по правилу [19]:
Решения уравнений Лапласа (3) для поправок к гидродинамическому ${{\psi }^{{\left( m \right)}}}\left( {\vec {r},t} \right)$ и электрическому ${{\Phi }^{{\left( k \right)}}}\left( {\vec {r},t} \right)$ потенциалам, удовлетворяющие граничным условиям (4), (5), а также поправки к равновесной форме поверхности капли ${{\xi }^{{\left( m \right)}}}\left( {\theta ,t} \right)$ запишем в виде рядов по полиномам Лежандра:
(15)
$\begin{gathered} {{\psi }^{{\left( m \right)}}}\left( {r,\theta ,{{T}_{0}},{{T}_{1}}} \right) = \mathop \sum \limits_{n{\kern 1pt} = {\kern 1pt} 0}^\infty D_{n}^{{\left( m \right)}}\left( {r,\theta ,{{T}_{0}},{{T}_{1}}} \right){{r}^{n}}{{P}_{n}}\left( \mu \right), \\ \left( {m = 1;2} \right), \\ \end{gathered} $(16)
$\begin{gathered} {{\Phi }^{{\left( k \right)}}}\left( {r,\theta ,{{T}_{0}}} \right) = \mathop \sum \limits_{n{\kern 1pt} = {\kern 1pt} 0}^\infty F_{n}^{{\left( k \right)}}\left( {r,\theta ,{{T}_{0}}} \right){{r}^{{ - \left( {n{\kern 1pt} + {\kern 1pt} 1} \right)}}}{{P}_{n}}\left( \mu \right), \\ \left( {k = {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2};{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}} \right), \\ \end{gathered} $(17)
$\begin{gathered} {{\xi }^{{\left( m \right)}}}\left( {\theta ,{{T}_{0}},{{T}_{1}}} \right) = \mathop \sum \limits_{n{\kern 1pt} = {\kern 1pt} 0}^\infty M_{n}^{{\left( m \right)}}\left( {\theta ,{{T}_{0}},{{T}_{1}}} \right){{P}_{n}}\left( \mu \right), \\ \left( {m = 1;2} \right). \\ \end{gathered} $(18)
$\begin{gathered} r = 1{\kern 1pt} :\,\,\,\,\frac{{\partial {{\xi }^{{\left( 1 \right)}}}}}{{\partial {{T}_{0}}}} = \frac{{\partial {{\psi }^{{\left( 1 \right)}}}}}{{\partial r}}, \\ \frac{{\partial {{\psi }^{{\left( 1 \right)}}}}}{{\partial {{T}_{0}}}} = \left( {2 + {{{\hat {L}}}_{\theta }}} \right){{\xi }^{{\left( 1 \right)}}},\,\,\,\,{{{\hat {L}}}_{\theta }} \equiv \frac{1}{{\sin \theta }}\frac{\partial }{{\partial \theta }}\left( {\sin \theta \frac{\partial }{{\partial \theta }}} \right), \\ \mathop \smallint \limits_0^\pi {{\xi }^{{\left( 1 \right)}}}\sin \theta d\theta = 0,\,\,\,\,\mathop \smallint \limits_0^\pi {{\xi }^{{\left( 1 \right)}}}\cos \theta \sin \theta d\theta = 0. \\ \end{gathered} $Выражения для поправок первого порядка к коэффициентам разложений (15), (17) несложно найти из системы (18) в виде
(19)
$\begin{gathered} M_{0}^{{\left( 1 \right)}}\left( {{{T}_{0}},{{T}_{1}}} \right) = 0,\,\,\,\,M_{1}^{{\left( 1 \right)}}\left( {{{T}_{0}},{{T}_{1}}} \right) = 0,\,\,\,\,D_{0}^{{\left( 1 \right)}}\left( {{{T}_{0}},{{T}_{1}}} \right) = 0, \\ D_{n}^{{\left( 1 \right)}}\left( {{{T}_{0}},{{T}_{1}}} \right) = \frac{1}{n}\frac{{\partial M_{n}^{{\left( 1 \right)}}\left( {{{T}_{0}},{{T}_{1}}} \right)}}{{\partial {{T}_{0}}}},\,\,\,\,\left( {n \geqslant 1} \right). \\ \end{gathered} $(20)
$\begin{gathered} \frac{{{{\partial }^{2}}}}{{\partial T_{0}^{2}}}M_{n}^{{\left( 1 \right)}}\left( {{{T}_{0}},{{T}_{1}}} \right) + \omega _{{n,s}}^{2}M_{n}^{{\left( 1 \right)}}\left( {{{T}_{0}},{{T}_{1}}} \right) = 0, \\ \omega _{{n,s}}^{2} = n\left( {n - 1} \right)\left( {n + 2} \right), \\ \end{gathered} $Решением уравнения (20) являются гармонические функции по времени ${{T}_{0}}$ с коэффициентами, зависящими от времени ${{T}_{1}}$:
(21)
$\begin{gathered} M_{n}^{{\left( 1 \right)}}\left( {{{T}_{0}},{{T}_{1}}} \right) = \\ = A_{n}^{{\left( 1 \right)}}\left( {{{T}_{1}}} \right)\exp \left( {i{{\omega }_{{n,s}}}{{T}_{0}}} \right) + {\text{к}}{\text{.с}}{\text{.,}}\,\,\,\,\left( {n \geqslant 2} \right), \\ A_{n}^{{\left( 1 \right)}}\left( {{{T}_{1}}} \right) \equiv a_{n}^{{\left( 1 \right)}}\left( {{{T}_{1}}} \right)\exp \left[ {ib_{n}^{{\left( 1 \right)}}\left( {{{T}_{1}}} \right)} \right]. \\ \end{gathered} $4. Задача порядка 3/2 по ${\mathbf{\varepsilon }}$. Система уравнений для определения коэффициентов $F_{n}^{{\left( {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} \right)}}$ в решении (16) получается из условий (8), (10) путем группировки слагаемых $ \sim {\kern 1pt} {{\varepsilon }^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}$:
(22)
$\begin{gathered} r = 1{\kern 1pt} :\,\,\,\,{{\Phi }^{{\left( {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} \right)}}} - 3{{\beta }_{E}}{{\xi }^{{\left( 1 \right)}}}{{P}_{1}}\left( \mu \right) = \Phi _{s}^{{\left( {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} \right)}}, \\ \mathop \smallint \limits_0^\pi \frac{{\partial {{\Phi }^{{\left( {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} \right)}}}}}{{\partial r}}\sin \theta d\theta = 0. \\ \end{gathered} $Подставляя разложение (16) при $k = {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}$ и решение первого порядка (17) в систему уравнений (22), определим коэффициенты $F_{n}^{{\left( {{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}} \right)}}\left( {{{T}_{0}}} \right)$ в виде:
(23)
$\begin{gathered} F_{0}^{{\left( {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} \right)}}\left( {{{T}_{0}}} \right) = 0,\,\,\,\,\Phi _{s}^{{\left( {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} \right)}} = 0, \\ F_{n}^{{\left( {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} \right)}}\left( {{{T}_{0}}} \right) = 3{\kern 1pt} {{\beta }_{E}} \times \\ \times \,\,\left( {\mu _{{n{\kern 1pt} - {\kern 1pt} 1}}^{ + }M_{{n{\kern 1pt} - {\kern 1pt} 1}}^{{\left( 1 \right)}}\left( {{{T}_{0}},{{T}_{1}}} \right) + \mu _{{n{\kern 1pt} + {\kern 1pt} 1}}^{ - }M_{{n{\kern 1pt} + {\kern 1pt} 1}}^{{\left( 1 \right)}}\left( {{{T}_{0}},{{T}_{1}}} \right)} \right),\,\,\,\,\left( {n \geqslant 1} \right), \\ \mu _{n}^{ + } = \frac{{n + 1}}{{2n + 1}},\,\,\,\,\mu _{n}^{ - } = \frac{n}{{2n + 1}}. \\ \end{gathered} $5. Задача второго порядка малости по ε. Для определения поправок второго порядка малости к найденному решению (т.е. для отыскания функций ${{\xi }^{{\left( 2 \right)}}}\left( {\theta ,t} \right)$, ${{\psi }^{{\left( 2 \right)}}}\left( {\vec {r},t} \right)$) приведем систему уравнений, получающуюся из (6)–(10) приравниванием слагаемых при ${{\varepsilon }^{2}}$:
(24)
$\begin{gathered} r = 1{\kern 1pt} :\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \\ \frac{{\partial {{\xi }^{{\left( 2 \right)}}}}}{{\partial {{T}_{0}}}} + \frac{{\partial {{\xi }^{{\left( 1 \right)}}}}}{{\partial {{T}_{1}}}} = \frac{{\partial {{\psi }^{{\left( 2 \right)}}}}}{{\partial r}} + \frac{{{{\partial }^{2}}{{\psi }^{{\left( 1 \right)}}}}}{{\partial {{r}^{2}}}} \times \\ \times \,\,\left[ {{{\xi }^{{\left( 1 \right)}}} + {{\beta }_{e}}h\left( \theta \right)} \right] - \left[ {\frac{{\partial {{\xi }^{{\left( 1 \right)}}}}}{{\partial \theta }} + {{\beta }_{e}}\frac{{\partial h\left( \theta \right)}}{{\partial \theta }}} \right]\frac{{\partial {{\psi }^{{\left( 1 \right)}}}}}{{\partial \theta }}, \\ - \frac{{\partial {{\psi }^{{\left( 2 \right)}}}}}{{\partial {{T}_{0}}}} - \frac{{\partial {{\psi }^{{\left( 1 \right)}}}}}{{\partial {{T}_{1}}}} - \frac{{{{\partial }^{2}}{{\psi }^{{\left( 1 \right)}}}}}{{\partial r\partial {{T}_{0}}}}\left[ {{{\xi }^{{\left( 1 \right)}}} + {{\beta }_{e}}h\left( \theta \right)} \right] + P_{E}^{{\left( 2 \right)}} = \\ = - \left( {2 + {{{\hat {L}}}_{\theta }}} \right){{\xi }^{{\left( 2 \right)}}} + 2{{\xi }^{{\left( 1 \right)}}}\left( {1 + {{{\hat {L}}}_{\theta }}} \right){{\xi }^{{\left( 1 \right)}}} + \\ + \,\,2{{\beta }_{e}}h\left( \theta \right)\left( {{{{\hat {L}}}_{\theta }} - 4} \right){{\xi }^{{\left( 1 \right)}}}, \\ \mathop \smallint \limits_0^\pi \left[ {3{{\xi }^{{\left( 2 \right)}}} + 3{{{({{\xi }^{{\left( 1 \right)}}})}}^{2}} + 2{{\beta }_{e}}{{\xi }^{{\left( 1 \right)}}}{{P}_{2}}\left( \mu \right)} \right]\sin \theta d\theta = 0, \\ \mathop \smallint \limits_0^\pi \left[ {2{{\xi }^{{\left( 2 \right)}}} + 3{{{({{\xi }^{{\left( 1 \right)}}})}}^{2}} + 2{{\beta }_{e}}{{\xi }^{{\left( 1 \right)}}}{{P}_{2}}\left( \mu \right)} \right]\cos {\kern 1pt} \theta \sin {\kern 1pt} \theta d\theta = 0, \\ P_{E}^{{\left( 2 \right)}} = - \frac{3}{{4\pi }}\left[ {{{\beta }_{E}}{{P}_{1}}\left( \mu \right)\frac{{\partial {{\Phi }^{{\left( {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} \right)}}}}}{{\partial r}} + 6\beta _{E}^{2}{{{\left( {{{P}_{1}}\left( \mu \right)} \right)}}^{2}}{{\xi }^{{\left( 1 \right)}}}} \right]. \\ \end{gathered} $Подставляя в систему уравнений (24) разложения (15) при m = 1; 2 и решение порядка 3/2 из (23), получим выражения для коэффициентов $M_{n}^{{\left( 2 \right)}}\left( {{{T}_{0}}} \right)$, $D_{n}^{{\left( 2 \right)}}\left( {{{T}_{0}}} \right)$ в виде:
(25)
$\begin{gathered} M_{0}^{{\left( 2 \right)}}\left( {{{T}_{0}}} \right) = - \mathop \sum \limits_{k{\kern 1pt} = {\kern 1pt} {\kern 1pt} 0}^\infty \frac{1}{{\left( {2k + 1} \right)}}{{\left( {M_{k}^{{\left( 1 \right)}}\left( {{{T}_{0}},{{T}_{1}}} \right)} \right)}^{2}} - \\ - \,\,\frac{2}{{15}}{{\beta }_{e}}M_{2}^{{\left( 1 \right)}}\left( {{{T}_{0}},{{T}_{1}}} \right), \\ M_{1}^{{\left( 2 \right)}}\left( {{{T}_{0}}} \right) = - \mathop \sum \limits_{k{\kern 1pt} = {\kern 1pt} 0}^\infty \frac{{9k}}{{\left( {2k + 1} \right)\left( {2k - 1} \right)}} \times \\ \times \,\,M_{{k{\kern 1pt} - {\kern 1pt} 1}}^{{\left( 1 \right)}}\left( {{{T}_{0}},{{T}_{1}}} \right)M_{k}^{{\left( 1 \right)}}\left( {{{T}_{0}},{{T}_{1}}} \right) - \frac{9}{{35}}{{\beta }_{e}}M_{3}^{{\left( 1 \right)}}\left( {{{T}_{0}},{{T}_{1}}} \right), \\ D_{0}^{{\left( 2 \right)}}\left( {{{T}_{0}}} \right) = 0,\,\,\,\,D_{n}^{{\left( 2 \right)}}\left( {{{T}_{0}}} \right) = \\ = \frac{1}{n}\left\{ {\frac{{\partial M_{n}^{{\left( 2 \right)}}\left( {{{T}_{0}}} \right)}}{{\partial {{T}_{0}}}} + \frac{{\partial M_{n}^{{\left( 1 \right)}}\left( {{{T}_{0}},{{T}_{1}}} \right)}}{{\partial {{T}_{1}}}} + } \right.\frac{1}{3}{{\beta }_{e}}{{N}_{0}} - \\ - \,\,\mathop \sum \limits_{m{\kern 1pt} = {\kern 1pt} {\kern 1pt} 0}^\infty \mathop \sum \limits_{k{\kern 1pt} = {\kern 1pt} {\kern 1pt} 0}^\infty \left[ {m\left( {m - 1} \right){{K}_{{m,k,n}}} - {{\alpha }_{{m,k,n}}}} \right] \times \\ \left. { \times \,\,\frac{1}{m}\frac{{\partial M_{m}^{{\left( 1 \right)}}\left( {{{T}_{0}},{{T}_{1}}} \right)}}{{\partial {{T}_{0}}}}M_{k}^{{\left( 1 \right)}}\left( {{{T}_{0}},{{T}_{1}}} \right)} \right\},\,\,\,\,\left( {n \geqslant 1} \right), \\ {{N}_{0}} = \frac{{\partial M_{{n{\kern 1pt} + {\kern 1pt} 2}}^{{\left( 1 \right)}}\left( {{{T}_{0}},{{T}_{1}}} \right)}}{{\partial {{T}_{0}}}}\left[ {\frac{{{{\alpha }_{{2,n{\kern 1pt} + {\kern 1pt} 2,n}}}}}{{\left( {n + 2} \right)}} - {{K}_{{2,n{\kern 1pt} + {\kern 1pt} 2,n}}}\left( {n + 1} \right)} \right] + \\ + \,\,\frac{{\partial M_{n}^{{\left( 1 \right)}}\left( {{{T}_{0}},{{T}_{1}}} \right)}}{{\partial {{T}_{0}}}}\left[ {\frac{{{{\alpha }_{{2,n,n}}}}}{n} - {{K}_{{2,n,n}}}\left( {n - 1} \right)} \right] + \\ + \,\,\frac{{\partial M_{{n{\kern 1pt} - {\kern 1pt} 2}}^{{\left( 1 \right)}}\left( {{{T}_{0}},{{T}_{1}}} \right)}}{{\partial {{T}_{0}}}}\left[ {\frac{{{{\alpha }_{{2,n{\kern 1pt} - {\kern 1pt} 2,n}}}}}{{\left( {n - 2} \right)}} - {{K}_{{2,n{\kern 1pt} - {\kern 1pt} 2,n}}}\left( {n - 3} \right)} \right], \\ {{K}_{{m,k,n}}} = {{\left[ {C_{{k0,m0}}^{{n0}}} \right]}^{2}}, \\ {{\alpha }_{{m,k,n}}} = - \sqrt {m\left( {m + 1} \right)k\left( {k + 1} \right)} C_{{m0,k0}}^{{n0}}C_{{m{\kern 1pt} - {\kern 1pt} 1,k1}}^{{n0}}, \\ \end{gathered} $Используя решение первого порядка (21), запишем неоднородное дифференциальное уравнение для определения амплитудных коэффициентов $M_{n}^{{\left( 2 \right)}}\left( {{{T}_{0}}} \right)$ при $n \geqslant 2$ в виде:
(26)
$\begin{gathered} \frac{{{{\partial }^{2}}}}{{\partial T_{0}^{2}}}M_{n}^{{\left( 2 \right)}}\left( {{{T}_{0}}} \right) + \omega _{n}^{2}M_{n}^{{\left( 2 \right)}}\left( {{{T}_{0}}} \right) = \\ = {{G}_{n}}\exp \left( {i{{\omega }_{n}}{{T}_{0}}} \right) + {{L}_{{n,1}}}A_{{n{\kern 1pt} - {\kern 1pt} 2}}^{{\left( 1 \right)}}\left( {{{T}_{1}}} \right)\exp \left( {i{{\omega }_{{n - 2}}}{{T}_{0}}} \right) + \\ + \,\,{{L}_{{n,2}}}A_{{n{\kern 1pt} + {\kern 1pt} 2}}^{{\left( 1 \right)}}\left( {{{T}_{1}}} \right)\exp \left( {i{{\omega }_{{n{\kern 1pt} + {\kern 1pt} 2}}}{{T}_{0}}} \right) + \\ + \,\,\mathop \sum \limits_{m{\kern 1pt} = {\kern 1pt} {\kern 1pt} 0}^\infty \mathop \sum \limits_{k{\kern 1pt} = {\kern 1pt} {\kern 1pt} 0}^\infty \left\{ {\lambda _{{m,k,n}}^{{\left( + \right)}}A_{m}^{{\left( 1 \right)}}\left( {{{T}_{1}}} \right)A_{k}^{{\left( 1 \right)}}\left( {{{T}_{1}}} \right)\exp \left[ {i\left( {{{\omega }_{m}} + {{\omega }_{k}}} \right){{T}_{0}}} \right]\mathop + \limits^{} } \right. \\ \left. {\mathop + \limits^{} \,\,\lambda _{{m,k,n}}^{{\left( - \right)}}A_{m}^{{\left( 1 \right)}}\left( {{{T}_{1}}} \right)\bar {A}_{k}^{{\left( 1 \right)}}\left( {{{T}_{1}}} \right)\exp \left[ {i\left( {{{\omega }_{m}} - {{\omega }_{k}}} \right){{T}_{0}}} \right]} \right\} + {\text{к}}{\text{.с}}{\text{.}} \\ \end{gathered} $Требование исключения из решений уравнения (25) секулярных членов показывает, что $a_{n}^{{\left( 1 \right)}}$ не зависит от времени ${{T}_{1}}$ и $b_{n}^{{\left( 1 \right)}}$ линейно зависит от ${{T}_{1}}$:
$b_{n}^{{\left( 1 \right)}}\left( {{{T}_{1}}} \right) = - \frac{{{{L}_{{n,0}}}}}{{2{{\omega }_{n}}}}{{T}_{1}} + b_{n}^{{\left( 0 \right)}}$, где $b_{n}^{{\left( 0 \right)}}$ – константа, определяемая из начальных условий.
Следовательно, общее решение уравнения (26) при $n \geqslant 2$ будет представлено в виде:
(27)
$\begin{gathered} M_{n}^{{\left( 2 \right)}}\left( {{{T}_{0}}} \right) = A_{n}^{{\left( 2 \right)}}\exp \left( {i{{\omega }_{n}}{{T}_{0}}} \right) + \\ + \,\,N_{n}^{{\left( - \right)}}A_{{n{\kern 1pt} - {\kern 1pt} 2}}^{{\left( 1 \right)}}\left( {{{T}_{1}}} \right)\exp \left( {i{{\omega }_{{n{\kern 1pt} - {\kern 1pt} 2}}}{{T}_{0}}} \right) + \\ + \,\,N_{n}^{{\left( + \right)}}A_{{n{\kern 1pt} + {\kern 1pt} 2}}^{{\left( 1 \right)}}\left( {{{T}_{1}}} \right)\exp \left( {i{{\omega }_{{n{\kern 1pt} + {\kern 1pt} 2}}}{{T}_{0}}} \right) + \\ + \,\,\mathop \sum \limits_{m{\kern 1pt} = {\kern 1pt} {\kern 1pt} 0}^\infty \mathop \sum \limits_{k{\kern 1pt} = {\kern 1pt} {\kern 1pt} 0}^\infty \left\{ {N_{{m,k,n}}^{{\left( + \right)}}A_{m}^{{\left( 1 \right)}}\left( {{{T}_{1}}} \right)A_{k}^{{\left( 1 \right)}}{\kern 1pt} \left( {{{T}_{1}}} \right){{ \times }^{{^{{^{{^{{}}}}}}}}}{\kern 1pt} } \right. \\ \times \,\,\exp \left[ {i\left( {{{\omega }_{m}} + {{\omega }_{k}}} \right){{T}_{0}}} \right]\mathop + \limits^{} \\ \left. {\mathop + \limits^{} \,\,N_{{m,k,n}}^{{\left( - \right)}}A_{m}^{{\left( 1 \right)}}\left( {{{T}_{1}}} \right)\bar {A}_{k}^{{\left( 1 \right)}}{\kern 1pt} \left( {{{T}_{1}}} \right)\exp \left[ {i\left( {{{\omega }_{m}} - {{\omega }_{k}}} \right){{T}_{0}}} \right]} \right\} + {\text{к}}{\text{.с}}{\text{.,}} \\ N_{n}^{{\left( - \right)}} \equiv \frac{{{{L}_{{n,1}}}}}{{\omega _{n}^{2} - \omega _{{n{\kern 1pt} - {\kern 1pt} 2}}^{2}}},\,\,\,\,N_{n}^{{\left( + \right)}} \equiv \frac{{{{L}_{{n,2}}}}}{{\omega _{n}^{2} - \omega _{{n{\kern 1pt} + {\kern 1pt} 2}}^{2}}}, \\ N_{{m,k,n}}^{{\left( \pm \right)}} \equiv \frac{{\lambda _{{m,k,n}}^{{\left( \pm \right)}}}}{{\omega _{n}^{2} - {{{\left( {{{\omega }_{m}} \pm {{\omega }_{k}}} \right)}}^{2}}}}. \\ \end{gathered} $Начальные условия (11) после подстановки в них разложений (13) превратятся в систему уравнений для функций первого и второго порядков малости:
Удовлетворяя начальным условиям в первом приближении по $\varepsilon $, получим:
(28)
$a_{n}^{{\left( 1 \right)}} = \frac{1}{2}\mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } {{h}_{j}}{{\delta }_{{n,j}}},\,\,\,\,b_{n}^{{\left( 1 \right)}} = 0,\,\,\,\,(j \in \Xi ,\,\,n = 0,\,1,\,2,\,\, \ldots ),$(29)
$\begin{gathered} a_{n}^{{\left( 2 \right)}} = - \frac{1}{2}\mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } {{h}_{j}}\left( {N_{n}^{{\left( - \right)}}{{\delta }_{{n{\kern 1pt} - {\kern 1pt} 2,j}}} + N_{n}^{{\left( + \right)}}{{\delta }_{{n{\kern 1pt} + {\kern 1pt} 2,j}}}} \right) - \\ - \,\,\mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } {\kern 1pt} {\kern 1pt} \mathop \sum \limits_{q{\kern 1pt} \in {\kern 1pt} \Xi } \frac{{{{h}_{j}}{{h}_{q}}}}{4}\left( {N_{{j,q,n}}^{{\left( + \right)}} + N_{{j,q,n}}^{{\left( - \right)}}} \right),\,\,\,\,b_{n}^{{\left( 2 \right)}} = 0. \\ \end{gathered} $В итоге, используя выражения (28), (29), запишем амплитуды первого и второго порядков малости в решении (17) для формы возмущенной поверхности капли:
(30)
$\begin{gathered} M_{0}^{{\left( 1 \right)}}\left( t \right) = M_{1}^{{\left( 1 \right)}}\left( t \right) = 0, \\ M_{j}^{{\left( 1 \right)}}\left( t \right) = \mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } {{h}_{j}}\cos \left( {\omega _{j}^{ + }t} \right), \\ \omega _{j}^{ + } = {{\omega }_{j}} - \varepsilon \frac{{{{L}_{{j,0}}}}}{{2{{\omega }_{j}}}}, \\ M_{0}^{{\left( 2 \right)}}\left( t \right) = - \mathop \sum \limits_{j \in \Xi } \left[ {\frac{{h_{j}^{2}}}{{\left( {2j + 1} \right)}}{{{\left( {\cos \left( {{{\omega }_{j}}t} \right)} \right)}}^{2}}} \right. + \\ \left. {^{{^{{^{{^{{^{{}}}}}}}}}} + \,\,\frac{2}{{15}}{{\beta }_{e}}{{h}_{j}}{{\delta }_{{j,2}}}\cos \left( {{{\omega }_{j}}t} \right)} \right], \\ M_{1}^{{\left( 2 \right)}}\left( t \right) = - \mathop \sum \limits_{j \in \Xi } \left[ {\frac{{9j{{h}_{{j - 1}}}{{h}_{j}}}}{{\left( {2j - 1} \right)\left( {2j + 1} \right)}}} \right. \times \\ \left. { \times \,\,\cos \left( {{{\omega }_{{j - 1}}}t} \right)\cos \left( {{{\omega }_{j}}t} \right) + \frac{9}{{35}}{{\beta }_{e}}{{h}_{j}}{{\delta }_{{j,3}}}\cos \left( {{{\omega }_{j}}t} \right)} \right], \\ M_{n}^{{\left( 2 \right)}}\left( t \right) = \mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } {{h}_{j}}\left[ {N_{n}^{{\left( - \right)}}{{\delta }_{{n{\kern 1pt} - {\kern 1pt} 2,j}}}\cos \left( {{{\omega }_{{n - 2}}}t} \right)} \right. + \\ + \,\,N_{n}^{{\left( + \right)}}{{\delta }_{{n{\kern 1pt} + {\kern 1pt} 2,j}}}\cos \left( {{{\omega }_{{n{\kern 1pt} + {\kern 1pt} 2}}}t} \right) - \\ \left. { - \,\,\left( {N_{n}^{{\left( - \right)}}{{\delta }_{{n{\kern 1pt} - {\kern 1pt} 2,j}}} + N_{n}^{{\left( + \right)}}{{\delta }_{{n{\kern 1pt} + {\kern 1pt} 2,j}}}} \right)\cos \left( {{{\omega }_{n}}t} \right)} \right] + \mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } \mathop \sum \limits_{q{\kern 1pt} \in {\kern 1pt} \Xi } \frac{{{{h}_{j}}{{h}_{q}}}}{2} \times \\ \times \,\,\left[ {N_{{j,q,n}}^{{\left( + \right)}}\left( {\cos \left( {\left( {{{\omega }_{j}} + {{\omega }_{q}}} \right)t} \right) - \cos \left( {{{\omega }_{n}}t} \right)} \right)} \right. + \\ \left. { + \,\,N_{{j,q,n}}^{{\left( - \right)}}\left( {\cos \left( {\left( {{{\omega }_{j}} - {{\omega }_{q}}} \right)t} \right) - \cos \left( {{{\omega }_{n}}t} \right)} \right)} \right],\,\,\,\,\left( {n \geqslant 2} \right). \\ \end{gathered} $(31)
$\begin{gathered} r\left( {\theta ,t} \right) = 1 + \frac{1}{3}{{e}^{2}}{{P}_{2}}\left( \mu \right) + \\ + \,\,\varepsilon \mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } M_{j}^{{\left( 1 \right)}}\left( t \right){{P}_{j}}\left( \mu \right) + {{\varepsilon }^{2}}\mathop \sum \limits_{n{\kern 1pt} = {\kern 1pt} 0}^\infty M_{n}^{{\left( 2 \right)}}\left( t \right){{P}_{n}}\left( \mu \right), \\ \end{gathered} $6. Задача порядка 5/2 по ε. Для нахождения коэффициентов $F_{n}^{{\left( {{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}} \right)}}$ в решении (16) приведем систему уравнений, получающуюся из условий (8), (10) путем группировки слагаемых $ \sim {\kern 1pt} {{\varepsilon }^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}$:
(32)
$\begin{gathered} r = 1{\kern 1pt} :\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \\ {{\Phi }^{{\left( {{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}} \right)}}} + \left[ {{{\xi }^{{\left( 1 \right)}}} + \frac{1}{3}{{\beta }_{e}}{{P}_{2}}\left( \mu \right)} \right]\frac{{\partial {{\Phi }^{{\left( {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} \right)}}}}}{{\partial r}} + \\ + \,\,3{{\beta }_{E}}\left\{ {\left[ {{{{({{\xi }^{{\left( 1 \right)}}})}}^{2}} - {{\xi }^{{\left( 2 \right)}}}} \right] + {{\beta }_{e}}\left[ {\frac{3}{5} - {{{\left( {{{P}_{1}}\left( \mu \right)} \right)}}^{2}}} \right]{{\xi }^{{\left( 1 \right)}}}} \right\} \times \\ \times \,\,{{P}_{1}}\left( \mu \right) = \Phi _{s}^{{\left( {{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}} \right)}}, \\ \mathop \smallint \limits_0^\pi \left\{ {\frac{{\partial {{\Phi }^{{\left( {{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}} \right)}}}}}{{\partial r}} - \frac{{\partial {{\Phi }^{{\left( {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} \right)}}}}}{{\partial \theta }}\frac{{\partial {{\xi }^{{\left( 1 \right)}}}}}{{\partial \theta }} + } \right. \\ + \,\,\left( {2\frac{{\partial {{\Phi }^{{\left( {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} \right)}}}}}{{\partial r}} + \frac{{{{\partial }^{2}}{{\Phi }^{{\left( {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} \right)}}}}}{{\partial {{r}^{2}}}}} \right){{\xi }^{{\left( 1 \right)}}} + \\ + \,\,\frac{1}{3}{{\beta }_{e}}\left[ {\left( {2\frac{{\partial {{\Phi }^{{\left( {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} \right)}}}}}{{\partial r}} + \frac{{{{\partial }^{2}}{{\Phi }^{{\left( {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} \right)}}}}}{{\partial {{r}^{2}}}}} \right){{P}_{2}}\left( \mu \right) - } \right. \\ - \,\,\frac{{\partial {{\Phi }^{{\left( {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} \right)}}}}}{{\partial \theta }}\frac{{\partial {{P}_{2}}\left( \mu \right)}}{{\partial \theta }} + \\ + \,\,3{{\beta }_{E}}\left( {\left( {\frac{6}{5}\left( {4{{P}_{3}}\left( \mu \right) + {{P}_{1}}\left( \mu \right)} \right) - {{P}_{1}}\left( \mu \right){{\xi }^{{\left( 1 \right)}}}} \right){{\xi }^{{\left( 1 \right)}}}} \right. - \\ \left. {\left. {\left. { - \,\,2{{P}_{2}}\left( \mu \right)\frac{{\partial {{P}_{1}}\left( \mu \right)}}{{\partial \theta }}\frac{{\partial {{\xi }^{{\left( 1 \right)}}}}}{{\partial \theta }}} \right)} \right]} \right\}\sin \theta d\theta = 0. \\ \end{gathered} $Подставляя в (32) разложения (17) при m = 1; 2 и решение (16) при k = 3/2; 5/2, получим выражения для $F_{n}^{{\left( {{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}} \right)}}\left( {{{T}_{0}}} \right)$ в виде:
(33)
$\begin{gathered} F_{0}^{{\left( {{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}} \right)}}\left( {{{T}_{0}}} \right) = 0, \\ \Phi _{s}^{{\left( {{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}} \right)}} = - 6{\kern 1pt} {{\beta }_{E}}\left[ {\mathop \sum \limits_{n{\kern 1pt} = {\kern 1pt} 0}^\infty \frac{{n\left( {n - 2} \right)}}{{\left( {2n - 1} \right)\left( {2n + 1} \right)}}M_{n}^{{\left( 1 \right)}}\left( {{{T}_{0}},{{T}_{1}}} \right)} \right. \times \\ \times \,\,\left. {M_{{n{\kern 1pt} - {\kern 1pt} 1}}^{{\left( 1 \right)}}\left( {{{T}_{0}},{{T}_{1}}} \right) + \frac{1}{{35}}{{\beta }_{e}}M_{3}^{{\left( 1 \right)}}\left( {{{T}_{0}},{{T}_{1}}} \right)} \right], \\ F_{n}^{{\left( {{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}} \right)}}\left( {{{T}_{0}}} \right) = {{\beta }_{E}} \times \\ \times \left\{ {3\left[ {\mu _{{n{\kern 1pt} - {\kern 1pt} 1}}^{ + }M_{{n{\kern 1pt} - {\kern 1pt} 1}}^{{\left( 2 \right)}}\left( {{{T}_{0}},{{T}_{1}}} \right) + \mu _{{n{\kern 1pt} + {\kern 1pt} 1}}^{ - }M_{{n{\kern 1pt} + {\kern 1pt} 1}}^{{\left( 2 \right)}}\left( {{{T}_{0}},{{T}_{1}}} \right)} \right]\mathop + \limits^{} } \right. \\ + \,\,{{\beta }_{e}}\left[ {M_{{n{\kern 1pt} - {\kern 1pt} 3}}^{{\left( 1 \right)}}\left( t \right){{l}_{1}}\left( n \right) + M_{{n{\kern 1pt} - {\kern 1pt} 1}}^{{\left( 1 \right)}}\left( t \right){{l}_{2}}\left( n \right)} \right. + \\ \left. { + \,\,M_{{n{\kern 1pt} + {\kern 1pt} 1}}^{{\left( 1 \right)}}\left( t \right){{l}_{3}}\left( n \right) + M_{{n{\kern 1pt} + {\kern 1pt} 3}}^{{\left( 1 \right)}}\left( t \right){{l}_{4}}\left( n \right)} \right] + \\ + \,\,3\mathop \sum \limits_{m{\kern 1pt} = {\kern 1pt} 1}^\infty {\kern 1pt} {\kern 1pt} \mathop \sum \limits_{k{\kern 1pt} = {\kern 1pt} 2}^\infty {{K}_{{m,k,n}}}M_{k}^{{\left( 1 \right)}}\left( {{{T}_{0}},{{T}_{1}}} \right) \times \\ \left. { \times \,\,\left[ {\mu _{{m{\kern 1pt} - {\kern 1pt} 1}}^{ + }M_{{m{\kern 1pt} - {\kern 1pt} 1}}^{{\left( 1 \right)}}\left( {{{T}_{0}},{{T}_{1}}} \right) + \mu _{{m{\kern 1pt} + {\kern 1pt} 1}}^{ - }M_{{m{\kern 1pt} + {\kern 1pt} 1}}^{{\left( 1 \right)}}\left( {{{T}_{0}},{{T}_{1}}} \right)} \right]} \right\},\,\,\,\,\left( {n \geqslant 1} \right), \\ \end{gathered} $7. Поверхностная плотность заряда. Определим поверхностную плотность $\nu \left( {\vec {r},t} \right)$ индуцированных внешним электростатическим полем зарядов, распределенных по возмущенной поверхности нелинейно осциллирующей проводящей капли, по известной формуле:
(34)
$\begin{gathered} \nu \left( {\vec {r},t} \right) = {{\left. {\frac{{{{E}_{n}}\left( {\vec {r},t} \right)}}{{4\pi }}} \right|}_{{r{\kern 1pt} = {\kern 1pt} r\left( {\theta ,t} \right)}}} = \\ = {{\left. { - \frac{1}{{4\pi }}\left( {\vec {n}\left( {\vec {r},t} \right),\nabla \Phi \left( {\vec {r},t} \right)} \right)} \right|}_{{r{\kern 1pt} = {\kern 1pt} r\left( {\theta ,t} \right)}}}, \\ \end{gathered} $Подставляя в (34) разложение (13), с учетом (2), (14), а также вектор нормали к возмущенной поверхности капли в виде разложения по степеням малого параметра $\varepsilon $ с точностью до слагаемых $ \sim {\kern 1pt} {{\varepsilon }^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}$:
(35)
$\begin{gathered} \vec {n}\left( {\vec {r},t} \right) = \left[ {1 - \frac{1}{2}{{\varepsilon }^{2}}{{{\left( {{{\beta }_{e}}\frac{{\partial h\left( \theta \right)}}{{\partial \theta }} + \frac{{\partial {{\xi }^{{\left( 1 \right)}}}\left( {\theta ,t} \right)}}{{\partial \theta }}} \right)}}^{2}}} \right]{{{\vec {e}}}_{r}} + \\ + \,\,\left\{ { - \varepsilon \left( {{{\beta }_{e}}\frac{{\partial h\left( \theta \right)}}{{\partial \theta }} + \frac{{\partial {{\xi }^{{\left( 1 \right)}}}\left( {\theta ,t} \right)}}{{\partial \theta }}} \right) + } \right. \\ + \,\,{{\varepsilon }^{2}}\left[ {\left( {{{\xi }^{{\left( 1 \right)}}}\left( {\theta ,t} \right) + {{\beta }_{e}}h\left( \theta \right)} \right)} \right. \times \\ \left. {\left. { \times \,\,\left( {{{\beta }_{e}}\frac{{\partial h\left( \theta \right)}}{{\partial \theta }} + \frac{{\partial {{\xi }^{{\left( 1 \right)}}}\left( {\theta ,t} \right)}}{{\partial \theta }}} \right) - \frac{{\partial {{\xi }^{{\left( 2 \right)}}}\left( {\theta ,t} \right)}}{{\partial \theta }}} \right]} \right\}{{{\vec {e}}}_{\theta }}, \\ \end{gathered} $Учитывая вид функций ${{\xi }^{{\left( 1 \right)}}}\left( {\theta ,t} \right)$ и ${{\xi }^{{\left( 2 \right)}}}\left( {\theta ,t} \right)$ из (31) и решение для поправок порядков 3/2 и 5/2 к электрическому потенциалу:
(36)
$\begin{gathered} {{\Phi }^{{\left( {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} \right)}}}\left( {\vec {r},t} \right) = 3{\kern 1pt} {{\beta }_{E}}\mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } \left[ {\mu _{{j{\kern 1pt} - {\kern 1pt} 1}}^{ + }M_{{j{\kern 1pt} - {\kern 1pt} 1}}^{{\left( 1 \right)}}\left( t \right) + \mu _{{j{\kern 1pt} + {\kern 1pt} 1}}^{ - }M_{{j{\kern 1pt} + {\kern 1pt} 1}}^{{\left( 1 \right)}}\left( t \right)} \right] \times \\ \times \,\,{{r}^{{ - \left( {j{\kern 1pt} + {\kern 1pt} 1} \right)}}}{{P}_{j}}\left( \mu \right), \\ {{\Phi }^{{\left( {{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}} \right)}}}\left( {\vec {r},t} \right) = {{\beta }_{E}}\mathop \sum \limits_{n{\kern 1pt} = {\kern 1pt} 0}^\infty \left[ {3\left( {\mu _{{n{\kern 1pt} - {\kern 1pt} 1}}^{ + }M_{{n{\kern 1pt} - {\kern 1pt} 1}}^{{\left( 2 \right)}}\left( t \right) + \mu _{{n{\kern 1pt} + {\kern 1pt} 1}}^{ - }M_{{n{\kern 1pt} + {\kern 1pt} 1}}^{{\left( 2 \right)}}\left( t \right)} \right)\mathop + \limits^{} } \right. \\ + \,\,3\mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } {\kern 1pt} {\kern 1pt} \mathop \sum \limits_{i{\kern 1pt} \in {\kern 1pt} \Xi } {{K}_{{j,i,n}}}M_{i}^{{\left( 1 \right)}}\left( t \right) \times \\ \left. { \times \,\,\left( {\mu _{{j{\kern 1pt} - {\kern 1pt} 1}}^{ + }M_{{j{\kern 1pt} - {\kern 1pt} 1}}^{{\left( 1 \right)}}\left( t \right) + \mu _{{j{\kern 1pt} + {\kern 1pt} 1}}^{ - }M_{{j{\kern 1pt} + {\kern 1pt} 1}}^{{\left( 1 \right)}}\left( t \right)} \right)} \right] \times \\ \times \,\,{{r}^{{ - \left( {n{\kern 1pt} + {\kern 1pt} 1} \right)}}}{{P}_{n}}\left( \mu \right) + {{\beta }_{e}}\mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } \left[ {M_{{j{\kern 1pt} - {\kern 1pt} 3}}^{{\left( 1 \right)}}\left( t \right){{l}_{1}}\left( j \right) + M_{{j{\kern 1pt} - {\kern 1pt} 1}}^{{\left( 1 \right)}}\left( t \right){{l}_{2}}\left( j \right)} \right. + \\ \left. { + \,\,M_{{j{\kern 1pt} + {\kern 1pt} 1}}^{{\left( 1 \right)}}\left( t \right){{l}_{3}}\left( j \right) + M_{{j{\kern 1pt} + {\kern 1pt} 3}}^{{\left( 1 \right)}}\left( t \right){{l}_{4}}\left( j \right)} \right]{{r}^{{ - \left( {j{\kern 1pt} + {\kern 1pt} 1} \right)}}}{{P}_{j}}\left( \mu \right) \\ \end{gathered} $(37)
$\begin{gathered} \nu \left( {\vec {r},t} \right) = \frac{3}{{4\pi }}{{\beta }_{E}}{{\varepsilon }^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} \times \\ \times \,\,\left\{ {{{P}_{1}}\left( \mu \right) + \varepsilon \left[ {\frac{2}{5}{{\beta }_{e}}{{P}_{3}}\left( \mu \right) + } \right.} \right. \\ + \,\,\left. {\mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } \left( {M_{{j{\kern 1pt} - {\kern 1pt} 1}}^{{\left( 1 \right)}}\left( t \right){{k}_{1}}\left( j \right) + M_{{j{\kern 1pt} + {\kern 1pt} 1}}^{{\left( 1 \right)}}\left( t \right){{k}_{2}}\left( j \right)} \right){{P}_{j}}\left( \mu \right)} \right] + \\ + \,\,{{\varepsilon }^{2}}\left[ {{{\beta }_{e}}\sum\limits_{j{\kern 1pt} \in {\kern 1pt} {{\Xi }}} {\left[ {M_{{j{\kern 1pt} - {\kern 1pt} 3}}^{{\left( 1 \right)}}\left( t \right){{k}_{3}}\left( j \right) + M_{{j{\kern 1pt} - {\kern 1pt} 1}}^{{\left( 1 \right)}}\left( t \right){{k}_{4}}\left( j \right)} \right.} } \right. + \\ \left. {^{{^{{^{{^{{}}}}}}}} + \,\,M_{{j{\kern 1pt} + {\kern 1pt} 1}}^{{\left( 1 \right)}}\left( t \right){{k}_{5}}\left( j \right) + M_{{j{\kern 1pt} - {\kern 1pt} 3}}^{{\left( 1 \right)}}\left( t \right){{k}_{6}}\left( j \right)} \right]{{P}_{j}}\left( \mu \right) + \\ + \,\,\mathop \sum \limits_{n{\kern 1pt} = {\kern 1pt} {\kern 1pt} 0}^\infty \left( {\left[ {M_{{n{\kern 1pt} - {\kern 1pt} 1}}^{{\left( 2 \right)}}\left( t \right){{k}_{1}}\left( n \right) + M_{{n{\kern 1pt} + {\kern 1pt} 1}}^{{\left( 2 \right)}}\left( t \right){{k}_{2}}\left( n \right)} \right]} \right. + \\ + \,\,\mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } {\kern 1pt} {\kern 1pt} \mathop \sum \limits_{i{\kern 1pt} \in {\kern 1pt} \Xi } {{K}_{{j,i,n}}}M_{i}^{{\left( 1 \right)}}\left( t \right) \times \\ \left. {\left. {^{{^{{^{{}}}}}} \times \,\,\left. {\left[ {M_{{j{\kern 1pt} - {\kern 1pt} 1}}^{{\left( 1 \right)}}\left( t \right){{k}_{7}}\left( {j,n} \right) + M_{{j{\kern 1pt} + {\kern 1pt} 1}}^{{\left( 1 \right)}}\left( t \right){{k}_{8}}\left( {j,n} \right)} \right]} \right){{P}_{n}}\left( \mu \right)} \right]} \right\}. \\ \end{gathered} $Из вида выражения (37) следует, что в отсутствии возмущения поверхностная плотность индуцированного заряда определяется двумя первыми слагаемыми в фигурных скобках.
8. Величины индуцированных зарядов. Величины разноименных индуцированных зарядов каждой из половинок возмущенной поверхности капли $r\left( {\theta ,t} \right)$ определяются уравнениями:
(38)
$\begin{gathered} {{q}_{ \pm }}\left( {\vec {r},t} \right) = \mathop \smallint \limits_{{{S}_{{1,2}}}} d{{q}_{ \pm }}\left( {\vec {r},t} \right) = \mathop \smallint \limits_{{{S}_{{1,2}}}} \nu \left( {\vec {r},t} \right)d{{S}_{{1,2}}} = \\ = \mathop \smallint \limits_{{{S}_{{1,2}}}} {{\left. {\frac{{\nu \left( {\vec {r},t} \right)}}{{\left( {\vec {n}\left( {\vec {r},t} \right),{{{\vec {e}}}_{r}}} \right)}}{{r}^{2}}} \right|}_{{r{\kern 1pt} = {\kern 1pt} r\left( {\theta ,t} \right)}}}\sin \theta d\theta d\varphi , \\ {{S}_{1}} \equiv \left[ {r = r\left( {\theta ,t} \right);\,\,0 \leqslant \theta \leqslant \frac{\pi }{2};\,\,0 \leqslant \varphi \leqslant 2\pi } \right], \\ {{S}_{2}} \equiv \left[ {r = r\left( {\theta ,t} \right);\,\,\frac{\pi }{2} \leqslant \theta \leqslant \pi ;\,\,0 \leqslant \varphi \leqslant 2\pi } \right]. \\ \end{gathered} $Разложение для индуцированного заряда ведется по полуцелым степеням параметра $\varepsilon $, поскольку ${{E}_{0}} \sim {{\varepsilon }^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$. Таким образом, определим (38) с точностью до слагаемых порядка $ \sim {\kern 1pt} {{\varepsilon }^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}$.
В силу симметрии распределения индуцированного заряда капли относительно экваториальной плоскости рассмотрим положительно заряженную половинку возмущенной сфероидальной капли ${{S}_{1}}$.
Подставляя в (38) поверхностную плотность заряда (37), вектор нормали (35) и форму возмущенной поверхности капли (31) и интегрируя полученное выражение по поверхности ${{S}_{1}}$, найдем величину положительного индуцированного заряда в виде разложения по степеням малого параметра $\varepsilon $ с точностью до слагаемых $ \sim {\kern 1pt} {{\varepsilon }^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}$:
(39)
$\begin{gathered} {{q}_{ + }}\left( t \right) = \frac{3}{4}{{\beta }_{E}}{{\varepsilon }^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} \times \\ \times \,\,\left\{ {1 + \varepsilon \left( {\frac{1}{{15}}{{\beta }_{e}} + 2\varepsilon \mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } M_{j}^{{\left( 1 \right)}}\left( t \right){{G}_{1}}\left( j \right)} \right) + } \right. \\ + \,\,2{{\varepsilon }^{2}}\left[ {{{\beta }_{e}}\mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } M_{j}^{{\left( 1 \right)}}\left( t \right){{G}_{2}}\left( j \right) + } \right. \\ + \,\,\mathop \sum \limits_{n{\kern 1pt} = {\kern 1pt} {\kern 1pt} 0}^\infty \left( {\sum\limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } {\sum\limits_{i{\kern 1pt} \in {\kern 1pt} \Xi } {M_{i}^{{\left( 1 \right)}}\left( t \right){\kern 1pt} } \left( {M_{{j{\kern 1pt} - {\kern 1pt} 1}}^{{\left( 1 \right)}}\left( t \right){{L}_{1}}{{{\left( {j,i,n} \right)}}^{{^{{^{{^{{^{{}}}}}}}}}}}} \right. + {\kern 1pt} } } \right. \\ \left. {\left. {\left. {\left. {^{{^{{^{{^{{^{{^{{^{{^{{}}}}}}}}}}}}}}}} + \,\,M_{{j{\kern 1pt} + {\kern 1pt} 1}}^{{\left( 1 \right)}}\left( t \right){{L}_{2}}\left( {j,i,n} \right)} \right) + M_{n}^{{\left( 2 \right)}}\left( t \right){{G}_{1}}\left( n \right)} \right)} \right]} \right\}, \\ \end{gathered} $В итоге, учитывая выражения для амплитудных коэффициентов $M_{j}^{{\left( 1 \right)}}\left( t \right)$ и $M_{n}^{{\left( 2 \right)}}\left( t \right)$ из (30) и переходя от формальных параметров ${{\beta }_{e}}$, ${{\beta }_{E}}$ физическим обозначениям, получим аналитическое выражение для разноименных индуцированных зарядов в размерном виде:
(40)
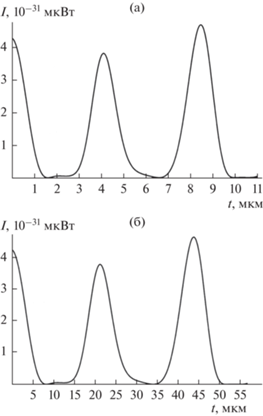
$\begin{gathered} {{q}_{ \pm }}\left( t \right) = \pm \frac{3}{2}\sqrt {\pi {{\varepsilon }_{0}}} {{E}_{0}}{{R}^{2}}\left\{ {1 + \frac{1}{{15}}{{e}^{2}} + 2\varepsilon \mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } {{h}_{j}} \times } \right. \\ \times \,\,\left[ {{{G}_{1}}\left( j \right)\cos \left( {\omega _{j}^{ + }t} \right) + {{e}^{2}}} \right.\left\{ {G_{1}^{ + }\left( j \right)\cos \left( {{{\omega }_{j}}t} \right)} \right. + \\ \left. {\left. { + \,\,G_{2}^{ + }\left( j \right)\cos \left( {{{\omega }_{{j{\kern 1pt} - {\kern 1pt} 2}}}t} \right) + G_{3}^{ + }\left( j \right)\cos \left( {{{\omega }_{{j{\kern 1pt} + {\kern 1pt} 2}}}t} \right)} \right\}} \right] + \\ + \,\,{{\varepsilon }^{2}}\sum\limits_{n{\kern 1pt} = {\kern 1pt} 0}^\infty {\sum\limits_{j{\kern 1pt} \in {\kern 1pt} {{\Xi }}} {\sum\limits_{i{\kern 1pt} \in {\kern 1pt} {{\Xi }}} {\left[ {{{S}_{1}}\left( {j,i,n} \right)\left\{ {\cos \left[ {\left( {{{\omega }_{i}} + {{\omega }_{{j{\kern 1pt} - {\kern 1pt} 1}}}} \right)t} \right]} \right.} \right.} } } + \\ \left. { + \,\,\cos \left[ {\left( {{{\omega }_{i}} - {{\omega }_{{j{\kern 1pt} - {\kern 1pt} 1}}}} \right)t} \right]} \right\} + {{S}_{2}}\left( {j,i,n} \right) \times \\ \times \,\,\left\{ {\cos \left[ {\left( {{{\omega }_{i}} + {{\omega }_{{j{\kern 1pt} + {\kern 1pt} 1}}}} \right)t} \right] + \cos \left[ {\left( {{{\omega }_{i}} - {{\omega }_{{j{\kern 1pt} + {\kern 1pt} 1}}}} \right)t} \right]} \right\} + \\ + \,\,{{S}_{3}}\left( {j,i,n} \right)\left\{ {\cos \left[ {\left( {{{\omega }_{i}} + {{\omega }_{j}}} \right)t} \right] - \cos \left( {{{\omega }_{n}}t} \right)} \right\} + \\ \left. {^{{^{{^{{^{{^{{^{{^{{}}}}}}}}}}}}}}\left. { + \,\,{{S}_{4}}\left( {j,i,n} \right)\left\{ {\cos \left[ {\left( {{{\omega }_{i}} - {{\omega }_{j}}} \right)t} \right] - \cos \left( {{{\omega }_{n}}t} \right)} \right\}} \right]} \right\}, \\ \end{gathered} $Рис. 1.
Зависимость величины положительного индуцированного заряда капли ${{q}_{ + }}\left( t \right)$ в электростатическом поле от времени $t$ при начальном возбуждении равновесной формы поверхности капли возмущением вида ${{\varepsilon \left[ {{{P}_{2}}\left( \mu \right) + {{P}_{3}}\left( \mu \right)} \right]} \mathord{\left/ {\vphantom {{\varepsilon \left[ {{{P}_{2}}\left( \mu \right) + {{P}_{3}}\left( \mu \right)} \right]} 2}} \right. \kern-0em} 2}$, $\sigma = 73 \times {{10}^{{ - 3}}}\;\frac{{\text{Н}}}{{\text{м}}}$, $\rho = {{10}^{3}}$ кг/м3, ${{E}_{0}} = 50$ В/см ($\sim 4 \times {{10}^{{ - 4}}}{{E}_{{0{\text{кр}}}}}$). Кривая 1 соответствует линейным осцилляциям капли, кривая 2 – нелинейным осцилляциям. (а) $R = 10$ мкм, (б) $R = 30$ мкм.
Рисунки “а” и “б” рассчитаны для разных величин радиусов капли потому, что изменение радиуса приводит к заметным количественным изменениям рисунков, как по оси ординат, так и по оси абсцисс. На этот факт необходимо обратить внимание потому, что он влияет и ширину и на интенсивность излучения из реального облака.
Числовые (зависящие только от $j$) коэффициенты $G_{1}^{ + }\left( j \right)$–$G_{3}^{ + }\left( j \right)$, и коэффициенты ${{S}_{1}}\left( {j,i,n} \right)$–${{S}_{4}}\left( {j,i,n} \right)$, зависящие помимо $j$, $i$, $n$ от начальных амплитуд ${{h}_{i}}$, ${{h}_{j}}$, ${{h}_{{j{\kern 1pt} \pm {\kern 1pt} 1}}}$, приведены в приложении.
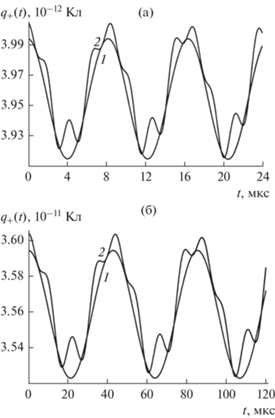
На рис. 2а–б для иллюстрации приведена зависимость от времени $t$ отклонения величины положительного индуцированного заряда капли $\Delta {{q}_{ + }}\left( t \right)$ от его стационарного значения $q_{ + }^{{\left( {{\text{eq}}} \right)}}$ = $ = \frac{3}{2}\sqrt {\pi {{\varepsilon }_{0}}} {{E}_{0}}{{R}^{2}}\left( {1 + \frac{1}{{15}}{{e}^{2}}} \right)$. Видно, что асимптотические расчеты второго порядка малости по $\varepsilon $ приводят к незначительной нелинейной поправке к величине ${{q}_{ + }}\left( t \right)$.
Рис. 2.
Зависимость от времени $t$ отклонения величины положительного индуцированного заряда капли $\Delta {{q}_{ + }}\left( t \right)$ в электростатическом поле от его равновесной величины, рассчитанная при тех же прочих значениях физических величин, что и на рис. 1. (а) $R = 10$ мкм, (б) $R = 30$ мкм.
9. Модель осциллирующего диполя. Разноименным равным по величине индуцированным зарядам ${{q}_{ + }}$ и ${{q}_{ - }}$ поставим в соответствие равновеликие точечные заряды (величина которых зависит от времени), разнесенные относительно друг друга на некоторое расстояние, меньшее диаметра капли. Эти заряды поместим на оси симметрии сфероида в положениях “эффективных” центров положительного и отрицательного зарядов, определенных соотношениями:
При капиллярных осцилляциях поверхности сфероида будет осциллировать величина “эффективного” индуцированного заряда и расстояние между центрами “эффективных” индуцированных зарядов. В результате получим “эффективный” диполь:
(41)
$\vec {d}\left( t \right) = {{q}_{ + }}\left( t \right)\left( {{{{\vec {R}}}_{{{{q}_{ + }}}}}\left( t \right) - {{{\vec {R}}}_{{{{q}_{ - }}}}}\left( t \right)} \right),$(42)
$I = \frac{2}{{3{{c}^{3}}}}{{\left( {\frac{{{{d}^{2}}\vec {d}\left( t \right)}}{{d{{t}^{2}}}}} \right)}^{2}}.$Заметим, что разложения для смещения центров разноименных индуцированных зарядов ведутся по целым степеням малого параметра $\varepsilon $, поэтому дальнейшие расчеты ${{\vec {R}}_{{{{q}_{ \pm }}}}}\left( t \right)$ проведем с точностью до слагаемых порядка $ \sim {\kern 1pt} {{\varepsilon }^{2}}$.
Для определения положения “эффективного” центра индуцированного заряда половинки капли учтем, что радиальный орт ${{\vec {e}}_{r}}$ сферической системы координат связан с ортами декартовой системы координат ${{\vec {e}}_{x}}$, ${{\vec {e}}_{y}}$, ${{\vec {e}}_{z}}$:
(43)
${{\vec {e}}_{r}} = {{\vec {e}}_{x}}\sin \theta \cos \varphi + {{\vec {e}}_{y}}\sin \theta \sin \varphi + {{\vec {e}}_{z}}\cos \theta .$Наконец, используя выражения для амплитуд $M_{j}^{{\left( 1 \right)}}\left( t \right)$ и $M_{n}^{{\left( 2 \right)}}\left( t \right)$ из (30) и переходя от формальных параметров ${{\beta }_{e}}$, ${{\beta }_{E}}$ физическим обозначениям, определим положение “эффективного” центра положительного индуцированного заряда капли в размерном виде:
(44)
$\begin{gathered} {{R}_{{qz}}}\left( t \right) = \frac{2}{3}R\left\{ {1 + \frac{1}{3}{{e}^{2}} + \varepsilon \mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } {{h}_{j}}\left\{ {{{J}_{1}}\left( j \right)\cos \left( {\omega _{j}^{ + }t} \right) + } \right.} \right. \\ + \,\,{{e}^{2}}\left[ {{{J}_{2}}\left( j \right)\cos \left( {{{\omega }_{j}}t} \right) + } \right. \\ \left. {\left. { + \,\,{{J}_{3}}\left( j \right)\cos \left( {{{\omega }_{{j{\kern 1pt} + {\kern 1pt} 2}}}t} \right) + {{J}_{4}}\left( j \right)\cos \left( {{{\omega }_{{j{\kern 1pt} - {\kern 1pt} 2}}}t} \right)} \right]} \right\} + \\ + \,\,{{\varepsilon }^{2}}\sum\limits_{n{\kern 1pt} = {\kern 1pt} 0}^\infty {\sum\limits_{j\, \in \,{{\Xi }}} {\sum\limits_{i\, \in \,{{\Xi }}} {\left[ {{{J}_{5}}\left( {j,i,n} \right)\left( {\cos \left[ {\left( {{{\omega }_{i}} + {{\omega }_{j}}} \right)t} \right]} \right.} \right.} } } + \\ \left. { + \cos \left[ {\left( {{{\omega }_{i}} - {{\omega }_{j}}} \right)t} \right]} \right) + {{J}_{6}}\left( {j,i,n} \right) \times \\ \times \,\,\left( {\cos \left[ {\left( {{{\omega }_{i}} + {{\omega }_{{j{\kern 1pt} - {\kern 1pt} 2}}}} \right)t} \right]} \right. + \\ \left. { + \,\,\cos \left[ {\left( {{{\omega }_{i}} - {{\omega }_{{j{\kern 1pt} - {\kern 1pt} 2}}}} \right)t} \right]} \right) + {{J}_{7}}\left( {j,i,n} \right) \times \\ \times \,\,\left( {\cos \left[ {\left( {{{\omega }_{i}} + {{\omega }_{{j{\kern 1pt} + {\kern 1pt} 2}}}} \right)t} \right] + } \right.\left. {\cos \left[ {\left( {{{\omega }_{i}} - {{\omega }_{{j{\kern 1pt} + {\kern 1pt} 2}}}} \right)t} \right]} \right) + \\ + \,\,{{J}_{8}}\left( {j,i,n} \right){\kern 1pt} \left( {\cos \left[ {\left( {{{\omega }_{i}} + {{\omega }_{{j{\kern 1pt} - {\kern 1pt} 1}}}} \right)t} \right] + \cos \left[ {\left( {{{\omega }_{i}} - {{\omega }_{{j{\kern 1pt} - {\kern 1pt} 1}}}} \right)t} \right]} \right) + \\ + \,\,{{J}_{9}}\left( {j,i,n} \right){\kern 1pt} \left( {\cos \left[ {\left( {{{\omega }_{i}} + {{\omega }_{{j{\kern 1pt} + {\kern 1pt} 1}}}} \right)t} \right] + \cos \left[ {\left( {{{\omega }_{i}} - {{\omega }_{{j{\kern 1pt} + {\kern 1pt} 1}}}} \right)t} \right]} \right) + \\ + \,\,{{J}_{{10}}}\left( {j,i,n} \right)\left\{ {\cos \left[ {\left( {{{\omega }_{i}} + {{\omega }_{j}}} \right)t} \right] - \cos \left( {{{\omega }_{n}}t} \right)} \right\} + \\ \left. {^{{^{{^{{^{{^{{^{{^{{}}}}}}}}}}}}}}\left. { + \,\,{{J}_{{11}}}\left( {j,i,n} \right)\left\{ {\cos \left[ {\left( {{{\omega }_{i}} - {{\omega }_{j}}} \right)t} \right] - \cos \left( {{{\omega }_{n}}t} \right)} \right\}} \right]} \right\}. \\ \end{gathered} $Числовые коэффициенты ${{J}_{1}}\left( j \right)$–${{J}_{4}}\left( j \right)$, зависящие только от $j$, и коэффициенты ${{J}_{5}}\left( {j,i,n} \right)$–${{J}_{{11}}}\left( {j,i,n} \right)$, зависящие помимо $j$, $i$, $n$ от начальных амплитуд ${{h}_{i}}$, ${{h}_{j}}$, ${{h}_{{j{\kern 1pt} \pm {\kern 1pt} 1}}}$, ${{h}_{{j{\kern 1pt} \pm {\kern 1pt} 2}}}$, в виду их чрезвычайной громоздкости приводятся в приложении.
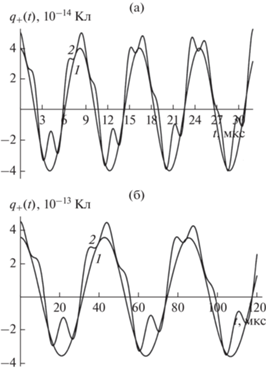
На рис. 3а–3б для иллюстрации приведена зависимость смещения центра положительного индуцированного заряда капли $\Delta {{R}_{{qz}}}\left( t \right)$ от его стационарного равновесного положения $R_{{qz}}^{{\left( {{\text{eq}}} \right)}}$ = $ = \frac{2}{3}R\left( {1 + \frac{1}{3}{{e}^{2}}} \right)$ от времени $t$. Несложно видеть, что нелинейная поправка к величине ${{R}_{{qz}}}\left( t \right)$, найденного в расчетах первого порядка малости, не дает существенный вклад в величину ${{R}_{{qz}}}\left( t \right)$.
Рис. 3.
Зависимость от времени $t$ смещения центра положительного индуцированного заряда капли $\Delta {{R}_{{qz}}}\left( t \right)$ от равновесного значения, рассчитанная при тех же прочих значениях физических величин, что на рис. 1. Кривая 1 соответствует $\Delta {{R}_{{qz}}}\left( t \right)$ при линейных осцилляциях капли, кривая 2 – при нелинейных осцилляциях. (а) $R = 10$ мкм, (б) $R = 30$ мкм.
Аналогичным образом для второй половинки сфероидальной капли найдем аналитическое выражение положения “эффективного” центра отрицательного индуцированного заряда в размерном виде:
(45)
$\begin{gathered} R_{{qz}}^{ - }\left( t \right) = - \frac{2}{3}R\left\{ {1 + \frac{1}{3}{{e}^{2}} + \varepsilon \mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } {{h}_{j}}} \right.\left\{ {J_{1}^{*}\left( j \right)\cos \left( {\omega _{j}^{ + }t} \right) + } \right. \\ + \,\,{{e}^{2}}\left[ {J_{2}^{*}\left( j \right)\cos \left( {{{\omega }_{j}}t} \right)} \right. + \\ \left. {\left. { + \,\,J_{3}^{*}\left( j \right)\cos \left( {{{\omega }_{{j{\kern 1pt} + {\kern 1pt} 2}}}t} \right) + J_{4}^{*}\left( j \right)\cos \left( {{{\omega }_{{j{\kern 1pt} - {\kern 1pt} 2}}}t} \right)} \right]} \right\} + \\ + \,\,{{\varepsilon }^{2}}\sum\limits_{n{\kern 1pt} = {\kern 1pt} 0}^\infty {\sum\limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } {\sum\limits_{i{\kern 1pt} \in {\kern 1pt} \Xi } {\left[ {J_{5}^{*}\left( {j,i,n} \right)} \right.} } } \left( {\cos \left[ {\left( {{{\omega }_{i}} + {{\omega }_{j}}} \right)t} \right]} \right. + \\ \left. { + \,\,\cos \left[ {\left( {{{\omega }_{i}} - {{\omega }_{j}}} \right)t} \right]} \right) + J_{6}^{*}\left( {j,i,n} \right){\kern 1pt} \left( {\cos \left[ {\left( {{{\omega }_{i}} + {{\omega }_{{j{\kern 1pt} - {\kern 1pt} 2}}}} \right)t} \right]} \right.{\kern 1pt} {\kern 1pt} + \\ \left. { + \,\,\cos \left[ {\left( {{{\omega }_{i}} - {{\omega }_{{j{\kern 1pt} - {\kern 1pt} 2}}}} \right)t} \right]} \right) + J_{7}^{*}\left( {j,i,n} \right) \times \\ \times \,\,\left( {\cos \left[ {\left( {{{\omega }_{i}} + {{\omega }_{{j{\kern 1pt} + {\kern 1pt} 2}}}} \right)t} \right] + \cos \left[ {\left( {{{\omega }_{i}} - {{\omega }_{{j{\kern 1pt} + {\kern 1pt} 2}}}} \right)t} \right]} \right) + \\ + \,\,J_{8}^{*}\left( {j,i,n} \right)\left( {\cos {\kern 1pt} \left[ {\left( {{{\omega }_{i}} + {{\omega }_{{j{\kern 1pt} - {\kern 1pt} 1}}}} \right)t} \right] + \cos {\kern 1pt} \left[ {\left( {{{\omega }_{i}} - {{\omega }_{{j{\kern 1pt} - {\kern 1pt} 1}}}} \right){\kern 1pt} t} \right]} \right) + \\ + \,\,J_{9}^{*}\left( {j,i,n} \right)\left( {\cos {\kern 1pt} \left[ {\left( {{{\omega }_{i}} + {{\omega }_{{j{\kern 1pt} + {\kern 1pt} 1}}}} \right)t} \right] + \cos {\kern 1pt} \left[ {\left( {{{\omega }_{i}} - {{\omega }_{{j{\kern 1pt} + {\kern 1pt} 1}}}} \right){\kern 1pt} t} \right]} \right) + \\ + \,\,J_{{10}}^{*}\left( {j,i,n} \right)\left\{ {\cos \left[ {\left( {{{\omega }_{i}} + {{\omega }_{j}}} \right)t} \right] - \cos \left( {{{\omega }_{n}}t} \right)} \right\} + \\ \left. {\left. { + \,\,J_{{11}}^{*}\left( {j,i,n} \right)\left\{ {\cos \left[ {\left( {{{\omega }_{i}} - {{\omega }_{j}}} \right)t} \right] - \cos \left( {{{\omega }_{n}}t} \right)} \right\}} \right]} \right\}, \\ \end{gathered} $Подставляя (40), (44), (45) в (41), найдем проекцию вектора дипольного момента на ось $z$:
(46)
$\begin{gathered} + \,\,{{f}_{9}}\left( {j,i,n} \right){\kern 1pt} \left( {\cos {\kern 1pt} \left[ {\left( {{{\omega }_{i}} + {{\omega }_{{j{\kern 1pt} - {\kern 1pt} 1}}}} \right){\kern 1pt} t} \right] + \cos {\kern 1pt} \left[ {\left( {{{\omega }_{i}} - {{\omega }_{{j{\kern 1pt} - {\kern 1pt} 1}}}} \right)t} \right]} \right) + \\ + \,\,{{f}_{{10}}}\left( {j,i,n} \right){\kern 1pt} \left( {\cos {\kern 1pt} \left[ {\left( {{{\omega }_{i}} + {{\omega }_{{j{\kern 1pt} + {\kern 1pt} 1}}}} \right){\kern 1pt} t} \right] + \cos {\kern 1pt} \left[ {\left( {{{\omega }_{i}} - {{\omega }_{{j{\kern 1pt} + {\kern 1pt} 1}}}} \right)t} \right]} \right) + \\ + \,\,{{f}_{{11}}}\left( {j,i,n} \right)\left( {\cos \left[ {\left( {{{\omega }_{i}} + {{\omega }_{j}}} \right)t} \right] - \cos \left( {{{\omega }_{n}}t} \right)} \right) + \\ \left. {\left. {\left. {^{{^{{^{{}}}}}} + \,\,{{f}_{{12}}}\left( {j,i,n} \right)\left( {\cos \left[ {\left( {{{\omega }_{i}} - {{\omega }_{j}}} \right)t} \right] - \cos \left( {{{\omega }_{n}}t} \right)} \right)} \right]} \right\}} \right\}, \\ {{f}_{1}}\left( j \right) = {{J}_{1}}\left( j \right) + J_{1}^{*}\left( j \right) + 4{{G}_{1}}\left( j \right), \\ {{f}_{2}}\left( j \right) = \frac{1}{{15}}\left( {{{J}_{1}}\left( j \right) + J_{1}^{*}\left( j \right)} \right) + \\ + \,\,{{J}_{2}}\left( j \right) + J_{2}^{*}\left( j \right) + 4G_{1}^{ + }\left( j \right) + \frac{4}{3}{{G}_{1}}\left( j \right), \\ \end{gathered} $Рис. 4.
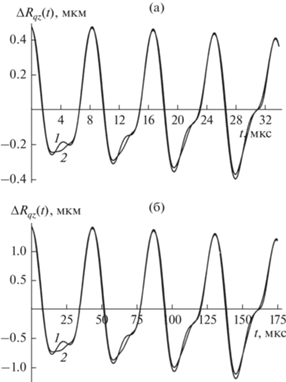
Зависимость от времени $t$ величины проекции ${{d}_{z}}\left( t \right)$ дипольного момента на ось z, рассчитанная при тех же прочих значениях физических величин, что на рис. 1. Кривая 1 соответствует ${{d}_{z}}\left( t \right)$ при линейных осцилляциях капли, кривая 2 – при нелинейных осцилляциях. (а) $R = 10$ мкм, (б) $R = 30$ мкм.
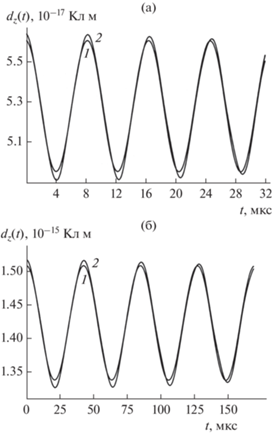
В частности, из рис. 5 несложно видеть, что поправка второго порядка малости по $\varepsilon $ к величине стационарного значения $d_{z}^{{\left( {{\text{eq}}} \right)}} = \sqrt {4\pi {{\varepsilon }_{0}}} {{E}_{0}}{{R}^{3}} \times $ × $\left( {1 + \frac{1}{3}{{e}^{2}}} \right)\left( {1 + \frac{1}{{15}}{{e}^{2}}} \right)$ в (46) определяется более высокими частотами, чем поправка первого порядка малости.
Рис. 5.
Зависимость от времени $t$ поправки $\Delta {{d}_{z}}\left( t \right)$ к величине стационарного значения проекции дипольного момента на ось z, рассчитанная при тех же прочих значениях физических величин, что на рис. 1. Кривая 1 – поправка $\Delta {{d}_{z}}\left( t \right)$ первого порядка малости по $\varepsilon $, кривая 2 – $\Delta {{d}_{z}}\left( t \right)$ второго порядка малости по $\varepsilon $. (а) $R = 10$ мкм, (б) $R = 30$ мкм.
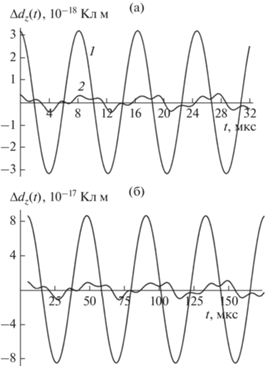
На рис. 6 и рис. 7 приведены зависимости частот осцилляций капли для линейной и нелинейной поправок к величине $d_{z}^{{\left( {{\text{eq}}} \right)}}$ от радиуса капли. Видно, что с ростом размера капли частоты ее осцилляций убывают по примерно гиперболическому закону.
Рис. 6.
Зависимость от радиуса капли частоты ее осцилляций $\omega _{2}^{ + }$ для поправки первого порядка малости по $\varepsilon $ к $d_{z}^{{\left( {{\text{eq}}} \right)}}$, рассчитанная при тех же прочих значениях физических величин, что и на рис. 1.
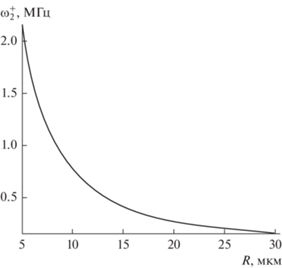
Рис. 7.
Зависимость от радиуса капли частот ее осцилляций ${{\omega }_{n}}$ для поправки второго порядка малости по $\varepsilon $ к величине стационарного значения $d_{z}^{{\left( {{\text{eq}}} \right)}}$, рассчитанная при тех же прочих значениях физических величин, что на рис. 1. Кривая 1 соответствует частоте осцилляций капли ${{\omega }_{3}} - {{\omega }_{2}}$, кривая 2 – ${{\omega }_{2}}$, кривая 3 – ${{\omega }_{3}}$, кривая 4 – $2{{\omega }_{2}}$, кривая 5 – ${{\omega }_{4}}$, кривая 6 – ${{\omega }_{2}} + {{\omega }_{3}}$, кривая 7 – $2{{\omega }_{3}}$, кривая 8 – ${{\omega }_{5}}$.
На основе (42) с учетом (46), заменяя в функциях косинусы и синусы на их максимальные значения, для проводимого качественного анализа, получим аналитическое выражение для интенсивности дипольного излучения нелинейно осциллирующей незаряженной капли во внешнем электростатическом поле в размерном виде:
(47)
$\begin{gathered} I = \frac{{2\pi {{\varepsilon }_{0}}}}{{3{{c}^{3}}}}E_{0}^{2}{{R}^{6}}\left\{ {\varepsilon \mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } {{h}_{j}}} \right.\left[ {{{f}_{1}}\left( j \right)\omega {{{_{j}^{ + }}}^{2}}} \right. + \\ \left. { + \,\,{{e}^{2}}\left\{ {{{f}_{2}}\left( j \right)\omega _{j}^{2} + {{f}_{3}}\left( j \right)\omega _{{j{\kern 1pt} + {\kern 1pt} 2}}^{2} + {{f}_{4}}\left( j \right)\omega _{{j{\kern 1pt} - {\kern 1pt} 2}}^{2}} \right\}} \right] + \\ + \,\,{{\varepsilon }^{2}}\left\{ {2\mathop \sum \limits_{i{\kern 1pt} \in {\kern 1pt} \Xi } \mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } {{h}_{j}}{{h}_{i}}{{f}_{5}}\left( {j,i} \right){{\omega }_{i}}{{\omega }_{j}}} \right. + \\ + \,\,\mathop \sum \limits_{n{\kern 1pt} = {\kern 1pt} 0}^\infty \mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } \mathop \sum \limits_{i{\kern 1pt} \in {\kern 1pt} \Xi } \left[ {{{f}_{6}}\left( {j,i,n} \right)\left\{ {{{{\left( {{{\omega }_{i}} + {{\omega }_{j}}} \right)}}^{2}} + {{{\left( {{{\omega }_{i}} - {{\omega }_{j}}} \right)}}^{2}}} \right\}} \right. + \\ + \,\,{{f}_{7}}\left( {j,i,n} \right)\left\{ {{{{\left( {{{\omega }_{i}} + {{\omega }_{{j{\kern 1pt} - {\kern 1pt} 2}}}} \right)}}^{2}} + {{{\left( {{{\omega }_{i}} - {{\omega }_{{j{\kern 1pt} - {\kern 1pt} 2}}}} \right)}}^{2}}} \right\} + \\ + \,\,{{f}_{8}}\left( {j,i,n} \right)\left\{ {{{{\left( {{{\omega }_{i}} + {{\omega }_{{j{\kern 1pt} + {\kern 1pt} 2}}}} \right)}}^{2}} + {{{\left( {{{\omega }_{i}} - {{\omega }_{{j{\kern 1pt} + {\kern 1pt} 2}}}} \right)}}^{2}}} \right\} + \\ + \,\,{{f}_{9}}\left( {j,i,n} \right)\left\{ {{{{\left( {{{\omega }_{i}} + {{\omega }_{{j{\kern 1pt} - {\kern 1pt} 1}}}} \right)}}^{2}} + {{{\left( {{{\omega }_{i}} - {{\omega }_{{j{\kern 1pt} - {\kern 1pt} 1}}}} \right)}}^{2}}} \right\} + \\ + \,\,{{f}_{{10}}}\left( {j,i,n} \right)\left\{ {{{{\left( {{{\omega }_{i}} + {{\omega }_{{j{\kern 1pt} + {\kern 1pt} 1}}}} \right)}}^{2}} + {{{\left( {{{\omega }_{i}} - {{\omega }_{{j{\kern 1pt} + {\kern 1pt} 1}}}} \right)}}^{2}}} \right\} + \\ + \,\,{{f}_{{11}}}\left( {j,i,n} \right)\left\{ {{{{\left( {{{\omega }_{i}} + {{\omega }_{j}}} \right)}}^{2}} + \omega _{n}^{2}} \right\} + \\ {{\left. {\left. {\left. { + \,\,{{f}_{{12}}}\left( {j,i,n} \right)\left\{ {{{{\left( {{{\omega }_{i}} - {{\omega }_{j}}} \right)}}^{2}} - \omega _{n}^{2}} \right\}} \right]} \right\}} \right\}}^{2}}. \\ \end{gathered} $Осцилляции большой амплитуды облачных капель могут быть вызваны различными причинами: коагуляцией; дроблением на более мелкие в результате процессов столкновения или в результате реализации электростатической неустойчивости; гидродинамическим и электрическим взаимодействием близко пролетающих капель; аэродинамическим взаимодействием с развитой мелкомасштабной турбулентностью, характерной для грозовых облаков. Амплитуды колебаний облачных капель, согласно данным натурных наблюдений [25, 26], могут достигать десятков процентов от радиуса капли. При нижеследующих оценках будем принимать безразмерную амплитуду осцилляций $\varepsilon $ равную $0.1$. Величина параметра Тейлора $w = 4\pi {{\varepsilon }_{0}}{{E_{0}^{2}R} \mathord{\left/ {\vphantom {{E_{0}^{2}R} \sigma }} \right. \kern-0em} \sigma }$ для капель в существующих в грозовых облаках электростатических полях [18] много меньше критического значения параметра ${{w}_{{{\text{кр}}}}}$ [4], т.е. большая часть облачных капель находится весьма далеко от предела неустойчивости по отношению к индуцированному заряду.
На рис. 8 приведена рассчитанная по (47) зависимость интенсивности излучения $I$ от величины напряженности внешнего электрического поля ${{E}_{0}}$. Видно, что с увеличением ${{E}_{0}}$ интенсивность излучения быстро увеличивается.
Рис. 8.
Зависимость интенсивности $I$ дипольного электромагнитного излучения нелинейно осциллирующей незаряженной капли в однородном электростатическом поле от величины напряженности внешнего электростатического поля, рассчитанная при тех же прочих значениях физических величин, что и на рис. 1.
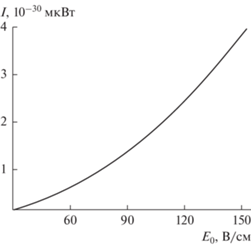
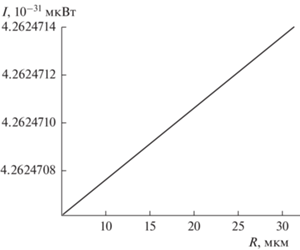
Рис. 9 иллюстрирует зависимость $I$ от радиуса капли $R$. Видно, что она весьма слаба.
Рис. 9.
Зависимость интенсивности $I$ дипольного электромагнитного излучения нелинейно осциллирующей незаряженной капли в однородном электростатическом поле от радиуса капли, рассчитанная при тех же прочих значениях физических величин, что и на рис. 1.
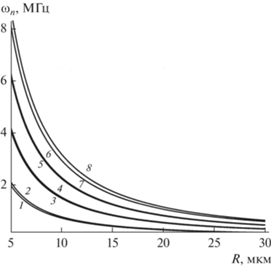
Зависимость интенсивности излучения $I$ от времени $t$, рассчитанная при фиксированных значениях $R$ и ${{E}_{0}}$ по точному выражению (42) с учетом (40), (46) (без замены косинусов и синусов на их максимальные значения) показана на рис. 10а–10б.
Рис. 10.
Зависимость интенсивности дипольного электромагнитного излучения нелинейно осциллирующей в однородном электростатическом поле незаряженной капли от времени $t$, рассчитанная по (42) с учетом (40), (46) и тех же прочих значениях физических величин, что и на рис. 1. (а) $R = 10$ мкм, (б) $R = 30$ мкм.
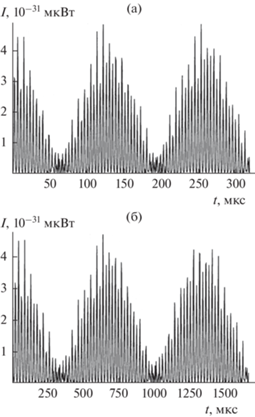
Масштаб изменения времени, принятый на рис. 10, весьма велик, и трудно угадать форму отдельных зубцов. В этой связи на рис. 11а–11б приведена форма отдельных зубцов из начала рис. 10 (в самой левой его части).
ЗАКЛЮЧЕНИЕ
Дипольное электромагнитное излучение незаряженной капли во внешнем электростатическом поле обуславливается неравномерным изменением во времени величины ее индуцированного внешним электростатическим полем осциллирующего дипольного момента. Квадратичные расчеты интенсивности дипольного излучения, выполненные на основе метода многих масштабов, показали их качественное сходство с ранее исследованным дипольным излучением от осциллирующей заряженной капли и некоторое количественное различие [14]. Оказалось, что частота квадратичных поправок к частотам для капли в электростатическом поле в несколько раз выше частоты линейных осцилляций, также как и для заряженной капли. Но зависимость интенсивности электромагнитного излучения от радиуса капли, осциллирующей в электростатическом поле, во много раз слабее, чем от осциллирующей заряженной капли. Исследование временной эволюции интенсивности электромагнитного излучения от единичной капли показало, что излучение имеет вид “биений” – серии пакетов, составленных из элементарных (несущих) волн.
Список литературы
Сивухин Д.В. Общий курс физики. Т. 3. Электричество. Часть вторая. М.: Наука, 1996.
Френкель Я.И. // ЖЭТФ. 1936. Т. 6. № 4. С. 348.
O’Konski C.J., Thacher H.C. // J. Phys. Chem. 1953. V. 57. P. 955.
Taylor G.I. // Proc. Roy. Soc., London. 1964. V. A280. P. 383.
Калечиц В.И., Нахутин И.Е., Полуэктов П.П. // ДАН СССР. 1982. Т. 262. № 6. С. 1344.
Богатов Н.А. // Сборник тез. докл. VI Международной конференции ”Солнечно-земные связи и физика предвестников землетрясений“. Петропавловск-Камчатский: ДВО РАН, 2013. С. 10.
Shiryaeva S.O., Grigoriev A.I., Kolbneva N.Yu. // Surface Engineering and Applied Electrochemistry. 2016. V. 52. № 2. P.162.
Левич В.Г. Курс теоретической физики. Т. 1. М.: Физматгиз, 1969.
Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. 2. Теория поля. М.: Наука, 1973.
Григорьев А.И., Ширяева С.О., Колбнева Н.Ю. Электромагнитное излучение капли, осциллирующей в грозовом облаке. Москва–Берлин: Изд. Директ-Медиа, 2021.
Качурин Л.Г. Физические основы воздействия на атмосферные процессы. Л.: Гидрометеоиздат, 1990.
Белоцерковский А.В., Дивинский Л.И. Активно-пассивная радиолокация грозовых и грозоопасных очагов в облаках / Под ред. Качурина Л.Г. и Дивинского Л.И. СПб.: Гидрометеоиздат, 1992.
Горелик А.Г., Козлов А.И., Стерлядкин В.В. // Научный вестник МГТУ ГА. 2012. № 176. С. 25.
Григорьев А.И., Колбнева Н.Ю., Ширяева С.О. // Изв. РАН. МЖГ. 2018. № 2. С. 62.
Григорьев А.И., Колбнева Н.Ю., Ширяева С.О. // Изв. РАН. МЖГ. 2019. № 5. С. 70.
Григорьев А.И., Ширяева С.О., Белавина Е.И. // ЖТФ. 1989 Т. 59. № 6. С. 27.
Мазин И.П., Шметер С.М. Облака. Строение и физика образования. Л.: Гидрометеоиздат, 1983.
Мазин И.П., Хргиан А.Х., Имянитов И.М. Облака и облачная атмосфера. Справочник. Л.: Гидрометеоиздат, 1989.
Найфе А.Х. Методы возмущений. М.: Мир, 1976.
Стрэттон Дж.А. Теория электромагнетизма. М.: ОГИЗ-Гостехиздат, 1948.
Смайт В. Электростатика и электродинамика. М.: ИЛ, 1954.
Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. 8. Электродинамика сплошных сред. М.: Наука, 1982.
Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. 6. Гидродинамика. М.: Наука, 1986.
Лагалли М. Векторное исчисление в применении к математической физике. М.: Изд. URSS, 2010.
Beard K.V., Tokay A.A. // Geophysical Research Letters. 1991. V. l8. № 12. P. 2257.
Стерлядкин В.В. // Известия АН СССР. ФАО. 1988. Т. 24. № 6. С.613.
Варшалович Д.А., Москалев А.Н., Херсонский В.К. Квантовая теория углового момента. Л.: Наука, 1975.
Дополнительные материалы отсутствуют.
Инструменты
Коллоидный журнал