Коллоидный журнал, 2022, T. 84, № 2, стр. 228-248
Аналитическое исследование модифицированного уравнения Пуассона–Больцмана и его применение для ионистора с цилиндрическими порами
1 School of Physics and Electronics, Central South University
410083 Hunan, Changsha, China
* E-mail: chixiayzsq@163.com
Поступила в редакцию 07.10.2021
После доработки 23.12.2021
Принята к публикации 24.02.2022
- EDN: QVAFAU
- DOI: 10.31857/S0023291222020100
Аннотация
Получено приближенное аналитическое решение модифицированного уравнения Пуассона-Больцмана для симметричного электролита в цилиндрической поре. Выведены выражения для отношения плотности поверхностного заряда $\sigma $ к потенциалу поверхности ${{\psi }_{{\text{s}}}}$, распределения потенциала и концентрации ионов. Выражение для ${\sigma \mathord{\left/ {\vphantom {\sigma {{{\psi }_{{\text{s}}}}}}} \right. \kern-0em} {{{\psi }_{{\text{s}}}}}}$ с высокой точностью согласуется с численным решением для всех значений ${{\psi }_{{\text{s}}}}$ и радиусов пор ${{r}_{{{\text{cyl}}}}}$. На его основе проанализированы электрическая емкость и зависимость плотности запасенной энергии от потенциала электрода цилиндрических пор ионистора. Полученные данные хорошо согласуются с предыдущими аналитическими и численными результатами. Показано, что влияние объемной молярной концентрации $c$ в основном проявляется в том, что высокие значения $c$ снижают максимальную плотность запасенной энергии ${{E}_{{{\text{sat}}}}}$ и пороговый потенциал электродов ${{U}_{{{\text{sat}}}}}$, при котором достигается ${{E}_{{{\text{sat}}}}}$, а также в уменьшении области нулевой энергии вблизи потенциала нулевого заряда. При этом влияние концентрации оказывается важным только в тонких порах. Кроме того, показано, что хотя увеличение размера иона уменьшает ${{E}_{{{\text{sat}}}}}$, оно также уменьшает и ${{U}_{{{\text{sat}}}}}$. Более того, оно приводит к переходу от двугорбой к колоколообразной форме кривой дифферинциальной емкости. В то же время, увеличение валентности ионов, так же, как и увеличение размеров пор, наоборот, увеличивает и ${{E}_{{{\text{sat}}}}}$, и ${{U}_{{{\text{sat}}}}}$.
1. ВВЕДЕНИЕ
Многие процессы, определяющие поведение биологических и физикохимических систем, такие, как фолдинг белков и макромолекул [1, 2], кристаллизация и устойчивость коллоидных растворов [3, 4], диссоциация ионов [5, 6], ионная селективность в порах [7], электроосмотическое течение в гидрофобных порах [8], а также связывание сильнозаряженных био-полиэлектролитов [9, 10], существенным образом зависят от образования двойных электрических слоев (ДЭС) вблизи заряженных поверхностей. В этих процессах, благодаря своей дальнодействующей природе, неионспецифичные электростатические взаимодействия играют важную роль и, в том числе, в большой степени определяют и сложное ион-специфичное поведение. Процессы, упомянутые выше, коренным образом связаны с концентрацией ионов и распределением электростатического потенциала вокруг заряженных поверхностей в водных растворах.
С другой стороны, по мере того, как эффективное хранение электрической энергии становится все более востребованным, особое внимание исследователи уделяют новому подходу по хранению энергии, заключающемуся в использовании электрохимических конденсаторов, называемых также ионисторами, суперконденсаторами и ДЭС-конденсаторами [11–15]. При этом для теоретических расчетов емкости и зависимости плотности запасенной энергии от потенциала электрода в ионисторах требуется знать взаимосвязь между поверхностным потенциалом и плотностью поверхностного заряда.
Одним из наиболее широко используемых методов для описания поведения растворов электролитов является приближение среднего поля, опирающееся на уравнение Пуассона−Больцмана (ПБ) [16–24]. В силу простоты и способности эффективно предсказывать термодинамические свойства, подход ПБ широко используется для моделирования распределения ионов вблизи заряженных поверхностей [25–31]. Несмотря на эти результаты, подход ПБ является континуальным подходом с рядом приближений, включающих приближение среднего поля, точечность ионов, термодинамическое равновесие в системе и пренебрежение статистическими корреляциями [32, 33]. Так, хотя этот подход хорошо описывает распределение ионов и результирующие силы для плоских и криволинейных поверхностей, известно, что он существенно переоценивает концентрацию ионов вблизи заряженных поверхностей. Эти недостатки подхода ПБ наиболее ярко проявляются вблизи сильно заряженных поверхностей и для электролитов с мультивалентными ионами.
Необходимо отметить, что подходы статистической механики, такие, как классическая теория функционала плотности (classical density functional theory, CDFT) или модель Изинга, за последние десятилетия существенно продвинулись в описании поля действия поверхностных сил жидкости [33–39]. Статистико-механические подходы широко применяются для систем, где существенным образом проявляются эффекты, не учтенные в теории ПБ: дискретность размера ионов [40–42], перезарядка[43–45], притяжение одинаково заряженных поверхностей [46–51], а также инверсия ион-специфичности [52–53]. Все эти эффекты связаны с высокой плотностью поверхностного заряда, большой концентрацией ионов или присутствием мультивалентных противоионов.
Однако, решения в рамках CDFT подхода исключительно численные. Поэтому старый подход Пуассона−Больцмана [54] по-прежнему используется многими исследователями. Были предложены несколько методов для учета конечности размеров ионов в рамках теории ПБ. Первый из таких подходов основан на модели слоя Штерна – области, окружающей заряженную поверхность, в которую не могут проникать ионы [55, 56]. Этот подход феноменологичен, менее строг, чем статистические методы и оставляет вопросы в определении толщины слоя Штерна. Другие подходы, включают в себя различные модификации уравнений Пуассона−Больцмана (МПБ) [57–62], которые учитывают размеры ионов.
Получение аналитических решений для ПБ и МПБ уравнений имеет важную теоретическую и практическую ценность. Хотя сами уравнения имеют ту же форму для заряженных поверхностей с различной геометрией, сложность и способ их решения существенно различаются для разных форм поверхности из-за отличий в граничных условиях. В целом, ПБ уравнения для ДЭС, формирующегося вблизи плоских заряженных поверхностей, решаются легко [63–65]. Однако, для криволинейных поверхностей, в силу сложности получающихся цилиндрических и сферических операторов, точных аналитических решений для уравнений ПБ и МПБ часто не существует, что приводит к необходимости получения приближенных аналитических решений [66–71]. Хотя значительное количество исследований направлено на изучение ДЭС, формирующегося вокруг заряженных частиц [72–75], с развитием пористых материалов все больше процессов затрагивают формирование ДЭС в тонких порах [76–79].
Данная работа направлена на решение двух задач. Первая состоит в получении приближенных аналитических решений уравнений МПБ для ДЭС, формирующегося в цилиндрической поре с симметричным +z/–z водным электролитом. Полученные аналитически уравнения для распределения потенциала, концентрации ионов и зависимости между плотностью поверхностного заряда и потенциалом поверхности будут сравнены с результатами численных решений уравнений МПБ. Вторая задача состоит в исследовании, на основе полученных уравнений, емкости и зависимости плотности запасенной энергии от потенциала электрода цилиндрической поры ионистора.
Статья организована следующим образом. В разделе 2 мы кратко описываем наше аналитическое решение уравнений МПБ. В разделе 3 представлена всесторонняя проверка предложенного решения. Затем полученные аналитические выражения используются для изучения емкости и зависимости плотности запасенной энергии от потенциала электрода цилиндрической поры ионистора. Выводы работы представлены в разделе 4.
2. АНАЛИТИЧЕСКОЕ РЕШЕНИЕ УРАВНЕНИЙ МПБ
Для потенциала $\psi $, создаваемого заряженной поверхностью в симметричном +z/–z электролите, уравнения МПБ записываются следующим образом [57]:
(1)
${{\nabla }^{2}}\psi = \frac{{2ze{{c}_{b}}}}{\varepsilon }\frac{{\operatorname{sh} \left( {\frac{{ze\psi }}{{{{k}_{{\text{B}}}}T}}} \right)}}{{1 + 2{{\phi }_{0}}{{{\operatorname{sh} }}^{2}}\left( {\frac{{ze\psi }}{{2{{k}_{{\text{B}}}}T}}} \right)}},$Для раствора соли в бесконечно длинной цилиндрической поре радиуса ${{r}_{{{\text{cyl}}}}}$ и равномерно заряженной стенки поры (см. рис. 1) уравнение (1) сводится к
(2)
$\frac{{{{d}^{2}}\psi }}{{d{{r}^{2}}}} + \frac{1}{r}\frac{{d\psi }}{{dr}} = \frac{{2ze{{c}_{b}}}}{\varepsilon }\frac{{\operatorname{sh} \left( {\frac{{ze\psi }}{{{{k}_{{\text{B}}}}T}}} \right)}}{{1 + 2{{\phi }_{0}}{{{\operatorname{sh} }}^{2}}\left( {\frac{{ze\psi }}{{2{{k}_{{\text{B}}}}T}}} \right)}}.$(3)
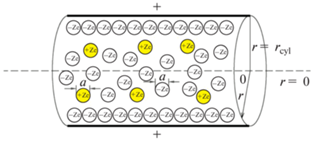
$\begin{gathered} \frac{{d\psi }}{{dr}} = 0,\,\,\,\,r = 0, \\ \frac{{d\psi }}{{dr}} = \frac{\sigma }{\varepsilon },\,\,\,\,~r = {{r}_{{{\text{cyl\;}}}}}, \\ \end{gathered} $Рис. 1.
Схема двойного электрического слоя, сформированного в +z/–z электролите внутри бесконечно длинной поры радиусом ${{r}_{{{\text{cyl}}}}}$ и равномерно заряженной за счет адсорбции положительных ионов поверхностью.
Вводя обозначение для приведенного электростатического потенциала $y = \frac{{ze\psi \left( r \right)}}{{{{k}_{{\text{B}}}}T}}$ (чтобы избежать путаницы, отметим, что для двух точек, $r = {{r}_{{{\text{cyl}}}}}$ и $r = 0~$, приведенные потенциалы ${{\psi }_{{\text{s}}}}$ и ${{\psi }_{0}}$ обозначаются стандартными символами $\psi _{{\text{s}}}^{*}$ и $\psi _{0}^{*}$, соответственно) и параметр экранирования (обратная дебаевская длина) $\kappa = {{\left( {\frac{{2{{z}^{2}}{{e}^{2}}{{c}_{b}}}}{{\varepsilon {{k}_{{\text{B}}}}T}}} \right)}^{{\frac{1}{2}}}}$, уравнение (2) с соответствующими граничными условиями (3) может быть записано следующим образом:
(4)
$\frac{{{{d}^{2}}y}}{{d{{{\left( {\kappa r} \right)}}^{2}}}} + \frac{1}{{\kappa r}}\frac{{dy}}{{d\left( {\kappa r} \right)}} = \frac{{\operatorname{sh} \left( y \right)}}{{1 + 2{{\phi }_{0}}{{{\operatorname{sh} }}^{2}}\left( {\frac{y}{2}} \right)}},$(5)
$\begin{gathered} \frac{{dy}}{{d\kappa r}} = 0,\,\,\,\,\kappa r = 0, \\ \frac{{dy}}{{d\kappa r}} = \frac{{ze\sigma }}{{\kappa \varepsilon {{k}_{{\text{B}}}}T}} = \sigma {\kern 1pt} *,\,\,\,\,\kappa r = \kappa {{r}_{{{\text{cyl}}}}}, \\ \end{gathered} $Для решения уравнений (4) и (5) мы применяем метод решения уравнений ПБ, впервые предложенный в работе [80] для ДЭС, окружающего цилиндрические и сферические частицы.
Уравнение (4) может быть приведено к следующему виду:
(6)
$\frac{{{{d}^{2}}y}}{{d{{{\left( {\kappa r} \right)}}^{2}}}} + \frac{1}{{\kappa r}}\frac{{dy}}{{d\kappa r}} = f\left( y \right)\frac{{df\left( y \right)}}{{dy}},$Проводя замену переменной $x = \frac{{{{K}_{0}}\left( {\kappa {{r}_{{{\text{cyl}}}}}} \right)}}{{{{K}_{0}}\left( {\kappa r} \right)}}$ (где ${{K}_{n}}$ – модифицированная функция Бесселя второго рода n-ного порядка), уравнение 6 можно записать как
(7)
$\begin{gathered} {{x}^{2}}\frac{{{{d}^{2}}y}}{{d{{x}^{2}}}} + x\frac{{dy}}{{dx}} = f\left( y \right)\frac{{df\left( y \right)}}{{dy}} - \\ - \,\,\left[ {1 + {{{\left\{ {\frac{{{{K}_{0}}\left( {\kappa r} \right)}}{{{{K}_{1}}\left( {\kappa r} \right)}}} \right\}}}^{2}}} \right]\left[ {f\left( y \right)\frac{{df\left( y \right)}}{{dy}} + x\frac{{dy}}{{dx}}} \right]. \\ \end{gathered} $С соответствующими граничными условиями
(8)
$\begin{gathered} \frac{{dy}}{{dx}} = 0,\,\,\,\,x \to 0, \\ \frac{{dy}}{{dx}} = \beta \sigma {\kern 1pt} *,\,\,\,\,x = 1, \\ \end{gathered} $где $\beta = \frac{{{{K}_{0}}\left( {\kappa {{r}_{{{\text{cyl}}}}}} \right)}}{{{{K}_{1}}\left( {\kappa {{r}_{{{\text{cyl}}}}}} \right)}}.$
Для x → 0, уравнение (7) сводится к
(9)
${{x}^{2}}\frac{{{{d}^{2}}y}}{{d{{x}^{2}}}} + x\frac{{dy}}{{dx}} = f\left( y \right)\frac{{df\left( y \right)}}{{dy}}.$(10)
${{\left( {x\frac{{dy}}{{dx}}} \right)}^{2}} = {{f}^{2}}\left( y \right) - {{f}^{2}}(\psi _{0}^{*}).$Предполагая, что поверхность заряжена положительно, имеем:
Подставляя уравнение (12) в уравнение (7) и заменяя κr на $\kappa {{r}_{{{\text{cyl}}}}}$, получаем(13)
$\begin{gathered} {{x}^{2}}\frac{{{{d}^{2}}y}}{{d{{x}^{2}}}} + x\frac{{dy}}{{dx}} = f\left( y \right)\frac{{df\left( y \right)}}{{dy}} - \\ - \,\,\left( {1 + {{\beta }^{2}}} \right)\left[ {f\left( y \right)\frac{{df\left( y \right)}}{{dy}} + f(y,\psi _{0}^{*})} \right]. \\ \end{gathered} $(14)
$\begin{gathered} {{x}^{2}}\frac{{{{d}^{2}}y}}{{d{{x}^{2}}}} + x\frac{{dy}}{{dx}} = f\left( y \right)\frac{{df\left( y \right)}}{{dy}} - \\ - \,\,\alpha \left[ {f\left( y \right)\frac{{df\left( y \right)}}{{dy}} + f(y,\psi _{0}^{*})} \right]. \\ \end{gathered} $(15)
$\frac{1}{2}d{{\left( {x\frac{{dy}}{{dx}}} \right)}^{2}} = \left( {1 - \alpha } \right)f\left( y \right)df\left( y \right) - \alpha \left[ {f(y,\psi _{0}^{*})dy} \right].$Интегрирование (15) с учетом граничных условий (8) дает
где $F(y,\psi _{0}^{*})$ = $f(y,\psi _{0}^{*})\left[ {1 - \alpha - \frac{{2\alpha }}{{{{f}^{2}}(y,\psi _{0}^{*})}}} \right. \times $ $ \times \,\,{{\left. {{\kern 1pt} \int_{\psi _{0}^{*}}^y {f(u,\psi _{0}^{*})du} } \right]}^{{^{{\frac{1}{2}}}}}}.$С учетом граничных условий и уравнения (16) соотношение между σ* и $\psi _{{\text{s}}}^{*}~$ запишется следующим образом:
(17)
$\begin{gathered} \sigma {\kern 1pt} * = \frac{1}{\beta }f(\psi _{{\text{s}}}^{*},\psi _{0}^{*}) \times \\ \times \,\,{{\left[ {1 - \alpha - \frac{{2\alpha }}{{{{f}^{2}}(\psi _{{\text{s}}}^{*},\psi _{0}^{*})}}\mathop \smallint \limits_{\psi _{0}^{*}}^{\psi _{s}^{*}} f(u,\psi _{0}^{*}){\kern 1pt} du} \right]}^{{\frac{1}{2}}}}. \\ \end{gathered} $Интегрирование уравнения (16) дает трансцендентное выражение для связи между переменной x и приведенным потенциалом y:
(18)
$\mathop \smallint \limits_y^{\psi _{{\text{s}}}^{*}} \frac{{dy}}{{F(y,\psi _{0}^{*})}} = - \ln x.$(19)
${{c}^{ \pm }}\left( {\mathbf{r}} \right) = \frac{{{{c}_{b}}{{e}^{{ \mp \frac{{ze\psi }}{{{{k}_{{\text{B}}}}T}}}}}}}{{1 + 2{{\phi }_{0}}{{{\operatorname{sh} }}^{2}}\left( {\frac{{ze\psi }}{{2{{k}_{{\text{B}}}}T}}} \right)}}.$3. ПРОВЕРКА И ПРИМЕНЕНИЕ В СЛУЧАЕ ИОНИСТОРА
В большинстве аналитических решений для ДЭС, формирующегося внутри пор различной геометрии, предполагается, что потенциал в центре поры равен нулю. Однако такое предположение оправдано только для больших пор. Для тонких пор это в общем случае неверно, поскольку малый размер не позволяет потенциалу снизиться от потенциала стенки до нуля в центре поры. Предложенный метод решения не требует $\psi \left( {r = 0} \right) = 0$, что соответствует рассмотрению общего случая. Однако, решение требует, чтобы потенциал в центре поры был задан. В нашей работе мы определяем $\psi \left( {r = 0} \right)$, или $\psi _{0}^{*}$, из условия электронейтральности:
(20)
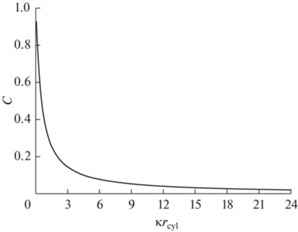
$\mathop \smallint \limits_0^{{{r}_{{{\text{cyl}}}}}} 2\pi r{{\rho }_{{{\text{ele}}}}}\left( r \right)dr + 2\pi {{r}_{{{\text{cyl}}}}}\sigma = 0.$Рис. 2.
Зависимость корректирующего фактора $C$ как функция приведенного (с учетом параметра экранирования $\kappa $) радиуса поры $\kappa {{r}_{{{\text{cyl}}}}}$.
Проверку корректности аналитического решения можно разделить на три части: проверка электростатического потенциала $y\left( {\kappa r} \right)$, распределение концентрации ионов ${{c}^{ \pm }}\left( r \right)~$ и соотношения между σ* и $\psi _{{\text{s}}}^{*}~$. Сравнение предложенных аналитических выражений с точным численным решением представлено на рис. 3–6 для $y\left( {\kappa r} \right)$, рис. 7–12 для ${{c}^{ \pm }}\left( r \right)$, и рис. 13–14 для соотношения между σ* и $\psi _{{\text{s}}}^{*}~$. Численное решение МПБ уравнений было получено с использованием функции DBVPMS из пакета IMSL включенного в Visual Fortran Professional Edition. Для безразмерных уравнений МПБ все величины, описывающие систему, можно сгруппировать в несколько безразмерных параметров: радиус цилиндрической поры $\kappa {{r}_{{{\text{cyl}}}}}$, плотность поверхностного заряда σ* или потенциал поверхности $\psi _{{\text{s}}}^{*}~$, объемная доля ϕ0. Соответственно, один набор безразмерных величин $\kappa {{r}_{{{\text{cyl}}}}}$, $\psi _{{\text{s}}}^{*}~$ и ϕ0 может соответствовать набору разных реальных систем. Во всех представленных примерах используются только безразмерные величины. В то же время, для некоторых случаев, в основном для высоких потенциалов $\psi _{{\text{s}}}^{*}~$ и малых $\kappa {{r}_{{{\text{cyl}}}}}$, численные методы не сходятся и для них численные результаты не представлены.
Рис. 3.
Распределение безразмерного электростатического потенциала $y = \frac{{ze\psi }}{{{{k}_{{\text{B}}}}T}}$ внутри поры. Безразмерный потенциал поверхности $\psi _{{\text{s}}}^{*}$ меняется от 5 до 50 с шагом 5. Рассматриваются два безразмерных размера пор: $\kappa {{r}_{{{\text{cyl}}}}} = 1.2$ и $\kappa {{r}_{{{\text{cyl}}}}} = 2$. Результаты численных расчетов показаны символами, а результаты аналитических расчетов линиями. Объемная мольная доля соли $~c = 0.1\,\,{\text{M}}$.
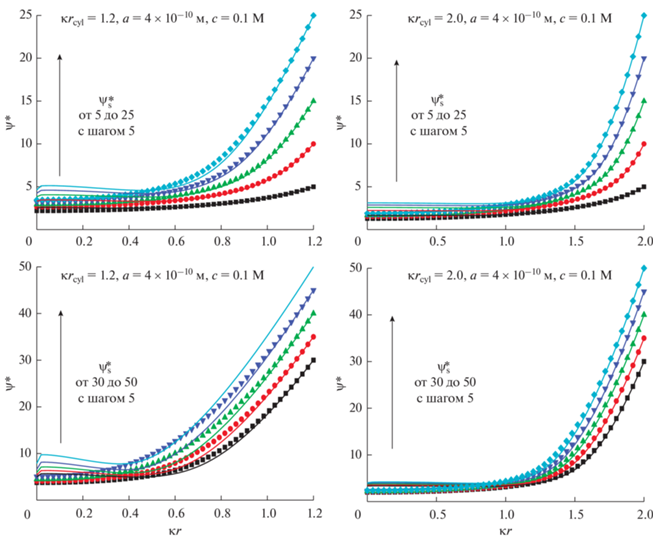
Рис. 4.
Распределение безразмерного электростатического потенциала $y = \frac{{ze\psi }}{{{{k}_{{\text{B}}}}T}}$ внутри поры. Безразмерный потенциал поверхности $\psi _{{\text{s}}}^{*}$ меняется от 5 до 50 с шагом 5. Рассматриваются два безразмерных размера пор: $\kappa {{r}_{{{\text{cyl}}}}} = 4$ и $\kappa {{r}_{{{\text{cyl}}}}} = 8$. Результаты численных расчетов показаны символами, а результаты аналитических расчетов линиями. Объемная мольная доля соли $~c = 0.1\,\,{\text{M}}$.
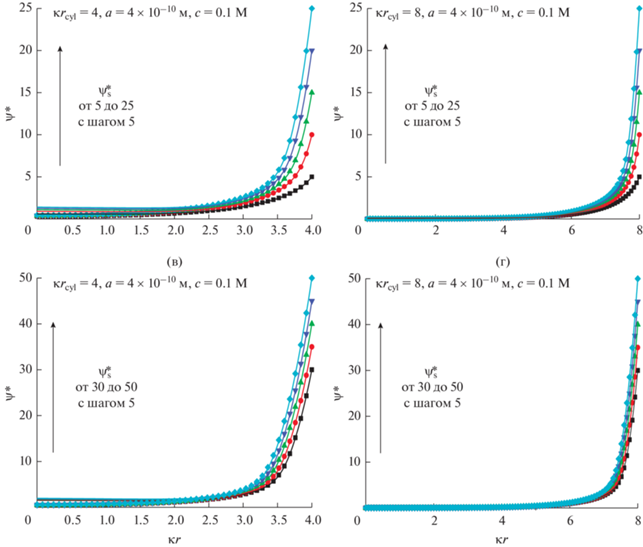
Рис. 5.
Распределение безразмерного электростатического потенциала $y = \frac{{ze\psi }}{{{{k}_{{\text{B}}}}T}}$ внутри поры. Безразмерный потенциал поверхности $\psi _{{\text{s}}}^{*}$ меняется от 5 до 50 с шагом 5; $\kappa {{r}_{{{\text{cyl}}}}} = 2$ (а) и $\kappa {{r}_{{{\text{cyl}}}}} = 3$ (б, в), $a = 5 \times {{10}^{{ - 10}}}~\,\,{\text{м}}$. Результаты численных расчетов показаны символами, а результаты аналитических расчетов линиями. Объемная мольная доля соли $~c = 1\,\,{\text{M}}$.
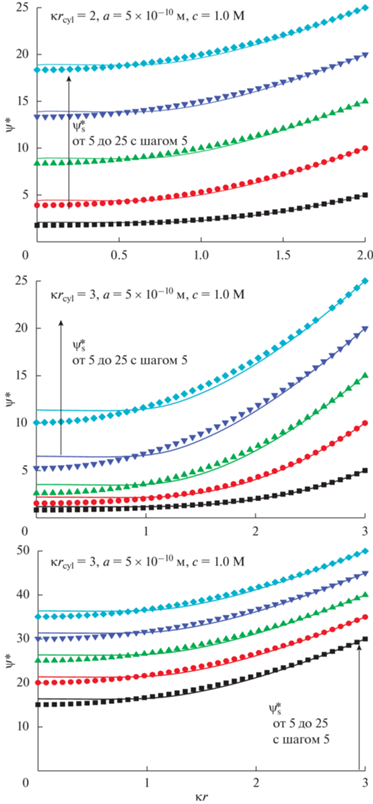
Рис. 6.
Распределение безразмерного электростатического потенциала $y = \frac{{ze\psi }}{{{{k}_{{\text{B}}}}T}}$ внутри поры. Безразмерный потенциал поверхности $\psi _{{\text{s}}}^{*}$ меняется от 5 до 50 с шагом 5; $\kappa {{r}_{{{\text{cyl}}}}} = 4$ (а, в) и $\kappa {{r}_{{{\text{cyl}}}}} = 8$ (б, г), $a = 5 \times {{10}^{{ - 10}}}{\text{\;м}}$. Результаты численных расчетов показаны символами, а результаты аналитических расчетов линиями. Объемная мольная доля соли $~c = 1\,\,{\text{M}}$.
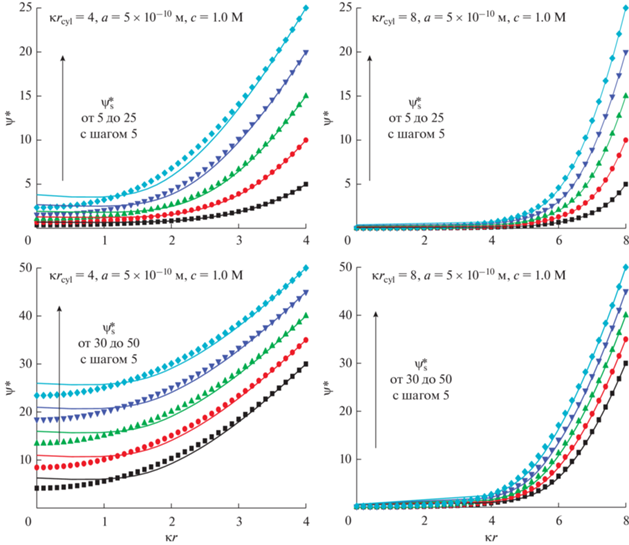
Рис. 7.
Распределение концентраций ионов ${{c}^{ \pm }}\left( {\kappa r} \right)$ внутри поры. Безразмерный потенциал поверхности $\psi _{{\text{s}}}^{*}$ меняется от 5 до 45; $\kappa {{r}_{{{\text{cyl}}}}} = 1.2$ (а, в) и $\kappa {{r}_{{{\text{cyl}}}}} = 2$ (б, г), $a = 4 \times {{10}^{{ - 10}}}{\text{\;м}}$. Результаты численных расчетов показаны символами, а результаты аналитических расчетов линиями. Объемная мольная доля соли $~c = 0.1\,\,{\text{M}}$.
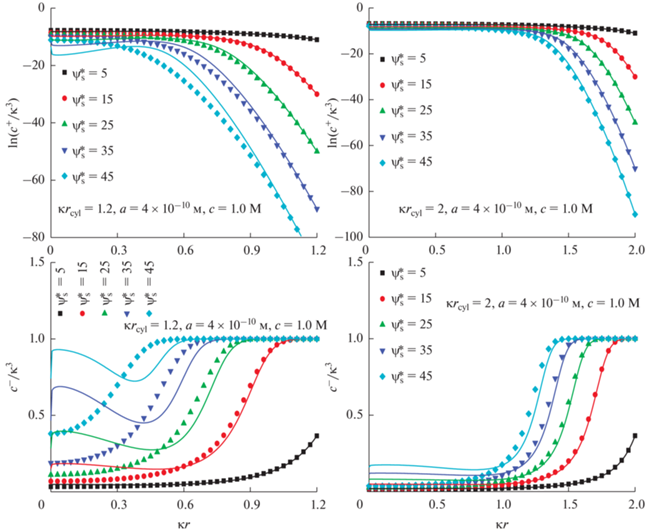
На основе анализа рис. 3–14 можно сформулировать следующие закономерности предложенных аналитических выражений. а) Соотношение между σ* и $\psi _{{\text{s}}}^{*}~$ всегда точно соответствует численному результату, вне зависимости от величины $\kappa {{r}_{{{\text{cyl}}}}}$. Позитивным является тот факт, что хотя в расчетах используется подгоночный параметр С, величина этого параметра зависит только от приведенного размера поры и применима для всех $\psi _{{\text{s}}}^{*}~$ без потери точности. б) Точность аналитического решения для распределения электростатического потенциала $y\left( {\kappa r} \right)$ зависит от местоположения в поре. Так, вблизи поверхности поры аналитическое выражение всегда близко к численным результатам, что является следствием высокой точности аналитического соотношения между σ* и $\psi _{{\text{s}}}^{*}~$. По мере приближения к центру поры аналитическое и численное решения постепенно расходятся. Необходимо подчеркнуть, что хотя $C\left( {\kappa {{r}_{{{\text{cyl}}}}}} \right)$ определяется из предположения равенства численного и аналитического значений $\psi _{0}^{*}~$ в уравнении (17), величина $\psi _{0}^{*}~$ из уравнения (19), определяемая из выражений для ${{c}^{ \pm }}\left( r \right)$ и условия электронейтральности, не совпадает с численным значением. Учитывая это несоответствие, можно было бы ожидать невысокую точность уравнения (17). Несколько неожиданно, но, как видно из рис. 13–14, точность остается достаточно высокой. Для больших $\kappa {{r}_{{{\text{cyl}}}}}$, как показано на рис. 2, $C\left( {\kappa {{r}_{{{\text{cyl}}}}}} \right)$ стремится к нулю по мере роста радиуса поры, что соответствует исчезновению влияния корректирующего множителя. Однако и для достаточно маленьких $\kappa {{r}_{{{\text{cyl}}}}}$ небольшие изменения $\psi _{0}^{*}$ в выражении для σ* и $\psi _{{\text{s}}}^{*}~$ не приводят к значимым отличиям для итогового соотношения между σ* и $\psi _{{\text{s}}}^{*}~$. в) Что касается точности аналитического выражения (19) для распределения концентрации ионов ${{c}^{ \pm }}\left( r \right)$, оно в целом похоже на поведение $y\left( {\kappa r} \right)$, т.е. вблизи поверхности поры наблюдается почти идеальное совпадение, а вблизи центра – существенное отклонение аналитического и численного решений. Сравнивая результаты, можно сказать, что точность выражения (19) ниже точности выражения (18). Причина этого может быть связана с тем, что отклонения в концентрации положительных и отрицательных ионов частично компенсируют друг друга, и итоговая плотность заряда ${{\rho }_{{{\text{ele}}}}}\left( r \right)$ слабо отличается от численных результатов. г) Для достаточно больших величин поверхностного потенциала по мере его роста концентрация противоионов перестает расти. Вместо этого наблюдается утолщение слоя противоионов, толщина которого растет с ростом потенциала и отрицательно коррелирует с $\kappa {{r}_{{{\text{cyl}}}}}$. Это соответствует достижению максимальной плотности противоионов, допустимой с учетом эффектов исключенного объема, и дальнейшее утолщение слоя связано с условием электронейтральности. Очевидно, что чем меньше $\kappa {{r}_{{{\text{cyl}}}}}$, тем толще должен быть слой противоионов для выполнения условий электронейтральности, что и объясняет отрицательную корреляцию между $\kappa {{r}_{{{\text{cyl}}}}}$ и толщиной слоя. Поскольку уравнения МПБ учитывают конечность размеров ионов за счет дополнительного члена в знаменателе правой части, не удивительно, что МПБ теория предсказывает достижение максимальной концентрации ионов у поверхности. Интересно отметить, что аналитическое решение верно отражает достижение максимальной концентрации и образования слоя противоионов, и согласуется с численным решением касательно как самой концентрации, так и ширины слоя.
Рис. 8.
Распределение концентраций ионов ${{c}^{ \pm }}\left( {\kappa r} \right)$ внутри поры. Безразмерный потенциал поверхности $\psi _{{\text{s}}}^{*}$ меняется от 5 до 45; $\kappa {{r}_{{{\text{cyl}}}}} = 4$ (а, в) и $\kappa {{r}_{{{\text{cyl}}}}} = 8$ (б, г), $a = 4 \times {{10}^{{ - 10}}}{\text{\;м}}$. Результаты численных расчетов показаны символами, а результаты аналитических расчетов линиями. Объемная мольная доля соли $~c = 0.1\,\,{\text{M}}$.
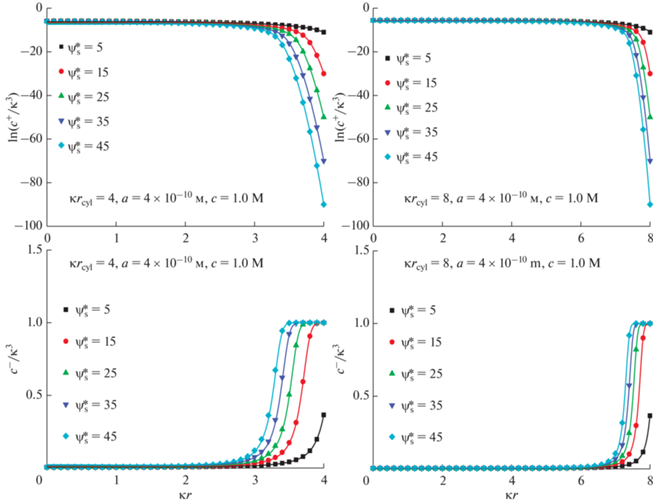
Рис. 9.
Распределение концентраций ионов ${{c}^{ \pm }}\left( {\kappa r} \right)$ внутри поры. Безразмерный потенциал поверхности $\psi _{{\text{s}}}^{*}$ меняется от 5 до 45; $\kappa {{r}_{{{\text{cyl}}}}} = 1.2$ (а, в) и $\kappa {{r}_{{{\text{cyl}}}}} = 2$ (б, г), $a = 5 \times {{10}^{{ - 10}}}{\text{\;м}}$. Результаты численных расчетов показаны символами, а результаты аналитических расчетов линиями. Объемная мольная доля соли $~c = 1\,\,{\text{M}}$.
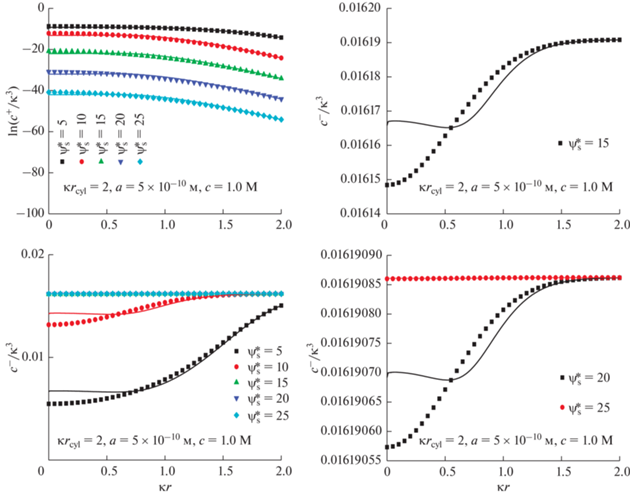
Рис. 10.
Распределение концентраций ионов ${{c}^{ \pm }}\left( {\kappa r} \right)$ внутри поры. Безразмерный потенциал поверхности $\psi _{{\text{s}}}^{*}$ меняется от 5 до 50; $\kappa {{r}_{{{\text{cyl}}}}} = 3$; $a = 5 \times {{10}^{{ - 10}}}\,\,~{\text{м}}$. Результаты численных расчетов показаны символами, а результаты аналитических расчетов линиями. Объемная мольная доля соли $~c = 1\,\,{\text{M}}$.
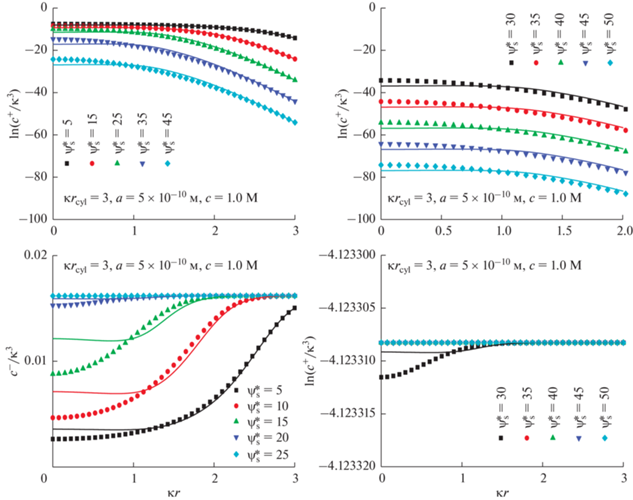
Рис. 11.
Распределение концентраций ионов ${{c}^{ \pm }}\left( {\kappa r} \right)$ внутри поры. Безразмерный потенциал поверхности $\psi _{{\text{s}}}^{*}$ меняется от 5 до 45; $\kappa {{r}_{{{\text{cyl}}}}} = 4$; $a = 5 \times {{10}^{{ - 10}}}{\text{\;м}}$. Результаты численных расчетов показаны символами, а результаты аналитических расчетов линиями. Объемная мольная доля соли $~c = 1\,\,{\text{M}}$.
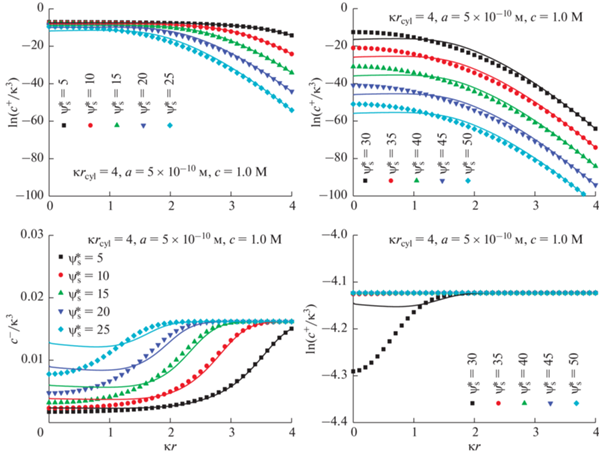
Рис. 12.
Распределение концентраций ионов ${{c}^{ \pm }}\left( {\kappa r} \right)$ внутри поры. Безразмерный потенциал поверхности $\psi _{{\text{s}}}^{*}$ меняется от 5 до 45; $\kappa {{r}_{{{\text{cyl}}}}} = 8$; $a = 5 \times {{10}^{{ - 10}}}{\text{\;м}}$. Результаты численных расчетов показаны символами, а результаты аналитических расчетов линиями. Объемная мольная доля соли $~c = 1\,\,{\text{M}}$.
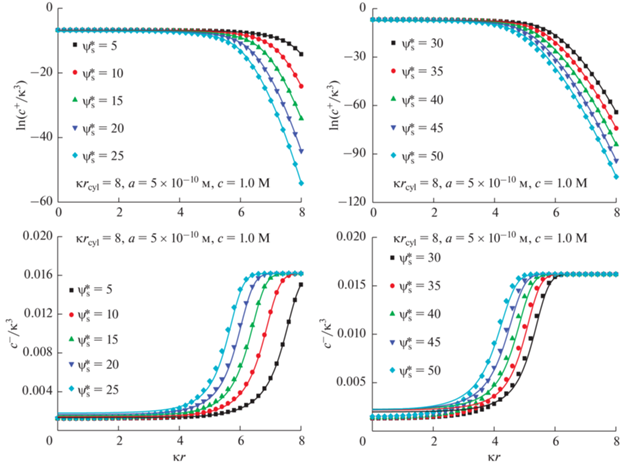
Рис. 13.
Заряжение поверхности поры как функция потенциала $\psi _{{\text{s}}}^{*}$ . $\kappa {{r}_{{{\text{cyl}}}}} = 1.2,~2,~4,~8~$, $a = 4 \times {{10}^{{ - 10}}}{\text{\;м}}$. Объемная мольная доля соли $~c = $ 0.025 (а), 0.1 (б), 0.4 (в), 1.2 М (г).
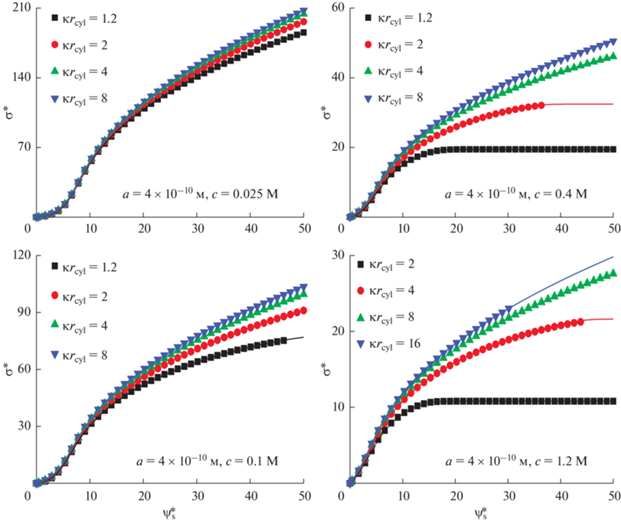
Поскольку аналитическое соотношение между σ* и $\psi _{{\text{s}}}^{*}~$ в рамках МПБ теории является очень точным, представляется возможным и интересным применить это выражение для анализа емкости и зависимости плотности запасенной энергии от потенциала электрода цилиндрической поры ионистора. С этой целью мы рассмотрим соответствующие выражения для удельной дифференциальной емкости ${{C}_{{\text{d}}}}~$ и плотности хранения энергии на единицу площади двойного электрического слоя ионистора $E$. Величину ${{C}_{{\text{d}}}}$ можно получить напрямую из аналитического соотношения σ* и $\psi _{{\text{s}}}^{*}~$:
Величина $E$ может быть получена из ${{C}_{{\text{d}}}}$ следующим образом:(23)
$E\left( U \right) = \mathop \smallint \limits_0^U {{C}_{{\text{d}}}}(\psi _{{\text{s}}}^{'}){\kern 1pt} \psi _{{\text{s}}}^{'}{\kern 1pt} d\psi _{{\text{s}}}^{'},$В этой работе мы исследовали влияние молярной концентрации соли $c$, размера $a$ и валентности $z$ на ${{C}_{{\text{d}}}}$ и $E$. Соответствующие результаты показаны ниже, для вычислений использовались относительная диэлектрическая проницаемость ${{\varepsilon }_{{\text{r}}}} = 7$ и абсолютная температура $T = {\text{298}}{\text{.15}}^\circ {\text{C}}$. В этих расчетах мы предполагали достаточно низкое значение ${{\varepsilon }_{{\text{r}}}}$, поскольку концентрация растворителя значительно меняется с напряжением (а именно падает при росте напряжения [78, 79]), что приводит к изменению значения ${{\varepsilon }_{{\text{r}}}}$. Этот эффект может быть весьма значителен для тонких пор и существенно снижает величину ${{\varepsilon }_{{\text{r}}}}$ для мелкопористых систем. Поэтому, для учета этого эффекта, мы берем малые величины ${{\varepsilon }_{{\text{r}}}}$.
Рис. 14.
Заряжение поверхности поры как функция потенциала $\psi _{{\text{s}}}^{*}$ . $\kappa {{r}_{{{\text{cyl}}}}} = 1.2,~2,~4,~8~$; $a = 2 \times {{10}^{{ - 10}}}{\text{\;}}$ (а) и $6 \times {{10}^{{ - 10}}}{\text{\;м}}$ (б). Объемная мольная доля соли $~c = 0.1\,\,{\text{M}}$.
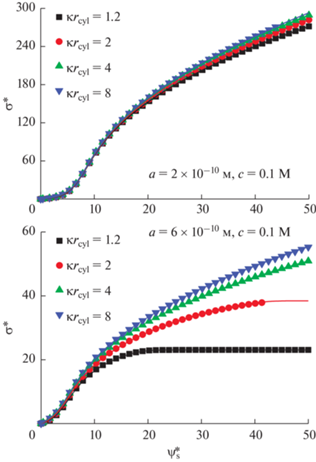
Рис. 15 показывает, что с ростом концентрации $c$ форма кривой ${{C}_{{\text{d}}}}$–U меняется от двугорбой к колоколообразной. Эти результаты согласуются с результатами моделирования [81] и CDFT расчетами [77–79]. Более того, были обнаружены два новых явления. Во-первых, максимальная плотность энергии ${{E}_{{{\text{sat}}}}}$ падает с ростом концентрации $c$. Объемная концентрация соли выступает основной движущей силой адсорбции ионов в пору, и с увеличением значения с адсорбция может происходить при меньших потенциалах электрода. С другой стороны, плотность энергии $E$, согласно уравнению (23), положительно коррелирует с потенциалом поверхности ${{\psi }_{{\text{s}}}}$. Соот-ветственно, это объясняет отрицательную корреляцию между $E$ и $c$. Также, поскольку адсорбция ионов становится легче при больших значениях $c$, пороговое значение потенциала электрода ${{U}_{{{\text{sat}}}}}$, при котором плотность хранения энергии достигает максимального значения, падает с ростом концентрации.
Рис. 15.
Кривые удельной дифференциальной емкости ${{C}_{{\text{d}}}}$ и емкости запасенной энергии $E$. Для пор с радиусом равным размерам ионов.
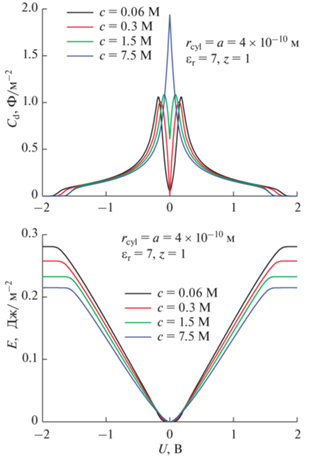
Во-вторых, существует область вблизи потенциала нулевого заряда, при котором плотность запасенной энергии Е близка к нулю, что указывает на чрезвычайно низкую ионную адсорбционную способность в этой области. Поскольку, как сказано выше, объемная концентрация соли играет роль движущей силы адсорбции ионов, становится понятным уменьшение ширины области нулевой энергии с ростом концентрации, т.е. плотность хранения энергии при том же напряжении электродов становится выше при росте $c$.
На рис. 16 показано влияние размеров ионов на ${{C}_{{\text{d}}}}$ и $E$ при двух различных концентрациях. Во-первых, практически отсутствует влияние концентрации на ${{C}_{{\text{d}}}}~$и $E$. Причиной этого может выступать тот факт, что эффект концентрации зависит от радиуса поры. Вследствие взаимосвязи адсобрции ионов и объемной концентрации соли, с повышением концентрации в порах растет избыток ионов. Очевидно, что чем меньше пора, тем более явно становится выражен эффект избыточности и, соответственно, ярче проявляется влияние концентрации.
Рис. 16.
Кривые удельной дифференциальной емкости ${{C}_{{\text{d}}}}$ и емкости запасенной энергии $E$ для пор с радиусом много больше размеров ионов. Объемная мольная доля соли $~c = 0.1\,\,{\text{M}}$ (а, в), $c = 1\,\,{\text{M}}$ (б, г).
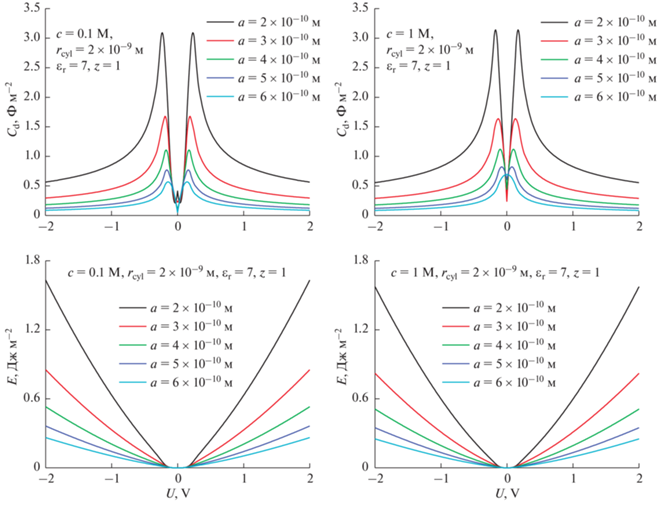
Во-вторых, в отличие от случая, проиллюстрированного на рис. 15, в котором максимальная плотность энергии ${{E}_{{{\text{sat}}}}}$ достигается задолго до того, как потенциал электрода достигнет 2 В, для пор большего размера плотность энергии при 2 В далека от ${{E}_{{{\text{sat}}}}}$. Это объясняется тем, что в большие поры может адсорбироваться больше ионов, требуется больший потенциал, чтобы удерживать эти ионы внутри пор, и величина порогового потенциала электрода ${{U}_{{{\text{sat}}}}}$ становится выше. Соответственно, величина ${{E}_{{{\text{sat}}}}}$ растет с увеличением размера пор.
В-третьих, увеличение размеров уменьшает плотность запасенной энергии. Это объясняется тем, что с ростом размера ионов меньшее их количество может разместиться внутри поры. Более того, для достижения той же плотности запасенной энергии для больших по размеру ионов требуется больший потенциал электродов. Это связано с тем фактом, что при том же количестве адсорбированных ионов ионам с большими размерами соответствует большая свободная энергия из-за сильного межионного отталкивания.
В-четвертых, величина ${{U}_{{{\text{sat}}}}}$ имеет тенденцию к уменьшению с увеличением размера иона, поскольку, при прочих равных, когда плотность запасенной энергии достигает ${{E}_{{{\text{sat}}}}}$, количество адсорбированных ионов тем меньше, чем больше размер иона.
На рис. 17 показано влияние валентности ионов z на ${{C}_{{\text{d}}}}~$ и $E$ для двух радиусов пор, ${{r}_{{{\text{cyl}}}}} = 1.5a$ и ${{r}_{{{\text{cyl}}}}} = 8a$. Анализ полученных данных позволяет сделать несколько выводов.
Рис. 17.
Кривые удельной дифференциальной емкости ${{C}_{{\text{d}}}}$ и емкости запасенной энергии $E$ для пор с радиусом ${{r}_{{{\text{cyl}}}}} = 6 \times {{10}^{{ - 10}}}~\,\,{\text{м}}$ (а, в) и ${{r}_{{{\text{cyl}}}}} = 3.2 \times {{10}^{{ - 10}}}~{\text{м}}$ (б, г). Объемная мольная доля соли $~c = 1\,\,{\text{M}}$.
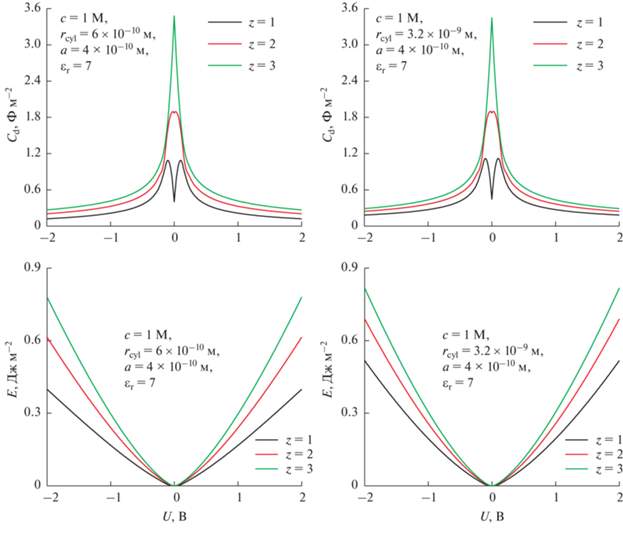
Во-первых, было обнаружено, что плотность запасенной энергии $E$ весьма чувствительна к валентности ионов. Более того, валентность положительно коррелирует с потенциалом электрода. Это объясняется тем, что с увеличением валентности ионов при одном и том же потенциале электрода растет заряд и, соответственно, плотность запасенной энергии $E$. Поскольку электростатические силы положительно коррелируют с произведением z и потенциала электрода, понятно, почему эффект z становится более ярко выраженным при увеличении потенциала электрода. Однако с увеличением валентности также растет и межионное электростатическое отталкивание, что затрудняет адсорбцию ионов. Поэтому для увеличения адсорбции необходимо повышать потенциал электрода, что следует из роста кривой ${{C}_{{\text{d}}}}~$при увеличении валентности.
Во-вторых, валентность иона существенно влияет на эффект размера пор. Большие поры способствуют повышению $E$, и наиболее выражен этот эффект при низкой валентности ионов. В то же время, хотя поры больших размеров могут вмещать больше ионов, чем мелкие, основной эффект увеличения запасаемой электрической энергии возникает за счет многовалентности иона.
Представлялось интересным рассмотреть предельный случай плоской поверхности в рамках уравнения (17). Когда радиус поры стремится к бесконечности $\kappa {{r}_{{{\text{cyl}}}}} \to \infty $, значение $\psi _{0}^{*}$, очевидно, стремится к нулю. Как показано на рис. 2, значение $C$ в этом случае также стремится к нулю и, более того, $\mathop {{\text{lim}}}\limits_{\kappa {{r}_{{{\text{cyl}}}}}{\kern 1pt} \to {\kern 1pt} \infty } \beta = \mathop {{\text{lim}}}\limits_{\kappa {{r}_{{{\text{cyl}}}}}{\kern 1pt} \to {\kern 1pt} \infty } \frac{{{{K}_{0}}\left( {\kappa {{r}_{{{\text{cyl}}}}}} \right)}}{{{{K}_{1}}\left( {\kappa {{r}_{{{\text{cyl}}}}}} \right)}} = 1$. В результате уравнение (17) сводится к
(24)
$\sigma {\kern 1pt} * = \pm 2\sqrt {\frac{1}{{2{{\phi }_{0}}}}\ln \left( {1 + 2{{\phi }_{0}}{{{\operatorname{sh} }}^{2}}\left( {\frac{{\psi _{{\text{s}}}^{*}}}{2}} \right)} \right)} ,$Уравнение (24) – это уравнение Грэма в рамках уравнений МПБ для заряженной плоскости. Интересно было сравнить уравнение (24) с уравнением Грэма в рамках классического подхода ПБ, которое для 25°С и раствора одновалентной (+1: –1) соли записывается в виде [82]:
(25)
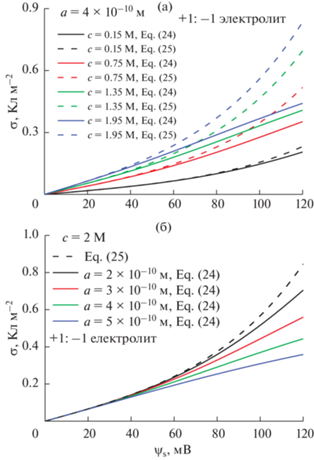
$\sigma = 0.117\sqrt c \operatorname{sh} \left( {\frac{{{{\psi }_{{\text{s}}}}}}{{51.4}}} \right),$Рис. 18.
Сравнение зависимости плотности поверхностного заряда $\sigma $ от потенциала поверхности $\psi _{{\text{s}}}^{*}$ в рамках ПБ и МПБ подходов для плоской заряженной поверхности, для различных концентраций (а) и различных размеров ионов (б). Рассматривается симметричный +1: –1 электролит при температуре 298.15 K.
ВЫВОДЫ
В представленной работе выведено приближенное аналитическое решение для модифицированного уравнения Пуассона-Больцмана, описывающего двойной электрический слой для симметричного +z/–z электролита внутри бесконечно длинной цилиндрической поры с однородно заряженными стенками. После проверки корректности аналитического решения оно было применено для анализа емкости и зависимости плотности запасенной энергии от потенциала электрода цилиндрической поры ионистора. По результатам анализа можно сделать следующие выводы.
1) В отличие от большинства имеющихся в литературе работ, в предложенном решении не предполагается, что потенциал в центре поры $\psi _{0}^{*}$ равен нулю. Значение потенциала может быть определено из условия электронейтральности. Хотя в решении используется корректирующий фактор $C$, величина $C$ зависит только от безразмерного радиуса поры $\kappa {{r}_{{{\text{cyl}}}}}$ и не зависит от потенциала поверхности. Поэтому использование этого фактора не усложняет решение, но повышает его точность. Для удобства использования в будущем, на рис. 2 приведена зависимость $C\left( {\kappa {{r}_{{{\text{cyl}}}}}} \right)$. Хотя предложенный подход плохо описывает поры с малыми, по сравнению с дебаевской длиной, радиусами, он позволяет с высокой точностью исследовать случаи, когда потенциал в центре поры не только не равен нулю, но и достаточно велик.
2) Полученное соотношение между плотностью поверхностного заряда σ * и поверхностным потенциалом $\psi _{{\text{s}}}^{*}$ оказывается очень близким к численному значению для всего интервала $\psi _{{\text{s}}}^{*}$ и $\kappa {{r}_{{{\text{cyl}}}}}$. Однако, согласие аналитических выражений для распределения потенциала $y\left( {\kappa r} \right)$ и концентрации ионов ${{c}^{ \pm }}\left( {\kappa r} \right)$ с численным расчетом оказывается хуже. В основном расхождения проявляются в центральной области поры при малых $\kappa {{r}_{{{\text{cyl}}}}}$ ($\kappa {{r}_{{{\text{cyl}}}}} < 2$). Для приповерхностных областей или при $\kappa {{r}_{{{\text{cyl}}}}} > 2$ хорошее согласие численных и аналитических результатов объясняется высокой точностью аналитического соотношения между плотностью поверхностного заряда и поверхностным потенциалом.
3) Анализ емкости и зависимости плотности запасенной энергии от потенциала электрода цилиндрической поры согласуется с имеющимися в литературе данными моделирования и расчетов в рамках классической теории функционала плотности. Кроме того, в этом анализе были получены следующие новые результаты. (а) Высокая концентрация соли $c$ снижает пороговый потенциал электрода ${{U}_{{{\text{sat}}}}}$, при котором достигается максимальная плотность запасенной энергии ${{E}_{{{\text{sat}}}}}$. С другой стороны, сама величина ${{E}_{{{\text{sat}}}}}$ снижается по мере роста концентрации. Влияние концентрации проявляется сильнее всего для пор с малым значением $\kappa {{r}_{{{\text{cyl}}}}}$. (б) Увеличение размера иона ведет к уменьшению значений ${{E}_{{{\text{sat}}}}}$ и ${{U}_{{{\text{sat}}}}}$. (в) Валентность иона положительно коррелирует с ${{E}_{{{\text{sat}}}}}$, чем больше валентность тем слабее ее эффект. (г) Пороговый потенциал электрода ${{U}_{{{\text{sat}}}}}$ зависит от нескольких факторов: объемной концентрации соли, размеров и валентности ионов, размера пор. В частности, ${{U}_{{{\text{sat}}}}}$ отрицательно коррелирует с объемной концентрацией соли и размером ионов и положительно с валентностью ионов и размером пор.
Список литературы
Kashiwagi Y., Nishio T., Ichikawa M.C., Shew Y., Umezawa N., Higuchi T., Sadakane K., Yoshikawa Y., Yoshikawa K. // Colloid Polym. Sci. 2019. V. 297. P. 397.
Kamenik A.S., Handle P.H., Hofer F., Kahler U., Kraml J., Liedl K.R. // J. Chem. Phys. 2020. V. 153. P. 185102.
Matsarskaia O., Da Vela S., Mariani A., Fu Z.D., Zhang F.J., Schreiber F. // J. Phys. Chem. B. 2019. V. 123. P. 1913.
Samukhina Y.V., Matyushin D.D., Polyakov P.A., Buryak A.K. // Colloid Journal. 2021. V. 83. P. 483.
Friedowitz S., Salehi A., Larson R.G., Qin J. // J. Chem. Phys. 2018. V. 149. P. 163335.
Portnov, I.V., Potemkin, I.I. // J. Phys. Chem. B. 2020. V. 124. P. 914.
Sabbatovskii, K.G., Sergeeva, I.P., Sobolev, V.D. // Colloid Journal. 2019. V. 81. P. 747.
Silkina, E.F., Asmolov, E.S., Vinogradova, O.I. // Phys. Chem. Phys. 2019. V. 21. P. 23036.
Penfold J., Thomas R.K. // J. Phys. Chem. B. 2020. V. 124. P. 6074.
Nikam R., Xu X., Kanduc M., Dzubiella J. // J. Chem. Phys. 2020. V. 153. P. 044904.
Duignan T.T., Zhao X.S. // J. Phys. Chem. C. 2019. V. 123. P. 4085.
Zhou S.// J. Phys. Chem. C. 2019. V. 123. P. 29638.
Lee H., Jin S., Yim S.// J. Phys. Chem. Solids. 2020. V. 138. P. 109264.
Singh A., Ojha A.K. // Chem. Phys. 2020. V. 530. P. 110607.
Yilmaz I., Gelir A., Yargi O., Sahinturk U., Ozdemir O.K. // J. Phys. Chem. Solids. 2020. V. 138. P. 109307.
Dolinnyi A.I. // Colloid Journal. 2019. V. 81. P. 642.
Frydel D. // J. Chem. Phys. 2019. V. 150. P. 194901.
Guerrero-Garcia G.I., Gonzalez-Tovar E., Chavez-Paez M., Wei T. // J. Mol. Liq. 2019. V. 277. P. 104.
Denton A.R., Alziyadi, M.O. // J. Chem. Phys. 2019. V. 151. P. 074903.
Okiyama Y., Watanable C., Fukuzawa K., Mochizuki Y., Nakano T., Tanaka S. // J. Phys. Chem. B. 2019. V. 123. P. 957.
Drab M., Gongadze E., Kralj-Iglic V., Iglic, A. // Entropy. 2022. V. 22. P. 1054.
Yu Y.K. // Phys. Rev. E. 2020. V. 102. P. 052404.
Buyukdagli S. // J. Phys. Chem. B. 2020. V. 124. P. 11299.
Bakhshandeh A., Santos A.P. dos, Levin Y. // J. Phys. Chem. B 2020. V. 124. P. 11762.
Hung H., Nguyen H.L., Huynh H.Q., Nguyen M.T. // Chem. Phys. 2018. V. 500. P. 26.
Stein C.J., Herbert J.M., Head-Gordon M. // J. Chem. Phys. 2019. V. 151. P. 224111.
Nikam R., Xu X., Kanduc M., Dzubiella J. // J. Chem. Phys. 2020. V. 153. P. 044904.
Dolinnyi A.I. // Colloid Journal. 2020. V. 82. P. 661.
Shavlov A.V., Dzhumandzhi V.A. // Phys. Lett. A. 2019. V. 383. P. 126030.
Okiyama Y., Watanable C., Fukuzawa K., Mochizuki Y., Nakano T., Tanaka S. // J. Phys. Chem. B. 2019. V. 123. P. 957.
Triandafilidi V., Hatzikiriakos S.G., Rottler J. // Soft Matt. 2020. V. 16. P. 1091.
Terao T. // Mol. Phys. 2020. e1831634 https://doi.org/10.1080/00268976.2020.1831634
Zhou S., Zhou R., Tian C. // J. Phys. Chem. Solids. 2021. V. 157. P. 110188.
Henderson D. // Fundamentals of Inhomogeneous Fluids. New York. Marcel Dekker, 1992.
Zhou S., Lamperski S., Sokołowska M. // J. Stat. Mech.-Theory E. 2017. Paper ID/ 073207.
Zhou S. // J. Stat. Phys. 2018. V. 170. P. 979.
Ras T., Szafarczyk M., Fuchs M. // Colloid Polym. Sci. 2020. V. 298. P. 803.
Zhou S., Zhou R. // Chinese J. Phys. 2021. V. 73. P. 391.
Zhou S., Lamperski S. // J. Phys. Chem. Solids. 2022. V. 161. P. 110440.
Lamperski S., Zhou S. // Microfluid Nanofluid. 2019. V. 23. P. 20.
Kiratidis A.L., Miklavcic S.J. // J. Chem. Phys. 2019. V. 150. P. 184502.
Shen G.L., Sun Y.H., Wang Y., Lu X.H., Ji X.Y. // J. Mol. Liq. 2020. V. 310. P. 113199.
Gillespie D., Khair A.S., Bardhan J.P., Pennathur S. // J. Colloid and Interface Sci. 2011. V.359. P. 520.
Medasani B., Ovanesyan Z. Thomas D.G., Sushko M.L., Marucho M. // J. Chem. Phys. 2014. V. 140. P. 204510.
Salerno K.M., Frischknecht A.L., Stevens M.J. // J. Phys. Chem. B. 2016. V. 120. P. 5927.
Zhou S. // J. Stat. Phys. 2017. V.169. P. 1019.
Zhou S. // J. Stat. Mech.-Theory E. 2019. Paper ID/033213.
Zhou S. // Mol. Phys. 2020. 118. https://doi.org/10.1080/00268976.2020.1778807
Samaj L., Trulsson M., Trizac E. // Phys. Rev. E. 2020. V. 102. P. 042604.
Zhou S. // J. Stat. Mech.-Theory E. 2020. Paper ID/073210.
Samaj L. // J. Stat. Phys. 2020. V. 181. P. 1699. https://doi.org/10.1007/s10955-020-02642-9
Goulding D., Hansen J.P., Melchionna S. // Phys. Rev. Lett. 2000. V. 85. P. 1132.
Yang G., Prasianakis N.I., Churakov S.V. // 2020. V. 68. P. 100.
Chenn I., Sigal I.M. // J. Stat. Phys. 2020. V. 180. P. 954.
Brown M.A., Bossa G.V., May S. // Langmuir. 2015. V. 31. P. 11477.
Daniels L., Scott M., Miskovic Z.L. // J. Chem. Phys. 2017. V. 146. P. 094101.
Borukhov I., Andelman D., Orland H. // Phys Rev. Lett. 1997. V. 79. P. 435.
Bhuiyan L.B., Outhwaite C.W., Henderson D. // J. Chem. Phys. 2005. V. 123. P. 034704.
Ohshima H. // Colloid Polym. Sci. 2019. V. 297. P. 35.
Xie D. X., Audi S.H., Dash R.K. // J. Comput. Chem. 2020. V. 41. P. 218.
Woelki S., Kohler H.H. // Chem. Phys. 2000. V. 261. P. 411.
Woelki S., Kohler H.H. // Chem. Phys. 2000. V. 261. P. 421.
D’yachkov L.G. // Phys. Lett. A. 2005. V. 340. P. 440.
Zhang W.Y., Wang Q.W., Zeng M., Zhao C.L. // Colloid Polym. Sci. 2018. V. 296. P. 1917.
Adar R.M., Andelman D. // Europ. Phys. J. E. 2018. V. 41. P. 11.
Tuinier R. // J. Colloid and Interface Sci. 2003. V. 258. P. 45.
D’yachkov L.G. // Technical Phys. Lett. 2005. V. 31. P. 204.
Tseng S., Jiang J.M., Hsu J.P. // J. Phys. Chem. B. 2005. V. 109. P. 8180.
Liu G.Z., Luo G.X. // Colloid Journal. 2013. V. 75. P. 565.
Murray H. // Solid-State Electronics. 2009. V. 53. P. 107.
Ohshima H. // Colloid Polym. Sci. 2018. V. 296. P. 647.
Tellez G., Trizac E. // J. Stat. Mech.-Theory E., 2016, Paper ID/P06018.
Tellez G., Trizac E. // J. Chem. Phys. 2019. V. 151. P. 124904.
Saboorian-Jooybari H., Chen Z.X. // Chem. Phys. 2019. V. 522. P. 147.
Djebbara L., Habchi M., Boussaid A. // Canadian J. Phys. 2019. V. 97. P. 656.
Mazzone V., Melchionna S., Marconi U.M.B. // J. Stat. Phys. 2015. V. 158. P. 1181.
Zhou S. // J. Stat. Mech.-Theory E. 2018, Paper ID/103203.
Zhou S. // Physica A. 2019. V. 533. P. 121905.
Zhou S. // J. Phys. Chem. Solids. 2021. V. 148. P. 109705.
White L.R. // J. Chem. Soc. Faraday Trans. 1977. V. 273. P. 577.
Bhuiyan L.B., Lamperski S. // Mol. Phys. 2013. V. 111. P. 807.
Israelachvili J.N. // Intermolecular and Surface Forces. Academic Press, 2011.
Дополнительные материалы отсутствуют.
Инструменты
Коллоидный журнал


