Коллоидный журнал, 2022, T. 84, № 3, стр. 251-262
Агрегация частиц алмаза и графита в водных электролитах AlCl3. электрооптические исследования
О. С. Везо 1, А. В. Войтылов 1, В. В. Войтылов 1, М. П. Петров 1, *, А. А. Трусов 1
1 Санкт-Петербургский государственный университет, физический факультет
198504 Санкт-Петербург,
Ульяновская ул. 1, Петродворец, Россия
* E-mail: m.p.petrov@spbu.ru
Поступила в редакцию 31.01.2022
После доработки 02.04.2022
Принята к публикации 02.04.2022
- EDN: DHXEHG
- DOI: 10.31857/S0023291222030132
Аннотация
В публикации рассмотрены возможности электрооптического метода при исследовании коагуляции, протекающей с высокой скоростью. Представлены результаты исследования агрегации частиц в водных коллоидах алмаза и графита, содержащих электролит AlCl3. Проведен сравнительный анализ скорости агрегирования частиц алмаза и графита при низких значениях их электрокинетических потенциалов. Показано, что при малых значениях электрокинетического потенциала изменение его на несколько милливольт меняет устойчивость коллоидов алмаза и графита в несколько раз. Исследования показали, что в изоэлектрической точке скорость образования парных агрегатов у частиц графита в пять раз выше, чем у частиц алмаза при близких счетных концентрациях частиц. Это свидетельствует о существенных различиях структурных составляющих поверхности, частиц алмаза и графита, препятствующих агрегированию. С помощью электрооптического метода были измерены релаксационные зависимости электрооптических эффектов, отвечающие разным промежуткам времени после начала коагуляции коллоидов. По этим зависимостям определены функции распределения частиц и агрегатов из них по размерам и проведен анализ изменения этих функций в процессе коагуляции. Была продемонстрирована эффективность метода и его применимость для изучения кинетики коагуляции при быстром ее протекании.
ВВЕДЕНИЕ
В данной работе представлены результаты исследования кинетики коагуляции водных коллоидов алмаза и графита электрооптическим методом. Рассмотрены возможности этого метода при изучении коагуляции коллоидов, протекающей с высокой скоростью. Коллоиды, содержащие наноразмерные частицы алмаза и графита, представляют как научный, так и практический интерес [1–3]. Водные коллоиды алмаза обладают высокой устойчивостью, если $\zeta $-потенциал частиц выше +30 мВ или меньше –30 мВ [4, 5]. Однако потенциалы поверхности природных и искусственных алмазов могут заметно отличаться даже в одной и той же дисперсионной среде. Высокая адсорбционная способность частиц позволяет модифицировать их поверхность в широких пределах [6–9]. Наноразмерные частицы графита практически всегда образуются в процессах получения наноалмаза [10], но могут быть получены при использовании и иных технологий [11, 12]. Частицы графита обладают высокой адсорбционной способностью. Они также перспективны в технике, медицине и биологии [13, 14].
Водные коллоиды графита менее устойчивы, чем коллоиды алмаза даже при более высоких $\zeta $-потенциалах частиц. Представляет интерес сравнительный анализ агрегативной устойчивости коллоидов алмаза и графита при низких значениях $\zeta $-потенциала частиц, когда электростатические силы расталкивания частиц малы и велико влияние структурной составляющей их поверхности на скорость их агрегирования. Для такого анализа требуются методы, позволяющие быстро определять скорости коагуляции коллоидов и исследовать коллоиды с низкой концентрацией частиц. При исследовании коллоидов с низкой концентрацией частиц обычно используются методики, основанные на изучении рассеяния света коллоидами [15]. При изучении полидисперсных систем и определении размеров агрегатов используется метод динамического светорассеяния, так как он позволяет определять распределения частиц по размерам [16, 17]. Для более детального анализа характеристик рассеянного коллоидами света, которые меняются в процессе коагуляции, используeтся комбинированный метод, использующий особенности статического и динамического светорассеяния [18–20]. При исследовании кинетики образования агрегатов из частиц также применим электрооптический метод [21, 22].
В данной работе исследовались скорости образования парных агрегатов из частиц в водных коллоидах искусственного алмаза и графита в области изоэлектрической точки. Для изменения заряда поверхности частиц использован электролит AlCl3. Ранее данный электролит использовался при изучении коагуляции коллоида естественного алмаза при более высоких значениях электрокинетического потенциала частиц, когда скорость коагуляции невысока [23].
Коллоиды алмаза и графита обладают ярко выраженными электрооптическими свойствами [24], а время определения релаксационных зависимостей электрооптического эффекта, необходимых для определения распределений частиц и агрегатов из них по размерам, крайне мало. Это позволило провести исследования при высокой скорости образования агрегатов и изучать коллоиды при низких концентрациях частиц, когда расстояние между ними многократно превышает их размеры.
МЕТОДИКА ИССЛЕДОВАНИЙ И ОСНОВНЫЕ СООТНОШЕНИЯ
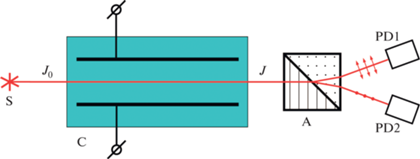
Коллоиды алмаза существенно рассеивают свет, а интенсивность и поляризация как рассеянного коллоидами, так и прошедшего сквозь них света, существенно меняются при изменении ориентационной упорядоченности частиц в них. Коллоиды графита рассеивают свет в меньшей степени, они содержат анизотропные частицы и тоже существенно меняют интенсивность и поляризацию рассеянного и прошедшего сквозь них света при ориентации частиц. По этой причине при исследовании коллоидов алмаза и графита было целесообразно использовать электрооптические эффекты, обусловленные поглощением и рассеянием света частицами [25]. Одна из оптических схем, удобных для электрооптических исследований в проходящем свете, представлена на рис. 1.
В кювете C, заполненной коллоидом, между плоскопараллельными электродами создается ориентационная упорядоченность частиц электрическим полем. Луч белого неполяризованного света от источника S проходит сквозь кювету, делится поляризатором A на два, поляризованных вдоль и перпендикулярно полю, и регистрируется фотоприемниками PD1 и PD2. Изменения интенсивности лучей, падающих на фотоприемники, можно отнести к двум разным эффектам, зависящему и независящему от их поляризации.
Первый эффект, который можно наблюдать с помощью приведенной оптической схемы, – это дихроизм. Он связан с влиянием поляризации падающего света на его ослабление коллоидом, в котором частицы имеют преимущественную ориентацию. Его величина определяется соотношением
Здесь ${{J}_{{||}}}$ и ${{J}_{ \bot }}$ – интенсивности прошедшего сквозь коллоид света и поляризованного параллельно и перпендикулярно электрическому полю, создающему ориентационную упорядоченность частиц, $J$ – интенсивность прошедшего света, когда коллоид изотропен, а частицы в нем ориентированы хаотично. Для коллоида алмаза дихроизм связан с рассеянием света частицами, а для частиц графита как с рассеянием, так и с его поглощением, что подтверждается результатами рентгеноструктурного анализа, приведенными ниже. В случае дихроизма, обусловленного анизотропией поглощения света, относительные изменения интенсивности прошедшего света, поляризованного параллельно и перпендикулярно падающему свету, возникающие при ориентации частиц, имеют противоположные знаки и отличаются по величине в два раза [26]. В случае рассеяния это не так и при ориентации частиц появляется изменение прошедшего света, не зависящее от его поляризации $\Delta J$. Общее соотношение, справедливое как для поглощающих, так и рассеивающих свет коллоидов можно представить в видеЕсли рассеяние коллоидом света мало по сравнению с его поглощением, то можно полагать, что $\Delta J = 0$. Изменение интенсивности $\Delta J$ рассеянного света также пренебрежимо мало в рассеивающих свет коллоидах, если частицы существенно меньше длины волны падающего света. Второй эффект обусловлен относительным изменением неполяризованной компоненты прошедшего света. Учитывая (2), его можно представить соотношением
(3)
$A \equiv \frac{{\Delta J}}{J} = \frac{1}{3}\frac{{{{J}_{{||}}} - J}}{J} + \frac{2}{3}\frac{{{{J}_{ \bot }} - J}}{J}.$Релаксационную зависимость дихроизма $N$ в полидисперсном коллоиде, содержащем как частицы, так и агрегаты из них, можно представить соотношением [27]
где ${{D}_{r}}(r) = \frac{{{{k}_{{\text{B}}}}T}}{{8\pi \eta {{r}^{3}}}}$.Здесь $\varphi (r)$ – функция распределения частиц и агрегатов из них по размерам $r$, $\Delta K$ – дихроический вес, $\eta $ – вязкость дисперсионной среды, ${{k}_{{\text{B}}}}$ – постоянная Больцмана, $T$ – температура. Так как ${{D}_{r}}$ – это константа вращательной диффузии, то $r$ – это гидродинамический радиус. Среднее значение константы вращательной диффузии
определяет характерное время $\tau $ релаксации электрооптического эффекта, увеличивающееся при образовании агрегатов. Из соотношения (4) следует Здесь ${{N}_{{\max }}}$ – максимальное значение эффекта $N$, соответствующее полной ориентации частиц и агрегатов вдоль поля. Оно может быть измерено и определяется соотношениемДля описания эффекта $A$ достаточно в соотношениях (4)–(6) заменить $N$ на $A$, а дихроический вес $\Delta K$ на оптический вес эффекта $A$, определяющий вклад частиц размера $r$ в эффект $A{{\,}_{{\max }}}$, наблюдаемый при полной ориентации частиц и агрегатов вдоль поля. Для определения функции распределения $\varphi (r)$ следует экспериментально определить релаксационную зависимость $N(t)$ и решить уравнение (4) относительно функции $f(r) = \Delta K\varphi (r)$ [28]. Дихроический вес $\,\Delta K$ зависит как от поперечного сечения частиц при их полной ориентации, так и отношения размеров частиц к длине волны падающего света [29]. В случае белого света можно приближенно считать, что для слабо вытянутых частиц алмаза $\,\Delta K$ меняется пропорционально квадрату размера частиц – ${{r}^{2}}$, а для плоских частиц графита – пропорционально квадрату размера частицы в плоскости.
Для проведения электрооптических исследований была собрана экспериментальная установка, оптическая часть которой соответствовала схеме, изображенной на рис. 1. Источником света S служил светодиод белого света, фотоприемниками ‑ PD1 и PD2 (фотодиоды). В качестве кюветы C использована ячейка Керра, а поляризатора A ‑ призма Волластона. Для создания поля в кювете использовался генератор, который вырабатывал импульсы электрического поля с заданными частотой, длительностью и величиной. По измеряемым с помощью фотоприемников значениям интенсивностей света ${{J}_{{||}}}$, ${{J}_{ \bot }}$ и $J$ в разные моменты времени и при разных величинах поля с помощью платы сбора данных определялись относительные изменения интенсивности обоих лучей $({{J}_{{||}}} - J){\text{/}}J$ и $({{J}_{ \bot }} - J){\text{/}}J$, а также временн${\text{ы}}'$е и полевые зависимости электрооптических эффектов $N$ и $A$, согласно формулам (1) и (3).
Для каждой исследованной коллоидной системы определялся ${{\zeta }}$-потенциал частиц. В области изоэлектрической точки частицы могут иметь заряд поверхности разного знака, и быстро коагулируют. Это требует измерений электрофоретической скорости отдельных частиц за малый промежуток времени. Для таких измерений была использована микро-электрофоретическая методика. Экспериментальная установка содержала микро-электрофоретическую ячейку с платиновыми электродами. Частицы алмаза, хорошо рассеивают свет, и можно было следить за их движением в темном поле микроскопа при помощи камеры на экране монитора, если их размеры 50 нм и более. Для проведения измерения более высоких значений $\zeta $-потенциала использовался Malvern Zetasiser (MADLS).
КОЛЛОИДЫ ДЛЯ ИССЛЕДОВАНИЙ
Коллоды алмаза и графита, как правило, полидисперсны. Для проведения электрооптических исследований кинетики коагуляции в них должна быть четко выраженная граница наименьших размеров частиц. Это необходимо для того, чтобы определить область размеров, в которой изменение наблюдаемых эффектов связано с изменением концентрации только частиц, а не их агрегатов, имеющих те же размеры. Также в исследуемом коллоиде не должно быть частиц больших размеров, концентрация которых может существенно измениться за время эксперимента по причине седиментации.
При получении коллоидных систем алмаза для исследований в качестве дисперсной фазы был использован коммерческий порошок с частицами размерами от нескольких нанометров до микрона фирмы “Сапфир”, полученный методом статического синтеза при высоких давлениях и температурах. Освобождение частиц от примесей и отмывка их поверхности проводились стандартными методами, включающими отстаивание (до 3 сут), центрифугирование (до 8000 g, время воздействия до 60 мин) и ультразвуковую обработку в водяной ванне (мощность 200 Вт, частота 22 кГц, длительность воздействия до 10 мин). Снимок частиц, полученный с использованием сканирующего электронного микроскопа представлен рис. 2, слева.
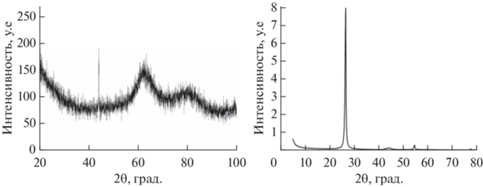
Согласно данным электронно-микроскопических исследований, корреляции между размерами и формой частиц не наблюдалось, и в электрооптических исследованиях их форму можно аппроксимировать эллипсоидами вращения. Для большинства частиц отношение наибольшего размера частиц к усредненному в перпендикулярном направлении, оно же отношение полуосей эллипсоидов, лежало в интервале 1.2–1.6. Многократными центрифугированием и ультразвуковой обработкой область размеров частиц была сужена до диапазона 100–500 нм. Контроль размеров производился по электронно-микроскопическим снимкам. Счетная доля частиц с размерами менее 100 нм не превышала 10%, а средний объем частицы в приготовленной для исследований дисперсной фазе, измеренный электронно-микроскопически, составил 2.3 × 10–14 см3. Базовая коллоидная система, используемая при исследованиях, содержала частицы полученной дисперсной фазы, взвешенные в дистиллированной воде. Добавление частиц к дистиллированной воде практически не меняло электропроводность системы, что свидетельствовало о низкой концентрации ионов на поверхности частиц. Был проведен рентгеноструктурный анализ состава частиц. Дифрактограмма рентгеноструктурного анализа, выполненая XRD-методом представлена на рис. 3, слева.
Кристаллической структуре алмаза соответствует пик, наблюдаемый под углом 2θ = 43.8° (111). Два других пика, свойственных алмазной кристаллической решётке (220 и 311), должны наблюдаться при 2θ = 75.2° и 2θ = 91.1° Они слегка смещены в область меньших углов и размыты, что свидетельствует о наличии поликристаллических структур в частицах. Согласно дифрактограмме, других форм углерода в частицах не было обнаружено.
Для получения коллоидных систем графита использованы частицы, полученные при распылении графитового анода в электрической дуге. Частицы графита сохранялись в смеси с частицами бентонита в лигносульфоновой кислоте с целью предотвращения их слипания. При получении дисперсной фазы графита, не содержащей частиц бентонита и других примесей, также как и в случае алмаза использовались отстаивание в воде, центрифугирование и ультразвуковая обработка. Для очистки поверхности частиц использовалось прокаливание дисперсной фазы графита при температуре более 500° в течение часа. Электронно-микроскопические исследования показали, что частицы имеют форму пластинок. Один из снимков представлен на рис. 2, справа. При высушивании на кварцевой подложке частицы графита также образуют агрегаты фрактального типа. У основной доли частиц, полученной дисперсной фазы, после центрифугирования размеры в плоскости частицы лежали в диапазоне от 100 до 500 нм. Доля частиц с размерами менее 100 нм не превышала 5–7%. При определении толщины частиц производилось их напыление платиной на кварцевой подложке под малым углом (7°), затем по электронно-микроскопическим снимкам измерялась длина тени частицы и рассчитывалась еe толщина. В электрооптическом эксперименте форма частиц аппроксимирована сплюснутыми эллипсоидами вращения, отношение полуосей которых не превышало 0.1. Средний объем частиц полученной дисперсной фазы графита составлял 1.9 × 10–14 см3 . Рентгеноструктурный анализ показал, что частицы содержали две полиморфные модификации графита. Основную долю составляла модификация 2H (2θ = 26.5°). В небольшом количестве также присутствовала модификация 3R (2θ = 42.3° и 2θ = = 54.5°). XRD-дифрактограмма дисперсной фазы графита представлена на рис. 3, справа. Базовая коллоидная система графита получалась, также как и базовая системы алмаза, удалением крупных и мелких частиц добавлением дисперсной фазы к воде, перемешиванием и ультразвуковой обработкой.
Для изучения состава поверхности частиц алмаза и графита в воде были выполнены исследования комбинационного рассеяния их базовых систем при длине волны падающего света 532 см. При исследовании системы алмаза на фоне спектра, свойственного водной дисперсионной среде, в которой взвешены частицы, можно выделить 3 пика (1332, 1430 и 1635 см–1), характеризующих частицы алмаза и их поверхность. Пик 1332 см–1 типичен для объемного алмаза пространственной группы ${\text{O}}_{h}^{7}$. Остальные пики отвечают молекулярным группам на поверхности частиц. Пик 1635 см–1 характерeн для деформационных поступательных и вращательных колебаний молекул ${{{\text{H}}}_{{\text{2}}}}{\text{O}}$. Пик 1430 см–1 слабо выражен и отвечает малой доле аморфной структуры углерода. Положение пиков отмечено на спектре интенсивности комбинационного рассеяния на рис. 4, слева.
Рис. 4.
Спектральные линии комбинационного рассеяния частиц алмаза (слева) и графита (справа) в воде.
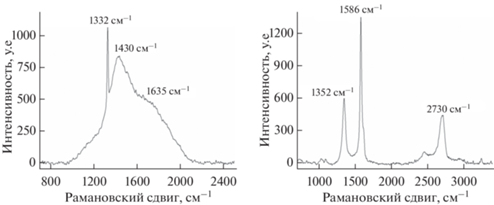
На рис. 4, справа, представлен разностный спектр комбинационного рассеяния базовой системой графита. Он характеризует как поверхность, так и приповерхностные слои частиц графита, так как они существенно поглощают свет. В спектре присутствуют основная линия, первого порядка, G (1586 см–1), линия второго порядка 2D (2713 см–1) и линия D1 (1357 см–1), соответствующая дефектам структуры графита. Отношение G/2D = 2.24. Высокое значение этого отношения можно объяснить небольшими добавками оксида углерода на поверхности частиц. При исследовании тонкой структуры линии D1 функциональных поверхностных групп также не было выявлено.
Для проведения исследования коагуляции были получены коллоидные системы с заданными концентрациями как частиц, так и электролита. Базовые системы алмаза и графита разбавлялись дистиллированной водой и к ним добавлялся водный раствор AlCl3. Концентрация Al-Cl3 во всех исследованных коллоидах не превышала 1 × 10–4 моль/л, объемная доля частиц алмаза была менее 0.01%, а графита менее 0.001%. При определении объемных долей $\Delta V{\text{/}}V$ и числа частиц в единице объeма $n$ измерялись плотности коллоидных систем и входящих в них электролитов с точностью 1 × 10–6 г/см3. При определении плотности использован плотномер DMA-5000. Для определения объемной доли частиц использовано соотношение
Здесь: $m$ – масса дисперсной фазы, $\Delta V$ и $V$ – объемы частиц и коллоидной системы, соответственно, ${{\rho }_{A}}$, $\rho $ и ${{\rho }_{0}}$ – плотности частиц, системы и электролита соответственно. Для плотности ${{\rho }_{A}}$ частиц использованы табличные данные плотности алмаза и графита. Величина $n$ равна отношению объемной доли частиц $\Delta V{\text{/}}V$ к среднему объему частицы $b$. Для еe определения, учитывая (7), можно использовалось соотношение(8)
$n = \frac{{\Delta V}}{V}\frac{1}{b} = \frac{1}{b}\frac{{\rho - {{\rho }_{0}}}}{{{{\rho }_{C}} - {{\rho }_{0}}}}.$Полученные таким образом коллоидные системы встряхивались и подвергались ультразвуковой обработке. Эти процедуры периодически повторялись с целью предотвращения образования агрегатов до начала исследований кинетики коагуляции.
РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ И ИХ ОБСУЖДЕНИЕ
Были проведены электрооптические исследования влияния скoрости образования парных агрегатов из частиц алмаза и графита при низких значениях $\zeta $-потенциала, значение которого варьировалось изменением концентрации AlCl3 в водных коллоидах. Кривые релаксации электрооптических эффектов $N(t)$ и $A(t)$ без добавления AlCl3 представлены на рис. 5.
Рис. 5.
Релаксационные зависимости эффектов $N$ (сплошная ) и $A$ (пунктир) коллоидов алмаза (слева) и графита (справа).
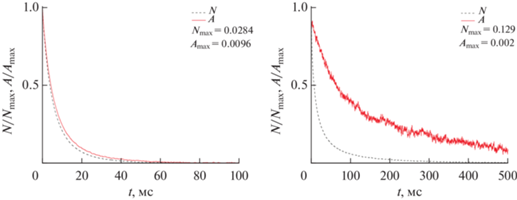
Как можно видеть для изотропных частиц алмаза, не поглощающих свет, эффект $A$, обусловленный неполяризованной компонентой изменения прозрачности коллоида сопоставим по величине с эффектом $N$, обусловленным влиянием поляризации на интенсивность проходящего сквозь коллоид света. А именно, ${{A}_{{\max }}}{\text{/}}{{N}_{{\max }}} = 0.34$. Это свидетельствует о высокой степени деполяризации рассеянного частицами алмаза света. Так как кривые $N(t)$ и $A(t)$ близки по форме, то эффект $A$, следует учитывать также как и эффект $N$, при электрооптических исследованиях как больших, так и малых частиц алмаза. Для коллоида графита ${{A}_{{\max }}}{\text{/}}{{N}_{{\max }}} = 0.016$, а время релаксации эфекта $A$ существенно выше времени релаксации эффекта $N$. Это указывает на то, что эффект $A$ крайне мал и создается только крупными частицами, размеры которых близки к длинам волн падающего света, и превышают их. Зависимости $N(t)$ были использованы для определения функций распределения $f(r)$ частиц алмаза и графита по размерам $r$ с дихроическим весом $\Delta \,K$. Они были определены как численное решение уравнения (4) [30]. Так как исследования проводились в белом свете, то при определении истинных функций распределения частиц по размерам $\varphi (r)$ полагалось что $\Delta K$ меняется пропорционально ${{r}^{2}}$. Функции $f(r)$ и $\varphi (r)$ для частиц алмаза и графита представлены на рис. 6.
Рис. 6.
Функции $f(r)$ (сплошная) и $\varphi (r)$ (пунктир) для коллоидов алмаза (слева) и графита (справа).
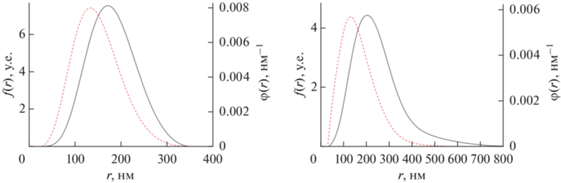
Для того, чтобы перейти от гидродинамических радиусов частиц $r$ к их геометрическим размерам, необходимо учитывать форму частиц. Если аппроксомировать частицы алмаза вытянутыми эллипсоидами вращения со средним отношением полуосей 1.5, то, учитывая влияние формы частиц на их константу вращательной диффузии [31], при определении больших полуосей эллипсоида $a$ можно использовать приближенное соотношение $R = 1.3r$. Для частиц графита, полагая что большая полуось $a$ эллипсоида вращения лежит в плоскости частицы, а отношение полуосей 0.1, можно использовать приближенное соотношение $R = 1.6r$. Необходимо учитывать, что даже в устойчивых коллоидах, к которым не добавлялись электролиты, малая доля (3–5)% частиц образуют агрегаты. Рассчитанные при использовании полученных функций $\varphi (r)$ значения средних объемов частиц составили $b = 2.8\,\, \times \,\,{{10}^{{ - 14}}}{\text{ с}}{{{\text{м}}}^{3}}$ для частиц алмаза и $b = 2.2\,\, \times \,\,{{10}^{{ - 14}}}{\text{ с}}{{{\text{м}}}^{3}}$ для частиц графита. Эти значения превышают средние объемы частиц, определенные при помощи электронного микроскопа, на 22% для частиц алмаза и на 16% для частиц графита. Полученные расхождения подтверждают существование агрегатов в коллоидах, которые не удается разрушить ультразвуковой обработкой. При изучении коагуляции такие агрегаты можно считать частицами. Также следует учитывать, что на результаты определения $b$ могла влиять неточность определения отношения полуосей эллипсоидов, которыми заменялись частицы при расчетах.
Для исследования влияния ионов на скорость агрегирования были приготовлены водные коллоиды: алмаза с объемной долей частиц $\Delta V{\text{/}}V = 1.1\,\, \times \,\,{{10}^{{ - 5}}}$ и графита объемной долей частиц $\Delta V{\text{/}}V = 1.0\,\, \times \,\,{{10}^{{ - 5}}}$. Эти значения рассчитывались по формуле (7). Значения плотностей коллоидов $\rho $ и ${{\rho }_{0}}$ электролитов определялись экспериментально, а плотности частиц ${{\rho }_{A}}$ для алмаза и графита считались равными 3.50 и 2.23 г/см3, соответственно. Рассчитанные по формуле (8) значения $n$ составили $0.39 \times {{10}^{9}}\,\,{\text{с}}{{{\text{м}}}^{{ - 3}}}$ для частиц алмаза и $0.45\,\, \times \,\,s{{10}^{9}}\,\,{\text{с}}{{{\text{м}}}^{{ - 3}}}$ для частиц графита. При определении $n$ использовались значения $b$, определенные электрооптическим методом. При таких концентрациях частиц рассеяние света частицами однократное, а величина электрооптических эффектов пропорциональна концентрации частиц. Значения $\zeta $-потенциала частиц графита и алмаза в таких системах составляли –56 и –37 мВ соответственно. Малые концентрации электролита AlCl3, содержащего катионы высокой валентности, позволяли менять $\zeta $-потенциал частиц, оставляя электропроводность коллоидных систем низкой. Это позволяло проводить электрооптические исследования, при которых изменения температуры коллоидных систем не превышали $ \pm \,0.5$°С. Ниже представлены результаты исследований при пяти концентрациях электролита, отвечающих низким значениям $\zeta $-потенциала частиц. Значения $\zeta $-потенциала частиц при этих концентрациях электролита, а также рН и электропроводности К коллоидных систем представлены в Табл. 1 и 2. Значения рН и К определялись лабораторными ph-метром (Hanna HI98127) и кондуктометром (Hanna HI98308). При расчете $\zeta $-потенциала частиц по электрофоретической подвижности использвана формула Смолуховского. Так как концентрация ионов в коллоидах была низкая, то значения дебаевского радиуса экранирования сопоставимы с размерами частиц. По этой причине коэффициент Генри не учитывался, так он для частиц разных размеров в полидисперснных коллоидах разный.
Таблица 1.
Коллоиды алмаза при 20°С
| ${{C}_{{{\text{AlC}}{{{\text{l}}}_{{\text{3}}}}}}} \times {{10}^{6}}{\text{, моль/л}}$ | $\zeta $, мВ | pH | $K \times {{10}^{6}}{\text{, С/см}}$ |
|---|---|---|---|
| 1.0 | –15.5 | 6.47 | 0.7 |
| 2.0 | –8.3 | 6.37 | 1.0 |
| 5.0 | $ \pm $0.5 | 6.16 | 2.1 |
| 10.0 | +9.1 | 6.06 | 3.1 |
| 20.0 | +9.5 | 5.84 | 6.2 |
Таблица 2.
Коллоиды графита при 20°С
| ${{C}_{{{\text{AlC}}{{{\text{l}}}_{{\text{3}}}}}}} \times {{10}^{6}}{\text{, моль/л}}$ | $\zeta $, мВ | pH | $K \times {{10}^{6}}{\text{, С/см}}$ |
|---|---|---|---|
| 1.0 | –40 | 6.37 | 1.6 |
| 4.0 | –2.8 | 6.14 | 2.4 |
| 6.0 | $ \pm $0.5 | 6.10 | 2.7 |
| 10.0 | +4.1 | 6.00 | 3.8 |
| 15.0 | +8.3 | 5.97 | 4.1 |
При образовании парных агрегатов скорость уменьшения концентрации отдельных частиц $n$ и увеличения концентрации парных агрегатов ${{n}_{p}}$ взаимосвязаны и определяются соотношениями [32]
(9)
$ - \frac{{dn}}{{d{{t}_{C}}}} = k{{n}^{2}}{\text{ и }}\frac{{d{{n}_{p}}}}{{d{{t}_{C}}}} = \frac{k}{2}{{n}^{2}},$Рис. 7.
Зависимости $\tau $ от ${{t}_{C}}$ для коллоидов алмаза (слева) и графита (справа) с добавками AlCl3.
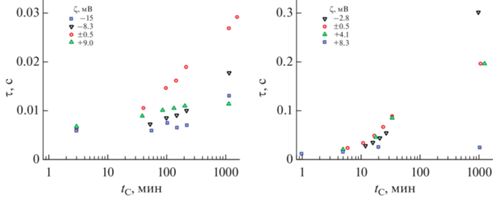
Как можно видеть из рисунка, скорости коагуляции коллоида алмаза на ранних еe этапах близки, когда частицы имеют $\zeta = - 8.3$ мВ и $\zeta = + 9.0$ мВ, и существенно отличаются от скорости коагуляции коллоида в изоэлектрической точке. Это указывает на то, что константа скорости коагуляции $k$ слабо зависит от знака заряда поверхности, но существенно зависит от потенциала поверхности даже при малых его значениях. У коллоида графита наблюдаются те же закономерности, но наблюдается более сильное влияние величины $\zeta $-потенциала на устойчивость коллоида графита, чем для коллоида алмаза. Так коллоид графита резко повышает устойчивость, если $\zeta $-потенциал частиц возрастает от $\zeta = + 4.1$ мВ до $\zeta = + 8.3$ мВ. Это связано с тем, что частицы графита имеют более тонкую гидратную оболочку, чем частицы алмаза.
Более детальное исследование кинетики коагуляции было проведено для коллоидов при концентрациях электролита, отвечающих изоэлектрической точке. Если $a$ – размер самых малых частиц, то можно полагать, что в области размеров $a < r < 2a$ доля агрегатов пренебрежимо мала. Число частиц в этой области размеров пропорционально вносимому ими вкладу в наблюдаемый электрооптический эффект. Согласно теории коагуляции, в области изоэлектрической точки, влияние размеров частиц на вероятность образования ими агрегатов пренебрежимо мало, а функции $\varphi (r)$ и$f(r)$, меняясь при коагуляции, должны оставаться подобными самим себе в области размеров $a < r < 2a$. Из этого следует, что если нормировка $f(r)$ определяется соотношением (6), то
Учитывая уравнение (9), зависимость отношения $\,{n \mathord{\left/ {\vphantom {n {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}}$ от времени ${{t}_{C}}$ также можно представить в виде
Таким образом, экспериментально определяя отношение функций $f(r){\text{/}}{{f}_{0}}(r)$, можно рассчитать период коагуляции ${{T}_{C}} = \frac{1}{{k{{n}_{0}}}}$.
Для коллоидов алмаза и графита в изоэлектрической точке были определены релаксационные кривые $N(t)$, отвечающие разным промежуткам времени ${{t}_{C}}$. Эти зависимости а также рассчитанные по ним функции распределения $f(r)$ представлены на рис. 8 и 9.
Рис. 8.
Релаксационные зависимости $N(t)$ и расчитанные по ним функции $f(r)$ частиц алмаза в водном электролите AlCl3 при $\zeta = 0$.
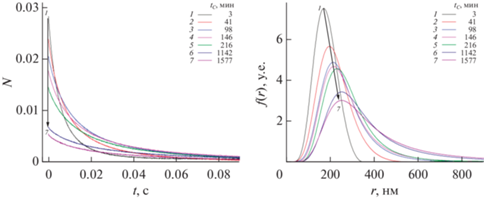
Рис. 9.
Релаксационные зависимости $N(t)$ и расчитанные по ним функции $f(r)$ частиц графита в водном электролите AlCl3 при $\zeta = 0$.
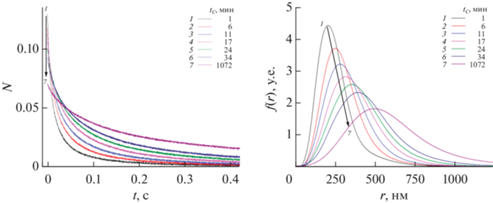
Размеры $a$ наименьших частиц были близки к 50 нм как для алмаза, так и графита. В области размеров $r$ от 50 до до 100 нм функции $f(r)$ оставались подобными (за исключением $f(r)$ при ${{t}_{C}} = 1072\,\,{\text{мин}}$), а отношение $f(r){\text{/}}{{f}_{0}}(r)$ в этой области размеров не зависело от $r$ и определялось только временем ${{t}_{C}}$ как для коллоидов алмаза, так и графита. По экспериментальным зависимостям $\,{n \mathord{\left/ {\vphantom {n {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}}$ от ${{t}_{C}}$, для коллоидов алмаза и графита были рассчитаны значения констант скоростей и периоды коагуляции. Для коллоида алмаза $k = 0.63\,\, \times \,\,{{10}^{{ - 12}}}{\text{ с}}{{{\text{м}}}^{3}}{\text{ }}{{{\text{с}}}^{{ - 1}}}$ и ${{T}_{C}} = 68\,\,{\text{мин}}$, а для коллоида графита $k = 3.1\,\, \times \,\,{{10}^{{ - 12}}}{\text{ с}}{{{\text{м}}}^{{\text{3}}}}{\text{ }}{{{\text{с}}}^{{ - 1}}}$ и ${{T}_{C}} = 12\,\,{\text{мин}}$. Зависимости $\,{n \mathord{\left/ {\vphantom {n {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}} - 1$ от ${{t}_{C}}$, определенные экспериментально а также рассчитанные по формуле (10) при этих значениях ${{T}_{C}}$, представлены на рис. 10.
Рис. 10.
Зависимости отношения ${{n}_{0}}{\text{/}}n$ от времени ${{t}_{C}}$ для коллоидов алмаза (слева) и графита (справа) с добавками ${\text{AlC}}{{{\text{l}}}_{3}}$ при $\zeta = 0$ частиц (точки – эксперимент, пунктир – теория).
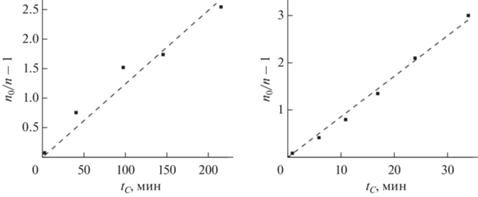
Можно заключить, что при столкновении частиц вероятность образовать агрегат из частиц графита существенно выше, чем из частиц алмаза. Так как ионно-электронная составляющая расклинивающего давления между частицами в изоэлектрической точке мала, то различие скоростей коагуляции частиц алмаза и графита определяется различием их молекулярных составляющих расклинивающего давления. В самом деле, расстояние между атомами углерода в алмазе меньше чем в графите, а значит их плотность на поверхности и, как следствие, плотность гидратной оболочки, определяющей молекулярную составляющую расклинивающего давления препятствующей агрегированию, выше. Поляризуемость химической связи между атомами углерода в sp3 гибридном состоянии в алмазе ниже, чем между атомами в sp2 гибридном состоянии в графите. В результате, дисперсионные силы притяжения, влияющие на расклинивающие давление, между частицами алмаза должны быть меньше чем между частицами графита.
ЗАКЛЮЧЕНИЕ
В данной работе показано, что предложенный метод, связанный с изучением электрооптических эффектов, применим для изучения кинетики коагуляции коллоидов на ранних еe этапах, если электропроводность коллоидов не слишком высокая и импульсы электрического поля позволяют создать ориентационную упорядоченность частиц без разогрева системы, способного повлиять на процесс коагуляции. Данным методом, связанным с измерениями релаксационных зависимостей наведенной электрическим полем оптической анизотропии коллоидов, также как и методом динамического светорассеяния, связанным с измерением автокорреляционных функций интенсивности рассеянного света, можно определять размеры и распределения по размерам агрегатов из частиц, а также скорости изменения концентраций частиц и агрегатов в процессе коагуляции. Преимущество электрооптического метода в том, что для измерения релаксационных зависимостей электрооптического эффекта необходимо меньшее время, чем для измерения автокорреляционных функций светорассеяния в методе динамического светорассеяния. Это позволяет изучать электрооптическими методами более быстрые процессы коагуляции, чем это можно сделать методом динамического светорассеяния. Также возможно изучать не только изменение интенсивности рассеянных световых волн, но и наведенную полем оптическую анизотропию, которая у частиц и агрегатов из них разная. Это предоставляет возможность различать эффекты, создаваемые частицами и агрегатами из них. Недостаток электрооптического метода связан с ограниченной областью допустимых значений электропроводности исследуемых коллоидов.
При исследовании было показано, что при низкой концентрации частиц даже крайне малые доли многовалентного электролита AlCl3 существенно меняют электрокинетические и электрооптические свойства водных коллоидов алмаза и графита. Это связано с тем, что катионы высокой валентности практически полностью адсорбируются поверхностью частиц, если концентрация ионов мала. Показано, что в области изоэлектрической точки изменение электрокинетического потенциала частиц алмаза и графита даже на несколько милливольт способно в несколько раз изменить скорость коагуляции водных коллоидов, содержащих эти частицы. Показано, что в изоэлектрической точке константа скорости коагуляции у частиц графита в 4.9 раза больше чем у частиц алмаза. В изоэлектрической точке силы электростатического взаимодействия частиц пренебрежимо малы и наблюдаемое различие скоростей коагуляции частиц алмаза и графита следует связывать с более плотной гидратной оболочкой частиц алмаза, препятствующей агрегированию.
Список литературы
Бердичевский Г.М. и др. // Вопросы биологической, медицинской и фармацевтической химии. 2021. Т. 24. № 1. С. 31.
Кузнецов Н.М. и др. // Тез. докл. Полимеры-2020. С. 50. Полимеры в стратегии научно-технического развития РФ. “Полимеры-2020”. 2020. С. 50.
Илларионов И.Е. и др. // Литейное производство. 2018. № 9. С. 25.
Голикова Е.В. и др. // Физика и химия стекла. 2011. Т. 37 № 4. С. 518.
Riddick T.M. Control of Colloid Stability through Zeta Potential. 1968. V. 1. Wynnewood, PA: Livingston.
Wang Tao и др. // Journal of Colloid and Interface Science. 2017. V. 499. P. 102.
Гусаков Г.А. и др. // Журнал прикладной спектроскопии. 2020. Т. 87. № 1. С. 33.
Krueger Anke, Daniel Lang // Advanced Functional Materials. 2012. V. 22. № 5. P. 890.
Соловьёва К.Н. и др. // Южно-Сибирский научный вестник. 2020. № 6. С. 96.
Пепекин В.И. // Химическая физика. 2010. Т. 29. № 9. Р. 52.
Иони Ю.В. и др. // Неорганические материалы. 2011. Т. 47. № 6. С. 671.
Юдина Т.Ф. и др. // Известия высших учебных заведений. Химия и химическая технология. 2018. Т. 61 № 9–10.
Юдина Т.Ф. и др. // Известия высших учебных заведений. Химия и химическая технология. 2013. Т. 56. № 7. С. 80.
Казилин Е.Е. и др. // Перспективные материалы. 2008. № 6. С. 21.
Gregor Trefalt и др. . // Chimia 2013. V. 67. № 11. P. 772. https://doi.org/10.2533/chimia
Дешабо В.А. и др. // Вести газовой науки. 2019. Т. 1 № 38. С. 172.
Вережников В.Н. и др. // Коллоид. журн. 2014. Т. 76. № 6. С. 717.
Савченко Е.А. и др. . / Сборник трудов ИТНТ. 2019. С. 428.
Величко Е.Н. и др. // Известия высших учебных заведений России. Радиоэлектроника. 2020. Т. 23. № 1. С. 25.
Helmut Holthoff et al. // Langmuir. 1996. V. 12. № 23. P. 5541. https://doi.org/10.1021/la960326e
Klemeshev S.A. et al. // Diamond and Related Materials. 2016. V. 69. P. 177.
Везо О.С. и др. // Опт. Спектр. 2020. Т. 128. № 6. С. 713.
Голикова Е.В. и др. // Коллоид. журн. 1986. Т. 48. № 5. С. 1005.
Klemeshev S.A. et al. // Colloids and Surfaces A: Physicochemical and Engineering Aspects. 2014. V. 456. P. 114.
Петров М.П. и др. // Опт. спектр. 2011. Т. 111. № 5. С. 871.
Fredericq Eugene, Claude Houssier. “Electric dichroism and electric birefringence.” 1973.
Spartakov A.A. et al. / Molecular and Colloidal Electro-Optics. CRC Press, 2016. P. 193–228.
Войтылов В.В. и др. // Опт. спектр. 1978. Т. 44. № 3. С. 604.
Ван де Хюлст Г. Рассеяние света малыми частицами. М: Ин. Лит. 1961.
Бабаджанянц Л.К. и др. // Высокомолекулярные соединения. Серия А. 2010. Т. 52. № 7. Р. 1329.
Цветков В.Н., Эскин В.Е., Френкель С.Я. Структура макромолекул в растворах. М.: Наука, 1964.
Smoluchowski M.V. // Phys. Z. 1916. V. 17. № 22. P. 557.
Дополнительные материалы отсутствуют.
Инструменты
Коллоидный журнал