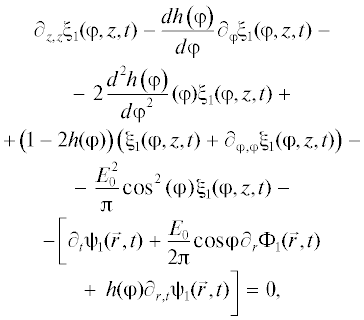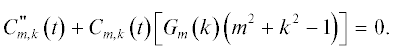Коллоидный журнал, 2022, T. 84, № 3, стр. 263-273
О критических условиях реализации неустойчивости азимутальных мод поверхностно однородно и неоднородно индуцированно заряженных струй электропроводных жидкостей и их электродиспергирование
А. И. Григорьев 1, *, С. О. Ширяева 2
1 Институт проблем механики им. А.Ю. Ишлинского
119526 Москва, пр-кт Вернадского, д. 101, к. 1, Россия
2 Ярославский государственный университет им. П.Г. Демидова
150000 Ярославль, ул. Советская, 14, Россия
* E-mail: grigorai@mail.ru
Поступила в редакцию 12.01.2022
После доработки 16.03.2022
Принята к публикации 21.03.2022
- EDN: KPVKCK
- DOI: 10.31857/S0023291222030065
Аннотация
Аналитическими асимптотическими методами исследуются критические условия реализации электростатической неустойчивости различных азимутальных мод электропроводных жидкостей по отношению к внешним электростатическим полям, в которых поверхность струй приобретает индуцированные заряды. В качестве таких внешних полей выбраны перпендикулярные к оси симметрии невозмущенной струи однородное электростатическое поле, в котором струя принимает эллиптическую в поперечном сечении форму, и радиальное осесимметричное. Выведено аналитическое выражение для произвольной азимутальной моды капиллярных волн на поверхности эллиптической струи. Оказалось, что критические условия реализации электростатической неустойчивости азимутальных мод не зависят от их начальных амплитуд (несмотря на наличие взаимодействия между модами), но определяются радиусом струи, коэффициентом поверхностного натяжения жидкости, величиной напряженности внешнего электростатического поля и наличием стационарной деформации равновесной формы струи по сравнению с круговой в поперечном сечении. Для эллиптической струи построены временные зависимости амплитуд неустойчивых азимутальных волн при различных начальных условиях.
ВВЕДЕНИЕ
Целью настоящего исследования является исследование критических условий реализации неустойчивости нескольких первых азимутальных мод струи идеальной несжимаемой электропроводной жидкости в электростатических полях разного вида (разной геометрии), перпендикулярных оси симметрии невозмущенной капиллярным волновым движением струи.
Но начнем с краткого перечисления основных этапов развития представлений об электростатической неустойчивости заряженной поверхности электропроводной жидкости.
В конце позапрошлого века Релей строго теоретическим путем вывел критерий электростатической неустойчивости сильно заряженной сферической капли идеальной несжимаемой электропроводной жидкости [1]. Его вывод был весьма краток, а его значение столь велико, что спустя почти век его расчеты были повторены более детально [2]. Критерий Релея в системе СИ имеет вид:
где $W$– безразмерный параметр Рэлея, характеризующий устойчивость капли по отношению к собственному заряду; ${{\varepsilon }_{0}}$ – электрическая постоянная; $Q$ и $R$ – заряд и радиус капли; ${{\sigma }}$ – коэффициент поверхностного натяжения жидкости. Если принять, что указанный заряд на поверхности сферической капли сформировался в результате индуцирования центрально симметричным внешним электростатическим полем напряженностью ${{E}_{0}}$, то указанный критерий можно переписать через напряженность ${{E}_{0}}$ в виде:(1)
$\begin{gathered} W \equiv \frac{{{{Q}^{2}}}}{{64{{\pi }^{2}}{{\varepsilon }_{0}}{{\sigma }}{{R}^{3}}}} \equiv \frac{{{{{\left( {4{{\pi }}{{R}^{2}}{{{{\chi }}}_{d}}} \right)}}^{2}}}}{{64{{\pi }^{2}}{{\varepsilon }_{0}}{{\sigma }}{{R}^{3}}}} \equiv \\ \equiv \,\,\frac{{{{{\left( {4{{\pi }}{{R}^{2}}{{\varepsilon }_{0}}{{E}_{0}}} \right)}}^{2}}}}{{64{{\pi }^{2}}{{\varepsilon }_{0}}{{\sigma }}{{R}^{3}}}} \equiv \frac{{{{\varepsilon }_{0}}E_{0}^{2}R}}{{16{{\sigma }}}} \geqslant 1, \\ \end{gathered} $Этот критерий неоднократно проверялся (см., например, [3–5], хотя успешная экспериментальная проверка его справедливости началась в середине 20 века и продолжается до сих пор по мере улучшения качества измерительной техники) и при всех проверках он подтвердился с точностью до единиц процентов от искомой величины.
С начала прошлого века были проведены и исследования устойчивости незаряженной капли электропроводной жидкости во внешнем однородном электростатическом поле ${{E}_{0}}$, итог которым был подведен в [6] выводом безразмерного критерия Тейлора, который экспериментально установил и численным расчетом подтвердил, что на пороге потери устойчивости сферической каплей радиуса $R$ (принимающей, однако, форму вытянутого по полю ${{\vec {E}}_{0}}$ сфероида), вид:
Если этот критерий привести к виду (1), он запишется как:
т.е. окажется примерно в двадцать раз слабее (1) (напомним, что $W$ и ${{w}_{d}}$ – безразмерные параметры). Впоследствии выводы [6] были подтверждены в более точных экспериментах [7, 8].Невольно напрашивается предположение, что такое положение дел: различия в величине критериев электростатической устойчивости однородно и неоднородно заряженных капель должно иметь место и для струй.
Струи и капли – геометрически различные объекты. Какие могут быть основания для переноса на струи изученных закономерностей реализации неустойчивости заряженных капель? А таковые имеются: на сферической заряженной капле и на цилиндрической струе кругового сечения в радиальном электростатическом поле поверхностные плотности заряда хоть и не идентичны, но однородны по поверхности капли и по поверхности струи.
На незаряженной капле в однородном электростатическом поле и на струе в перпендикулярном ее оси однородном электростатическом поле ${{\vec {E}}_{0}}$ индуцированный заряд не только распределен неоднородно, но он еще и имеет противоположные знаки на стороне струи, обращенной к полю, и на противоположной. И капля, и струя несжимаемой электропроводной жидкости в однородном электростатическом поле принимают эллиптические в сечении формы: капля – вытянутого по полю сфероида [6–9], а струя – эллиптическую в перпендикулярном сечении [10].
Первые исследования устойчивости струй начались еще в конце 19-го века и связаны c именем Рэлея, который создал строгую теорию капиллярного распада струй и провел эксперименты по исследованию влияния электризации струи на закономерности капиллярного распада струи на капли. Но первое теоретическое исследование устойчивости заряженных струй связано с именем Бассета А.Б. [11], который в конце 19-го века (не без ошибок, но впервые) получил дисперсионное уравнение для заряженной струи. Допущенные им ошибки были исправлены Дж. Тейлором [12] только через семьдесят пять лет. Оба эти исследователя установили явный вид параметра устойчивости заряженной струи в виде $w \equiv {{{{{{\mu }}}^{2}}} \mathord{\left/ {\vphantom {{{{{{\mu }}}^{2}}} {{{\pi }}{{\varepsilon }_{0}}R{{\sigma }}}}} \right. \kern-0em} {{{\pi }}{{\varepsilon }_{0}}R{{\sigma }}}}$, где ${{\mu }}$ – электрический заряд, приходящийся на единицу длины струи; $R$ – радиус цилиндрической струи; ${{\sigma }}$ – коэффициент поверхностного натяжения жидкости. Но Бассет [11], изучал устойчивость струи только по отношению к осесимметричной моде капиллярных волн, а Тейлор [12] изучил еще и изгибную моду (при неустойчивости которой конец струи совершает хлыстообразное движение) не затрагивая более высоких азимутальных мод. По итогам исследований [11, 12] был получен критерий неустойчивости нулевой и первой азимутальных мод в виде:
Параметр устойчивости заряженной струи может быть переопределен с использованием напряженности внешнего электростатического поля ${{E}_{0}}$, (физической величины, измеряемой приборами, в отличии от ${{\mu }}$) через серию тождественных преобразований:
(3)
$w \equiv \left( {{{{{{{\mu }}}^{2}}} \mathord{\left/ {\vphantom {{{{{{\mu }}}^{2}}} {{{\pi }}{{\varepsilon }_{0}}{{\sigma }}R}}} \right. \kern-0em} {{{\pi }}{{\varepsilon }_{0}}{{\sigma }}R}}} \right) \equiv \left( {{{{\text{4}}{{{{\pi }}}^{2}}{{\chi }}_{j}^{2}{{R}^{2}}} \mathord{\left/ {\vphantom {{{\text{4}}{{{{\pi }}}^{2}}{{\chi }}_{j}^{2}{{R}^{2}}} {{{\pi }}{{\varepsilon }_{0}}\sigma R}}} \right. \kern-0em} {{{\pi }}{{\varepsilon }_{0}}\sigma R}}} \right) \equiv \left( {{{{{\varepsilon }_{0}}E_{0}^{2}R} \mathord{\left/ {\vphantom {{{{\varepsilon }_{0}}E_{0}^{2}R} {{\sigma }}}} \right. \kern-0em} {{\sigma }}}} \right),$В [13–15] была изучена неустойчивость произвольных азимутальных мод заряженной круглой струи проводящей жидкости, но только в [15] критические условия реализации неустойчивости произвольной азимутальной моды были выражены в аналитическом виде:
(4)
$w \geqslant \frac{{\left( {{{{(kR)}}^{2}} + {{m}^{2}} - 1} \right){{K}_{m}}\left( {kR} \right)}}{{{{K}_{m}}\left( {kR} \right) + kR\frac{{d{{K}_{m}}\left( {kR} \right)}}{{d\left( {kR} \right)}}}},$Аналогичная (4) зависимость, но для струи во внешнем однородном электростатическом поле напряжeнностью ${{E}_{0}}$ перпендикулярном к оси симметрии невозмущенной струи получена недавно [10] в виде:
(5)
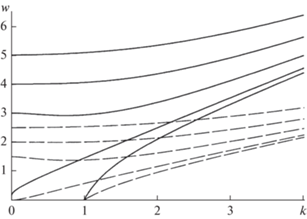
$\begin{gathered} w = \frac{{\left( {{{m}^{2}} + {{{\left( {kR} \right)}}^{2}} - 1} \right)}}{{{{H}_{{m + 1}}}\left( {kR} \right) + {{H}_{{m - 1}}}\left( {kR} \right) + 2}}, \\ {{H}_{j}}\left( {kR} \right) \equiv \frac{{kRK_{j}^{'}\left( {kR} \right)}}{{{{K}_{j}}\left( {kR} \right)}}, \\ \end{gathered} $На рис. 1 сплошными кривыми нанесены зависимости $w = w(k)$ рассчитанные по (4) для первых пяти азимутальных мод капиллярных волн (волновое число $k$ обезразмерено на $R$). Пунктирными линиями на том же рисунке нанесены безразмерные зависимости, рассчитанные по (5). Кривые расположены снизу вверх в порядке возрастания номеров азимутальных мод. Как видно, критические условия реализации неустойчивости различных азимутальных мод на эллиптической в сечении струе в два раза ниже, чем на круглой.
Рис. 1.
Критические зависимости ${\text{w}} = {\text{w}}(k)$ значений безразмерного полевого параметр w от безразмерного волнового числа $k$ для первых пяти азимутальных мод капиллярных волн на поверхности струи, расположенных снизу вверх в порядке возрастания номеров азимутальных мод. Самая нижняя линия соответствует $m = 0$, самая верхняя $m = 4$. Сплошными линиями нанесены зависимости для волн на поверхности круглой струи в радиальном электростатическом поле, пунктирными – эллиптической струи в ортогональном однородном.
В проводимом рассмотрении, когда приходится иметь дело со струей во внешнем однородном электростатическом поле ${{\vec {E}}_{0}}$, перпендикулярном оси симметрии невозмущенной струи, на разных сторонах струи (ориентированной по направлению внешнего однородного электростатического поля и в противоположном направлении) индуцированные заряды имеют разные знаки и поэтому естественно пользоваться определением полевого параметра как: $w \equiv \left( {{{{{\varepsilon }_{0}}E_{0}^{2}R} \mathord{\left/ {\vphantom {{{{\varepsilon }_{0}}E_{0}^{2}R} {{\sigma }}}} \right. \kern-0em} {{\sigma }}}} \right)$.
Отмеченное на рис. 1 снижение напряженности внешнего электростатического поля, при которой становятся неустойчивыми высокие азимутальные моды для эллиптической струи по сравнению с круглой струей, вполне объяснимо из общефизических соображений. Напряженность радиального электростатического поля на поверхности круглой в сечении струи имеет во всех точках поверхности одинаковую величину, а для струи эллиптического сечения напряженность электростатического поля на вершинах эллипса имеет максимум (достигаемый при меньшей напряженности внешнего поля), где и реализуется неустойчивость.
В заключение краткого обзора электростатической неустойчивости заряженной поверхности жидкости следует пару слов сказать о неустойчивости плоской поверхности жидкости во внешнем однородном электростатическом поле. Она также имеет место и была исследована в середине тридцатых годов прошлого столетия теоретически [17, 18], а позднее, [19–21] – экспериментально. Но поскольку в данном рассмотрении речь фактически идет о неустойчивости струй, заряженных индуцированным внешним электростатическом полем зарядом, то закономерности электростатической неустойчивости плоской заряженной поверхности жидкости оставим за пределами проводимого рассмотрения. Но, тем не менее, отметим, что сильно заряженная поверхность жидкости независимо от ее геометрии на стадии развития неустойчивости покрывается эмитирующими выступами так называемыми “конусами Тейлора” (см., например, фотографии в [21] и [22], стр. 247, для плоской и сферической форм), с вершин которых начинается эмиссия сильно заряженных капелек или струек, уносящих избыточный заряд, приводящий к развитию неустойчивости.
Целью настоящего рассмотрения будем считать исследование критических условий реализации неустойчивости высоких ($m \geqslant 2$) азимутальных мод капиллярных волн на поверхности струи, как наименее изученных: экспериментальное их изучение застопорено зажиганием коронного разряда в газовой среде в окрестности струи [23, 24].
1. Вывод аналитического выражения для m-й азимутальной моды капиллярных волн на поверхности эллиптической струи
Будем решать асимптотическими методами задачу об исследовании устойчивости капиллярных волн на бесконечной струе радиуса $R$ идеальной несжимаемой электропроводной жидкости с коэффициентом поверхностного натяжения ${{\sigma }}$, массовой плотностью ${{\rho }}$, движущейся в вакууме с постоянной скоростью, в инерциальной системе отсчета, движущейся вместе со струей с той же скоростью. Все рассмотрение проведем в цилиндрической системе координат $\left( {r,{{\varphi }},z} \right)$, связанной с осью симметрии невозмущенной струи. Иными словами, влиянием окружающей среды будем пренебрегать.
Движение жидкости в струе будем полагать потенциальным с гидродинамическим потенциалом ${{\psi }}(\vec {r},t)$. Будем считать, что струя находится в однородном электростатическом поле ${{\vec {E}}_{0}}$. Примем также, что ${{\vec {E}}_{0}}$ перпендикулярно оси симметрии невозмущенной капиллярным волновым движением струи, в котором струя принимает в поперечном сечении эллиптическую форму с эксцентриситетом $e$ [10].
Потенциал электрического поля в окрестности струи, поверхность которой возмущена капиллярным волновым движением, обозначим ${{\Phi }}(\vec {r},t)$.
Поскольку течение жидкости в струе генерируется возмущением ее поверхности, то величина гидродинамического потенциала течения жидкостей имеет тот же порядок малости, что и амплитуда капиллярных волн в капле ${{\psi }}(\vec {r},t)\sim {{\Phi }}(\vec {r},t) \sim \varepsilon $.
В качестве малых параметров задачи примем безразмерную амплитуду капиллярных волн на струе $\varepsilon $ и квадрат эксцентриситета эллипса в перпендикулярном сечении струи ${{e}^{2}}$. Азимутальный параметр $m$ будет целочисленным, произвольным. Все расчеты проведем в безразмерных переменных, в которых $R = {{\rho }} = {{\sigma }} = {{\left[ {4{{\pi }}{{{{\varepsilon }}}_{0}}} \right]}^{{ - 1}}} = 1$ (${{\varepsilon }_{0}}$ – электрическая постоянная). Остальные физические величины задачи будут выражены в долях своих характерных значений:
(6)
$\begin{gathered} \left[ r \right] = R,\,\,\,\,\left[ z \right] = R,\,\,\,\,\left[ \xi \right] = R,\,\,\,\,\left[ P \right] = {\sigma \mathord{\left/ {\vphantom {\sigma R}} \right. \kern-0em} R}, \\ \left[ t \right] = \sqrt {{{{{R}^{3}}\rho } \mathord{\left/ {\vphantom {{{{R}^{3}}\rho } \sigma }} \right. \kern-0em} \sigma }} ,\,\,\,\,\left[ \omega \right] = \sqrt {{\sigma \mathord{\left/ {\vphantom {\sigma {{{R}^{3}}\rho }}} \right. \kern-0em} {{{R}^{3}}\rho }}} , \\ \end{gathered} $Математическая формулировка линеаризованной по $\varepsilon $ и ${{e}^{2}}$ задачи в указанных безразмерных переменных будет иметь вид:
(7)
${{\Delta }}{{{{\psi }}}_{{\text{1}}}}\left( {r,\varphi ,z,t} \right) = 0,\,\,\,\,{{\Delta }}{{{{\Phi }}}_{{\text{1}}}}\left( {r,\varphi ,z,t} \right) = 0,$(8)
$\begin{gathered} r \to 0{\kern 1pt} :{{\psi }_{1}}\left( {r,\varphi ,z,t} \right) \to 0, \\ r \to \infty {\kern 1pt} :{{\Phi }_{1}}\left( {r,\varphi ,z,t} \right) \to 0, \\ \end{gathered} $(9)
$\begin{gathered} r = 1{\kern 1pt} : - {{\partial }_{t}}{{\xi }_{1}}\left( {\varphi ,z,t} \right) + \left( {{{\partial }_{r}}{{\psi }_{1}}\left( {r,\varphi ,z,t} \right)} \right. - \\ - \,\,\left. {\frac{{dh\left( \varphi \right)}}{{d\varphi }}{{\partial }_{\varphi }}{{\psi }_{1}}(\vec {r},t) + h\left( \varphi \right){{\partial }_{{r,r}}}{{\psi }_{1}}(\vec {r},t)} \right) = 0, \\ \end{gathered} $(11)
${{\Phi }_{1}}(\vec {r},t) - 2{{E}_{0}}\cos {\kern 1pt} {{\varphi }}{{{{\xi }}}_{1}}({{\varphi }},z,t) = 0,$(12)
$\begin{gathered} \mathop \smallint \limits_a^{a + {{\lambda }}} \mathop \smallint \limits_0^{2{{\pi }}} \left( {1 + h({{\varphi }})} \right){{{{\xi }}}_{1}}({{\varphi }},z,t)dzd{{\varphi }} = 0, \hfill \\ \int\limits_a^{a + \lambda } {\int\limits_0^{2\pi } {{{\partial }_{r}}{{\Phi }_{1}}(r,\varphi ,z{{{\left. {,t)} \right|}}_{{r = 1}}}dzd\varphi = 0} } . \hfill \\ \end{gathered} $В задаче (7)–(12) $\vec {r}$ – радиус-вектор; ${{\partial }_{t}}$, ${{\partial }_{r}}$ и ${{\partial }_{\varphi }}$ – обозначение частных производных по времени и цилиндрическим координатам; $h({{\varphi }}) \equiv \frac{{E_{0}^{2}}}{{12{{\pi }}}}\cos \left( {2{{\varphi }}} \right)$ – эллиптическая поправка к форме круглой струи, имеющая первый порядок малости по ${{e}^{2}}$. Искомыми функциями являются: ${{\xi }}\left( {{{\varphi }},z,t} \right)$ – тепловое возмущение равновесной поверхности струи капиллярным волновым движением, на основании этой величины и вводится первый малый параметр: $\varepsilon \equiv \left( {{{\max \left| {{{\xi }}\left( {{{\varphi }},z,t} \right)} \right|} \mathord{\left/ {\vphantom {{\max \left| {{{\xi }}\left( {{{\varphi }},z,t} \right)} \right|} R}} \right. \kern-0em} R}} \right)$; ${{{{\psi }}}_{{\text{1}}}}\left( {\vec {r},t} \right)$ – поправка первого порядка малости по $\varepsilon $, к гидродинамическому потенциалу скоростей [25], ${{\Phi }_{{\text{1}}}}\left( {\vec {r},t} \right)$ – поправка первого порядка малости по $\varepsilon $ к электрическому потенциалу [26].
Говоря о тепловом волновом движении, мы имеем в виду, что тепловые волны возбуждаются уже тепловым движением молекул жидкости [18]. Амплитуды таких волн $\sim \sqrt {{{\kappa T} \mathord{\left/ {\vphantom {{\kappa T} \sigma }} \right. \kern-0em} \sigma }} $, где $\kappa $ – постоянная Больцмана, $T$ – абсолютная температура жидкости [18]. Для большинства жидкостей эти амплитуды, не превышают одной десятой нанометра $ \sim {{10}^{{ - 10}}}\,\,{\text{м}}$. Если радиус струи принять $R \sim {{10}^{{ - 4}}}\,\,{\text{м}}$, то $\varepsilon \sim {{10}^{{ - 6}}}$. Вторым малым параметром будет величина квадрата эксцентриситета эллипса в поперечном сечении струи ${{e}^{2}}$.
В записанной выше формулировке решаемой задачи: (7) уравнения Лапласа для гидродинамического и электрического потенциалов, а (8) – граничные условия в нуле и на бесконечности к ним; (9) и (10) кинематическое и динамическое гидродинамические условия; (11) – условие эквипотенциальности поверхности струи. Интегральные условия (12) – условия постоянства объема участка струи длиной, равной длине капиллярной волны ${{\lambda }}$, и сохранения заряда на нем.
Решения уравнений Лапласа (7) для функций ${{{{\psi }}}_{1}}(r,{{\varphi }},z,t)$ и ${{\Phi }_{1}}(r,{{\varphi }},z,t)$, гармонические по координатам ${{\varphi }}$ и $z$, удовлетворяющие условиям ограниченности, будем искать в виде:
(13)
$\begin{gathered} {{{{\psi }}}_{1}}\left( {r,{{\varphi }},z,t} \right) = \\ = \mathop \sum \limits_{m = 0}^\infty \mathop \smallint \limits_0^\infty \left( {{{A}_{{m,k}}}\left( t \right){\text{exp(}}im{{\varphi )exp(}}ikz{\text{)}}{{I}_{m}}\left( {kr} \right)} \right)dk, \\ {{\Phi }_{1}}\left( {r,{{\varphi }},z,t} \right) = \\ = \mathop \sum \limits_{m = 0}^\infty \mathop \smallint \limits_0^\infty \left( {{{B}_{{m,k}}}\left( t \right){\text{exp(}}im{{\varphi )exp(}}ikz{\text{)}}{{K}_{m}}\left( {kr} \right)} \right)dk, \\ \end{gathered} $Поскольку функция ${{{{\xi }}}_{1}}\left( {{{\varphi }},z,t} \right)$, связана с ${{{{\psi }}}_{1}}(r,{{\varphi }},z,t)$ кинематическим граничным условием, будем искать выражение для нее в виде:
(14)
${{{{\xi }}}_{1}}\left( {{{\varphi }},z,t} \right) = \mathop \sum \limits_{m = 0}^\infty \mathop \smallint \limits_0^\infty {{С}_{{m,k}}}(t){\text{exp(}}im{{\varphi )exp(}}ikz{\text{)}}dk,$Подставляя выражения (13)–(14) в условия (9)–(10), выразим ${{A}_{{m,k}}}\left( t \right)$ и ${{B}_{{m,k}}}\left( t \right)$ через ${{С}_{{m,k}}}\left( t \right)$. Результаты подставим в динамическое граничное условие первого порядка по $\varepsilon $ и получим систему связанных обыкновенных дифференциальных уравнений второго порядка относительно неизвестных функций ${{С}_{{m,k}}}\left( t \right)$, описывающих временную эволюцию возмущения поверхности струи. Двумя верхними штрихами обозначается вторая производная по времени.
Появление взаимодействия мод, обычно проявляющееся во втором порядке малости по малому параметру, объясняется тем, что в рассматриваемой задаче имеются два малых параметра: $\varepsilon $ и ${{е}^{2}}$. Взаимодействие волн описывается слагаемыми $ \sim \varepsilon {{е}^{2}}$ как и для эллипсоидальной капли [27].
В нулевом порядке малости по ${{е}^{2}}$ легко получить систему несвязанных уравнений:
Решениями этих уравнений являются гармонические функции времени:
(17)
${{С}_{{m,k}}}\left( t \right) = {{{{\alpha }}}_{{m,k}}}{\text{exp(}}i{{{{\omega }}}_{{m,k}}}t{\text{),}}$Решения системы (15) в линейном по ${{е}^{2}}$ приближении будем искать, подставляя в систему (15) вместо амплитуд ${{C}_{{m + 2,k}}}\left( t \right)$ решения системы (16) нулевого порядка, вида (17). В результате получим систему несвязанных неоднородных дифференциальных уравнений второго порядка для отыскания функций ${{С}_{{m,k}}}\left( t \right)$:
Общее решение системы (18) ищется по стандартным для неоднородных дифференциальных уравнений правилам [28], и имеет вид:
(19)
$\begin{gathered} {{С}_{{m,k}}}\left( t \right) = {{\alpha }_{{m,k}}}{\text{exp(}}i{{\omega }_{{m,k}}}t{\text{)}} + \\ + \,\,w\left[ {{{{{\alpha }}}_{{m + 2,k}}}{\text{exp(}}i{{{{\omega }}}_{{m + 2,k}}}t{\text{)}}\frac{{\left( {{{\omega }}_{{m + 2,k}}^{2}{{{\rm A}}_{m}}\left( k \right) - {{\Gamma }_{m}}\left( k \right)} \right)}}{{{{\omega }}_{{m,k}}^{2} - {{\omega }}_{{m + 2,k}}^{2}}} + } \right. \\ \left. { + \,\,{{\alpha }_{{m - 2,k}}}{\text{exp(}}i{{{{\omega }}}_{{m - 2,k}}}t{\text{)}}\frac{{\left( {{{\omega }}_{{m - 2,k}}^{2}{{{\rm X}}_{m}}\left( k \right) - {{{\rm N}}_{m}}\left( k \right)} \right)}}{{{{\omega }}_{{m,k}}^{2} - {{\omega }}_{{m - 2,k}}^{2}}}} \right]. \\ \end{gathered} $Это выражение справедливо с точностью $ \sim {{e}^{2}}\varepsilon $. Слагаемые более высоких порядков малости, чем $ \sim {{e}^{2}}\varepsilon $, должны быть отброшены.
Выражение (14) после подстановки в него (19) и даст аналитическое выражение для формы $m$-й азимутальной моды капиллярных волн на поверхности эллиптической струи.
Из (19) видно, что амплитудные функции ${{С}_{{m,k}}}\left( t \right)$ зависят от амплитуд соседних мод одной ними четности. В этой связи представляется целесообразным численно исследовать поведение ${{С}_{{m,k}}}\left( t \right)$ при варьировании соседних мод. Интересно найти ответ на вопрос: можно ли, варьируя начальные условия для нижней моды (с $m \leqslant 1$), повлиять на критические условия релизации электростатической неустойчивость высокой азимутальной моды с $m \geqslant 2$?
2. Численный анализ
Чтобы построить по (19) графики амплитуд ${{С}_{{m,k}}}\left( t \right)$ необходимо задаться начальными условиями, а именно, начальными значениями безразмерных амплитуд ${{{{\alpha }}}_{{m,k}}}$.
Азимутальный параметр $m$ формально изменяется от $0$ до $\infty $. На практике никто осознанно не исследовал экспериментально устойчивость струй со значениями $m \geqslant 3$ [23–24]. Причина этого в том, что для струй хорошо проводящих жидкостей с круговым поперечным сечением уже для моды $m = 2$ экспериментальным исследованиям мешает коронный разряд в окрестности струи, а моды с $m \geqslant 3$ становятся неустойчивыми при более высоких значениях напряженности электростатического поля [17]. Исследования устойчивости высоких азимутальных мод с $m \geqslant 3$ пока возможны только теоретическим образом, как это, например, проделано в [17] для радиального поля.
Для всех мод примем, что начальная амплитуда меняется между принятыми малыми параметрами от $\varepsilon $ до ${{e}^{2}}$.
На рис. 2–5 приведены графики зависимости безразмерных амплитуд ${{С}_{{m,k}}}\left( t \right)$ от безразмерного времени, рассчитанные по (19), т.е. для струй в однородном поперечном электростатическом поле, при различных значениях полевого параметра w, безразмерного волнового числа $k$ и различных значений начальных амплитуд ${{\alpha }_{{0,k}}},\;\;{{\alpha }_{{2,k}}},\;\;{{\alpha }_{{4,k}}}$ (связанных по (19) между собой), графики ${{С}_{{m,k}}}\left( t \right)$ для $m = 2$. Сравнение графиков между собой позволяет выяснить роль каждого из указанных параметров.
Рис. 2.
Графики зависимости безразмерного амплитудного коэффициента ${{С}_{{m,k}}}\left( t \right)$ для четных азимутальных мод от безразмерного времени $t$, рассчитанные при: (а) $m = 2;\,\,\,\,w = 1.5;\;\;k = 1.5;\;\;{{\alpha }_{{0,k}}} = 0.6;$ ${{\alpha }_{{2,k}}} = 0.000001;\;\;{{\alpha }_{{4,k}}} = 0.000001$; (б) $m = 2;\;\;w = 1.5;$ $k = 1.5;\;\;{{\alpha }_{{0,k}}} = 0.1;$ ${{\alpha }_{{2,k}}} = 0.000001;\;\;{{\alpha }_{{4,k}}} = 0.000001$; (в) $m = 2;\;\;w = 1.5;\;\;k = 1.5;\;\;{{\alpha }_{{0,k}}} = 0.000001;$ ${{\alpha }_{{2,k}}} = 0.000001;$ ${{\alpha }_{{2,k}}} = 0.000001;\;\;{{\alpha }_{{4,k}}} = 0.000001$.
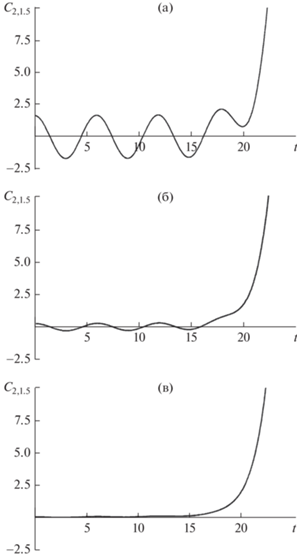
Рис. 3.
Графики зависимости безразмерного амплитудного коэффициента ${{С}_{{m,k}}}\left( t \right)$ для четных азимутальных мод от безразмерного времени $t$, рассчитанные при различных масштабах по оси ординат: а) $m = 2;\;\;w = 1.5;\;\;k = 1.5;$ ${{\alpha }_{{0,k}}} = 0.000001;$ ${{\alpha }_{{2,k}}} = 0.000001;$ ${{\alpha }_{{4,k}}} = 0.000001$; (б) $m = 2;\,\,\,\,w = 1.5;$ $k = 1.5;\;\;{{\alpha }_{{0,k}}} = 0.000001;$ ${{\alpha }_{{2,k}}} = 0.000001;$ ${{\alpha }_{{4,k}}} = 0.000001$.
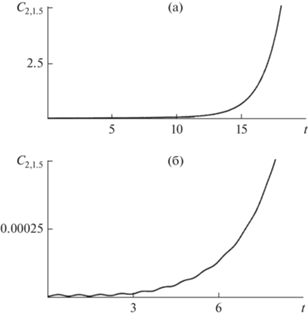
Рис. 4.
График зависимости безразмерного амплитудного коэффициента ${{С}_{{m,k}}}\left( t \right)$ от безразмерного времени $t$, рассчитанный при $m = 2;\;\;w = 1.45;\;\;k = 1.5;\;$ ${{\alpha }_{{0,k}}} = 0.6;\;\;{{\alpha }_{{2,k}}} = 0.000001;\;\;{{\alpha }_{{4,k}}} = 0.000001$. По сравнению с рис. 2а уменьшена величина полевого параметра с $w = 1.5$ до $w = 1.45$.
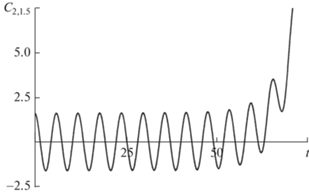
Рис. 5.
(а) График зависимости безразмерного амплитудного коэффициента ${{С}_{{m,k}}}\left( t \right)$ для четных азимутальных мод от безразмерного времени $t$, рассчитанный при $m = 2;\;\;w = 1.45;\;\;k = 1.5;\;{{\alpha }_{{0,k}}} = 0.6;\;\;{{\alpha }_{{2,k}}} = 0.1;\;$ α4,k = = 0.000001. По сравнению с рис. 4 увеличено ${{\alpha }_{{2,k}}}$ до ${{\alpha }_{{2,k}}} = 0.1$. (б) График зависимости безразмерного амплитудного коэффициента ${{С}_{{m,k}}}\left( t \right)$ от безразмерного времени $t$, рассчитанный при $m = 2;$ $w = 1.45;\;\;k = 1.5;$ $m = 2;\,\,\,\,k = 1.5;$ ${{\alpha }_{{0,k}}} = 0.6;\;\;{{\alpha }_{{2,k}}} = 0.000001;$ ${{\alpha }_{{4,k}}} = 0.1$. По сравнению с рис. 4 увеличено ${{\alpha }_{{4,k}}}$ до ${{\alpha }_{{4,k}}} = 0.1$. (в) График зависимости безразмерного амплитудного коэффициента ${{С}_{{m,k}}}\left( t \right)$ от безразмерного времени $t$, рассчитанный при $m = 2;\;\;w = 1.45;\;k = 1.5;\;$ ${{\alpha }_{{0,k}}} = 0.6;\;\;{{\alpha }_{{2,k}}} = 0.1;\;\;{{\alpha }_{{4,k}}} = 0.1$. По сравнению с рис. 4 увеличено ${{\alpha }_{{2,k}}}$ до ${{\alpha }_{{2,k}}} = 0.1$ и ${{\alpha }_{{4,k}}}$ до ${{\alpha }_{{4,k}}} = 0.1$.
Чтобы на основании приведенных графиков построить размерные зависимости перепишем безразмерную зависимость ${{С}_{{m,k}}}\left( t \right)$ в размерном виде, используя масштабы обезразмеривания (6):
(20)
${{С}_{{m,k}}}\left( t \right) \Rightarrow \frac{{{{{\tilde {С}}}_{{m,k}}}}}{R}\left( {t\sqrt {\frac{\sigma }{{{{R}^{3}}{{\rho }}}}} } \right).$В правой стороне выражения (20) все физические величины размерные, а ${{\tilde {С}}_{{m,k}}}$ – размерная амплитуда капиллярной волны на поверхности струи. Из (20) следуют качественные и количественные зависимости амплитуды капиллярной волны от физико-химических свойств жидкости. Так, например, необходимо исследовать зависимость характерного размерного времени реализации неустойчивости $\tilde {t}$ от физико-химических свойств жидкости и радиуса струи при $m = 2$. Из рис. 2 следует, что при ${{С}_{{m,k}}}\left( t \right) \approx 20$ безразмерная амплитуда азимутальной капиллярной волны с $m = 2$ начинает неограниченно расти (претерпевает неустойчивость). Тогда из (20) следует, что при сохранении неизменной величины аргумента $t\sqrt {\frac{\sigma }{{{{R}^{3}}{{\rho }}}}} $ можно найти зависимости характерного размерного времени реализации неустойчивости $\tilde {t}$ от размерных характеристик струи: радиуса струи $\tilde {R}$, плотности жидкости ${{\tilde {\rho }}}$ и величины коэффициента поверхностного натяжения $\tilde {\sigma }$ в виде:
По несложному такому правилу следует обрабатывать все графики данной статьи.
На рис. 2а–2в приведены графики, различающиеся начальной амплитудой осесимметричной моды ${{\alpha }_{{0,k}}}$. Расчeты показывают, что изменение начальной амплитуды ${{\alpha }_{{0,k}}}$ от тепловой до максимально возможной, характерного времени реализации неустойчивости не меняет. Начальная амплитуда ${{\alpha }_{{0,k}}}$ сказывается лишь на внешнем виде графика.
Из рис. 3а–3б, где приведены разномасштабные по оси ординат вариации рис. 2в видно, что примерно экспоненциальный рост ${{С}_{{2,k}}}\left( t \right)$ начинается с начала изменения времени $t$, но на рис. 2 он маскируется малой скоростью прироста величины ${{С}_{{2,k}}}\left( t \right)$. На рис. 3б проявляется волнистость растущей амплитуды ${{С}_{{2,k}}}\left( t \right)$ обусловленная сравнимостью начальной амплитуды тепловых волн ${{{{\alpha }}}_{{4,k}}}$ с масштабом изменения графика по оси ординат.
На рис. 4 приведен график зависимости от времени амплитудного множителя ${{С}_{{2,k}}}\left( t \right)$, отличающийся от рис. 2а только значением полевого параметра: принято, что $w = 1.45$, т.е. на $0.05$ меньше чем на рис. 2а. Но столь незначительное уменьшение полевого параметра привело к увеличению характерного времени реализации неустойчивости более чем в три раза.
На рис. 5а–5в приведены графики зависимости от времени амплитудного множителя ${{С}_{{2,k}}}\left( t \right)$ при различных значениях начальных амплитуд ${{{{\alpha }}}_{{m + 2,k}}}$ и ${{{{\alpha }}}_{{m + 4,k}}}$, которые принимают значения $0.1$, в начале врозь, а затем и одновременно, при сохранении значений прочих параметров такими, как на рис. 4. Принимаемые значения начальных амплитуд ${{{{\alpha }}}_{{m + 2,k}}}$ и ${{{{\alpha }}}_{{m + 4,k}}}$ на рис. 5а–5в не соответствуют реальной физической ситуации, но позволяют судить о тенденции изменения графиков при варьировании величин начальных амплитуд.
Из рис. 5а видно, что увеличение начальной амплитуды ${{{{\alpha }}}_{{2,k}}}$ в 100 000 раз приводит к сокращению характерного времени реализации неустойчивости в 4–5 раз. Из рис. 5б видно, увеличение начальной амплитуды ${{{{\alpha }}}_{{4,k}}}$ в 100 000 раз не приводит к заметному изменению характерного времени реализации неустойчивости по сравнению с рис. 4, но кривая нарастания ${{С}_{{2,k}}}\left( t \right)$ амплитуды азимутальной моды с $m = 2$ становится более сложной (соответствует прямому сложению двух колебаний с ${{\alpha }_{{0,k}}} = 0.6$ и ${{{{\alpha }}}_{{4,k}}} = 0.1$).
Из рис. 5в видно, что когда ${{{{\alpha }}}_{{2,k}}} = 0.1$ и ${{{{\alpha }}}_{{4,k}}} = 0.1$, кривая ${{С}_{{2,k}}}\left( t \right)$ претерпевает неустойчивость как на рис. 5а и сохраняет сложность рис. 5в.
Можно сделать вывод, что когда увеличивается начальная амплитуда неустойчивой моды, тогда сокращается время реализации неустойчивости, а когда растут амплитуды мод, связанных согласно (18), они просто складываются.
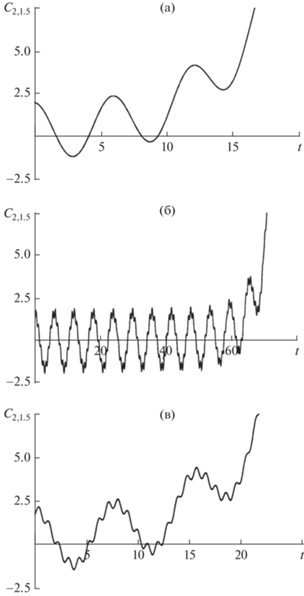
Сказанное касается и нечетных азимутальных мод: так, если согласно (18) рассмотреть взаимодействующие моды с $m = 1$, $m = 3$ и $m = 5$, и принять, что ${{\alpha }_{{1,k}}} = 0.6;\;\;{{\alpha }_{{3,k}}} = 0.000001;\;\;{{\alpha }_{{5,k}}} = 0.000001$, то зависимости от времени амплитудного множителя ${{С}_{{3,k}}}\left( t \right)$ примут вид, приведенный на рис. 6. На рис. 6а–6в приведены графики для различных околокритических значений полевого параметра $w \approx {{w}_{{{\text{cr}}}}}$ азимутальной моды с $m = 3$ и волнового числа k = 1.5. Отметим, что при k = 1.5 найдено критическое значение полевого параметра ${\text{w}}$ с точностью до пятого знака после запятой ${{w}_{{{\text{cr}}}}} = 2.0256$. Легко видеть, что характерное время реализации неустойчивости значительно увеличивается по мере приближения w к критическому значению сверху ${{w}_{{{\text{cr}}}}}$. Оно, тем меньше, чем значительнее принятое значение w превышает ${{w}_{{{\text{cr}}}}}$.
Рис. 6.
Графики зависимости безразмерного амплитудного коэффициента ${{С}_{{m,k}}}\left( t \right)$ для нечетных азимутальных мод от безразмерного времени $t$, рассчитанные при: (а) $m = 3;\;\;w = 2.1;\;\;k = 1.5;\;\;{{\alpha }_{{1,k}}} = 0.6;$ ${{\alpha }_{{3,k}}} = 0.000001;$ ${{\alpha }_{{5,k}}} = 0.000001$; (б) $m = 3;\;\;w = 2.0265;$ $k = 1.5;\;\;{{\alpha }_{{1,k}}} = 0.6;$ ${{\alpha }_{{3,k}}} = 0.000001;\;\;{{\alpha }_{{5,k}}} = 0.000001$; (в) $m = 3;\;\;w = 2.02561;\;\;k = 1.5;\;\;{{\alpha }_{{1,k}}} = 0.6;$ ${{\alpha }_{{3,k}}} = 0.000001;$ ${{\alpha }_{{5,k}}} = 0.000001$; (г) $m = 3;\;\;w = 2.0256;$ $k = 1;\;\;{{\alpha }_{{1,k}}} = 0.6;$ ${{\alpha }_{{3,k}}} = 0.000001;\;\;{{\alpha }_{{5,k}}} = 0.000001$.

Если ввести превышение величины полевого параметра w над критическим значением ${{w}_{{{\text{cr}}}}}$: $\Delta w \equiv w - {{w}_{{{\text{cr}}}}}$, то можно сформулировать высказанное в предыдущем абзаце утверждение следующим образом: характерное безразмерное время реализации неустойчивости ${{\tau }}$ быстро растет со стороны больших значений w при $\Delta w \to {\text{0}}$.
На рис. 6г приведена зависимость ${{С}_{{3,k}}}\left( t \right)$ при тех же значениях начальных амплитуд мод капиллярных волн, что и на рис. 6в, и k = 1 при критическом значении полевого параметра ${{w}_{{{\text{cr}}}}} = 2.0256$ для волнового числа k = 1.5. Видно, что характерное время реализации неустойчивости при уменьшении значения волнового числа на треть сократилось в 80 раз.
3. Электродиспергирование
В экспериментальных исследованиях при реализации неустойчивости первых двух азимутальных мод с m = 0 и m = 1 от свободного торца струи отрываются заряженные капли с размерами примерно равными диаметру струи, разве что при реализации неустойчивости изгибной азимутальной моды (m = 1) отрыву капель с торца струи способствуют также и центробежные силы. При реализации электростатической неустойчивости азимутальных мод с $m \geqslant 2$ с поверхности струи выбрасываются дочерние струйки с диаметрами на два порядка величины меньшими чем диаметр родительской струи, которые в свою очередь распадаются на капельки. В итоге, функция распределения капель по размерам, на которые распадается струя, весьма широка. Про функцию рапределения капель по зарядам можно только гадать. Но, скорее всего, заряды близки к критическим для реализации электростатической неустойчивости капель [29].
Следует указать, что в данной постановке задачи, при пренебрежении влиянием окружающей среды, критические условия определяются двумя характеристиками: полевым безразмерным параметром w и волновым числом $k$. В более общей постановке, с учетом влияния наличия среды, необходимо учесть и величину параметра Вебера ${\text{We}}$ (см., например, таблицы в [30]). Движение жидкой струи относительно газообразной среды вызывает появление на поверхности струи вязкой жидкости напряжений или в более простой модели идеальной жидкости – появление тангенциального скачка поля скоростей, сопровождающегося возникновением неустойчивости Кельвина−Гельмгольца [23].
4. Область применимости
Следует отметить, что проведенное исследование базировалось на модели идеальной несжимаемой электропроводной жидкости. Это означает, что влияние вязкости жидкости и ее электропроводности на критические условия и закономерности реализации неустойчивости высоких азимутальных мод капиллярных волн на струе выпало из рассмотрения. В этой связи можно отметить, что вязкость жидкости на критические условия электростатической неустойчивости не влияет [31] и скажется лишь на времени реализации неустойчивости и на феноменологии явления [32]. Что касается электропроводности жидкости, то ее влияние на реализацию неустойчивости струи пока исследуется лишь на качественном уровне (на уровне использования характерных времен релаксации заряда) потому, что в модельную математическую постановку задачи об электростатическом распаде струи электропроводность не входит. A priori, из общефизических представлений ясно, что электропроводность должна сказываться на феноменологии явления реализации электростатической неустойчивости струй. Но для указания, каким образом будет осуществлено ее влияние, пока не хватает экспериментальных данных.
Пока можно лишь выделить область значений физических величин, в которой применимо приведенное рассмотрение. Согласно [32] безразмерный коэффициент кинематической вязкости жидкости записывается в виде:
а безразмерная удельная электропроводность как: где $\gamma $ – удельная электропроводность; ${{\varepsilon }_{d}}$ – диэлектрическая проницаемость; $\nu $ – коэффициент кинематической вязкости.Проведенное рассмотрение будет справедливо при малых безразмерных вязкостях и больших безразмерных удельных электропроводностях, т.е. в области значений физических параметров, в которых
ЗАКЛЮЧЕНИЕ
Выведено аналитическое выражение для произвольной $m$-й азимутальной моды капиллярных волн на поверхности эллиптической струи. Найдены критические условия реализации электростатической неустойчивости высоких азимутальных мод эллиптической струи во внешнем однородном электростатическом поле и для прямой круговой струи в радиально симметричном электростатическом поле. Оказалось, что по сравнению со струей в радиальном электростатическом поле устойчивость эллиптической струи существенно снижается, а связано это с различиями распределения индуцированного заряда по поверхности струи.
Для эллиптической в перпендикулярном сечении струи построены зависимости амплитуд капиллярных волн для различных азимутальных чисел $m$ от времени. Обнаружено, что капиллярные волны для различных $m$ (четных и нечетных раздельно) на поверхности эллиптической струи взаимодействуют между собой, благодаря эллиптическому искажению круговой формы поперечного сечения. На круглой струе взаимодействия нет. Переноса энергии между капиллярными волнами, соответствующими различным азимутальным модам, связанными взаимодействием, не обнаружено, в отличие от капиллярных волн на капле [27].
Показано, что величина начальной амплитуды ${{\alpha }_{{0,k}}}$ для четных мод или ${{\alpha }_{{1,k}}}$ для нечетных, характерного времени реализации неустойчивости ${{\tau }}$ не меняет и сказывается лишь на внешнем виде графика. Увеличение начальной амплитуды моды, за которой ведется наблюдение (например, ${{\alpha }_{{2,k}}}$), приводит к сокращению времени реализации неустойчивости ${{\tau }}$. На характерное время реализации неустойчивости ${{\tau }}$ основное влияние оказывает превышение величины полевого параметра ${\text{w}}$ над критическим при заданном волновом числе $k$ его значением: $\Delta w \equiv w - {{w}_{{{\text{cr}}}}}$, что вполне естественно, т.к. с ростом $\Delta w$ увеличивается и инкремент неустойчивости капиллярных волн и наоборот: при уменьшении $\Delta w$ снижается и величина инкремента, стремясь к нулю при $\Delta w \to {\text{0}}$.
Обнаружено, что на критические условия электростатической неустойчивости влияют лишь: искажение равновесной формы струи, величина коэффициента поверхностного натяжения жидкости, радиус струи и длина волны, на которой исследуется неустойчивость. Изменение начальных амплитуд азимутальных мод капиллярных волн сказывается лишь на характерном времени реализации неустойчивости. Критические условия реализации электростатической неустойчивости при этом не меняются.
Работа, выполнена по теме государственного задания (№ госрегистрации АААА-А20-120011690131).
Список литературы
Rayleigh (Strutt J.W.) // Phil. Mag. 1882. V. 14. P. 184.
Hendrics C.D., Schneider J.M. // J. Amer. Phys. 1963. V. 1. № 6. P. 450.
Duft D., Lebbeus H., Huber B.A. // Phys. Rev. Lett. 2002. V. 89. № 8. P. 1.
Duft D., Achtzehn T., Muller R. et al. // Nature. 2003. V. 421. № 6919. P.128.
Grimm R.L., Beauchamp J.L. // J. Phys. Chem. B. 2005. V. 109. P. 8244.
Taylor G.I. // Proc. Roy. Soc., London. 1964. V. A280. P. 383.
Inculet I.I. // IEEE Transactions on Industry Applications. 1989. V. 25. № 5. P. 945.
Inculet I.I., Floryan J.M., Haywood R.J. // IEEE Transactions on Industry Applications. 1992. V. 28. № 5. P. 1203.
O’Konski C.T., Harris F.E. // J. Phys. Chem. 1957. V. 61. P. 1172.
Григорьев А.И., Ширяева С.О. // Изв. РАН. МЖГ. 2021. № 2. С. 29.
Basset A.B. // Amer. J. Math. 1894. V. 16. P. 93.
Taylor G. // Proc. Roy. Soc., London. 1969. V. A313. P. 453.
Saville D. // Phys. of Fluids. 1971. V. 14. № 6. P. 1095.
Ширяева С.О., Григорьев А.И., Левчук Т.В., Рыбакова М.В. // ЖТФ. 2003. Т. 73. Вып. 4. С. 5.
Григорьев А.И. // ЖТФ.2009. Т. 79. № 4. С. 36.
Справочник по специальным функциям / Под ред. Абрамовиц М., Стиган И. М.: Наука, 1979.
Tonks L. A // Phys. Rev. 1935. V. 48. P. 562.
Френкель Я. И. // ЖЭТФ. 1936. Т. 6. № 4. С. 348.
Taylor G.I., McEwan A.D. // J. Fluid Mech. 1965. V. 22. № 1. P. 1.
Шутов А.А. // ЖТФ. 2002. Т. 72. № 8. С. 126.
Габович М.Д. // УФН. 1983. Т. 140. № 1. С. 137.
Остроумов Г.А. Взаимодействие электрических и гидродинамических полей. М.: Наука, 1979.
Cloupeau M., Prunet Foch B. // J. Aerosol Sci. 1994. V. 25. № 6. P. 1021.
Jaworek A., Krupa A. // J Aerosol Sci. 1999. V. 30. № 7. P. 873.
Ландау Л.Д., Лифшиц Е.М. Гидродинамика. М.: Наука, 1986.
Ландау Л.Д., Лифшиц Е.М. Теория поля. М.: Наука, 1973.
Ширяева С.О., Григорьев А.И., Корниенко Д.О. // ЖТФ. 2010. Т. 80. № 11. С. 11.
Степанов В.В. Курс дифференциальных уравнений. М.: ГосТехТеорИздат, 1953.
Grigor'ev A.I., Shiryaeva S.O. // J. Aerosol Sci. 1994. V. 25. № 6. P. 1079.
Григорьев А.И., Ширяева С.О. // Изв. РАН. МЖГ. 2021. № 3. С. 48.
Левич В.Г. Физико-химическая гидродинамика. М.: Физматгиз, 1959.
Григорьев А.И., Ширяева С.О. // КЖ. 2021. Т. 83. № 5. С. 532
Дополнительные материалы отсутствуют.
Инструменты
Коллоидный журнал