Космические исследования, 2019, T. 57, № 3, стр. 212-228
Совместная оптимизация управления и основных траекторных и проектных параметров межпланетного космического аппарата с электроракетной двигательной установкой
В. Г. Петухов 1, *, А. В. Иванюхин 1, 2, **, Ву Сан Вук 3, ***
1 Научно-исследовательский институт прикладной механики и электродинамики МАИ
г. Москва, Россия
2 Российский университет дружбы народов
г. Москва, Россия
3 Московский авиационный институт
г. Москва, Россия
* E-mail: vgpetukhov@gmail.com
** E-mail: ivanyukhin.a@yandex.ru
*** E-mail: sanukk@hanmail.net
Поступила в редакцию 23.02.2018
После доработки 30.03.2018
Принята к публикации 20.04.2018
Аннотация
Исследована задача совместной оптимизации программ управления вектором тяги и основных траекторных и проектных параметров межпланетного космического аппарата с электроракетной двигательной установкой (ЭРДУ) с целью максимизации полезной массы КА. Для математических моделей регулируемой по тяге и однорежимной ЭРДУ с постоянной скоростью истечения и для фиксированной длительности перелета по гелиоцентрической траектории получены необходимые условия совместной оптимальности программы управления вектором тяги, вектора отлетного гиперболического избытка скорости, даты отлета, удельного импульса ЭРДУ, максимальной мощности ЭРДУ и системы электроснабжения КА. Показано, что для ряда представляющих практический интерес задач оптимальное значение тяги ЭРДУ равно ее минимально допустимому значению. Полученные результаты могут представлять интерес на ранних этапах проектирования межпланетных КА с ЭРДУ и для обоснования выбора основных параметров разрабатываемых электроракетных двигателей.
ВВЕДЕНИЕ
В настоящее время электроракетные двигательные установки (ЭРДУ) все чаще применяются в качестве маршевых двигательных установок околоземных и межпланетных космических аппаратов (КА). Основной причиной использования ЭРДУ в этом качестве является их большой удельный импульс, который позволяет достичь больших значений характеристической скорости с малыми затратами рабочего тела. Основным недостатком ЭРДУ является малое значение тяги, которая пропорциональна доступной для питания ЭРДУ электрической мощности на борту КА и обратно пропорциональна величине удельного импульса. Малая величина тяги приводит к необходимости длительной работы ЭРДУ для реализации требуемого приращения характеристической скорости и к большой длительности перелета. Для увеличения тяги ЭРДУ требуется либо уменьшить ее удельный импульс, либо увеличить электрическую мощность. Уменьшение удельного импульса приводит к увеличению затрат рабочего тела, а увеличение электрической мощности – к увеличению массы ЭРДУ и бортовых систем, обеспечивающих электропитание ЭРДУ. Очевидно, для каждой конкретной космической транспортной операции ограниченной длительности должны существовать оптимальные значения удельного импульса и электрической мощности (или тяги) ЭРДУ, обеспечивающие максимум полезной массы КА, под которой будем понимать конечную массу КА за вычетом массы ЭРДУ с системой хранения и подачи рабочего тела (СХПРТ) и обеспечивающих работу ЭРДУ бортовых систем.
В традиционной постановке задач оптимизации траекторий КА с ЭРДУ основные проектные параметры – начальная масса, мощность системы электропитания, тяга и удельный импульс ЭРДУ – считаются заданными. Это, безусловно, оправдано, когда проектный облик КА сформирован и выбраны средства его выведения. Однако на начальных этапах проектирования КА необходимо получить представление о том, какие значения проектных параметров КА и ЭРДУ обеспечат наилучшие характеристики при выполнении рассматриваемой космической транспортной операции. Несмотря на ограниченные возможности выбора многих из этих параметров на практике, знание их оптимальных значений и достижимых значений показателей эффективности космической миссии при оптимальных проектных параметрах позволяет принять обоснованные технические решения на ранних стадиях разработки КА.
Основные проектные параметры КА с ЭРДУ можно условно разделить на две категории. К первой категории отнесем параметры, определяющие уровень используемых технологий. Для обеспечения максимальной эффективности космической транспортной операции их значения должны быть максимальными или минимальными, но фактически они ограничены используемыми технологиями и не могут быть улучшены в рамках реализации конкретного проекта. К таким параметрам относится, например, удельная масса солнечных батарей и других элементов системы электроснабжения КА, удельная масса и тяговый к.п.д. ЭРДУ, баковый коэффициент (отношение конечной массы СХПРТ к массе рабочего тела, используемого для создания тяги). Ко второй категории отнесем параметры, которые могут выбираться при проектировании КА и ЭРДУ. К таким параметрам может относиться установленная электрическая мощность солнечных батарей, максимальная и минимальная потребляемая электрическая мощность ЭРДУ, удельный импульс ЭРДУ. Оптимальные значения этих параметров, обеспечивающие максимум полезной массы КА, будут связаны с параметрами траектории перелета. Поэтому большой практический интерес представляет совместная оптимизация траектории и основных проектных параметров КА второй категории. Такая совместная оптимизация позволяет оценить максимально достижимые показатели эффективности, обосновать основные характеристики системы электроснабжения КА и ЭРДУ, выбрать наиболее подходящие электроракетные двигатели (ЭРД) для реализации конкретного проекта, а также обосновать основные параметры вновь проектируемых ЭРД.
В литературе задача оптимизации основных проектных параметров часто называется параметрической, в отличие от динамической задачи – задачи оптимизации траектории [1]. Хорошо известно, что для идеально-регулируемого двигателя (в случае, когда ограничена только мощность, пропорциональная произведению тяги на скорость истечения ЭРДУ, а значения собственно тяги и скорости истечения могут изменяться произвольно в рамках этого ограничения) динамическая задача полностью отделяется от параметрической и может быть решена самостоятельно, а решение параметрической задачи определяется простыми соотношениями с использованием результатов решения динамической задачи [2].
Для задачи с ограниченной тягой и скоростью истечения ЭРДУ такого разделения задачи оптимизации на динамическую и параметрическую части не известно. Поэтому типичный подход к совместной оптимизации траектории и основных проектных параметров КА с ЭРДУ до настоящего времени состоит в решении последовательности задач с различными значениями проектных параметров и построении зависимостей показателей эффективности полученных решений (например, полезной массы КА) от значений варьируемых проектных параметров [1, 3, 4]. Такой подход требует больших вычислительных затрат, отличается невысокой точностью оптимизации основных проектных параметров и может иметь проблемы со сходимостью при изменении свойств оптимальной траектории с изменением значений варьируемых параметров.
Поэтому в настоящей работе рассматривается подход, основанный на использовании необходимых условий оптимальности принципа максимума для одновременной оптимизации траектории и основных проектных параметров, который позволяет существенно снизить вычислительные затраты на решение задачи и, с использованием метода продолжения, обеспечить хорошую сходимость к оптимальному решению. Используемые здесь идеи совместной оптимизации уже были представлены в работах [5, 6]. Похожий подход использовался в работе [7] при анализе марсианской пилотируемой экспедиции. В настоящей работе представлены необходимые условия оптимальности основных проектных параметров для случаев, когда электрическая мощность ЭРДУ постоянна или зависит от гелиоцентрического удаления КА. Первый случай соответствует однорежимной ЭРДУ с ядерной или солнечной бортовой энергоустановкой. В этом случае, при использовании солнечной энергоустановки, ее мощность должна быть достаточна для обеспечения работы ЭРДУ на максимальном требуемом гелиоцентрическом удалении. Второй случай соответствует ЭРДУ, мощность и тяга которой непрерывно регулируется при изменении доступной мощности бортовой солнечной энергоустановки.
В данной работе рассматривается комбинированная схема межпланетного перелета между двумя планетами с фиксированной длительностью. В рамках этой схемы КА с ЭРДУ выводится на отлетную траекторию от планеты отправления с помощью средств выведения, использующих двигательные установки большой тяги. Задана либо начальная масса КА, либо зависимость начальной массы КА на отлетной траектории от значения отлетного гиперболического избытка скорости (в работе использовались аппроксимации таких зависимостей, представленных в табличной форме в руководствах пользователей средствами выведения [8, 9], с помощью полиномов 6-го порядка). Гелиоцентрическая траектория КА формируется ЭРДУ. Рассматривается задача оптимизации траекторий прямых гелиоцентрических перелетов между двумя планетами в рамках допущений метода точечных сфер действия [10–12], участок движения внутри сферы действия планеты назначения не анализируется. Оптимизация траектории, помимо вычисления оптимального управления (программы управления вектором тяги ЭРДУ), может включать в себя оптимизацию ряда траекторных параметров (даты отлета, величины и направления отлетного гиперболического избытка скорости). Одновременная оптимизация управления, траекторных и проектных параметров позволяет получить представление о наилучшем варианте проектируемой космической миссии и сделать некоторые заключения о свойствах и возможности использования таких оптимальных решений.
Фактически, эта статья является продолжением серии статей [13–15], посвященных оптимизации траекторий КА с идеально-регулируемым двигателем, двигателем ограниченной и минимальной тяги, и использует аналогичный подход к постановке и решению задач оптимального управления.
1. ПРОСТАЯ ПРОЕКТНАЯ МОДЕЛЬ КА С ЭРДУ
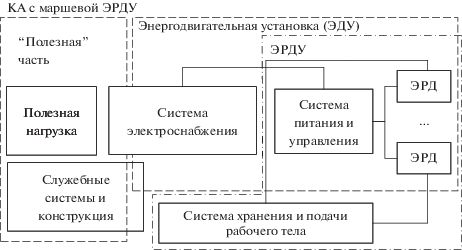
Для задачи совместной оптимизации траектории и основных проектных параметров будем рассматривать простую проектную модель КА. В рамках этой проектной модели будем считать, что в состав КА входят “полезная” часть, энергодвигательная установка (ЭДУ) и СХПРТ. Рассматриваемая схема деления КА на составные части представлена на рис. 1. Задачей оптимизации является максимизация массы “полезной” части КА, в состав которой входит полезная нагрузка (целевая аппаратура) и часть системы электроснабжения (СЭС) и других служебных систем КА, которые обеспечивают функционирование полезной нагрузки. В состав ЭДУ входит часть СЭС, необходимая только для обеспечения работы ЭРДУ, система питания и управления (СПУ) ЭРДУ и собственно ЭРД. СХПРТ представляет собой баки для хранения рабочего тела ЭРДУ с трубопроводами и арматурой для обеспечения подачи рабочего тела к ЭРД. Следует отметить, что принятая схема деления КА на составные части не вполне традиционна. Она обусловлена только удобством представления проектной модели КА для решения рассматриваемой задачи оптимизации.
Система электроснабжения состоит из первичного источника мощности (ядерной энергоустановки или солнечных батарей с одноосными приводами), аккумуляторных батарей и аппаратуры регулирования и контроля для стабилизации напряжения на шине питания КА. Если используются солнечные батареи, то ось их вращения перпендикулярна направлению вектора тяги ЭРДУ, что позволяет с помощью трехосной ориентации КА и поворота плоскости солнечных батарей независимо ориентировать вектор тяги ЭРДУ в нужном направлении, а нормаль к рабочей плоскости солнечных батарей – по направлению к Солнцу для обеспечения генерации максимально возможной мощности в каждый момент времени.
Электрическая мощность ЭРДУ в начале полета на гелиоцентрическом удалении 1 а. е. PBOL является одним из выбираемых проектных параметров КА. Зависимость электрической мощности ЭРДУ P от гелиоцентрического удаления r в общем случае представляется в виде
где в случае использования солнечных батарей и регулируемой по мощности ЭРДУ $\rho \left( {r,{{r}_{{\min }}}} \right)$ = = $\min \left( {{{r}^{{ - k}}},r_{{\min }}^{{ - k}}} \right),$ rmin – гелиоцентрическое удаление КА, на котором достигается максимальная мощность ЭРДУ (r и rmin выражается в астрономических единицах), а k – параметр, зависящий от типа и конструктивных особенностей солнечной батареи и имеющий значение в пределах от 1.7 до 2.0. Ограничение максимальной мощности солнечных батарей связано с ограничением мощности, которую можно передать через приводы солнечных батарей, ограниченной мощностью аппаратуры регулирования напряжения на шине питания КА и необходимостью обеспечения теплового режима солнечных батарей при приближении КА к Солнцу, для чего необходим отворот нормали к рабочей плоскости солнечных батарей от направления на Солнце. В случае использования однорежимной (нерегулируемой) ЭРДУ и ядерной энергоустановки (или солнечных батарей с мощностью, достаточной для обеспечения работы ЭРДУ и служебных систем КА на максимальном гелиоцентрическом удалении), ρ(r, rmin) ≡ 1.Масса солнечных батарей для обеспечения работы ЭРДУ пропорциональна их начальной мощности на удалении 1 а. е. от Солнца PBOL, а масса приводов солнечных батарей (через которые передается вырабатываемая солнечными батареями электрическая мощность), масса аппаратуры регулирования и контроля СЭС КА и масса ЭРДУ (собственно двигателей, механизмов их ориентации, системы питания и управления ЭРДУ) пропорциональна максимальной вырабатываемой солнечными батареями электрической мощности PBOLρ(rmin, rmin) на гелиоцентрическом удалении менее rmin, равной максимальной потребляемой мощности регулируемой ЭРДУ. Масса заправленной СХПРТ пропорциональна массе рабочего тела ЭРДУ. Таким образом, начальную массу КА m0 с регулируемой по мощности ЭРДУ после отделения от средств выведения можно представить в следующем виде:
(2)
$\begin{gathered} {{m}_{0}} = {{m}_{u}} + {{m}_{{{\text{Э Д У }}}}} + {{m}_{{{\text{С Х П Р Т }}}}} = \\ = {{m}_{u}} + {\text{ }}[{{\gamma }_{1}} + {{\gamma }_{2}}\rho \left( {{{r}_{{{\text{min}}}}},{{r}_{{{\text{min}}}}}} \right)]{{P}_{{BOL}}} + {\text{ }}\left( {1 + {{a}_{t}}} \right){{m}_{p}},\quad \\ \end{gathered} $где mu – полезная масса КА, mЭДУ – масса ЭДУ, mСХПРТ – масса СХПРТ, γ1 – удельная масса солнечных батарей (в единицах массы на единицу вырабатываемой на гелиоцентрическом удалении 1 а. е. электрической мощности), γ2 – удельная масса аппаратуры регулирования и контроля и приводов солнечных батарей части СЭС для питания ЭРДУ и собственно ЭРДУ (в единицах массы на единицу максимальной расчетной потребляемой электрической мощности ЭРДУ), at – баковый коэффициент, равный отношению сухой массы СХПРТ и невыработанных остатков рабочего тела в конце полета к массе использованного рабочего тела, mp – масса использованного к концу полета рабочего тела ЭРДУ. Очевидно, что при использовании однорежимной ЭРДУ ρ(rmin, rmin) = 1, поэтому выражение для начальной массы КА упрощается:
(3)
$\begin{gathered} {{m}_{0}} = {{m}_{u}} + {{m}_{{{\text{Э Д У }}}}} + {{m}_{{{\text{С Х П Р Т }}}}} = \\ = {{m}_{u}} + {{\gamma }_{3}}{{P}_{{BOL}}} + \left( {1 + {{a}_{t}}} \right){{m}_{p}}, \\ \end{gathered} $где γ3 = γ1 + γ2.
К числу оптимизируемых проектных параметров КА, помимо электрической мощности PBOL, относится эффективная скорость истечения ЭРДУ c. Тяга T, скорость истечения c, полный тяговый к.п.д. η и потребляемая мощность ЭРДУ P связаны известным соотношением:
Полный тяговый к.п.д., в общем случае, может зависеть от c и P, а скорость истечения c – от P. Однако эти зависимости во многом определяются конкретным исполнением ЭРДУ, в частности числом используемых в ЭРДУ двигателей и мощностью одного двигателя. Поэтому на этапе предварительного проектирования КА, для выбора основных параметров ЭРДУ будем считать полный тяговый к.п.д. η заданным и постоянным на всей траектории, а выбираемое значение скорости истечения c – постоянным и не зависящим от текущей мощности питания ЭРДУ. Очевидно, что с учетом (4) значение тяги может быть вычислено с помощью выражения
Таким образом, выбираемыми (оптимизируемыми) проектными параметрами являются начальная электрическая мощность ЭРДУ PBOL, скорость истечения ЭРДУ c и, в общем случае, гелиоцентрическое удаление rmin, на котором достигается максимальная расчетная мощность СЭС и ЭРДУ КА. Начальная масса КА определяется характеристиками средств выведения КА и величиной отлетного гиперболического избытка скорости V∞0, который тоже может оптимизироваться. Остальные перечисленные в этом разделе проектные параметры (η, at, γ1, γ2, γ3, k) относятся к первой группе проектных параметров, определяющих уровень используемых технологий. Они должны задаваться в качестве исходных данных для решения задачи совместной оптимизации траектории и основных проектных параметров PBOL, c, rmin.
2. ФУНКЦИОНАЛ, УРАВНЕНИЯ ДВИЖЕНИЯ И УПРАВЛЕНИЕ
Рассмотрим задачу совместной оптимизации основных проектных параметров КА и траектории прямого гелиоцентрического перелета между двумя заданными планетами за фиксированное время. Задачей совместной оптимизации траектории является максимизация полезной массы КА mu, что эквивалентно минимизации функционала:
(6)
$\begin{gathered} {{J}_{1}} = - {{m}_{u}} = - {{m}_{0}}\left( {{{V}_{{\infty 0}}}} \right) + \\ + \,\,\left[ {{{\gamma }_{1}} + {{\gamma }_{2}}\rho \left( {{{r}_{{\min }}},{{r}_{{\min }}}} \right)} \right]{{P}_{{BOL}}} + \left( {1 + {{a}_{t}}} \right){{m}_{p}}. \\ \end{gathered} $Так как, в рамках принятых допущений все удельные массы, входящие в эту формулу заданы и постоянны, а уравнение для изменения массы КА m можно представить в виде
(7)
$\frac{{dm}}{{dt}} = - \delta \frac{T}{c} = - \delta \frac{{2\eta P\left( {{{P}_{{BOL}}},r,{{r}_{{\min }}}} \right)}}{{{{c}^{2}}}},$(8)
$\begin{gathered} {{J}_{2}} = - {{m}_{0}}\left( {{{V}_{{\infty 0}}}} \right) + {{\gamma }_{3}}{{P}_{{BOL}}} + \\ + \,\,\left( {1 + {{a}_{t}}} \right)\int\limits_{{{t}_{0}}}^{{{t}_{f}}} {\delta \frac{{2\eta P\left( {{{P}_{{BOL}}},r,{{r}_{{\min }}}} \right)}}{{{{c}^{2}}}}dt} , \\ \end{gathered} $Приведем задачу оптимального управления к форме Лагранжа, для чего внесем постоянный на траектории внеинтегральный член функционала J2 под знак интеграла, предварительно разделив все слагаемые в правой части выражения для J2 на положительную постоянную (1 + at). В результате получим функционал, эквивалентный функционалу J1, который будет использоваться в дальнейших выкладках:
(9)
$\begin{gathered} J = \int\limits_{{{t}_{0}}}^{{{t}_{f}}} {\left[ { - \frac{{{{m}_{0}}\left( {{{V}_{{\infty 0}}}} \right)}}{{\Delta t \cdot \left( {1 + {{a}_{t}}} \right)}} + \gamma {{P}_{{BOL}}}} \right.} + \\ \left. { + \,\,\delta \frac{{2\eta P\left( {{{P}_{{BOL}}},r,{{r}_{{\min }}}} \right)}}{{{{c}^{2}}}}} \right]dt, \\ \end{gathered} $Уравнения движения КА с ЭРДУ на гелиоцентрическом участке траектории имеют вид:
(10)
$\frac{{d{\mathbf{r}}}}{{dt}} = {\mathbf{v}},\,\,\,\,\frac{{d{\mathbf{v}}}}{{dt}} = {{\Omega }_{{\mathbf{r}}}} + \delta \frac{T}{m}{{{\mathbf{e}}}_{T}},\,\,\,\,\frac{{dm}}{{dt}} = - \delta \frac{T}{c},$Управлять движением КА можно выбором программы ориентации вектора тяги eT(t) и программы включения-выключения ЭРДУ δ(t). Целью управления является достижение заданного конечного многообразия в фазовом пространстве за заданное время перелета с минимальным значением функционала (9).
3. УСЛОВИЯ ОПТИМАЛЬНОСТИ МОЩНОСТИ И СКОРОСТИ ИСТЕЧЕНИЯ
В общем случае оптимизируемыми проектными параметрами являются начальная электрическая мощность ЭРДУ PBOL, гелиоцентрическое удаление КА rmin, на котором достигается максимальная мощность СЭС и ЭРДУ КА, и скорость истечения ЭРДУ c. Для вывода условий оптимальности этих величин, введем соответствующие фиктивные фазовые переменные. Так как эти оптимизируемые величины постоянны на траектории, дифференциальные уравнения, описывающие их изменение, имеют тривиальный вид:
(11)
$\frac{{d{{P}_{{BOL}}}}}{{dt}} = 0,\,\,\,\,\frac{{d{{r}_{{\min }}}}}{{dt}} = 0,\,\,\,\,\frac{{dc}}{{dt}} = 0.$Полная система дифференциальных уравнений рассматриваемой динамической системы в гелиоцентрической инерциальной системе координат, после замены тяги на ее выражение через потребляемую электрическую мощность, скорость истечения и тяговый к.п.д. ЭРДУ, примет вид:
(12)
$\begin{gathered} \frac{{d{\mathbf{r}}}}{{dt}} = {\mathbf{v}},\,\,\,\,\frac{{d{\mathbf{v}}}}{{dt}} = {{\Omega }_{{\mathbf{r}}}} + {\delta }\frac{{2{\eta }P}}{{mc}}{{{\mathbf{e}}}_{T}},\,\,\,\,\frac{{dm}}{{dt}} = - \delta \frac{{2{\eta }P}}{{{{c}^{2}}}}, \\ \frac{{d{{P}_{{BOL}}}}}{{dt}} = 0,\,\,\,\,\frac{{d{{r}_{{\min }}}}}{{dt}} = 0,\,\,\,\,\frac{{dc}}{{dt}} = 0, \\ \end{gathered} $Функция Понтрягина рассматриваемой задачи оптимального управления имеет вид:
(13)
$\begin{gathered} H = \frac{{{{m}_{0}}\left( {{{V}_{{\infty 0}}}} \right)}}{{\Delta t \cdot \left( {1 + {{a}_{t}}} \right)}} - \gamma {{P}_{{BOL}}} - \delta \frac{{2\eta P}}{{{{c}^{2}}}} + {\mathbf{p}}_{r}^{T}{\mathbf{v}} + \\ + \,\,{\mathbf{p}}_{v}^{T}{{\Omega }_{{\mathbf{r}}}} + {\delta }\frac{{2{\eta }P}}{{mc}}{\mathbf{p}}_{v}^{T}{{{\mathbf{e}}}_{T}} - \delta \frac{{2{\eta }P}}{{{{c}^{2}}}}{{p}_{m}}, \\ \end{gathered} $(14)
$\begin{gathered} H = \frac{{{{m}_{0}}\left( {{{V}_{{\infty 0}}}} \right)}}{{\Delta t \cdot \left( {1 + {{a}_{t}}} \right)}} - \gamma {{P}_{{BOL}}} + {\mathbf{p}}_{r}^{T}{\mathbf{v}} + \\ + \,\,{\mathbf{p}}_{v}^{T}{{\Omega }_{{\mathbf{r}}}} + \delta \frac{{2\eta P}}{c}S, \\ \end{gathered} $(15)
${{{\mathbf{e}}}_{T}} = \frac{{{{{\mathbf{p}}}_{v}}}}{{{{p}_{v}}}},\,\,\,\,\delta = \left\{ \begin{gathered} 1,\,\,\,\,S > 0, \hfill \\ 0,\,\,\,\,S \leqslant 0, \hfill \\ \end{gathered} \right.$Уравнения оптимального движения имеют вид:
(17)
$\begin{gathered} \frac{{d{\mathbf{r}}}}{{dt}} = {\mathbf{v}},\,\,\,\,\frac{{d{\mathbf{v}}}}{{dt}} = {{\Omega }_{{\mathbf{r}}}} + \delta \frac{{2{\eta }P}}{{mc}}\frac{{{{{\mathbf{p}}}_{v}}}}{{{{p}_{v}}}},\,\,\,\,\frac{{dm}}{{dt}} = - \delta \frac{{2\eta P}}{{{{c}^{2}}}}, \\ \frac{{d{{P}_{{BOL}}}}}{{dt}} = 0,\,\,\,\,\frac{{d{{r}_{{\min }}}}}{{dt}} = 0,\,\,\,\,\frac{{dc}}{{dt}} = 0, \\ \frac{{d{{{\mathbf{p}}}_{r}}}}{{dt}} = - {{\Omega }_{{{\mathbf{rr}}}}}{{{\mathbf{p}}}_{v}} - \delta \frac{{2\eta }}{c}{{P}_{{BOL}}}\frac{{\partial \rho \left( {r,{{r}_{{\min }}}} \right)}}{{\partial r}}\frac{{\mathbf{r}}}{r}S, \\ \frac{{d{{{\mathbf{p}}}_{v}}}}{{dt}} = - {{{\mathbf{p}}}_{r}},\,\,\,\,\frac{{d{{p}_{m}}}}{{dt}} = \delta \frac{{2\eta P}}{c}\frac{{{{p}_{v}}}}{{{{m}^{2}}}},\,\,\,\,\frac{{d{{p}_{{P\;BOL}}}}}{{dt}} = \gamma \left( {{{r}_{{\min }}}} \right) - \\ - \,\,\delta \frac{{2\eta }}{c}\rho \left( {r,{{r}_{{\min }}}} \right)S,\,\,\,\,\frac{{d{{p}_{c}}}}{{dt}} = \delta \frac{{2\eta }}{{{{c}^{2}}}}P \cdot \left( {\frac{{{{p}_{v}}}}{m} - 2\frac{{{{p}_{m}} + 1}}{c}} \right), \\ \frac{{d{{p}_{{r\min }}}}}{{dt}} = \frac{{\partial \gamma \left( {{{r}_{{\min }}}} \right)}}{{\partial {{r}_{{\min }}}}}{{P}_{{BOL}}} - \delta \frac{{2\eta }}{c}{{P}_{{BOL}}}\frac{{\partial {\rho }\left( {r,{{r}_{{\min }}}} \right)}}{{\partial {{r}_{{\min }}}}}S, \\ \end{gathered} $Так как значения PBOL, rmin и c оптимизируются, они свободны на обеих концах траектории. Поэтому, в силу условий трансверсальности, сопряженные к ним переменные должны принимать нулевые значения на левом и правом концах траектории:
(18)
$\begin{gathered} {{p}_{{P\,BOL}}}\left( {{{t}_{0}}} \right) = 0,\,\,\,\,{{p}_{c}}\left( {{{t}_{0}}} \right) = 0,\,\,\,\,{{p}_{{r\min }}}\left( {{{t}_{0}}} \right) = 0, \\ {{p}_{{P\,BOL}}}\left( {{{t}_{f}}} \right) = 0,\,\,\,\,{{p}_{c}}\left( {{{t}_{f}}} \right) = 0,\,\,\,\,{{p}_{{r\min }}}\left( {{{t}_{f}}} \right) = 0. \\ \end{gathered} $Эти условия должны быть добавлены к начальным и конечным условиям краевой задачи принципа максимума в случае оптимизации PBOL, rmin и c совместно с траекторией. Очевидно, что приведенные условия оптимальности PBOL, rmin и c можно переписать в виде равенства нулю следующих интегралов:
(19)
$\begin{gathered} \int\limits_{{{t}_{0}}}^{{{t}_{f}}} {\left[ {\gamma \left( {{{r}_{{\min }}}} \right) - \delta \frac{{2\eta }}{c}\rho \left( {r,{{r}_{{\min }}}} \right)S} \right]} dt = 0, \\ \int\limits_{{{t}_{0}}}^{{{t}_{f}}} {\left[ {\delta \frac{{2\eta }}{{{{c}^{2}}}}P \cdot \left( {\frac{{{{p}_{v}}}}{m} - 2\frac{{{{p}_{m}} + 1}}{c}} \right)} \right]} dt = 0, \\ \int\limits_{{{t}_{0}}}^{{{t}_{f}}} {\left[ {\frac{{\partial \gamma \left( {{{r}_{{\min }}}} \right)}}{{\partial {{r}_{{\min }}}}}{{P}_{{SA\,BOL}}} - \delta \frac{{2\eta }}{c}{{P}_{{SA\,BOL}}}\frac{{\partial \rho \left( {r,{{r}_{{\min }}}} \right)}}{{\partial {{r}_{{\min }}}}}S} \right]} dt = 0. \\ \end{gathered} $Естественно, что при рассмотрении однорежимной ЭРДУ, необходимые условия оптимальности для rmin должны быть исключены из рассмотрения.
4. КРАЕВЫЕ УСЛОВИЯ И УСЛОВИЯ ОПТИМАЛЬНОСТИ ТРАЕКТОРНЫХ ПАРАМЕТРОВ
В рамках метода точечных сфер действия, длительности планетоцентрических участков считаются нулевыми, вектор положения КА в момент начала или окончания гелиоцентрического участка траектории совпадает с гелиоцентрическим радиус-вектором планеты, а вектор скорости КА в эти моменты времени равен сумме векторов гелиоцентрической скорости планеты и гиперболического избытка скорости КА. Поэтому, в начальный момент времени t0 краевые условия можно записать в виде:
(20)
$\begin{gathered} {\mathbf{r}}\left( {{{t}_{0}}} \right) = {{{\mathbf{r}}}_{{pl0}}}\left( {{{t}_{0}}} \right),\,\,\,\,{\mathbf{v}}\left( {{{t}_{0}}} \right) = {{{\mathbf{v}}}_{{pl0}}}\left( {{{t}_{0}}} \right) + {{{\mathbf{V}}}_{{\infty 0}}}, \\ m\left( {{{t}_{0}}} \right) = {{m}_{0}}\left( {{{V}_{{\infty 0}}}} \right), \\ \end{gathered} $Если значение отлетного гиперболического избытка скорости V∞0 = |V∞0| в начальный момент времени t0 задано и не равно 0, то условие на начальный вектор гелиоцентрической скорости КА из (20) может быть переписано в виде
(21)
$\psi = \frac{1}{2}{{\left[ {{\mathbf{v}}\left( {{{t}_{0}}} \right) - {{{\mathbf{v}}}_{{pl0}}}\left( {{{t}_{0}}} \right)} \right]}^{2}} - \frac{1}{2}V_{{\infty 0}}^{2}.$Краевое условие (21) приводит к условию трансверсальности
(22)
$\begin{gathered} {{{\mathbf{p}}}_{v}}\left( {{{t}_{0}}} \right) = {{{\mu }}_{{V0}}} \cdot {{\left( {\frac{{\partial \psi }}{{\partial {\mathbf{v}}\left( {{{t}_{0}}} \right)}}} \right)}^{T}} = \\ = {{\mu }_{{V0}}} \cdot \left[ {{\mathbf{v}}\left( {{{t}_{0}}} \right) - {{{\mathbf{v}}}_{{pl0}}}\left( {{{t}_{0}}} \right)} \right] = {{{\mu }}_{{V0}}}{{{\mathbf{V}}}_{{\infty 0}}}, \\ \end{gathered} $При достаточно малых значениях V∞0 (точнее, при V∞0, меньшем некоторого критического значения) неопределенный множитель Лагранжа μV0 положителен, поэтому уравнение (22) может быть переписано в виде
(23)
${{{\mathbf{V}}}_{{\infty 0}}} = {{V}_{{\infty 0}}}\frac{{{{{\mathbf{p}}}_{v}}\left( {{{t}_{0}}} \right)}}{{{{p}_{v}}\left( {{{t}_{0}}} \right)}},$(24)
$\begin{gathered} {\mathbf{r}}\left( {{{t}_{0}}} \right) = {{{\mathbf{r}}}_{{pl0}}}\left( {{{t}_{0}}} \right),\,\,\,\,{\mathbf{v}}\left( {{{t}_{0}}} \right) = {{{\mathbf{v}}}_{{pl0}}}\left( {{{t}_{0}}} \right) + {{V}_{{\infty 0}}}\frac{{{{{\mathbf{p}}}_{v}}\left( {{{t}_{0}}} \right)}}{{{{p}_{v}}\left( {{{t}_{0}}} \right)}}, \\ m\left( {{{t}_{0}}} \right) = {{m}_{0}}\left( {{{V}_{{\infty 0}}}} \right). \\ \end{gathered} $При нулевом отлетном гиперболическом избытке скорости начальные условия (24) упрощаются:
(25)
$\begin{gathered} {\mathbf{r}}\left( {{{t}_{0}}} \right) = {{{\mathbf{r}}}_{{pl0}}}\left( {{{t}_{0}}} \right),\,\,\,\,{\mathbf{v}}\left( {{{t}_{0}}} \right) = {{{\mathbf{v}}}_{{pl0}}}\left( {{{t}_{0}}} \right), \\ m\left( {{{t}_{0}}} \right) = {{m}_{0}}\left( 0 \right). \\ \end{gathered} $В общем случае, для произвольного (возможно, достаточно большого) значения V∞0, начальные условия (24) следует переписать в виде
(26)
$\begin{gathered} {\mathbf{r}}\left( {{{t}_{0}}} \right) = {{{\mathbf{r}}}_{{pl0}}}\left( {{{t}_{0}}} \right),\,\,\,\,{\mathbf{v}}\left( {{{t}_{0}}} \right) = {{{\mathbf{v}}}_{{pl0}}}\left( {{{t}_{0}}} \right) + {{{\mathbf{V}}}_{{\infty 0}}}, \\ m\left( {{{t}_{0}}} \right) = {{m}_{0}}\left( {{{V}_{{\infty 0}}}} \right),\,\,\,\,{{{\mathbf{p}}}_{v}}\left( {{{t}_{0}}} \right) = {{\mu }_{{V0}}}{{{\mathbf{V}}}_{{\infty 0}}}, \\ {\mathbf{V}}_{{\infty 0}}^{T}{{{\mathbf{V}}}_{{\infty 0}}} - V_{{\infty 0}}^{2} = 0, \\ \end{gathered} $Выведем необходимые условия оптимальности вектора отлетного гиперболического избытка скорости, считая известной зависимость начальной массы КА на отлетной траектории m0 от величины отлетного гиперболического избытка скорости V∞0:
Введем фиктивную фазовую переменную V∞0:
(28)
${{d{{V}_{{\infty 0}}}} \mathord{\left/ {\vphantom {{d{{V}_{{\infty 0}}}} {dt}}} \right. \kern-0em} {dt}} = 0.$Дифференциальное уравнение для сопряженной к V∞0 переменной имеет вид:
(29)
$\frac{{d{{p}_{{V\infty 0}}}}}{{dt}} = - \frac{{\partial H}}{{\partial {{V}_{{\infty 0}}}}} = - \frac{1}{{\Delta t \cdot \left( {1 + {{a}_{t}}} \right)}}\frac{{\partial {{m}_{0}}}}{{\partial {{V}_{{\infty 0}}}}}.$В конечный момент времени tf значение переменной V∞0 не задано, поэтому
Так как правая часть (29) – постоянная, то
(31)
${{p}_{{V\infty 0}}}\left( {{{t}_{0}}} \right) = \frac{1}{{1 + {{a}_{t}}}}\frac{{\partial {{m}_{0}}}}{{\partial {{V}_{{\infty 0}}}}}.$В начальный момент времени t0 должны выполняться следующие условия, связанные с величиной отлетной скорости:
(32)
$\begin{gathered} \psi = \\ = \left( \begin{gathered} {{\left( {{\mathbf{v}}\left( {{{t}_{0}}} \right) - {{{\mathbf{v}}}_{{pl0}}}\left( {{{t}_{0}}} \right)} \right)}^{T}}\left( {{\mathbf{v}}\left( {{{t}_{0}}} \right) - {{{\mathbf{v}}}_{{pl0}}}\left( {{{t}_{0}}} \right)} \right) - V_{{\infty 0}}^{2} \hfill \\ m\left( {{{t}_{0}}} \right) - {{m}_{0}}\left( {{{V}_{{\infty 0}}}} \right) \hfill \\ \end{gathered} \right) = 0. \\ \end{gathered} $Отсюда следует, что при t = t0 значения переменных, сопряженных к скорости, отлетному гиперболическому избытку скорости и массе, должны удовлетворять следующим условиям:
(33)
$\begin{gathered} {{{\mathbf{p}}}_{v}}\left( {{{t}_{0}}} \right) = 2{{{\mu }}_{1}}\left( {{\mathbf{v}}\left( {{{t}_{0}}} \right) - {{{\mathbf{v}}}_{{pl0}}}} \right),\,\,\,\,{{p}_{{V\infty 0}}}\left( {{{t}_{0}}} \right) = \\ = - 2{{\mu }_{1}}{{V}_{{\infty 0}}} - {{\mu }_{2}}\frac{{\partial {{m}_{0}}}}{{\partial {{V}_{{\infty 0}}}}},\,\,\,\,{{p}_{m}}\left( {{{t}_{0}}} \right) = {{\mu }_{2}}, \\ \end{gathered} $Второе и третье уравнения (33), с учетом (31), позволяют получить следующее выражение для неопределенного множителя Лагранжа μ1:
(34)
${{{\mu }}_{1}} = - \frac{1}{{2{{V}_{{\infty 0}}}}}\left[ {{{p}_{m}}\left( {{{t}_{0}}} \right) + \frac{1}{{1 + {{a}_{t}}}}} \right]\frac{{\partial {{m}_{0}}}}{{\partial {{V}_{{\infty 0}}}}}.$Подставляя это выражение в первое уравнение (33), получим необходимое условие оптимальности для оптимального вектора отлетного гиперболического избытка скорости ${{{\mathbf{V}}}_{{\infty 0}}} = {\mathbf{v}}\left( {{{t}_{0}}} \right) - {{{\mathbf{v}}}_{{pl0}}}\,:$
(35)
${{{\mathbf{p}}}_{v}}\left( {{{t}_{0}}} \right) = - \frac{1}{{{{V}_{{\infty 0}}}}}\left[ {{{p}_{m}}\left( {{{t}_{0}}} \right) + \frac{1}{{1 + {{a}_{t}}}}} \right]\frac{{\partial {{m}_{0}}}}{{\partial {{V}_{{\infty 0}}}}}{{{\mathbf{V}}}_{{\infty 0}}}.$Как и в случае с заданной величиной отлетного гиперболического вектора скорости, сопряженный к скорости вектор на оптимальной траектории должен быть параллельным вектору начального (отлетного) гиперболического избытка скорости. Оптимальная величина отлетного гиперболического избытка скорости определяется с помощью вытекающего из (35) условия в виде:
(36)
${{p}_{v}}\left( {{{t}_{0}}} \right) = - \left[ {{{p}_{m}}\left( {{{t}_{0}}} \right) + \frac{1}{{1 + {{a}_{t}}}}} \right]\frac{{\partial {{m}_{0}}}}{{\partial {{V}_{{\infty 0}}}}}.$Краевые условия в конечный момент времени tf для задачи сопровождения (подлета к планете назначения с нулевым гиперболическим избытком скорости) имеют вид:
(37)
${\mathbf{r}}\left( {{{t}_{f}}} \right) = {{{\mathbf{r}}}_{{plf}}}\left( {{{t}_{f}}} \right),\,\,\,\,{\mathbf{v}}\left( {{{t}_{f}}} \right) = {{{\mathbf{v}}}_{{plf}}}\left( {{{t}_{f}}} \right),$В последнем случае конечные условия (38) должны быть дополнены условиями трансверсальности
В случае, если момент отлета от планеты отправления t0 не задан, но время перелета Δt фиксировано, условие трансверсальности для определения оптимального значения t0 имеет следующий вид:
(40)
$\begin{gathered} {\mathbf{p}}_{{r0}}^{T}{{{\mathbf{V}}}_{{\infty 0}}} + {\mathbf{p}}_{{v0}}^{T}\left( {{{\Omega }_{{{\mathbf{r}}0}}} - {{{\mathbf{a}}}_{{pl0}}}} \right) - \\ - \,\,{\mathbf{p}}_{{vf}}^{T}\left( {{{\Omega }_{{{\mathbf{r}}f}}} - {{{\mathbf{a}}}_{{plf}}}} \right) + {{\delta }_{0}}{{T}_{0}}{{S}_{0}} - {{\delta }_{f}}{{T}_{f}}{{S}_{f}} = 0, \\ \end{gathered} $(41)
$\begin{gathered} {\mathbf{p}}_{{r0}}^{T}{{{\mathbf{V}}}_{{\infty 0}}} + {\mathbf{p}}_{{v0}}^{T}\left( {{{\Omega }_{{{\mathbf{r}}0}}} - {{{\mathbf{a}}}_{{pl0}}}} \right) - {\mathbf{p}}_{{rf}}^{T}{{{\mathbf{V}}}_{{\infty f}}} - \\ - \,\,{\mathbf{p}}_{{vf}}^{T}{{\Omega }_{{{\mathbf{r}}f}}} + {{\delta }_{0}}{{T}_{0}}{{S}_{0}} - {{\delta }_{f}}{{T}_{f}}{{S}_{f}} = 0, \\ \end{gathered} $Во всех рассматриваемых вариантах конечное значение массы КА m(tf) не задано, поэтому к конечным условиям должно быть добавлено условие трансверсальности на сопряженную к массе переменную
5. КРАЕВАЯ ЗАДАЧА И МЕТОД ЕЕ РЕШЕНИЯ
Рассматриваемая задача оптимизации свелась к краевой задаче для системы обыкновенных дифференциальных уравнений (17) с начальными условиями (24), (25) или (26), к которым добавляются нужные дополнительные начальные условия из трех первых уравнений (18) при необходимости оптимизации PBOL, c и rmin. При необходимости оптимизации величины V∞0 к начальным условиям добавляется (36). Конечными условиями являются (37) или (38), (39), дополненные условиями трансверсальности (42), и, при необходимости, дополнительными условиями трансверсальности в конечный момент времени на сопряженные к PBOL, c и rmin переменные из числа трех последних уравнений (18). При необходимости оптимизации t0 к перечисленным начальным и конечным условиям добавляются смешанные условия (40) или (41), содержащие значения фазовых переменных на обеих концах траектории.
Неизвестными параметрами краевой задачи являются значения сопряженных переменных pr, pv и pm в начальный момент времени t0 и, при необходимости, значения основных проектных параметров PBOL, c и rmin и траекторных параметров V∞0 и t0. Для удовлетворения необходимых условий оптимальности необходимо вычислить такие значения этих параметров, чтобы удовлетворялись шесть конечных условий (37) для задачи сопровождения или шесть граничных условий (38), (39) для задачи пролета, одно условие трансверсальности (42) и, при необходимости, три условия трансверсальности для PBOL, c и rmin в момент tf (три последние уравнения (18)), условие оптимальности V∞0 (36) и условие оптимальности t0 (40) или (41). Таким образом, порядок краевой задачи (число неизвестных переменных и число краевых условий, которые необходимо удовлетворить) может изменяться от 7 при проведении оптимизации только управления до 12 при проведении совместной оптимизации управления и всех рассматриваемых проектных и траекторных параметров.
Для решения краевой задачи используется метод непрерывного продолжения по параметру (ньютоновской гомотопии), редуцирующий краевую задачу к задаче Коши [13, 14]. В качестве начального приближения для неизвестных параметров краевой задачи используется решение задачи оптимизации перелета с идеально-регулируемым двигателем ограниченной мощности [13], при необходимости используется метод продолжения по гравитационному параметру для вычисления экстремали с заданным числом целых оборотов вокруг Солнца [13]. В качестве начального значения скорости истечения может приниматься ее среднее значение на решении с идеально-регулируемым двигателем заданной мощности. Начальное приближение для V∞0 может быть выбрано нулевым, а для t0 – произвольной величиной внутри интересующего диапазона изменения даты отлета. Довольно сложным оказался вопрос выбора начального приближения для rmin, на практике это начальное приближение подбиралось вручную для обеспечения сходимости решения краевой задачи. В правых частях системы дифференциальных уравнений оптимального движения была реализована гомотопия между правыми частями дифференциальных уравнений для КА с идеально-регулируемым двигателем [13] и КА с рассматриваемым однорежимным или регулируемым двигателем ограниченной тяги и постоянной скорости истечения [14]. При начальном значении параметра продолжения τ = 0 правые части этих дифференциальных уравнений совпадают с правыми частями дифференциальных уравнений для КА с идеально-регулируемым двигателем, а при конечном значении параметра продолжения τ = 1 – с правыми частями системы (17).
Для регуляризации процесса продолжения при решении краевой задачи с разрывным управлением, используется “естественное” сглаживание функции тяги в предложенном в работе [14] виде:
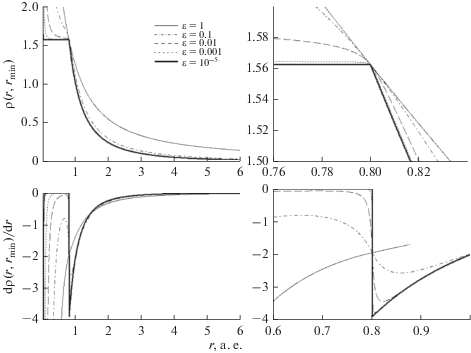
В правые части уравнений оптимального движения входит функция ρ(r, rmin), имеющая излом в точке r = rmin и ее производная, имеющая разрыв в этой точке. Для облегчения решения краевой задачи принципа максимума используется гладкая аппроксимация этой функции вида:
Зависимость сглаженного представления функции ρ(r, rmin) и ее производной от r представлена на рис. 2. Видна гладкость этих зависимостей и практическая неотличимость сглаженной функции от оригинальной при ε = 10–5.
6. ЧИСЛЕННЫЕ ПРИМЕРЫ
Рассмотрим приложение разработанного метода к задачам оптимизации перелетов КА с ЭРДУ к Марсу и Меркурию.
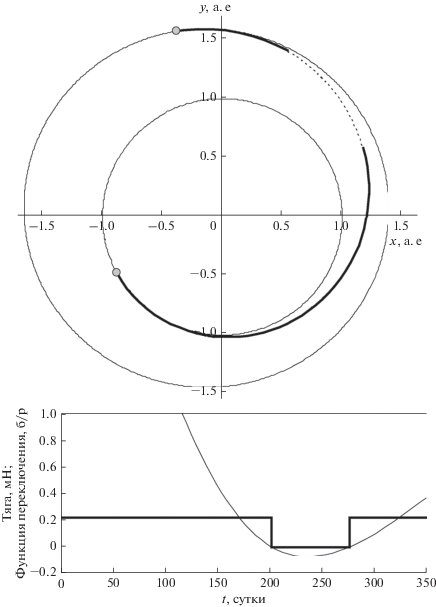
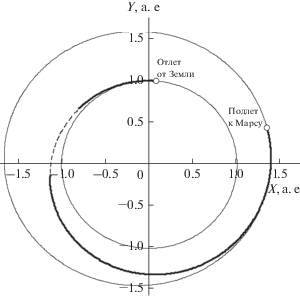
В первом примере рассмотрим задачу оптимизации перелета КА с маршевой ЭРДУ к Марсу для даты отлета от Земли 20.IV.2035, нулевого отлетного гиперболического избытка скорости, длительности перелета Δt = 350 суток и начальной массы КА m0 = 1000 кг. На рис. 3 приведен пример оптимальной траектории с оптимальными параметрами ЭРДУ для следующих значений проектных параметров, определяющих уровень используемых технологий: к.п.д. ЭРДУ η = 0.5, удельная масса ЭДУ γ3 = 40 кг/кВт, относительная масса СХПРТ at = 0.1. В результате решения оптимизационной задачи, кроме оптимальной программы управления, определены оптимальные для данного случая значения удельного импульса тяги Iуд = c/g0 = 2374 с (g0 = 9.80665 м/с2 – стандартное ускорение свободного падения), тяги T = 220.39 мН и электрической мощности ЭРДУ P = 5131 Вт. Затраты рабочего тела ЭРДУ на оптимальной траектории составляют mp = 224.89 кг, а полезная масса КА – mu = 547.39 кг.
В верхней части рис. 3 приведена проекция оптимальной траектории на плоскость эклиптики (участки работы ЭРДУ обозначены толстыми линиями, а участок пассивного полета КА – пунктиром). Тонкими линиями обозначены орбиты Земли и Марса. Круглыми маркерами обозначены положения Земли в момент отлета КА и положение Марса в момент прибытия к нему КА. На нижней части рисунка представлены зависимости от времени функции переключения S (тонкая линия) и тяги T (толстая линия).
В табл. 1 представлены результаты совместной оптимизации траектории перелета к Марсу и основных проектных параметров ЭРДУ для различных значений проектных параметров η, γ3, и at, характеризующих уровень используемой технологии. Оптимальное значение удельного импульса растет с уменьшением γ и с увеличением η и at, а оптимальное значение электрической мощности ЭРДУ растет с уменьшением η и γ и с увеличением at. Конечно, максимальное значение полезной массы КА достигается при максимальном значении к.п.д. ЭРДУ и минимальных значениях удельной массы ЭДУ и относительной массы СХПРТ.
Таблица 1.
Результаты совместной оптимизации траектории перелета к Марсу и основных проектных параметров ЭРДУ для различных значений проектных параметров, характеризующих уровень используемой технологии
| № п/п | η | γ3, кг/кВт | at | Iуд, с | T, мН | m(tf), кг | mp, кг | mЭДУ, кг | mu, кг | P, Вт |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.7 | 40 | 0.1 | 2869 | 222.66 | 809.95 | 190.05 | 178.99 | 611.96 | 4474 |
| 2 | 0.5 | 40 | 0.1 | 2374 | 220.39 | 775.11 | 224.89 | 205.23 | 547.39 | 5131 |
| 3 | 0.5 | 80 | 0.1 | 1580 | 214.05 | 681.77 | 318.23 | 265.28 | 384.67 | 3316 |
| 4 | 0.5 | 40 | 0.2 | 2494 | 221.02 | 784.69 | 215.31 | 216.24 | 525.39 | 5406 |
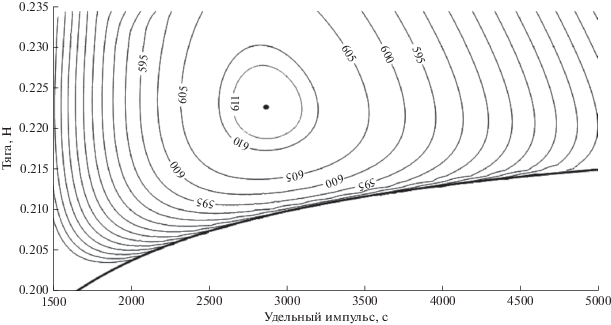
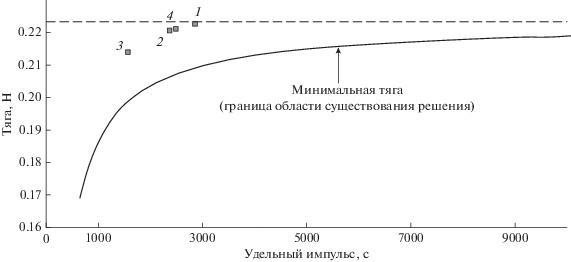
На рис. 4 квадратными маркерами обозначены результаты оптимизации основных проектных параметров ЭРДУ, представленные на плоскости удельный импульс–тяга. Номера у маркеров соответствуют варианту из табл. 1. Сплошной линией на этом рисунке представлена зависимость минимальной тяги от удельного импульса тяги, ограничивающая снизу область существования решений, пунктирной линией – асимптотическое значение минимальной тяги при стремлении удельного импульса к бесконечности. Кривая минимальной тяги была получена с использованием методики, приведенной в [15–17].
Рис. 4.
Оптимальные значения удельного импульса тяги и тяги ЭРДУ (квадратные маркеры) для траектории перелета к Марсу при различных значениях проектных параметров, характеризующих уровень используемых технологий.
В табл. 2 приведены результаты совместной оптимизации основных проектных параметров ЭРДУ и траектории КА для η = 0.7, γ3 = 40 кг/кВт и at = 0.1, длительности перелета Δt = 350 суток и начальной массы КА m0 = 1000 кг для различных значений отлетного гиперболического избытка скорости V∞0. Оптимальная электрическая мощность ЭРДУ монотонно снижается с ростом V∞0, оптимальное значение тяги имеет минимум, а оптимальный удельный импульс тяги – максимум по V∞0. Полезная масса КА монотонно растет с ростом V∞0, так как в рассматриваемом случае начальная масса КА на отлетной от Земли траектории не снижается с ростом V∞0.
Таблица 2.
Зависимость оптимальных значений основных проектных параметров от значения отлетного от Земли гиперболического избытка скорости на траектории перелета к Марсу
| V∞0, м/с | T, мН | Iуд, с | m(tf), кг | mp, кг | mЭДУ, кг | mu, кг | P, Вт |
|---|---|---|---|---|---|---|---|
| 0 | 222.66 | 2869 | 809.95 | 190.05 | 178.99 | 611.96 | 4474 |
| 1000 | 160.77 | 3206 | 849.56 | 150.44 | 144.44 | 690.08 | 3611 |
| 2000 | 137.08 | 3214 | 869.71 | 130.29 | 123.43 | 733.25 | 3086 |
| 3000 | 137.43 | 2997 | 879.46 | 120.54 | 115.40 | 752.01 | 2885 |
| 3500 | 140.02 | 2896 | 881.94 | 118.06 | 113.63 | 756.49 | 2841 |
На рис. 5 приведены изолинии полезной массы КА на плоскости удельный импульс–тяга ЭРДУ для случая, соответствующего первым строкам табл. 1 и 2. Максимум полезной массы (около 612 кг) достигается в точке, отмеченной круглым маркером. Этот максимум довольно пологий – при отклонении удельного импульса от оптимального значения на 300 с (на 10.5%) или отклонении тяги от оптимального значения на величину до 7 мН (на 3.1%) полезная масса уменьшается только на 2 кг (0.3%). Линии уровня полезной массы ограничены снизу кривой минимальной тяги (толстая линия на рис. 5). При значениях тяги и удельного импульса, лежащих на этой кривой, на траектории перелета отсутствуют пассивные участки, поэтому любое снижение величины тяги ниже этой линии приводит к невозможности реализации перелета за заданное время [15–17].
Для оптимизации величины V∞0 необходима зависимость m0(V∞0), определяемая характеристиками средств выведения КА на отлетную траекторию. Представим ее в виде аппроксимирующего полинома
В табл. 3 представлены коэффициенты ai, определенные методом наименьших квадратов из данных, представленных в руководствах пользователя для ракеты-носителя (РН) “Союз-2.1Б” с разгонным блоком (РБ) “Фрегат” [8] и РН “Протон-М” с РБ “Бриз-М” [9]. Для приведенных значений коэффициентов V∞0 задается в м/с, а масса определяется в кг.
Таблица 3.
Коэффициенты разложения аппроксимирующих зависимостей начальной массы КА от отлетного гиперболического избытка скорости
| i | “Союз-2.1Б” + “Фрегат” | “Протон-М” + “Бриз-М” |
|---|---|---|
| 0 | 2.033309 · 103 | 6.474400 · 103 |
| 1 | –5.623431 · 10–2 | 2.820072 · 10–2 |
| 2 | 5.265562 · 10–5 | –1.869981 · 10–4 |
| 3 | –8.146719 · 10–8 | 5.229323 · 10–8 |
| 4 | 3.631484 · 10–11 | –1.776752 · 10–11 |
| 5 | –7.845370 · 10–15 | 3.061888 · 10–15 |
| 6 | 6.651509 · 10–19 | –1.902993 · 10–19 |
Результаты совместной оптимизации основных проектных параметров КА, отлетного гиперболического избытка скорости и управления вектором тяги ЭРДУ представлены в табл. 4. Как и прежде, используются значения к.п.д. ЭРДУ, удельной массы ЭДУ и относительной массы СХПРТ из первой строки табл. 1, t0 = 20.IV.2035, Δt = 350 суток.
Таблица 4.
Зависимость оптимальных значений основных проектных параметров от значения отлетного от Земли гиперболического избытка скорости на траектории перелета к Марсу
| РН | V∞0, м/с | T, мН | Iуд, с | m0, кг | mp, кг | mЭДУ, кг | mu, кг | P, Вт |
| “Союз-2.1Б” | 1376.4 | 287.51 | 3257 | 1939.16 | 272.17 | 262.40 | 1377.38 | 6560 |
| “Протон-М” | 1474.2 | 906.41 | 3254 | 6212.56 | 858.93 | 826.42 | 4441.32 | 20 661 |
Оптимальные значения удельного импульса и V∞0 получились близкими для случая использования РН “Союз-2.1Б” с РБ “Фрегат” и РН “Протон-М” с РБ “Бриз-М”. Оказалось, что в обоих случаях гелиоцентрические траектории не содержат пассивных участков, то есть оптимальное значение тяги оказалось равным минимальному ее значению. В связи с этим возникает вопрос, насколько такая ситуация характерна при совместной оптимизации основных проектных параметров КА и величины отлетного гиперболического избытка скорости.
Рассмотрим КА с однорежимной ЭРДУ и со следующими параметрами, определяющими уровень используемых технологий: γ3 = 50 кг/кВт, at = 0.1, η = 0.7. В табл. 5–7 представлены оптимальные траекторные и проектные параметры как функции от смещения даты старта Δt0 от номинальной даты 20.IV.2035 для длительности перелета 250, 300 и 350 суток соответственно. В качестве средства выведения КА на отлетную траекторию рассматривается РН “Союз-2.1Б” с РБ “Фрегат”.
Таблица 5.
Зависимость оптимальных параметров от смещения даты старта (длительность перелета 250 суток)
| Δt0, сут | T, Н | c, м/с | V∞0, м/с | m0, кг | mp, кг | P, Вт | mu, кг |
|---|---|---|---|---|---|---|---|
| 10 | 0.5845 | 18 181.0 | 1740.7 | 1891.8 | 492.7 | 7590.8 | 970.3 |
| 20 | 0.5370 | 18 732.0 | 1734.1 | 1892.8 | 450.4 | 7185.7 | 1038.0 |
| 30 | 0.4894 | 19 297.1 | 1770.1 | 1887.6 | 409.5 | 6745.8 | 1099.8 |
| 40 | 0.4428 | 19 822.6 | 1885.4 | 1870.4 | 369.3 | 6269.5 | 1150.7 |
| 50 | 0.3995 | 20 300.8 | 2115.1 | 1833.4 | 332.4 | 5792.9 | 1178.1 |
| 60 | 0.3633 | 20 630.3 | 2413.8 | 1780.1 | 300.6 | 5353.5 | 1181.8 |
| 70 | 0.3367 | 20 739.6 | 2822.6 | 1697.8 | 276.1 | 4988.3 | 1144.7 |
| 80 | 0.3219 | 20 632.1 | 3312.9 | 1585.9 | 261.6 | 4743.6 | 1060.9 |
| 90 | 0.3154 | 20 288.2 | 3857.1 | 1451.4 | 254.4 | 4570.3 | 943.0 |
Таблица 6.
Зависимость оптимальных параметров от смещения даты старта (длительность перелета 300 суток)
| Δt0, сут | T, Н | c, м/с | V∞0, м/с | m0, кг | mp, кг | P, Вт | mu, кг |
|---|---|---|---|---|---|---|---|
| –10 | 0.4044 | 23 280.0 | 1403.1 | 1936.0 | 401.8 | 6725.3 | 1157.7 |
| 0 | 0.3714 | 23 955.6 | 1436.2 | 1932.1 | 371.1 | 6354.7 | 1206.1 |
| 10 | 0.3384 | 24 668.8 | 1478.4 | 1926.9 | 341.2 | 5963.4 | 1253.4 |
| 20 | 0.3075 | 25 399.5 | 1571.4 | 1915.0 | 313.5 | 5578.8 | 1291.2 |
| 30 | 0.2849 | 25 685.3 | 1689.7 | 1899.0 | 287.5 | 5227.3 | 1321.4 |
| 40 | 0.2653 | 25 899.0 | 1863.6 | 1873.7 | 265.6 | 4908.7 | 1336.2 |
| 50 | 0.2495 | 26 041.5 | 2125.8 | 1831.6 | 248.3 | 4640.3 | 1326.5 |
| 60 | 0.2382 | 26 093.6 | 2419.7 | 1779.0 | 236.6 | 4439.3 | 1296.8 |
| 70 | 0.2374 | 25 372.1 | 2802.6 | 1702.1 | 228.6 | 4301.7 | 1235.6 |
| 80 | 0.2442 | 24 417.1 | 3228.5 | 1606.0 | 227.4 | 4259.9 | 1142.9 |
| 90 | 0.2572 | 23 439.6 | 3659.8 | 1500.5 | 233.3 | 4306.3 | 1028.6 |
Таблица 7.
Зависимость оптимальных параметров от смещения даты старта (длительность перелета 350 суток)
| Δt0, сут | T, Н | c, м/с | V∞0, м/с | m0, кг | mp, кг | P, Вт | mu, кг |
|---|---|---|---|---|---|---|---|
| –50 | 0.3431 | 27 021.6 | 1198.8 | 1958.6 | 383.9 | 6621.3 | 1205.3 |
| –40 | 0.3266 | 27 410.1 | 1249.6 | 1953.3 | 360.3 | 6394.1 | 1237.3 |
| –30 | 0.3105 | 27 764.1 | 1319.1 | 1945.7 | 338.2 | 6157.8 | 1265.8 |
| –20 | 0.2943 | 28 069.9 | 1383.7 | 1938.3 | 317.0 | 5900.2 | 1294.6 |
| –10 | 0.2786 | 28 330.6 | 1478.5 | 1926.9 | 297.4 | 5637.5 | 1317.9 |
| 0 | 0.2636 | 28 534.0 | 1568.1 | 1915.5 | 279.3 | 5372.3 | 1339.6 |
| 10 | 0.2489 | 28 676.9 | 1651.0 | 1904.4 | 262.4 | 5098.0 | 1360.8 |
| 20 | 0.2355 | 28 771.8 | 1768.6 | 1887.8 | 247.5 | 4840.3 | 1373.5 |
| 30 | 0.2243 | 28 811.2 | 1869.1 | 1872.9 | 235.4 | 4615.8 | 1383.1 |
| 40 | 0.2150 | 28 793.2 | 1991.0 | 1853.8 | 225.8 | 4421.9 | 1384.4 |
| 50 | 0.2076 | 28 743.7 | 2188.2 | 1820.9 | 218.4 | 4261.4 | 1367.7 |
| 60 | 0.2021 | 28 653.6 | 2415.5 | 1779.8 | 213.3 | 4137.1 | 1338.3 |
| 70 | 0.1980 | 28 516.8 | 2737.5 | 1715.8 | 210.0 | 4033.3 | 1283.2 |
| 80 | 0.2022 | 27 732.1 | 3123.8 | 1630.5 | 210.4 | 4004.4 | 1198.9 |
| 90 | 0.2188 | 26 300.8 | 3480.7 | 1545.0 | 218.9 | 4110.9 | 1098.6 |
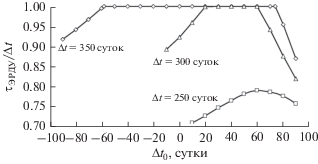
На рис. 6 представлены зависимости отношения времени работы ЭРДУ τЭРДУ к полному времени перелета Δt от смещения даты отлета от Земли относительно даты 20.IV.2035 для Δt = 250, 300 и 350 суток. Видно, что для достаточно больших Δt (300 и 350 суток) оптимизация тяги, скорости истечения, гиперболического избытка скорости и даты пуска приводит к оптимальным траекториям без пассивных участков при достаточно большой продолжительности перелета, причем диапазон дат старта в окрестности оптимального значения, при которых тяга ЭРДУ равна минимальной, расширяется при увеличении длительности перелета.
Рис. 6.
Зависимость отношения времени работы ЭРДУ к полному времени перелета от смещения даты отлета при оптимальном отлетном гиперболическом избытке скорости.
Гелиоцентрические траектории перелета к Марсу характеризуются относительно небольшой угловой дальностью. Интересно сравнить свойства таких траекторий и оптимальных траекторий с большим количеством витков вокруг Солнца. Максимальное число витков требуется на прямых траекториях перелета к Меркурию, поэтому рассмотрим совместную оптимизацию программы управления вектором тяги, основных траекторных и проектных параметров КА с однорежимной ЭРДУ на примере решения задачи перелета от Земли к Меркурию. Гиперболический избыток скорости КА при подлете к Меркурию задается нулевым (рассматривается задача сопровождения), величина отлетного гиперболического избытка скорости V∞0 и число целых витков КА вокруг Солнца nrev оптимизируются, дата отлета t0 и длительность перелета Δt перебираются. Как и в предыдущем примере, принимаем γ3 = 50 кг/кВт, at = 0.1, η = 0.7. В качестве средства выведения КА на отлетную траекторию рассматривается РН “Протон-М” с РБ “Бриз-М”.
В табл. 8 представлены основные параметры оптимальных траекторий перелета к Меркурию для длительности перелета в диапазоне 1000–3600 сут, а на рис. 7 – проекции оптимальных траекторий перелета к Меркурию на плоскость эклиптики и зависимости тяги T и функции переключения S от времени для длительности перелета 1000, 2400 и 3000 суток.
Таблица 8.
Основные параметры оптимальных траекторий перелета к Меркурию
| t0 | Δt, сутки | nrev, | T, мН | Iуд, с | V∞0, м/с | m0, кг | mp, кг | P, Вт | mu, кг | τЭРДУ/Δt |
|---|---|---|---|---|---|---|---|---|---|---|
| 23.IV.2025 | 1000 | 6 | 1021.7 | 4394.1 | 1904.6 | 6044.9 | 2007.9 | 31447.1 | 2263.9 | 0.98017 |
| 4.V.2025 | 1200 | 7 | 870.4 | 4895.3 | 1883.5 | 6054.0 | 1839.0 | 29845.2 | 2538.8 | 0.97833 |
| 13.V.2025 | 1800 | 11 | 614.3 | 6207.2 | 1621.3 | 6159.5 | 1553.8 | 26710.5 | 3114.8 | 0.99000 |
| 10.V.2026 | 2400 | 15 | 481.5 | 7291.1 | 1375.3 | 6245.7 | 1391.3 | 24589.9 | 3485.8 | 0.99641 |
| 13.V.2025 | 3000 | 19 | 397.1 | 8244.3 | 1219.0 | 6294.0 | 1270.9 | 22931.3 | 3749.5 | 0.99829 |
| 13.V.2025 | 3600 | 23 | 339.7 | 9096.2 | 1078.5 | 6333.0 | 1182.8 | 21645.7 | 3949.6 | 0.99855 |
Рис. 7.
Оптимальные траектории перелета к Меркурию (вверху) и зависимости тяги T и функции переключения S от времени для длительности перелета 1000, 2400 и 3000 суток.
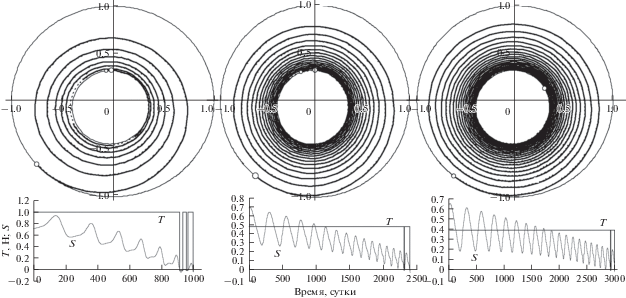
Из приведенных в таблице данных видно, что в рассмотренном диапазоне длительности перелета гипотезу об оптимальности минимальной тяги при оптимальном значении отлетного гиперболического избытка скорости и близкой к оптимальной дате старта для перелета к Меркурию подтвердить не удалось, хотя полученные значения оптимальной тяги оказались близкими к минимальному ее значению. С увеличением длительности перелета, суммарная длительность пассивных участков уменьшается, достигая 0.145% от общей длительности перелета при Δt = 3600 суток. Фактически, при Δt ≥ 2400 суток на траектории присутствует только один небольшой пассивный участок на последнем витке, величина которого уменьшается с ростом Δt. Вполне возможно, что при дальнейшем росте Δt траектория не будет содержать пассивных участков и, следовательно, оптимальным станет минимальное значение тяги.
В заключение рассмотрим совместную оптимизацию управления и основных траекторных и проектных параметров для перелета к Марсу при использовании РН “Союз-2.1Б” с РБ “Фрегат” для выведения КА на отлетную траекторию. Рассмотрим следующие значения основных проектных параметров первой категории: удельная масса солнечных батарей γ1 = 10 кг/кВт, удельная масса приводов солнечных батарей, других элементов СЭС и ЭРДУ γ2 = 15 кг/кВт, at = 0.1, η = 0.7.
В результате решения краевой задачи с заданной длительностью перелета Δt = 400 суток и начальным приближением для даты старта 1.I.2031 г., были получены следующие оптимальные значения основных траекторных и проектных параметров: величина отлетного гиперболического избытка скорости V∞0 = 1144.144 м/с, дата отлета – 17.XII.2030 6 часов 32 минут 22.3 с, PBOL = 12741.533 Вт, c = 33102.249 м/с, rmin = 1.36252356 а. е. Оптимальная масса КА при отлете 1964.147 кг, масса рабочего тела ЭРДУ mp = 261.372 кг, конечная масса СХПРТ – 26.137 кг, масса СЭС и ЭРДУ – 244.092 кг, а полезная масса КА – mu = 1432.546 кг.
Оптимальная траектория перелета от Земли к Марсу показана на рис. 8. На рис. 9 представлено оптимальное управление, включая зависимости от времени тяги и функции переключения (верхний левый график), тангажа и рысканья (верхний правый график), зависимость гелиоцентрического удаления КА от времени (нижний левый график) и зависимости от времени сопряженных переменных pP BOL, pc, and prmin (нижний правый график). Функции pP BOL(t) и pc(t) имеют угловые точки в моменты переключения тяги t*: S(t*) = 0, а функция prmin(t) имеет угловую точку при t*: r(t*) = rmin.
Рис. 9.
Зависимость от времени тяги T, функции переключения S, углов тангажа и рысканья, гелиоцентрического удаления КА и переменных, сопряженных к PBOL, c и rmin на оптимальной траектории перелета к Марсу.
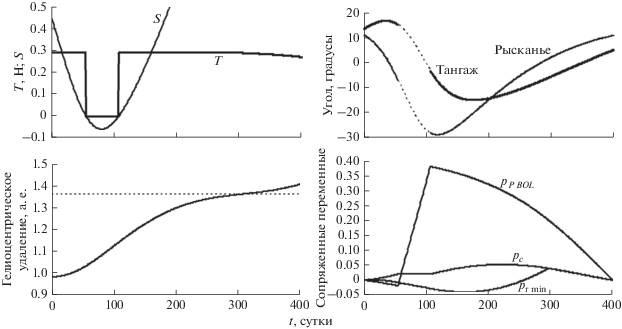
Оказалось неожиданным относительно большое оптимальное значение rmin. Фактически, тяга уменьшается только на последней четверти перелета и в результате дросселируется только до 93.2% от максимального значения 0.290272 Н. Максимальная потребляемая ЭРДУ мощность равна 6863.39 Вт, немногим больше половины мощности PBOL, генерируемой солнечными батареями на гелиоцентрическом удалении 1 а. е.
ЗАКЛЮЧЕНИЕ
В статье приведены необходимые условия совместной оптимальности управления вектором тяги ЭРДУ, даты отлета, вектора отлетного гиперболического избытка скорости и основных проектных параметров КА с ЭРДУ для прямого перелета между двумя планетами в центральном ньютоновском гравитационном поле Солнца за фиксированное время. Рассмотрены варианты однорежимного ЭРДУ с фиксированными значениями тяги и удельного импульса и регулируемой по тяге (потребляемой мощности) ЭРДУ с фиксированным удельным импульсом.
В типичных случаях зависимость полезной массы КА с ЭРДУ от величины тяги и удельного импульса в районе максимума оказалась достаточно пологой: для перелета к Марсу длительностью около года изменение удельного импульса на 10% и тяги на 3% от оптимального значения приводит к уменьшению полезной массы на 0.3%.
Обнаружено, что в ряде случаев, при достаточно большой продолжительности перелета, близкой к оптимальной дате отлета, оптимальном значении отлетного гиперболического избытка скорости и удельного импульса, оптимальное значение тяги равно минимальному ее значению. На таких траекториях ЭРДУ работает постоянно (отсутствуют пассивные участки траектории). Такие оптимальные траектории обнаружены для перелетов Земля–Марс длительностью 300 сут и выше, однако их не удалось обнаружить для перелетов Земля–Меркурий длительностью до 3600 сут с оптимальной угловой дальностью. Все найденные оптимальные траектории перелета к Меркурию содержат, по крайней мере, один пассивный участок малой длительности. Возможно, это связано с относительно большими значениями эксцентриситета и наклонения орбиты Меркурия или с недостаточно большой общей длительностью перелета.
Полученные необходимые условия оптимальности, помимо прочих проектных параметров КА, позволяют определять оптимальную установленную мощность СЭС и оптимальную максимальную мощность, потребляемую регулируемой солнечной ЭРДУ. Рассмотренный пример оптимизации перелета к Марсу КА с регулируемой солнечной ЭРДУ показал, что при небольшой удельной массе элементов СЭС и ЭРДУ оптимальная установленная мощность СЭС может быть в два раза больше оптимальной максимальной мощности, потребляемой ЭРДУ, при этом оптимальное текущее значение тяги регулируемой ЭРДУ не снижается ниже 90% от оптимального максимального значения. В этом случае замена регулируемой по мощности ЭРДУ на однорежимную нерегулируемую ЭРДУ не приведет к заметному снижению полезной массы КА.
Работа выполнена за счет средств гранта Российского научного фонда (соглашение № 16-19-10429).
Список литературы
Гродзовский Г.Л., Иванов Ю.Н., Токарев В.В. Механика космического полета с малой тягой. М.: Наука, 1966.
Irving J.H. Low thrust flight: variable exhaust velocity in gravitational fields. (In Seifert H.S. (eds.)): Space Technology, John Wiley and Sons Inc., New York, 1959.
Vavrina M.A., Englander J.A., Ghosh A.R. Coupled low-thrust trajectory and system optimization via multi-objective hybrid optimal control. AAS/AIAA Space Flight Mechanics Meeting, American Astronautical Soc. Paper 2015–397, 2015.
Kwon K., Lantoine G., Russell R.P., Mavris D.N. A study on simultaneous design of a Hall Effect Thruster and its low-thrust trajectory // Acta Astronautica. 2016. V. 119. P. 34–47.
Petukhov V.G. Joint Optimization of the Low-Thrust Trajectory and the Main Design Parameters of Electric Propulsion System. IAC-15-C1.1.5. Jerusalem, 2015.
Петухов В.Г., Иванюхин А.В. Совместная оптимизация основных проектных параметров электроракетной двигательной установки и траектории космического аппарата // Известия РАН. Энергетика. 2016. № 2. С. 92–101.
Климов С.С. Совместная оптимизация траекторий и энергосиловых параметров марсианских экспедиционных комплексов с электроракетными двигательными установками // Космонавтика и ракетостроение, 2017. № 4(97). С. 71–83.
Proton launch system mission planner’s guide. Revision 7. International Launch Services. 2009.
Soyuz user’s manual. Arianespace. Issue 2. Revision 0. March 2012.
Егоров В.А., Гусев Л.И. Динамика перелетов между Землей и Луной. М.: Наука, 1980.
Механика космического полета / Мишин В.П. (ред.). М.: Машиностроение, 1989.
Bate R.R., Mueller D.D., White J.E. Fundamentals of Astrodynamics. New York: Dover Publications, 1971.
Петухов В.Г. Оптимизация межпланетных траекторий космических аппаратов с идеально-регулируемым двигателем методом продолжения // Космич. исслед. Т. 46. № 3. 2008. С. 224–237. (Cosmic Research. P. 219).
Петухов В.Г. Метод продолжения для оптимизации межпланетных траекторий с малой тягой // Космич. исслед. Т. 50. № 3. 2012. С. 258–270. (Cosmic Research. P. 249).
Иванюхин А.В., Петухов В.Г. Задача минимизации тяги и ее приложения // Космич. исслед. Т. 53. № 4. 2015. С. 320–321. (Cosmic Research. P. 300).
Petukhov V.G. Minimum-Thrust Problem and Its Application to Trajectory Optimization with Thrust Switchings. IAC-13-C1.6.2. Beijing, 2013.
Иванюхин А.В. Область существования решений в задаче оптимального управления космическим аппаратом с ограниченной тягой // Современная математика. Фундаментальные направления. 2016. Т. 62. С. 100–123.
Дополнительные материалы отсутствуют.
Инструменты
Космические исследования