Космические исследования, 2019, T. 57, № 5, стр. 347-360
Сравнительный проектно-баллистический анализ использования химической и электроракетной двигательных установок в проекте солнечного зонда
М. С. Константинов *
Научно-исследовательский институт прикладной механики и электродинамики МАИ
г. Москва, Россия
* E-mail: mkonst@bk.ru
Поступила в редакцию 25.03.2019
После доработки 02.04.2019
Принята к публикации 25.04.2019
Аннотация
Анализируется возможность реализации проекта солнечного зонда с выведением исследовательского КА на систему гелиоцентрических орбит с относительно малым радиусом перигелия и достаточно большим наклонением к солнечному экватору (наклонение последней гелиоцентрической орбиты к плоскости солнечного экватора должно быть не менее 30°). Проведен сравнительный проектно-баллистический анализ возможности использования химической и электроракетной двигательных установок (ЭРДУ) при выведении КА на рассматриваемую систему гелиоцентрических орбит. Анализируемые транспортные системы предполагают использование ракеты-носителя “Союз-2.1б” и химического разгонного блока “Фрегат” при старте КА от Земли. Двигательные установки собственно КА различны. В одном случае используется химическая двигательная установка, в другом – солнечная электроракетная двигательная установка на базе одного стационарного плазменного двигателя типа СПД-140. Время выведения КА на последнюю гелиоцентрическую орбиту рассматриваемой системы орбит ограничено сверху пятью годами. Показано, что использование ЭРДУ позволяет значительно увеличить массу КА на рабочих орбитах (с 910 до 1600 кг).
ВВЕДЕНИЕ
В настоящее время реализуется проект “Parker Solar Probe” исследования Солнца, который предполагает использование системы гелиоцентрических орбит с малым радиусом перигелия (https://solarprobe.gsfc.nasa.gov/ Solar Probe Plus; https://www.nasa.gov/content/goddard/parker-solar-probe). Запуск КА в рамках этого проекта осуществлен NASA 12.VIII.2018 года. Использование мощной ракеты-носителя тяжелого класса “Delta 4 Heavy” позволило обеспечить большой гиперболический избыток скорости при старте от Земли и КА по “крутой” траектории достиг окрестности Венеры уже на 48 сутки полета. У Венеры был осуществлен первый гравитационный маневр, позволивший вывести КА на первую из предполагаемых 25 рабочих гелиоцентрических орбит. Радиус перигелия этой орбиты ~24 млн км (~34.7 радиуса Солнца, RS). Проект предполагает использование схемы полета с семью гравитационными маневрами у Венеры. Использование предполагаемой последовательности гравитационных маневров у Венеры позволит обеспечить совсем низкие пролеты околосолнечного пространства (минимальный радиус перигелия предполагается равным ~6 млн км, около 9-ти радиусов Солнца).
Особенностью рабочих орбит в проекте “Parker Solar Probe” является то, что их плоскость практически совпадает с плоскостью орбиты Венеры. Плоскость орбиты Венеры наклонена к плоскости эклиптики на ~3.4° и, что очень важно, на ~3.9° к плоскости солнечного экватора. При этом склонение КА, находящегося на используемых рабочих орбитах по отношению к плоскости солнечного экватора, не может быть более 3.9°. Поэтому исследовать полярные области Солнца в рамках проекта “Parker Solar Probe” не представляется возможным.
Для реализации исследований полярных областей Солнца необходимы рабочие гелиоцентрические орбиты с большим наклонением к плоскости солнечного экватора. Часто выставляется требование о наклонении не менее 30°. Это требование может быть реализовано в таких проектах, как проект Европейского космического агентства “Solar Orbiter” (https://space.skyrocket.de/doc_sdat/solar-orbiter.htm, http://sci.esa.int/solar-orbiter/) и российский проект “Интергелио-Зонд” [1, 2]. В этих проектах, также, как и в проекте “Parker Solar Probe” предполагается использовать гравитационные маневры у Венеры. Но при реализации внеэклиптических наблюдений Солнца (в отличие от проекта “Parker Solar Probe”) нет возможности использовать резонансные с Венерой орбиты с неполным числом витков вокруг Солнца. Важным дополнительным обстоятельством в этих проектах является ограничение снизу радиуса перигелия используемых рабочих орбит (из-за существующих тепловых проблем). Так в проекте “Интергелио-Зонд” не предполагается сближаться КА с Солнцем на расстояние меньшее 60 радиусов Солнца (0.279 а.е.). Отказ от рабочих орбит с малым радиусом перигелия приводит к дополнительным сложностям. КА на каждой резонансной орбите делает целое число витков относительно Солнца. Периоды на каждой рабочей орбиты из используемой последовательности достаточно велики, исключается принципиальная возможность использовать такие резонансные перелеты, при которых изменяется положение Венеры при гравитационных маневрах у нее. При этом возрастает время реализации всей миссии, что вызывает трудности, связанные с ограниченным ресурсом используемых систем КА.
Оптимизации схемы выведения КА на систему рабочих орбит для внеэклиптического исследования Солнца посвящено много исследований. В работе [3] проанализированы несколько систем рабочих гелиоцентрических орбит, возможные резонансные последовательности этих орбит, проанализирована возможность выведения КА на систему гелиоцентрических рабочих орбит с использованием транспортной системы на базе РН “Союз-2.1б”, химического разгонного блока “Фрегат” и ЭРДУ на базе двух двигателей типа RIT-22. Выбранная система рабочих орбит характеризовалась узким диапазоном радиуса перигелия рабочих орбит (50…70 RS). Последняя рабочая орбита имеет наклонение более 30 градусов к плоскости эклиптики. Было показано, что на рабочие орбиты может быть выведен КА довольно большой массы (более 1830 кг). Заметим, что рассмотренная в работе схема использовала рабочие орбиты с радиусом перигелия меньшим 60 RS, что неприемлемо по требованиям разработчиков проекта “Интергелио-Зонд”. Кроме того, минимальное время выведения КА на последнюю рабочую орбиту рассматривалось относительно большим (6 лет). В [4] приведены результаты проектно-баллистического анализа аналогичной транспортной системы и показано, что для эпох запуска 2017 и 2018 годов можно обеспечить выведение КА массой 1645…1669 кг на рабочую орбиту с эклиптическим наклонением 25°…27°, не нарушая ограничение по минимальному сближению КА с Солнцем.
В [5] проанализирована возможность использования двигательной установки на базе двигателя типа RIT-22 для реализации гелиоцентрического перелета Земля–Земля. Рассмотрены две системы рабочих орбит, отличающихся диапазонами радиуса перигелия используемых рабочих орбит (30…50 и 40…60 RS). Требуемое эклиптическое наклонение конечной рабочей орбиты принято равным 30°. В [6] проанализирована возможность использования той же двигательной установки (на базе двигателя типа RIT-22). Рассматривается система рабочих орбит с диапазонами радиуса перигелия используемых рабочих орбит от 60 до 104 RS, наклонение конечной рабочей орбиты 27°.
В [7, 8] проанализирована возможность использования стационарного плазменного двигателя типа СПД-140Д для реализации гелиоцентрического перелета Земля–Земля. Было показано, что использование двигателя типа СПД-140Д позволяет достичь заданных параметров гелиоцентрической орбиты и провести комплекс экспериментов в течение заданного срока (5 лет) активного существования КА “Интергелио-Зонд” В [8] приведены результаты анализа варианта использования ХДУ для реализации рассматриваемого варианта выведения солнечного зонда. В [9] рассмотрена схема прямого выведения (без использования гравитационных маневров) с использованием ЭРДУ на базе RIT-22 на рабочую гелиоцентрическую орбиту с радиусом перигелия 70 RS и наклонением к плоскости эклиптики 30°. В [10] для схемы прямого выведения показана возможность увеличения массы, доставляемой на рабочую гелиоцентрическую орбиту, при увеличении удельного импульса двигателя. В частности, показано, что увеличение удельного импульса СПД с 1600 до 3000 с может позволить увеличить массу КА на целевой орбите более чем 1.6 раз. Анализируется проблема оптимальной электрической мощности и оптимальной тяги ЭРДУ. Авторы [11] проанализировали влияние величины мощности солнечной энергетической установки на характеристики проекта “Интергелио-Зонд” в варианте использования ЭРДУ.
В [12] проанализирована возможность использования химических ракетных двигателей, обеспечивающих условия для гравитационных маневров при выведении на рабочие орбиты.
Сформулируем несколько особенностей постановки задачи проектирования траектории выведения КА на гелиоцентрические орбиты для исследования Солнца настоящего исследования. Прежде всего, в большинстве опубликованных исследований с использованием гравитационных маневров у Венеры при выведении КА на внеэклиптическую орбиту рассматриваются очень большие величины гиперболического избытка скорости при гравитационном маневре. Величина этого избытка считается примерно равной половине величины гелиоцентрической скорости Венеры. Постулируется, что, если величина гиперболического избытка скорости равна 17.5 км/с, то всегда последовательность гравитационных маневров у Венеры может обеспечить наклонение орбиты КА к плоскости эклиптики 30°. Ошибочность такого подхода заключается в двух обстоятельствах. Первое – при гиперболическом избытке скорости равном половине величины гелиоцентрической скорости Венеры можно действительно гарантировать наклонение рабочей орбиты 30° к плоскости орбиты Венеры. Но эта плоскость не совпадает с плоскостью эклиптики. Второе важное обстоятельство заключается в том, что важнее анализировать наклонение рабочей орбиты к плоскости солнечного экватора, а не к плоскости эклиптики.
В настоящей работе траектория выведения на рабочие орбиты, включая параметры гравитационных маневров, будет выбираться из анализа наклонения рабочих орбит не к плоскости эклиптики, а к плоскости солнечного экватора. При этом (важное обстоятельство) величина гиперболического избытка скорости при гравитационных маневрах будет рассматриваться как выбираемый параметр схемы перелета. Забегая вперед отметим, что эта величина при гравитационных маневрах у Венеры будет существенно меньше половины гелиоцентрической скорости Венеры.
Отметим еще одно свойство настоящего исследования, которое включает сравнительный проектно-баллистический анализ возможности использования в проекте ХДУ и ЭРДУ. Принципиально такая задача была исследована в работе [13]. В ней сравнение вариантов с разными типами двигательных установок проводилось с использованием критерия эффективности, рассматриваемого в виде свертки различных показателей. С искусственно выбранными авторами работы коэффициентами складывались массовые, временные и другие показатели проекта. Среди других показателей рассматривалось наклонение последней рабочей орбиты. При этом, например, в варианте с химической двигательной установкой это эклиптическое наклонение рабочей орбиты было всего 17°. Постановка задачи в настоящем исследовании выбрана другой, анализируемая транспортная задача будет одной и той же для рассмотренных вариантов транспортной космической системы.
1. ТРАНСПОРТНАЯ КОСМИЧЕСКАЯ СИСТЕМА
Рассматриваемая транспортная система базируется на РН “Союз-2.1б”, химическом разгонном блоке “Фрегат”. Для собственно КА рассматриваются две альтернативы. В одном случае КА имеет солнечную ЭРДУ. В другом случае КА располагает ХДУ. Выведение КА на опорную орбиту производится РН “Союз 2” с космодрома Байконур.
Химический разгонный блок “Фрегат” обеспечивает старт КА с опорной орбиты и уход из окрестности Земли с некоторой величиной гиперболического избытка скорости (эта величина является выбираемым параметром схемы перелета). Зависимость массы КА после отделения химического разгонного блока “Фрегат” как функция величины гиперболического избытка скорости приведена на рис. 1 [14].
Рис. 1.
Масса КА, выведенного на гиперболическую отлетную траекторию (кг), как функция величины гиперболического избытка скорости (км/с). РН “Союз 2.1б” и ХРБ “Фрегат”.
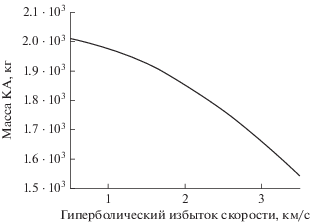
Из представленного графика видно, при использовании РН “Союз 2.1б” и ХРБ “Фрегат” можно обеспечить выведение КА на гиперболическую отлетную от Земли траекторию с величиной гиперболического избытка скорости до 3.5 км/с. Масса выведенного на гиперболическую траекторию КА является монотонно убывающей функцией величины гиперболического избытка скорости. При максимальном гиперболическом избытке скорости (3.5 км/с) эта масса меньше 1550 кг. При таких характеристиках реализовывать траектории полета аналогичные используемым траекториям в проекте “Parker Solar Probe” невозможно.
Удельный импульс химического ракетного двигателя КА (маршевой химической двигательной установки) полагается равным 300 с. Его тяга не анализируется. Затраты топлива рассчитываются по формуле Циолковского, при этом пренебрегается потерями в скорости. В дальнейшем будет использован термин маршевая двигательная установка для того, чтобы подчеркнуть существование корректирующей химической двигательной установки в варианте использования ЭРДУ.
Характеристики ЭРДУ приняты следующими: удельный импульс 1670 с; тяга двигателя 290 мН (используется один двигатель типа СПД140). Потребляемая электрическая мощность двигателем (5 кВт) и тяга работающей ЭРДУ принимаются постоянными, не зависящими от гелиоцентрического расстояния КА.
2. АНАЛИЗИРУЕМАЯ СХЕМА ВЫВЕДЕНИЯ НА РАБОЧИЕ ГЕЛИОЦЕНТРИЧЕСКИЕ ОРБИТЫ
Анализируемая схема выведения на рабочие гелиоцентрические орбиты аналогична схеме, рассмотренной в работах [3–5]. Она включает в себя следующие участки:
1) выведение КА на околоземную орбиту с помощью РН “Союз-2.1б”;
2) выведение КА на отлетную от Земли траекторию с помощью ХРБ “Фрегат” с последующим его отделением;
3) участок перелета по гелиоцентрической траектории Земля–Земля. На этом участке предполагается возможность работы двигательной установки КА (или ЭРДУ или маршевой ХДУ);
4) пассивный гравитационный маневр у Земли;
5) участок гелиоцентрического перелета Земля–Венера (на нем не предполагается работа маршевых двигательных установок);
6) последовательность пассивных гравитационных маневров у Венеры с выведением на последовательность гелиоцентрических рабочих орбит. На этих орбитах не предполагается включение маршевых двигательных установок.
После гравитационного маневра у Земли двигательная установка КА используется только для коррекции траектории и для решения задач управления ориентацией.
Таким образом, на гелиоцентрической траектории КА используются гравитационные маневры у Земли и Венеры. Минимальная высота пролета Земли и Венеры при проведении гравитационных маневров принята равной 400 км. Координаты и компоненты вектора скорости планет определяются с использованием эфемеридного программного обеспечения JPL DE403.
Для реализации серии гравитационных маневров у Венеры КА выводится на гелиоцентрическую орбиту, находящуюся в орбитальном резонансе k:m с Венерой. На такой орбите КА совершает k оборотов вокруг Солнца за время, которое нужно Венере, чтобы совершить m оборотов вокруг Солнца (орбитальный период Венеры примерно равен 224.7 суток). В процессе перелета гравитационные маневры используются для перевода КА из одного резонанса в другой с целью управления радиусом перигелия и наклонением орбиты КА. Синодический период Венеры, через который повторяются окна пуска, равен 1.6 года. В статье рассмотрена эпоха запуска 2027 года.
3. ПОСТАНОВКА ЗАДАЧИ ОПТИМИЗАЦИИ СХЕМЫ ВЫВЕДЕНИЯ НА РАБОЧИЕ ГЕЛИОЦЕНТРИЧЕСКИЕ ОРБИТЫ
Анализируемая транспортная операция выведения на систему рабочих гелиоцентрических орбит для исследования Солнца формулируется так:
1. Наклонение последней рабочей орбиты к плоскости солнечного экватора должно быть не менее 30°;
2. Радиусы перигелия (rp) всех рабочих орбит должны быть больше 60 радиусов Солнца (RS) и меньше 100 этих радиусов. То есть должно удовлетворяться ограничение 60RS ≤ rp ≤ 100RS;
3. Время выведение на последнюю рабочую орбиту должно быть не более 5-ти лет.
Выбираемыми характеристиками проектируемой траектории выведения на рабочие орбиты являются:
1. Число используемых гравитационных маневров у Венеры;
2. Величина гиперболического избытка скорости при гравитационных маневрах у Венеры;
3. Величина гиперболического избытка скорости при гравитационном маневре у Земли;
4. Порядки резонансов всех рабочих гелиоцентрических орбит кроме последней рабочей орбиты;
5. Даты всех характерных событий на траектории выведения (старта, гравитационного маневра у Земли, гравитационных маневров у Венеры);
6. Величина и направление гиперболического избытка скорости при старте от Земли;
7. Программа управления движением КА на гелиоцентрическом перелете Земля–Земля.
В варианте использования ЭРДУ – количество активных участков на траектории перелета, даты начала и конца этих участков, направление тяги ЭРДУ на активных участках.
В варианте использования маршевой ХДУ – количество импульсов скорости, даты сообщения КА этих импульсов скорости, их величина и направление;
8. Параметры всех используемых на перелете гравитационных маневров (они рассматриваются пассивными).
Отметим, что некоторые из перечисленных выбираемых параметров нельзя рассматривать как независимые выбираемые параметры. Например, фиксация даты гравитационного маневра у Земли и даты первого гравитационного маневра у Венеры полностью определяют траекторию гелиоцентрического перелета Земля–Венера, а значит и величину, и направление гиперболических скоростей отлета от Земли и подлета к Венере. Ниже будут выделен независимый набор оптимизируемых характеристик схемы перелета.
Критерием оптимизации рассматривается масса КА, доставленного на рабочие орбиты. Так как все гравитационные маневры рассматриваются пассивными и маршевый двигатель не используется на всех гелиоцентрических участках, кроме первого участка перелета Земля–Земля, то критерием оптимизации можно рассматривать массу КА в момент его подлета к Земле для гравитационного маневра у нее. Эта масса максимизируется.
4. МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧИ ОПТИМИЗАЦИИ СХЕМЫ ВЫВЕДЕНИЯ НА РАБОЧИЕ ГЕЛИОЦЕНТРИЧЕСКИЕ ОРБИТЫ
Опишем математические модели движения КА на отдельных участках выведения.
Участок геоцентрической траектории при старте КА. Участок геоцентрической траектории при старте КА из окрестности Земли описывается зависимостью mo(V∞start), приведенной на рис. 1, связывающей величину гиперболического избытка скорости V∞start с массой КА в начале гелиоцентрической траектории отлета от Земли (массой КА после отделения ХРБ). Использовалась аппроксимация зависимости в виде кубической параболы. Она позволяла легко рассчитывать производную этой функции по величине гиперболического избытка скорости $\frac{{d{{m}_{{\text{o}}}}}}{{d{{V}_{{\infty {\text{start}}}}}}},$ используемую в условии оптимальности величины гиперболического избытка скорости при старте.
Методически целесообразно привести математическую модель, которая используется при описании пассивного гравитационного маневра у любого небесного тела (Земли или Венеры).
Математическая модель пассивного гравитационного маневра. Используется следующая математическая модель гравитационного маневра [15, 16]. В рамках метода грависфер нулевой протяженности в результате пассивного гравитационного маневра происходит мгновенное изменение вектора гелиоцентрической скорости КА, эквивалентное развороту вектора гиперболического избытка скорости на некоторый угол, ограниченный сверху минимально допустимой высотой пролета планеты.
Рассматриваются следующие два параметра гравитационного маневра:
– угол β между векторами подлетного ${\mathbf{V}}_{\infty }^{ - }$ и отлетного ${\mathbf{V}}_{\infty }^{ + }$ гиперболического избытка скорости при гравитационном маневре (он ограничен сверху максимальной величиной β ≤ βmax). βmax зависит от величины гиперболического избытка скорости V∞, минимального радиуса перицентра пролетной гиперболы rπmin и величины гравитационного параметра небесного тела, у которого осуществляется гравитационный маневр μpl$\left( {{{\beta }_{{\max }}} = 2\arcsin \left[ {{{{\left( {1 + \frac{{{{r}_{{\pi \min }}}V_{\infty }^{2}}}{{{{\mu }_{{pl}}}}}} \right)}}^{{ - 1}}}} \right]} \right)$.
– и угол γ, определяющий положение плоскости пролетной гиперболы (угол поворота плоскости пролетной гиперболы относительно вектора подлетного гиперболического избытка скорости [15]). На угол γ никаких ограничений не накладывается.
Вектор гиперболического избытка скорости после гравитационного маневра можно подсчитать по известным компонентам подлетного вектора гиперболического избытка скорости (в произвольной, например, эклиптической системе координат) по следующему соотношению [15, 16]:
Модель оптимального движения КА на гелиоцентрическом перелете Земля–Земля
Случай использование ЭРДУ. Исследуется движение КА на гелиоцентрическом участке Земля-Земля. Движение КА на этом участке перелета анализируется в гелиоцентрической эклиптической системе координат. Учитывается притяжение КА Солнцем и тяга ЭРДУ. Общий используемый метод оптимизации – принцип максимума Понтрягина. Уравнения оптимального движения записываются в следующем традиционном безразмерном виде [16]:
Оптимальный закон функции включения-выключения двигателя δ получается из условия максимума гамильтониана и используется в виде: $\delta = \left\{ \begin{gathered} {\text{1, е с л и }}\psi > 0; \hfill \\ {\text{0, е с л и }}\psi \leqslant 0, \hfill \\ \end{gathered} \right.$ где функция переключения ψ имеет вид: $\psi = \frac{{{{\lambda }_{V}}}}{m} - \frac{{{{\lambda }_{m}}}}{w}{\text{.}}$ В последнем соотношении используется безразмерный удельный импульс w.
Траектория гелиоцентрического перелета Земля–Земля полностью определяется следующими 10-ю скалярными выбираемыми параметрами: – датой старта to; и датой гравитационного маневра у Земли t1; – вектором сопряженных переменных в начальной точке гелиоцентрического перелета: λr(to); λV(to), λm(to); величиной вектора гиперболического избытка скорости при старте V∞start (направление этого вектора при оптимальной его величине коллинеарно базису вектору λV(to) в начальной точке гелиоцентрического перелета).
В конечной точке траектории перелета необходимо удовлетворить три скалярных условия попадания в окрестность Земли для гравитационного манера около нее r(t1) = rE(t1). Остальные 7 степеней свободы (10–3) должны использоваться на оптимизацию траектории перелета (должны удовлетворять условиям оптимальности). Легко записать условие оптимальности величины гиперболического избытка скорости: ${{\lambda }_{V}}({{t}_{o}}) + {{\lambda }_{m}}({{t}_{o}})\frac{{d{{m}_{o}}}}{{d{{V}_{{\infty \,{\text{start}}}}}}}{\text{ = 0}}{\text{.}}$ Это равенство позволяет исключить из вектора выбираемых характеристик рассматриваемого участка траектории один из параметров краевой задачи (например, λm(to)). Чем мы и воспользовались.
Случай использование химической ракетной двигательной установки. При анализе использования маршевой химической двигательной установки целесообразно исследовать траекторию от старта КА из окрестности Земли до гравитационного маневра у Венеры. При этом было рассмотрено несколько схем перелета:
1. Использование одного импульса скорости на гелиоцентрической траектории перелета Земля- Земля и одного импульса скорости на траектории Земля–Венера.
2. Использование двух импульсов скорости на гелиоцентрической траектории перелета Земля–Земля и одного импульса скорости на траектории Земля–Венера.
3. Использование двух импульсов скорости на гелиоцентрическом перелете от Земли к Венере (без гравитационного маневра у Земли).
Самым рациональным оказался перелет с одним импульсом скорости на гелиоцентрическом перелете Земля–Земля и пассивный перелет (без импульса скорости) Земля–Венера (оптимальная величина этого импульса скорости оказалась равна нулю). При использовании этого перелета масса КА, доставляемая к Венере для системы гравитационных маневров у нее, оказывалась наибольшей. Приведем математическую модель, описывающую такую схему гелиоцентрического перелета. Идея рассмотрения описываемой модели использовалась при оптимизации сложных схем межпланетного перелета [15].
Каждый гелиоцентрический участок траектории рассматривается состоящим из двух сегментов. Для рассматриваемого гелиоцентрического участка вводятся две дополнительные выбираемые характеристики. Вектор гиперболического избытка скорости при отлете от планеты для рассматриваемого участка (три скалярных параметра) и время движения на первом сегменте рассматриваемого участка. По дате начала участка, определяется положение и гелиоцентрическая скорость анализируемой планеты. Находится вектор гелиоцентрической начальной скорости КА (как сумма вектора скорости планеты и вектора гиперболического избытка скорости). По положению и скорости КА в начальной точке рассматриваемого гелиоцентрического участка определяются элементы орбиты КА (в рамках задачи двух тел Солнце–КА). Используя время перелета на первом сегменте траектории, определяется вектор положения и вектор скорости КА в конце первого сегмента траектории. Анализируется второй сегмент рассматриваемого участка. Используя решение уравнения Ламберта, находятся элементы орбиты КА на втором сегменте траектории. Находятся вектора гелиоцентрических скоростей КА в начале и конце второго сегмента траектории. Эти векторы позволяют найти требуемый импульс скорости при переходе от первого сегмента участка ко второму сегменту и гиперболический избыток скорости при подлете ко второй планете рассматриваемого гелиоцентрического участка. При этом удается рассматривать траекторию перелета Земля–Земля–Венера как функцию следующих 11 скалярных параметров: трех дат пролета планет to, t1, t2; векторов гиперболических избытков скорости отлета от Земли при старте и после гравитационного маневра, времени перелета на первых сегментах траектории каждого из двух гелиоцентрических участков. Задание этих 11 параметров дает возможность рассчитать: требуемую массу КА в начальной точке гелиоцентрического перелета при старте от Земли (используется величина гиперболического избытка скорости); требуемые импульсы скорости на гелиоцентрических участках траектории и, наконец, импульс скорости при гравитационном маневре у Земли.
Заметим, что введение активного гравитационного маневра является методическим приемом, который позволяет легко “замыкать” задачу поиска оптимальной схемы импульсного перелета. Импульс скорости при гравитационном маневре рассматривался выполняемым на участке подлета или отлета от планеты. Использовался следующий алгоритм:
– Сравниваются величины подлетного ${\mathbf{V}}_{\infty }^{ - }$ и отлетного ${\mathbf{V}}_{\infty }^{ + }$ векторов гиперболического избытка скорости и выбирается минимальная величина из них min V∞;
– Вычисляется максимально допустимый угол поворота вектора гиперболического избытка скорости при величине гиперболического избытка скорости равного min V∞:
– Вычисляется угол βreal между векторами гиперболического избытка скорости при подлете к планете и отлете от нее (используется скалярное произведение этих векторов);
– В том случае, если требуемый угол поворота вектора гиперболического избытка скорости больше максимально допустимого (βreal > βmax), требуемая величина импульса скорости при гр-авитационном маневре вычисляется с использованием соотношения $\Delta {{V}_{{{\text{swingy}}}}}$ $ = \,\sqrt {V_{\infty }^{{ - 2}}\, + \,V_{\infty }^{{ + 2}}\, - \,2V_{\infty }^{ - }V_{\infty }^{ + }{\kern 1pt} \cos ({{\beta }_{{{\text{real}}}}}\, - \,{{\beta }_{{\max }}})} .$
– Если требуемый угол поворота вектора гиперболического избытка скорости не превышает максимально допустимого (βreal ≤ βmax), величина импульса скорости при гравитационном маневре вычисляется так: $\Delta {{V}_{{{\text{swingby}}}}} = \left| {V_{\infty }^{ + } - V_{\infty }^{ - }} \right|.$
Суммарный импульс скорости, рассчитанный как сумма модулей трех импульсов скорости (на гелиоцентрических участках перелета и при гравитационном маневре), позволяют найти массу КА при подлете к Венере (используется формула Циолковского).
Нахождение рациональной схемы перелета сводится к нахождению таких параметров схемы перелета, которые максимизируют конечную массу КА при удовлетворении двух ограничений. Первое из них обеспечивает определенную величину гиперболического избытка скорости при подлете к Венере. Второе ограничение приводит к использованию пассивного гравитационного маневра у Венеры.
Заметим, что существует возможность рассматривать схему полета, использующую пассивный гравитационный маневр у Земли. Для этого достаточно в качестве выбираемых параметров схемы перелета вместо компонент вектора гиперболического избытка скорости рассматривать параметры гравитационного маневра (выше введенные углы β и γ). При этом угол поворота вектора гиперболического избытка скорости β должен быть меньше максимального угла поворота βmax.
Модель движения КА на гелиоцентрическом перелете Земля–Венера. На гелиоцентрическом перелете Земля–Венера не предполагается работа маршевой двигательной установки. Поэтому траектория анализируется в рамках задачи двух тел. Ее характеристики полностью определяются датами начала t1 и конца участка t2. Сам анализ ведется с использованием уравнения Ламберта. Угловая дальность гелиоцентрического перелета Земля–Венера предполагается малой (по крайней мере, меньше 360°). Поэтому решение уравнения Ламберта всегда существует, и оно единственное. На полученном решении легко определяются гиперболические избытки скорости отлета от Земли и подлета к Венере. Легко анализируется зависимости этих гиперболических избытков от дат t1 и t2: $V_{{\infty {\text{Earth}}}}^{ + }({{t}_{1}},{{t}_{2}});$ $V_{{\infty {\text{Venus}}}}^{ - }({{t}_{1}},{{t}_{2}}).$
Анализ возможной последовательности резонансов гелиоцентрических рабочих орбит после гравитационных маневров у Венеры. В [3] приведен достаточно подробный анализ возможной цепочки резонансов анализируемых гелиоцентрических орбит. В настоящей работе из-за существенного ограничения времени выведения на последнюю рабочую орбиту (5 лет) и ограничения снизу величины радиуса перигелия рабочих орбит (эта величина должна быть больше 60 радиусов Солнца) допустимый набор резонансных орбит очень сильно сужается. Использование орбит с периодом равным или меньшим половине периода орбиты Венеры (в частности резонанса 2 : 1, когда КА делает два витка вокруг Солнца за время одного витка Венеры) невозможно, так как перигелий орбиты меньше 60 RS.
Несложно оценить максимальное число оборотов Венеры, которые она может сделать за время нахождения КА на резонансных орбитах. С учетом времени перелета по траектории Земля–Земля–Венера максимальное количество витков Венеры вокруг Солнца равно 6. При этом принципиально возможные порядки резонансов рабочих орбит оказываются следующими: 1 : 1; 3 : 2; 4 : 3 и 5 : 3.
Практика показала, что резонансной орбитой 5 : 3 не удается воспользоваться, так как радиус перигелия орбиты оказывается меньше 60 RS. Комбинирование оставшихся трех резонансов позволят утверждать, что наиболее интересным вариантом является вариант, в котором используются каждый из трех резонансов. В итоге для подробного анализа была выбрана следующая последовательность резонансных орбит: 1 : 1, 4 : 3 и 3 : 2. Как мы покажем ниже, использование такой последовательности позволяет за 5 лет обеспечить выведение КА на гелиоцентрическую орбиту, наклонение которой к плоскости солнечного экватора равно 30°, радиус перигелия всех рабочих орбит находится в диапазоне 60…100 RS.
Постановка задачи оптимизации выведения КА на систему рабочих гелиоцентрических орбит с использованием ЭРДУ на траектории гелиоцентрического перелета Земля–Земля. Задача формулируется как краевая задача принципа максимума. Выбираемая величина гиперболического избытка скорости при гравитационных маневрах у Венеры $V_{{\infty {\text{Venus}}}}^{ * }$ рассматривается как внешний оптимизируемый параметр схемы перелета. Эта величина перебиралась от достаточно большой (как выше отмечалось, во многих публикациях она рассматривается равной 17.5 км/с) до некоторой минимальной величины, при которой последовательность гравитационных маневров может обеспечить необходимое наклонение последней рабочей орбиты к плоскости солнечного экватора. Эта оптимальная величина гиперболического избытка скорости для рассматриваемой эпохи запуска (2027 год) оказалась равной 15.45 км/с.
Формулировка краевой задачи принципа максимума рассматривалась следующей. Неизвестные параметры краевой задачи: дата старта to; дата гравитационного маневра у Земли t1; дата первого гравитационного маневра у Венеры t2; векторы сопряженных переменных к радиус-вектору и вектору скорости КА в начальной точке гелиоцентрического перелета λr(to); λV(to); величина вектора гиперболического избытка скорости при старте V∞start. Учитывалось время выведения наконечную рабочую орбиту. В расчетах оно принималось равным 5 лет. Для выбранной последовательности резонансных орбит время перелета КА после первого гравитационного маневра у Венеры равно шести периодам орбиты Венеры (3.691 года). Поэтому дата подлета КА к Венере для первого гравитационного маневра около нее t2 связана с датой старта следующим соотношением: t2 = = t0 + 1.309 года и не рассматривается, как независимый выбираемый параметр.
Перечисленные независимые выбираемые параметры краевой задачи (9 скалярных параметров) выбирались из условия удовлетворения следующих краевых условий:
– условие попадания КА в окрестность Земли для гравитационного маневра у нее r(t1) = rE(t1);
– условие оптимальности величины гиперболического избытка скорости при старте от Земли ${{\lambda }_{V}}({{t}_{{\text{o}}}}) + {{\lambda }_{m}}({{t}_{o}})\frac{{d{{m}_{o}}}}{{d{{V}_{{\infty {\text{start}}}}}}}{\text{ = 0;}}$
– условие обеспечения требуемой величины гиперболического избытка скорости при первом подлете к Венере $V_{{\infty {\text{Venus}}}}^{ - }({{t}_{1}},{{t}_{2}}) = V_{{\infty {\text{Venus}}}}^{{\text{*}}};$
– условие обеспечения величины гиперболического избытка скорости при подлете к Земле для гравитационного маневра $V_{{\infty \,{\text{Earth}}}}^{ - } = V_{{\infty \,{\text{Earth}}}}^{ + }({{t}_{1}},{{t}_{2}})$;
– условие оптимальности направления вектора гиперболического избытка скорости при гравитационном маневре у Земли.
Условия оптимальности направления вектора гиперболического избытка скорости при гравитационном маневре у Земли имеют различные формы записи в зависимости от величины вектора гиперболического избытка скорости и угла поворота этого вектора. Угол поворота вектора гиперболического избытка скорости не может быть больше максимального, определяемого величиной гиперболического избытка скорости ${{\beta }_{{\max }}}({{V}_{\infty }}).$ Если угол β равен максимально допустимому значению, то из условий оптимальности следует, что базис-вектор λV в момент подлета КА к Земле для гравитационного маневра должен принадлежать плоскости гравитационного манера. То есть смешенное произведение трех векторов λV(t1), ${\mathbf{V}}_{{\infty {\text{Earth}}}}^{ - }$ и ${\mathbf{V}}_{{\infty {\text{Earth}}}}^{ + }$ должно быть равно нулю: $({{{\mathbf{\lambda }}}_{{\mathbf{V}}}}({{t}_{1}}),$ $[{\mathbf{V}}_{{\infty {\text{Earth}}}}^{ - } \times {\mathbf{V}}_{{\infty {\text{Earth}}}}^{ + }]) = 0.$
То есть должны удовлетворяться два условия. Одно из которых только что приведено, а второе имеет вид: $\beta = {{\beta }_{{\max }}}({{V}_{\infty }}).$
Если угол β меньше максимально допустимого значения $\beta < {{\beta }_{{\max }}}({{V}_{\infty }}),$ то из условий оптимальности следует, что базис-вектор λV в момент подлета к Земле должен быть коллинеарен вектору гиперболического избытка скорости при подлете к Земле. То есть в этом случае должны выполняться другие условия, но их тоже два:
В приведенных равенствах используются проекции на прямоугольную систему координат базис-вектора в момент подлета КА к Земле и проекции вектора подлетного гиперболического избытка скорости.
Последнее 9-ое условие есть условие оптимальности даты старта to и связанных с нею дат t1 и t2. Для случая коллинеарности базис-вектора и вектора гиперболического избытка скорости оно имеет следующий вид:
Методические особенности, использованные для оптимизации исследуемой миссии. Серьезных новых методических приемов не было использовано при оптимизации рассматриваемой транспортной операции. Можно отметить, что проблема сходимости используемых итерационных процедур остается не до конца решенной. Трудности появляются, как всегда, при изменении структуры оптимального управления (появление новых или исчезновение старых активных или пассивных участков). Свою трудность добавляет “негладкий” переход от варианта, когда гравитационный маневр у Земли выполняется с максимальным углом поворота вектора гиперболического избытка скорости, к варианту, когда гравитационный маневр выполняется с углом поворота вектора гиперболического избытка скорости меньшего максимального. В отличие от предыдущих исследований, когда сглаживание функции тяги осуществлялось с использованием соотношения $\delta = \frac{1}{2}\left( {\frac{\psi }{{\left| \psi \right| + \varepsilon }} + 1} \right),$ обратив внимание на то, эта функция имеет разрыв второй производной при нулевом значении функции переключения ψ, мы использовали другую функцию: $\delta = 1 + \frac{2}{\pi }{\text{arctg}}\left( {\frac{\Psi }{\varepsilon }} \right).$ Она не имеет разрывов производных любого порядка. К сожалению, ощутимых преимуществ замена не дала.
5. РЕЗУЛЬТАТЫ ПРОЕКТНО-БАЛЛИСТИЧЕСКОГО АНАЛИЗА ПРИ ИСПОЛЬЗОВАНИИ ЭРДУ НА ТРАЕКТОРИИ ПЕРЕЛЕТА ЗЕМЛЯ–ЗЕМЛЯ
Выше был отмечен важный результат численного анализа. Оказалось, что максимальная масса КА, доставляемого на систему рабочих гелиоцентрических орбит, при фиксированной величине наклонения конечной рабочей орбиты к плоскости солнечного экватора (30°) соответствует минимальной величине гиперболического избытка скорости при гравитационных маневрах у Венеры, обеспечивающее их это наклонение. Для рассматриваемой транспортной системы эта величина оказалась равна 15.45 км/с. Приведем характеристики оптимальной траектории выведения на систему рабочих орбит и проектно-баллистические характеристики КА для варианта гиперболического избытка скорости у Венеры равного 15.45 км/с.
Временные характеристики приведены в табл. 1.
Таблица 1.
Временные характеристики траектории выведения на систему гелиоцентрических орбит. Использование ЭРДУ
| Дата старта от Земли | 7.II.2027 года (юлианская дата 2 461 443.58822) |
| Время гелиоцентрического перелета Земля–Земля | 418.912 суток |
| Дата гравитационного маневра у Земли | 1.I.2028 года (юлианская дата 2 461 862.5) |
| Время гелиоцентрического перелета Земля–Венера | 59.111 суток |
| Дата первого гравитационного маневра у Венеры | 30.V.2028 года (юлианская дата 2 461 921.61105) |
| Время нахождения на первой рабочей орбите | 224.698 суток |
| Дата второго гравитационного маневра у Венеры | 9.I.2029 года (юлианская дата 246 2146.30908) |
| Время нахождения на второй рабочей орбите | 674.094 суток |
| Дата третьего гравитационного маневра у Венеры | 14.XI.2030 года (юлианская дата 2 462 820.40316) |
| Время нахождения на третьей рабочей орбите | 449.396 суток |
| Дата последнего гравитационного маневра у Венеры | 7.II.2032 года (юлианская дата 2 463 269.79922) |
| Время от даты старта до выведения на последнюю рабочую орбиту | 5 лет |
Массовые характеристики и величины гиперболических избытков скорости приведены в табл. 2.
Таблица 2.
Массовые и некоторые другие характеристики проекта выведения КА на систему гелиоцентрических орбит. Использование ЭРДУ
| Величина гиперболического избытка скорости при старте от Земли | 1425.492 м/с |
| Масса КА после отделения ХРБ | 1899.90 кг |
| Требуемая масса ксенона для реализации перелета Земля–Земля | 299.36 кг |
| Масса КА при гравитационном маневре у Земли | 1600.537 кг |
| Величина гиперболического избытка скорости при гравитационном маневре у Земли | 7458.672 м/с |
| Величина гиперболического избытка скорости при гравитационных маневрах у Венеры | 15.45 км/с |
Масса КА, доставляемого на рабочие орбиты, оказывается достаточно большой 1600 кг. Требуемая масса топлива менее 300 кг. Неплохой для реализации результат.
Характеристики рабочих орбит приведены в табл. 3. Строки таблицы соответствуют последовательности гравитационных маневров. Первая строка дает характеристики траектории перелета Земля–Венера, которая не рассматривается как рабочая орбита. Обозначение ГМ1, ГМ2 и т.д. обозначает номер гравитационного маневра, учитывая гравитационный маневр у Земли.
Таблица 3.
Характеристики рабочих гелиоцентрических орбит КА. Использование ЭРДУ
| Событие | Дата маневра | Время от даты старта, годы | Порядок резонанса | Период орбиты, сутки |
Радиус перигелия, RS |
Наклонение к плоскости эклиптики, градусы | Наклонение к плоскости солнечного экватора, градусы |
|---|---|---|---|---|---|---|---|
| ГМ1 | 1.IV.2028 | 1.147 | – | – | 86.729 | 0.656 | 7.552 |
| ГМ2 | 30.V.2028 | 1.309 | 1/1 | 224.7 | 97.278 | 9.422 | 16.581 |
| ГМ3 | 9.I.2029 | 1.924 | 3/4 | 168.5 | 79.824 | 15.19 | 22.352 |
| ГМ4 | 14.XI.2030 | 3.770 | 2/3 | 149.8 | 76.166 | 20.342 | 27.505 |
| ГМ5 | 7.II.2032 | 5.000 | – | 167.4 | 99.481 | 22.865 | 30.028 |
В последнем столбце таблицы приведены величины наклонения орбиты по отношению к плоскости солнечного экватора. Интересно то, что орбита гелиоцентрического перелета Земля–Венера, имеющая очень малое наклонение к плоскости эклиптики (менее 0.7°), имеет существенное наклонение к плоскости солнечного экватора (более 7.5°).
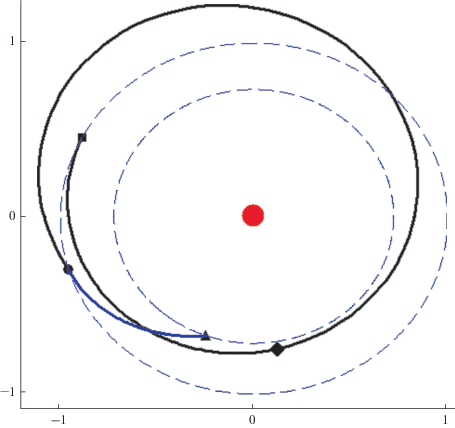
На рис. 2 показана проекция на плоскость эклиптики траектории гелиоцентрического перелета Земля–Земля–Венера. Тонкими линиями показаны орбиты Земли и Венеры. Квадратом и треугольником отмечены начальная и конечная точки гелиоцентрического перелета Земля–Земля соответственно. Пунктирными линиями показаны пассивные участки траектории перелета Земля–Земля. Активные участки траектории показаны сплошной линией. Направление тяги на этих участках показаны отрезками прямых в отдельных точках активных участков. Траектория перелета Земля–Венера показана штрихпунктирной линией.
Рис. 2.
Проекция на плоскость эклиптики траектории гелиоцентрического перелета Земля–Земля–Венера. Использование ЭРДУ.
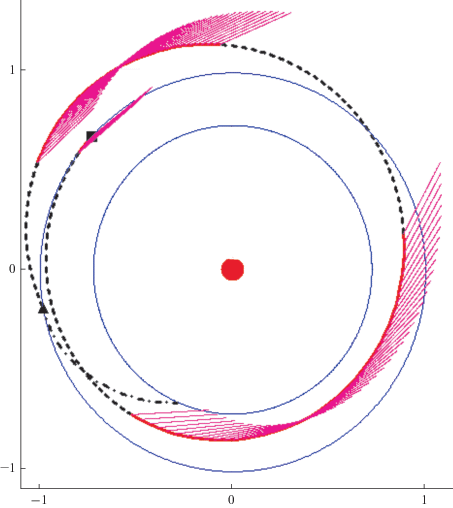
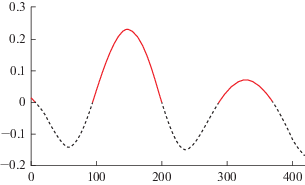
На траектории перелета Земля–Земля есть три активных и три пассивных участка. Их продолжительность хорошо видна на рис. 3. На нем показана функция переключения двигателя ψ вдоль всей перелетной траектории. Функция переключения 5 раз меняет свой знак. Траектория начинается очень коротким активным участком (его продолжительность 6.467 суток). Продолжительность последующего участка (он пассивный) 87.335 суток. Его сменяет активный участок продолжительностью 106.344 суток. Продолжительность второго пассивного участка равна 86.847 суток. Затем следует последний активный участок траектории. Его продолжительность 82.857 суток. КА подлетает к Земле (для гравитационного маневра у нее) на пассивном участке. Его продолжительность 49.062 суток.
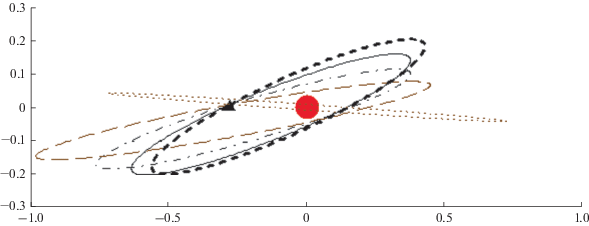
На рис. 4 приведена проекция на плоскость эклиптики системы рабочих гелиоцентрических орбит. Орбита Венеры показана точками. Треугольником показано положение Венеры в момент гравитационных маневров около нее. Первая рабочая орбита показана тонкой пунктирной линией. Афелий этой орбиты находится в районе орбиты Земли (радиус афелия 0.994 а.е.). Вторая рабочая орбита показана штрихпунктирной линией. Видно, что орбита имеет существенно меньший радиус афелия (0.823 а.е.). Третья рабочая орбита (последняя резонансная орбита) показана сплошной линией. Она имеет самой малый радиус перигелия (76.166 RS). Четвертая рабочая орбита показана жирной пунктирной линией. Эксцентриситет этой орбиты самый малый (0.221).
Рис. 4.
Проекция на плоскость эклиптики системы рабочих гелиоцентрических орбит. Использование ЭРДУ.
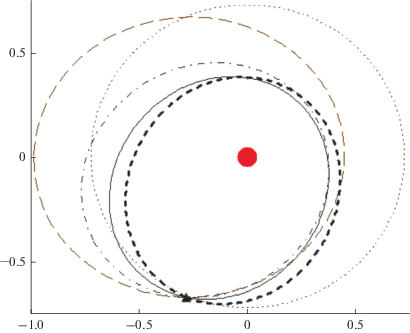
На рис. 5 показана проекция на плоскость xz эклиптической системы координат системы рабочих орбит. Использованы те же обозначения, что на предыдущем рис. 4. Видно, что последняя рабочая орбита наиболее сильно наклонена к плоскости эклиптики. На этой орбите имеются области, где КА удаляется от плоскости эклиптики более чем на 0.2 а.е.
6. РЕЗУЛЬТАТЫ ПРОЕКТНО-БАЛЛИСТИЧЕСКОГО АНАЛИЗА ПРИ ИСПОЛЬЗОВАНИИ ХИМИЧЕСКОЙ ДВИГАТЕЛЬНОЙ УСТАНОВКИ
Величину гиперболического избытка скорости при гравитационных маневрах у Венеры (она обеспечивает требуемое наклонение последней рабочей орбиты к плоскости солнечного экватора) оставляем той же (15.45 км/с), что и для варианта использования ЭРДУ. Приведем характеристики оптимальной траектории выведения на систему рабочих орбит и проектно-баллистические характеристики КА.
Оптимальной оказалась схема перелета Земля–Земля с одним импульсом скорости на траектории этого гелиоцентрического перелета.
Оптимальная дата старта КА от Земли оказалась равна 22.II.2027 года (сместилась на более позднюю дату на 15 дней по отношению к варианту использования ЭРДУ). Оптимальная величина гиперболического избытка скорости при старте от Земли равна 2.769 км/с (очень сильно увеличилась в сравнении с вариантом использования ЭРДУ, когда он был равен 1.425 км/c). КА на начальном участке гелиоцентрической траектории двигается по орбите с эксцентриситетом 0.141482, радиусом перигелия 0.748 а.е., радиусом афелия 0.995 а.е. Начальная точка траектории очень близка к афелию (ее истинная аномалия равна 195.339°). Длительность участка гелиоцентрического перелета до импульса скорости равна 107.753 суток. Угловая дальность полета на участке 125.932°. Истинная аномалия точки траектории, в которой дается импульс скорости 321.271°. Дата этого импульса скорости 10.VI.2027 года. Величина импульса скорости равна 1.675 км/с. Практически он просто разгоняет КА, почти не изменяя направления скорости КА. Благодаря импульсу скорости КА переходит на гелиоцентрическую орбиту со следующими характеристиками: радиус афелия 1.244 а.е., радиус перигелия 0.758 а.е., эксцентриситет орбиты 0.243109. Истинная аномалия начальной точки участка траектории после импульса скорости оказывается равна 337.311°. Угловая дальность полета на участке 278.588°. Орбита КА пересекает орбиту Земли. КА “сверху” подлетает к Земле для гравитационного маневра у Земли. В момент подлета к Земле КА имеет гелиоцентрическую скорость 29.766 км/с, очень близкую к гелиоцентрической скорости Земли. Но вектор скорости КА имеет весьма большую отрицательную радиальную компоненту скорости (истинная аномалия этой точки орбиты равна 255.899°). При этом величина гиперболического избытка скорости относительно Земли оказывается равной 7.775 км/с (она немного увеличилась по сравнению с вариантом использования ЭРДУ 7.459 км/с).
Оптимальное время гелиоцентрического перелета Земля–Земля оказалось равным 409.971 суток (уменьшилось примерно на 13.4 суток по отношению к варианту с ЭРДУ).
Гравитационный маневр у Земли выполняется с высотой перигея пролетной гиперболы равной 533.042 км, немного превышающей минимально допустимую высоту 400 км. При этом угол поворота вектора гиперболического избытка скорости равен 58.483°. Благодаря гравитационному маневру КА переходит на орбиту со следующими характеристиками: радиус перигелия 0.409 а.е., радиус афелия 1.012 а.е. (очень близок к орбите Земли), эксцентриситет орбиты 0.424658, наклонение к плоскости эклиптики 0.469°. Начальная точка гелиоцентрического перелета близка к афелию перелетной орбиты (истинная аномалия ее 189.771°).
Время гелиоцентрического перелета Земля–Венера оказалось рано 54.422 суток (уменьшилось примерно на 4.7 суток по отношению к варианту с ЭРДУ). Угловая дальность перелета 52.473°.
Масса КА после отделения ХРБ оказывается равной 1675.55 кг. Реализация импульса скорости на траектории гелиоцентрического перелета Земля–Земля требует 764.12 кг топлива (без учета потерь в скорости). При этом масса КА в момент подлета к Земле для гравитационного маневра оказывается равной 911.43 кг.
Характеристики гелиоцентрических рабочих орбит, на которые выводится КА в варианте использования химической двигательной установки отличаются незначительно (в третьей значащей цифре). Поэтому мы посчитали возможным их не приводить.
На рис. 6 показана проекция на плоскость эклиптики траектории гелиоцентрического перелета Земля–Земля–Венера для варианта использования химической двигательной установки. Пунктирными линиями показаны орбиты Земли и Венеры. Начальная и конечная точки гелиоцентрического перелета Земля–Земля показаны квадратом и кружочком. Точка подлета КА к Венере показана треугольником. Точка, где КА сообщается импульс скорости, отмечена ромбом.
7. СРАВНИТЕЛЬНЫЙ АНАЛИЗ ВОЗМОЖНОСТИ ИСПОЛЬЗОВАНИЯ РАССМОТРЕННЫХ ДВИГАТЕЛЬНЫХ УСТАНОВОК
Проведенный анализ показывает, что принципиально можно реализовать выведения КА на систему гелиоцентрических орбит для исследования Солнца, используя оба типа двигательных установок. Вопрос состоит только в том, какой набор научных инструментов удастся поместить на КА, в связи относительно небольшой их массой. Принципиально, можно увеличить массу КА на рабочих орбитах многими способами. Среди них можно отметить: вариант использования более тяжелых ракет-носителей; вариант увеличения длительности выведения на рабочие орбиты (увеличение длительности всего на 0.6 года, позволит включить в схему перелета еще одну орбиту с резонансом 2 : 3, это даст возможность увеличить массу выводимого КА); уменьшение нижней допустимой границы радиуса перигелия рабочих орбит (например, до 50 RS). Достаточно уменьшить границу для одной промежуточной рабочей орбиты.
Масса КА, выводимого на рабочие орбиты в варианте использование ЭРДУ, оказывается существенно больше варианта использования химической двигательной установки (1600 кг по отношению к 910 кг). Даже полагая, что масса солнечной электроракетной двигательной установки с электрической мощностью 5 кВт может иметь массу 200 кг (удельная масса установки 40 кг/кВт), то и в этом случае выигрыш в массе полезной нагрузки будет достигать несколько сотен кг.
ЗАКЛЮЧЕНИЕ
Проведен проектно-баллистический анализ двух вариантов реализации проекта солнечного зонда, предполагающего использовании системы гелиоцентрических орбит с относительно низким перигелием (радиус которого находится в диапазоне 60…100 RS), и достаточно большим наклонением к плоскости солнечного экватора (наклонение последней орбиты рассматриваемой системы 30°). Время выведения КА на последнюю рабочую орбиту ограничивалось сверху 5 годами. Варианты реализации проекта отличаются типом двигательной установки КА.
Использование постановки задачи, включающей: а) ограничение наклонения рабочих о-рбит по отношению к плоскости солнечного экватора, а не наклонение орбит к плоскости э-клиптики; б) рассмотрение величины гиперболического избытка скорости, как выбираемого параметра схемы перелета, дало возможность получить траектории выведения на систему рабочих орбит с заданными характеристиками и малым (5 лет) временем выведения на последнюю рабочую орбиту.
Показано, использование солнечной ЭРДУ обеспечивает выведение на рабочие орбиты КА существенно большей массой, чем в варианте ХДУ (1600 кг против 910 кг).
Исследование выполнено при поддержке Российского научного фонда. Проект № 16-19-10429.
Список литературы
Kuznetsov V.D., Zelenyi L.M., Zimovets I.V. et al. The Sun and heliosphere explorer – the InterhelioProbe mission // Geomagnetism and Aeronomy. 2016. V. 56. № 7. Р. 781.
INTERHELIOPROBE Project. Workshop Proceedings / Ed. Kuznetsov V. Tarusa, 2011 May 11.
Константинов М.С., Тейн М. Оптимизация траектории выведения космического аппарата на систему гелиоцентрических орбит // Космич. исслед. 2017. Т. 55. № 3. С. 214.
Konstantinov M.S., Petukhov V.G., Thein M. The one mission for S exploration // Proceedings 63rd International Astronautical Congress, 2012. P. 1745.
Konstantinov M.S., Petukhov V.G., Thein M. Optimization of the spacecraft insertion into the system of heliocentric orbits for S exploration // Proceeding of the 65-th International Astronautical Congress. Toronto, Canada, 2014. P. 11.
Konstantinov M.S., Petukhov V.G., Loeb H.W. Application of RIT-22 Thruster for InterhelioProbe Mission // Электронный журнал “Труды МАИ”. 2012. № 60.
Konstantinov M.S., Petukhov V.G. One Version of a Space Transport System for Research of the S // 62nd International Astronautical Congress. Cape Town, South Africa, 2011.
Платов И.В., Симонов А.В., Константинов М.С. Особенности разработки комбинированной двигательной установки и схемы полета космического аппарата “ИНТЕРГЕЛИО-ЗОНД” // Вестник Сибирского государственного аэрокосмического университета им. академика М.Ф. Решетнева. 2015. Т. 16. № 1. С. 198.
Константинов М.С., Тейн M. Оптимизация траектории выведения космического аппарата на рабочую гелиоцентрическую орбиту // Электронный журнал “Труды МАИ”. 2013. № 67.
Константинов М.С., Тейн Мин. Рациональные характеристики солнечной энергетической установки КА с ЭРДУ при прямом выведении на гелиоцентрическую орбиту для исследования Солнца // Известия РАН. Энергетика. 2018. № 3. С. 93.
Константинов М.С., Петухов В.Г., Тейн М. Анализ влияния мощности солнечной энергетической установки на характеристики проекта “ИНТЕРГЕЛИО-ЗОНД” при использовании электроракетных двигателей // Известия РАН. Энергетика. 2016. № 2. С. 102.
Константинов М.С., Тейн M. Анализ одной схемы полета КА для исследования Солнца // Электронный журнал “Труды МАИ”. 2013. № 71.
Платов И.В., Симонов А.В., Константинов М.С. Выбор рационального варианта построения комбинированной двигательной установки и схемы полета космического аппарата “ИНТЕРГЕЛИ0-30НД” // Вестник НПО им. С.А. Лавочкина. 2015. № 4(30). С. 31.
Константинов М.С. Анализ возможностей космической транспортной системы при использовании электроракетной двигательной установки и гравитационного маневра у Земли в начале межпланетного перелета // Некоторые аспекты современных проблем механики и информатики. М.: ИКИ РАН, 2018. С. 153–165. https://doi.org/10.21046/aspects-2018-153-165
Konstantinov M.S., Thein M. Method of Interplanetary Trajectory Optimization for the Spacecraft with Low Thrust and Swing-bys // Acta Astronautica. V. 136. 2017. P. 297.
Константинов М.С., Петухов В.Г., Тейн М. Оптимизация траекторий гелиоцентрических перелетов. Издательство МАИ, 2015.
Дополнительные материалы отсутствуют.
Инструменты
Космические исследования