Космические исследования, 2019, T. 57, № 5, стр. 339-346
Анализ влияния электромагнитного излучения стационарных плазменных двигателей на помехоустойчивость канала связи “Земля–космический аппарат”
А. П. Плохих 1, *, Н. А. Важенин 1, Г. А. Попов 1
1 Научно-исследовательский институт прикладной механики и электродинамики МАИ
г. Москва, Россия
* E-mail: riame@sokol.ru
Поступила в редакцию 27.03.2019
После доработки 18.04.2019
Принята к публикации 25.04.2019
Аннотация
Рассматривается полный цикл исследований, связанных с получением знаний о спектрально-временных характеристиках излучения стационарных плазменных двигателей (СПД), разработкой математических и имитационных моделей такого излучения и оценками его влияния на помехоустойчивость систем космической связи. По результатам проведенного имитационного моделирования оценивается достоверность передачи информации в цифровых каналах связи Земля–КА. Исследуется зависимость вероятности битовой ошибки как функции битовых отношений сигнал-шум и сигнал-помеха от СПД. В качестве показателя помехоустойчивости канала связи в присутствии излучения СПД, рассматривается его энергетический проигрыш относительно эталонной системы. Проводятся расчеты энергетического потенциала радиолиний дальнего и ближнего космоса. Оценивается энергетический проигрыш радиолиний на трассе Земля–Марс и в пределах геостационарной орбиты. Даются рекомендации по снижению влияния излучения СПД.
ВВЕДЕНИЕ
Успешное использование стационарных плазменных двигателей при решении многообразных задач в ближнем и дальнем Космосе подтвердило их надежность и эффективность. В тоже время, углубленные исследования свойств и характеристик СПД показали, что при интеграции СПД с космическим аппаратом и его системами необходимо учитывать некоторые особенности их функционирования. Так анализ многочисленных результатов экспериментальных исследований собственного электромагнитного излучения СПД показал, что это излучение кроме тепловой компоненты содержит широкополосный импульсный случайный процесс, спектральная плотность которого лежит в пределах от десятков кГц до единиц ГГц [1, 2]. Данное излучение может представлять собой помеху для канала “Земля–КА” систем космической связи, в особенности дальней, и его необходимо учитывать на этапе проектирования таких систем. В связи с этим актуальной является задача анализа воздействия такого рода помех на помехоустойчивость систем космической связи.
С целью уточнения данных о спектрально-временных характеристиках излучения, создаваемого ЭРД, необходимо обеспечить проведение прецизионных измерений в наземных условиях. При этом основная проблема заключается в одновременном обеспечении требуемого для работы двигателя уровня вакуума и необходимого уровня “безэховости” в измерительной зоне. В качестве примера одного из вариантов успешной реализации представлен, разработанный авторами, измерительный комплекс, основу которого составляет мобильная безэховая камера (БЭК) с интегрированным радиопрозрачным вакуумным отсеком (РВО) (рис. 1) [3]. Мобильная БЭК установлена на рельсовом пути и может перемещаться относительно основной вакуумной камеры, оборудованной системой откачки.
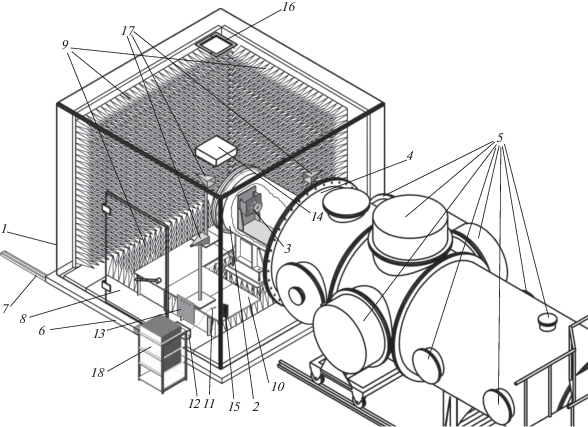
Рис. 1.
Конструкция измерительного комплекса: 1 – БЭК; 2 – радиопрозрачный вакуумный цилиндр; 3 – ЭРД; 4 – основная вакуумная камера; 5 – система откачки; 6 – подвижная платформа; 7 – рельсовый путь; 8 – дверь; 9 – радиопоглощающее покрытие; 10 – диэлектрический помост; 11 – сетевой удлинитель; 12 – проходной сетевой фильтр; 13 – панель с проходными разъемами; 14 – реверсивный вентилятор; 15 – пульт управления вентилятором; 16 – дополнительное окно вентиляции; 17 – измерительные антенны; 18 – стойка с измерительным оборудованием.
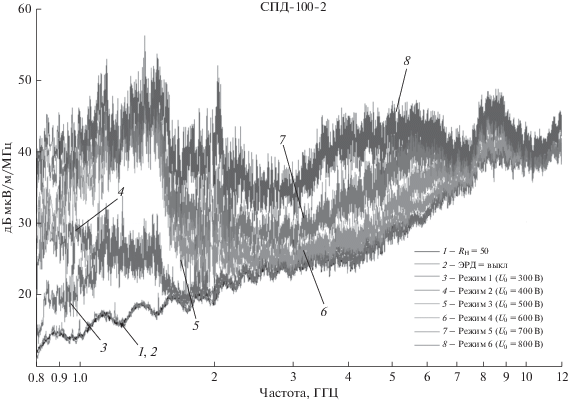
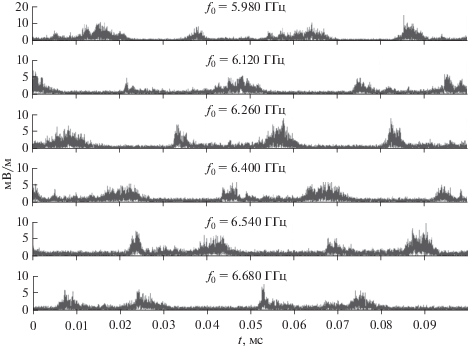
Надежную стыковку двух вакуумных объемов обеспечивает быстроразъемное вакуумное соединение, описанное в [4]. Над напольными пирамидальными поглощающими покрытиями сформирован подиум из диэлектрического листового материала, на котором расположены измерительные антенны, перекрывающие заданный частотный диапазон. С помощью проходных разъемов сигналы от антенн выводятся за пределы БЭК, где располагается аппаратура спектрально временного анализа. В качестве примеров на рис. 2 представлены зависимости уровня фона и излучения СПД-100 от частоты для различных режимов его работы, а на рис. 3 амплитудная огибающая излучения СПД для различных частотных диапазонов, подтверждающая его импульсный характер.
База данных результатов экспериментальных измерений характеристик собственного излучения СПД в радиодиапазоне служит основой для разработки математических и имитационных моделей такого излучения. Данные модели необходимы для анализа влияния излучения СПД на помехоустойчивость бортовых радиосистем космической связи и разработки соответствующих конструктивно-технологических и программно-алгоритмических решений минимизирующих это влияние.
На основе статистического анализа большого объема экспериментальных данных предложены две обобщенные математические модели излучения СПД в радиодиапазоне, первая – на основе модифицированной модели Фурутсу–Ишида, а вторая – на основе моделей Холла и стробированного гауссовского шума [5, 6].
Случайный процесс ${{n}_{\Sigma }}\left( t \right),$ описывающий излучение СПД, может быть представлен в виде суммы импульсного процесса (ИП) ${{u}_{p}}\left( t \right)$ и широкополосного (теплового) шума $n\left( t \right)$
Или в комплексной форме
(2)
${{\dot {n}}_{\Sigma }}\left( t \right) = {{\dot {u}}_{p}}\left( t \right) + \dot {n}\left( t \right) = \left( {{{{\dot {U}}}_{p}}\left( t \right) + \dot {N}\left( t \right)} \right)\exp \left( {j{{\omega }_{0}}t} \right),$где ω0 – центральная частота спектра, ${{\dot {U}}_{p}}\left( t \right)$ – комплексная огибающая импульсного процесса, $\dot {N}\left( t \right)$ – комплексная огибающая теплового шума.
Модифицированная модель Фурутсу–Ишида:
(3)
${{\dot {U}}_{p}}\left( t \right) = \sum\limits_{i = 1}^\infty {{{u}_{0}}\left( {t - \sum\limits_{l = 1}^i {{{T}_{{pl}}}} } \right)\exp \left( { - j\left( {{{\varphi }_{{oi}}} + {{\varphi }_{{opi}}}\left( t \right)} \right)} \right).} $Модифицированная модель Холла:
(4)
${{\dot {U}}_{p}}\left( t \right) = \sum\limits_{i = 1}^\infty {{{u}_{0}}\left( {t - \sum\limits_{l = 1}^i {{{T}_{{pl}}}} } \right)\exp \left( { - j{{\varphi }_{{oi}}}} \right) \cdot {{{\dot {n}}}_{p}}\left( t \right),} $где ${{u}_{0}}\left( t \right)$ – функция, описывающая форму одиночного импульса,
${{T}_{{pl}}}$ – временной интервал между l-м и (l – 1)-м импульсами в последовательности,
${{\varphi }_{{oi}}}$ – начальный фазовый сдвиг для каждого импульса ИП,
${{\varphi }_{{opi}}}\left( t \right)$ – закон изменения фазы в пределах i-го импульса.
Для имитационного моделирования функционирования радиосистемы связи с учетом влияния собственного излучения СПД в радиодиапазоне был разработан специализированный программный комплекс, осуществляющий имитационное моделирование передаваемого информационного сигнала, тепловых шумов и импульсной помехи, формируемой СПД, а также алгоритмов обработки принимаемой смеси сигнала и помех [7–9].
Разработанный программный комплекс осуществляет имитационное моделирование цифровой радиосистемы передачи данных и обеспечивает учет воздействия на эту систему собственного излучения СПД на основе формирования реализации комплексной огибающей сигнала, имитирующей импульсную и тепловую компоненты собственного излучения СПД. Использование данного программно-алгоритмического комплекса позволяет оценивать вероятность битовой ошибки при передаче информации в зависимости от отношений сигнал-шум и сигнал-помеха от СПД.
ОЦЕНКА ВЛИЯНИЯ ЭЛЕКТРОМАГНИТНОГО ИЗЛУЧЕНИЯ СПД В РАДИОДИАПАЗОНЕ НА ХАРАКТЕРИСТИКИ ПОМЕХОУСТОЙЧИВОСТИ РАДИОСИСТЕМ КОСМИЧЕСКОЙ СВЯЗИ
Для описания качества функционирования радиосистем связи в условиях помех обычно используют такие показатели, как достоверность передачи информации и помехоустойчивость системы связи.
Достоверность передачи информации в цифровых системах связи принято оценивать с помощью такого показателя, как вероятность битовой ошибки (Bit Error Rate – BER), которая характеризует вероятность неправильного приема бита полезной информации. Вероятность битовой ошибки зависит от многих факторов: методов модуляции и демодуляции, вида и алгоритмов кодирования и декодирования, вида и характеристик помех и т.п.
Помехоустойчивость систем связи обычно описывается энергетическим проигрышем (выигрышем) рассматриваемой системы относительно некоторой эталонной системы. Под энергетическим проигрышем понимается показатель, определяющий во сколько раз необходимо увеличить отношение сигнал-шум на входе рассматриваемой системы, чтобы ее достоверность передачи информации сравнялась с аналогичным показателем эталонной системы.
Вероятность битовой (BER) ошибки рассматривается как функция битовых отношений сигнал-шум (ОСШ) и сигнал-импульсная помеха (ОСИП). Рассмотрим параметры, характеризующие полезный сигнал и помехи в рассматриваемой задаче. Радиосигнал зададим средней мощностью на входе линейной части приемника (ЛЧП) Ps, длительностью двоичного информационного символа τs и энергией в символе Es = Psτs, Nbit – количество бит, приходящееся на один канальный символ.
Широкополосную гауссовскую шумовую помеху будем характеризовать постоянной в пределах полосы ЛЧП односторонней спектральной плотностью мощности N0.
Для описания случайной импульсной помехи (ИП), моделирующей импульсную составляющую излучения СПД, на входе линейной части приемника (ЛЧП) введем среднюю длительность одного импульса ${{\bar {\tau }}_{p}};$ средний период повторения импульсов ${{\bar {T}}_{p}};$ коэффициент перекрытия А = ${{\bar {\tau }}_{p}}$/${{\bar {T}}_{p}};$ скважность Q = 1/А = ${{\bar {T}}_{p}}$/${{\bar {\tau }}_{p}};$ среднюю мощность одного импульса ${{\bar {P}}_{{p1}}};$ среднюю мощность ИП ${{\bar {P}}_{p}} = {{\bar {P}}_{{p1}}}A.$
Также будем использовать параметры, характеризующие взаимосвязь полезного сигнала, шума и ИП:
Можно показать, что битовое ОСШ определяется как
где ${{\bar {P}}_{n}} = {{{{N}_{0}}} \mathord{\left/ {\vphantom {{{{N}_{0}}} {{{\tau }_{s}}}}} \right. \kern-0em} {{{\tau }_{s}}}}$ – средняя мощность шума в эквивалентной шумовой полосе СФ $\Delta {{F}_{n}} = {1 \mathord{\left/ {\vphantom {1 {{{\tau }_{s}}}}} \right. \kern-0em} {{{\tau }_{s}}}};$а битовое ОСИП (здесь помеха – импульсная составляющая излучения СПД)
Авторами рассматривались радиосистемы с различными методами модуляции несущего сигнала, например, такими, как ФМн-2/BPSK, ФМн-4/QSPK, ФМн-8/8PSK, ФМн-16/16PSK, КАМ-16/16QAM и КАМ-64/64QAM, которые нашли применение в радиосистемах космической связи (РСКС). Ниже в качестве примера приводятся результаты, полученные для ФМн-2 и КАМ-64.
Результаты оценки зависимости вероятности битовой ошибки в радиосистемах космической связи с модуляцией ФМн-2 от ОСШ и ОСИП, полученные на основе имитационного моделирования для модели радиоизлучения СПД приведены на рис. 4. На данных графиках зависимости BER от битовых ОСШ и ОСИП построены для средней скважности СИП Q = 10 и значения параметра µ = 1, характеризующего соотношение длительности канального символа и средней длительности импульса помехи.
Рис. 4.
Зависимость BER от битовых отношений сигнал-шум и сигнал-импульсная помеха для модуляции ФМн-2, μ = 1.
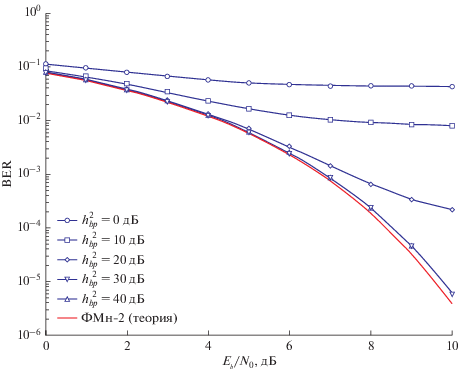
Как видно из представленных графиков, в зависимости от текущих значений ОСШ и ОСИП излучение ЭРД в радиодиапазоне может приводить к увеличению вероятности битовой ошибки от нескольких раз до нескольких десятков раз. При µ = 1.0 и ОСШ 10 дБ BER увеличивается с 4.5 ⋅ 10–6 до 4.5 ⋅ 10–1. В случае µ = 10 и ОСШ 10 дБ BER увеличивается с 6 ⋅ 10–6 до 8 ⋅ 10–2, а при µ = 100 и ОСШ 10 дБ BER увеличивается с 4 ⋅ 10–6 до 1 ⋅ 10–1.
Результаты оценки зависимости вероятности битовой ошибки в РСКС с модуляцией КАМ-64 от ОСШ и ОСИП, полученные на основе имитационного моделирования, приведены на рис. 5. Зависимости BER от битовых ОСШ и ОСИП построены для средней скважности СИП Q = 10 и µ = 1.0.
Рис. 5.
Зависимость BER от битовых отношений сигнал-шум и сигнал-импульсная помеха для модуляции КАМ-64, μ = 1.
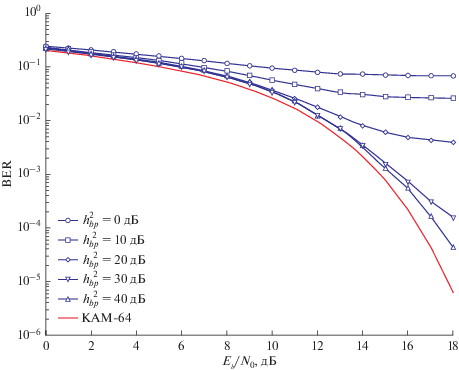
Анализ полученных результатов показывает, что для всех рассмотренных значений параметра µ при уменьшении ОСИП от 40 до 0 дБ наблюдается рост вероятности битовой ошибки. Так, при µ = 1.0 и ОСШ 18 дБ BER увеличивается с 3 ⋅ 10–5 до 6.5 ⋅ 10–2.
При этом энергетический проигрыш для модуляции ФМн-2 в зависимости от текущих значений ОСШ и ОСИП может варьироваться от десятых долей децибела до 3 и более дБ (рис. 6). Наименьшие энергетические потери порядка 0.1–0.2 дБ во всем рассмотренном диапазоне отношений сигнал-шум имеют место при отношениях сигнал-помеха от ЭРД превышающих 30 дБ. Для КАМ-64 энергетический проигрыш составляет соответственно от 1 до 6 и более децибел (рис. 7). При этом наименьшие энергетические потери порядка 0.5–1.0 дБ во всем рассмотренном диапазоне отношений сигнал-шум имеют место так же при отношениях сигнал-помеха от ЭРД превышающих 30 дБ.
Рис. 6.
Зависимость энергетического проигрыша EL1 от суммарного отношения сигнал-шум и отношения сигнал-импульсная помеха для модуляций ФМн-2, μ = 1.
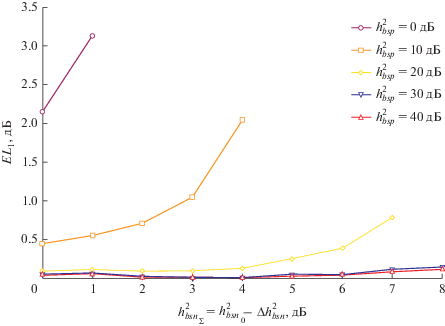
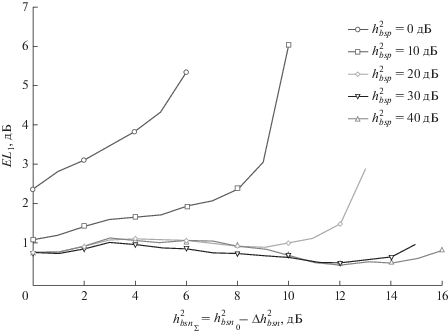
Рис. 7.
Зависимость энергетического проигрыша EL1 от суммарного отношения сигнал-шум и отношения сигнал-импульсная помеха для модуляций КАМ-64.
На основании проведенного моделирования были проведены расчеты энергетического бюджета командных радиолиний для случаев ближнего и дальнего космоса. Так в табл. 1 приведены исходные данные и результаты расчетов радиолинии связи с КА, находящегося на орбите Марса. Данные расчеты показывают, что для радиолинии “Земля–Марс” при приеме командно-программной информации (КПИ) на остронаправленную антенну энергетический проигрыш за счет влияния ЭРД может составлять около 11 дБ. В случае связи с КА, находящимся на геостационарной орбите, энергетический проигрыш за счет влияния излучения ЭРД не превышает 2.7 дБ.
Таблица 1.
Энергетический бюджет радиолинии “Земля–Марс”
| Параметры | Остронаправленная антенна |
|---|---|
| Исходные данные: | |
| Максимальная дальность связи, км | 360 000 000.00 |
| Частота несущей, ГГц | 7.20 |
| Вид модуляции | ИКМ-ФМн-ФМ |
| Битовая скорость передачи информации, бит/с | 512 000.00 |
| Параметры передающей системы: | |
| Мощность передатчика, дБВт | 43.01 |
| Коэффициент усиления передающей антенны, дБ | 72.51 |
| Параметры приемной системы: | |
| Коэффициент усиления приемной антенны, дБ | 39.70 |
| Уровень боковых лепестков приемной антенны, дБ | –20.00 |
| Добротность приемной системы, дБ 1/К | 12.71 |
| Пороговое ОСШ, дБ | 9.60 |
| Чувствительность приемника для порогового ОСШ, дБВт | –134.92 |
| Потери в тракте распространения(1: | |
| Потери распространения в свободном пространстве, дБ | 280.71 |
| Энергетические характеристики при выключенном СПД: | |
| Средняя мощность информационной компоненты сигнала на входе МШУ приемника, дБВт | –131.51 |
| Битовое отношение сигнал-шум, дБ | 13.01 |
| Энергетические характеристики с учетом теплового излучения СПД: | СПД-100-2 Up = 800 В |
| Расстояние от СПД до приемной антенны, м | 2.00 |
| Увеличение шумовой температуры за счет излучения СПД, градусы К | 174.61 |
| Суммарное битовое отношение сигнал-шум, дБ | 11.71 |
| Энергетические характеристики с учетом импульсной компоненты излучения СПД: | |
| Экспериментальные данные импульсного излучения СПД: | СПД-100 Up = 800 В |
| Параметр Рэлея пикового значения импульсов в апертуре приемной антенны, В/м | 1.6 ⋅ 10–3 |
| Средняя длительность импульсов по уровню Ep, с | 4 ⋅ 10–6 |
| Средний интервал следования импульсов, с | 5 ⋅ 10–5 |
| Средняя скважность импульсов | 12.50 |
| Результаты расчета влияния теплового и импульсного излучения СПД: | |
| Суммарное битовое отношение сигнал-шум, дБ | 11.71 |
| Битовое отношение сигнал-импульсная помеха, дБ | –7.04 |
| Энергетический проигрыш EL1 по сравнению с гауссовским каналом (без СПД), дБ | 11.29 |
В качестве мер повышения помехоустойчивости радиолиний, функционирующих в условиях воздействия излучения СПД, могут быть предложены: снижение уровня излучения СПД в диапазоне работы радиолинии за счет выбора соответствующих режимов работы СПД; выбор компоновки КА (оптимальное взаимное расположение ЭРД и приемных антенн); выбор оптимального диапазона частот, используемого радиолинией; разработка и реализация алгоритмов приема и обработки сигналов, устойчивых к воздействию импульсного и теплового излучения СПД; в частности использование методов борьбы с импульсными помехами и помехоустойчивого кодирования в канале связи.
ЗАКЛЮЧЕНИЕ
1. Рассмотрен полный цикл процедур, связанных с получением знаний о спектрально-временных характеристиках излучения ЭРД типа СПД, разработке математических и имитационных моделей такого излучения и оценок его влияния на помехоустойчивость систем космической связи.
2. Результаты имитационного моделирования показали, что величина энергетических потерь, связанная с влиянием собственного излучения СПД в радиодиапазоне, для модуляции ФМн-2 варьируется от десятых долей дБ до 3 и более децибел. Наименьшие энергетические потери порядка 0.1–0.2 дБ во всем рассмотренном диапазоне отношений сигнал-шум имеют место при отношениях сигнал-помеха от ЭРД превышающих 30 дБ.
3. Для модуляции КАМ-64 величина энергетических потерь варьируется от 1 до 6 и более децибел. Наименьшие энергетические потери порядка 0.5–1.0 дБ во всем рассмотренном диапазоне отношений сигнал-шум имеют место при отношениях сигнал-помеха от ЭРД превышающих 30 дБ.
4. Наиболее существенное влияние собственного излучения СПД, проявляется в диапазоне рабочих отношений сигнал-шум порядка 8…12 дБ и более и отношений сигнал-помеха меньших 15–20 дБ.
5. Проведены расчеты энергетического потенциала радиолиний дальнего и ближнего космоса. Показано, что для радиолинии “Земля–Марс” энергетический проигрыш за счет влияния ЭРД может составлять около 11 дБ. В случае связи с КА, находящимся на геостационарной орбите, энергетический проигрыш за счет влияния излучения ЭРД для рассмотренного режима работы СПД не превышает 2.7 дБ.
Список литературы
Plokhikh A., Vazhenin N., Kim V. et al. Study for the Influence of Stationary Plasma Thruster Operating Models on Its Electromagnetic Emission. IEPC-2011-094. 32 International Electric Propulsion Conference. 11–15 September, 2011, Wiesbaden, Germany.
Beiting E.J., Garrett M.L., Pollard J.E. et al. Temporal Characteristics of Radiated Emission from SPT-100 Hall Thrusters in the L, S, and C Bands // 29th International Electric Propulsion Conference. Princeton University. October 31–November 4. 2005. P. 222.
Важенин Н.А., Плохих А.П., Попов Г.А., Арбатский В.М. Испытательный стенд. Патент РФ N 107769 от 19.04.2011г.
Арбатский В.М., Важенин Н.А., Плохих А.П., Попов Г.А., Испытательный стенд. Патент РФ N 124664 от 24.09.2012г.
Spaulding A.D., Middleton D. Optimum Reception in Impulsive Interference Environment. Coherent detection // IEEE Trans. on Communication Technology. 1977. V. Com-25. № 9. Part I: P. 910–923. Part II: P. 924–934.
Middleton D. Canonical Non-Gaussian Noise Models: Their Implications for Measurement and for Prediction of Receiver Performance // IEEE Trans. on Communication Technology. 1979. V. EMC-21. № 3. P. 209–220.
Важенин Н.А., Волковский А.С. Помехоустойчивость систем цифровой передачи информации при совместном воздействии шумовых и импульсных помех // Вестник Московского авиационного института. 2010. Т. 17. № 6. С. 109–119.
Важенин Н.А., Плохих А.П. Имитационное моделирование электромагнитного излучения стационарных плазменных двигателей // Известия Академии наук. Энергетика. 2014. № 6. С. 118–131.
Важенин Н.А., Плохих П.П., Фоменков А.И. Воздействие электромагнитного излучения стационарных плазменных двигателей на канал связи “Земля–космический аппарат” // Известия Академии наук. Энергетика. 2017. № 3. С. 74–85.
Дополнительные материалы отсутствуют.
Инструменты
Космические исследования