Космические исследования, 2019, T. 57, № 5, стр. 373-385
Применение угловой независимой переменной и ее регуляризирующего преобразования в задачах оптимизации траекторий с малой тягой
В. Г. Петухов *
Научно-исследовательский институт прикладной механики и электродинамики МАИ
г. Москва, Россия
* E-mail: vgpetukhov@gmail.com
Поступила в редакцию 26.03.2019
После доработки 26.03.2019
Принята к публикации 25.04.2019
Аннотация
Рассматривается целесообразность использования истинной долготы или связанного с ней угла в качестве независимой переменной в задачах оптимизации многовитковых траекторий космических аппаратов с малой тягой. Вводится вспомогательная долгота, которая используется в дальнейшем в качестве новой независимой переменной вместо времени. Показано преимущество использования вспомогательной долготы в качестве независимой переменной в задаче оптимизации траекторий с фиксированной угловой дальностью и оптимальным временем перелета. Рассмотрены задачи оптимизации траекторий космических аппаратов с идеально-регулируемым двигателем ограниченной мощности и двигателем ограниченной тяги с постоянной скоростью истечения. Рассмотрена возможность улучшения сходимости методов решения задач оптимизации траекторий с двигателем ограниченной тяги за счет совместного использования сглаживающей аппроксимации релейной функции переключения тяги и регуляризирующего преобразования независимой переменной, растягивающего ее значения в окрестности моментов переключения тяги. На основе полученных результатов предложен метод решения задач оптимизации многовитковых перелетов, представлены численные примеры его использования.
ВВЕДЕНИЕ
К настоящему времени разработано множество численных методов оптимизации траекторий космических аппаратов (КА) с малой тягой, хороший обзор по ранним работам в этой области приведен в [1], а по современным работам – в [2]. Одним из наиболее эффективных является подход, основанный на использовании необходимых условий оптимальности в форме принципа максимума для редукции задачи оптимального управления в краевую задачу для системы обыкновенных дифференциальных уравнений, с последующим сведением этой краевой задачи к задаче Коши с помощью метода продолжения по параметру [3–9].
Применение этого подхода сталкивается с определенными трудностями при оптимизации многовитковых траекторий, связанными, в частности, с проблемой выбора согласованных значений угловой дальности и длительности перелета. Одной из проблем является возможность существования множества локальных экстремумов решения таких задач, поэтому выполнение необходимых условий оптимальности никоим образом не гарантирует того, что получено наилучшее решение. Более того, несогласованный выбор угловой дальности и длительности траектории может приводить к оптимальным решениям, не имеющим практического значения из-за слишком близкого пролета притягивающего центра или из-за слишком большого удаления от него. В работах [3, 4, 7, 8], для вычисления оптимальных траекторий встречи с фиксированной длительностью и угловой дальностью, предложен метод продолжения по гравитационному параметру. Однако и с помощью этого метода оптимальную угловую дальность приходится находить перебором целого числа витков, а это оказывается весьма трудоемким при большом числе витков и больших вычислительных затратах на вычисление каждой оптимальной траектории. Существование множества локальных экстремалей со своими областями притяжения в пространстве неизвестных параметров краевой задачи принципа максимума снижает устойчивость численных методов, так как на границах этих областей притяжения вырождается матрица частных производных от невязок краевой задачи по ее неизвестным параметрам, так или иначе используемая во всех непрямых методах решения задачи оптимизации траекторий.
В задаче перелета с малой тягой между некомпланарными эллиптической и круговой орбитами ранее обнаружено существование двух типов траекторий, удовлетворяющих необходимым условиям оптимальности, которые в работе [6] названы C- и E-решениями. При угле между плоскостями начальной и конечной орбитами, меньшем критического, существует только решение C-типа, в противном случае существуют оба типа решения. Анализ задачи оптимального быстродействия показывает, что для заданной длительности перелета для каждого типа траекторий, удовлетворяющих необходимым условиям оптимальности, может существовать множество решений с разной угловой дальностью. На рис. 1 представлена характерная зависимость конечной массы КА от угловой дальности перелета для C-решения (аналогичная зависимость для другого перелета была приведена в работе [10]). Видно, что при конечной массе КА 885.19 кг (пунктирная линия на рис. 1), соответствующей в данном случае длительности перелета 80.88373 суток, существует 10 различных решений с разной угловой дальностью – от 69.6 до 73.8 витков.
Рис. 1.
Типичная зависимость конечной массы КА от угловой дальности перелета для траекторий на минимум времени перелета C-типа.
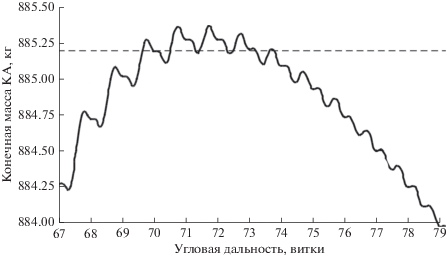
График на рис. 1 получен для задачи минимизации времени перелета между начальной эллиптической орбитой, имеющей высоту перигея 10 000 км, высоту апогея 60 000 км, наклонение 30°, нулевые значения аргумента перигея и долготы восходящего узла и геостационарной орбитой (круговой орбитой высотой 35 793 км с нулевым наклонением). Все высоты здесь и далее приведены относительно среднего радиуса Земли 6371 км, гравитационный параметр Земли принят равным 398 600.44 км3/с2. Начальная точка траектории имеет истинную долготу 150°, начальная масса КА принята равной 1000 кг, тяга двигательной установки – 0.29 Н, удельный импульс тяги – 1800 с.
Из рис. 1 видно, что для фиксированной угловой дальности существует единственное решение с минимальным временем перелета. Можно предположить, что качественно картина не изменится и для задачи на минимум затрат топлива, по крайней мере при величине тяги, близкой к минимальной: возможно существование множества решений с разной угловой дальностью при фиксированном времени перелета и существует единственное решение данного типа (например, E- или C-) с фиксированной угловой дальностью и оптимальным временем перелета.
Из приведенного анализа следует, что решение задачи оптимизации перелета с фиксированной угловой дальностью и оптимальной длительностью перелета должно быть проще решения задачи с оптимальной угловой дальностью хотя бы потому, что в первом случае, в отличие от второго, существует не более одного решения для заданного семейства (например, E- или C-) экстремалей. В связи с этим логично использовать в качестве независимой переменной вместо времени какую-либо величину, связанную с угловым положением КА на орбите, например, истинную долготу L. Такой прием использовался в целом ряде работ, например, [11, 12]. Его недостатком является существенное усложнение структуры оптимального управления (из-за наличия в знаменателях правых частей дифференциальных уравнений движения реактивного ускорения) и возможность нарушения монотонности изменения истинной долготы по времени при достаточно больших значениях реактивного или возмущающего ускорения. Вероятно, первый из этих недостатков, является одной из причин использования прямых методов оптимизации в [11, 12]. В этой статье истинная долгота разбивается на две части: вспомогательную долготу K и отклонение истинной долготы от вспомогательной LK, причем в качестве новой независимой переменной рассматривается именно вспомогательная долгота K. Такой прием позволяет избежать обеих указанных проблем. Позже в этой работе будет показано, что для случая, когда действующие на КА внешние силы не зависят от времени, оптимизация траекторий с фиксированной угловой дальностью с использованием дифференциальных уравнений движения с K в качестве независимой переменной автоматически приводит к выполнению необходимого условия оптимальности по длительности перелета.
Использование вспомогательной долготы в качестве независимой переменной, как будет показано далее, оказалось крайне эффективным при оптимизации межорбитальных траекторий КА с идеально-регулируемым двигателем ограниченной мощности, позволяя рассчитывать траектории с любой представляющей практический интерес угловой дальностью.
Существует, однако, еще одна значительная трудность, которая связана с использованием подхода, основанного на применении принципа максимума и метода продолжения, для решения задач максимизации конечной массы КА или минимизации затрат рабочего тела на перелет. Эта трудность связана с негладкой зависимостью невязок краевой задачи от начальных значений сопряженных переменных, которые требуется найти (угловые точки в этой зависимости появляются при равенстве нулю локального максимума или минимума функции переключения в какой-либо точке траектории, то есть при рождении или исчезновении пассивных или активных участков траектории). Выходом из этой ситуации является использование сглаженного представления релейной функции тяги [8]. Для обеспечения сходимости уровень сглаживания должен быть достаточно большим, а для достижения необходимой точности решения – малым. Использование достаточно точной гладкой аппроксимации релейной функции тяги приводит к существенному – на порядки – изменению производных по времени правых частей дифференциальных уравнений движения в окрестности точек включения и выключения тяги [8]. Как следствие, уравнения движения становятся жесткими, что существенно снижает эффективность применяемых численных методов. В этой работе рассматривается возможность использования преобразования независимой переменной K к новой независимой переменной – фиктивной вспомогательной долготе s, обеспечивающей растяжение масштаба по этой новой независимой переменной в окрестности точек переключения тяги, то есть в окрестности нуля функции переключения. Близким известным аналогом такого преобразования в небесной механике является преобразование Зундмана [13], обеспечивающее растяжение фиктивного времени при близком сближении КА с притягивающим центром.
1. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДВИЖЕНИЯ
Рассматривается задача оптимизации перелета КА с двигателем малой тяги в центральном ньютоновском гравитационном поле. Дифференциальные уравнения движения КА под действием сил гравитации и тяги в модифицированных равноденственных элементах p, ex, ey, ix, iy, L [13] имеют вид:
(1)
$\begin{gathered} \frac{{dp}}{{dt}} = \delta \frac{T}{m}\sqrt {\frac{p}{\mu }} \frac{{2p}}{q}\cos \vartheta \cos \psi , \\ \frac{{d{{e}_{x}}}}{{dt}} = \delta \frac{T}{m}\sqrt {\frac{p}{\mu }} \left[ {\sin L\sin \vartheta \cos \psi + _{{_{{_{{}}^{{}}}}^{{}}}}^{{^{{^{{^{{}}}}}}}}} \right. \\ + \,\,\left. {\frac{{\left( {q + 1} \right)\cos L + {{e}_{x}}}}{q}\cos \vartheta \cos \psi - \frac{{{{e}_{y}}\xi }}{q}\sin \psi } \right], \\ \frac{{d{{e}_{y}}}}{{dt}} = \delta \frac{T}{m}\sqrt {\frac{p}{\mu }} \left[ { - \cos L\sin \vartheta \cos \psi + _{{_{{_{{_{{_{{_{{}}}}}}}}}}}}^{{^{{^{{^{{}}}}}}}}} \right. \\ \left. { + \,\,\frac{{\left( {q + 1} \right)\sin L + {{e}_{y}}}}{q}\cos \vartheta \cos \psi + \frac{{{{e}_{x}}\xi }}{q}\sin \psi } \right], \\ \frac{{d{{i}_{x}}}}{{dt}} = \delta \frac{T}{m}\sqrt {\frac{p}{\mu }} \frac{{{{s}^{2}}}}{{2q}}\cos L\sin \psi , \\ \frac{{d{{i}_{y}}}}{{dt}} = \delta \frac{T}{m}\sqrt {\frac{p}{\mu }} \frac{{{{s}^{2}}}}{{2q}}\sin L\sin \psi , \\ \frac{{dL}}{{dt}} = \sqrt {\mu p} {{\left( {\frac{q}{p}} \right)}^{2}} + \delta \frac{T}{m}\sqrt {\frac{p}{\mu }} \frac{\xi }{q}\sin \psi ,\,\,\,\,\frac{{dm}}{{dt}} = - \delta \frac{T}{c}, \\ \end{gathered} $Введем в рассмотрение вспомогательную долготу K, подчиняющуюся дифференциальному уравнению
и отклонение истинной долготы от вспомогательной LK = L – K, которое, в соответствии с (1) и (2), подчиняется дифференциальному уравнениюЗаменяя в системе (1) шестое уравнение на (2) и (3), получим следующую систему дифференциальных уравнений:
(4)
$\begin{gathered} \frac{{dp}}{{dt}} = \delta \frac{T}{m}\sqrt {\frac{p}{\mu }} \frac{{2p}}{q}\cos \vartheta \cos \psi , \\ \frac{{d{{e}_{x}}}}{{dt}} = \delta \frac{T}{m}\sqrt {\frac{p}{\mu }} \left[ {\sin L\sin \vartheta \cos \psi + \frac{{\left( {q + 1} \right)\cos L + {{e}_{x}}}}{q}} \right. \times \\ \times \,\,\left. {\cos \vartheta \cos \psi - \frac{{{{e}_{y}}\xi }}{q}\sin \psi } \right],\,\,\,\,\frac{{d{{e}_{y}}}}{{dt}} = \delta \frac{T}{m}\sqrt {\frac{p}{\mu }} \times \\ \times \left[ { - \cos L\sin \vartheta \cos \psi + \frac{{\left( {q + 1} \right)\sin L + {{e}_{y}}}}{q}} \right. \times \\ \times \,\,\left. {\cos \vartheta \cos \psi + \frac{{{{e}_{x}}\xi }}{q}\sin \psi } \right],\,\,\,\,\frac{{d{{i}_{x}}}}{{dt}} = \delta \frac{T}{m} \times \\ \times \,\,\sqrt {\frac{p}{\mu }} \frac{{{{s}^{2}}}}{{2q}}\cos L\sin \psi ,\frac{{d{{i}_{y}}}}{{dt}} = \delta \frac{T}{m}\sqrt {\frac{p}{\mu }} \frac{{{{s}^{2}}}}{{2q}}\sin L\sin \psi , \\ \frac{{d{{L}_{K}}}}{{dt}} = \delta \frac{T}{m}\sqrt {\frac{p}{\mu }} \frac{\xi }{q}\sin \psi , \\ \frac{{dm}}{{dt}} = - \delta \frac{T}{c},\,\,\,\,\frac{{dK}}{{dt}} = \sqrt {\mu p} {{\left( {\frac{q}{p}} \right)}^{2}}. \\ \end{gathered} $В системе (4) истинная долгота L во всех уравнениях заменяется на ее выражение через вспомогательную долготу K и отклонение истинной долготы LK: L = K + LK. Если величины реактивного ускорения T/m и массового расхода T/c малы, то уравнения движения (4) сводятся к системе дифференциальных уравнений с 7 медленными переменными p, ex, ey, ix, iy, LK, m и одной быстрой K.
Заметим, что правые части системы (4) не зависят явным образом от времени, а правая часть дифференциального уравнения для K положительна для любых значений фазовых координат при p > 0. Таким образом, если исключить случай вырождения оскулирующей орбиты в отрезок прямой линии, можно провести замену независимой переменной t на K с использованием соотношения
(5)
$dK = \frac{{dK}}{{dt}}dt \Rightarrow \frac{d}{{dK}} = \frac{{dt}}{{dK}}\frac{d}{{dt}} = \frac{1}{{\sqrt {\mu p} }}{{\left( {\frac{p}{q}} \right)}^{2}}\frac{d}{{dt}}.$В итоге получим следующую систему дифференциальных уравнений:
(6)
$\begin{gathered} \frac{{dp}}{{dK}} = \delta \frac{T}{m}\frac{{2{{p}^{3}}}}{{\mu {{q}^{3}}}}\cos \vartheta \cos \psi , \\ \frac{{d{{e}_{x}}}}{{dK}} = \delta \frac{T}{m}\frac{{{{p}^{2}}}}{{\mu {{q}^{2}}}}\left[ {\sin L\sin \vartheta \cos \psi + \frac{{\left( {q + 1} \right)\cos L + {{e}_{x}}}}{q}} \right. \times \\ \times \,\,\left. {\cos \vartheta \cos \psi - \frac{{{{e}_{y}}\xi }}{q}\sin \psi } \right], \\ \frac{{d{{e}_{y}}}}{{dK}} = \delta \frac{T}{m}\frac{{{{p}^{2}}}}{{\mu {{q}^{2}}}}\left[ { - \cos L\sin \vartheta \cos \psi } \right. + \\ + \,\,\frac{{\left( {q\, + \,1} \right)\sin L\, + \,{{e}_{y}}}}{q}\cos \vartheta \cos \psi + \left. { + \frac{{{{e}_{x}}\xi }}{q}\sin \psi } \right], \\ \frac{{d{{i}_{x}}}}{{dK}} = \delta \frac{T}{m}\frac{{{{p}^{2}}{{s}^{2}}}}{{2\mu {{q}^{3}}}}\cos L\sin \psi , \\ \frac{{d{{i}_{y}}}}{{dK}} = \delta \frac{T}{m}\frac{{{{p}^{2}}{{s}^{2}}}}{{2\mu {{q}^{3}}}}\sin L\sin \psi ,\,\,\,\,\frac{{d{{L}_{K}}}}{{dK}} = \delta \frac{T}{m}\frac{{{{p}^{2}}}}{{\mu {{q}^{3}}}}\xi \sin \psi , \\ \frac{{dm}}{{dK}} = - \delta \frac{T}{c}\sqrt {\frac{{{{p}^{3}}}}{\mu }} \frac{1}{{{{q}^{2}}}}. \\ \end{gathered} $При необходимости, система может быть дополнена уравнением для времени
Далее в статье ограничимся рассмотрением задачи перелета между двумя заданными точками с фиксированной угловой дальностью ΔK и свободным временем перелета. В этом случае, без потери общности, начальные условия движения задаются для фиксированного значения начальной вспомогательной долготы K0 в виде
(8)
$\begin{gathered} p\left( {{{K}_{0}}} \right) = {{p}_{0}},\,\,\,\,{{e}_{x}}\left( {{{K}_{0}}} \right) = {{e}_{{x0}}},\,\,\,\,{{e}_{y}}\left( {{{K}_{0}}} \right) = {{e}_{{y0}}}, \\ {{i}_{x}}\left( {{{K}_{0}}} \right) = {{i}_{{x0}}},\,\,\,\,{{i}_{y}}\left( {{{K}_{0}}} \right) = {{i}_{{y0}}}, \\ {{L}_{K}}\left( {{{K}_{0}}} \right) = 0,\,\,\,\,m\left( {{{K}_{0}}} \right) = {{m}_{0}}, \\ \end{gathered} $(9)
$\begin{gathered} p\left( {{{K}_{f}}} \right) = {{p}_{f}},\,\,\,\,{{e}_{x}}\left( {{{K}_{f}}} \right) = {{e}_{{xf}}}, \\ {{e}_{y}}\left( {{{K}_{f}}} \right) = {{e}_{{yf}}},\,\,\,\,{{i}_{x}}\left( {{{K}_{f}}} \right) = {{i}_{{xf}}}, \\ {{i}_{y}}\left( {{{K}_{f}}} \right) = {{i}_{{yf}}},\,\,\,\,{{L}_{K}}\left( {{{K}_{f}}} \right) = 0. \\ \end{gathered} $Далее будем рассматривать две математические модели двигательной установки КА: модель идеально-регулируемого двигателя ограниченной мощности (ОМ-модель, [7]) и модель нерегулируемого двигателя ограниченной тяги с постоянной скоростью истечения (ОТ-модель, [8]). В рамках ОМ-модели величины тяги T и скорости истечения c могут произвольно изменяться при выполнении единственного ограничения, заключающегося в постоянстве реактивной мощности: Tc/2 = const, а в рамках ОТ-модели значения тяги и скорости истечения принимаются постоянными. ОМ-задача используется в качестве вспомогательной при решении ОТ-задачи.
2. ОПТИМИЗАЦИЯ ТРАЕКТОРИЙ С ИДЕАЛЬНО-РЕГУЛИРУЕМЫМ ДВИГАТЕЛЕМ ОГРАНИЧЕННОЙ МОЩНОСТИ
Рассмотрим задачу оптимизации траектории КА с идеально-регулируемым двигателем ограниченной мощности, то есть задачу минимизации функционала
(10)
${{J}_{1}} = \frac{1}{2}\int\limits_{{{t}_{0}}}^{{{t}_{f}}} {{{a}^{2}}dt} = \frac{1}{2}\int\limits_{{{K}_{0}}}^{{{K}_{f}}} {\frac{{{{a}^{2}}}}{{{{q}^{2}}}}} \sqrt {\frac{{{{p}^{3}}}}{\mu }} dK,$Как известно [1, 7, 15], ОМ-задача разделяется на динамическую (включающую уравнения для всех фазовых переменных, кроме массы КА) и параметрическую (включающую уравнение для массы КА) части. Поэтому для анализа динамической части ОМ-задачи уравнения движения удобно переписать в виде:
(11)
$\begin{gathered} \frac{{dp}}{{dK}} = \frac{{2{{p}^{3}}}}{{\mu {{q}^{3}}}}{{a}_{t}},\,\,\,\,\frac{{d{{e}_{x}}}}{{dK}} = \frac{{{{p}^{2}}}}{{\mu {{q}^{2}}}} \times \\ \times \,\,\left[ {\sin L \cdot {{a}_{r}} + \frac{{\left( {q + 1} \right)\cos L + {{e}_{x}}}}{q}{{a}_{t}} - \frac{{{{e}_{y}}\xi }}{q}{{a}_{n}}} \right], \\ \frac{{d{{e}_{y}}}}{{dK}} = \frac{{{{p}^{2}}}}{{\mu {{q}^{2}}}} \times \\ \times \,\,\left[ { - \cos L \cdot {{a}_{r}} + \frac{{\left( {q + 1} \right)\sin L + {{e}_{y}}}}{q}{{a}_{t}} + \frac{{{{e}_{x}}\xi }}{q}{{a}_{n}}} \right], \\ \frac{{d{{i}_{x}}}}{{dK}} = \frac{{{{p}^{2}}{{s}^{2}}}}{{2\mu {{q}^{3}}}}\cos L \cdot {{a}_{n}}, \\ \frac{{d{{i}_{y}}}}{{dK}} = \frac{{{{p}^{2}}{{s}^{2}}}}{{2\mu {{q}^{3}}}}\sin L \cdot {{a}_{n}},\,\,\,\,\frac{{d{{L}_{K}}}}{{dK}} = \frac{{{{p}^{2}}}}{{\mu {{q}^{3}}}}\xi \cdot {{a}_{n}}, \\ \end{gathered} $(12)
$\begin{gathered} p\left( {{{K}_{0}}} \right) = {{p}_{0}},\,\,\,\,{{e}_{x}}\left( {{{K}_{0}}} \right) = {{e}_{{x0}}},\,\,\,\,{{e}_{y}}\left( {{{K}_{0}}} \right) = {{e}_{{y0}}}, \\ {{i}_{x}}\left( {{{K}_{0}}} \right) = {{i}_{{x0}}},\,\,\,\,{{i}_{y}}\left( {{{K}_{0}}} \right) = {{i}_{{y0}}},\,\,\,\,{{L}_{K}}\left( {{{K}_{0}}} \right) = 0. \\ \end{gathered} $Функция Понтрягина задачи оптимального управления (9), (10), (11), (12) имеет вид
(13)
${{H}_{1}} = - \frac{1}{2}\frac{{{{a}^{2}}}}{{{{q}^{2}}}}\sqrt {\frac{{{{p}^{3}}}}{\mu }} + \frac{{{{p}^{2}}}}{{{{q}^{3}}\mu }}{{{\mathbf{A}}}^{T}}{\mathbf{a}},$(14)
$\begin{gathered} {{A}_{t}} = 2p \cdot {{p}_{p}} + \left[ {\left( {q + 1} \right)\cos L + {{e}_{x}}} \right]{{p}_{{ex}}} + \\ + \,\,\left[ {\left( {q + 1} \right)\sin L + {{e}_{y}}} \right]{{p}_{{ey}}}, \\ {{A}_{r}} = q \cdot \left( {\sin L \cdot {{p}_{{ex}}} - \cos L \cdot {{p}_{{ey}}}} \right), \\ {{A}_{n}} = \xi \cdot \left( { - {{e}_{y}}{{p}_{{ex}}} + {{e}_{x}}{{p}_{{ey}}}} \right. + \left. {{{p}_{{LK}}}} \right) + \\ + \,\,\frac{{{{s}^{2}}}}{2}\left( {\cos L \cdot {{p}_{{ix}}} + \sin L \cdot {{p}_{{iy}}}} \right), \\ \end{gathered} $Здесь следует сделать замечание по поводу оптимальности времени перелета в рассматриваемой постановке. Правые части системы не зависят от времени t. Эту систему можно расширить дифференциальным уравнением для времени (7), правая часть которого также не зависит от времени. Функция Понтрягина для такой расширенной системы примет вид $H_{1}^{t} = {{H}_{1}} + \frac{1}{{\sqrt {\mu p} }}{{\left( {\frac{p}{q}} \right)}^{2}}{{p}_{t}},$ где pt – сопряженная ко времени переменная. Без потери общности можно положить, что t(K0) = 0. Необходимым условием оптимальности времени перелета будет pt(Kf) = 0. Из независимости функции Понтрягина от времени следует, что dpt/dK ≡ 0. Следовательно, для выполнения необходимого условия оптимальности по t требуется, чтобы pt(K0) = 0, но отсюда следует что pt(K) ≡ 0 и $H_{1}^{t} \equiv {{H}_{1}}.$ Следовательно, на решении задачи оптимального управления (9), (10), (11), (12) автоматически выполняются необходимые условия оптимальности времени перелета. Используемые здесь для доказательства оптимальности времени перелета свойства задачи оптимального управления справедливы и для далее рассматриваемого случая перелета с ограниченной тягой, поэтому рассматриваемые далее решения ОТ-задачи также удовлетворяют необходимому условию оптимальности по времени перелета.
Из условия максимума функции Понтря-гина (13) по управлению a легко получить выражение для оптимального управления:
подставляя которое в (13) получим выражение для гамильтониана рассматриваемой задачи оптимального управления: где $k = \frac{1}{{2{{q}^{4}}}}\sqrt {\frac{{{{p}^{5}}}}{{{{\mu }^{3}}}}} .$ Очевидно, что уравнения оптимального движения примут вид(17)
$\frac{{d{\mathbf{x}}}}{{dK}} = \frac{{\partial {{H}_{1}}}}{{\partial {\mathbf{p}}}},\,\,\,\,\frac{{d{\mathbf{p}}}}{{dK}} = - \frac{{\partial {{H}_{1}}}}{{\partial {\mathbf{x}}}},$Краевая задача (9), (12), (17) решалась методом продолжения по параметру [3–9] с использованием метода комплексного шага [16, 17] для высокоточного вычисления производных от невязок краевой задачи при K = Kf от p0 и с коррекцией решения методом Ньютона после каждого шага численного интегрирования дифференциальных уравнений метода продолжения по параметру продолжения.
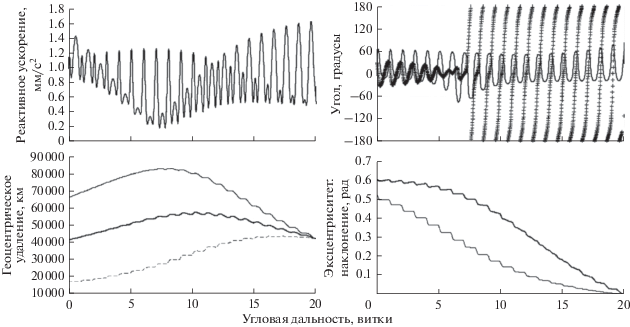
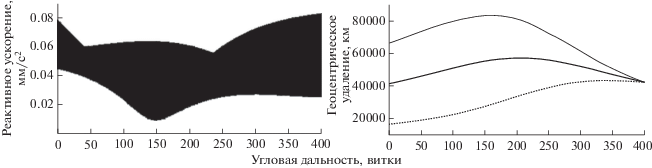
Приведем численные примеры расчета оптимальных ОМ-траекторий. Выберем начальные и конечные условия такими же, как в численном примере, приведенном ранее во введении к этой статье, однако в угловую дальность перелета зафиксируем 20 витками в первом случае и 400 витками во втором. На рис. 2 для траектории с угловой дальностью 20 витков представлены зависимости величины оптимального реактивного ускорения (левый верхний график), углов тангажа и рысканья (правый верхний график), радиусов перигея, апогея и большой полуоси (левый нижний график), эксцентриситета и наклонения (правый нижний график) от угловой дальности. На рис. 3 для траектории с угловой дальностью 400 витков представлены зависимости величины оптимального реактивного ускорения (левый график) и радиусов перигея, апогея и большой полуоси (правый график) от угловой дальности. Зависимость для угла рысканья представлена маркерами “+”, для радиуса апогея и наклонения – сплошной тонкой линией, для большой полуоси и эксцентриситета – сплошной толстой линией, для радиуса перигея – пунктирной линией.
Из рис. 1 и 2 видно, что увеличение угловой дальности не приводит к качественному изменению вида оптимального управления и зависимости траекторных параметров от угловой дальности. Увеличение угловой дальности в 20 раз привело к почти 20-кратному уменьшению величины реактивного ускорения и, естественно, к существенному уменьшению амплитуды короткопериодических колебаний траекторных параметров.
Следует отметить, что рассмотренный в данной статье подход к оптимизации ОМ-задачи позволил существенно улучшить сходимость и скорость решения. Это позволяет практически снять методическое ограничение на максимально допустимую угловую дальность перелета (в [7], при формулировке ОМ-задачи в декартовых координатах, практически допустимая угловая дальность ограничивалась 50–100 витками).
3. ОПТИМИЗАЦИЯ ТРАЕКТОРИЙ С ДВИГАТЕЛЕМ ОГРАНИЧЕННОЙ ТЯГИ С ПОСТОЯННОЙ СКОРОСТЬЮ ИСТЕЧЕНИЯ
Теперь рассмотрим задачу минимизации массы рабочего тела для перелета с двигателем ограниченной тяги с постоянной скоростью истечения, то есть задачу минимизации функционала
(18)
${{J}_{2}} = \int\limits_{{{t}_{0}}}^{{{t}_{f}}} {\delta \frac{T}{m}dt} = \int\limits_{{{K}_{0}}}^{{{K}_{f}}} {\delta \frac{T}{{{{q}^{2}}m}}\sqrt {\frac{{{{p}^{3}}}}{\mu }} dK} $Функция Понтрягина рассматриваемой задачи имеет вид:
(19)
$\begin{gathered} {{H}_{2}} = \delta T{{k}_{1}} \cdot \left[ {{{k}_{2}} \cdot \left( {{{A}_{r}}\sin \vartheta \cos \psi + } \right._{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}^{{^{{^{{}}}}}}} \right. \\ + \,\,\left. {{{A}_{t}}\cos \vartheta \cos \psi + {{A}_{n}}\sin \psi } \right)\left. { - \frac{{{{p}_{m}} + 1}}{c}} \right], \\ \end{gathered} $Максимизируя функцию Понтрягина (19) по δ, ϑ, ψ, получим выражения для оптимального управления:
(20)
$\begin{gathered} \sin \vartheta = {{{{A}_{r}}} \mathord{\left/ {\vphantom {{{{A}_{r}}} {{{A}_{{rt}}},}}} \right. \kern-0em} {{{A}_{{rt}}},}}\,\,\,\,\cos \vartheta = {{{{A}_{t}}} \mathord{\left/ {\vphantom {{{{A}_{t}}} {{{A}_{{rt}}},}}} \right. \kern-0em} {{{A}_{{rt}}},}} \\ \sin \psi = {{{{A}_{n}}} \mathord{\left/ {\vphantom {{{{A}_{n}}} {A,}}} \right. \kern-0em} {A,}}\,\,\,\,\cos \psi = {{{{A}_{{rt}}}} \mathord{\left/ {\vphantom {{{{A}_{{rt}}}} {A,}}} \right. \kern-0em} {A,}} \\ \end{gathered} $(21)
$\delta = {{\left( {1 + \operatorname{sign} S} \right)} \mathord{\left/ {\vphantom {{\left( {1 + \operatorname{sign} S} \right)} 2}} \right. \kern-0em} 2},\,\,\,\,S \ne 0;\,\,\,\,\delta \in \left[ {0;1} \right],\,\,\,\,S = 0,$Подставляя выражения для оптимального управления (20), (21) в функцию Понтрягина (19), получим выражение для гамильтониана задачи оптимального управления:
Уравнения оптимального движения примут вид
(23)
$\frac{{d{\mathbf{x}}}}{{dK}} = \frac{{\partial {{H}_{2}}}}{{\partial {\mathbf{p}}}},\,\,\,\,\frac{{d{\mathbf{p}}}}{{dK}} = - \frac{{\partial {{H}_{2}}}}{{\partial {\mathbf{x}}}},$(24)
$\begin{gathered} p\left( {{{K}_{f}}} \right) = {{p}_{f}},\,\,\,\,{{e}_{x}}\left( {{{K}_{f}}} \right) = {{e}_{{xf}}},\,\,\,\,{{e}_{y}}\left( {{{K}_{f}}} \right) = {{e}_{{yf}}}, \\ {{i}_{x}}\left( {{{K}_{f}}} \right) = {{i}_{{xf}}},\,\,\,\,{{i}_{y}}\left( {{{K}_{f}}} \right) = {{i}_{{yf}}}, \\ {{L}_{K}}\left( {{{K}_{f}}} \right) = 0,\,\,\,\,{{p}_{m}}\left( {{{K}_{f}}} \right) = 0. \\ \end{gathered} $Таким образом, задача оптимального управления (6), (8), (9), (18) сводится к краевой задаче для системы обыкновенных дифференциальных уравнений (23) с краевыми условиями (8) и (24). Для решения этой краевой задачи требуется удовлетворить 7 конечных условий (24) подбором 7 начальных значений вектора сопряженных переменных p0 = p(K0).
Основной сложностью при решении краевой задачи (8), (23), (24) является, как указывалось ранее, негладкая зависимость невязок в конечных условиях (24) от p0. Угловые точки в этой зависимости появляются при рождении или исчезновении пассивных или активных участков траектории в процессе решения задачи [8], что соответствует прохождению минимумов или максимумов функции переключения S через нулевое значение. Появление этих угловых точек приводит к разрыву в зависимости производных от невязок краевой задачи по элементам p0, а следовательно – к отказам численных методов типа метода Ньютона или метода продолжения, требующих непрерывности этих зависимостей.
Для решения указанной проблемы используется сглаживание функции тяги [8]. Такое сглаживание может быть проведено с использованием какой-либо аналитической аппроксимации функции Хевисайда, например
(25)
$\delta \left( S \right) \approx \frac{1}{2}\left( {\frac{S}{{\left| S \right| + \varepsilon \left( \tau \right)}} + 1} \right),$(26)
$\delta \left( S \right) \approx \frac{1}{2}\left( {1 + \frac{2}{\pi }\operatorname{arctg} \frac{S}{{\varepsilon \left( \tau \right)}}} \right),$(27)
$\delta \left( S \right) \approx {{\left[ {1 + \exp \left( { - \frac{S}{{\varepsilon \left( \tau \right)}}} \right)} \right]}^{{ - 1}}},$(28)
$\delta \left( S \right) \approx \frac{1}{2}\left( {1 + \operatorname{th} \frac{S}{{\varepsilon \left( \tau \right)}}} \right).$Сглаживание функции тяги позволяет обеспечить возможность применения методов типа метода продолжения для решения краевых задач с переключениями тяги, однако остается проблема резкого изменения правых частей дифференциальных уравнений оптимального движения в окрестности точек переключения в конце процесса продолжения, которые делают интегрируемую систему уравнений жесткой, приводят к потери точности интегрирования и могут привести к отказу метода решения краевой задачи.
В рамках данной работы была сделана попытка преодолеть эту проблему введением регуляризирующего преобразования независимой переменной, растягивающего интервал интегрирования в окрестности нулевого значения функции переключения, аналогично известному в небесной механике преобразованию Зундмана, растягивающему интервал интегрирования в окрестности нулевого удаления КА от притягивающего центра [13]. Новая независимая переменная s – фиктивная дополнительная долгота – в данной работе определяется следующим преобразованием:
где εS – малая положительная постоянная, обеспечивающая возможность прохождения точки S = 0 в процессе численного интегрирования без использования дополнительных приемов (в данной работе, при использовании безразмерных переменных с единицами измерений физических величин, отнесенными к ГСО и начальной массе КА, использовалось значение εS = 10–10).Краевая задача (6), (8), (24), как и ОМ-задача, решалась методом продолжения по параметру с использованием метода комплексного шага для высокоточного вычисления производных от невязок краевой задачи при s = sf от p0 и с коррекцией решения методом Ньютона после каждого шага численного интегрирования дифференциальных уравнений метода продолжения по параметру продолжения. Для аппроксимации функции тяги использовалось выражение (26) с ε(τ) = 1 – τ + 10–5τ. В качестве начального приближения использовалось решение ОМ-задачи, дополненное начальным условием pm(s0) = 0. Для обеспечения равенства нулю невязок краевой задачи в процессе продолжения, вместо системы (23) использовалась система дифференциальных уравнений
(30)
$\begin{gathered} \frac{{d{\mathbf{x}}}}{{ds}} = \sqrt {{{S}^{2}} + {{\varepsilon }_{S}}} \frac{{\left( {1 - \tau } \right)k + \tau \delta T{{k}_{1}}{{k}_{2}}}}{{1 - \tau + \tau A}}{{{\mathbf{A}}}^{\operatorname{T} }}\frac{{\partial {\mathbf{A}}}}{{\partial {\mathbf{p}}}}, \\ \frac{{d{\mathbf{p}}}}{{ds}} = - \sqrt {{{S}^{2}} + {{\varepsilon }_{S}}} \frac{{\left( {1 - \tau } \right)\left( {\frac{1}{2}\frac{{\partial k}}{{\partial {\mathbf{x}}}}{{A}^{2}} + k{{{\mathbf{A}}}^{\operatorname{T} }}\frac{{\partial {\mathbf{A}}}}{{\partial {\mathbf{x}}}}} \right) + \tau \delta T \cdot \left[ {\frac{{\partial {{k}_{1}}}}{{\partial {\mathbf{x}}}}SA + {{k}_{1}} \cdot \left( {\frac{{\partial {{k}_{2}}}}{{\partial {\mathbf{x}}}}{{A}^{2}} + {{k}_{2}}{{{\mathbf{A}}}^{\operatorname{T} }}\frac{{\partial {\mathbf{A}}}}{{\partial {\mathbf{x}}}}} \right)} \right]}}{{1 - \tau + \tau A}}, \\ \frac{{dK}}{{ds}} = \sqrt {{{S}^{2}} + {{\varepsilon }_{S}}} . \\ \end{gathered} $В этой системе осуществлен переход от вспомогательной долготы K к фиктивной вспомогательной долготе s в качестве независимой переменной, введено дополнительное дифференциальное уравнение для K, так как текущее значение К необходимо для вычисления истинной долготы L в правых частях других уравнений системы, и скомбинированы правые части дифференциальных уравнений для ОМ- и ОТ-задачи таким образом, чтобы при τ = 0 система (30) соответствовала системе уравнений для ОМ-задачи, а при τ = 1 – системе уравнений для ОТ-задачи. Численное интегрирование этой системы проводилось от s = 0 до s = sf, при котором достигается нуль функции f(s) = K(s)–Kf.
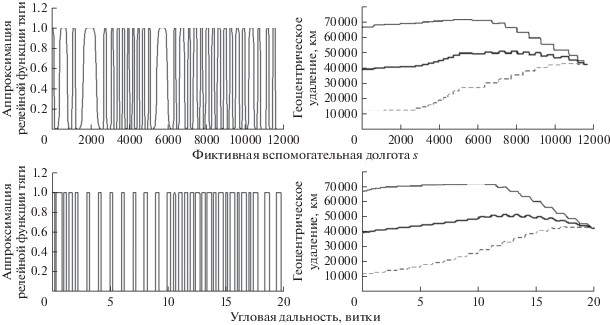
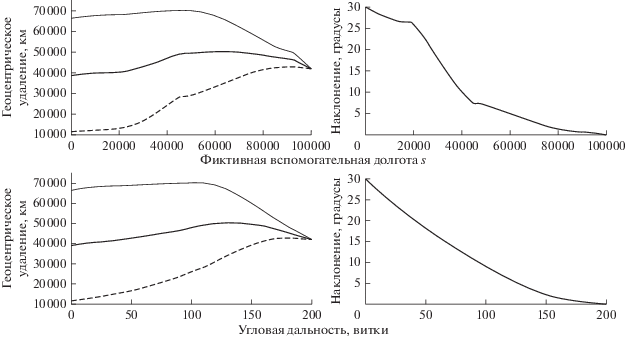
Приведем численные примеры расчета оптимальных ОТ-траекторий с использованием описанного метода. На рис. 4 и 5 приведены результаты расчета оптимальной ОТ-траектории перелета с начальной орбиты, имеющей высоту перигея 5000 км, высоту апогея 60 000 км, наклонение 30°, нулевые значения аргумента перигея и долготы восходящего узла, на ГСО (круговая экваториальная орбита высотой 35793 км). Истинная долгота КА в начальной точке перелета выбрана равной 150°, начальная масса КА равна 1000 кг, тяга – 1.5 Н, удельный импульс – 1800 с. На рис. 4 слева представлены зависимости функции переключения тяги от фиктивной вспомогательной долготы s (вверху) и от угловой дальности по вспомогательной долготе K (внизу). Из сравнения этих графиков видно, что переход к фиктивной вспомогательной долготе весьма эффективен с точки зрения сглаживания релейной функции тяги при численном интегрировании. Справа на рис. 4 представлены зависимости большой полуоси (толстая сплошная линия), радиуса апогея (тонкая сплошная линия) и радиуса перигея (пунктирная линия) от s (вверху) и от угловой дальности по K (внизу). Из сравнения этих графиков видно, что диапазон изменения производных от траекторных параметров по s превышает диапазон изменения производных по K, что объясняется большим диапазоном изменения dK/ds и, разумеется, снижает эффективность использования s в качестве независимой переменной.
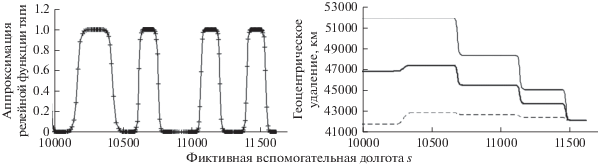
Однако, как показано на рис. 5, где приведены графики тех же параметров от s в увеличенном масштабе, зависимости траекторных параметров от s все же остаются достаточно гладкими.
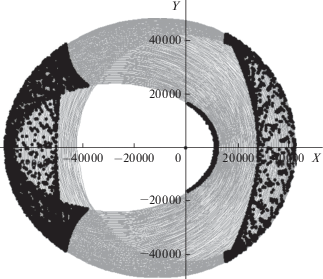
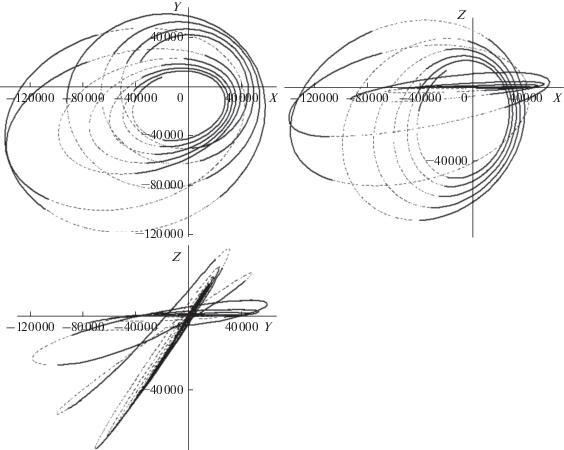
Разработанный метод тестировался и на траекториях с угловой дальностью в сотни витков. На рис. 6 и 7 представлены результаты расчета траекторий межорбитального перелета с теми же граничными условиями, что и в предыдущем примере, но с угловой дальностью по истинной долготе в 200 витков для КА с начальной массой 1000 кг, тягой 0.166 Н и удельным импульсом 1500 с. Проекция оптимальной траектории на плоскость экватора представлена на рис. 6 (пассивные участки обозначены тонкими сплошными линиями, активные участки – линиями с маркерами).
На рис. 7 представлены зависимости большой полуоси (толстая сплошная линия), радиуса апогея (тонкая сплошная линия) и радиуса перигея (пунктирная линия) от s (вверху слева) и угловой дальности по K (внизу слева), а также наклонения от s (вверху справа) и угловой дальности по K (внизу справа). На верхних графиках хорошо заметны три различные фазы движения КА, соответствующие разным конфигурациям активных и пассивных участков на витках: на первой фазе (до s ≈ 20 000) на каждом витке траектории имеются два активных участка (в окрестности перигея и апогея), на второй фазе (до s ≈ 45 000) на каждом витке существует единственный активный участок в районе апогея и на третьей фазе на каждом витке снова имеются перигейный и апогейный активные участки.
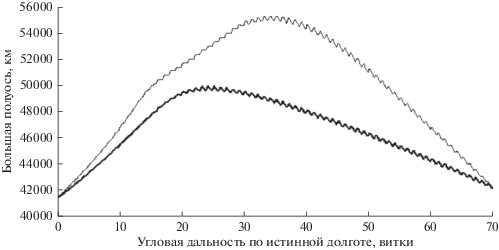
На рис. 8 и 9 представлены результаты сравнения траекторий перелета с переключениями тяги, оптимальным временем и фиксированной угловой дальностью в 70 витков и траектории с минимальным временем перелета с той же угловой дальностью для параметров граничных орбит, КА и его двигательной установки, приведенных в примере во введении к этой статье. На рис. 8 представлены проекции траекторий перелета на координатные плоскости инерциальной геоцентрической экваториальной системы координат J2000 (слева – траектория с переключениями тяги, справа – траектория с минимальным временем перелета). Пассивные участки траектории отображены пунктирной линией, активные – сплошной. Масса КА, доставляемая на конечную орбиту с использованием траектории с выключениеми тяги составляет 891.546 кг, что на 6.355 кг больше, чем масса КА, доставляемого по траектории оптимального быстродействия (885.191 кг), требуемые затраты рабочего тела составляют соответственно 108.454 и 114.809 кг. Увеличение конечной массы КА на траектории с пассивными участками объясняется снижением потерь характеристической скорости за счет выключения двигателя на участках с минимальной эффективностью тяги. Для обеспечения возможности появления пассивных участков при фиксированной угловой дальности требуется увеличение длительности перелета, что достигается увеличением большой полуоси на траектории перелета с пассивными участками по сравнению с траекторией оптимального быстродействия. Это хорошо видно на рис. 9, где представлены зависимости больших полуосей траекторий перелета от угловой дальности (тонкая линия – для траектории с пассивными участками, толстая линия – для оптимального быстродействия).
Рис. 8.
70-витковая ОТ-траектория. Слева – минимальные затраты рабочего тела, справа – минимальное время перелета.
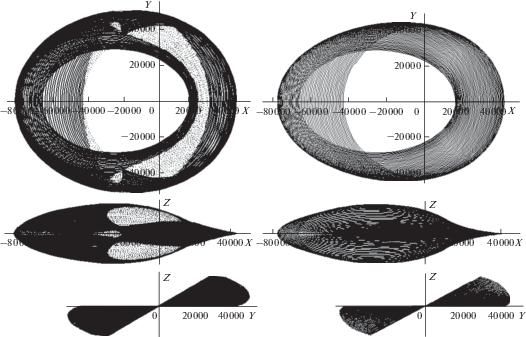
Рис. 9.
Изменение большой полуоси на перелета за минимальное время (толстая линия) и с минимальными затратами рабочего тела (тонкая линия).
В следующем примере демонстрируется возможность применения разработанного метода для расчета менее симметричных траекторий. На рис. 10 приведены проекции на координатные плоскости оптимальной ОТ-траектории перелета при большом отклонении линии апсид от плоскости конечной орбиты. В качестве конечной орбиты, по-прежнему, принята ГСО, а в качестве начальной – орбита с высотой перигея 10 000 км, высотой апогея 60 000 км, наклонением 48.8°, аргументом перигея 70°, долготой восходящего узла 0°. Начальная истинная долгота равна 150°, угловая дальность перелета – 10 витков, начальная масса КА – 1000 кг, тяга – 3 Н, удельный импульс 1520 с. Активные участки траектории показаны сплошными линиями, а пассивные – пунктирными.
ЗАКЛЮЧЕНИЕ
В работе введено разделение истинной долготы на вспомогательную долготу и ее отклонение от истинной долготы. Преимуществами использования в качестве независимой переменной в задачах оптимизации траекторий КА вспомогательной долготы по сравнению с истинной долготой являются: 1) более простая форма дифференциальных уравнений движения; 2) более простой вид выражений для оптимального управления и 3) монотонность зависимости вспомогательной долготы от времени при любых значениях реактивного ускорения.
Рассмотрена задача оптимизации траекторий с фиксированной угловой дальностью и свободным временем перелета. Результаты вычислительных экспериментов позволяют сделать предположение, что в отличие от задачи оптимального быстродействия, рассмотренная задача имеет единственную экстремаль в заданном семействе траекторий, удовлетворяющих необходимым условиям оптимальности. Показано, что для перелетов в центральном ньютоновском гравитационном поле и в случае наличия возмущений, независящих от времени, использование вспомогательной долготы в качестве независимой переменной позволяет автоматически удовлетворить необходимые условия оптимальности времени перелета.
Для оптимизации траекторий использовался подход, основанный на использовании принципа максимума и метода продолжения. Использование в качестве независимой переменной вспомогательной долготы позволило разработать вычислительно устойчивый быстродействующий метод вычисления оптимальных многовитковых траекторий КА с идеально-регулируемым двигателем ограниченной мощности с фиксированной угловой дальностью и оптимальным временем перелета, с помощью которого возможна оптимизация траекторий с любым, представляющим практический интерес, числом витков.
Для оптимизации траекторий КА с двигателем ограниченной тяги с постоянной скоростью истечения предложено совместное использование сглаживающего преобразования релейной функции переключения тяги и регуляризирующего преобразования независимой переменной (вспомогательной долготы К) к фиктивной вспомогательной долготе s. Это преобразование растягивает интервал изменения независимой переменной в окрестности быстрого изменения правых частей дифференциальных уравнений движения вблизи моментов переключения тяги. Приведенные численные примеры демонстрируют работоспособность и устойчивость численного метода, основанного на предложенных подходах.
Работа выполнена за счет средств гранта Российского научного фонда (соглашение № 16-19-10429).
Список литературы
Гродзовский Г.Л., Иванов Ю.Н., Токарев В.В. Механика космического полета с малой тягой. М.: Наука, 1966.
Shirazi A., Ceberio J., Lozano J. Spacecraft trajectory optimization: a review of models, objectives, approaches and solutions // Progress in Aerospace Sciences. A-ugust 2018. P. 76–98.
Petukhov V.G. One Numerical Method to Calculate Optimal PowerLimited Trajectories. IEPC-95-221. M., 1995.
Eneev T.M., Egorov V.A., Efimov G.B. et al. Some Methodical Problems of Low-Thrust Trajectory Optimization. ПРЕПРИНТ ИПМ РАН. № 110. 1996. P. 1–24.
Haberkorn T., Martinon P., Gergaud J. Low thrust minimum-fuel orbital transfer: a homotopic approach // J. Guidance, Control, and Dynamics. 2004. V. 27. № 6. P. 1046–1060
Петухов В.Г. Оптимизация многовитковых перелетов между некомпланарными эллиптическими орбитами // Космич. исслед. 2004. Т. 42. № 3. С. 260–279 (Cosmic Research. P. 250).
Петухов В.Г. Оптимизация межпланетных траекторий космических аппаратов с идеально-регулируемым двигателем методом продолжения // Космич. исслед. 2008. Т. 46. № 3. С. 224–237. (Cosmic Research. P. 219).
Петухов В.Г. Метод продолжения для оптимизации межпланетных траекторий с малой тягой // Космич. исслед. 2012. Т. 50. № 3. С. 258–270. (Cosmic Research. P. 249).
Иванюхин А.В., Петухов В.Г. Задача минимизации тяги и ее приложения // Космич. исслед. 2015. Т. 53. № 4. С. 320–321. (Cosmic Research. P. 300).
Ахметшин Р.З. Плоская задача оптимального перелета космического аппарата с малой тягой с высокой эллиптической орбиты на геостационар // Космич. исслед. 2004. Т. 42. № 3. С. 248–259 (Cosmic Research. P. 238).
Graham K.F., Rao A.V. Minimum-Time Trajectory Optimization of Low-Thrust Earth-Orbit Transfers with Eclipsing // J. Spacecraft and Rockets. 2016. V. 53. № 2. P. 289–303.
Betts J.T. Optimal low-thrust orbit transfers with eclipsing // Optimal Control Applications and Methods. 2015. V. 36. № 2. P. 218–240.
Sundman K. Memoire sur le problem des trios corps // Acta Mathematica. 1912. V. 36. P. 105–179.
Walker M.J.H., Ireland B., Owens J. A Set of Modified Equinoctial Elements // Celestial Mechanics. 1985. V. 36. P. 409–419; 1986. V. 38. P. 391.
Irving J.H. Low thrust flight: variable exhaust velocity in gravitational fields / In Seifert H.S. // Space Technology. New York, John Wiley and Sons Inc., 1959.
Lyness J.N., Moller C.B. Numerical differentiation of analytic functions // SIAM J. Numer. Anal. 1967. № 4. P. 202–210.
Martins J.R.R.A., Sturdza P., Alonso J.J. The complex-step derivative approximation // ACM Transaction on Mathematical Software. 2003. V. 29. № 3. P. 245–262.
Lawden D.F. Calculation of singular extremal rocket trajectories // J. Guidance, Control, and Dynamics. 1992. V. 15. № 6. P. 1361–1365.
Константинов М.С. Сравнительный проектно-баллистический анализ использования химической и электроракетной двигательных установок в проекте солнечного зонда // Космич. исслед. 2019. Т. 57. № 5. С. 347–360.
Дополнительные материалы отсутствуют.
Инструменты
Космические исследования