Космические исследования, 2020, T. 58, № 2, стр. 165-176
Низкоэнергетические квазиоптимальные траектории с малой тягой к точкам либрации и гало-орбитам
А. В. Иванюхин 1, 2, *, В. Г. Петухов 1, **
1 Научно-исследовательский институт прикладной механики и электродинамики МАИ
г. Москва, Россия
2 Российский университет дружбы народов
г. Москва, Россия
* E-mail: ivanyukhin.a@yandex.ru
** E-mail: vgpetukhov@gmail.com
Поступила в редакцию 03.04.2019
После доработки 03.04.2019
Принята к публикации 25.04.2019
Аннотация
В работе рассматривается задача расчета прямых и низкоэнергетических траекторий космического аппарата с малой тягой к точкам либрации системы Земля–Луна и на гало-орбиты вокруг них. Предлагается метод решения задачи, заключающийся в вычислении устойчивых многообразий точек либрации или гало-орбит и расчете траекторий перелета космического аппарата с малой тягой с начальной круговой околоземной орбиты в заданную точку этого многообразия с использованием квазиоптимального управления с обратной связью. При фиксированной конечной массе космического аппарата, последний этап вычислений сводится к решению задачи Коши. Приводятся численные примеры расчета прямых и низкоэнергетических траекторий перелета к точкам либрации и на гало-орбиты с оптимизацией точки выхода на устойчивые многообразия для низкоэнергетических перелетов.
ВВЕДЕНИЕ
В начальный период практической космонавтики достижение и исследование Луны являлись одними из наиболее приоритетных задач. В этот период был проделан огромный объем работ по механике полета к Луне, позволивший успешно реализовать перелеты лунных автоматических и пилотируемых космических аппаратов. В Советском Союзе пионерские работы по исследованию лунных траекторий были проведены В.А. Егоровым [1–3]. Вскоре после завершения программы “Аполлон” была прекращена и отечественная лунная программа, и исследования Луны с помощью КА на длительное время прекратились. Современное возобновление интереса к Луне связано со значительным расширением планируемых программ исследований, что привело к необходимости рассмотрения новых вариантов целевых окололунных орбит и новых схем выведения КА на эти орбиты.
Одним из перспективных вариантов окололунных орбит базирования являются квазипериодические орбиты вокруг точек либрации L1 и L2 системы Земля–Луна. Гало-орбиты вокруг точки либрации L2 целесообразно использовать для размещения КА-ретрансляторов с целью обеспечения радиосвязи посадочных КА на обратной стороне Луны с Землей, что уже реализовано КА КНР Цюэцяо [4]. Орбиты, связанные с точкой либрации L1, в частности почти прямолинейную гало-орбиту (Near Rectilinear Halo Orbits, NRHO), планируется использовать в качестве орбиты базирования международной лунной орбитальной станции [5, 6]. Эта орбита базирования обладает рядом преимуществ по сравнению с низкой окололунной орбитой. Например, с нее постоянно открыты окна для траекторий возвращения на Землю.
Точки либрации и гало-орбиты являются частными решениями задачи трех тел [7–12]. Коллинеарные точки либрации L1/L2 и орбиты вокруг них, в рамках ограниченной задачи трех тел, существуют в окрестности тела меньшей массы любой системы из двух гравитирующих небесных тел, обращающихся вокруг общего барицентра, в том числе в системах Земля–Луна и Солнце–Земля. Исторически, первые полеты были реализованы в окрестность коллинеарных точек либрации системы Солнце–Земля. Среди КА, выведенных на орбиты вокруг этих точек можно перечислить ISEE-3, S-OHO, Genesis, ACE, WMAP, Herschel, Plank. В настоящее время готовятся к реализации новые проекты такие как “Спектр-РГ”, “Спектр-М”, JWST, Euclid [11]. На орбиты вокруг точек либрации L1/L2 системы Земля–Луна выводились 2 КА проекта ARTEMIS [12] и КА Цюэцяо [4, 11].
Требования по повышению эффективности выведения лунных КА на целевые орбиты стимулировало изучение низкоэнергетических перелетов к Луне, на которых особенности движения КА в гравитационном поле двух или трех небесных тел используются для снижения требуемых затрат характеристической скорости [11, 13–21]. Разные типы низкоэнергетических перелетов были реализованы в рамках выполнения проектов Hiten, ARTEMIS, GRAIL [11].
Другим направлением повышения эффективности лунных миссий является использование для их реализации электроракетных двигательных установок (ЭРДУ) с высоким удельным импульсом тяги, позволяющих существенно (в разы) сократить требуемые затраты рабочего тела на перелет. К настоящему времени успешно реализован перелет на окололунную орбиту КА с ЭРДУ SMART-1 [19], планируется использование ЭРДУ для выведения базового модуля PPE лунной орбитальной станции [5], рассматриваются варианты многоразовых межорбитальных буксиров для транспортировки грузов между околоземными и окололунными орбитами [23]. Теоретические аспекты перелетов к Луне с малой тягой и численные методы для их расчета и оптимизации рассматривались во многих работах, например в [20–25], однако следует отметить, что до настоящего времени не проведено достаточно полного теоретического исследования особенностей лунных траекторий с малой тягой, а разработанные численные методы имеют существенные ограничения по применению.
В силу особенностей траекторий КА с ЭРДУ и для достижения максимальной эффективности космических транспортных операций в системе Земля–Луна заманчивой оказывается возможность рассмотрения оптимальных низкоэнергетических траекторий перелета с малой тягой. Попытки рассмотрения таких траекторий уже делались, например в [20, 21], но необходимо признать, что задача оптимизации таких траекторий оказалась очень сложной и требует дальнейшего изучения.
В этой статье делается попытка рассмотрения квазиоптимальных низкоэнергетических траекторий с малой тягой к точкам либрации L1/L2 системы Земля-Луна и гало-орбитам вокруг них. В качестве управления используется квазиоптимальное управление с обратной связью (КОУ-СОС), построенное на основе ряда свойств и массива численных решений задачи многовиткового межорбитального перелета в центральном ньютоновском поле с малой тягой за минимальное время между некомпланарными эллиптической и круговой орбитами. КОУСОС было синтезировано и представлено в [26–28], там же показана близость квазиоптимального решения к оптимальному в невозмущенной задаче и устойчивость к КОУСОС по отношению к возмущающим ускорениям и ошибкам управления. В работах [27, 29, 30] уже делались попытки применения КОУСОС для расчета траекторий перелета к Луне с малой тягой: в [27] и [30] – к точке либрации L1 и на орбиту вокруг Луны со стыковкой геоцентрического и селеноцентрического участков в L1, а в [29] – на орбиту вокруг Луны со стыковкой геоцентрического и селеноцентрического участков пассивной траекторией временного захвата на орбиту вокруг Луны.
В отличие от предыдущих работ, в этой статье будут проанализированы траектории, состоящие из участка квазиоптимального движения с малой тягой и участка движения по устойчивому многообразию к точкам либрации L1/L2 или гало-орбитам вокруг этих точек. По результатам численного анализа будет представлена оценка возможного выигрыша от использования низкоэнергетических траекторий с участками движения по устойчивым многообразиям по сравнению с прямым выведением в точки либрации или на гало-орбиты.
1. ТОЧКИ ЛИБРАЦИИ, ГАЛО-ОРБИТЫ, УСТОЙЧИВЫЕ МНОГООБРАЗИЯ
Для определения основных эффектов, влияющих на движение КА в системе Земля-Луна, рассмотрим математическую постановку ограниченной круговой задачи трех тел (ОКЗТТ).
Пусть три материальных точки (тела) P1, P2 и P3, движутся под действием сил взаимного притяжения. Тела P1 и P2 имеют массы m1 и m2 (m1 > m2), а масса тела P3 пренебрежимо мала, и не влияет на движение P1 и P2. То есть, тела P1 и P2 движутся вокруг их общего центра масс, и в случае, когда они движутся по круговым орбитам, задача называется ограниченной круговой задачей трех тел. Запишем движение третьего тела в безразмерной синодической барицентрической системе координат. Пусть единицей длины будет расстояние между P1 и P2, единицей массы сумма m1 и m2, а единицу времени выберем так, чтобы период обращения этих точек вокруг их центра масс был равен 2π. Направим ось x вдоль вектора от P1 к P2, ось z по вектору кинетического момента этих точек, а ось у пусть дополняет систему до правой тройки. Тогда уравнения движения P3 можно записать в виде [7–9]:
(1)
$\left\{ \begin{gathered} \ddot {x} - 2\dot {y} = {{U}_{x}} \hfill \\ \ddot {y} + 2\dot {x} = {{U}_{y}} \hfill \\ \ddot {z} = {{U}_{z}} \hfill \\ \end{gathered} \right.,$Точки либрации являются стационарными решениями системы (1). Кроме того, система уравнений имеет один первый интеграл, найденный Якоби, который задает кривые нулевой скорости (v = 0), ограничивающие область возможных движений точки P3:
где J – константа Якоби, v – скорость точки P3.Поскольку система (1) автономна, обладает первым интегралом и стационарным решением, к ней применима теорема Ляпунова о существовании периодических решений: плоских и вертикальных орбит Ляпунова [9]. Численный анализ решений системы (1) показывает, что она обладает следующими решениями в окрестности коллинеарных точек либрации [12]:
– периодические – гало-орбиты, для которых периоды в плоскости XY и перпендикулярно к ней совпадают;
– квазипериодические орбиты, для которых периоды в плоскости XY и перпендикулярно к ней не совпадают, при этом выделяют два типа орбит: квазигало-орбиты (если периоды в среднем равны) и орбиты Лиссажу (если периоды рационально соизмеримы).
Важные исследования этих орбит были сделаны Робертом Фаркуаром – в своей диссертации он описал инженерную методику построения гало-орбит, а через несколько лет в работе [32] с помощью метода Линдстеда-Пуанкаре было получено приближенное решение, которое впоследствии много раз уточнялось другими авторами путем учета дополнительных членов ряда. Наиболее известна в этом смысле работа Ричардсона [33]. Кроме того, в 1973 г. Фаркуаром и Кэмелом было обнаружено, что гало-орбита может возникнуть только при достижении константы Якоби определенной величины, т.е. при определенной амплитуде осцилляций в орбитальной плоскости XY. В работе 1973 г. дана оценка минимальной амплитуды по оси Y для гало-орбит около точки либрации L2 равная 32379 км. Таким образом, гало-орбиты возникают как бифуркация семейства плоских орбит Ляпунова.
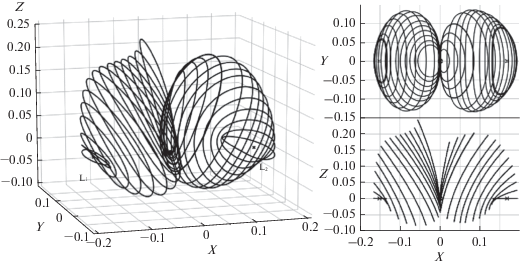
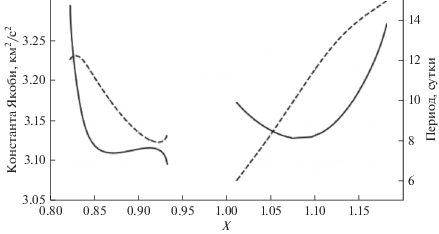
На рис. 1 приведено семейство северных гало-орбит около точки L1 системы Земля–Луна. Бифуркация “рождения” этого семейства гало-орбит происходит при достижении константы Якоби величины 3.291618348 км2/c2, а константа Якоби самой точки либрации равна 3.306124298 км2/c2. На рис. 2 представлены графики, иллюстрирующие связь между координатой X апоселения, периодом и константой Якоби.
Рис. 2.
Зависимость периода (пунктирная линия) и константы Якоби (сплошная линия) от координаты X апоселения.
Семейство южных гало-орбит абсолютно симметрично приведенному выше и отличается лишь знаком у координаты Z.
Вблизи периодического решения линейная относительная динамика описывается следующими уравнениями:
(3)
$\left( {\begin{array}{*{20}{c}} {\delta {\mathbf{\dot {r}}}} \\ {\delta {\mathbf{\dot {v}}}} \end{array}} \right) = {{\left. {\mathbf{A}} \right|}_{{\left( {\begin{array}{*{20}{c}} {{{{\mathbf{r}}}_{{{\text{ref}}}}}} \\ {{{{\mathbf{v}}}_{{{\text{ref}}}}}} \end{array}} \right)}}}\left( {\begin{array}{*{20}{c}} {\delta {\mathbf{r}}} \\ {\delta {\mathbf{v}}} \end{array}} \right),$решение этих уравнений можно записать в форме
(4)
$\left( {\begin{array}{*{20}{c}} {\delta {\mathbf{r}}\left( t \right)} \\ {\delta {\mathbf{v}}\left( t \right)} \end{array}} \right) = {\mathbf{\Phi }}\left( {t,{{t}_{0}}} \right)\left( {\begin{array}{*{20}{c}} {\delta {\mathbf{r}}\left( {{{t}_{0}}} \right)} \\ {\delta {\mathbf{v}}\left( {{{t}_{0}}} \right)} \end{array}} \right),$где матрица перехода Φ(t, t0) вычисляется как решение уравнений в вариациях на заданном периодическом решении $\left( {{{{\mathbf{r}}}_{{{\text{ref}}}}},{{{\mathbf{v}}}_{{{\text{ref}}}}}} \right){\text{:}}$
(5)
${\mathbf{\dot {\Phi }}}\left( {t,{{t}_{0}}} \right) = {\mathbf{A}}\left( t \right){\mathbf{\Phi }}\left( {t,{{t}_{0}}} \right),\,\,\,\,{\mathbf{\Phi }}\left( {{{t}_{0}},{{t}_{0}}} \right) = {{{\mathbf{E}}}_{{6 \times 6}}},$а сама периодическая траектория является решением системы (1).
Проинтегрировав совместно уравнения (1) и (5) на периоде заданного решения P, получим матрицу монодромии M = Φ(t0 + P, t0). Для типичных, неустойчивых, орбит вокруг коллинеарных точек либрации эта матрица имеет шесть собственных значений со свойствами
(6)
$\begin{gathered} {{\mu }_{1}} > 1,\,\,\,\,{{\mu }_{2}} = \mu _{1}^{{ - 1}} < 1,\,\,\,\,{{\mu }_{3}} = {{\mu }_{4}} = 1, \\ {{\mu }_{5}} = \mu _{6}^{*},\,\,\,\,\left| {{{\mu }_{5}}} \right| = \left| {{{\mu }_{6}}} \right| = 1, \\ \end{gathered} $где μ5 и μ6 – комплексно сопряженные числа.
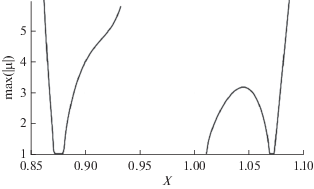
Величины первых двух мультипликаторов μ1 и μ2 – определяет свойства устойчивости периодических орбит. Как известно, в семействе гало-орбит есть островки устойчивости, для которых максимальная величина всех мультипликаторов не превосходит 1 [6, 34]. Зависимость этого параметра от координаты X апоселения приведена на рис. 3.
Рис. 4.
Устойчивое многообразие L1 (сплошная линия) и L2 (пунктирная линия) во вращающейся барицентрической системе координат.

Помимо самих точек либрации и орбит около них большой интерес с точки зрения проектирования перелетов в окрестности Луны представляют инвариантные многообразия, связанные с точками либрации и периодическими орбитами вокруг них.
Существуют два множества асимптотических траекторий, связанных с точками либрации и периодическими орбитами вокруг коллинеарных точек либрации: устойчивые и неустойчивые многообразия. Траектории устойчивого многообразия стремятся к точке либрации или орбите при t → ∞, в то время как траектории неустойчивого многообразия стремятся к точке либрации или орбите при t → –∞ Наличие таких траекторий для точек либрации следует из наличия положительного и отрицательного собственного значения у матрицы линеаризованной системы (1). Аналогичная ситуация наблюдается и для периодических решений: орбит Ляпунова и гало-орбит.
Для определения инвариантных устойчивых и неустойчивых многообразий точек либрации необходимо сделать малый сдвиг из нее в направлении соответствующего собственного вектора и проинтегрировать систему в обратном и прямом времени:
(7)
$\left( {\begin{array}{*{20}{c}} {{{{\mathbf{r}}}_{s}}} \\ {{{{\mathbf{v}}}_{s}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{{{\mathbf{r}}}_{L}}} \\ {{{{\mathbf{v}}}_{L}}} \end{array}} \right) + \varepsilon {{{\mathbf{\Lambda }}}_{s}},\,\,\,\,\left( {\begin{array}{*{20}{c}} {{{{\mathbf{r}}}_{u}}} \\ {{{{\mathbf{v}}}_{u}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{{{\mathbf{r}}}_{L}}} \\ {{{{\mathbf{v}}}_{L}}} \end{array}} \right) + \varepsilon {{{\mathbf{\Lambda }}}_{u}},$где $\left( {{{{\mathbf{r}}}_{L}},{{{\mathbf{v}}}_{L}}} \right)$ – координаты и скорость точки либрации, ${{{\mathbf{\Lambda }}}_{s}}$ – собственный вектор соответствующий отрицательному собственному значению (устойчивому многообразию), ${{{\mathbf{\Lambda }}}_{u}}$ – собственный вектор соответствующий положительному собственному значению (неустойчивому многообразию), ε – малый параметр.
Вид устойчивых инвариантных многообразий для точек либрации L1 и L2 системы Земля–Луна в ОКЗТТ приведен на рис. 4.
В случае периодических орбит у точек либрации каждая точка на периодической орбите связана с некоторой асимптотической траекторией, принадлежащей устойчивому и неустойчивому многообразию этой орбиты. Заменяя координаты и скорость точки либрации на координаты и скорости точки на периодическом решении, и используя собственные векторы матрицы монодромии, связанные с μ2 и μ1, можно получить эти многообразия.
Для использования этих решений в рамках возмущенной эфемеридной модели необходимо сделать переход из вращающейся системы координат, связанной с барицентром системы или точкой либрации в неподвижную экваториальную геоцентрическую или селеноцентрическую систему координат, связанную с эпохой J2000.
Введем мгновенную синодическую систему координат связанную с текущим положением и скоростью Луны $\left( {{{{\mathbf{r}}}_{{\text{M}}}},{{{\mathbf{v}}}_{{\text{M}}}}} \right)$в геоцентрической системе координат J2000. Для этого запишем единичные векторы этой системы в системе J2000 $\left( {{{{\mathbf{e}}}_{x}},{{{\mathbf{e}}}_{y}},{{{\mathbf{e}}}_{z}}} \right){\text{:}}$
(8)
${{{\mathbf{e}}}_{x}} = \frac{{{{{\mathbf{r}}}_{{\text{M}}}}}}{{\left| {{{{\mathbf{r}}}_{{\text{M}}}}} \right|}},\,\,\,\,{{{\mathbf{e}}}_{z}} = \frac{{{{{\mathbf{r}}}_{{\text{M}}}} \times {{{\mathbf{v}}}_{{\text{M}}}}}}{{\left| {{{{\mathbf{r}}}_{{\text{M}}}} \times {{{\mathbf{v}}}_{{\text{M}}}}} \right|}},\,\,\,\,{{{\mathbf{e}}}_{y}} = {{{\mathbf{e}}}_{z}} \times {{{\mathbf{e}}}_{x}}$и мгновенную угловую скорость вращения Луны:
(9)
$\dot {\vartheta } = \frac{{\left| {{{{\mathbf{r}}}_{{\text{M}}}} \times {{{\mathbf{v}}}_{{\text{M}}}}} \right|}}{{{{{\left| {{{{\mathbf{r}}}_{{\text{M}}}}} \right|}}^{2}}}}.$После этого положение и скорость относительно Земли в инерциальной системе координат можно получить из координат в синодической системе относительно Земли в следующем виде:
(10)
$\left( {\begin{array}{*{20}{c}} {{{{\mathbf{r}}}_{{{\text{J}}2000}}}} \\ {{{{\mathbf{v}}}_{{{\text{J}}2000}}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{{{\mathbf{e}}}_{x}}}&{{{{\mathbf{e}}}_{y}}}&{{{{\mathbf{e}}}_{z}}}&0&0&0 \\ {\dot {\vartheta }{{{\mathbf{e}}}_{y}}}&{ - \dot {\vartheta }{{{\mathbf{e}}}_{x}}}&0&{{{{\mathbf{e}}}_{x}}}&{{{{\mathbf{e}}}_{y}}}&{{{{\mathbf{e}}}_{z}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {\left| {{{{\mathbf{r}}}_{{\text{M}}}}} \right| \cdot {\mathbf{r}}} \\ {\left| {{{{\mathbf{v}}}_{{\text{M}}}}} \right| \cdot {\mathbf{v}}} \end{array}} \right),$где $\left( {{\mathbf{r}},{\mathbf{v}}} \right)$ – безразмерные положение и скорость в синодической системе координат.
Преобразование (10) соответствуют введению координат Нехвилла в ограниченной эллиптической задаче трех тел [7–9].
2. КВАЗИОПТИМАЛЬНОЕ УПРАВЛЕНИЕ С ОБРАТНОЙ СВЯЗЬЮ
КОУСОС [26–28] получено для математической модели возмущенного движения КА, использующей равноденственные элементы $h = \sqrt {\frac{p}{\mu }} ,$ ${{e}_{x}} = e\cos \left( {\Omega + \omega } \right),$ ${{e}_{y}} = e\sin \left( {\Omega + \omega } \right),$ ${{i}_{x}} = {\text{tg}}\frac{i}{2}\cos \Omega ,$ ${{i}_{y}} = {\text{tg}}\frac{i}{2}\sin \Omega $ и $F = \nu + \omega + \Omega $ [35], где p – фокальный параметр, e – эксцентриситет, ω – аргумент перицентра, i – наклонение, Ω – долгота восходящего узла, ν – истинная аномалия, μ – гравитационный параметр центрального тела (для геоцентрических траекторий – гравитационный параметр Земли). КОУСОС определяет углы ориентации вектора тяги ЭРДУ в орбитальной системе координат – углы тангажа ϑ (угол между трансверсальным направлением и проекцией вектора тяги на оскулирующую орбитальную плоскость) и рысканья ψ (угол между оскулирующей орбитальной плоскостью и векторам тяги) в виде
Применение КОУСОС к расчету траекторий к точкам либрации или на гало-орбиты оказывается возможным потому, что оскулирующая геоцентрическая орбита точек либрации L1/L2 и точек на значительных интервалах движения по гало-орбитам и устойчивым многообразиям точек либрации и гало-орбит является эллиптической. Поэтому возможна реализация следующей схемы вычислений:
1) Фиксируется время t1 прибытия КА в конечную точку (точку либрации, заданную точку на гало-орбите или в заданную точку на устойчивом многообразии точки либрации или гало-орбиты) и задается начальное приближение для массы КА в этой точке m1;
2) Дифференциальные уравнения геоцентрического движения КА с направлением тяги, обратным вычисляемому с использованием КОУСОС, интегрируются в обратном направлении по времени от конечной точки до достижения малой окрестности начальной круговой геоцентрической орбиты. В результате этого интегрирования определяется масса КА на начальной геоцентрической орбите m0;
3) Пункты 1–2 определяют функциональную зависимость m0(m1). Каким-либо стандартным численным методом определяется корень уравнения m0(m1) – $m_{0}^{*}$ = 0, где $m_{0}^{*}$ – заданная начальная масса КА на начальной круговой геоцентрической орбите. В результате, определяется m1 и траектория перелета от начальной орбиты до конечной точки.
Вычисленная таким образом траектория может состоять только из активного участка с КОУСОС либо из активного участка с КОУСОС и пассивного участка движения по устойчивому многообразию от точки выключения малой тяги до точки либрации или гало-орбиты. Первый (полностью активный) тип траекторий назовем траекторией прямого перелета с малой тягой, а второй тип траекторий – низкоэнергетической траекторией с малой тягой.
Разумеется, использование КОУСОС накладывает ряд ограничений на рассматриваемые траектории перелета к точкам либрации и на гало-орбиты. Во-первых, начальная околоземная орбита должна быть круговой. Во-вторых, точка окончания участка перелета с малой тягой должна иметь оскулирующий геоцентрический эксцентриситет, меньший единицы. В-третьих, в случае пересечения траекторией сферы Хилла Луны на участке работы ЭРДУ появляется высокая вероятность отказа КОУСОС. Однако имеющиеся возможности КОУСОС все же позволяют провести быстрые качественные оценки возможностей многих типов перелетов к Луне с малой тягой и, на взгляд авторов, должны быть использованы.
Для облегчения анализа, с целью получения качественной оценки возможностей низкоэнергетических перелетов с малой тяги, откажемся от решения однопараметрической краевой задачи для определения массы КА в конце работы ЭРДУ. Вместо этого зафиксируем массу КА в точке выключения ЭРДУ, тогда задача расчета одной квазиоптимальной траектории сведется просто к интегрированию уравнений возмущенного движения с заданным управлением в обратном времени. Заметим, что при анализе оптимальных низкоэнергетических перелетов с малой тягой для каждой траектории придется решать крайне сложную и трудоемкую задачу оптимального управления со многими локальными экстремумами. Собственно, это соображение и является оправданием использования на первом этапе исследований упрощенного вида управления – КОУСОС – вместо оптимального управления.
3. ПРИМЕРЫ ТРАЕКТОРИЙ ПЕРЕЛЕТА
В качестве примера рассмотрим перелеты в системе Земля–Луна к точкам либрации L1, L2 и гало-орбитам около них. Расчеты будем проводить с учетом возмущения от Солнца в системе координат J2000 связанной с Землей, в этом случае уравнения описывающие пассивное движения КА имеют вид:
(11)
$\begin{gathered} {\mathbf{\ddot {r}}} = - \frac{{{{\mu }_{{\text{E}}}}{\mathbf{r}}}}{{{{{\left| {\mathbf{r}} \right|}}^{3}}}} + {{\mu }_{{\text{S}}}}\left( {\frac{{{\mathbf{r}} - {{{\mathbf{r}}}_{{\text{S}}}}}}{{{{{\left| {{\mathbf{r}} - {{{\mathbf{r}}}_{{\text{S}}}}} \right|}}^{3}}}} + \frac{{{{{\mathbf{r}}}_{{\text{S}}}}}}{{{{{\left| {{{{\mathbf{r}}}_{{\text{S}}}}} \right|}}^{3}}}}} \right) + \\ + \,\,{{\mu }_{{\text{M}}}}\left( {\frac{{{\mathbf{r}} - {{{\mathbf{r}}}_{{\text{M}}}}}}{{{{{\left| {{\mathbf{r}} - {{{\mathbf{r}}}_{{\text{M}}}}} \right|}}^{3}}}} + \frac{{{{{\mathbf{r}}}_{{\text{M}}}}}}{{{{{\left| {{{{\mathbf{r}}}_{{\text{M}}}}} \right|}}^{3}}}}} \right), \\ \end{gathered} $где μE, μS, μM – гравитационные параметры Земли, Солнца и Луны, а rS, rM –геоцентрические радиус-векторы Солнца и Луны соответственно. Векторы положения и скорости Солнца и Луны вычисляются с помощью эфемеридного обеспечения JPL DE405.
Рассматривается задача доставки в заданную дату 12.IV.2026 00.00 UTС в окрестность одной из точек либрации (на гало-орбиту или в саму точку) КА конечной массой 1000 кг, оснащенный ЭРДУ с двигателем СПД-140Д, имеющим тягу 290 мН и удельный импульс 1770 с (https://fakel-russia.com/ images/gallery/produczia/fakel_spd_print.pdf). В начальный момент времени КА находится на круговой геосинхронной орбите (то есть на орбите с радиусом 42164 км) с наклонением 51.8°.
В качестве целевых (конечных) орбит, кроме точек либрации L1 и L2, рассмотрим следующие три гало-орбиты:
1) Северная гало-орбита у точки либрации L1, обладающая свойством орбитальной устойчивости (максимальный мультипликатор Флоке равен 1), с координатами апоселения в синодической барицентрической безразмерной системе координат (0.8730990324388, 0.0, 0.1906425182060, 0.0, 0.2354475477314, 0.0), периодом 9.677 дня и константой Якоби 3.108604 км2/с2. Введем для этой орбиты обозначение L1HO.
2) Северная гало-орбита у точки либрации L1, относящаяся к классу почти прямолинейных орбит (NRНO) с максимальным по модулю мультипликатором Флоке 5.32, не обладающая свойством орбитальной устойчивости. Ее апоселений имеет координаты (0.9306744714248, 0.0, 0.2304688230602, 0.0, 0.1037746566261, 0.0), период равен 8.047 суткам, а константа Якоби равна 3.1038796 км2/с2. Эту орбиту обозначим L1NRHO.
3) Северная гало-орбита у точки L2 (обозначение – L2HO) достаточно больших размеров, обладающая свойством орбитальной устойчивости, с координатами апоселения (1.0806959653822, 0.0, 0.2023606276413, 0.0, –0.1986289716256, 0.0), периодом 10.265 сут и константой Якоби 3.1266148 км2/с2.
Рассматриваемые траектории перелета КА с ЭРДУ к точке либрации или на целевую гало-орбиту состоят из двух участков движения. На первом участке осуществляется перелет КА с работающей ЭРДУ с начальной геосинхронной орбиты в какую-либо точку устойчивого многообразия рассматриваемой точки либрации или гало-орбиты. После достижения устойчивого многообразия ЭРДУ выключается и КА совершает пассивный перелет по этому многообразию до точки либрации или целевой гало-орбиты.
На первом участке ЭРДУ работает постоянно, а ориентация вектора тяги вычисляется с помощью алгоритма КОУСОС. Фактически расчет первого участка траектории производится после вычисления устойчивого многообразия с помощью интегрирования уравнений движения КА с работающей ЭРДУ в обратном времени от заданной точки устойчивого многообразия до близкой окрестности геосинхронной орбиты заданного наклонения. Выход из интегрирования происходит при достижении заданного значения большой полуоси 42164 км, при этом типичная ошибка по наклонению меньше 0.025°, а по эксцентриситету – меньше 0.005. Для определения оптимальных точек выхода на устойчивые многообразия проводились вычисления траекторий с КОУСОС, заканчивающихся во всех вычисленных точках этих многообразий (обычно – на интервале движения от 0 до 120 сут с шагом 0.1 сут). В результате определялись зависимости длительности первого участка траектории (активного участка траектории перелета с начальной геосинхронной орбиты до устойчивого многообразия с использованием КОУСОС) и требуемой массы рабочего тела ЭРДУ на перелет от длительности второго участка траектории (участка пассивного движения по устойчивому многообразию до точки либрации или гало-орбиты).
Для определения устойчивых многообразий воспользуемся выражениями (7), (8)–(10) и проинтегрируем уравнения (11). Для точек либрации в этом нет никакой неоднозначности, т.к. собственный вектор, задающий в их малой окрестности устойчивое многообразие всегда один. В случае неустойчивых гало-орбит появляется возможность выбора точки выхода на орбиту, для каждой из которых существует своя асимптотическая траектория. А в случае орбитально-устойчивых гало-орбит чисто вещественных мультипликаторов нет, зато есть две пары комплексно сопряженных. В данной работе для этих орбит за направление для определения устойчивого многообразия брались вещественные части собственных векторов, соответствующих таким мультипликаторам. В итоге был организован перебор по точкам на гало-орбитах и подходящим направлениям, в результате которого оказалось, что на заданную дату прибытия в эфемеридной модели наиболее близкими к Земле оказались “ветви” многообразия, исходящие из окрестности апоселения и периселения для орбит у L1 и L2 соответственно. Для дальнейших расчетов выбирались именно эти многообразия.
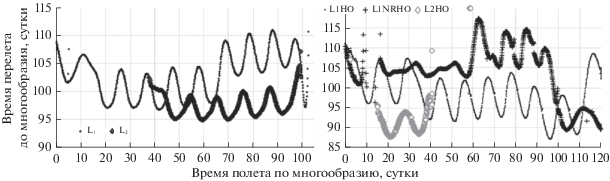
На рис. 5 представлены зависимости длительности активного участка на траектории перелета от начальной геосинхронной орбиты до устойчивого многообразия от длительности дальнейшего пассивного полета по устойчивому многообразию до точек либрации L1, L2 (слева) и орбит L1HO, L1HRHO, L2HO (справа). Не для всех точек устойчивых многообразий удалось найти решения, так как не всюду выполнялись условия применимости КОУСОС. Например, решения не были найдены для точек устойчивых многообразий, на которых оскулирующий геоцентрический эксцентриситет превышал единицу, для большинства точек внутри сферы Хилла Луны, для ряда траекторий с близким сближением с Луной на активном участке траектории, приводящим к выходу КА на гиперболические геоцентрические траектории или на траектории столкновения с Луной.
Рис. 5.
Зависимость длительности активного участка траектории от длительности полета по устойчивому многообразию.
В табл. 1 приведено сравнение основных параметров перелета с начальной геосинхронной орбиты к точкам либрации и на гало-орбиты. В этой таблице введены следующие обозначения Δtс – длительность пассивного движения КА по устойчивому многообразию после выключения ЭРДУ, ΔtΣ – суммарная длительность перелета, Δtm – длительность перелета с начальной геосинхронной орбиты до устойчивого многообразия с работающей ЭРДУ, mp – требуемые затраты рабочего тела ЭРДУ, δtΣ – увеличение суммарной длительности перелета по сравнению с длительностью либо прямого перелета (если такая траектория найдена), либо перелета с минимальной длительностью движения по устойчивому многообразию, δmp – снижение затрат рабочего тела ЭРДУ по сравнению с затратами на прямом перелете (если такая траектория найдена), либо на перелете с минимальной длительностью движения по устойчивому многообразию.
Таблица 1.
Сравнение основных параметров перелета к точкам либрации и на гало-орбиты
| Δtс | ΔtΣ | Δtm | mp | δtΣ | δmp | ||
|---|---|---|---|---|---|---|---|
| сутки | сутки | сутки | кг | % | сутки | % | кг |
| Перелет к L1 | |||||||
| 0.0 | 108.908 | 108.908 | 157.209 | – | – | – | – |
| 20.8 | 117.895 | 97.095 | 140.158 | 8.253 | 8.988 | 10.846 | 17.051 |
| 41.8 | 138.565 | 96.765 | 139.681 | 27.231 | 29.657 | 11.150 | 17.529 |
| Перелет к L2 | |||||||
| 37.7 | 140.080 | 102.380 | 147.787 | ||||
| 48.4 | 143.494 | 95.094 | 137.269 | 2.437 | 3.414 | 7.117 | 10.518 |
| 59.4 | 154.317 | 94.917 | 137.014 | 10.163 | 14.237 | 7.290 | 10.773 |
| Перелет на L1HO | |||||||
| 0.0 | 111.052 | 111.052 | 160.304 | ||||
| 11.2 | 107.106 | 95.906 | 138.442 | –3.553 | –3.946 | 13.638 | 21.863 |
| 96.3 | 183.396 | 87.096 | 125.724 | 65.145 | 72.344 | 21.572 | 34.580 |
| Перелет на L1NRHO | |||||||
| 0.0 | 110.454 | 110.454 | 159.441 | ||||
| 6.3 | 107.215 | 100.915 | 145.672 | –2.932 | –3.239 | 8.636 | 13.769 |
| 103.8 | 193.285 | 89.485 | 129.172 | 74.992 | 82.831 | 18.985 | 30.269 |
| Перелет на L2HO | |||||||
| 0.6 | 127.443 | 126.843 | 183.100 | ||||
| 2.4 | 109.582 | 107.182 | 154.718 | –14.015 | –17.861 | 15.500 | 28.381 |
| 21.3 | 109.051 | 87.751 | 126.669 | –14.432 | –18.392 | 30.819 | 56.430 |
Для каждой конечной точки либрации или орбиты в табл. 1 приведены основные параметры перелетов для траекторий с минимальным временем пассивного движения по устойчивому многообразию, траекторий, соответствующих первому локальному минимуму и глобальному минимуму длительности активного участка (среди найденных решений) в зависимости от длительности пассивного движения (рис. 5).
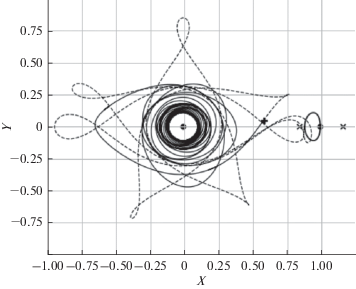
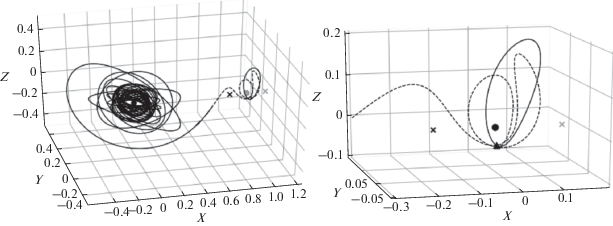
На рис. 6 и 7 приведены проекции траекторий перелета на мгновенную плоскость движения Луны в барицентрических оскулирующих переменных Нехвилла для решений, соответствующих глобальному минимуму длительности активного участка для перелета на L1HO и L1NRHO из таблицы 1.
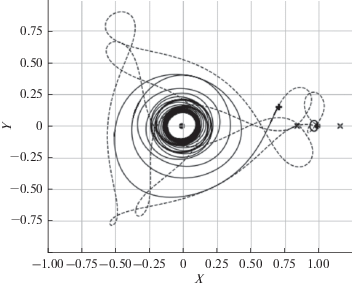
На рис. 8 приведены траектория перелета на L2HO для решения, соответствующего глобальному минимуму длительности активного участка (слева) из табл. 1 и участок движения по этой траектории вблизи Луны в увеличенном масштабе (справа).
ЗАКЛЮЧЕНИЕ
В работе предложен метод расчета пространственных траекторий перелета КА с малой тягой с круговой околоземной орбиты к точкам либрации L1, L2 системы Земля–Луна и на гало-орбиты вокруг них, включая прямые перелеты и низкоэнергетические перелеты, состоящие из активного участка перелета с начальной геоцентрической орбиты к устойчивому многообразию и участка пассивного движения КА по этому многообразию.
В качестве управления на прямых траекториях и на активных участках низкоэнергетических траекторий используется квазиоптимальное управление с обратной связью, позволяющее свести задачу вычисления траектории перелета к однопараметрической краевой задаче (если задана начальная масса КА) или к задаче Коши (если задана конечная масса КА).
Разработанный метод использовался для численного анализа траекторий перелета с наклонной геосинхронной орбиты к точкам либрации и на гало-орбиты. Простота и высокое быстродействие этого метода позволило провести оптимизацию точек выхода на устойчивые многообразия с помощью расчета множества квазиоптимальных траекторий, выходящих на эти многообразия с шагом по времени 0.1 сут на интервале до 120 сут. Низкоэнергетические траектории с оптимальным временем выхода КА на устойчивое многообразие всегда имеют преимущество перед прямыми перелетами. Для перелета в L1 массу рабочего тела ЭРД-У на низкоэнергетических траекториях удается сократить примерно на 11% по сравнению с прямыми перелетами при увеличении общего времени перелета на 8–27%. Для перелета к L2 прямого перелета с использованием КОУСОС найти не удалось, в этом классе траекторий обнаружены только низкоэнергетические перелеты. Для них увеличение общей длительности перелета на 2.4% приводит к снижению требуемых затрат рабочего тела ЭРДУ на 7%. Для перелетов на гало-орбиты, низкоэнергетические перелеты позволяют добиться не только сокращения массы рабочего тела ЭРДУ (в некоторых случаях – на 30–56%), но и сократить, в ряде вариантов, общую длительность перелета.
Оптимизация точек выхода на устойчивые многообразия показала, что в рассматриваемом случае перелета с круговой геосинхронной орбиты минимальное время работы ЭРДУ и минимальные затраты рабочего тела ЭРДУ достигаются на траекториях, выходящих в точки устойчивого многообразия с минимальным оскулирующим эксцентриситетом и с радиусом апогея, меньшим радиуса Луны. Значения других оскулирующих элементов точки сопряжения активного и пассивного участков траектории (большой полуоси, радиуса перигея и наклонения) оказывает на характеристики перелета существенно меньшее влияние.
Работа выполнена за счет средств гранта Российского научного фонда (соглашение № 16-19-10429).
Список литературы
Егоров В.А. О некоторых задачах динамики полета к Луне // УФН. 1957. Т. 43. № 1. С. 73–117.
Егоров В.А. Пространственная задача достижения Луны. М.: Наука, 1965.
Егоров В.А., Гусев Л.И. Динамика перелетов между Землей и Луной. М.: Наука. 1980.
Wu W., Tang Y., Zhang L., Qiao, D. Design of communication relay mission for supporting lunar-farside soft landing // Science China Information Sciences. 2018. V. 61. № 4. P. 14.
Melissa L., McGuire M.L., Burke L.M., McCarty S.L. et al. Low thrust cis-lunar transfers using a 40 kW-classsolar electric propulsion spacecraft // AAS. 17-583. P. 1–21.
Davis D.C. et al. Stationkeeping and Transfer Trajectory Design for Spacecraft in Cislunar Space // AAS/AIAA Astrodynamics Specialist Conference, Washington, 2017. AAS. 17-826.
Маркеев А.П. Точки либрации в небесной механике и космодинамике. М.: Наука, 1978.
Себехей В. Теория орбит: ограниченная задача трех тел. М.: Наука, 1982.
Дубошин Г.Н. Небесная механика. Аналитические и качественные методы. М.: Наука, 1964.
Ильин И.С., Сазонов В.В., Тучин А.Г. Гало-орбиты в окрестности точки либрации L2 системы Солнце–Земля // Космич. исслед. 2014.Т. 52. № 3. С. 201–217. (Cosmic Research. P
Parker J.S., Anderson R.L. Low-energy lunar trajectory design. John Wiley & Sons, 2014. V. 12.
Folta D.C., Pavlak T.A., Haapala A.F. et al. Earth–Moon Libration Point Orbit Stationkeeping: Theory, Modeling, and Operations // Acta Astronautica. 2014. V. 94. № 1. P. 421–433.
Белбруно Э. Динамика захвата и хаотические движения в небесной механике с приложениями к конструированию малоэнергетических перелетов. Ижевск, НИЦ РХД, 2011.
Belbruno E.A., Miller J.K. Sun-Perturbed Earth-to-Moon Transfers with Ballistic Capture // J. Guidance, Control and Dynamics. 1993. V. 16. № 4. P. 770–775.
Uesugi K. Results of the MUSES-A “HITEN” mission // Advances in Space Research. 1996. V. 18. № 11. P. 69–72.
Лидов М.Л., Ляхова В.А., Тесленко Н.М. Одноимпульсный перелет на условно-периодическую орбиту в окрестности точки системы Земля–Солнце // Космич. исслед. 1987. Т. 25. № 2. С. 163–185.
Ивашкин В.В. О траекториях полета точки к Луне с временным захватом ее Луной // ДАН. 2002. Т. 387. № 2. С. 196–199.
Ivashkin V.V. On Trajectories for the Earth-to-Moon Flight with Capture by the Moon // AAS Publications, Scienceand Technology Series. 2004. V. 108. Paper AAS 03-723. P. 157–166.
Foing B.H., Racca G.D. et al. SMART-1 after lunar capture: First results and perspectives // J. Earth System Science. 2005. V. 114. № 6. P. 687–697.
Ozimek M.T., Howell K.C. Low-Thrust Transfers in the Earth–Moon System, Including Applications to Libration Point Orbits // J. Guidance, Control, and Dynamics. 2010. V. 33. № 2.
Mingotti G., Topputo F., Bernelli-Zazzera F. Low-energy, low-thrust transfers to the Moon // Celest. Mech. Dyn. Astr. 2009. V. 105. P. 61–74.
Shimmin R. Trajectory design for a very-low-thrust lunar mission // PhD thesis. University of Adelaide. 2012. P. 1–204.
Архангельский Н.И., Акимов В.Н., Кувшинова Е.Ю., Синицын А.А. Выбор параметров эллиптической орбиты базирования для повышения безопасности применения многоразовых ядерных буксиров // Космическая техника и технологии. 2016. Т. 13. № 2. С. 45–54.
Kluever C.A., Pierson B.L. Optimal Low-Thrust Earth-Moon Transfers with a Switching Function // J. Astronautical Sciences. 1994. V. 42. № 3. P. 269–284.
Kluever C.A., Pierson B.L. Optimal Low-Thrust Three-Dimensional Earth-Moon Trajectories // J. Guidance, Control and Dynamics. 1995. V. 18. № 4.
Петухов В.Г. Квазиоптимальное управление с обратной связью для многовиткового перелета с малой тягой между некомпланарными эллиптической и круговой орбитами // Космич. исслед. 2011. Т. 49. № 2. С. 128–137. (Cosmic Research. P. 121)
Petukhov V.G., Svotina V.V. Robust Suboptimal Feedback Control for Low-Thrust Transfers between Noncoplanar Elliptical and Circular Orbits. 3rd European Conference for Aero-Space Sciences (EUCASS-2009). France, Versailles, 2009.
Петухов В.Г. Робастное квазиоптимальное управление с обратной связью для перелета с малой тягой между некомпланарными эллиптической и круговой орбитами // Вестник МАИ. 2010. Т. 17. № 3. С. 50–58.
Ивашкин В.В., Петухов В.Г. Траектории перелета с малой тягой между орбитами спутников Земли и Луны при использовании орбиты захвата Луной. Препринт ИПМ им. М.В. Келдыша РАН. 2008. № 81.
Petukhov V.G., Konstantinov M.S. Spacecraft Insertion into Earth-Moon L1 and Lunar Orbit. IAC-09-D2.3.11, 2009.
Petukhov V.G., Popov G.A., Svotina V.V. Suboptimal Low-Thrust Trajectories for Lunar Missions. GLUC-2010-2.2.P3. Global Lunar Conference, 31 May–3 June 2010, IAF Beijing, China.
Farquhar R.W., Kamel A.A. Quasi-Periodic Orbits About the Translunar Libration Point // Celestial Mechanics. 1973. V. 7. № 4. P. 458–473.
Richardson D.L. Analytic construction of periodic orbits about the collinear points // Celestial mechanics. 1980. V. 22. № 3. P. 241–253.
Breakwell J.V., Brown J.V. The Halo Family of 3-Dimensional Periodic Orbits in the Earth-Moon Restricted 3-body Problem // Celestial Mechanics. 1979. V. 20. № 4. P. 389–404.
Brouke R.A., Cefola P.J. On the Equinoctial Orbital Elements // Celestial Mechanics. 1972. V. 5. P. 303–310.
Дополнительные материалы отсутствуют.
Инструменты
Космические исследования