Космические исследования, 2020, T. 58, № 4, стр. 331-343
Выбор структуры систем спутников для метеорологии и обнаружения очагов лесных пожаров на основе векторной модели обзора Земли
Научно-производственная корпорация “Космические системы мониторинга, информационно управляющие
и электромеханические комплексы” им. А.Г. Иосифьяна
г. Москва, Россия
* E-mail: ntk.vniiem@bk.ru
** E-mail: saulskiy@gmail.com
Поступила в редакцию 03.04.2019
После доработки 18.11.2019
Принята к публикации 16.01.2020
Аннотация
Используя “векторную модель обзора Земли”, показано, что рассматриваемые системы спутников должны иметь “эквидистантную” структуру, формируемую равными сдвигами по долготе узлов орбит и по фазе спутников. Для сравнения вариантов структуры разработана на основе “векторной модели обзора Земли” компьютерная программа, вычисляющая все перерывы обзора с их частотами для очередного варианта системы спутников за доли секунды. Проанализировав все возможные варианты, выработаны рекомендации по выбору структуры систем из 4-х метеоспутников типа МЕТЕОР-М и из 5 и 6 спутников с широкозахватными инфракрасными радиометрами, впервые испытанными на спутнике КАНОПУС-В-ИК. Одним из дополнительных результатов стало то, что в рассмотренных вариантах частота максимального перерыва обзора, широко применяемого в качестве критерия эффективности систем наблюдения Земли, оказалась меньше 0.01. В связи с этим сделан вывод о практической нецелесообразности использования этого критерия. Цель статьи – демонстрация возможностей применения введенной в статьях [1–4] “векторной модели обзора Земли” для анализа и выбора спутниковой структуры космических систем наблюдения Земли.
ПОСТРОЕНИЕ И СВОЙСТВА ВЕКТОРНОЙ МОДЕЛИ ОБЗОРА ШИРОТЫ ЗЕМЛИ
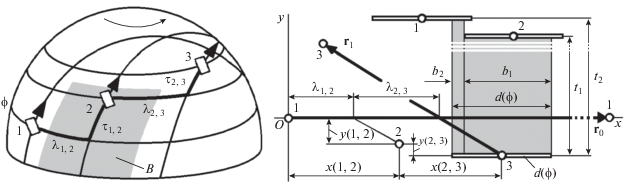
Векторная модель обзора Земли, далее коротко – модель, строится для любой широты φ. Схема построения дана на рис. 1. Там слева показана система спутников 1, 2 и 3, а справа – ее модель. Орбиты круговые с одинаковыми высотами h и наклонениями i. Структура системы задана сдвигами: λ1, 2, λ2, 3 для долгот восходящих узлов орбит и τ1, 2 , τ2, 3 для фаз спутников внутри орбит. На модели структура отображается в виде “спутниковых узлов”, отражающих моменты прохода трасс спутников через широту ϕ. Узлы (кружочки на рис. 1) изображаются в системе координат xOy, где по горизонтали откладываются долготы x точек широты φ, а по вертикали – время y. Поэтому абсциссой узла служит долгота точки, через которую прошла трасса, а ординатой – момент времени, когда это случилось. Все угловые величины на модели удобно (но не обязательно) измерять в радианах, а время – в драконических периодах обращения спутников ${{T}_{{dr}}}$, т.е. в витках орбиты (coils).
Помещая узел 1-го спутника в начало координат, находим позиции узлов 2 и 3 спутников по следующим формулам, учитывающим межвитковый сдвиг $l$ трасс спутников, появляющийся на любом витке орбиты из-за вращения Земли:
(1)
$x\left( {1,2} \right) = {{{\lambda }}_{{1,2}}} + {{l~{{{\tau }}_{{1,2}}}} \mathord{\left/ {\vphantom {{l~{{{\tau }}_{{1,2}}}} {\left( {2{\pi }} \right)}}} \right. \kern-0em} {\left( {2{\pi }} \right)}},\,\,\,\,y\left( {1,2} \right) = {{ - ~{{{\tau }}_{{1,2}}}} \mathord{\left/ {\vphantom {{ - ~{{{\tau }}_{{1,2}}}} {\left( {2{\pi }} \right)}}} \right. \kern-0em} {\left( {2{\pi }} \right)}};$(2)
$x\left( {2,3} \right) = {{{\lambda }}_{{2,3}}} + {{l~{{{\tau }}_{{2,3}}}} \mathord{\left/ {\vphantom {{l~{{{\tau }}_{{2,3}}}} {\left( {2{\pi }} \right)}}} \right. \kern-0em} {\left( {2{\pi }} \right)}},\,\,\,\,y\left( {2,3} \right) = {{ - ~{{{\tau }}_{{2,3}}}} \mathord{\left/ {\vphantom {{ - ~{{{\tau }}_{{2,3}}}} {\left( {2{\pi }} \right)}}} \right. \kern-0em} {\left( {2{\pi }} \right)}}.$Каждому спутнику соответствует бесконечное множество узлов на модели, возникающих при различных прохождениях его трассы через широту ϕ, а также за счет смещения по горизонтали на целое число периодов 2π. Чтобы найти все спутниковые узлы, введем два первых “шаг-вектора”:
(3)
${{{\mathbf{r}}}_{0}} = \left( {{{x}_{0}};{{Y}_{0}}} \right) = \left( {2{\pi };0} \right),\,\,\,\,{{{\mathbf{r}}}_{1}} = \left( {{{x}_{1}};{{Y}_{1}}} \right) = \left( { - l;1} \right).$Здесь и далее проекции векторов на оси координат записываются в скобках, где 1-е число – это проекция на ось Ox, а 2-е – на ось Oy. Ординаты шаг-векторов всегда являются целыми числами и обозначаются прописными буквами Y.
Для получения всех узлов некоторого спутника, достаточно прибавлять к вектору ${\mathbf{r}}$, задающему какой-либо его узел, следующую комбинацию из шаг-векторов ${{{\mathbf{r}}}_{0}}$ и ${{{\mathbf{r}}}_{1}}$ с любыми, но целочисленными коэффициентами ${{W}_{0}}$ и ${{W}_{1}}$:
Цель построения модели – расчет всех перерывов обзора на широте φ, а, в конце концов, на поясе широт, представляемом как набор узеньких поясов. Для достижения цели нужно сначала через каждый узел модели провести “спутниковый след”, или кратко “след”, являющийся отрезком прямой линии. Его длина $d\left( \phi \right)$ равна участку широты $~\phi $ (в радианах), пересеченному полосой обзора спутника. На рис. 1 слева одна из таких полос, обозначенная как B, выделена затенением. На том же рис. 1 справа, т.е. на модели, показаны 3 “следа”, между которыми образовались вертикальные столбики, также выделенные затенением. Высоты столбиков ${{t}_{1}}$и ${{t}_{2}}$ равны искомым перерывам обзора, а их частоты ${{f}_{1}}$ и ${{f}_{2}}$ вычисляются по следующим формулам:
(5)
${{f}_{1}} = {{{{b}_{1}}} \mathord{\left/ {\vphantom {{{{b}_{1}}} {d\left( \phi \right)}}} \right. \kern-0em} {d\left( \phi \right)}},\,\,\,\,{{f}_{2}} = {{{{b}_{2}}} \mathord{\left/ {\vphantom {{{{b}_{2}}} {d\left( \phi \right)}}} \right. \kern-0em} {d\left( \phi \right)}},$Вот так реализуется 1-е свойство модели: обеспечивается расчет всех перерывов обзора с их частотами на любой широте Земли, а потому и на всем широтном поясе.
Описанная выше картина из столбиков перерывов обзора называется “подмоделью”. Вся модель целиком состоит из подмоделей на следах всех спутников.
Для приближенного вычисления следа $~d\left( \phi \right)$ предлагается формула [1–4]:
(6)
$d\left( \phi \right) = B{{\left( {2{\pi } - l~{\text{cos}}i} \right)} \mathord{\left/ {\vphantom {{\left( {2{\pi } - l~{\text{cos}}i} \right)} {(2{\pi }{{R}_{{\text{E}}}}\sqrt {{{{\cos }}^{2}}\phi - {{{\cos }}^{2}}i} )}}} \right. \kern-0em} {(2{\pi }{{R}_{{\text{E}}}}\sqrt {{{{\cos }}^{2}}\phi - {{{\cos }}^{2}}i} )}},$Точный, но громоздкий способ расчета $d\left( \phi \right)$ содержится, например, в [5].
Для системы из K спутников обе пары формул (1) и (2) обобщаются так:
(7)
$\begin{gathered} x\left( {k,t} \right) = {{{\lambda }}_{{k,t}}} + {{l~{{{\tau }}_{{k,t}}}} \mathord{\left/ {\vphantom {{l~{{{\tau }}_{{k,t}}}} {\left( {2{\pi }} \right)}}} \right. \kern-0em} {\left( {2{\pi }} \right)}},\,\,\,\,y\left( {k,t} \right) = {{ - ~{{{\tau }}_{{k,t}}}} \mathord{\left/ {\vphantom {{ - ~{{{\tau }}_{{k,t}}}} {\left( {2{\pi }} \right)}}} \right. \kern-0em} {\left( {2{\pi }} \right)}}, \\ 1 \leqslant k < t \leqslant K. \\ \end{gathered} $Очевидно, существуют следующие обратные выражения к (7):
(8)
$\begin{gathered} {{{\lambda }}_{{k,t}}} = x\left( {k,t} \right) + l~y\left( {k,t} \right), \\ {{{\tau }}_{{k,t}}} = - 2{\pi }~y\left( {k,t} \right),\,\,\,\,{\text{\;}}1 \leqslant k < t \leqslant K. \\ \end{gathered} $В (8) можно подставлять координаты любой пары узлов k-го и t-го спутников. Значения ${{{\lambda }}_{{k,t}}}$ и ${{{\tau }}_{{k,t}}}$ могут выходить за рамки привычного сегмента [0, 2π). Во избежание этого рекомендуется заменить (8) на следующие формулы:
(9)
$\begin{gathered} {{{\lambda }}_{{k,t}}} = {\text{mod}}\left( {2{\pi };x\left( {k,t} \right) + l~y\left( {k,t} \right)} \right), \\ {{{\tau }}_{{k,t}}} = 2{\pi }~{\text{mod}}\left( {1; - y\left( {k,t} \right)} \right), \\ \end{gathered} $Из (7) и (9) вытекает 2-е свойство модели: структура системы спутников и ее модель на широте Земли взаимно однозначно соответствуют друг другу.
Это свойство, как будет показано позже, позволяет находить лучшие структуры просто путем перемещения цепочек спутниковых узлов на (векторной) модели.
Наряду с первыми “шаг-векторами” ${{{\mathbf{r}}}_{0}}$ и ${{{\mathbf{r}}}_{1}}$ из (3), применяются и дальнейшие “шаг–векторы” ${{{\mathbf{r}}}_{j}} = \left( {{{x}_{j}};{{Y}_{j}}} \right),$ $j = \,\,~2$, 3, … , вычисляемые из следующей рекуррентной процедуры, в которой исходными служат ${{{\mathbf{r}}}_{0}}$ и ${{{\mathbf{r}}}_{1}}$:
(10)
${{{\mathbf{r}}}_{{j + 1}}} = {{{\mathbf{r}}}_{{j - 1}}} + E\left( {\left| {{{{{x}_{{j - 1}}}} \mathord{\left/ {\vphantom {{{{x}_{{j - 1}}}} {{{x}_{j}}}}} \right. \kern-0em} {{{x}_{j}}}}} \right|} \right),\,\,\,\,j = 1,2,3, \ldots .$Целочисленная функция $E\left( z \right)$ равна целой части аргумента z.
Как и (4), комбинация с целочисленными множителями ${{W}_{j}}$ и ${{W}_{{j + 1}}}$
(11)
${\mathbf{\Delta r}} = {{W}_{j}}{{{\mathbf{r}}}_{j}} + {{W}_{{j + 1}}}{{{\mathbf{r}}}_{{j + 1}}}$До сих пор для простоты изложения фактически рассматривался “односторонний” обзор, реализуемый на восходящих сторонах орбит. При “двустороннем” обзоре на широте ϕ к картине “восходящих” узлов и следов добавляется точно такая же “нисходящая” картина, но передвинутая на “вектор перехода” ${\mathbf{\rho }}\left( \phi \right) = \left( {x\left( \phi \right);y\left( \phi \right)} \right)$ со следующими координатами [2–4]:
(12)
$\begin{gathered} x\left( \phi \right) = {\pi } - {l \mathord{\left/ {\vphantom {l 2}} \right. \kern-0em} 2} - 2{{\sin }^{{ - 1}}}({{{\text{tg}}\phi } \mathord{\left/ {\vphantom {{{\text{tg}}\phi } {{\text{tg}}i}}} \right. \kern-0em} {{\text{tg}}i}}) + \\ + \,\,l{{\sin }^{{ - 1}}}{{({{\sin \phi } \mathord{\left/ {\vphantom {{\sin \phi } {\sin i}}} \right. \kern-0em} {\sin i}})} \mathord{\left/ {\vphantom {{({{\sin \phi } \mathord{\left/ {\vphantom {{\sin \phi } {\sin i}}} \right. \kern-0em} {\sin i}})} {\pi }}} \right. \kern-0em} {\pi }}{\text{,}} \\ \end{gathered} $(13)
$y\left( \phi \right) = 0.5 - {{\sin }^{{ - 1}}}{{({{\sin \phi } \mathord{\left/ {\vphantom {{\sin \phi } {\sin i}}} \right. \kern-0em} {\sin i}})} \mathord{\left/ {\vphantom {{({{\sin \phi } \mathord{\left/ {\vphantom {{\sin \phi } {\sin i}}} \right. \kern-0em} {\sin i}})} {\pi }}} \right. \kern-0em} {\pi }}.$Смещение узлов t-го спутника относительно узлов k-го спутника фиксируется “вектором смещения” ${\mathbf{\rho }}\left( {k,t,\phi ,V} \right)$ = $\left( {x\left( {k,t,\phi ,V} \right);y\left( {k,t,\phi ,V} \right)} \right)$, определяемым так:
(14)
${\mathbf{\rho }}\left( {k,t,\phi ,V} \right) = {\mathbf{\rho }}\left( {k,t} \right) + V~{\mathbf{\rho }}\left( \phi \right),$0 при смещении: от восходящих узлов k-го спутника к восходящим узлам t-го спутника или от нисходящих узлов k-го спутника к нисходящим узлам t-го спутника,
1 при смещении от восходящих узлов k-го спутника к нисходящим t-го спутника,
–1 при смещении от нисходящих узлов k-го спутника к восходящим t-го спутника.
При двустороннем обзоре для K спутников возникает 2K подмоделей, одна половина которых имеется на восходящих следах, а другая – на нисходящих.
Ряд дополнительных свойств векторной модели содержится в [1–4].
ВЕКТОРНАЯ МОДЕЛЬ ДЛЯ СИСТЕМ СПУТНИКОВ НА ИЗОМАРШРУТНЫХ ОРБИТАХ
Спутники наблюдения Земли обычно выводятся на изомаршрутные орбиты. Далее рассматриваются только системы спутников на изомаршрутных орбитах. Трассы таких орбит повторяется через целое число витков T и целое число суток L. Удобно ввести новую единицу e вместо радианов для измерения долгот на оси абсцисс:
За счет e происходят изменения в формулах предыдущего раздела. Шаг-векторы ${{{\mathbf{r}}}_{j}} = \left( {{{x}_{j}};{{Y}_{j}}} \right)$ заменяются на “большие” шаг-векторы ${{{\mathbf{R}}}_{j}} = \left( {{{X}_{j}};{{Y}_{j}}} \right)$, где абсцисса ${{X}_{j}}$[e] также стала целым числом, как и ордината ${{Y}_{j}}$ [витков], что очень удобно:
(16)
$\begin{gathered} {{X}_{j}} = {{T~{{x}_{j}}} \mathord{\left/ {\vphantom {{T~{{x}_{j}}} {\left( {2\pi } \right)}}} \right. \kern-0em} {\left( {2\pi } \right)}},\,\,\,\,{{X}_{0}} = T,\,\,\,\,{{X}_{1}} = - L, \\ {{{\mathbf{R}}}_{0}} = \left( {T;0} \right),\,\,\,\,{{{\mathbf{R}}}_{1}} = \left( { - L;1} \right); \\ \end{gathered} $(17)
${{{\mathbf{R}}}_{{j + 1}}} = {{{\mathbf{R}}}_{{j - 1}}} + E\left( {\left| {{{{{X}_{{j - 1}}}} \mathord{\left/ {\vphantom {{{{X}_{{j - 1}}}} {{{X}_{j}}}}} \right. \kern-0em} {{{X}_{j}}}}} \right|} \right),\,\,\,\,j = 1,2,3, \ldots ,J,$Комбинация (11) заменяется на $~{\mathbf{\Delta R}} = {{W}_{j}}{{{\mathbf{R}}}_{j}} + $ $~ + \,\,{{W}_{{j + 1}}}{{{\mathbf{R}}}_{{j + 1}}}.$
След $d\left( \phi \right)$ в радианах превращается в след $D\left( \phi \right)$ [e], вычисляемый так:
(19)
$D\left( \phi \right) = B{{\left( {T - L~{\text{cos}}i} \right)} \mathord{\left/ {\vphantom {{\left( {T - L~{\text{cos}}i} \right)} {(2{\pi }{{R}_{{\text{E}}}}}}} \right. \kern-0em} {(2{\pi }{{R}_{{\text{E}}}}}}\sqrt {{{{\cos }}^{2}}\phi - {{{\cos }}^{2}}i} ).$Обозначения долгот $~x\left( {k,t} \right),$ $x\left( \phi \right),$ $x\left( {k,t,\phi ,V} \right)$ сохраняются, но теперь они даны в единицах (15), поэтому формулы (7), (9) и (12) преобразуются к следующим видам:
(20)
$\begin{gathered} x\left( {k,t} \right) = {{\left( {T~{{{\lambda }}_{{k,t}}} + L~{{{\tau }}_{{k,t}}}} \right)} \mathord{\left/ {\vphantom {{\left( {T~{{{\lambda }}_{{k,t}}} + L~{{{\tau }}_{{k,t}}}} \right)} {\left( {2{\pi }} \right)}}} \right. \kern-0em} {\left( {2{\pi }} \right)}}, \\ y\left( {k,t} \right) = {{ - ~{{{\tau }}_{{k,t}}}} \mathord{\left/ {\vphantom {{ - ~{{{\tau }}_{{k,t}}}} {\left( {2{\pi }} \right)}}} \right. \kern-0em} {\left( {2{\pi }} \right)}},\,\,\,\,1 \leqslant k < t \leqslant K, \\ \end{gathered} $(21)
$\begin{gathered} {{{\lambda }}_{{k,t}}} = 2{\pi \;mod}{{\left( {T;x\left( {k,t} \right) + L~y\left( {k,t} \right)} \right)} \mathord{\left/ {\vphantom {{\left( {T;x\left( {k,t} \right) + L~y\left( {k,t} \right)} \right)} T}} \right. \kern-0em} T}, \\ {{{\tau }}_{{k,t}}} = 2{\pi }~{\text{mod}}\left( {1; - y\left( {k,t} \right)} \right), \\ \end{gathered} $(22)
$\begin{gathered} x\left( \phi \right) = {T \mathord{\left/ {\vphantom {T 2}} \right. \kern-0em} 2} - {L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0em} 2} - T{{\sin }^{{ - 1}}}{{({{{\text{tg}}\phi } \mathord{\left/ {\vphantom {{{\text{tg}}\phi } {{\text{tg}}i}}} \right. \kern-0em} {{\text{tg}}i}})} \mathord{\left/ {\vphantom {{({{{\text{tg}}\phi } \mathord{\left/ {\vphantom {{{\text{tg}}\phi } {{\text{tg}}i}}} \right. \kern-0em} {{\text{tg}}i}})} {\pi }}} \right. \kern-0em} {\pi }} + \\ + \,\,L{{\sin }^{{ - 1}}}{{({{\sin \phi } \mathord{\left/ {\vphantom {{\sin \phi } {\sin i}}} \right. \kern-0em} {\sin i}})} \mathord{\left/ {\vphantom {{({{\sin \phi } \mathord{\left/ {\vphantom {{\sin \phi } {\sin i}}} \right. \kern-0em} {\sin i}})} {\pi }}} \right. \kern-0em} {\pi }}{\text{.}} \\ \end{gathered} $Вместо ${{{\lambda }}_{{k,t}}}$ и ${{{\tau }}_{{k,t}}}$ в радианах можно применять те же параметры, но в градусах, обозначая их ${\lambda }_{{k,t}}^{^\circ }$ и ${\tau }_{{k,t}}^{^\circ }$; формулы (20) и (21) изменяются так:
(23)
$\begin{gathered} x\left( {k,t} \right) = {{(T~{\lambda }_{{k,t}}^{^\circ } + L{\text{\;}}{\tau }_{{k,t}}^{^\circ })} \mathord{\left/ {\vphantom {{(T~{\lambda }_{{k,t}}^{^\circ } + L{\text{\;}}{\tau }_{{k,t}}^{^\circ })} {360}}} \right. \kern-0em} {360}}, \\ y\left( {k,t} \right) = {{ - {\tau }_{{k,t}}^{^\circ }} \mathord{\left/ {\vphantom {{ - {\tau }_{{k,t}}^{^\circ }} {360}}} \right. \kern-0em} {360}},\,\,\,\,1 \leqslant k < t \leqslant K; \\ \end{gathered} $(24)
$\begin{gathered} {\lambda }_{{k,t}}^{^\circ } = 360~{\text{mod}}{{\left( {T;x\left( {k,t} \right) + L~y\left( {k,t} \right)} \right)} \mathord{\left/ {\vphantom {{\left( {T;x\left( {k,t} \right) + L~y\left( {k,t} \right)} \right)} T}} \right. \kern-0em} T}; \\ {\tau }_{{k,t}}^{^\circ } = 360~{\text{mod}}\left( {1; - y\left( {k,t} \right)} \right). \\ \end{gathered} $Для подстановки в формулу (14) координаты векторов ${\mathbf{\rho }}\left( {k,t} \right)$ определяются из пар формул (20) или (23), а координаты$~{\mathbf{\rho }}\left( \phi \right)$ – из (22) и (13).
АЛГОРИТМ РАСЧЕТА ПЕРЕРЫВОВ ОБЗОРА И ИХ ЧАСТОТ НА ПОЯСЕ ШИРОТ ЗЕМЛИ
Расчет перерывов производится по подмоделям на всех восходящих и нисходящих (если обзор двусторонний) следах спутников заданной системы.
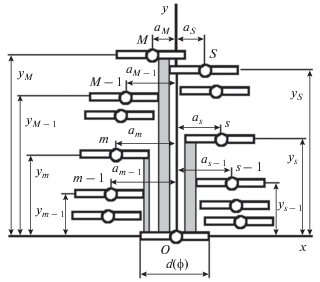
На рис. 2 дан вид подмодели для произвольной широты Земли [4]. Она состоит из узлов и следов над следом очередного k-го спутника, становящегося “базовым”. В ней присутствуют только те узлы, следы в которых образуют столбики перерывов над “базовым” следом. “Базовый” узел стал началом координат подмодели. Различаются два набора узлов: левый, состоящий из узлов слева от оси ординат, и правый – из узлов правее той же оси. Узлы левого набора фиксируем номерами 1, 2, … , m, … , M, а правого – 1, 2, …, s, …, S. Абсолютные величины абсцисс узлов левого набора обозначим ${{a}_{m}}$, а правого – ${{a}_{s}}$. Ординаты узлов: ${{y}_{m}}$ и ${{y}_{s}}.$
Для обоих наборов узлов подмодели выполняются следующие условия:
1) абсолютные величины абсцисс обязаны быть не больше длины следа (19):
2) с ростом номеров узлы приближаются к оси ординат и повышаются:
(26)
$\begin{gathered} {{a}_{m}} > {{a}_{{m + 1}}}\,\,\,\,{\text{и}}\,\,\,\,~{{y}_{m}} < {{y}_{{m + 1~}}}, \\ {{a}_{s}} > {{a}_{{s + 1}}}\,\,\,\,~{\text{и}}\,\,\,\,{{y}_{s}} < {{y}_{{s + 1}}}; \\ \end{gathered} $3) для высших узлов с номерами $M$ (левый набор) и $S$ (правый набор)
4) если $~{{y}_{M}} > {{y}_{S}}$, то для узлов с номерами $m \leqslant M - 1~$ и $s \leqslant S$
а если $~{{y}_{M}} < $ ${{y}_{S}}$, то данное условие реализуется для $m \leqslant M~$ и $s \leqslant S - 1$; наконец, при $~{{y}_{M}} = ~{{y}_{S}}$ то же самое условие действует для $m \leqslant M - 1~$ и $~s \leqslant S - $1.Для построения подмодели на следе k-го спутника нужно перебирать восходящие и нисходящие узлы спутников с номерами t = 1, 2, …, K, включая и k-й. Из них отбираются наборы узлов подмодели, удовлетворяющие условиям (25)–(28).
Восходящие (нисходящие) узлы t-го спутника, выделяемые для подмодели k-го спутника, задаются “бета-векторами” $~{{{\mathbf{\beta }}}_{{j,p}}} = \left( {{{x}_{{j,p}}};{{y}_{{j,p}}}} \right)$, вычисляемыми в процедуре, напоминающей расчет шаг-векторов, которые можно считать “альфа-векторами”. Индекс $j$ – номер этапа процедуры, $p$ – номер подэтапа внутри j-го этапа.
На рис. 3 показано построение последовательности бета-векторов [4]. Первыми выделяются ${{{\mathbf{\beta }}}_{{0,0}}}$ и ${{{\mathbf{\beta }}}_{{1,0}}}$, задающие узлы, ближайшие к началу координат подмодели слева сверху и справа сверху. Вначале находим промежуточный вектор ${\mathbf{\gamma }}$ = = (${{x}_{\gamma }}$; ${{y}_{\gamma }})$:
(29)
${\mathbf{\gamma }} = ~~{\mathbf{\rho }}(k,t,\phi ,V)~\,\, - \,\,U(y(k,t,\phi ,V)\,\,--\,\,~1~)~{{{\mathbf{R}}}_{1}}$Используя ${\mathbf{\gamma }}$ и шаг-вектор ${{{\mathbf{R}}}_{0}}$ из (16), определяем первые бета-векторы:
(30)
${{{\mathbf{\beta }}}_{{0,0}}} = ~\,{\mathbf{\gamma }} - U({{{{x}_{\gamma }}} \mathord{\left/ {\vphantom {{{{x}_{\gamma }}} {\left( T \right)}}} \right. \kern-0em} {\left( T \right)}}){{{\mathbf{R}}}_{0}},\,\,\,\,{{{\mathbf{\beta }}}_{{1,0}}} = {{{\mathbf{\beta }}}_{{0,0}}}~ + {{{\mathbf{R}}}_{0}}.$Дальнейшие бета-векторы определяются рекуррентно по этапам и подэтапам, используя шаг-векторы ${{{\mathbf{R}}}_{1}},~{{{\mathbf{R}}}_{2}},~ \ldots ~$, вычисленные в процедуре (17):
(31)
$\begin{gathered} {{{\mathbf{\beta }}}_{{1,p}}} = ~\,\,{{{\mathbf{\beta }}}_{{1,0}}} + ~p~{{{\mathbf{R}}}_{1}},\,\,\,\,p = 1,2, \ldots ,E\left( {\left| {{{{{x}_{{1,0~}}}} \mathord{\left/ {\vphantom {{{{x}_{{1,0~}}}} {{{X}_{1}}}}} \right. \kern-0em} {{{X}_{1}}}}~} \right|} \right), \\ {{{\mathbf{\beta }}}_{{2,0}}} = ~\,\,{{{\mathbf{\beta }}}_{{1,0}}} + \left( {~E\left( {\left| {{{{{x}_{{1,0~}}}} \mathord{\left/ {\vphantom {{{{x}_{{1,0~}}}} {{{X}_{1}}}}} \right. \kern-0em} {{{X}_{1}}}}~} \right|} \right) + 1} \right){{{\mathbf{R}}}_{1}}; \\ {{{\mathbf{\beta }}}_{{2,p}}} = \,\,~{{{\mathbf{\beta }}}_{{2,0}}} + ~p~{{{\mathbf{R}}}_{2}},~\,\,\,\,~p = 1,2, \ldots ,E\left( {\left| {{{{{x}_{{2,0~}}}} \mathord{\left/ {\vphantom {{{{x}_{{2,0~}}}} {{{X}_{2}}}}} \right. \kern-0em} {{{X}_{2}}}}~} \right|} \right), \\ {{{\mathbf{\beta }}}_{{3,0}}} = \,\,~{{{\mathbf{\beta }}}_{{2,0}}} + \left( {~E\left( {\left| {{{{{x}_{{2,0~}}}} \mathord{\left/ {\vphantom {{{{x}_{{2,0~}}}} {{{X}_{2}}}}} \right. \kern-0em} {{{X}_{2}}}}~} \right|} \right) + 1} \right){{{\mathbf{R}}}_{2}}; \\ .................................................................. \\ {{{\mathbf{\beta }}}_{{j,p}}} = \,\,~{{{\mathbf{\beta }}}_{{j,0}}} + ~p~{{{\mathbf{R}}}_{j}},~\,\,\,\,~p = 1,2, \ldots ,E(\left| {{{{{x}_{{j,0~}}}} \mathord{\left/ {\vphantom {{{{x}_{{j,0~}}}} {{{X}_{j}}}}} \right. \kern-0em} {{{X}_{j}}}}~} \right|), \\ {{{\mathbf{\beta }}}_{{j + 1,0}}} = ~\,\,{{{\mathbf{\beta }}}_{{j,0}}} + \left( {~E\left( {\left| {{{{{x}_{{j,0~}}}} \mathord{\left/ {\vphantom {{{{x}_{{j,0~}}}} {{{X}_{j}}}}} \right. \kern-0em} {{{X}_{j}}}}~} \right|} \right) + 1} \right){{{\mathbf{R}}}_{j}}. \\ \end{gathered} $$E\left( z \right)$ – целая часть z. Ввиду (18) и (27), последним становится “нулевой” вектор $\left( {j + 1} \right)$-го этапа, вычисляемый после наступления любого из следующих условий:
(32)
$j = J~\,\,\,\,{\text{или}}\,\,\,\,~\left| {{{X}_{j}}} \right| \leqslant \,\,~D\left( \phi \right) < \left| {{{X}_{{j - 1}}}} \right|,$Как только найден очередной бета-вектор, нужно, используя условия (25)–(28), попытаться встроить его узел в левый или правый набор узлов, сформированный к данному моменту. При этом могут быть удалены некоторые из прежних узлов.
Если хоть в одной из подмоделей для широты ϕ не выполнено условие (27), то данная система спутников не обеспечивает сплошной обзор этой широты.
Вслед за событием пересечения широты ϕ полосой обзора k-го спутника на восходящей (нисходящей) стороне его орбиты, возникают перерывы обзора, которые видны на восходящей (нисходящей) подмодели, отображающей результаты этого события. Перерывы – это ординаты узлов подмодели, а их частоты вычисляются по формулам, приведенным ниже. Они выведены по рис. 2 с учетом условий (25)–(28) и с добавлением в подмоделях слева и справа условных узлов с ${{a}_{0}} = D\left( \phi \right)$ и ${{y}_{0}} = 0.$
Если наивысшим являлся узел M левого набора, то частота ${{f}_{M}}$ его перерыва ${{y}_{M}}$
(33)
${{f}_{M}} = {{\left( {{{a}_{{M - 1}}} + {{a}_{S}} - D\left( \phi \right)} \right)} \mathord{\left/ {\vphantom {{\left( {{{a}_{{M - 1}}} + {{a}_{S}} - D\left( \phi \right)} \right)} {D\left( \phi \right)}}} \right. \kern-0em} {D\left( \phi \right)}}.$Частоты ${{f}_{m}}$ и ${{f}_{s}}$ перерывов ${{y}_{m}}$ и ${{y}_{s}}$ вычисляются по формулам
(34)
$\begin{gathered} {{f}_{m}} = {{\left( {{{a}_{{m - 1}}} - {{a}_{m}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{a}_{{m - 1}}} - {{a}_{m}}} \right)} {D\left( \phi \right)}}} \right. \kern-0em} {D\left( \phi \right)}} \\ {\text{для}}\,\,\,\,m = 1,2, \ldots ,M - 1; \\ \end{gathered} $(35)
$\begin{gathered} {{f}_{s}} = {{\left( {{{a}_{{s - 1}}} - {{a}_{s}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{a}_{{s - 1}}} - {{a}_{s}}} \right)} {D\left( \phi \right)}}} \right. \kern-0em} {D\left( \phi \right)}} \\ {\text{для}}\,\,\,\,s = 1,2, \ldots ,S. \\ \end{gathered} $Если же наивысшим был узел $S$ правого набора, то в (33)–(35) происходят очевидные перемены. При ${{y}_{M}} = {{y}_{S}}$ частота этого (наибольшего) перерыва равна:
(36)
${{f}_{M}} = {{f}_{S}} = {{\left( {{{a}_{{M - 1}}} + {{a}_{{S - 1}}} - D\left( \phi \right)} \right)} \mathord{\left/ {\vphantom {{\left( {{{a}_{{M - 1}}} + {{a}_{{S - 1}}} - D\left( \phi \right)} \right)} {D\left( \phi \right)}}} \right. \kern-0em} {D\left( \phi \right)}}.$Ординаты подмоделей на всех широтах ϕ объединяем в перечень перерывов обзора ${{t}_{1}} < {{t}_{2}} < \ldots < {{t}_{n}} < \ldots < {{t}_{{{{n}_{{{\text{max}}}}}}}}$. Их частоты ${{f}_{1}}$, ${{f}_{2}}$, …, ${{f}_{n}}$, …, ${{f}_{{{{n}_{{{\text{max}}}}}}}}$ определяются, исходя из равных вероятностей событий пересечения широты φ всеми спутниками.
При двустороннем обзоре широты $\phi $ частота ${{f}_{n}}\left( \phi \right)$ перерыва ${{t}_{n}}$ для системы из K спутников вычисляется, как средняя от частот ${{f}_{{n,k}}}\left( {\phi ,k,A} \right)$ и ${{f}_{{n,k}}}\left( {\phi ,k,D} \right)$, найденных по всем восходящим (A) и нисходящим (D) подмоделям:
(37)
$\begin{gathered} {{f}_{n}}\left( \phi \right) = \sum\limits_{k = 1}^K {{{({{f}_{{n,k}}}\left( {\phi ,k,A} \right) + {{f}_{{n,k}}}\left( {\phi ,k,D} \right))} \mathord{\left/ {\vphantom {{({{f}_{{n,k}}}\left( {\phi ,k,A} \right) + {{f}_{{n,k}}}\left( {\phi ,k,D} \right))} {\left( {2K} \right)}}} \right. \kern-0em} {\left( {2K} \right)}}} , \\ n = 1,~2, \ldots ,~{{n}_{{{\text{max}}}}}. \\ \end{gathered} $Для K-спутникового одностороннего обзора эта формула, естественно, упрощается:
(38)
${{f}_{n}}\left( \phi \right) = \sum\limits_{k = 1}^K {{{({{f}_{{n,k}}}\left( {\phi ,k} \right)} \mathord{\left/ {\vphantom {{({{f}_{{n,k}}}\left( {\phi ,k} \right)} K}} \right. \kern-0em} K}} ,$От относительных (безразмерных) частот ${{f}_{n}}\left( \phi \right)$ переходим к частотам ${{g}_{n}}\left( \phi \right)$ перерывов ${{t}_{n}}$ за виток (орбиты), т.е. за драконический период ${{T}_{{dr}}}$:
(39)
$\begin{gathered} {{g}_{n}}\left( \phi \right) = {{{{f}_{n}}\left( \phi \right)} \mathord{\left/ {\vphantom {{{{f}_{n}}\left( \phi \right)} {{{t}_{{{\text{mid}}}}}}}} \right. \kern-0em} {{{t}_{{{\text{mid}}}}}}}\left( \phi \right)\,\,\left[ {{1 \mathord{\left/ {\vphantom {1 {{\text{виток}}}}} \right. \kern-0em} {{\text{виток}}}}} \right],~ \\ {{t}_{{{\text{mid}}}}}\left( \phi \right) = \sum\limits_{n = 1}^{{{n}_{{{\text{max}}}}}} {{{t}_{n}}~{{f}_{n}}\left( \phi \right)} \,\,\left[ {{\text{витков}}} \right], \\ \end{gathered} $Для расчета частот ${{g}_{n}}$ на поясе широт [${{\phi }_{{{\text{min}}}}},~{{\phi }_{{{\text{max}}}}}$] нужно сначала разделить его на M малых поясов $\left[ {{{\phi }_{{{\text{min}}}}} + \left( {m - 1} \right){\Delta }\phi ,{{\phi }_{{{\text{min}}}}} + m~{\Delta }\phi } \right]$, $m = 1,~2,~ \ldots ,~M$ с шагом ${\Delta }\phi = {{\left( {{{\phi }_{{{\text{max}}}}} - {{\phi }_{{{\text{min}}}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{\phi }_{{{\text{max}}}}} - {{\phi }_{{{\text{min}}}}}} \right)} M}} \right. \kern-0em} M}$. Найдя по формулам (33)–(35) частоты ${{g}_{n}}({{\phi }_{m}}$) для средних широт малых поясов ${{\phi }_{m}} = {{\phi }_{{{\text{min}}}}} + \left( {m - 0.5} \right){\Delta }\phi $, вычисляются искомые частоты:
(40)
$~{{g}_{n}} = {{\sum\limits_{m = 1}^M {{{f}_{n}}\left( {{{\phi }_{m}}} \right)} ~\cos {{\phi }_{m}}~} \mathord{\left/ {\vphantom {{\sum\limits_{m = 1}^M {{{f}_{n}}\left( {{{\phi }_{m}}} \right)} ~\cos {{\phi }_{m}}~} {\sum\limits_{m = 1}^M {\cos {{\phi }_{m}}} }}} \right. \kern-0em} {\sum\limits_{m = 1}^M {\cos {{\phi }_{m}}} }}~\,\,\left[ {{1 \mathord{\left/ {\vphantom {1 {{\text{виток}}}}} \right. \kern-0em} {{\text{виток}}}}} \right].$Для получения частот $g_{n}^{*}$ за сутки нужно ${{g}_{n}}$ умножить на 24 и разделить на ${{T}_{{dr}}}$ в часах:
(41)
$g_{n}^{*} = {{24~{{g}_{n}}} \mathord{\left/ {\vphantom {{24~{{g}_{n}}} {{{T}_{{dr}}}{\text{\;}}}}} \right. \kern-0em} {{{T}_{{dr}}}{\text{\;}}}}\,\,\left[ {{1 \mathord{\left/ {\vphantom {1 {{\text{сутки}}}}} \right. \kern-0em} {{\text{сутки}}}}} \right].$Наконец, находим средний период ${{t}_{{{\text{mid}}}}}$ и частоты ${{f}_{n}}$ перерывов ${{t}_{n}}$ на поясе широт:
(42)
${{t}_{{{\text{mid}}}}} = {1 \mathord{\left/ {\vphantom {1 {\sum\limits_{n = 1}^{{{n}_{{{\text{max}}}}}} {{{g}_{n}}} }}} \right. \kern-0em} {\sum\limits_{n = 1}^{{{n}_{{{\text{max}}}}}} {{{g}_{n}}} }},\,\,\,\,{{f}_{n}} = {{g}_{n}}~{{t}_{{{\text{mid}}}}},\,\,\,\,n = 1,~2,~ \ldots ,~{{n}_{{{\text{max}}}}}.$Заметим, что в [2–4] для расчета ${{f}_{n}}$ складывались частоты ${{f}_{n}}\left( \phi \right)$ по широтам пояса, что было неправильно, хотя и не приводило к серьезным ошибкам.
На основе описанного алгоритма разработана компьютерная программа расчета перерывов обзора и их частот на любом поясе широт Земли для системы из любого числа спутников с любой структурой. Быстродействие программы можно оценить по следующим примерам расчетов на простом домашнем компьютере Acer, Aspire 23820 для системы из K спутников МЕТЕОР-М с полосами обзора 2900 км на поясе [0°,80°]:
A) шаг ${\Delta }\phi ^\circ {\text{\;}}$ = 1°, время расчета: 0.05 с при K = 4, около 1 с при K = 100, 70 c при K = 1000;
B) ${\Delta }\phi ^\circ $ = 0.1°, время расчета: 0.35 с при K = 4, 11 с при K = 100, 16 мин при K = 1000.
Результаты при ${\Delta }\phi $ = 1° и 0.1° почти совпадают, поэтому рекомендуется шаг ${\Delta }\phi $ = 1°.
КРИТЕРИИ ЭФФЕКТИВНОСТИ ПЕРИОДИЧЕСКОГО ОБЗОРА
Для применения набора перерывов ${{t}_{n}}$ и их частот ${{g}_{n}}$ и ${{f}_{n}}$, нужно предложить и обосновать критерии в виде функций от этого набора, оценивающих качество обзора.
Простейший критерий – максимальный перерыв обзора ${{T}_{{{\text{max}}}}}$ = ${{t}_{{{{n}_{{{\text{max}}}}}}}}$, широко применяемый из-за простоты его расчета. Он сразу выделяется из набора ${{t}_{n}}$, но его частота, как будет показано далее, столь мала, что он не является полноценным показателем. Дополнительно рассматривается T99 = ${{t}_{m}}$ при следующем условии:
(43)
$\sum\limits_{n = 1}^{m - 1} {{{f}_{n}}} < 0.99\,\,\,\,{\text{и}}\,\,\,\,\sum\limits_{n = 1}^m {{{f}_{n}}} \geqslant 0.99.$При оценке работы спутников метеорологии и для обнаружения очагов лесных пожаров естественным критерием является $F\left( a \right)$ – “частота ошибок” на “рабочих интервалах” a [часов]. Метеоспутники должны всюду обеспечивать съемки на регулярно чередующихся интервалах a, привязанных к синоптическим срокам. Пожар нужно обнаружить не более, чем за a [часов] с момента возгорания. В обоих случаях частота ошибок, т.е. пропуска съемок на интервалах a, определяется одинаково:
(44)
$\begin{gathered} F\left( a \right) = \sum\limits_{n = m}^{{{n}_{{{\text{max}}}}}} {\left( {{{t}_{n}} - {a \mathord{\left/ {\vphantom {a {{{T}_{{dr}}}}}} \right. \kern-0em} {{{T}_{{dr}}}}}} \right)~} {{g}_{n}},\,\,\,\,{{t}_{{m~}}}{{T}_{{dr}}} > a, \\ {{t}_{{m - 1~}}}{{T}_{{dr}}} \leqslant a,\,\,\,\,{{T}_{{dr}}}\,\,{\text{и}}\,\,a\,\,{\text{даны}}\,\,{\text{в}}\,\,{\text{часах}}\,\,[h]. \\ \end{gathered} $Еще один критерий – “эффективный период” ${{T}_{{{\text{ef}}}}}$ $\left[ {{\text{витков}}} \right]$ из [2–4]. Это условно постоянный перерыв на поясе широт. Пусть потери $u\left( {{{t}_{n}}} \right)$ из-за перерывов ${{t}_{n}}$ равны
${{T}_{{{\text{ef}}}}}$ вычисляется из условия равенства удельных потерь для набора перерывов ${{t}_{n}}$, $n = 1,~2,~ \ldots ,~{{n}_{{{\text{max}}}}},$ и для одного ${{T}_{{{\text{ef}}}}}$. Находим и приравниваем удельные потери за виток (орбиты) в обоих случаях: $c\sum\nolimits_{n = 1}^{{{n}_{{{\text{max}}}}}} {t_{n}^{b}{{g}_{n}}} = c~T_{{{\text{ef}}}}^{{b - 1}}$. Решаем это уравнение:
(46)
${{T}_{{{\text{ef}}}}} = \sqrt[{b - 1}]{{\sum\limits_{n = 1}^{{{n}_{{{\text{max}}}}}} {t_{n}^{b}{{g}_{n}}} }}.$В [2–4] считалось, что $b$ = 2. Однако, рассмотрим задачу мониторинга развития чрезвычайной ситуации (ЧС). При росте ущерба во времени (от начала ЧС) в степени $h$
(47)
$\begin{gathered} u\left( {{{t}_{n}}} \right) = v\int\limits_0^{{{t}_{n}}} {dx} \int\limits_x^{{{t}_{n}}} {{{{\left( {{{t}_{n}} - x} \right)}}^{h}}~dy} = \\ = {{v~t_{n}^{{h + 2}}} \mathord{\left/ {\vphantom {{v~t_{n}^{{h + 2}}} {\left( {\left( {h + 1} \right)\left( {h + 2} \right)} \right)}}} \right. \kern-0em} {\left( {\left( {h + 1} \right)\left( {h + 2} \right)} \right)}}; \\ v,h - \,\,{\text{константы}}. \\ \end{gathered} $Всегда $h > 0$, а чаще $h > 1$, поэтому здесь оказалось $b \gg 2$. Значит, выбор $b$ в (46) требует индивидуального анализа для разных задач наблюдения Земли.
ВЫБОР СТРУКТУРЫ СИСТЕМЫ ИЗ 4-Х МЕТЕОСПУТНИКОВ ТИПА МЕТЕОР-М
Применим векторную модель для выбора структуры системы из 4-х спутников типа МЕТЕОР-М [6] для регулярного обзора Земли на рабочих интервалах 3 и 3.5 часа.
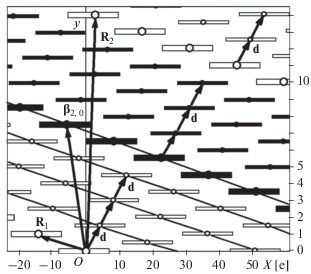
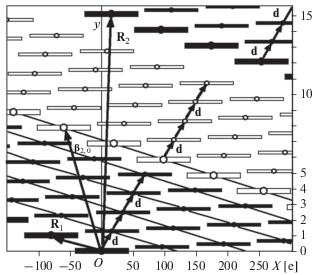
На рис. 4 дана модель системы для экватора. Обзор двусторонний. Восходящие узлы и следы белые, нисходящие – черные. Узлы и следы 1-го спутника крупные, остальные – мелкие. Позиции узлов соответствуют изомаршрутной орбите с периодом повторения T= 199 [витков] и L = 14 [суток].
Из (15), (16) и (17) на рис. 4: ${{{\mathbf{R}}}_{0}} = \left( {199e;0} \right)$, ${{{\mathbf{R}}}_{1}} = \left( { - 14e;1} \right)$, $~{{{\mathbf{R}}}_{2}} = \left( {3e;14} \right)$.
Из (14), (20), (22), (13) при k = t = 1, ϕ = 0, V = 1: ${\mathbf{\rho }}\left( {1,~1,~0,~1} \right) = {\mathbf{\rho }}\left( 0 \right) = \left( {{T \mathord{\left/ {\vphantom {T 2}} \right. \kern-0em} 2} - {L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0em} 2};~0.5} \right).$
Из (29), (30):
(48)
$\begin{gathered} {\mathbf{\gamma }} = {\mathbf{\rho }}\left( 0 \right),\,\,\,\,{{{\mathbf{\beta }}}_{{1,0}}} = {\mathbf{\rho }}\left( 0 \right) = \\ = \left( {{T \mathord{\left/ {\vphantom {T 2}} \right. \kern-0em} 2} - {L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0em} 2};0.5} \right) = \left( {92.5e;0.5} \right). \\ \end{gathered} $Из (31):
(49)
$\begin{gathered} {{{\mathbf{\beta }}}_{{2,0}}} = {{{\mathbf{\beta }}}_{{1,0}}} + Q~{{{\mathbf{R}}}_{1}} = \left( { - 5.5e;~7.5} \right), \\ {\text{где}}\,\,Q = {\text{E}}\left( {\left| {{{{{x}_{{1,0}}}} \mathord{\left/ {\vphantom {{{{x}_{{1,0}}}} {{{X}_{1}}}}} \right. \kern-0em} {{{X}_{1}}}}} \right|} \right) + 1 = 7. \\ \end{gathered} $Съемочный прибор – радиометр МСУ-МР с полосой захвата B = 2900 км [6]. Из (19) при наклонении i = 98.8° вычисляем длину следов на рис. 4: $D\left( {0^\circ } \right) = 14.8e.$
Положения цепочек узлов (со следами) 1‑го спутника на рис. 4 менять нельзя: они зафиксированы по параметрам орбиты. Остальные цепочки можно перемещать параллельно самим себе. В результате, вследствие 2-го свойства модели, возникают различные варианты спутниковых структур, из которых нужно выбрать лучшую по критерию частоты ошибок $F\left( a \right)$ на рабочем интервале $~a$.
Для минимизации перерывов обзора, равных, ввиду 1-го свойства модели, вертикальным интервалам между следами, нужно расположить цепочки восходящих узлов спутников 2, 3, 4 равномерно между восходящей и нисходящей цепочкой узлов спутника 1. Возникает набор моделей, а потому и спутниковых структур, называемых “эквидистантными”. Они получаются при смещении цепочек узлов спутников 2, 3, 4 по наклонным линиям на рис. 4, находящимся на равных расстояниях друг от друга и от нисходящей цепочки спутника 1. Цепочки узлов спутников 2, 3, 4 задаются векторами
“Эквидистантная” модель имеет равные сдвиги Δx и Δy между соседними узлами:
(50)
$\begin{gathered} {{{\lambda }}_{{1,k}}} = \left( {k - 1} \right){\Delta \lambda ,}\,\,\,\,{{{\tau }}_{{1,k}}} = \left( {k - 1} \right){\Delta \tau }, \\ k = 1,2, \ldots ,K. \\ \end{gathered} $Подставляя координаты вектора ${\mathbf{d}}$ в (24) и учитывая (48) и (49), получаем:
${\Delta \tau } = 2{\pi \;mod}\left( {1; - 0.5 + Q + m} \right) = q$, $q$ – любое число от 0 до $2{\pi }$, т.е. $0^\circ \leqslant {\Delta \tau }^\circ \leqslant 360^\circ $. Найденный на основе модели, т.е. теоретически, сдвиг ${\Delta \lambda }$ соответствует практике формирования систем метеоспутников. Для 4-х спутников он равен 45°.
Осталось найти наилучший сдвиг по фазе 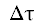 , при котором достигается минимум критерия (44) частоты ошибок обзора $F\left( a \right)$ на рабочих интервалах $a$ = 3h и $a~$ = 3.5h.
, при котором достигается минимум критерия (44) частоты ошибок обзора $F\left( a \right)$ на рабочих интервалах $a$ = 3h и $a~$ = 3.5h.
Используя компьютерную программу расчета перерывов обзора и их частот для системы из 4‑х спутников типа МЕТЕОР-М при всех ${\Delta \tau }$ от $0^\circ $ до 360° и вычисляя затем значения $F\left( {3h} \right)$ и $F\left( {3.5h} \right)$, а также ${{T}_{{{\text{max}}}}}$, T99 из (43) и ${{T}_{{{\text{ef}}}}}$ из (46) при $b$ = 3, построены графики на рис. 5. Расчеты велись на поясе широт [0°, 80°], так как на более высоких широтах безошибочный обзор гарантирован. Шаг по широтам ${\Delta }\phi ^\circ $ = 0.1°.
Рис. 5.
Графики критериев эффективности для системы МЕТЕОР-М в зависимости от сдвига фаз $\Delta \tau ^\circ $ . Значения ${{T}_{{{\text{max}}}}}$, $T99$, ${{T}_{{{\text{ef}}}}}$ даны в витках орбиты.
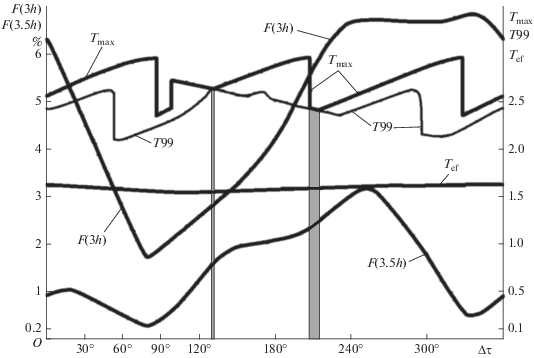
На графиках $F\left( {3h} \right)$ и $F\left( {3.5h} \right)$ наименьшие частоты 1.7 и 0.27% возникли при сдвиге $\sim $80°, который и рекомендуется для системы из 4-х спутников типа МЕТЕОР-М.
Графики ${{T}_{{{\text{max}}}}}$ и T99 отличаются друг от друга всюду, кроме узких (зачерненных на рис. 5) диапазонов 130°–131° и 208°–215°, где они совпадают. Ввиду (43), это означает, что частота перерывов ${{T}_{{{\text{max}}}}}$ почти всегда меньше 1%. Поэтому ${{T}_{{{\text{max}}}}}$ не следует применять для оценки качества обзора. К тому же ${{T}_{{{\text{max}}}}}$ неудобен из-за того, что его минимумы соседствуют с максимумами после скачкообразных падений графика.
Вывод о непригодности ${{T}_{{{\text{max}}}}}$ вытекает и из табл. 1, где даны относительные частоты диапазонов перерывов обзора для систем со следующими сдвигами фаз: 80°, что соответствует минимуму $F\left( {3h} \right)$; 90°, что чуть правее минимума для ${{T}_{{{\text{max}}}}}$.
Таблица 1.
Относительные частоты диапазонов перерывов, %, для системы из 4-х спутников типа МЕТЕОР-М, $\Delta \tau ^\circ $ – сдвиг фаз, град
| $\Delta \tau ^\circ $ | Диапазоны перерывов обзора, витки орбиты | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0–0.1 | 0.1–0.2 | 0.2–0.3 | 0.3–0.4 | 0.4–0.5 | 0.5–0.6 | 0.6–0.7 | 0.7–0.8 | 0.8–0.9 | 0.9–1.0 | |
| 80° | 2.23 | 3.30 | 6.86 | 2.87 | 4.08 | 2.30 | 0.05 | 18.54 | 0.02 | 17.23 |
| 90° | 2.23 | 1.73 | 8.81 | 3.38 | 3.13 | 2.33 | 0.41 | 16.93 | 0.42 | 17.31 |
| $\Delta \tau ^\circ $ | Диапазоны перерывов обзора, витки орбиты | |||||||||
| 1.0–1.1 | 1.1–1.2 | 1.2–1.3 | 1.3–1.4 | 1.4–1.5 | 1.5–1.6 | 1.6–1.7 | 1.7–1.8 | 1.8–1.9 | 1.9–2.0 | |
| 80° | 0.33 | 0.99 | 1.82 | 1.50 | 0.11 | – | – | 30.41 | 1.29 | 1.87 |
| 90° | 0.17 | 0.62 | 1.32 | 2.05 | 1.05 | 0.01 | – | 31.25 | 0.40 | 1.41 |
| $\Delta \tau ^\circ $ | Диапазоны перерывов обзора, витки орбиты | |||||||||
| 2.0–2.1 | 2.1–2.2 | 2.2–2.3 | 2.3–2.4 | 2.4–2.5 | 2.5–2.6 | 2.6–2.7 | 2.7–2.8 | 2.8–2.9 | 2.9–3.0 | |
| 80° | 2.00 | 1.51 | 0.59 | – | – | – | – | – | 0.05 | 0.05 |
| 90° | 1.85 | 1.75 | 1.17 | 0.27 | – | – | – | – | – | – |
Сравнение по диапазонам вызвано тем, что общее число перерывов слишком велико для записи всех их в таблице: 3466 для сдвига 80°, и 3450 – для 90°.
Для сдвига 80° есть крупные перерывы 2.8–3.0 витка, но их общая частота ничтожна: 0.01%, а для сдвига 90° частота наибольшего диапазона 2.3–2.4 витка равна 0.27%; следовательно, в обоих случаях частоты ${{T}_{{{\text{max}}}}}$ пренебрежимо малы.
Частоты перерывов свыше 2.2 и 2.0 витков для сдвига 80° равны 0.69 и 4.20%, а для 90° – 1.44 и 5.04%. Значит, большие перерывы для сдвига 90° возникают чаще, чем для 80°, поэтому главный критерий $F\left( a \right)$ минимизируется при сдвиге 80°.
По графику критерия ${{T}_{{{\text{ef}}}}}$ видно, что в данном случае он слабо зависит от сдвига фаз. Его важная роль проявится в следующей статье по теме векторной модели.
ВЫБОР СТРУКТУРЫ СИСТЕМЫ ДЛЯ ОБНАРУЖЕНИЯ ОЧАГОВ ЛЕСНЫХ ПОЖАРОВ
Рассмотрим пример применения векторной модели обзора Земли для выбора структуры системы из 5 и 6 спутников с инфракрасными (ИК) радиометрами с полосами захвата 2000 км, впервые испытанными на спутнике КАНОПУС-В-ИК [7].
Назначение ИК-радиометров – обнаружение очагов лесных пожаров (ООЛП) на поясе широт [43°, 70°], соответствующем основной территории лесов России. Время обнаружения не должно превышать 2 часа, поэтому критерием для выбора спутниковой структуры служит частота ошибок $F\left( {2h} \right)$ на рабочем интервале $~a$ = 2 часа.
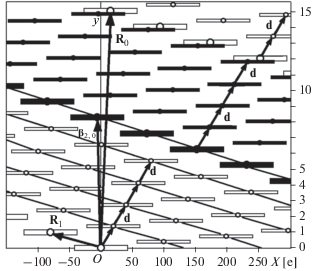
На рис. 6 и 7 даны 2 варианта моделей системы для широты ϕ = 43°. Обзор двусторонний. Восходящие узлы и следы белые, нисходящие черные. Для 1-го спутника узлы и следы крупные, остальные – мелкие. Позиции узлов соответствуют изомаршрутной орбите с периодом повторения T = = 1200 [витков] и L = 79 [суток].
На рис. 6 начало координат помещено в восходящий узел 1-го спутника, а на рис. 7 – в нисходящий узел того же спутника. Число спутников K = 5. Полоса захвата, найденная по формуле (19) при наклонении i = 97.4°, равна $D(43^\circ ) = 36.95e.$
Как и для системы МЕТЕОР-М, действует принцип равномерного распределения цепочек узлов 2-го – K-го спутников между цепочками узлов 1-го спутника и возникают “эквидистантные” модели. Однако, ввиду того, что модели для ООЛП строятся не на экваторе, а на нижней широте пояса ϕ = 43° = 0.7505 [рад], появляются 2 типа эквидистантных моделей (и структур). Для 1-го типа на рис. 6 заполнение пространства между цепочками узлов 1-го спутника происходит от восходящей цепочки до нисходящей, а для 2-го на рис. 7 – от нисходящей до восходящей.
Сначала рассмотрим 1-й тип модели, представленный на рис. 6.
Из (15), (16) и (17) на рис. 4:
(52)
$\begin{gathered} {{{\mathbf{R}}}_{0}} = \left( {1200e;0} \right),\,\,\,\,{{{\mathbf{R}}}_{1}} = \left( { - 79e;1} \right), \\ ~{{{\mathbf{R}}}_{2}} = \left( {15e;15} \right). \\ \end{gathered} $Из (13), (14), (20), (22), k = t = 1, ϕ = 43°, V = 1:
(53)
${\mathbf{\rho }}\left( {1,~1,~\phi ,~1} \right) = {\mathbf{\rho }}\left( \phi \right) = \left( {x\left( \phi \right);y\left( \phi \right)} \right),$(54)
$\begin{gathered} x\left( \phi \right) = {T \mathord{\left/ {\vphantom {T 2}} \right. \kern-0em} 2} - {L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0em} 2} - T{{\sin }^{{ - 1}}}{{({{{\text{tg}}\phi } \mathord{\left/ {\vphantom {{{\text{tg}}\phi } {{\text{tg}}i}}} \right. \kern-0em} {{\text{tg}}i}})} \mathord{\left/ {\vphantom {{({{{\text{tg}}\phi } \mathord{\left/ {\vphantom {{{\text{tg}}\phi } {{\text{tg}}i}}} \right. \kern-0em} {{\text{tg}}i}})} {\pi }}} \right. \kern-0em} {\pi }} + \\ + \,\,L{{\sin }^{{ - 1}}}{{({{\sin \phi } \mathord{\left/ {\vphantom {{\sin \phi } {\sin i}}} \right. \kern-0em} {\sin i}})} \mathord{\left/ {\vphantom {{({{\sin \phi } \mathord{\left/ {\vphantom {{\sin \phi } {\sin i}}} \right. \kern-0em} {\sin i}})} {\pi }}} \right. \kern-0em} {\pi }}, \\ \end{gathered} $(55)
$y\left( \phi \right) = 0.5 - {{\sin }^{{ - 1}}}{{({{\sin \phi } \mathord{\left/ {\vphantom {{\sin \phi } {\sin i}}} \right. \kern-0em} {\sin i}})} \mathord{\left/ {\vphantom {{({{\sin \phi } \mathord{\left/ {\vphantom {{\sin \phi } {\sin i}}} \right. \kern-0em} {\sin i}})} {\pi }}} \right. \kern-0em} {\pi }}{\text{.}}$Из (29), (30):
(56)
$\begin{gathered} {\mathbf{\gamma }} = {\mathbf{\rho }}\left( \phi \right),\,\,\,\,{{{\mathbf{\beta }}}_{{1,0}}} = \left( {{{x}_{{1,0}}};{{y}_{{1,0}}}} \right) = \\ = {\mathbf{\rho }}\left( \phi \right) = \left( {625.95e;0.26} \right). \\ \end{gathered} $Из (31):
(57)
$\begin{gathered} {{{\mathbf{\beta }}}_{{2,0}}} = {{{\mathbf{\beta }}}_{{1,0}}} + Q~{{{\mathbf{R}}}_{1}} = \left( { - 6.05e;~8.26} \right), \\ {\text{где}}\,\,Q = E\left( {\left| {{{{{x}_{{1,0}}}} \mathord{\left/ {\vphantom {{{{x}_{{1,0}}}} {{{X}_{1}}}}} \right. \kern-0em} {{{X}_{1}}}}} \right|} \right) + 1 = 8. \\ \end{gathered} $Цепочки узлов 2-го $ - $ K-го спутников фиксируются одинаковыми векторами
(58)
$\begin{gathered} {\mathbf{d}} = \left( {{\Delta }x;~{\Delta }y} \right) = {{\left( {~{{{\mathbf{\beta }}}_{{2,0}}} + m~{{{\mathbf{R}}}_{1}}} \right)} \mathord{\left/ {\vphantom {{\left( {~{{{\mathbf{\beta }}}_{{2,0}}} + m~{{{\mathbf{R}}}_{1}}} \right)} K}} \right. \kern-0em} K}, \\ K - {\text{число спутников}},~\,\,m - {\text{любое число}}. \\ \end{gathered} $Подставляя в (24) координаты ${\mathbf{d}}$, определяемые из (52)–(57), получаем сдвиги по долготе узла орбиты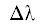 и по фазе ${\Delta \tau }$ для эквидистантой системы спутников:
и по фазе ${\Delta \tau }$ для эквидистантой системы спутников:
(59)
$\begin{gathered} {\Delta \lambda } = 2{\pi }~{\text{mod}}{{\left( {1;0.5 - {{{\sin }}^{{ - 1}}}{{({{{\text{tg}}\phi } \mathord{\left/ {\vphantom {{{\text{tg}}\phi } {{\text{tg}}i}}} \right. \kern-0em} {{\text{tg}}i}})} \mathord{\left/ {\vphantom {{({{{\text{tg}}\phi } \mathord{\left/ {\vphantom {{{\text{tg}}\phi } {{\text{tg}}i}}} \right. \kern-0em} {{\text{tg}}i}})} {\pi }}} \right. \kern-0em} {\pi }}} \right)} \mathord{\left/ {\vphantom {{\left( {1;0.5 - {{{\sin }}^{{ - 1}}}{{({{{\text{tg}}\phi } \mathord{\left/ {\vphantom {{{\text{tg}}\phi } {{\text{tg}}i}}} \right. \kern-0em} {{\text{tg}}i}})} \mathord{\left/ {\vphantom {{({{{\text{tg}}\phi } \mathord{\left/ {\vphantom {{{\text{tg}}\phi } {{\text{tg}}i}}} \right. \kern-0em} {{\text{tg}}i}})} {\pi }}} \right. \kern-0em} {\pi }}} \right)} K}} \right. \kern-0em} K} = \\ = {{1.0773~{\pi }} \mathord{\left/ {\vphantom {{1.0773~{\pi }} K}} \right. \kern-0em} K} = {{193.914^\circ } \mathord{\left/ {\vphantom {{193.914^\circ } K}} \right. \kern-0em} K}, \\ {\Delta \tau } = 2{\pi \;mod}\left( {1; - y\left( \phi \right) + Q + m} \right) = q, \\ ~q--{\text{любое число от }}0{\text{ до }}2{\pi }, \\ {\text{\;}}0^\circ \leqslant {\Delta \tau }^\circ \leqslant 360^\circ . \\ \end{gathered} $На основе (59) сдвиги по долготе ${\Delta \lambda }$ равны 38.78° для K = 5 и 32.32° для K = 6, а для выбора сдвигов по фазе ${\Delta \tau }$ нужно построить и исследовать графики для $F\left( {2h} \right)$.
Далее рассмотрим 2-й тип эквидистантой модели. Он изображен на рис. 7.
Соотношения (52), (54), (55) сохраняются, а в (53) происходит смена знака:
Вследствие этого, выражения (56) и (57) претерпевают следующие перемены:
(60)
$\begin{gathered} {\mathbf{\gamma }} = - {\mathbf{\rho }}\left( \phi \right) + {{{\mathbf{R}}}_{1}},\,\,\,{{{\mathbf{\beta }}}_{{1,0}}} = \left( {{{x}_{{1,0}}};{{y}_{{1,0}}}} \right) = \\ = - {\mathbf{\rho }}\left( \phi \right) + {{{\mathbf{R}}}_{1}} + {{{\mathbf{R}}}_{0}} = \left( {495.05e;0.74} \right). \\ \end{gathered} $(61)
$\begin{gathered} {{{\mathbf{\beta }}}_{{2,0}}} = {{{\mathbf{\beta }}}_{{1,0}}} + Q~{{{\mathbf{R}}}_{1}} = \left( { - 57.95e;~7.74} \right), \\ {\text{где}}\,\,Q = E\left( {\left| {{{{{x}_{{1,0}}}} \mathord{\left/ {\vphantom {{{{x}_{{1,0}}}} {{{X}_{1}}}}} \right. \kern-0em} {{{X}_{1}}}}} \right|} \right) + 1 = 7. \\ \end{gathered} $Формула (58) для вектора ${\mathbf{d}}$ сохраняется. По-дставляя в (24) его координаты, определяемые из (52)–(55), (58), (60), (61), находим искомые сдвиги ${\Delta \lambda }$ и ${\Delta \tau }$:
(62)
$\begin{gathered} {\Delta \lambda } = 2{\pi }~{\text{mod}}{{\left( {1;0.5 + {{{\sin }}^{{ - 1}}}{{({{{\text{tg}}\phi } \mathord{\left/ {\vphantom {{{\text{tg}}\phi } {{\text{tg}}i}}} \right. \kern-0em} {{\text{tg}}i}})} \mathord{\left/ {\vphantom {{({{{\text{tg}}\phi } \mathord{\left/ {\vphantom {{{\text{tg}}\phi } {{\text{tg}}i}}} \right. \kern-0em} {{\text{tg}}i}})} {\pi }}} \right. \kern-0em} {\pi }}} \right)} \mathord{\left/ {\vphantom {{\left( {1;0.5 + {{{\sin }}^{{ - 1}}}{{({{{\text{tg}}\phi } \mathord{\left/ {\vphantom {{{\text{tg}}\phi } {{\text{tg}}i}}} \right. \kern-0em} {{\text{tg}}i}})} \mathord{\left/ {\vphantom {{({{{\text{tg}}\phi } \mathord{\left/ {\vphantom {{{\text{tg}}\phi } {{\text{tg}}i}}} \right. \kern-0em} {{\text{tg}}i}})} {\pi }}} \right. \kern-0em} {\pi }}} \right)} K}} \right. \kern-0em} K} = \\ = {{0.9227~{\pi }} \mathord{\left/ {\vphantom {{0.9227~{\pi }} K}} \right. \kern-0em} K} = {{166.086^\circ } \mathord{\left/ {\vphantom {{166.086^\circ } K}} \right. \kern-0em} K}, \\ {\Delta \tau } = 2{\pi \;mod}\left( {1;y\left( \phi \right) + 1 + Q + m} \right) = q, \\ ~q - {\text{любое число от }}0{\text{ до}}\,\,{\text{2}}\pi {\text{,}} \\ 0^\circ \leqslant {\Delta \tau }^\circ \leqslant 360^\circ . \\ \end{gathered} $Как и следовало ожидать, сумма долготных сдвигов, вычисляемых из (59) для 1-го и (62) для 2-го типа эквидистантных спутниковых структур, равна ${{2{\pi }} \mathord{\left/ {\vphantom {{2{\pi }} K}} \right. \kern-0em} K}$.
Из (62) для 2-го типа долготный сдвиг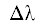 равен 33.22° при K = 5 и 27.68° при K = 6. Выбор ${\Delta \tau }$, как и для 1-го типа, должен быть основан на графиках критерия $F\left( {2h} \right)$.
равен 33.22° при K = 5 и 27.68° при K = 6. Выбор ${\Delta \tau }$, как и для 1-го типа, должен быть основан на графиках критерия $F\left( {2h} \right)$.
Применяя компьютерную программу, находим перерывы обзора и их частоты для систем из 5 и 6 спутников ООЛП при всех ${\Delta \tau }$ от $0^\circ $ до 360°. Пояс широт [43°, 70°], шаг по широте ${\Delta }\phi ^\circ $ = 0.1°. Вычисляем $F\left( {2h} \right)$ из (44), а также выделяем ${{T}_{{{\text{max}}}}}$. Строим графики на рис. 8. По ним видно, что по критерию $F\left( {2h} \right)$ 1-й тип моделей лучше 2-го. Приводим для 1-го типа наименьшие значения $F\left( {2h} \right)$ и соответствующие сдвиги фаз ${\Delta \tau }^\circ $:
Рис. 8.
Графики критериев эффективности для системы ООЛП в зависимости от сдвига фаз $\Delta \tau ^\circ $. Значения ${{T}_{{{\text{max}}}}}$ даны в витках орбиты.
7.29% при сдвиге фаз 264° для системы из 5 спутников,
1.33% при сдвиге фаз 291° для системы из 6 спутников.
Итак, для обнаружения очагов лесных пожаров с минимальной частотой ошибок 1.33% рекомендуется эквидистантная система 1-го типа из 6 спутников с широкозахватными ИК-радиометрами на борту, имеющая следующие сдвиги:
32.32° – по долготе узлов орбит, 291° – по фазе спутников внутри орбит.
На рис. 8 есть также график ${{T}_{{{\text{max}}}}}$ для 1-го типа систем из 6 спутников. График скачкообразный, а абсциссы его минимумов не дают лучших значений $F\left( {2h} \right)$.
Частоты ${{T}_{{{\text{max}}}}}$ малы, что следует и из табл. 2. Там даны относительные частоты диапазонов перерывов для систем со следующими сдвигами фаз: 291°, что приводит к минимуму $F\left( {3h} \right)$; 228°, что немного правее минимума для ${{T}_{{{\text{max}}}}}$. В 1-м случае имеются большие перерывы вплоть до 2.3 витка, но их частоты ничтожны и даже сумма частот перерывов более 1.3 витка меньше 1.2%. Во 2-м случае наибольший перерыв гораздо меньше и лежит в диапазоне 1.4–1.5 витка с общей частотой 1.1%; однако сумма частот перерывов более 1.3 витка подскакивает до 34.5%. Поэтому главный критерий $F\left( {2h} \right)$ достигает минимума не во 2-м, а в 1-м варианте при сдвиге фаз 291°.
Таблица 2.
Относительные частоты диапазонов перерывов, %, для системы 1-го типа из 6 спутников с ИК-радиометрами для обнаружения очагов лесных пожаров, $\Delta \tau ^\circ $ сдвиг фаз, град
| $\Delta \tau ^\circ $ | Диапазоны перерывов обзора, витки орбиты | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0–0.1 | 0.1–0.2 | 0.2–0.3 | 0.3–0.4 | 0.4–0.5 | 0.5–0.6 | 0.6–0.7 | 0.7–0.8 | 0.8–0.9 | 0.9–1.0 | |
| 291° | 3.88 | 20.72 | 0.60 | – | – | – | – | 0.38 | 2.84 | 26.89 |
| 228° | 6.69 | – | 0.29 | 27.44 | 1.36 | 1.14 | 1.07 | – | – | 24.91 |
| $\Delta \tau ^\circ $ | Диапазоны перерывов обзора, витки орбиты | |||||||||
| 1.0–1.1 | 1.1–1.2 | 1.2–1.3 | 1.3–1.4 | 1.4–1.5 | 1.5–1.6 | 1.6–1.7 | 1.7–1.8 | 1.8–1.9 | 1.9–2.0 | |
| 291° | 4.53 | 35.01 | 3.98 | 0.03 | – | – | – | – | – | 0.16 |
| 228° | – | – | 2.60 | 33.40 | 1.10 | – | – | – | – | – |
| $\Delta \tau ^\circ $ | Диапазоны перерывов обзора, витки орбиты | |||||||||
| 2.0–2.1 | 2.1–2.2 | 2.2–2.3 | 2.3–2.4 | 2.4–2.5 | 2.5–2.6 | 2.6–2.7 | 2.7–2.8 | 2.8–2.9 | 2.9–3.0 | |
| 291° | – | 0.76 | 0.22 | – | – | – | – | – | – | – |
| 228° | – | – | – | – | – | – | – | – | – | – |
Подтверждается вывод о нецелесообразности ${{T}_{{{\text{max}}}}}$ для оценки качества обзора.
ВЕКТОРНАЯ МОДЕЛЬ ДЛЯ НЕПРЕРЫВНОГО M-КРАТНОГО ОБЗОРА
Идея отображения спутниковой структуры в виде векторной модели обзора Земли хорошо работает, как показано в [8, 9], также и для непрерывного глобального и зонального наблюдения с любой кратностью M = 1, 2, 3, ….
Реализация идеи путем изображения на плоскости в координатах “долгота – время” “спутниковых узлов” и “следов” сохраняется для непрерывного обзора с некоторыми изменениями. Основное вызвано тем, что спутники непрерывного обзора имеют круговые “зоны видимости” на Земле. Поэтому “след”, отображающий во времени пересечение широты, приобретает вид сложной выпуклой фигуры [8].
Вместо 1-го свойства модели периодического обзора, обеспечившего расчет всех перерывов обзора и их частот, на модели непрерывного наблюдения действует удобный принцип достижения M-кратного покрытия заданной зоны Земли: для любой широты не должно быть участков, попадающих менее, чем в M следов. Развивая этот принцип, в [8] выведена теорема, сводящая анализ сплошности M-кратного покрытия к простой проверке вхождения в зоны видимости M или более спутников конечного числа точек пересечения границ этих зон. Реализуя теорему, создана компьютерная программа расчета и выбора спутниковых структур по критерию минимума радиуса спутниковой зоны видимости. Программа применима для широкого класса “систем с линейной структурой” [8, 9]. В него, как подклассы, входят все известные типы структур непрерывного обзора: “дельта-системы” Дж. Уолкера [10], “кинематически правильные системы” (КПС) с 1-й и 2-й группой симметрии (соответственно КПС-1 и КПС-2) Г.В. Можаева [11–13], “полярные” и “околополярные” системы [14–17], а также новый класс “компактных систем” [8, 9].
В [8, 9] при разных кратностях обзора, числах спутников и поясах широт лучшими были представители от всех классов, кроме околополярных систем. Дельта-системы и эквивалентные им КПС-1, стали лучшими для глобального обзора с четной кратностью и заняли растущие места среди лучших систем при увеличении нечетной кратности [9]. Для однократного глобального обзора, согласно [8], до 19 спутников лидировали дельта-системы (КПС-1), затем до 38 спутников выигрывали КПС-2, далее попеременно были лучшими полярные и компактные структуры. Для однократного обзора пояса широт $ \pm $65° при числе спутников до 200 чаще побеждали компактные системы [8].
ЗАКЛЮЧЕНИЕ
Для полноценного анализа эффективности космических систем наблюдения Земли нужен алгоритм расчета всех перерывов обзора и частот их возникновения на заданной области земного шара. Для его разработки в [2–4] предложена “векторная модель обзора Земли”. В данной статье модель уточнена и конкретизирована для систем спутников на “изомаршрутных” орбитах, трассы которых повторяются через целое число суток и целое число витков. Получен алгоритм и компьютерная программа, обладающая высоким быстродействием. Например, расчет перерывов обзора и их частот на поясе широт [0°, 80°] с шагом 1° для системы из 4-х спутников длится несколько сотых долей секунды, а для 100 спутников – около секунды.
Потенциал векторной модели и программы на ее базе продемонстрирован на двух примерах. В них произведен выбор спутниковой структуры для двух возможных и актуальных систем. Первая состоит из спутников типа МЕТЕОР-М и предназначена для глобального метеорологического мониторинга. Спутники второй системы должны быть снабжены широкозахватными инфракрасными радиометрами для обнаружения очагов лесных пожаров. Подобный прибор испытан на спутнике КАНОПУС-В-ИК.
Опираясь на свойства модели, показано, что в обоих примерах лучшая структура – “эквидистантная”. Она обеспечивает равномерную минимизацию перерывов обзора.
Выведены формулы для расчета долгот узлов орбит эквидистантных систем.
Используя расчеты по компьютерной программе, выбраны фазы спутников, минимизирующие “частоту ошибок” на заданных “рабочих интервалах” времени.
Попутно установлено, что во всех рассмотренных вариантах спутниковых структур максимальные перерывы обзора, широко используемые для оценки работы систем мониторинга Земли, возникали с пренебрежимо малой частотой, не достигающей 0.01. Учитывая это, не рекомендуется использование максимальных перерывов обзора в роли критериев при выборе структуры систем наблюдения Земли.
Принципы построения векторной модели обзора Земли, сформулированные для периодического наблюдения, сохраняются и для систем непрерывного обзора Земли с различной кратностью и могут эффективно применяться для выбора их структуры.
Список литературы
Саульский В.К. Векторный метод синтеза орбит и структуры систем спутников для периодического обзора Земли // Космич. исслед. 2016. Т. 54. № 4. С. 334–346. (Cosmic Research. P. 313–324).
Саульский В.К. Анализ систем спутников для периодического обзора Земли // Космич. исслед. 2017. Т. 55. № 4. С. 290–304. (Cosmic Research. P. 275 – 289).
Saulskiy V.K. Vector Model of Multi-Satellite Earth Survey and Its Use Directions // Advances in the Astronautical Sciences. 2017. V. 161. P. 1111–1127.
Горбунов А.В., Саульский В.К. Векторная модель обзора Земли и направления ее использования // Вопросы электромеханики. Труды ВНИИЭМ. 2017. Т. 156. № 1. С. 21–32.
Саульский В.К. Использование “следограмм” для расчета периодического землеобзора // Исслед. Земли из космоса. 1994. № 2. С. 65–74.
Акимов Н.П., Бадаев К.В., Гектин Ю.М. и др. Многозональное сканирующее устройство малого разрешения МСУ-МР для космического информационного комплекса “Метеор-М”. Принцип работы, эволюция, перспективы // Ракетно-космическое приборостроение и информационные системы. 2015. Т. 2. Вып. 4. С. 30–39.
Акимов Н.П., Бадаев К.В., Гектин Ю.М. и др. Первые результаты работы ИК-радиометра МСУ-ИК-СРМ в составе КА “Канопус-В-ИК” // Ракетно-космическое приборостроение и информационные системы. 2018. Т. 5. Вып. 4. С. 34–45.
Саульский В.К. Многоспутниковые системы с линейной структурой и их применение для непрерывного обзора Земли // Космич. исслед. 2005. Т. 43. № 1. С. 36–63 (Cosmic Research. P. 34–51).
Саульский В.К. Многократный непрерывный обзор Земли на основе многоспутниковых систем с линейной структурой // Космич. исслед. 2009. Т. 47. № 2. С. 64–175 (Cosmic Research. P. 144–155).
Walker J.G. Circular Orbit Patterns Providing Continuous Whole Earth Coverage. Royal Aircraft Establishment. Technical Report. November 1970. № 70211.
Можаев Г.В. К проблеме оптимизации орбит спутниковых систем, предназначенных для непрерывного обзора Земли // Третий Всесоюзный съезд по теоретической и прикладной механике. Москва, 25 января–1февраля 1968 г. М.: Наука, 1968. С. 215.
Можаев Г.В. Задача о непрерывном обзоре Земли и кинематически правильные спутниковые системы // Космич. исслед. 1972. Т. 10. № 6. С. 833–840. 1973. Т. 11. № 1. С. 59–69.
Можаев Г.В. Возможности кинематически правильных систем с группами симметрии второго типа в задаче непрерывного однократного обзора Земли // Космич. исслед. 2005. Т. 43. № 3. С. 215–223.
Luders R.D. Satellite Networks for Continuous Zonal Coverage // American Rocket Society. 1961. V. 31. P. 179–184.
Rider L. Optimized Polar Orbit Constellation for Redundant Earth Coverage // Astronautical Sci. 1985. V. 33. № 2. P. 147–161.
Adams W.S., Rider L. Circular Polar Constellations Providing Continuous Single or Multiple Coverage Above a Specified Latitude // Astronautical Sci. 1987. V. 35. № 2. P. 155–192.
Ulybyshev Y. Near-Polar Satellite Constellations for Continuous Global Coverage // Spacecraft and Rockets. 1999. V. 36. № 1. P. 92–99.
Дополнительные материалы отсутствуют.
Инструменты
Космические исследования